Transfer Learning for Class Imbalance Problems with Inadequate Data

Abstract

A fundamental problem in data mining is to effectively build robust classifiers in the presence of skewed data distributions. Class imbalance classifiers are trained specifically for skewed distribution datasets. Existing methods assume an ample supply of training examples as a fundamental prerequisite for constructing an effective classifier. However, when sufficient data is not readily available, the development of a representative classification algorithm becomes even more difficult due to the unequal distribution between classes. We provide a unified framework that will potentially take advantage of auxiliary data using a transfer learning mechanism and simultaneously build a robust classifier to tackle this imbalance issue in the presence of few training samples in a particular target domain of interest. Transfer learning methods use auxiliary data to augment learning when training examples are not sufficient and in this paper we will develop a method that is optimized to simultaneously augment the training data and induce balance into skewed datasets. We propose a novel boosting based instance-transfer classifier with a label-dependent update mechanism that simultaneously compensates for class imbalance and incorporates samples from an auxiliary domain to improve classification. We provide theoretical and empirical validation of our method and apply to healthcare and text classification applications.

1. Introduction

One of the fundamental problems in machine learning is to effectively build robust classifiers in the presence of class imbalance. Imbalanced learning is a well-studied problem and many sampling techniques, cost-sensitive algorithms, kernel-based techniques, and active learning methods have been proposed in the literature [1]. Though there have been several attempts to solve this problem, most of the existing methods always assume an ample supply of training examples as a fundamental prerequisite for constructing an effective classifier tackling class imbalance problems. In other words, the existing imbalanced learning algorithms only address the problem of “Relative Imbalance” where the number of samples in one class is significantly higher compared to the other class and there is an abundant supply of training instances. However, when sufficient data for model training is not readily available, the development of a representative hypothesis becomes more difficult due to an unequal distribution between its classes.

Many datasets related to medical diagnoses, natural phenomena, or demographics are naturally imbalanced datasets and will typically have an inadequate supply of training instances. For example, datasets for cancer diagnosis in minority populations (benign or malignant), or seismic wave classification datasets (earthquake or nuclear detonation) are small and imbalanced. “Absolute Rarity” refers to a dataset where the imbalance problem is compounded by a supply of training instances that is not adequate for generalization. Many of such practical datasets have high dimensionality, small sample size and class imbalance. The minority class within a small and imbalanced dataset is considered to be a “Rare Class”. Classification with “Absolute Rarity” is not a well-studied problem because the lack of representative data, especially within the minority class, impedes learning.

To address this challenge, we develop an algorithm to simultaneously rectify for the skew within the label space and compensate for the overall lack of instances in the training set by borrowing from an auxiliary domain. We provide a unified framework that can potentially take advantage of the auxiliary data using a “knowledge transfer” mechanism and build a robust classifier to tackle this imbalance issue in the presence of fewer training samples in the target domain. Transfer learning algorithms [2, 3] use auxiliary data to augment learning when training examples are not sufficient. In the presence of inadequate number of samples, the transfer learning algorithms will improve learning on a small dataset (referred to as target set) by including a similar and possibly larger auxiliary dataset (referred to as the source set). In this work, we will develop one such method optimized to simultaneously augment the training data and induce balance into the skewed datasets.

This paper presents the first method for rare dataset classification within a transfer learning paradigm. In this work, we propose a classification algorithm to address the problem of “Absolute Rarity” with an instance-transfer method that incorporates the best-fit set of auxiliary samples that improve balanced error minimization. Our transfer learning framework induces balanced error optimization by simultaneously compensating for the class imbalance and the lack of training examples in “Absolute Rarity”. To achieve this goal, we utilize ensemble-learning techniques that iteratively construct a classifier that is trained with the weighted source and target samples that best improve balanced classification. Our transfer learning algorithm will include label information while performing knowledge transfer.

This paper effectively combines two important machine learning concepts: the concept of compensating for the skew within the label space (which belongs to the domain of “Imbalanced Learning”) and the concept of extracting knowledge from an auxiliary dataset to compensate for the overall lack of samples (which belongs to a family of methods known as “instance-based transfer learning”). We aim to construct a hypothesis and uncover the separating hyperplane with only a handful of training examples with data that is complex in both the feature and label spaces. The complexity of the data skewness and the rarity of training examples prohibit hypothesis construction by human experts or standard algorithms and thus we present a solution that can be applied when nothing else suffices. The main contributions of this paper are as follows:

1. Present a complete categorization of several recent works and highlight the need for a new type of specialized algorithms to solve a niche but important problem that is not addressed in the current literature.

2. Propose a novel transfer learning algorithm, Rare-Transfer, optimized for transfer within the label space to effectively handle rare class problems.

3. Provide theoretical and empirical analysis of the proposed Rare-Transfer algorithm.

4. Demonstrate the superior performance of the proposed algorithm compared to several existing methods in the literature using various real-world examples.

The rest of the paper is organized as follows: In Section 2, we describe the different types of datasets and briefly discuss the related methods suitable for each type. Section 3 presents the motivation for a unified balanced optimization framework. Section 4 describes our algorithm, “Rare-Transfer”, which addresses the “Absolute Rarity” problem. Section 5 presents the theoretical analysis of the proposed algorithm. For further validation, Section 6 presents empirical analysis of our framework and is followed by experimental results on real-world data in Section 7. Finally, we discuss possible extensions and conclude our work.

2. Characterization of Existing Machine Learning Domains

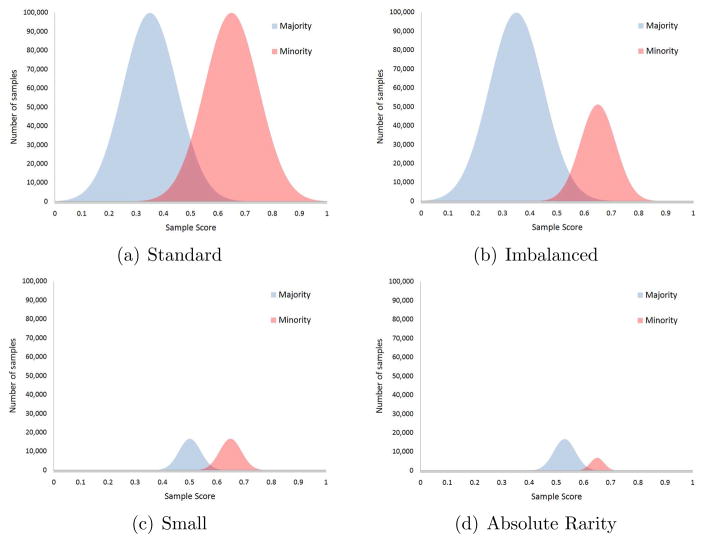
To describe datasets in terms of both size and imbalance, we use the “Label-Dependent” view in Figure 1. The sub-figures present a binary classification problem with normally distributed samples within each class¹ (thus we describe it as label-dependent since the distributions are normal within each label). Figure 1 illustrates the different datasets with an overview of the related machine learning fields² that can improve learning.

Figure 1.

Label-Dependent view of different type of datasets.

1. Standard dataset: Figure 1(a) depicts a standard dataset with a relatively equal number of samples within each class (balanced class distribution) and an adequate number of samples for generalization. To learn from balanced datasets, equal importance is assigned to all classes and thus maximizing the overall arithmetic accuracy is the chosen optimization objective. A variety of standard machine learning and data mining approaches can be applied for standard datasets as such methods serve as the foundation for the algorithms that are modified for any peculiar feature set or distribution.

2. Imbalanced dataset: The dataset in Figure 1(b) is a relatively-imbalanced dataset. It is relatively-imbalanced because there is a between-class imbalance where one class encompass the majority of the training set. The balance is relative since both minority and majority training subsets contain adequate training samples. For example, email spam classification is a relatively imbalanced problem since 97% (majority) of emails sent over the net are considered unwanted emails [4] and with around 200 billion messages of spam sent per day [5], the number of non-spam emails (minority) is also a large dataset. A dataset where the number samples belonging to different classes is highly disproportionate is considered to be an “imbalanced dataset” with the postulation that the imbalance is relative [1]. Because the majority class overwhelms the minority class, imbalanced learning models are biased to improve learning on the minority class (without any consideration to the availability of training examples).

3. Small dataset: The dataset in Figure 1(c) is a balanced dataset with a training sample size that is inadequate for generalization. One method to determine the number of samples required for training is to rely on the “Probably Approximately Correct (PAC)” learning theory [6]. PAC is applied to determine if the ratio of the dimensions of the data to the number of training samples is too high where the hypothesis space would thus be exceedingly large. If that ratio is too high, learning becomes difficult and prone to model over-fitting. PAC gives a theoretic relationship between the number of samples needed in terms of the size of hypothesis space and the number of dimensions. The simplest example is a binary dataset with binary classes and d dimensions with hypothesis space of size 2^2d, requiring O (2ⁿ) samples [7].

4. Rare Dataset (Dataset with “Absolute Rarity”): The dataset in Figure 1(d) is imbalanced as well as small and thus its imbalance is termed as “Absolute Rarity”. Weiss [8] presents a good overview of the problems encountered when analyzing and evaluating such datasets. Different solutions are outlined for handling “Absolute Rarity” with a discussion of solutions for segmentation, bias and noise associated with these datasets. In [9], an end-to-end investigation of rare categories in imbalanced datasets in both the supervised and unsupervised settings is presented.

3. Learning with “Absolute Rarity”

A “Rare Dataset”³ is a label-skewed and small dataset and presents a set of challenges that are not studied in existing literature. This section examines the parameters that are relevant for the study of “Rare Datasets”.

3.1. Effect of Data Size on Learning

3.1.1. In a Balanced Dataset

The first impediment to learning with “Absolute Rarity” is the fact that the small size of the training set, regardless of imbalance, impedes learning. When the number of training examples is not adequate to generalize to instances not present in the training data, it is not theoretically possible to use a learning model as the model will only overfit the training set. The term “adequate” is a broad term as many factors including data complexity, number of dimensions, data duplication, and overlap complexity have to be considered [1]. Computational learning theory [7] provide a general outline to estimate the difficulty of learning a model, the required number of training examples, the expected learning and generalization error and the risk of failing to learn or generalize.

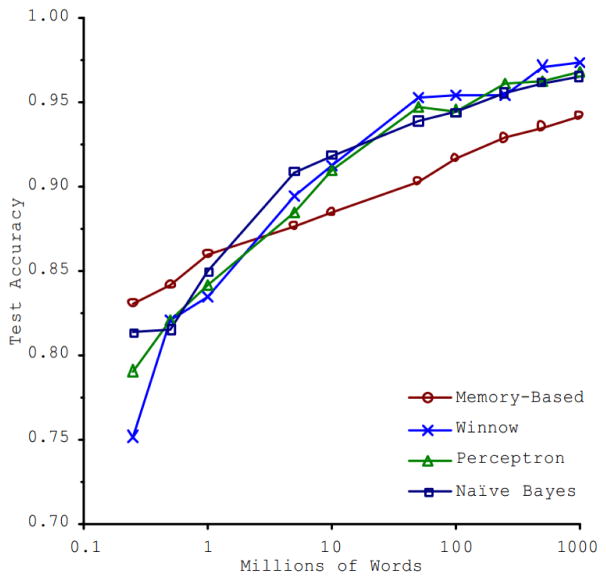
A study in [10] found that the size of training set is the factor with the most significant impact on classification performance. Figure 2 depicts 4 different algorithms that are trained at different training set sizes and demonstrates that increasing the training sets’ size improves the classification performance of all the algorithms. To assert that increasing the number of training examples, combined with an error minimizing classifier, yields results where the training and the generalization errors are similar is an intuitive and crucial finding as it demonstrates that the choice of a classification model is less important than the overall size of the training set.

Figure 2.

Learning Curves for Confusion Set Disambiguation [10].

3.1.2. In an Imbalanced Dataset

The second impediment to learning with “Absolute Rarity” is the between-class imbalance where a majority of samples belong to an overrepresented class and a minority of samples belong to an underrepresented class [1]. The imbalanced classification study in [11] found that the most significant effect on a classifier’s performance in an imbalanced classification problem is not the ratio of imbalance but it is the number of samples in the training set. This is an important finding as it demonstrates that the lack of data in “Absolute Rarity” intensifies the label imbalance problem. As the number of the training examples increased, the error rate caused by imbalance decreased [12] and thus increasing the number of training samples makes the classifiers less sensitive to the between-class imbalance [11].

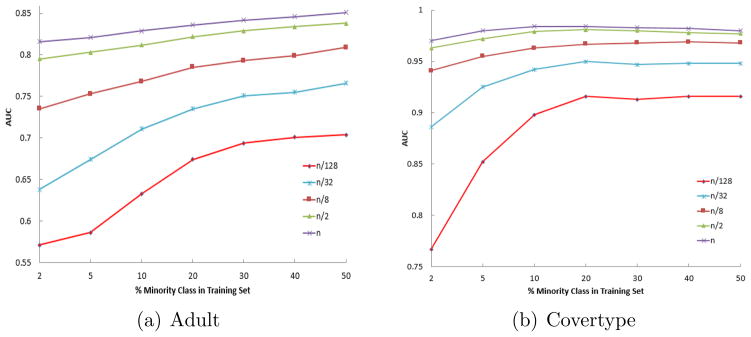
Figure 3 demonstrates how the lack of training examples degrades learning in an imbalanced dataset [11]. The ROC curve illustrates the performance of a binary classifier where the x-axis represents the False Positive Rate (1-Specificity) and the y-axis represents the True Positive Rate and is an accepted metric in imbalanced learning problems. Figure 3 presents the Area Under the ROC curve (AUC) [13] results in [11] where a classifier was trained for two imbalanced datasets [14] with different subsets of training sets (with a total of n samples). AUC is a simple summary of the ROC performance and can be calculated by using the trapezoidal areas created between ROC points and is thus equivalent to the Wilcoxon-Mann-Whitney statistic [15]. The results demonstrate that increasing the size of the training set directly improves learning for imbalanced datasets.

Figure 3.

AUC for imbalanced datasets at different training sample sizes [11].

4. The Proposed Rare-Transfer Algorithm

4.1. Notations

Consider a domain (D) comprised of instances (X ∈ ℝ^d) with d features. We can specify a mapping function, F, to map the feature space to the label space as “X → Y” where Y ∈ {−1, 1}. If no source or target instances are defined, then n will simply refer to the number of instances in a dataset; otherwise, we will denote the domain with n auxiliary instances as the source domain (D_src) and define (D_tar) as the target domain with m ≪ n instances. Instances that belong to the majority class will be defined as X_majority and those that belong to the minority class will be defined as X_minority. n^l is the number of source samples that belong to label l while ε^l is the error rate for label l and denotes the misclassification rate for samples with true label l. N defines the total number of boosting iterations, w is a weight vector. A weak classifier at a given boosting iteration (t) will be defined as f̈^t and its classification error is denoted by ε^t. 1I is an indicator function and is defined as:

$$1\mathrm{I}\left[y\ne \ddot{f}\right]=\{\begin{array}{cc}1& y\ne \ddot{f}\\ 0& y=\ddot{f}\end{array}$$ (1)

4.2. Boosting-based Transfer Learning

Boosting-based transfer learning algorithms apply ensemble methods to both source and target instances with an update mechanism that incorporates only the source instances that are useful for target instance classification. These methods perform this form of mapping by giving more weight to source instances that improve target training and decreasing the weights for instances that induce negative transfer.

TrAdaBoost [16] is the first and most popular transfer learning method that uses boosting as a best-fit inductive transfer learner. TrAdaBoost trains a base classifier on the weighted source and target set in an iterative manner. After every boosting iteration, the weights of misclassified target instances are increased and the weights of correctly classified target instances are decreased. This target update mechanism is based solely on the training error calculated on the normalized weights of the target set and uses a strategy adapted from the classical AdaBoost [17] algorithm. The Weighted Majority Algorithm (WMA) [18] is used to adjust the weights of the source set by iteratively decreasing the weight of misclassified source instances by a constant factor and preserving the current weights of correctly classified source instances. The basic idea is that the weight of source instances that are not correctly classified on a consistent basis would converge and would not be used in the final classifier’s output since that classifier only uses boosting iterations $\frac{N}{2}\to N$ for convergence [16].

TrAdaBoost has been extended to many transfer learning problems. A multi-source learning [19] approach was proposed to import knowledge from many sources. Having multiple sources increases the probability of integrating source instances that are better fit to improve target learning and thus this method can reduce negative transfer. A model-based transfer in “TaskTrAd-aBoost” [20] extends this algorithm to transferring knowledge from multiple source tasks to learn a specific target task. Since closely related tasks share some common parameters, suitable parameters that induce positive transfer are integrated from multiple source tasks. Some of the prominent applications of TrAdaBoost include multi-view surveillance [20], imbalanced classification [21], head-pose estimation [22], visual tracking [23], text classification [16] and several other problems [2].

TransferBoost [24] is an AdaBoost based method for boosting when multiple source tasks are available. It boosts all source weights for instances that belong to tasks exhibiting positive transferability to the target task. TransferBoost calculates an aggregate transfer term for every source task as the difference in error between the target only task and the target plus each additional source task. AdaBoost was extended in [25] for concept drift as a fixed cost is pre-calculated using Euclidean distance (as one of two options) as a measure of relevance between source and target distributions. This relevance ratio thus gives more weights to data that is near in the feature space and share a similar label. This ratio is finally incorporated to the update mechanism via AdaCost [26].

Many problems have been noted when using TrAdaBooost. The authors in [27] reported that there was a weight mismatch when the size of source instances is much larger than that of target instances. This required many iterations for the total weight of the target instances to approach that of the source instances. In [28], it was noted that TrAdaBoost yielded a final classifier that always predicted one label for all instances as it substantially unbalanced the weights between the different classes. Even the original implementation of TrAdaBoost in [16] re-sampled the data at each step to balance the classes. Finally, various researchers observed that beneficial source instances that are representative of the target concept tend to have a quick and stochastic weight convergence. This quick convergence was examined by Eaton and desJardins [24] as they observed that in TrAdaBoost’s reweighing scheme, the difference between the weights of the source and target instances only increased and that there was no mechanism in place to recover the weight of source instances in later boosting iterations when they become beneficial. TrAdaBoost was improved in [29] where dynamic reweighing separated the two update mechanisms of AdaBoost and WMA for better classification performance.

4.3. The Proposed Rare-Transfer Algorithm

To overcome the limitations in boosting-based transfer learning and simultaneously address imbalance in “Absolute Rarity”, we present the “Rare-Transfer” algorithm (shown in algorithm 1). The algorithm exploits transfer learning concepts to improve classification by incorporating auxiliary knowledge from a source domain to a target domain. Simultaneously, balanced classification is improved as the algorithm allocates higher weights to the subset of auxiliary instances that improve and balance the final classifier. The framework effectively combines the power of two boosting algorithms with AdaBoost [17] updating the target instances’ weights and the Weighted Majority Algorithm (WMA) [18], modified for balanced transfer, updating the source instances’ weights to incorporate auxiliary knowledge and skew for balanced classification via transfer from the source domain.

Algorithm 1.

Rare-Transfer Algorithm

Require:
• Source domain instances Dsrc = {(xsrci, ysrci)}
• Target domain instances Dtar = {(xtari, ytari)}
• Maximum number of iterations : N
• Base learner : f̈
Ensure: Target Classifier Output : {ḟ : X → Y} $$\stackrel{.}{f}=\mathit{sign}\left[{\prod }_{t=\frac{N}{2}}^N\left({{\beta }_{\mathit{tar}}^t}^{-{\ddot{f}}^t}\right)-{\prod }_{t=\frac{N}{2}}^N\left({{\beta }_{\mathit{tar}}^t}^{-\frac{1}{2}}\right)\right]$$
Procedure:
1:	Initialize the weights w for all instances D = {Dsrc ∪ Dtar}, where: wsrc = {wsrc1, …, wsrcn}, wtar = {wtar1, …, wtarm}, w = {wsrc ∪ wtar}
2:	Set ${\beta }_{\mathit{src}}=\frac{1}{1+\sqrt{\frac{2ln(n)}{N}}}$
3:	for t = 1 to N do
4:	Normalize Weights: $w=\frac{w}{{\displaystyle \sum _i^n}{w}_{{\mathit{src}}_i}+{\displaystyle \sum _j^m}{w}_{{\mathit{tar}}_j}}$
5:	Find the candidate weak learner f̈t : X → Y that minimizes error for D weighted according to w
6:	Calculate the error of f̈t on Dsrc: ${\epsilon }_{\mathit{src}}^t={\displaystyle \sum _{j=1}^n}\frac{\left[w_{\mathit{src}}^j\right]·1\mathrm{I}\left[y_{{\mathit{src}}_j}\ne {\ddot{f}}_j^t\right]}{{\displaystyle \sum _{i=1}^n}\left[w_{\mathit{src}}^i\right]}$
7:	Calculate the error of f̈t on Dtar: ${\epsilon }_{\mathit{tar}}^t={\displaystyle \sum _{j=1}^m}\frac{\left[w_{\mathit{tar}}^j\right]·1\mathrm{I}\left[y_{{\mathit{tar}}_j}\ne {\ddot{f}}_j^t\right]}{{\displaystyle \sum _{i=1}^m}\left[w_{\mathit{tar}}^i\right]}$
8:	Set $C^l=\left(1-{\epsilon }_{\mathit{src}}^l\right)$
9:	Set ${\beta }_{\mathit{tar}}=\frac{1-{\epsilon }_{\mathit{tar}}^t}{{\epsilon }_{\mathit{tar}}^t}$
10:	$w_{{\mathit{src}}_i}^{t+1}=C^l{w}_{{\mathit{src}}_i}^t{\beta }_{\mathit{src}}^{1\mathrm{I}\left[y_{{\mathit{src}}_i}\ne {\ddot{f}}_i^t\right]}$where i ∈ Dsrc
11:	$w_{{\mathit{tar}}_j}^{t+1}=w_{{\mathit{tar}}_j}^t{\beta }_{\mathit{tar}}^{1\mathrm{I}\left[y_{{\mathit{tar}}_j}\ne {\ddot{f}}_j^t\right]}$where j ∈ Dtar
12:	end for

The two algorithms operate separately and are only linked in:

1. Line 4 (Normalization): Both algorithms require normalization. The combined normalization causes an anomaly that we will address in subsequent analysis.

2. Line 5: Infusing source with target for training is how transfer learning is induced from the auxiliary dataset.

The target instances are updated in lines 7,9, and 11 as outlined by AdaBoost [17]. The weak learner in line 5 finds the separating hyperplane that forms the classification boundary and is used to calculate the target’s error rate ( ${\epsilon }_{\mathit{tar}}^t<0.5$) in line 7. This error is used in line 9 to calculate (β_tar > 1) which will then be used to update the target weights in line 11 as:

$$w_{{\mathit{tar}}_j}^{t+1}=w_{{\mathit{tar}}_j}^t{\beta }_{\mathit{tar}}^{1\mathrm{I}\left[y_{{\mathit{tar}}_j}\ne {\ddot{f}}_j^t\right]}$$ (2)

Similar to AdaBoost, a misclassified target instance’s weight increases after normalization and would thus gain more influence in the next iteration. Once boosting is completed, (t = N), the weak classifiers (f̈^t) weighted by β_tar are combined to construct a committee capable of non-linear approximation. The source instances are updated in lines 2 and 10 as done by the Weighted Majority Algorithm [18]. The static WMA update rate (β_src < 1) is calculated on line 2 and updates the source weights as:

$$w_{{\mathit{src}}_i}^{t+1}=w_{{\mathit{src}}_i}^t{\beta }_{\mathit{src}}^{1\mathrm{I}\left[y_{{\mathit{src}}_i}\ne {\ddot{f}}_i^t\right]}$$ (3)

Contrary to AdaBoost, WMA decreases the influence of an instance that is misclassified and gives it a lower relative weight in the subsequent iterations. This property is beneficial for transfer learning since the source instance’s contribution to the weak classifiers is dependent on its classification consistency. A consistently misclassified instance’s weight converges⁴ and its influence diminishes in subsequent iterations. In Algorithm 1, the WMA update mechanism in Equation (3) is actually modified in line 10 to incorporate the cost C^l for label-dependent transfer. This dynamic cost is calculated in line 8 and it promotes balanced transfer learning. Starting with equal initial weights and using standard weak classifiers that optimize for accuracy, these classifiers achieve low error rates for the majority and high error rate for the minority as they are overwhelmed with the majority label. The label dependent cost, C^l, controls the rate of convergence of the source instances and hence the weights converge slower⁵ for labels with high initial error rates (minority classes). As minority labels get higher normalized weights with each successive boosting iteration, the weak classifiers would subsequently construct more balanced separating hyperplanes. The $\frac{N}{2}\to N$ weak classifiers are used for the final output with the expectation that the most consistent and balanced mix of source instances would be used for learning the final classifier.

5. Theoretical Analysis of the Rare-Transfer Algorithm

We will refer to the cost C^l on line 9 as the “Correction Factor” and prove in section 5.1 that it prevents the source instances’ weights from early convergence. This improves transfer learning and addresses the lack of training data in a rare dataset. In section 5.2, we provide the motivation for balanced optimization and modify this “Correction Factor” to incorporate balanced optimization to simultaneously compensate for the lack of sufficient data and the class-imbalance within a rare dataset.

5.1. Correction for Transfer Learning

Definition 1

Given k instances at iteration t with normalized weight w and update rate β, the sum of the weights after one boosting iteration with error rate (ε^t) is calculated as:

$$\sum _{i=1}^k{w}^{t+1}={kw}^t(1-{\epsilon }^t)+{kw}^t({\epsilon }^t)\beta$$ (4)

We will now explain this in more detail with the help of an example. Given k = 10 instances at iteration t with normalized weights w = 0.1, assume that weak learner f̈ correctly classifies 6 instances (ε^t = 0.4). Sum of correctly classified instances at boosting iteration t + 1 is calculated as:

$$\begin{array}{l}\sum _{y={\ddot{f}}^t}{w}^{t+1}=0.1{\beta }^0+0.1{\beta }^0+0.1{\beta }^0+0.1{\beta }^0+0.1{\beta }^0+0.1{\beta }^0\\ =6(w^t){\beta }^0\{\text{since}(w^t=0.1)\}\\ =10(0.6)(w^t)\\ ={kw}^t(1-{\epsilon }^t)\{\text{since}(\mathrm{k}=10,{\epsilon }^t=0.4)\}\end{array}$$ (5)

On the other hand, the sum of misclassified instances at boosting iteration t + 1 is:

$$\begin{array}{l}\sum _{y\ne {\ddot{f}}^t}{w}^{t+1}=0.1{\beta }^1+0.1{\beta }^1+0.1{\beta }^1+0.1{\beta }^1\\ =4(w^t){\beta }^1\{\text{since}(w^t=0.1)\}\\ =10(0.4)(w^t)\beta \\ ={kw}^t({\epsilon }^t)\beta \{\text{since}(k=10,{\epsilon }^t=0.4)\}\end{array}$$ (6)

Thus, the sum of weights at boosting iteration “t+1” is calculated as:

$$\begin{array}{l}\sum _{i=1}^k{w}^{t+1}=\sum _{y={\ddot{f}}^t}{w}^{t+1}+\sum _{y\ne {\ddot{f}}^t}{w}^{t+1}\\ ={kw}^t(1-{\epsilon }^t)+{kw}^t({\epsilon }^t)\beta \end{array}$$ (7)

Proposition 1

All source instances are correctly classified by the weak learner:

$$y_{{\mathit{src}}_i}={\ddot{f}}_i^t,\forall i\in \{1,\dots ,n\}$$ (8)

Equation (8) is analogous to:

$$\sum _{i=1}^n{w}^{t+1}={nw}_{\mathit{src}}^t\left(1-{\epsilon }_{\mathit{src}}^t\right)+{nw}_{\mathit{src}}^t\left({\epsilon }_{\mathit{src}}^t\right){\beta }_{\mathit{src}}={nw}_{\mathit{src}}^t$$ (9)

This proposition is held true in subsequent analysis to theoretically demonstrate that even under ideal conditions with perfect auxiliary instances that consistently fit the classifiers, knowledge from these source instances is lost as their weights converge. A “Correction Factor” is calculated to conserve such instances and it will be later demonstrated that this correction is inversely proportional to classifier’s error and approaches unity (no correction needed) as error increases and the analysis deviates from this proposition.

Theorem 1 will examine the effect of the combined (source + target) normalization in line 4 of Algorithm 1.

Theorem 1

If no correction is included in Algorithm 1, source weights will improperly converge even when all instances are correctly classified.

Proof

In the Weighted Majority Algorithm, the weights are updated as:

$$w_{\mathit{src}}^{t+1}=\{\begin{array}{cc}\frac{w_{\mathit{src}}^t}{{\displaystyle \sum _{\{y_i=f_i\}}}{w}_{\mathit{src}}^t+{\displaystyle \sum _{\{y_i\ne f_i\}}}{\beta }_{\mathit{src}}{w}_{\mathit{src}}^t}& y_{\mathit{src}}={\ddot{f}}^t\\ \frac{{\beta }_{\mathit{src}}{w}_{\mathit{src}}^t}{{\displaystyle \sum _{\{y_i=f_i\}}}{w}_{\mathit{src}}^t+{\displaystyle \sum _{\{y_i\ne f_i\}}}{\beta }_{\mathit{src}}{w}_{\mathit{src}}^t}& y_{\mathit{src}}\ne {\ddot{f}}^t\end{array}$$ (10)

Equation (10) demonstrates that the weights for source instances that are correctly classified should not change after normalization as:

$$w_{\mathit{src}}^{t+1}=\frac{w_{\mathit{src}}^t}{{\displaystyle \sum _{i=1}^n}{w}_{{\mathit{src}}_i}^t}=w_{\mathit{src}}^t$$ (11)

Without correction, the normalized source weights in Algorithm 1 are updated as:

$$w_{\text{src}}^{\mathrm{t}+1}=\frac{w_{\mathit{src}}^t}{{\displaystyle \sum _i^n}{w}_{{\mathit{src}}_i}^t+{\displaystyle \sum _j^m}{w}_{{\mathit{tar}}_j}^t{\beta }_{\mathit{tar}}^{1\mathrm{I}\left[y_{{\mathit{tar}}_j}\ne {\ddot{f}}_j^t\right]}}$$ (12)

Equation (12) shows that, without correction, correctly classified source weights would still converge as:

$$\sum _j^m{w}_{{\mathit{tar}}_j}^t{\beta }_{\mathit{tar}}^{\left[y_{{\mathit{tar}}_j}\ne {\ddot{f}}_j^t\right]}=\sum _j^m{w}_{{\mathit{tar}}_j}^t{\left(\frac{1-{\epsilon }_{\mathit{tar}}^t}{{\epsilon }_{\mathit{tar}}^t}\right)}^{1\mathrm{I}\left[y_{{\mathit{tar}}_j}\ne {\ddot{f}}_j^t\right]}$$ (13)

Since all source weights persistently converge, all target weights would inversely increase since $({nw}_{\mathit{src}}^t+{mw}_{\mathit{tar}}^t)=1$. This will be referred to as “Weight Drift” since weight entropy drifts from source to target instances. “Weight Drift” negates transfer since the final classifier is comprised of the cascade of weak learners constructed in boosting iterations $\frac{N}{2}\to N$ (where the source instances’ weights could have already converged). With converged source weights, Algorithm 1 becomes analogous to the standard AdaBoost algorithm with target instances and no transfer learning.

Theorem 1 examined the cause of “Weight Drift” and Theorem 2 will outline the factors that control it.

Theorem 2

For n source instances, the number of target training samples (m) affects the convergence rate and thus the “Weight Drift”. “Weight Drift” is also stochastic since the rate of convergence at iteration t (without correction) is determined by that iteration’s target error rate ( ${\epsilon }_{\mathit{tar}}^t$).

Proof

The fastest rate⁶ of convergence is achieved by minimizing the weight for each subsequent boosting iteration ( $w_{\mathit{src}}^{t+1}$) as:

$$\underset{m,n,{\epsilon }_{\mathit{tar}}^t}{min}(w_{\mathit{src}}^{t+1})=\frac{w_{\mathit{src}}^t}{\underset{m,n,{\epsilon }_{\mathit{tar}}^t}{max}\left\{{\displaystyle \sum _{i=1}^n}{w}_{{\mathit{src}}_i}^t+{\displaystyle \sum _{j=1}^m}{w}_{{\mathit{tar}}_j}^t{\left(\frac{1-{\epsilon }_{\mathit{tar}}^t}{{\epsilon }_{\mathit{tar}}^t}\right)}^{1\mathrm{I}\left[y_{{\mathit{tar}}_j}\ne {\ddot{f}}_j^t\right]}\right\}}$$ (14)

Equation (14) shows that two factors can slow down the rate of convergence of correctly-classified source instances:

1. Maximizing the weak learner’s target error rate with ${\epsilon }_{\mathit{tar}}^t\to 0.5$(choosing an extremely weak learner or one that is only slightly better than random). Since the weak learner is weighted differently for each iteration, its error cannot be controlled and this factor will induce a stochastic effect.

2. Decreasing the number of target samples m, since rate of convergence accelerates when m/n → ∞. Attempting to slow the improper rate of convergence by reducing the number of target instances is counterproductive as the knowledge from the removed instances would be lost.

Theorem 2 demonstrated that a fixed cost cannot control the rate of convergence since the cumulative effect of m, n, and ${\epsilon }_{\mathit{tar}}^t$ is stochastic. A dynamic term has to be calculated to compensate for “Weight Drift” at every iteration. The calculation of a dynamic term is outlined in Theorem 3.

Theorem 3

A correction factor of $2(1-{\epsilon }_{\mathit{tar}}^t)$ can be applied to the source weights to prevent their “Weight Drift” and make the weights converge at a rate similar to that of the Weighted Majority Algorithm.

Proof

Un-wrapping the WMA source update mechanism of Equation (14), yields:

$$w_{\mathit{src}}^{t+1}=\frac{w_{\mathit{src}}^t}{{\displaystyle \sum _{i=1}^n}{w}_{{\mathit{src}}_i}^t+{\displaystyle \sum _{j=1}^m}{w}_{{\mathit{tar}}_j}^t{\left(\frac{1-{\epsilon }_{\mathit{tar}}^t}{{\epsilon }_{\mathit{tar}}^t}\right)}^{1\mathrm{I}\left[y_{{\mathit{tar}}_j}\ne {\ddot{f}}_j^t\right]}}=\frac{w_{\mathit{src}}^t}{{nw}_{\mathit{src}}^t+A+B}$$ (15)

Where A and B are defined as:

• A = Sum of correctly classified target weights at boosting iteration“t + 1”

  $$\begin{array}{l}A=\text{Sum}\text{of}\text{correctly}\text{classified}\text{target}\text{weights}\text{at}\text{boosting}\text{iteration}“\mathrm{t}+1”\\ ={mw}_{\mathit{tar}}^t(1-{\epsilon }_{\mathit{tar}}^t)\end{array}$$ (16)
• B = Sum of misclassified target weights at boosting iteration“t + 1”

  $$\begin{array}{l}B=\text{Sum}\text{of}\text{misclassified}\text{target}\text{weights}\text{at}\text{boosting}\text{iteration}“\mathrm{t}+1”\\ ={mw}_{\mathit{tar}}^t({\epsilon }_{\mathit{tar}}^t){\beta }_{\mathit{tar}}^t={mw}_{\mathit{tar}}^t({\epsilon }_{\mathit{tar}}^t){\left(\frac{1-{\epsilon }_{\mathit{tar}}^t}{{\epsilon }_{\mathit{tar}}^t}\right)}^{1\mathrm{I}\left[y_{{\mathit{tar}}_j}\ne {\ddot{f}}_j^t\right]}\\ ={mw}_{\mathit{tar}}^t(1-{\epsilon }_{\mathit{tar}}^t)\end{array}$$ (17)

Substituting for A and B, the source update is:

$$w_{\mathit{src}}^{t+1}=\frac{w_{\mathit{src}}^t}{{nw}_{\mathit{src}}^t+2{mw}_{\mathit{tar}}^t(1-{\epsilon }_{\mathit{tar}}^t)}$$ (18)

We will introduce and solve for a correction factor C^t to equate ( $w_{\mathit{src}}^{t+1}=w_{\mathit{src}}^t$) for correctly classified instances (as per the WMA).

$$w_{\mathit{src}}^t=w_{\mathit{src}}^{t+1}=\frac{C^t{w}_{\mathit{src}}^t}{C^t{nw}_{\mathit{src}}^t+2{mw}_{\mathit{tar}}^t(1-{\epsilon }_{\mathit{tar}}^t)}$$ (19)

Solving for C^t:

$$C^t=\frac{2{mw}_{\mathit{tar}}^t(1-{\epsilon }_{\mathit{tar}}^t)}{(1-{nw}_{\mathit{src}}^t)}=\frac{2{mw}_{\mathit{tar}}^t(1-{\epsilon }_{\mathit{tar}}^t)}{{mw}_{\mathit{tar}}^t}=2(1-{\epsilon }_{\mathit{tar}}^t)$$ (20)

Adding this correction factor to line 10 of Algorithm 1 equates its normalized update mechanism to the Weighted Majority Algorithm and subsequently prevents “Weight Drift”. Theorem 4 examines the effect this factor has on the update mechanism of the target weights.

Theorem 4

Applying a correction factor of $2(1-{\epsilon }_{\mathit{tar}}^t)$ to the source weights prevents “Weight Drift” and subsequently equates the target instances’ weight update mechanism in Algorithm 1 to that of AdaBoost.

Proof

In AdaBoost, without any source instances (n = 0), target weights for correctly classified instances would be updated as:

$$\begin{array}{l}{w}_{\mathit{tar}}^{t+1}=\frac{w_{\mathit{tar}}^t}{{\displaystyle \sum _{j=1}^m}{w}_{{\mathit{tar}}_j}^t{\left(\frac{1-{\epsilon }_{\mathit{tar}}^t}{{\epsilon }_{\mathit{tar}}^t}\right)}^{1\mathrm{I}\left[y_{{\mathit{tar}}_j}\ne {\ddot{f}}_j^t\right]}}\\ =\frac{w_{\mathit{tar}}^t}{A+B}=\frac{w_{\mathit{tar}}^t}{2{mw}_{\mathit{tar}}^t\left(1-{\epsilon }_{\mathit{tar}}^t\right)}=\frac{w_{\mathit{tar}}^t}{2(1)\left(1-{\epsilon }_{\mathit{tar}}^t\right)}\end{array}$$ (21)

Applying the “Correction Factor” to the source instances’ weight update prevents “Weight Drift” and subsequently equates the target instances’ weight update mechanism outlined in Algorithm 1 to that of AdaBoost since

$$\begin{array}{l}{w}_{\mathit{tar}}^{t+1}=\frac{w_{\mathit{tar}}^t}{{nw}_{\mathit{src}}^t+2{mw}_{\mathit{tar}}^t\left(1-{\epsilon }_{\mathit{tar}}^t\right)}=\frac{w_{\mathit{tar}}^t}{C^t{nw}_{\mathit{src}}^t+2{mw}_{\mathit{tar}}^t\left(1-{\epsilon }_{\mathit{tar}}^t\right)}\\ =\frac{w_{\mathit{tar}}^t}{2\left(1-{\epsilon }_{\mathit{tar}}^t\right){nw}_{\mathit{src}}^t+2{mw}_{\mathit{tar}}^t\left(1-{\epsilon }_{\mathit{tar}}^t\right)}\\ =2\frac{w_{\mathit{tar}}^t}{2\left(1-{\epsilon }_{\mathit{tar}}^t\right)({nw}_{\mathit{src}}^t+{mw}_{\mathit{tar}}^t)}=\frac{w_{\mathit{tar}}^t}{2\left(1-{\epsilon }_{\mathit{tar}}^t\right)(1)}\end{array}$$ (22)

It was proven that a dynamic cost can be incorporated into Algorithm 1 to correct for weight drifting from source to target instances. This factor would ultimately separate the source instance updates which rely on the WMA and β_src, from the target instance updates which rely on AdaBoost and ${\epsilon }_{\mathit{tar}}^t$. With these two algorithms separated, they can be joined for transfer learning by infusing “best-fit” source instances to each successive weak classifier.

The “Correction Factor” introduced in this section allows for strict control of the source weights’ rate of convergence and this property will be exploited to induce balance to “Absolute Rarity”. Balanced classifiers will be dynamically promoted by accelerating the rate of weight convergence of the majority label and slowing it for the minority label.

5.2. Correction for Learning with “Absolute Rarity”

Instance-transfer methods improve classification on a small dataset, but they also exacerbate the imbalance problem by constructing imbalanced classifiers. This outcome was even observed in generally balanced instance-transfer methods. It was noted by [28] that boosting for transfer learning sometimes yielded a final classifier that always predicted a single label. Dai et al. [16] re-sampled the data at each step to balance the class weight since they observed similar behavior. In this section, we examine the cause of this induced imbalance.

Proposition 2

For a class-imbalance problem, a standard classifier yields lower error rate for the majority label as compared to that of the minority since it optimizes:

$$\underset{\epsilon }{min}(n\epsilon )=\underset{{\epsilon }^l}{min}\left(\sum _{\forall l\in Y}{n}^l{\epsilon }^l\right)$$ (23)

In a class-imbalanced problem, where (n^l=majority ≫ n^l=minority), a traditional classifier optimizing Equation (23) can achieve high accuracy if it classifies all instances as majority instances. This proposition serves as a foundation for all imbalanced learning methods [30, 1, 31].

Theorem 5

In an imbalanced problem, the weighted majority algorithm, WMA, constructs a classifier where the minority instances’ weights decrease exponentially with every boosting iteration.

Proof

A misclassified source instance at boosting iteration t is updated via the WMA update mechanism and its t + 1 weight is adjusted to: $w_{\mathit{src}}^{t+1}={\beta }_{\mathit{src}}{w}_{\mathit{src}}^t$. The source update mechanism is set by β_src which is set to:

$$0<\left[{\beta }_{\mathit{src}}=\frac{1}{1+\sqrt{\frac{2ln(n)}{N}}}\right]<1$$ (24)

Since β_src < 1, a misclassified source instance’s weight would converge after normalization. Since weak classifiers at initial boosting iterations, with equally initialized weights, yield high error rates for minority labels (Proposition 2), the minority label’s weights would subsequently have less influence on the t + 1 classifier and would accelerate the rate of convergence as

$$\begin{array}{ll}{w}_{\mathit{src}}^{t+1}\ge w_{\mathit{src}}^t\hfill & if\left(y_{\mathit{src}}={\ddot{f}}^t\right)\hfill \\ w_{\mathit{src}}^{t+1}<w_{\mathit{src}}^t\hfill & if\left(y_{\mathit{src}}\ne {\ddot{f}}^t\right)\hfill \end{array}$$ (25)

Ignoring normalization, the minority label’s weights decrease exponentially as:

$$\begin{array}{lll}{w}_{\mathit{src}}^{t+1}\hfill & \hfill \approx \hfill & {\beta }_{\mathit{src}}{w}_{\mathit{src}}^t\hfill \\ w_{\mathit{src}}^{t+2}\hfill & \hfill \approx \hfill & {\beta }_{\mathit{src}}{w}_{\mathit{src}}^{t+1}\approx {\beta }_{\mathit{src}}{\beta }_{\mathit{src}}{w}_{\mathit{src}}^t\hfill \\ \hfill & \hfill ⋮\hfill & \hfill \\ w_{\mathit{src}}^{t+k}\hfill & \hfill \approx \hfill & {\beta }_{\mathit{src}}^k{w}_{\mathit{src}}^t\hfill \end{array}$$ (26)

Since the final classifier in Algorithm 1 is computed from the cascade of learners constructed in iterations $\frac{N}{2}\to N$, where the minority source weights could have already converged, the final output would be extremely imbalanced as it will have added only majority weights.

Conversely, updating the target instances via the AdaBoost update mechanism improves the performance on an imbalanced dataset particularly if the final classifier is computed using only the $\frac{N}{2}\to N$ boosting iterations. A mis-classified target instance at boosting iteration t is updated via the AdaBoost update mechanism and its t + 1 weight is adjusted to: $w_{\mathit{tar}}^{t+1}={\beta }_{\mathit{tar}}{w}_{\mathit{tar}}^t$. The target update for a misclassified instance’s weight is dependent on β_tar where

$$1<\left[{\beta }_{\mathit{tar}}=\frac{1-{\epsilon }_{\mathit{tar}}^t}{{\epsilon }_{\mathit{tar}}^t}\right]<\infty$$ (27)

Since β_tar > 1, a misclassified target instance’s weight would increase after normalization and the minority label’s weights would in turn have more influence on the t + 1 classifier and bias the classifier to improve learning on the minority as:

$$\begin{array}{ll}{w}_{\mathit{tar}}^{t+1}<w_{\mathit{tar}}^t\hfill & if\left(y_{\mathit{tar}}={\ddot{f}}^t\right)\hfill \\ w_{\mathit{tar}}^{t+1}\ge w_{\mathit{tar}}^t\hfill & if\left(y_{\mathit{tar}}\ne {\ddot{f}}^t\right)\hfill \end{array}$$ (28)

Since the final classifier is computed from the cascade of learners constructed in iterations $\frac{N}{2}\to N$, where the minority label’s instances have increased weights to compensate for the lack of its samples, the final output would be more balanced.

5.3. Label-Space Optimization

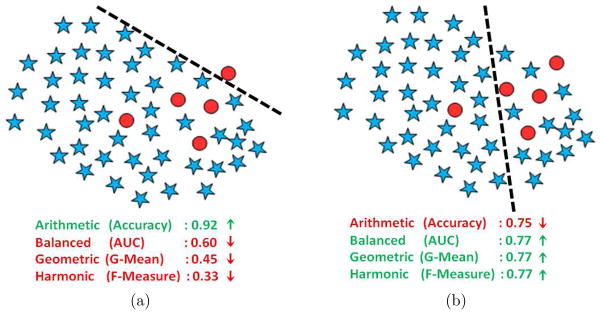
Instance-transfer can improve learning with “Absolute Rarity” as it compensates for the lack of training examples with a selective set of samples from an auxiliary domain. Since instance-transfer can also induce imbalance (as proved in the previous section), intuitive results will require a balanced optimization technique to address the class imbalance in “Absolute Rarity”. Figure 4 motivates for optimization with balanced measures to improve classification in imbalanced datasets. The two classifiers in Figure 4 are optimized with different types of accuracy measures⁷ where Figure 4(a) minimizes the Arithmetic error while Figure 4(b) minimizes the (Geometric [32]/ Balanced [33]/Harmonic [34]) errors. This example shows that given a constrained classifier (linear classifier in this example), the algorithm in Figure 4(b) obtains more intuitive results with a degraded arithmetic accuracy and an improved balanced (Geometric/Balanced/Harmonic) accuracy. Theorems 6, 7, and 8 prove that minimizing a label-dependent measure improves balanced statistical measures while Theorem 9 shows that a label-dependent optimization can improve the balanced statistics for “Absolute Rarity” in Algorithm 1.

Figure 4.

(a) Algorithm minimizing Arithmetic Error. (b) Algorithm minimizing Geometric/Balanced/Harmonic Error

Theorem 6

Maximizing the Balanced Accuracy (BAC) is equivalent to minimizing the sum of label-dependent errors independent of the number of samples within each class:

$$\underset{{\epsilon }^l}{max}(\mathit{BAC})=\underset{{\epsilon }^l}{min}\sum _{l\in Y}{\epsilon }_{\mathit{src}}^l$$

Proof

To prove theorem 6, we will start with a binary labeled example and extend to general form. With no optimization of the prediction threshold of a binary classifier (classifier threshold at a pre-set level), the Area under the ROC Curve (AUC) is equivalent to Balanced Accuracy (BAC) [35]. This Balanced Accuracy is the average accuracy of each class and in turn equates to the average of sensitivity and specificity. It is calculated as follows:

$$\begin{array}{l}\mathit{AUC}=\mathit{BAC}=\frac{1}{2}(\mathit{Sensitivity}+\mathit{Specificity})\\ =\frac{1}{2}\left[\left(\frac{\mathit{TruePositive}}{\mathit{TruePositive}+\mathit{FalseNegative}}\right)+\left(\frac{\mathit{TrueNegative}}{\mathit{TrueNegative}+\mathit{FalsePositive}}\right)\right]\\ =\sum _{l\in Y}\frac{0.5\left({\displaystyle \sum _{i=1}^n}\left(y_i^l=f_i^l\right)\right)}{{\displaystyle \sum _{i=1}^n}\left(y_i^l=f_i^l\right)+{\displaystyle \sum _{i=1}^n}\left(y_i^l\ne f_i^l\right)}=\sum _{l\in Y}\frac{0.5\left(n^l\left(1-{\epsilon }^l\right)\right)}{n^l\left(1-{\epsilon }^l\right)+n^l\left({\epsilon }^l\right)}=0.5\left(\sum _{l\in Y}\left(1-{\epsilon }^l\right)\right)\end{array}$$ (29)

Equation (29) can be maximized as follows:

$$\underset{{\epsilon }^l}{max}(\mathit{BAC})=\underset{{\epsilon }^l}{max}\left(0.5\left(\sum _{l\in Y}\left(1-{\epsilon }^l\right)\right)\right)=\underset{{\epsilon }^l}{min}\left(\sum _{l\in Y}{\epsilon }^l\right)$$ (30)

The optimization problem in Equation (30) is a constrained optimization problem which is minimized as follows:

$$\begin{array}{c}\underset{{\epsilon }^l}{min}\sum _{l\in Y}{\epsilon }^l\\ \text{s.t.}{\sum }_{\forall l\in Y}{n}^l{\epsilon }^l=\epsilon \end{array}$$ (31)

Theorem 7

Maximizing the Geometric Mean (G-Mean) is equivalent to minimizing the product of label-dependent errors and is independent of the number of samples within each class:

$$\underset{{\epsilon }^l}{max}(G-\mathit{Mean})=min\prod _{l\in Y}{\epsilon }_{\mathit{src}}^l$$

Proof

Similar to Theorem 6, we start with a binary labeled example and extend to general form:

$$\begin{array}{l}G-\mathit{Mean}=\sqrt{(\mathit{Sensitivity})(\mathit{Specificity})}\\ =\sqrt{\left(\frac{\mathit{TruePositive}}{\mathit{TruePositive}+\mathit{FalseNegative}}\right)\left(\frac{\mathit{TrueNegative}}{\mathit{TrueNegative}+\mathit{FalsePositive}}\right)}\\ =\sqrt{\prod _{l\in Y}\frac{{\displaystyle \sum _{i=1}^n}\left(y_i^l=f_i^l\right)}{{\displaystyle \sum _{i=1}^n}\left(y_i^l=f_i^l\right)+{\displaystyle \sum _{i=1}^n}\left(y_i^l\ne f_i^l\right)}}=\sqrt{\prod _{l\in Y}\frac{n^l\left(1-{\epsilon }^l\right)}{n^l\left(1-{\epsilon }^l\right)+n^l\left({\epsilon }^l\right)}}=\sqrt{\prod _{l\in Y}\left(1-{\epsilon }^l\right)}\end{array}$$ (32)

Maximizing the statistic in Equation (32), we have

$$\underset{{\epsilon }^l}{max}(G-\mathit{Mean})=\underset{{\epsilon }^l}{max}\left(\sqrt{\prod _{l\in Y}(1-{\epsilon }^l)}\right)=\underset{{\epsilon }^l}{min}\left(\prod _{l\in Y}{\epsilon }^l\right)$$ (33)

Similar to Equation (31), the optimization problem in Equation (33) is a constrained optimization problem and is minimized by

$$\begin{array}{c}\underset{{\epsilon }^l}{min}\prod _{l\in Y}{\epsilon }^l\\ \text{s.t.}{\sum }_{\forall l\in Y}{n}^l{\epsilon }^l=\epsilon \end{array}$$ (34)

Since both Equations (31) and (34) are constrained by the classifier’s error rate, modifying the weak learner to improve classification on one label can degrade classification on the other label (Figure 4).

Theorem 8

An improved G-Mean coupled with no degradation in the BAC will improve the F-Measure.

Proof

The harmonic mean of sensitivity and specificity is a particular realization of the F-measure [34] and is maximized as

$$\begin{array}{l}f-\mathit{measure}=\left[\frac{2(\mathit{Sensitivity})(\mathit{Specificity})}{\mathit{Sensitivity}+\mathit{Specificity}}\right]\\ =\left[\frac{{\displaystyle \prod _{l\in Y}}\frac{n^l\left(1-{\epsilon }^l\right)}{n^l\left(1-{\epsilon }^l\right)+n^l\left({\epsilon }^l\right)}}{{\displaystyle \sum _{l\in Y}}\frac{0.5\left(n^l\left(1-{\epsilon }^{\lambda }\right)\right)}{n^l\left(1-{\epsilon }^l\right)+n^l\left({\epsilon }^l\right)}}\right]=\left[\frac{{\displaystyle \prod _{l\in Y}}\left(1-{\epsilon }^l\right)}{0.5\left({\displaystyle \sum _{l\in Y}}\left(1-{\epsilon }^l\right)\right)}\right]\end{array}$$ (35)

Equation (35) can be optimized as

$$\begin{array}{l}\underset{{\epsilon }^l}{max}(f-\mathit{measure})=\underset{{\epsilon }^l}{max}\left[\frac{{\displaystyle \prod _{l\in Y}}\left(1-{\epsilon }^l\right)}{0.5\left({\displaystyle \sum _{l\in Y}}\left(1-{\epsilon }^l\right)\right)}\right]\\ ={\displaystyle \underset{{\epsilon }^l}{max}}\left[\frac{{(G-\mathit{Mean})}^2}{\mathit{BAC}}\right]=\underset{{\epsilon }^l}{min}\left[\frac{\left({\displaystyle \prod _{l\in Y}}{\epsilon }^l\right)}{{\displaystyle \sum _{l\in Y}}{\epsilon }^l}\right]\end{array}$$ (36)

Equation (36) proves a classifier that improves G-Mean (via balance) with no degradation in BAC (via Transfer) improves the F-measure.

Theorem 9

In an imbalanced dataset, a label-dependent update mechanism can improve the G-Mean without degrading the BAC performance.

Proof

In a balanced learning problem, all labels have an equal effect on BAC and G-Mean but as the label space gets more imbalanced, $\frac{n^{l=\text{majority}}}{n^{l=\text{minority}}}\to \infty$, the contribution of the minority label’s error rate to the classifier’s overall accuracy can thus be approximated as:

$$\sum _{\forall l\in Y}{n}^l{\epsilon }^l\approx \sum _{l\in \mathit{majority}}{n}^l{\epsilon }^l$$ (37)

Equation (37) demonstrates that biasing the classifier to favor the minimization of the minority label, in an imbalanced dataset, has minimal effect on the overall accuracy and the balanced arithmetic mean will not be degraded since the increased error of the majority label is negated by the decreased error of the minority label. On the other hand, G-Mean is the balanced geometric mean and is significantly improved if balance is induced.

5.3.1. Optimization for “Absolute Rarity”

Using definition 1, the sum of source instances’ weight is monotonically decreasing as:

$$\begin{array}{lll}{nw}_{\mathit{src}}^{t+1}\hfill & =\hfill & {nw}_{\mathit{src}}^t[1+{\epsilon }_{\mathit{src}}^t({\beta }_{\mathit{src}}-1)]\hfill \\ {nw}_{\mathit{src}}^{t+1}\hfill & \le \hfill & {nw}_{\mathit{src}}^t\text{since}({\beta }_{\mathit{src}}<1,{\epsilon }_{\mathit{src}}^t\ge 0)\hfill \end{array}$$ (38)

Similarly, the target instances’ weights are monotonically increasing:

$$\begin{array}{lll}{mw}_{\mathit{tar}}^{t+1}\hfill & =\hfill & {mw}_{\mathit{tar}}^t[1+{\epsilon }_{\mathit{tar}}^t({\beta }_{\mathit{tar}}-1)]\hfill \\ {\text{mw}}_{\mathit{tar}}^{t+1}\hfill & \le \hfill & {mw}_{\mathit{tar}}^t\text{since}({\beta }_{\mathit{tar}}>1,{\epsilon }_{\mathit{tar}}^t\ge 0)\hfill \end{array}$$ (39)

Line 4 of “Rare Transfer” normalizes the sum of all weights and thus, all source weights are monotonically converging. On the other hand, Theorem (5) demonstrated that the minority sources’ weights converge faster than the majority sources’ weights. To improve balanced classification, we include a “Label-Dependent Correction Factor” to dynamically slow the convergence of the source instances’ weights while simultaneously reducing the differential in the error between the minority and majority label. It is set to:

$$C^l=\left(1-{\epsilon }_{\mathit{src}}^l\right)$$ (40)

This factor dynamically slows convergence for the label with a higher error since the convergence rate is inversely correlated to the error. Biasing each label’s weights allows “Rare Transfer” to steer for the construction of a final classifier that includes a best-fit set of auxiliary samples and has an equal error on all labels.

6. Empirical Analysis

In this section, we provide empirical validation of our theorems. The first experiment demonstrates how a “Correction Factor” fixes the problem of “Weight Drift”. The second experiment examines the effect of “Label-Dependent” optimization on imbalanced learning.

6.1. “Weight Drift” and “Correction Factor”

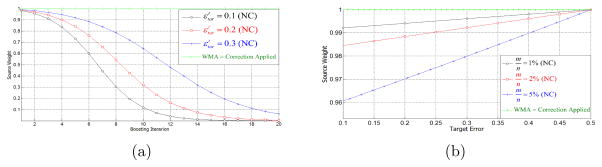
The first experiment demonstrates the effect of “Weight Drift” on source and target weights. In Figure 5(a), the number of instances was constant (n = 10000, m = 200), the source error rate was set to zero (as per Proposition 1) and the number of boosting iterations was set to N = 20. According to the WMA, the weights should not change when ${\epsilon }_{\mathit{src}}^t=0$. The ratio of the weights (with and without correction) to the weights of the WMA are plotted at different boosting iterations and with different target error rates ${\epsilon }_{\mathit{tar}}^t\in \{0.1,0.2,0.3\}$. This experiment validates the following theorems:

Figure 5.

The weights (relative to the WMA) for ideal source instances. (a) For 20 iterations with different error. (b) For 1 iteration with different target instances and error. (NC: No correction)

1. With correction, source weights converge even when correctly classified.

2. Applying our “Correction Factor” equates the weight update of Algorithm 1 to the WMA.

3. If correction is not applied, strong classifiers cause weights to converge at a faster rate than weak ones (Theorem 2).

The figure also demonstrates that for a strong learner with ${\epsilon }_{\mathit{tar}}^t\approx 0.1$, if no correction is applied, an “un-corrected” update mechanism would not transfer knowledge from all 10,000 source instances although they were never misclassified. The final classifier uses boosting iterations N/2 → N, or 10 → 20, where the weights of ideal source instances would have already lost over 85% of their value. Correction conserved these instances’ weights and thus helpful source instances would improve classification.

The second experiment validates the effect of the number of target instances, m, on the convergence rate (Theorem 2). The number of source instances was set (n = 1000), while the number of target instances was varied $\frac{m}{n}\in \{1\%,2\%,5\%\}$ and plotted for ${\epsilon }_{\mathit{tar}}^t\in \{0.1,\dots ,0.5\}$. The plot in Figure 5(b) shows how the source weights converge after a single boosting iteration and it can be observed that the rate of convergence is affected by m/n and the error rate ε_tar (which is also related to m). It can also be observed that as the error rate increases (ε → 0.5), less correction is required as the improper convergence rate approaches the correct WMA rate. This is expected since the “Correction Factor” ( $C=2(1-{\epsilon }_{\mathit{tar}}^t)$) is inversely proportional to ${\epsilon }_{\mathit{tar}}^t$ and its impact reaches unity (No Correction) as the target error rate increases.

$$\underset{{\epsilon }_{\mathit{tar}}^t\to 0.5}{lim}\{C\}=\underset{{\epsilon }_{\mathit{tar}}^t\to 0.5}{lim}\{2(1-{\epsilon }_{\mathit{tar}}^t)\}\approx \underset{{\epsilon }_{\mathit{src}}^t\to 0.5}{lim}\{2(1-{\epsilon }_{\mathit{src}}^t)\}=1$$ (41)

This is an important property because “Weight Drift” is most detrimental to learning at low error rates (where Proposition 1 was set).

It should be noted that for both plots in Figure 5, the weight lost by the source instances is drifting to the target instances. The plots for the target weights would look inversely proportional to the plots in Figure 5 since ${\displaystyle \sum _{i=1}^n}{w}_{{\mathit{src}}_i}^t+{\displaystyle \sum _{j=1}^m}{w}_{{\mathit{tar}}_j}^t=1$.

6.2. “WMA Imbalanced Drift” and “Rare Correction Factor”

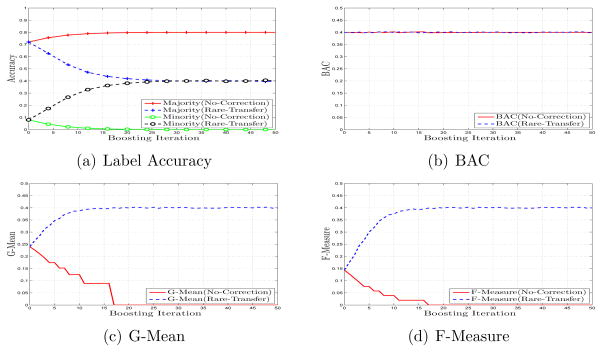
This section presents an empirical validation of Theorems 5, 6, 7, 8, and 9. A binary labeled classification problem was simulated with 900 majority instances, 100 minority instances and the weak classifier error rate was set to (ε = 0.2). Since this an imbalanced dataset and the weak classifier is weighted, error rate (ε^l) was correlated with the label’s relative weight as follows: ${\epsilon }^l=\frac{\epsilon {\displaystyle \sum _{i\in l}}{w}^i}{\sum w}$.

In Figure 6(a), we plot the accuracy for both labels and demonstrate that applying a label dependent correction factor to the weight update mechanism induces balance while the un-corrected WMA update mechanism minimizes only the majority label’s error and causes imbalance. This is reflected in the statistical measures as Figure 6(b) shows that inducing balance causes no change in BAC while significantly improving G-Mean in Figure 6(c). The improved G-Mean coupled with no degradation in BAC is reflected in the improved F-Measure in Figure 6(d).

Figure 6.

The effect of “Rare Correction” using various evaluation metrics.

7. Real-World Experimental Results

We will now provide the details on the performance of various algorithms under different evaluation metrics using real-world datasets.

7.1. Dataset Description

A Detailed description of the datasets used in our experiments is provided in Table 1.

Table 1.

Description of the datasets used in our experiments. For brevity, we used several acronyms which are explained here. Nu:Numeric, No:Nominal, CA:Caucasian, AA:African American, NReH:Not Re-Hospitalized, ReH:Re-Hospitalized, Emp:Employment, Rel:Religion, Park:Parkinson.

Dataset	Features	Source Majority	Source Minority	Target Majority	Target Minority
HF (Race)	Nu : 2 No : 20	AA NReH 4468 (78.0%)	AA ReH 1026 (17.9%)	CA NReH ≈183 (3.2%)	CA ReH ≈50 (0.9%)
HF (Age)	Nu : 1 No : 21	Over 50 NReH 4513 (75.4%)	Over 50 ReH 1182 (19.8%)	Under 50 NReH ≈241 (4.0%)	Under 50 ReH ≈50 (0.8%)
HF (Gender)	Nu : 2 No : 20	Male NReH 3366 (75.7%)	Male ReH 818 (18.4%)	Female NReH ≈211 (4.8%)	Female ReH ≈50 (1.1%)
Emp (Rel)	Nu : 5 No : 3	Muslim Un-employed 955 (74%)	Muslim Employed 298 (23%)	Non-Muslim Un-employed 15 (0.02%)	Non-Muslim Employed 7 (0.006%)
Park (Gender)	Nu : 19 No : 0	Male UPDRS≥10 3732 (89%)	Male UPDRS<10 276 (8%)	Female UPDRS≥10 112 (0.03%)	Female UPDRS<10 13(0.003%)
REC vs TALK	Nu : 500 No : 0	rec .autos .motorcycles 1009	talk .politics.guns .politics.misc 20,50,101 2%,5%,10%	rec .sports.baseball .sports.hockey 472,453,393 2%,5%,10%	talk .politics.mideast .religion.misc 10,23,39 2%,5%,10%
REC vs SCI	Nu : 500 No : 0	rec .autos .sports.baseball 1187	sci .sci.crypt .sci.space 24,59,119 2%,5%,10%	rec .motorcycles .sports.hockey 486,518,543 2%,5%,10%	sci .sci.electronics .sci.med 10,26,55 2%,5%,10%
SCI vs TALK	Nu : 500 No : 0	sci .sci.med .sci.electronics 840	talk .politics.misc .religion.misc 17,42,84 2%,5%,10%	sci .sci.crypt .sci.space 513,529,507 2%,5%,10%	talk .politics.guns .politics.mideast 10,26,51 2%,5%,10%

(i) HealthCare Demographics

We collected Heart Failure (HF) patient data from the Henry Ford Health System (HFHS) in Detroit. This dataset contains records for 8913 unique patients who had their first hospitalization with primary HF diagnosis. The goal is to predict if a patient will be re-admitted within 30 days after being discharged from the hospital and to apply the model to rural hospitals or to demographics with less data [36]. Re-hospitalization for HF occurs in around one-in-five patients within 30 days of discharge and is disproportionately distributed across the US population with significant disparities based on gender, age, ethnicity, geographic area, and socioeconomic status [37]. Other non-demographic features included length of hospital stay, ICU stay and dichotomous variables for whether a patient was diagnosed with diabetes, hypertension, peripheral vascular disease, transient ischemic attack, heart failure, chronic kidney disease, coronary artery disease, hemodialysis treatment, cardiac catheterization, right heart catheterization, coronary angiography, balloon pump, mechanical ventilation or general intervention. The average results with 50 minority samples (patient was re-hospitalized) is reported.

(ii) Employment Dataset

This dataset is a subset of the 1987 National Indonesia Contraceptive Prevalence Survey [38]. We used the dataset [14] to predict if a non-Muslim woman is employed based on her demographic and socio-economic characteristics. In the training set, only 22 of the 1275 were not Muslim and only 7 of them were employed.

(iii) Parkinson Dataset

This dataset [39] is composed of a range of biomedical voice measurements from people with early-stage Parkinson’s disease⁷. The goal is to predict if a female patient’s score on the Unified Parkinson’s Disease Rating Scale [40] is high (UPDRS≥10) or low (UPDRS<10). In the training set, only 125 of the 3732 participants were female and only 13 of them had a low UPDRS score.

(iv) Text Dataset

20 Newsgroups⁸ is a popular text collection that is partitioned across 20 groups with 3 cross-domain tasks and a two-level hierarchy as outlined in [41]. We used Term FrequencyInverse Document Frequency (TF-IDF) [42] to maintain around 500 features and imbalanced the dataset to generate a high dimensional, small and imbalanced dataset.

7.2. Experiment Setup

AdaBoost [17] was used as the standard baseline algorithm for comparison. We applied SMOTE [43], with 5 nearest neighbors (k = 5), before boosting to compare with an imbalanced classification method (SMOTE-AdaBoost). TrAdaBoost [16] was used as the baseline transfer learning algorithm. The non-transfer reference algorithms were trained with the target-only set and with the combined (target+source) set. Thirty boosting iterations were experimentally proven sufficient for training.

Base Learner (f̈)

We did not use decision stumps as weak learners since most data belongs to the source and it was not possible to keep the target error below 0.5 (as mandated by AdaBoost) for more than a few iterations. A strong classifier, full classification tree without pruning, is applied with a top-down approach where the tree is trimmed at the first level to achieve ${\epsilon }_{\mathit{tar}}^t<0.5$.

Cross Validation

Small datasets are prone to over-fit and terminate boosting and thus all algorithms were restarted with a new cross validation fold when any algorithm terminated before reaching 30 iterations. Random sub-sampling cross validation [44] was applied and each statistic was tabulated with the macro average [45] of 30 runs. Plots with two imbalance ratios across a variable size of minority samples are also presented.

7.3. Experimental Results

This section presents the classification results for the different balanced learning measures.

7.3.1. BAC Results

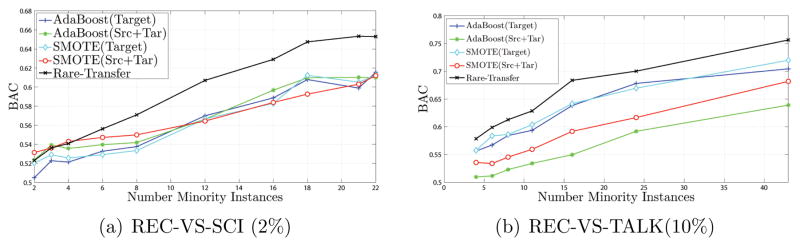
The BAC results presented in Table 2 show that Rare-Transfer improved the Balanced Accuracy. The improved performance is consistent even when the addition of auxiliary data seemed to degrade the performance as evident in the 20 Newsgroups dataset. This is proof that the “transfer learning” objective in our algorithm improved learning with only the best set of auxiliary instances. Figure 7 demonstrates that the improved performance is consistent across different datasets, imbalance ratios and absolute number of minority samples.

Table 2.

Comparison of Balanced Accuracy values on real-world datasets.

	AdaBoost (Target)	AdaBoost (Src+Tar)	SMOTE (Target)	SMOTE (Src+Tar)	TrAda Boost	Rare Transfer
HF(Gender)	0.518	0.512	0.524	0.549	0.502	0.562
HF(Race)	0.521	0.509	0.529	0.547	0.504	0.563
HF(Age)	0.526	0.511	0.538	0.535	0.503	0.556
Rec-Sci(2%)	0.564	0.571	0.566	0.569	0.558	0.594
Sci-Talk(2%)	0.544	0.541	0.544	0.540	0.543	0.571
Rec-Talk(2%)	0.569	0.534	0.577	0.547	0.561	0.610
Rec-Sci(5%)	0.635	0.622	0.635	0.645	0.608	0.664
Sci-Talk(5%)	0.602	0.591	0.607	0.596	0.582	0.632
Rec-Talk(5%)	0.635	0.569	0.642	0.602	0.609	0.672
Rec-Sci(10%)	0.696	0.680	0.699	0.706	0.649	0.706
Sci-Talk(10%)	0.662	0.639	0.672	0.647	0.620	0.679
Rec-Talk(10%)	0.714	0.628	0.722	0.673	0.640	0.736
Employment	0.506	0.509	0.510	0.523	0.524	0.513
Parkinson	0.649	0.659	0.761	0.762	0.862	0.885

Figure 7.

BAC values when the number of minority samples is varied.

7.3.2. G-Mean Results

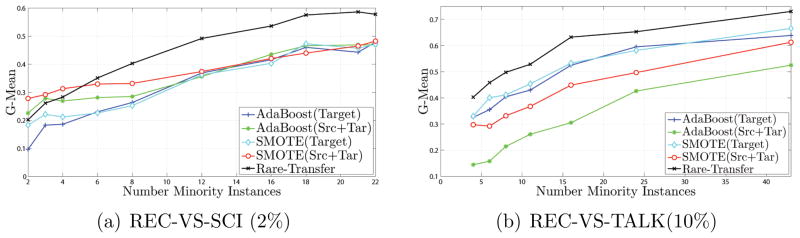
The results in Table 3 confirm that Rare-Transfer significantly improved the Geometric Mean. The results on the 20 Newsgroups (2%) dataset demonstrate improved performance with severe label imbalance and an extremely high features/samples ratio (10 minority samples, ≈500 majority samples, 500 features). Figure 8 shows that Rare-Transfer consistently yield superiorsresults even after the non-transfer algorithms construct representative hypotheses with more training samples.

Table 3.

Comparison of G-Mean values on real-world datasets

	AdaBoost (Target)	AdaBoost (Src+Tar)	SMOTE (Target)	SMOTE (Src+Tar)	TrAda Boost	Rare Transfer
HF(Gender)	0.336	0.212	0.444	0.459	0.117	0.518
HF(Race)	0.366	0.178	0.467	0.478	0.145	0.540
HF(Age)	0.346	0.141	0.447	0.357	0.164	0.478
Rec-Sci(2%)	0.324	0.362	0.338	0.379	0.384	0.430
Sci-Talk(2%)	0.270	0.271	0.277	0.292	0.339	0.380
Rec-Talk(2%)	0.343	0.221	0.378	0.293	0.387	0.460
Rec-Sci(5%)	0.500	0.492	0.501	0.561	0.512	0.592
Sci-Talk(5%)	0.433	0.423	0.446	0.464	0.471	0.541
Rec-Talk(5%)	0.502	0.340	0.516	0.450	0.491	0.591
Rec-Sci(10%)	0.615	0.605	0.623	0.671	0.581	0.674
Sci-Talk(10%)	0.563	0.531	0.584	0.575	0.531	0.637
Rec-Talk(10%)	0.647	0.483	0.661	0.597	0.569	0.702
Employment	0.422	0.452	0.467	0.483	0.331	0.378
Parkinson	0.518	0.570	0.715	0.741	0.841	0.874

Figure 8.

G-Mean values when the number of minority samples is varied.

7.3.3. F-Measure Results

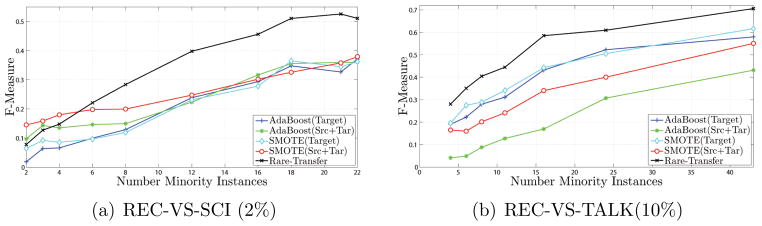
The F-Measure results are presented in Table 4 and demonstrate that Rare-Transfer constructs a more balanced classifier. The improvements are consistent at different imbalance ratios and sample sizes as shown in Figure 9. The figures also demonstrate that the classification models can construct classifiers that are more balanced when the overall size of the training set increases.

Table 4.

Comparison of F-Measure values on real-world datasets

	AdaBoost (Target)	AdaBoost (Src+Tar)	SMOTE (Target)	SMOTE (Src+Tar)	TrAda Boost	Rare Transfer
HF(Gender)	0.217	0.088	0.375	0.384	0.307	0.478
HF(Race)	0.256	0.062	0.412	0.418	0.055	0.519
HF(Age)	0.228	0.039	0.372	0.238	0.063	0.411
Rec-Sci(2%)	0.208	0.240	0.218	0.258	0.266	0.331
Sci-Talk(2%)	0.225	0.115	0.256	0.174	0.223	0.363
Rec-Talk(2%)	0.149	0.144	0.152	0.164	0.254	0.275
Rec-Sci(5%)	0.405	0.393	0.408	0.490	0.434	0.534
Sci-Talk(5%)	0.407	0.228	0.424	0.349	0.382	0.527
Rec-Talk(5%)	0.324	0.309	0.343	0.365	0.405	0.473
Rec-Sci(10%)	0.550	0.541	0.560	0.638	0.512	0.645
Sci-Talk(10%)	0.590	0.389	0.609	0.536	0.472	0.671
Rec-Talk(10%)	0.484	0.445	0.514	0.513	0.520	0.600
Employment	0.276	0.408	0.325	0.457	0.188	0.378
Parkinson	0.404	0.504	0.552	0.733	0.702	0.749

Figure 9.

F-Measure values when the number of minority samples is varied.

7.4. Discussion and Possible Extensions

Traditional imbalanced modifications including SMOTEBoost [46], over or under sampling [47] followed by transfer [48] or cost sensitive learning [26] are a straight-forward extension to Algorithm 1 and can further improve classification. Improvements, even minor, from methods optimized specifically for “Absolute Rarity” can have significant practical impact within real-world domains where only human expertise are currently applicable. For example, rare diseases are a substantial public health burden as extremely low percentage of people have a rare disease at some point and currently no global registry or classification codes exist. Rare methods can improve learning and encourage data collection and warehousing. Future work will test our approach using multi-resolution methods in distributed environments with multiple source sets [49, 50].

8. Conclusion

Learning with “Absolute Rarity” is an important and understudied area of research which is investigated in this paper. We discussed the impediments and proposed the first classification method optimized specifically for the problem of “Absolute Rarity”. Our framework simultaneously compensated for the lack of data and the presence of class-imbalance using a transfer learning paradigm with a balanced statistics objective. We theoretically analyzed and empirically verified our work and demonstrated its effectiveness with several real-world domains. We proposed possible extensions and motivated for more research for a problem with significant social and financial impact.

Biographies

Samir Al-stouhi is a research engineer at Honda R&D labs. He received his Ph.D. from the Electrical & Computer Engineering Department at Wayne State University. His research interests include transfer learning, multi-task learning and imbalanced learning. He also has few years of experience in Embedded Signal Processing.

Chandan K. Reddy is an Associate Professor in the Department of Computer Science at Wayne State University. He received his PhD from Cornell University and MS from Michigan State University. His primary research interests are in the areas of data mining and machine learning with applications to healthcare, bioinformatics, and social network analysis. His research is funded by the NSF, NIH, DOT, Susan G. Komen for the Cure Foundation. He has published over 50 peer-reviewed articles in leading conferences and journals. He received the Best Application Paper Award at the ACM SIGKDD conference in 2010 and was a finalist of the INFORMS Franz Edelman Award Competition in 2011. He is a senior member of IEEE and a life member of ACM.