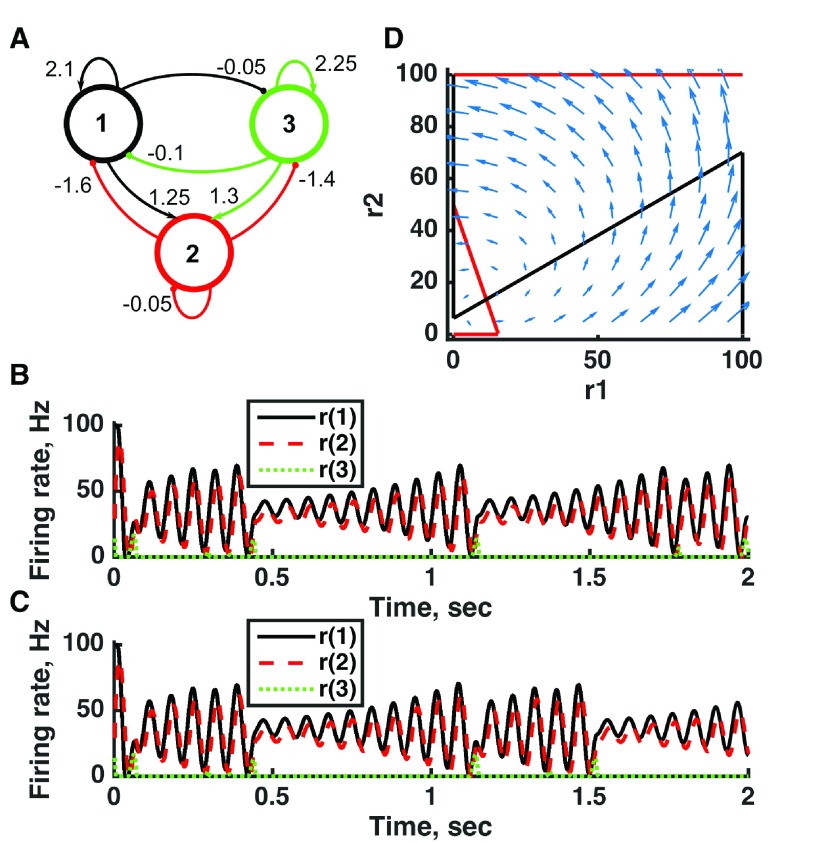
Figure 8. Chaotic activity in a threshold-linear three-unit circuit.

( A) Diagram of the model circuit. Arrows indicate excitatory connections, and balls indicate inhibitory connections between units. Architecture is identical to that of Figure 4 and Figure 7. ( B, C) Firing rate as a function of time in the coupled network, from two imperceptibly different initial conditions. No applied current is present. The miniscule difference in initial conditions is amplified over time, so, for example, unit 3 produces a small burst of activity after 1.5 s in ( D), but that burst is absent from ( C). ( D) Any particular combination of the firing rates of the three units (x-axis is rate of unit 1, y-axis is rate of unit 3) determines the way those firing rates change in time (arrows). Only a plane out of the full three-dimensional space of arrows is shown: the plane corresponding to dr(2)/dt = 0. Red line: nullcline for unit 2—the value of r(2) at which dr(2)/dt = 0 (its fixed point) given a value of r(1). Black line: nullcline for unit 1—the value of r(1) at which dr(1)/dt = 0 (its fixed point) given a value of r(2). The crossing points of the nullclines are unstable fixed points of the whole system. For parameters, see supporting Matlab code, “dynamics_three_units.m”.