Abstract
Selective and rapid enrichment of biomolecules is of great interest for biomarker discovery, protein crystallization, and in biosensing for speeding assay kinetics and reducing signal interferences. The current state of the art is based on DC electrokinetics, wherein localized ion depletion at the microchannel to nanochannel interface is used to enhance electric fields, and the resulting biomarker electromigration is balanced against electro-osmosis in the microchannel to cause high degrees of biomarker enrichment. However, biomarker enrichment is not selective, and the levels fall off within physiological media of high conductivity, due to a reduction in ion concentration polarization and electro-osmosis effects. Herein, we present a methodology for coupling AC electrokinetics with ion concentration polarization effects in nanoslits under DC fields, for enabling ultrafast biomarker enrichment in physiological media. Using AC fields at the critical frequency necessary for negative dielectrophoresis of the biomarker of interest, along with a critical offset DC field to create proximal ion accumulation and depletion regions along the perm-selective region inside a nanoslit, we enhance the localized field and field gradient to enable biomarker enrichment over a wide spatial extent along the nanoslit length. While enrichment under DC electrokinetics relies solely on ion depletion to enhance fields, this AC electrokinetic mechanism utilizes ion depletion as well as ion accumulation regions to enhance the field and its gradient. Hence, biomarker enrichment continues to be substantial in spite of the steady drop in nanostructure perm-selectivity within physiological media.
I. INTRODUCTION
Biomarker discovery requires the identification of variations in rare sets of biomolecules within bio-fluids that also contain common interfering species at million to billion-fold higher levels. Hence, there is a need for methods to cause rapid and selective enrichment of rare biomarkers versus the interfering species,1 preferably within physiological media, to maintain their ability to selectively bind with receptors, without needing buffer changes that lead to dilution. Since affinity methods based on antibody depletion can cause enrichment levels of no more than two to three orders of magnitude,2 there is a need for complementary enrichment modalities. A commonly investigated methodology for achieving highly enriched analyte plugs from dilute samples is through applying an electrokinetic force balance in conjunction with localized ion depletion to create a trap due to the sharp spatial profile in the field. Typically, ion concentration polarization (ICP) effects at the entrance of perm-selective nanochannels are used to cause sharp field gradients due to ion depletion at the anodic interface of microchannel to the nanochannel, and this is balanced against electro-osmosis within the microchannel3 to cause high degrees of biomarker enrichment.4 However, due to the abrupt field profile, the trapped biomarkers are co-localized within a tightly confined region, which limits the scope for spatially graded stacking toward selectivity. Furthermore, the degree of biomarker enrichment obtained by this method can fall sharply within physiological media of high conductivity, due to a reduction in electro-osmosis, as well as ICP effects. While a limited degree of biomarker enrichment can be obtained within conductive media through utilizing tighter nanochannels and/or higher applied fields to enhance ICP, these strategies are not practical due to fabrication challenges, disruptive electrothermal flow due to Joule heating,5,6 and electrical-double layer induced field screening.7 An alternate strategy is to carry out biomarker enrichment inside a nanoslit channel under the field profile due to ion conductivity gradients, where enhanced surface versus bulk conduction of ions can lead to more pronounced ICP than obtained at the microchannel interface to the nanoslit. In this manner, conductivity gradients enable extension of the field profile along the nanoslit length for enhancing the spatial extent for biomarker depletion,8 to achieve biomarker enrichment in parallel to spatially graded biomarker stacking.9 In this work, we implement a similar electrokinetic force balance due to ion conductivity gradients generated inside the nanoslit channel, rather than through field-enhanced ICP in the microchannel, by placing a surface charge non-uniformity inside the nanoslit to initiate ion accumulation proximal to ion depletion. Furthermore, instead of electroosmosis as the opposing force field, we utilize AC fields for frequency-selective negative dielectrophoresis (nDEP) from the high field regions, since nDEP continues to be a significant force field within media of high conductivity. In this manner, we utilize ion depletion effects to enhance the localized field and ion accumulation effects to enhance field gradient, thereby enhancing biomarker electrophoresis (EP) and nDEP trapping to cause ultrafast biomarker enrichment within physiological media.
Dielectrophoresis (DEP) enables selective trapping of bio-particles based on the characteristic frequency response of dielectric permittivity of the particle versus the medium10–14 for causing frequency-selective enrichment of target DNA15–17 and protein molecules,18,19 but only a few studies are reported in physiological media.20–23 Furthermore, the highly localized nature of DEP behavior, due to its dependence on ∇E2, limits its spatial extent.13,24 Herein, by initiating ICP at lateral perm-selective constrictions of large surface charge non-uniformity, we create conductivity differences across the nanoslit length to enhance the spatial extent for biomarker depletion. As a result, the localized field (E) is enhanced due to ion depletion at the constriction tips, whereas ion accumulation along the constriction sidewalls increases the field gradient (∇E), thereby dramatically enhancing the magnitude and spatial extent of nDEP, due to its ∇E2 dependence. Specifically in this work, we optimize nanoslit designs for enhanced surface conduction toward creating the ion conductivity gradients that increase the height and depth of the potential barrier for nDEP trapping, thereby exponentially enhancing localized biomarker numbers due to its Boltzmann distribution profile. While ICP effects have been extensively applied within prior work to cause ion gradients in the microchannel region interfacing the nanochannel,3 this is the first report on using ICP to initiate ion conductivity gradients inside the nanochannel, where surface charge-induced ion conduction effects can cause more pronounced ICP effects than within microchannels. As a result, the presented AC electrokinetic method can cause biomarker enrichment within physiological media of high conductivity for facile coupling to receptors to enable detection.25,26
II. RESULTS AND DISCUSSION
A. Device geometry for ICP-enhanced nDEP enrichment
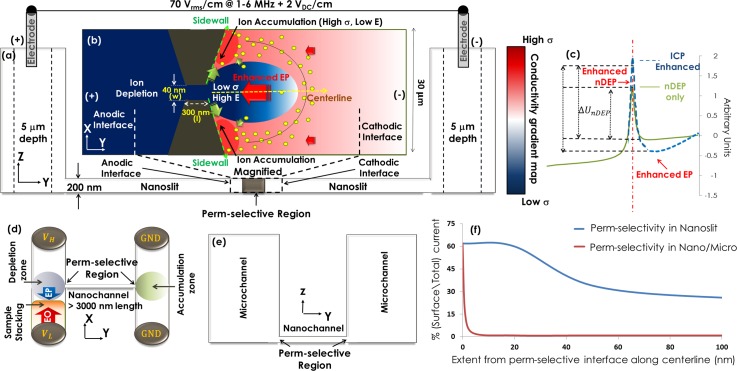
We begin with schematically illustrating the mechanism for generating ion conductivity gradients inside the nanoslit and illustrate its application toward enhancing the electrokinetic enrichment of biomarkers. The device geometry is subsequently optimized using the Poisson–Nernst–Plank (PNP) model to simulate the conductivity gradients and its application toward frequency-selective biomarker enrichment is validated using spatio-temporal profiles of fluorescently labeled streptavidin. Our prior work has implemented this methodology within various sensing paradigms for improving biomarker sensitivity.22,23 A cross-section view of the device geometry used within this work is schematically presented in Figure 1(a) (device images in S1, supplementary material), wherein glassy carbon modified Pt electrodes within the reservoirs leading to a microchannel on each side are used to initiate the discussed electrokinetic effects under a DC-offset (2 V/cm) AC field (70 Vrms/cm) that is set at the critical frequency required to cause optimal biomarker nDEP, which is 1 MHz for streptavidin, 3 MHz for Neuropeptide Y (NPY),22 and 4–6 MHz for Prostate Specific Antigen (PSA).23 The microchannels (5 μm depth) are connected by slit-shaped channels of 200 nm depth (henceforth called nanoslit). Within each nanoslit (300 μm length/200 nm depth), a lateral constriction (optimized at 300 nm length and 40 nm gap) with a sharp surface charge non-uniformity is used to initiate ICP (see magnified top-view in Figure 1(b)), whereas no significant ICP occurs at the micro/nanochannel interface due to the wide nanoslit entry points (30 μm width). The geometry of this constricted perm-selective region is designed so as to enable ion conductivity gradients over a wide extent across its cathodic interface, due to interaction of ion depletion and ion accumulation profiles under field-induced ICP conditions. First, the spatial extent of the constriction is designed to be short (l ∼ 300 nm) to reduce the length over which the voltage drop occurs inside the perm-selective region, thereby enhancing the localized field and extending ion depletion through a significant portion of the nanoslit, beyond the immediate perm-selective region. In this manner, due to enhanced surface conduction of counter-ions and the exclusion of co-ions in the perm-selective region, the ion depletion region extends from across the anodic interface through inside of the perm-selective region, up to portions across the cathodic interface inside the nanoslit, as reported within other similar geometries.27 Second, the sloping constriction geometry enables a sharp drop in the field profile along its sidewall directions versus a more gradual drop along the device centerline. As a result, ion accumulation at its cathodic interface is higher along the constriction sidewall directions and occurs within a short distance of the constriction tip, whereas the accumulation is lower along the device centerline direction and is pushed further away from the constriction tip. Due to current conservation, these ion conductivity gradients at the cathodic interface modify the localized field and nDEP trapping potential profiles. On one hand, the reduction in localized ion conductivity at the constriction tip due to the extension of ion depletion across from the anodic to the cathodic interface (σdepletion) increases the field at the constriction tip E. On the other hand, the sharp rise in localized ion conductivity along the sidewall directions due to the ion accumulation (σacc) creates a localized reduction in the field away from the constriction tip, thereby increasing the field gradient ∇E. In Figure 1(c), we represent these field profile changes in terms of alterations in the nDEP trapping potential profile, from the green solid line (nDEP with no ICP due to low DC field) to the blue dashed line (nDEP with ICP due to a critical DC field). Since nDEP depends on the product of the field and its gradient, its enhancement under these ICP conditions can be represented as a higher potential barrier to indicate the higher field at the constriction tips and a deeper potential well to indicate the steeper field gradient along the constriction sidewall. Hence, biomarker numbers (n) rise with the potential (U) as per the Boltzmann distribution: n = noexp(-U/kBT), thereby causing exponential biomarker enrichment with an increase in U (calculated in S5, supplementary material).
FIG. 1.
(a) Cross-section view of the nanoslit device. (b) Top-view of the lateral constriction used to initiate ICP in the nanoslit (biomarkers shown as green particles). (c) Alteration of electrokinetic trapping potential profile due to ICP enables exponential enhancement in biomarker numbers. The H-shaped ICP device from prior work: (d) top-view (e) cross-section. (f) Comparison of calculated surface to total ion current away from the perm-selective interface for the different geometries.
Furthermore, as a consequence of the extension in ion depletion along the cathodic interface to well beyond the immediate vicinity of the perm-selective region, the local ion conductivity along the centerline direction (σcenterline) remains low over an extended length away from the constriction tip. Hence, due to current conservation, the field enhancement arising from ion depletion at the constriction tips is extended along the centerline direction at the cathodic interface, whereas this field enhancement is abruptly lowered along the sidewall directions, due to ion accumulation within a short distance of the constriction tip. As a result, electrophoresis (EP) dominates along the nanoslit centerline due to field enhancement, whereas the nDEP trapping is enhanced along the sidewall in the vicinity of the constriction tip, thereby routing biomarkers from the off-sidewall directions toward localized nDEP traps at the constriction sidewall. In the absence of ICP effects, such as by using AC fields with a DC field that is not sufficient to create ICP, we would still have biomarker enrichment along the cathodic interface due to the balance of nDEP versus electrophoresis. However, in the presence of a critical DC field to cause ICP, the enhanced EP velocities and nDEP trapping alter the net spatial extent and magnitude of the trapping potential profile to exponentially enhance biomarker enrichment due to its Boltzmann distribution.
B. Comparison with DC electrokinetics at the micro/nanochannel interface
It is noteworthy to compare the current device geometry (Figure 1(a)), which enables the initiation of ICP effects inside the nanoslit channel, with the commonly used H-shaped device geometry (Figures 1(d) and 1(e)), where ion depletion due to ICP at the microchannel interface to nanochannel enhances the local field (by factor α1) for biomarker electrophoresis (FEP) versus electro-osmosis (FEO), as given by the force balance
| (1) |
With increasing media conductivity (σm), the increasing competition of bulk conduction with surface conduction in the nanochannel causes the level of ICP enhancement (α1) to drop, whereas the less thick electrical double-layer (EDL) causes FEO to drop, thereby reducing the net level of biomarker enrichment (Fnet). On the other hand, in the geometry of Figure 1(a), by initiating ICP inside the nanoslit rather than within the interfacing microchannel, we seek to maintain a significant level of ICP even within conductive physiological media, due to the strong influence of the surface charge non-uniformity (ρc) in the nanoslit on enhancing surface conduction over bulk conduction (which enhances FEP and FnDEP by factors of α2 and h, respectively, as per S2, supplementary material). With the H-shaped device geometry, on the other hand, ICP effects in the microchannel are less influenced by the surface charge non-uniformity created by the nanochannel/microchannel interface. This comparison of the influence of α1 (due to ICP at micro/nanochannel interface) versus that of α2 (due to ICP caused by the surface charge non-uniformity in nanoslit) is shown in Figure 1(f), in terms of the calculated surface to total ion current away from the perm-selective interface (details on method in S6, supplementary material). For the device geometry of Fig. 1(a), ICP due to the constriction-induced surface charge non-uniformity in the nanoslit enables an enhancement (due to α2) in surface conduction over an extent of 20 nm from the perm-selective interface, with only a gradual fall off over the next 80 nm to a steady enhanced level through the rest of the nanoslit channel length. In comparison, at the H-shaped device geometry, while the surface conduction effects are strong at the microchannel interface to the nanochannel due to the sharp field profile, this surface conduction drops off sharply within a few nanometers from the perm-selective interface into the microchannel, since the nanochannel surface charge presents a less weak influence on ion conduction within the microchannel. As a result, in order for ICP at the micro/nanochannel interface to maintain a significant degree of ion depletion within conductive physiological media, there is a need for tighter nanochannels and/or higher applied fields to enhance ICP conditions (or α1). These strategies are not practical due to fabrication challenges, disruptions from Joule heating induced electrothermal flow, and voltage drop due to field screening by the electrical-double layer. A second major difference between these two ICP-based electrokinetic biomarker enrichment methods arises from how the ICP is utilized. Within the H-shaped device geometry, while ICP at the sharp microchannel to nanochannel interface creates a region with ion depletion at the anodic interface and ion accumulation at the cathodic interface, these ion depletion and accumulation regions do not interact due to their spatial separation. In fact, a spatial separation of at least 300 μm is required, especially within media of successively higher levels of conductivity, to prevent co-ion leakage from the cathodic to anodic portion of the microchannel/nanochannel interface, since this leakage will reduce the level of depletion along the anodic interface. Due to this spatial separation, only the localized ion depletion at the anodic interface is used to enhance the fields for DC-based electrokinetic enrichment, thereby creating sharp field gradients, with no ability to spatially modulate the field profile. Within our constriction-based nanoslit device geometry, on the other hand, the proximity of the ion depletion and ion accumulation regions cause their interaction, so that both regions act together to modulate the field profiles and create localized traps for enhancing the spatial extent of biomarker trapping. In fact, to maximize the voltage drop across the perm-selective region for enabling higher localized fields, we prefer designs with a short perm-selective spatial extent (usually 300 nm), so that it is just sufficient to maintain ion depletion along the cathodic interface. The third distinguishing feature of our approach is that instead of an opposing electroosmotic force field, we utilize AC fields to initiate frequency-selective nDEP away from the constriction tips, since nDEP continues to be a significant force field even within media of high conductivity. This is apparent considering the force balance at the cathodic interface in Figure 1(a)
| (2) |
Hence, at higher σm, the drop in ICP-induced enhancement (α2 and h) can be arrested by using a sharper surface charge non-uniformity (ρc ∼ 0.08–0.3 C/m2) in the nanoslit, for enabling sufficient surface conduction versus increasing bulk conduction (Figure 1(f)). Furthermore, by using an opposing nDEP force field, a higher level of FnDEP in Eq. (2) is maintained at high σm, due to its dependence on the difference of particle versus medium conductivity: (σp-σm). In this manner, we continue to enhance the net biomarker transport toward the cathodic interface for biomarker enrichment within physiological media, since: (a) ICP effects that usually drop off within conductive media are sufficient within our device geometry, due to the significant role of surface conduction inside the nanoslit arising from the large surface charge non-uniformity of the lateral constriction (ρc), and (b) nDEP effects rise rather than fall within conductive media, thereby maintaining a localized opposing force balance. In the subsequent sections (Sec. II C. & D), we compute the ion conductivity profiles to optimize the device geometry for enhanced biomarker trapping, and experimentally validate these ion conductivity gradients by mapping spatio-temporal biomarker trapping profiles under various applied field magnitude and bulk media conductivity conditions.
C. Optimizing device geometry for enhancing nDEP
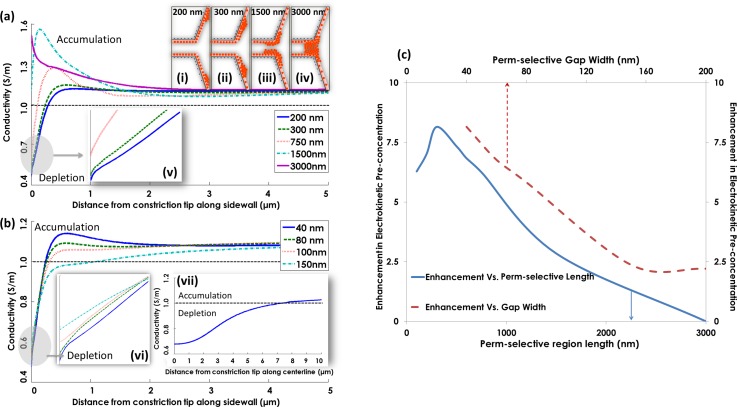
We consider optimization of the geometry of the perm-selective region within the nanoslit for enhancing electrokinetic biomarker enrichment under ICP conditions. Specifically, we compute ICP-induced ion conductivity profiles along the constriction sidewall and centerline directions, for varying lengths (l) and widths (d) of the perm-selective region, thereby enabling an assessment of the ensuing enhancement in nDEP. The angle of lateral constriction in the nanoslit is held constant at 30° to enable the highest possible field gradient (∇E), under the fabrication limitations. Due to the ∇E2 dependence of nDEP, we seek device geometries that promote ion depletion at the constriction tip to enhance the field (E) and initiate ion accumulation along the constriction sidewall to enhance the field gradient (∇E). Since the ion conductivity profiles in Figure 2 are computed in media with bulk conductivity of 1 S/m, the regions with localized conductivity less than 1 S/m exhibit ion depletion and those at greater than 1 S/m exhibit ion accumulation, with the insets (i–iv) indicating the respective region of counter-ion accumulation (solid orange circles). For the case of a perm-selective region with a large length (3000 nm), the surface charge non-uniformity has a greater electrostatic interaction length with counter-ions undergoing surface conduction. This will limit the level of surface conduction of counter-ions out of the perm-selective region, thereby causing counter-ion accumulation inside the perm-selective region, including at the constriction tips. As a result, the degree of ion depletion inside the perm-selective region is reduced, thereby limiting the degree of field enhancement at the constriction tip along the cathodic interface. The computed ion conductivity profile in Figure 2(a) for this case (3000 nm length of perm-selective region) shows no apparent ion depletion, with only a maximum in ion accumulation that occurs right at the constriction tips, as per inset (iv). For successively smaller length extents of the perm-selective region, the higher localized field and lower electrostatic interaction length with counter-ions enhances the net surface conduction. As a result, ion depletion at the constriction tips is enhanced (Figure 2(a), inset v) to cause further increases in the localized field (E). However, the level of ion accumulation along the sidewall direction is seen to gradually decrease with increasing perm-selective extent, thereby lowering the field gradient (∇E), with the peak region for ion accumulation being pushed further away from the constriction tip along the sidewall. This suggests that an optimal length extent of the perm-selective region is needed for maximum electrokinetic enhancement, due to its ∇E2 dependence. Hence, we compute an optimal perm-selective length for surface conduction enhanced nDEP (factor “h” in Eq. (2)), based on the product of the rise in potential energy barrier height due to field enhancement (E) under ion depletion (by factor β) and the deeper potential well due to field gradient (∇E) under ion accumulation (by factor κ), with details in S2 (supplementary material). It is apparent from the plot in Figure 2(c) that a perm-selective region with a length of 300 nm is optimal, since it is capable of causing ∼8-fold enhancement in level of electrokinetic trapping (factor “h” in Eq. (2)) at bulk media conductivity of 1 S/m to cause exponentially higher biomarker numbers (ehU) versus that for nDEP with no ICP (eU). At a smaller length of the perm-selective region (200 nm), while the degree of ion depletion is higher at the constriction tips (increasing E), the ion accumulation is lower and occurs too far away from the constriction tip to cause the necessary rise in ∇E2, for enhancing ICP-induced trapping. On the other hand, with gradual lowering of the constricting perm-selective gap, the enhanced exclusion of co-ions and surface conduction of counter-ions cause a higher level of ion depletion (Figure 2(b), inset vi), as well as ion accumulation.
FIG. 2.
(a) Ion conductivity profile along the constriction sidewall for different perm-selective lengths (gap width: 40 nm) within media of bulk conductivity of 1 S/m. Insets (i)–(iv) show schematic of counter-ion distribution for different perm-selective lengths and (v) shows a magnified view of the depletion for each perm-selective length. (b) Ion conductivity profile along the constriction sidewall for different perm-selective gap widths (length: 300 nm) at medium conductivity of 1 S/m. Inset (vi) shows a magnified view of the depletion at each constriction gap and inset (vii) shows ion conductivity profile along the constriction centerline for perm-selective region with 40 nm width and 300 nm length with media of bulk conductivity of 1 S/m. (c) Calculated electrokinetic enhancement (S2, supplementary material) due to ICP for different perm-selective lengths (solid blue line) and gap sizes (dashed red line).
This explains the monotonic rise in the net electrokinetic enhancement in Figure 2(c), for gaps varying from 160 nm to 40 nm. Finally, we compare the ion conductivity profile along sidewall (Figure 2(b)) versus centerline directions (Figure 2(b), inset vii). For the optimal perm-selective device geometry to enhance electrokinetic enrichment (40 nm constriction gap with a 300 nm length extent), the centerline direction undergoes ion depletion over a wide extent (∼7.5 μm from constriction tip), with more modest levels of ion accumulation thereafter, whereas the ion depletion region along the sidewall direction is localized within 0.5 μm from the constriction tip, followed by strong levels of ion accumulation. This quantitative picture is consistent with the schematic ion conductivity profiles, shown earlier in Figure 1(b) to explain the enrichment mechanism.
D. Dimensionless perm-selectivity factor for AC electrokinetic enhancement
A critical level of perm-selectivity is required to initiate the necessary ion conductivity gradients that arise due to spatially proximal ion depletion and ion accumulation regions, for enhancing the net electrokinetic enrichment. We describe the necessary perm-selective geometry by the following dimensionless analysis. The necessary perm-selectivity (PS) depends on the perm-selective gap length (l), its cross-sectional area (A: product of gap width to nanoslit depth), its surface charge distribution (ρc), the ion mobility (μ), and media conductivity (). We write this in terms of the following dimensionless parameter:
| (3) |
Unlike the case of DC electrokinetics, where maximum levels of perm-selectivity are needed, as achieved through reducing perm-selective gap (to reduce A) or increasing length (L) to exponentially increase PS, our AC electrokinetic mechanism prefers PS values in the range of , as determined by optimal L described in Figure 2(c). For PS values above , ion accumulation and depletion are too far spatially separated, so that accumulation occurs only on the cathodic side and depletion occurs only on the anodic side, as seen within ICP under DC electrokinetics. Such wide spatial separation of the ion accumulation and depletion regions coupled to ion accumulation at the cathodic side where trapping occurs under nDEP reduces the electric field and their gradients, thereby reducing the net nDEP trapping efficiency. On the other hand, at PS values less than ICP effects are not significant, thereby causing no significant enhancement in nDEP trapping due to ICP.
E. Influence of bulk media conductivity
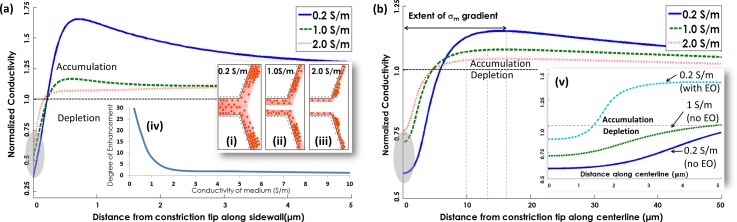
Conductivity of the bulk media (σm) determines the electrical double-layer (EDL) thickness within the perm-selective region (schematically shown within insets ((i)–(iii) in Figure 3(a)), so that the ensuing differences in surface conduction strongly influence the ion conductivity profiles along the cathodic interface of the constriction. At lower bulk media conductivities (σm = 0.2 S/m), the thicker EDL causes enhanced levels of co-ion exclusion and counter-ion surface conduction within the perm-selective region, which in turn enhances the levels of ion depletion and ion accumulation versus those achieved within media of higher conductivities (σm = 1 and 2 S/m). Figure 3 presents this information in terms of the normalized conductivity, i.e., as a ratio of the local conductivity to the bulk conductivity, with ion depletion in regions below unity and ion accumulation in regions above unity. Comparing Figures 3(a) and 3(b), it is clear that the degree of ion accumulation is significantly greater along the sidewall direction versus the centerline, and it peaks at well less than 0.5 μm from the constriction tip. Along the centerline direction, on the other hand, the effects of ion depletion from the perm-selective region continue to be apparent over several microns from the constriction tip, with the peak in ion accumulation occurring much further along, thereby creating a wide region for the localized ion conductivity gradient along the cathodic interface. These results are consistent with the schematic in Figure 1(b), showing ion depletion over a broad elliptical region along the off-sidewall directions and ion accumulation close to the sidewall directions.
FIG. 3.
Normalized ion conductivity profile for different bulk media conductivities (perm-selective length of 300 nm and gap width of 40 nm): (a) along the constriction sidewall, and (b) along the constriction centerline. Insets (i)–(iii) show a schematic of how the electrical double layer affects the counter-ion distribution; inset (iv) shows the net electrokinetic enhancement due to ICP effects within media of different bulk conductivities (neglecting electro-osmosis); and inset (v) shows the alteration of the extent of ion depletion when electro-osmosis effects are considered at σm of 0.2 S/m.
At σm of 1 S/m, there is no ion depletion beyond the constriction tip along the sidewall directions and ion accumulation peaks within 0.4 μm from the constriction tip, whereas along the centerline direction, the ion depletion extends to ∼5 μm from the constriction tip and the localized conductivity gradient due to differential ion accumulation extends to ∼13 μm. As a result, the computed enhancement in potential barrier for trapping due to ion conductivity gradients at σm of 1 S/m continues to be significant in Figure 3(c) (∼8-fold enhancement, with a conservative ρc: 0.08 C/m2), even though the EDL is not thick enough to ensure maximum co-ion exclusion and counter-ion surface conduction within the perm-selective region versus the respective level at σm of 0.2 S/m. However, while electro-osmotic effects on ion migration can be neglected at higher σm (≥1 S/m), since electrophoretic ion mobilities are significantly greater than electro-osmotic mobilities in nanochannels28–30 (see supplementary material, S3), this is not the case at σm of 0.2 S/m, where the two mobilities are comparable.31 The inset (v) of Fig. 3(b) shows the effect of including electro-osmosis at σm of 0.2 S/m, on the localized ion conductivity profiles. While the ion depletion region extends over a significant portion of the device centerline in the absence of disruptions from electro-osmotic flow (∼5 μm and ∼8 μm from constriction tip at 1 S/m and 0.2 S/m, respectively), it is significantly reduced due to disruptions from electro-osmotic flow at σm of 0.2 S/m (down to ∼1.5 μm). We attribute this lowering of ion depletion along the cathodic interface at σm of 0.2 S/m to the reduced co-ion leakage from the cathodic to anodic interface due to greater levels of co-ion exclusion at lower σm and the opposing influence of electro-osmotic flow. Hence, the degree of biomarker enrichment at lower σm is likely to be less optimal due to greater opposing electro-osmotic flow and lower localized nDEP trapping (see Eq. (2)), which suggests a more dispersed biomarker trapping profile with lowering σm, as validated subsequently. Assuming a Boltzmann distribution for biomarkers, the ∼5-fold enhanced potential barrier for electrokinetic trapping under ICP at σm of 1.6 S/m using a conservative estimate for the surface charge non-uniformity (ρc: 0.08 C/m2) in Fig. 3(a-iv) suggests >100× higher levels of preconcentration (ehU) than obtained solely under nDEP (S5, supplementary material) and up to 25-fold reduction in biomarker accumulation times (see S4, supplementary material).
F. Validation using spatio-temporal biomarker profiles
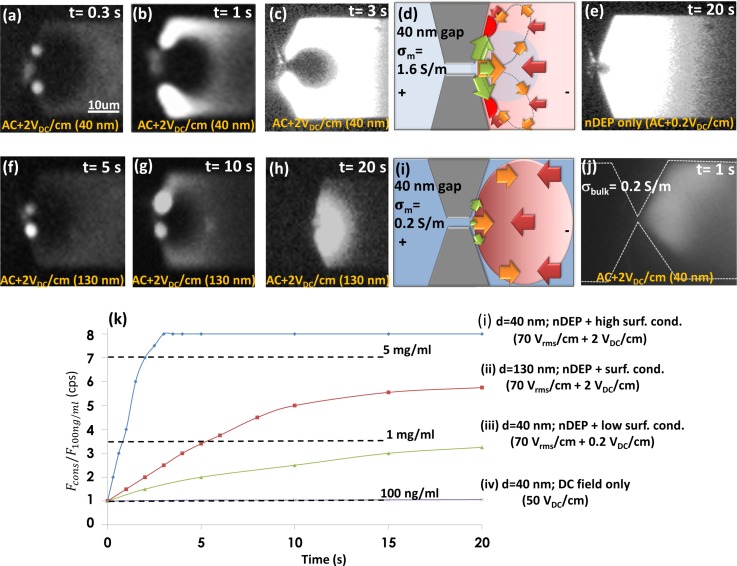
In order to explain how these conductivity gradients along the cathodic interface of the constriction region influence the profile and level of electrokinetic biomarker enrichment, we present spatio-temporal images and temporal plots of enrichment of labeled streptavidin at 1 MHz in Figures 4(a)–4(k), from a starting level of 100 ng/ml. The fluorescence intensity versus time plots for various conditions of nDEP induced electrokinetic trapping are determined by averaging the maximum intensities from 20 pixels along the sidewall direction and normalizing these fluorescence levels to those obtained under purely DC fields, where no perceptible rise in fluorescence is apparent. For comparison, we choose the following: (1) trapping within constriction gaps of varying size: ∼40 nm in Figures 4(a)–4(c) versus ∼130 nm in Figures 4(f)–4(h); (2) trapping under varying degrees of surface conduction for inducing ICP conditions, using a critical DC offset field (2 VDC/cm) to enhance ICP in Figure 4(c) versus a sub-critical DC offset field (0.2 VDC/cm) to obviate ICP conditions in Figure 4(e); and (3) trapping within physiological media, using PBS buffers with σm of 1.6 S/m versus 10-fold diluted PBS buffers with σm of 0.2 S/m (Figure 4(b) versus 4(j), after 1s trapping). For nanoslits with 40 nm constrictions (Figures 4(a)–4(c)), within 0.3 s of field application, a significant level of biomarker preconcentration is apparent along the constriction sidewall within 0.3 μm of the constriction tip and biomarker depletion over a broad elliptical region that extends ∼20 μm along the centerline is also clear. Over time, the biomarker depletion region remains more-or-less unchanged, while biomarker preconcentration gradually extends from the constriction sidewall directions to cover the off-sidewall directions. For the case of nanoslits with 130 nm constrictions, the profiles are somewhat similar (Figures 4(f)–4(h)), with initial preconcentration along constriction sidewalls and a biomarker depletion region along the centerline. However, the preconcentration is considerably slower, as apparent from the longer time intervals,32 and the biomarker depletion region extends no more than ∼3 μm along the centerline. For the case of trapping under nDEP conditions with a sub-critical DC field for initiating ICP, the biomarker enrichment rate is gradual (Figure 4(k)) and the trapping profile shows only a very small biomarker depletion region (∼0.3 μm along centerline in Figure 4(e)).
FIG. 4.
Fluorescence images of streptavidin preconcentration in physiological media (σm ∼ 1.6 S/m) from a starting level of 100 ng/ml, under an electrokinetic force balance due to 70 Vrms/cm (AC) plus 1.5 VDC/cm offset for: (a) t = 0.3 s, (b) t = 1 s, and (c) t = 3 s of enrichment at nanoslits with 40 nm constriction gap widths and (f) t = 5 s, (g) t = 10 s, and (h) t = 20 s of enrichment at nanoslits with 130 nm constriction gap widths. (d) Preconcentration under predominantly nDEP conditions (no ICP enhancement) after 20 s of enrichment; and (j) preconcentration under conditions similar to (a)–(c), but in media of 10-fold lower conductivity (σm ∼ 0.2 S/m). A schematic explanation of the biomarker preconcentration profile under the force balance of electrophoresis (red) vs. nDEP (Green) and enhanced second order electroosmosis (orange) is shown for: (d) physiological media, and (i) 10-fold diluted media. (k) Fluorescence intensity versus time averaged for 20 pixels along the constriction sidewall with highest intensity and normalized to fluorescence under purely DC fields.
Within 10-fold diluted PBS media (σm ∼ 0.2 S/m), the trapping is dispersed, with no biomarker depletion region, even with a critical DC field for initiating ICP alongside nDEP. These enrichment profiles under various field, media conductivity, and device geometries validate the role of σm gradients generated under ICP conditions along the cathodic interface of the constriction region inside the nanoslit (as described in Figures 2 and 3). As per the schematic in Figure 4(d) depicting biomarker and ion transport in nanoslits with constrictions of 40 nm gap, the high field due to ion depletion near the constriction tip and the high field gradient due to ion accumulation along the constriction sidewall cause a localized nDEP trap (green arrows) within ∼0.3 μm from the constriction tip along the sidewall, which correlates with region of maximum biomarker in Figures 4(a)–4(c). On the other hand, the high field along the device centerline arising from extension of ion depletion onward from the constriction tip drives biomarkers by electrophoresis (red arrows) away from the centerline toward the nDEP trapping region along the sidewall, correlating to the broad biomarker depletion region away from the off-sidewall directions up toward the device centerline. The localized σm gradients due to ICP at bulk σm of 1.6 S/m (Figure 3(a-iv)) that cause at least 5-fold enhancement in potential barrier for trapping (assuming a conservative ρc: 0.08 C/m2) suggest >100× higher levels of enrichment than obtained solely under nDEP (see S5, supplementary material). As per the fluorescence levels in Figure 4(k), this causes localized enhancement of >5000× in streptavidin concentration. In fact, our prior work quantified this at 104–105-fold concentration enhancement in the preconcentration region19 and ∼103-fold enhancement in analyte binding at capture probe surface.22,23 This is apparent from the sharp rise in fluorescence signal to saturation levels in Figure 4(k), within just 3 s (curve (i)). For the nanoslit with a constriction of 130 nm gap (Figures 4(f)–4(h)), the biomarker enrichment profile is quite similar to that for the equivalent device at 40 nm, but the lower level of nDEP trapping, as well as the ICP enhancement of electrokinetic trapping due to lower ion depletion levels, cause a less sharp rise in fluorescence signal versus time (Figure 4(k), curve (ii)) and smaller region of biomarker depletion. It is noteworthy that ICP-enhanced nDEP trapping with a 130 nm constriction gap is greater than that obtained under nDEP trapping conditions at a 40 nm constriction gap, with no significant ICP enhancement (Figure 4(k), curve (ii) vs. (iii)). This suggests that nDEP trapping within nanoslits containing larger constriction gaps (∼130 nm) can be enhanced over that obtained utilizing smaller constriction gaps (∼40 nm), by sufficiently increasing DC offset field to enhance surface conduction for inducing ICP. Within media of lower bulk conductivity (10-fold diluted PBS media at σm ∼ 0.2 S/m), the highly dispersed biomarker enrichment along the entire cathodic interface (Figure 4(j)) is explained by the schematic in Figure 4(i). Herein, the force balance is dominated solely by biomarker electrophoresis (red) versus electro-osmosis in the nanoslit (orange), with a minimal role for nDEP trapping (green), thereby explaining the absence of the biomarker depletion region along the centerline and the highly focused biomarker trapping region along the sidewall directions that are seen within phosphate-buffered saline (PBS) media.
III. METHODS
A. Theoretical formulation
Ion conductivity profiles were computed for perm-selective geometries within the nanoslit, assuming constant surface charge non-uniformity (ρc) through applying Neumann flux/source boundary condition as shown in Equation (5). We use a conservative estimate of: ρc,33 which is well lower than possible higher end estimates (ρc ).34 At equilibrium the electric potential, , distribution is governed by the Poisson equation35
| (4) |
To solve the Poisson equation, Dirichlet boundary condition was applied to inlet/outlet walls in reservoirs, where electrodes are inserted, to simulate the voltage source. All other boundaries are set to zero flux. In solution, is the number of ionic species, where and are the number density and valence of i-th ionic species, respectively. represent permittivity of vacuum and relative permittivity of the medium, respectively. Using a continuum treatment of the problem, in the absence of chemical reactions, the flux of each of these ionic species is described by Nernst–Planck equation, which represents the balance between convection, diffusion, and ionic drift due to presence electric field.33,36
| (5) |
With , are the diffusion coefficients of ion species, is the Boltzmann constant, is the temperature, is the molar concentration of species at each point of the device, and u is the fluid velocity vector. To solve this equation, all boundaries except inlet and outlet walls were assigned zero flux boundaries for both ionic species. Dirichlet boundary condition equal to bulk concentration is assigned to both inlet/outlet for both ionic species. In steady state, continuity equation requires. A closer examination of Equations (3) and (4) reveals their interdependence, thereby requiring them to be solved simultaneously. Together they are known as Poisson–Nernst–Plank (PNP) equations, which should be solved numerically, since analytical solutions are not available for their nonlinear form.33 Using standard boundary conditions for continuity of and of their first derivatives, we used COMSOL Multiphysics to solve these equations over 2D space to find the concentration distribution of ionic species at any point in the device. The only exceptions are at the constriction tip and within the walls of the perm-selective region, wherein the electrical boundary condition is set to account for the surface charge density (ρc)
| (6) |
Assuming incompressibility of the fluid, , Navier–Stockes equation, which governs the fluid momentum completes these set of equations
| (7) |
In this equation is the water density, is the pressure, is the water dynamic viscosity, and is the body force. In the nanoslit design, due to the high surface to volume ratio, we can neglect dielectric forces,37 and electric body force can be defined as follows, with , as the free charge density
| (8) |
To solve for fluid flow, the no-slip Dirichlet boundary condition was applied to walls of the microchannel, constriction, and perm-selective regions. Along these boundaries, a layered quadrilateral mesh with dense element distribution in the normal direction was used to resolve the thin boundary layers along the no-slip boundaries. However, for simulations in media of bulk conductivity of ≥1 S/m, the double layer thickness is within 1% of nano slit depth. Hence, in order to significantly lower computational requirements in our set of simulations within the microchannel region, which is very far from perm-selective zone, Dirichlet electroosmotic velocity boundary condition can be applied to the boundaries (walls) through choosing proper electroosmotic mobility for each bulk conductivity value.
After solving Equations (4), (5), and (7), the current through any particular cross-sectional area of the channel can be calculated38
| (9) |
Here, is the electrolyte electrical conductivity, s the electrical mobility, is the molar concentration, is the electrical potential distribution due to the external applied voltage, and finally F is the Faraday's constant. At steady state, non-uniform distribution of electric field, E, will cause the particles in the medium to experience dielectrophoretic force (FDEP). The average FDEP on a homogeneous spherical particle with electrical permittivity , conductivity , and radius, , suspended in a fluid with electrical permittivity and conductivity , is given by the following:
| (10) |
KCM is the Clausius–Mossotti factor, which depends on the frequency () of the applied field as given by: . Due to the DC offset of the applied voltage, particles in the medium will also experience electrophoresis (), which can be calculated from the following equation:
| (11) |
Here, is electrophoretic mobility, and is the friction coefficient for a spherical particle with radius a in a medium with viscosity of . Biomarker trapping occurs under electrokinetic force balance of and , under a zero net force on the particle,
| (12) |
denote the respective levels of local ICP-induced enhancement as a function of position and medium conductivity. Since all steady-state electrical forces are conservative vector fields, we can calculate scalar potential energy fields to describe the net electrokinetic force balance in terms of barriers and wells that affect particle trapping within the device. The potential field is given by the integral over the volume (dV) of the net electrokinetic force20
| (13) |
This integral in the presence of AC and DC fields is
| (14) |
is the offset voltage to enable electrophoresis (EP).
B. Experimental methods
Details of experimental device geometry and operation are available in prior work20,39,40 and in supplementary material S1. Alexa 488 labeled Streptavidin (∼60 kDa) was procured from Molecular Probes (Eugene, OR).
IV. CONCLUSIONS
A methodology for utilizing surface conduction versus bulk conduction effects in nanoslits to sharply enhance the spatial extent of negative dielectrophoresis is described to initiate ultrafast enrichment of biomarkers within physiological media. Using AC fields to generate negative dielectrophoresis and an offset DC field to initiate ion concentration polarization at surface charge non-uniformities in the nanoslit, the localized field intensity is enhanced due to ion depletion and the field gradient is enhanced due to proximal ion accumulation, thereby enhancing ∇E2 to enable biomarker enrichment in physiological media. The optimal device geometry for creating the charge non-uniformity inside the nanoslit is a sharp lateral constriction with a gap of ∼40 nm and a length of ∼300 nm, to enable an extension of the ion depletion region from the anodic interface up to the cathodic interface. As a result, ultrafast electrokinetic enrichment of biomarkers occurs within physiological media due to the highly focused trapping profile, whereas the trapping profiles are more dispersed within media of lower bulk conductivity, due to the lowered biomarker nDEP alongside the enhanced level of disruptions from electro-osmotic flow. Using a conservative estimate for the surface charge non-uniformity (ρc ), the ICP-induced enhancement in the potential barrier for electrokinetic trapping within physiological media (σm = 1.6 S/m) is ∼5-fold higher than in the absence of ICP. Using a Boltzmann distribution for biomarkers, this suggests >100× higher levels of enrichment than obtained solely under nDEP, as validated by experimental observations. Since this AC electrokinetic-based methodology causes ultrafast biomarker enrichment in conductive physiological media, wherein DC electrokinetic enrichment is limited, we envision its application for biomarker discovery, protein crystallization, and in biosensing for speeding assay kinetics and reducing assay interferences.
V. SUPPLEMENTARY MATERIAL
See supplementary material for a description of experimental device geometry (S1), methodology for calculating ICP-induced electrokinetic enhancement (S2), the influence of electro-osmotic disruptions on electrophoretic ion mobility at lower media conductivity (S3), influence of trapping potential enhancement on preconcentration (S5) and on reducing trapping time (S4), calculation of surface to total ion current in nanoslit (S6), and total nDEP enhancement in nanoslit at different medium conductivities (S7).
ACKNOWLEDGMENTS
We acknowledge support from U.S. Air Force FA2386-14-1-4070 and FA2386-15-1-4105, AS Nano Program and Core Facility, and Integrated Thematic Project (AS-103-TP-A01), Ministry of Science and Technology, Taiwan (103-2923-M-001-007-MY3 and 104-2119-M-001-011), and the NSF EAPSI Program.
References
- 1. Daniels J. S. and Pourmand N., Electroanalysis 19(12), 1239–1257 (2007). 10.1002/elan.200603855 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Polaskova V., Kapur A., Khan A., Molloy M. P., and Baker M. S., Electrophoresis 31(3), 471–482 (2010). 10.1002/elps.200900286 [DOI] [PubMed] [Google Scholar]
- 3. Kim S. J., Song Y. A., and Han J., Chem. Soc. Rev. 39(3), 912–922 (2010). 10.1039/b822556g [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Wang Y. C., Stevens A. L., and Han J. Y., Anal. Chem. 77(14), 4293–4299 (2005). 10.1021/ac050321z [DOI] [PubMed] [Google Scholar]
- 5. Castellanos A., Ramos A., Gonzalez A., Green N. G., and Morgan H., J. Phys. D: Appl. Phys. 36(20), 2584–2597 (2003). 10.1088/0022-3727/36/20/023 [DOI] [Google Scholar]
- 6. Srivastava S. K., Gencoglu A., and Minerick A. R., Anal. Bioanal. Chem. 399(1), 301–321 (2011). 10.1007/s00216-010-4222-6 [DOI] [PubMed] [Google Scholar]
- 7. Cong Y. Z., Katipamula S., Geng T., Prost S. A., Tang K. Q., and Kelly R. T., Electrophoresis 37(3), 455–462 (2016). 10.1002/elps.201500286 [DOI] [PubMed] [Google Scholar]
- 8. Hsu W. L., Harvie D. J. E., Davidson M. R., Jeong H., Goldys E. M., and Inglis D. W., Lab Chip 14(18), 3539–3549 (2014). 10.1039/C4LC00504J [DOI] [PubMed] [Google Scholar]
- 9. Inglis D. W., Goldys E. M., and Calander N. P., Angew. Chem., Int. Ed. 50(33), 7546–7550 (2011). 10.1002/anie.201100236 [DOI] [PubMed] [Google Scholar]
- 10. Pohl H. A., Appl. Phys. 22(7), 869–871 (1951). 10.1063/1.1700065 [DOI] [Google Scholar]
- 11. Jones T. B., Electromechanics of particles ( Cambridge University Press, Cambridge, New York, 1995). [Google Scholar]
- 12. Pethig R., Biomicrofluidics 4(2), 022811 (2010) 10.1063/1.3456626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Morgan H. and Green N. G., AC electrokinetics: Colloids and Nanoparticles ( Research Studies Press, Institute of Physics Pub., Distribution, North America, AIDC, Baldock, Hertfordshire, England, Philadelphia, PA, Williston, VT, 2003). [Google Scholar]
- 14. Gagnon Z. R., Electrophoresis 32(18), 2466–2487 (2011). 10.1002/elps.201100060 [DOI] [PubMed] [Google Scholar]
- 15. Chaurey V., Polanco C., Chou C. F., and Swami N. S., Biomicrofluidics 6(1), 012806 (2012) 10.1063/1.3676069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Swami N., Chou C. F., Ramamurthy V., and Chaurey V., Lab Chip 9(22), 3212–3220 (2009). 10.1039/b910598k [DOI] [PubMed] [Google Scholar]
- 17. Swami N. S., Chou C. F., and Terberueggen R., Langmuir 21(5), 1937–1941 (2005). 10.1021/la0493767 [DOI] [PubMed] [Google Scholar]
- 18. Lapizco-Encinas B. H., Ozuna-Chacon S., and Rito-Palomares M., J. Chromatogr. A 1206(1), 45–51 (2008). 10.1016/j.chroma.2008.05.077 [DOI] [PubMed] [Google Scholar]
- 19. Nakano A., Camacho-Alanis F., and Ros A., Analyst 140(3), 860–868 (2015). 10.1039/C4AN01503G [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Liao K. T., Tsegaye M., Chaurey V., Chou C. F., and Swami N. S., Electrophoresis 33(13), 1958–1966 (2012). 10.1002/elps.201100707 [DOI] [PubMed] [Google Scholar]
- 21. Liao K. T. and Chou C. F., J. Am. Chem. Soc. 134(21), 8742–8745 (2012). 10.1021/ja3016523 [DOI] [PubMed] [Google Scholar]
- 22. Sanghavi B. J., Varhue W., Chavez J. L., Chou C. F., and Swami N. S., Anal. Chem. 86(9), 4120–4125 (2014). 10.1021/ac500155g [DOI] [PubMed] [Google Scholar]
- 23. Sanghavi B. J., Varhue W., Rohani A., Liao K. T., Bazydlo L. A. L., Chou C. F., and Swami N. S., Lab Chip 15(24), 4563–4570 (2015). 10.1039/C5LC00840A [DOI] [PubMed] [Google Scholar]
- 24. Anand R. K., Johnson E. S., and Chiu D. T., J. Am. Chem. Soc. 137(2), 776–783 (2015). 10.1021/ja5102689 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Sanghavi B. J., Moore J. A., Chavez J. L., Hagen J. A., Kelley-Loughnane N., Chou C. F., and Swami N. S., Biosens. Bioelectron. 78, 244–252 (2016). 10.1016/j.bios.2015.11.044 [DOI] [PubMed] [Google Scholar]
- 26. Sanghavi B. J., Wolfbeis O. S., Hirsch T., and Swami N. S., Microchim. Acta 182(1–2), 1–41 (2015). 10.1007/s00604-014-1308-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Schiffbauer J., Park S., and Yossifon G., Phys. Rev. Lett. 110(20), 204504 (2013). 10.1103/PhysRevLett.110.204504 [DOI] [PubMed] [Google Scholar]
- 28. Haywood D. G., Harms Z. D., and Jacobson S. C., Anal. Chem. 86(22), 11174–11180 (2014). 10.1021/ac502596m [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Bahga S. S., Bercovici M., and Santiago J. G., Electrophoresis 31(5), 910–919 (2010). 10.1002/elps.200900560 [DOI] [PubMed] [Google Scholar]
- 30. Wu J., Gerstandt K., Zhang H. B., Liu J., and Hinds B. J., Nat. Nanotechnol. 7(2), 133–139 (2012). 10.1038/nnano.2011.240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Thormann W., Zhang C. X., Caslavska J., Gebauer P., and Mosher R. A., Anal. Chem. 70(3), 549–562 (1998). 10.1021/ac970513x [DOI] [PubMed] [Google Scholar]
- 32. Rohani A., Varhue W., Su Y. H., and Swami N. S., Biomicrofluidics 8(5), 052009 (2014). 10.1063/1.4897283 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Vlassiouk I., Smirnov S., and Siwy Z., Nano Lett. 8(7), 1978–1985 (2008). 10.1021/nl800949k [DOI] [PubMed] [Google Scholar]
- 34. Schoch R. B., Han J. Y., and Renaud P., Rev. Mod. Phys. 80(3), 839–883 (2008). 10.1103/RevModPhys.80.839 [DOI] [Google Scholar]
- 35. Daiguji H., Yang P. D., and Majumdar A., Nano Lett. 4(1), 137–142 (2004). 10.1021/nl0348185 [DOI] [Google Scholar]
- 36. Kirby B. J., Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices ( Cambridge University Press, New York, 2010). [Google Scholar]
- 37. Chaurey V., Rohani A., Su Y. H., Liao K. T., Chou C. F., and Swami N. S., Electrophoresis 34(7), 1097–1104 (2013). 10.1002/elps.201200456 [DOI] [PubMed] [Google Scholar]
- 38. Chein R. Y. and Chung B. G., J. Appl. Electrochem. 43(12), 1197–1206 (2013). 10.1007/s10800-013-0607-5 [DOI] [Google Scholar]
- 39. Su Y. H., Tsegaye M., Varhue W., Liao K. T., Abebe L. S., Smith J. A., Guerrant R. L., and Swami N. S., Analyst 139(1), 66–73 (2014). 10.1039/C3AN01810E [DOI] [PubMed] [Google Scholar]
- 40. Farmehini V., Rohani A., Su Y.-H., and Swami N., Lab Chip 14(21), 4183–4187 (2014). 10.1039/C4LC00801D [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary material for a description of experimental device geometry (S1), methodology for calculating ICP-induced electrokinetic enhancement (S2), the influence of electro-osmotic disruptions on electrophoretic ion mobility at lower media conductivity (S3), influence of trapping potential enhancement on preconcentration (S5) and on reducing trapping time (S4), calculation of surface to total ion current in nanoslit (S6), and total nDEP enhancement in nanoslit at different medium conductivities (S7).