Abstract
Structure dictates the function of many RNAs, but secondary RNA structure analysis is either labor intensive and costly or relies on computational predictions that are often inaccurate. These limitations are alleviated by integration of structure probing data into prediction algorithms. However, existing algorithms are optimized for a specific type of probing data. Recently, new chemistries combined with advances in sequencing have facilitated structure probing at unprecedented scale and sensitivity. These novel technologies and anticipated wealth of data highlight a need for algorithms that readily accommodate more complex and diverse input sources. We implemented and investigated a recently outlined probabilistic framework for RNA secondary structure prediction and extended it to accommodate further refinement of structural information. This framework utilizes direct likelihood-based calculations of pseudo-energy terms per considered structural context and can readily accommodate diverse data types and complex data dependencies. We use real data in conjunction with simulations to evaluate performances of several implementations and to show that proper integration of structural contexts can lead to improvements. Our tests also reveal discrepancies between real data and simulations, which we show can be alleviated by refined modeling. We then propose statistical preprocessing approaches to standardize data interpretation and integration into such a generic framework. We further systematically quantify the information content of data subsets, demonstrating that high reactivities are major drivers of SHAPE-directed predictions and that better understanding of less informative reactivities is key to further improvements. Finally, we provide evidence for the adaptive capability of our framework using mock probe simulations.
Keywords: RNA secondary structure, minimum free energy, probabilistic models, data-directed, statistical inference
INTRODUCTION
RNA plays a central role in various cellular functions, such as protein synthesis and gene regulation (Sharp 2009; Mortimer et al. 2014). It is widely accepted that the structure of an RNA is essential to its functionality, underlining the importance of deciphering structure. Experimental methods for secondary RNA structure analysis at high resolution, such as crystallography and nuclear magnetic resonance, have had much success, but are also labor intensive and costly. A computational high-precision approach that has been successfully applied is comparative sequence analysis, which infers a common structure among multiple homologous RNA sequences (Pace et al. 1999; Gutell et al. 2002). While this approach is highly accurate, it requires considerable manual labor to construct a model based on multiple sequence alignment. Alternative computational methods attempt to predict secondary structure from a single sequence in an automated fashion (Ding and Lawrence 2003; Markham and Zuker 2008; Lu et al. 2009; Reuter and Mathews 2010; Lorenz et al. 2011). The most widely used one seeks the structure with minimum free energy (MFE) based on a set of nearest-neighbor thermodynamic model (NNTM) parameters. While these methods are popular, they often result in low accuracy when utilizing sequence information alone (Low and Weeks 2010).
Structure probing experiments, such as SHAPE (selective 2′-hydroxyl acylation analyzed by primer extension), have emerged as powerful techniques for characterizing RNA structure (Ehresmann et al. 1987; Tullius and Greenbaum 2005; Wilkinson et al. 2006; Regulski and Breaker 2008). In these experiments, chemicals or enzymes modify RNA nucleotides in a structure-dependent manner (Weeks 2010). Modification events are detected during reverse transcription of the RNA and quantified by sequencing. Recently, advances in chemistry and sequencing have spurred the development of new probing techniques and massively parallel approaches to probing RNA structures on a transcriptome-wide scale and in living cells (Kertesz et al. 2010; Underwood et al. 2010; Lucks et al. 2011; Spitale et al. 2013; Ding et al. 2014; Hector et al. 2014; Kielpinski and Vinther 2014; Rouskin et al. 2014; Siegfried et al. 2014; Talkish et al. 2014; Cheng et al. 2015; Poulsen et al. 2015). Despite shared principles (NP Shih, K Choudhary, M Ledda, and S Aviran, in prep.), these techniques differ in the types of structural information they extract and in the statistical properties of the data they generate.
Propelled by these experimental advances, prediction algorithms that incorporate probing data as soft constraints to direct predictions have recently emerged (Deigan et al. 2009; Cordero et al. 2012; Sükösd et al. 2012; Washietl et al. 2012; Zarringhalam et al. 2012; Hajdin et al. 2013; Ouyang et al. 2013; Luntzer et al. 2015; Wu et al. 2015). While structure-probing data do not directly report pairing states of nucleotides (Sloma and Mathews 2015), they proved useful in improving the accuracy of MFE predictions (Deigan et al. 2009; Hajdin et al. 2013; Luntzer et al. 2015). In a pioneering work, Mathews, Weeks, and colleagues proposed to incorporate SHAPE data in the form of pseudo-energy terms derived from a linear–log formula (Deigan et al. 2009). Although this scheme works remarkably well with SHAPE data, it relies on a predefined relationship (i.e., linear–log) between a nucleotide's reactivity and its pairing likelihood. Moreover, it requires a grid-based optimization routine that essentially calibrates this relationship to fit the data. This may pose challenges in accommodating other types of probing data and in accounting for complex scenarios, thus warranting a more generic approach. This need is further substantiated by the plethora of novel and upcoming probing techniques and their anticipated utilization by a broad research community.
Recently, Eddy developed a probabilistic model and adjoined statistical inference framework as an alternative data-directed prediction approach (Eddy 2014). This probabilistic perspective also provided insights into likelihood-based calculation of pseudo-energy terms with respect to single-nucleotide structural states. These states can be as simple as paired versus unpaired, as pointed out by Eddy. As this framework derives pseudo-energy terms explicitly from a statistical model of the probing data, it is readily adaptable to a variety of probes and can also directly account for complex dependencies in structural information.
In this study, we implemented Eddy's framework and extended it to accommodate a further refinement of structural information. In particular, we implemented it at two structural contexts resolutions. A first and low resolution identifies paired and unpaired bases and a second, higher resolution further classifies paired bases as either helix-ends or stacked, resulting in three contexts. To the best of our knowledge, this is the first scheme that accounts for these three contexts in an explicit manner such that it affords full flexibility in modeling helix-end bases, independent of how the other two contexts are modeled. Our implementation of this approach at two single-nucleotide resolutions reveals its capability to readily account for different structural contexts and to ultimately improve prediction. To complement performance evaluations over existing SHAPE data and to account for their probabilistic nature, we also carried out analyses of model-based simulated data sets. Our analyses demonstrated that proper integration of more detailed structural contexts could lead to improved structure predictions. These analyses further revealed discrepancies, which we were able to partially reconcile by more detailed data modeling. Additionally, we made use of simulations to explore the robustness of all considered schemes to noisy inputs, and we found them all to be comparably and remarkably robust. To broaden the applicability of Eddy's framework, we proposed novel statistical preprocessing methods to standardize data translation into prediction algorithms.
To gain a better understanding of how SHAPE data direct structure prediction, we systematically divided our data into subsets and then evaluated their information content. We found that high reactivities are the main force driving structure prediction while a refinement of moderate reactivities is key to further performance improvements. To the best of our knowledge, this is the first time that SHAPE information content is systematically quantified. Notably, our approach to information content quantification generalizes to virtually all probing data. Finally, to provide concrete evidence of our framework's adaptive capabilities, we describe a thought experiment in which we evaluated the scheme's performances on data simulated from two mock probes.
RESULTS
Implementation of RNAprob
The probabilistic framework proposed by Eddy (referred to as RNAprob) was implemented within RNAstructure (Reuter and Mathews 2010) at two structural context resolutions. At low resolution, paired and unpaired bases are identified. At a higher resolution, paired bases are further classified as either helix-ends or stacked, resulting in three contexts. We refer to these as RNAprob-2 and RNAprob-3, respectively.
It is straightforward to implement RNAprob-2. Apart from a different pseudo-energy calculation, it diverges from the widely used approach proposed by Mathews and Weeks (referred to as RNAlin) (Deigan et al. 2009) in how these terms are fused with NNTM energy calculations: (i) ΔG′|unpaired is applied to each unpaired base; and (ii) ΔG′|paired is applied when i and j pair, as opposed to each time they form a stack in RNAlin (see Materials and Methods).
Implementation of RNAprob-3 is more challenging. The difficulty here lies in the fact that when i–j forms a stack with (i + 1)−(j − 1), we do not yet know how i–j will be extended in the context of a longer sequence. We therefore cannot determine its structural context (i.e., helix-end or stacked) and the appropriate pseudo-energy term. However, when i and j form a pair, we can set it as helix-end and later check if it is stacked. The basic idea is to verify and track the state of the nearest neighbors as a means of identifying potential stacked pairs. When necessary, the pseudo-energy term is retroactively adjusted accordingly (see Supplemental Material). This idea is an extension of that proposed by Mathews et al. (2004) to implement the first scheme that integrated chemical modification information into the dynamic programming paradigm.
Performances on real data and simulations
To evaluate performances of schemes, we assembled a set of 23 sequences with published reference structures and SHAPE profiles, summarized in Supplemental Table S1 (Deigan et al. 2009; Hajdin et al. 2013; Lavender et al. 2015). It features a wide range of sequence lengths (34–2904 nt) and diverse RNA types (rRNAs, riboswitches, viruses, and other functional RNAs).
Figure 1 compares RNAlin and RNAprob average performances on our data set (see leftmost bar in each group), distinguishing between four variants of RNAprob (see Materials and Methods) and featuring a no-SHAPE control (see Supplemental Table S2 for sequence-level summary). While RNAlin seemed to achieve higher performance on average compared to RNAprob, this difference was not statistically significant, indicating comparable average performances on real data (all P > 0.05 in pairwise paired t-tests); see Supplemental Material. Moreover, when examining performances at individual RNA resolution, neither approach consistently outperforms the other (Supplemental Table S2). Note that throughout this manuscript, we focus on average performances. This is because of the stochastic nature of the data, models, and methods we consider. In such cases, we believe that an average behavior of a system over a large and diverse data set provides a more comprehensive and robust assessment of its performance, as compared to detailed examination of individual, often short, sequences.
FIGURE 1.
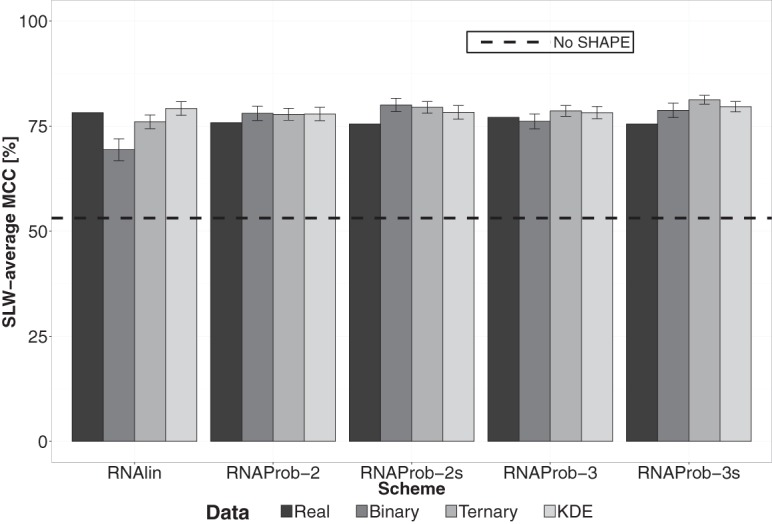
Performances on real data and simulations. “Real,” “Binary,” “Ternary,” and “KDE” represent SLW-average MCC for real data, simulated data generated using binary, ternary, and Gaussian kernel estimate models, respectively. Error bars represent standard deviations and the dashed line indicates SLW-average MCC for the no-SHAPE control.
To assess confidence in our performance evaluations in the absence of replicate data, we resorted to simulating replicates for each RNA using a previous model and methodology (Sükösd et al. 2013). Briefly speaking, we randomly sampled reactivities from modeled probability densities associated with structural contexts. Contexts were defined as either paired/unpaired (binary model) or helix-end/stacked/unpaired (ternary model) (see Fig. 2, top panel, red curves). This approach is thus only applicable when reference structures are available. For each RNA and each model, we generated 100 SHAPE profiles from which averages performances and error estimates were obtained.
FIGURE 2.
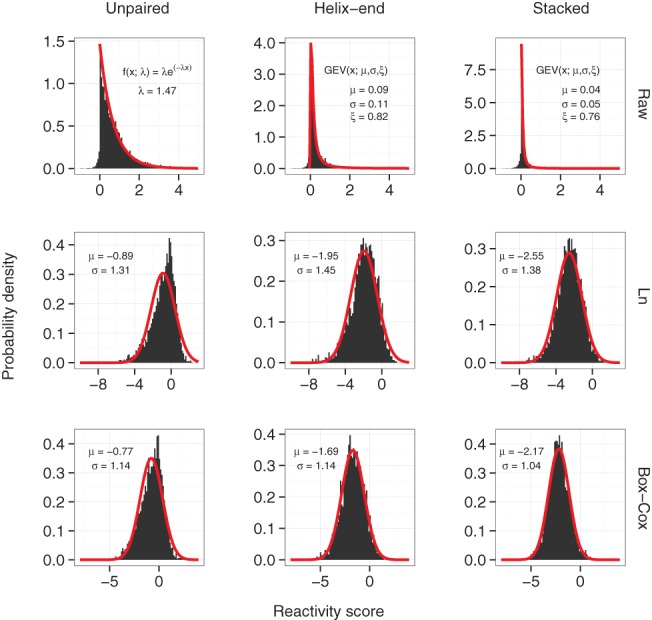
Reactivity distributions for unpaired, helix-end, and stacked bases. (Top) Untransformed, (middle) log-transformed, and (bottom) Box-Cox transformed data. Red lines correspond to fitted models. GEV represents the probability density function of the generalized extreme value distribution. Normal distributions N (μ, σ) were fitted for both logarithm (Ln) and Box-Cox transformed data. The parameters for the exponential decay and GEV distributions were derived from Sükösd et al. (2013).
Figure 1 reveals significant performance differences between schemes on simulated data. All four RNAprob variants consistently outperform RNAlin with both binary- and ternary-model simulated data (P < 0.05 in pairwise two-sample t-tests). These results differ from those obtained with real data. Furthermore, for each scheme, we found significant differences between performances on real data and simulations (P < 0.05, pairwise one-sample t-test). This was further confirmed by similar t-tests at the single RNA level (>18 RNAs for each scheme with P-values below 0.05). Taken together, these results highlight a “gap” between real data and simulations and warrant further modeling efforts to improve the power of this approach.
The observed gap could be attributed to fundamental differences between model and real data. In essence, the above model relies on the assumption that reactivity distributions follow known density functions, which might not capture all subtleties present in real data. We therefore resorted to simulating reactivities by randomly sampling from a Gaussian kernel density estimation (KDE) fit. KDE-based fitting allows for more realistic modeling by providing more flexibility to capture local variations in distributions (see Supplemental Material). Our results show that for KDE-based simulations, performances are closer to those with real data when compared to previous models implying a reduction in the gap (Fig. 1). Specifically, for RNAlin, RNAprob-2, and RNAprob-3, differences are insignificant when comparing SLW-average MCCs between real data and simulations (P > 0.05, one-sample t-tests). Yet, the gap is still present at the single RNA level (>18 RNAs for each scheme with P-values below 0.05).
RNAprob-2 and RNAprob-3 integrate different resolutions of statistical data characterization when determining base-pairing states from reactivities. Going the other direction, simulated data can also be generated using such different characterizations, with the binary model leading to less faithful realization of the data. From the perspective of information transmission and retrieval, a model used to generate data can be viewed as an “encoder,” while a scheme used to interpret them would be a “decoder.” Therefore, understanding the encoder-decoder relationship becomes necessary to compare performances of RNAprob variants across different simulation models. Figure 1 shows that RNAprob-2 outperforms RNAprob-3 with data generated using the binary model and the opposite with data generated using the ternary model. Furthermore, we observed the same trend with KDE-simulated data, where performances improved upon the replacement of the RNAProb-3s decoder with a KDE-based variant, and inversely when ternary-model simulations were used with a KDE-based decoder (Supplemental Fig. S6). These results suggest that matching a decoder to an encoder has the potential to enhance performance, in alignment with the fundamentals of information theory and communications systems design (Proakis and Salehi 2007; Cover and Thomas 2012). Taking this notion a step further, if we generated improved models of the data and concurrently integrated them into model-based decoding schemes such as RNAprob, then this has the potential to lead to better predictions.
Recently, McGinnis et al. (2015) showed that free 30S ribosome subunits are in the inactive state. In particular, the functionally important h28–h44 region contains an alternative structure inconsistent with the conventional reference. Here, we are interested in exploring whether RNAprob correctly predicts structure in this region. We found that the alternative substructure was correctly predicted within the MFE structures reported by RNAprob-2 and RNAprob-2s. In contrast, RNAprob-3, RNAprob-3s, and RNAlin identified it within the third, fifth, and sixth reported (suboptimal) structures, with energy differences of 1.5, 1.4, and 4.5 from the corresponding MFE structure, respectively. Despite this positive outcome, we stress that ranking of predicted structures is very sensitive to subtle changes in the ensemble and the NNTM model. Therefore, we do not know how generalizable this result is.
Characterizing SHAPE information content
Inclusion of SHAPE reactivities can dramatically improve structure prediction, but their relative contribution remains unclear. This raises the question: Are all reactivities equally important to structure prediction? To address this, we separated reactivities into subsets and quantified their information content. Subsets are typically obtained by categorizing reactivities as unreactive (<0.4), moderately (0.4–0.85), and highly reactive (>0.85), using knowledge-based thresholds (Hajdin et al. 2013). More simply, reactivities could be separated into equal-width bins. While these approaches are legitimate, they result in bins of different mass, i.e., containing varying numbers of data points. Consequently, analysis may be biased by bins of larger mass, which might play a greater role in determining structures. To overcome this, we opted for equal-mass bins with quantiles determined separately for each RNA (exact ranges are given in Supplemental Table S3). We then used leave-one-in and leave-one-out analyses to quantify information content in each subset (see Materials and Methods).
Figure 3 shows that the top 20% reactivities yield the strongest boost and most dramatic drop in prediction performances for the leave-one-in and leave-one-out strategies, respectively. This highlights the dominant role of this quintile in directing prediction and implies its ample information content. The bottom 20% reactivities also play a major role in driving performances, albeit to a lesser extent. In contrast, moderate reactivities (40%–80%) have limited impact on prediction (P > 0.05 in one-tailed two-sample t-tests). This is better illustrated by the ∪-shape across quintiles in the leave-one-in analysis, and the ∩-shape in the leave-one-out analysis (Fig. 3, in particular the “Simulated” panel).
FIGURE 3.
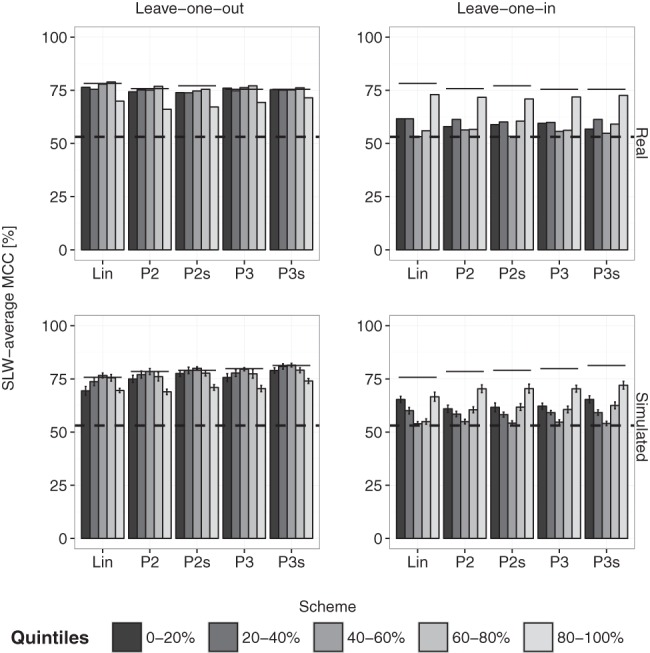
Performances using leave-one-out and leave-one-in cross-validations. Plots in the upper and lower panels indicate SLW-average MCCs for real data and simulations (N = 20), respectively. The bottom dashed line represents the performance for the no-SHAPE control and scheme-specific upper lines represent performances with entire SHAPE profiles. Scheme acronyms {Lin, P2, P3, P2s, and P3s} stand for {RNAlin, RNAprob-2, RNAprob-3, RNAprob-2s, and RNAprob-3s}, respectively. Errors bars represent standard deviations.
To further confirm the relative contribution of quintiles, we incrementally reconstructed SHAPE profiles by sequentially adding quintiles in descending order of information content: 80%–100%, 0%–20%, 60%–80%, 20%–40%, and 40%–60%. Results were normalized so that 0% indicates no-SHAPE control and 100% corresponds to performance with complete data. Figure 4 shows that the top quintile contributes between 80% and 60% of the maximum gain for real and simulated data, respectively. For simulated data, the remaining 40% performance gain is driven by the 0%–20% and 60%–80% quintiles. For real data, all RNAprob variants display the same trend as in simulations, but intriguingly, RNAlin uses another quintile (20%–40%) to recover full performance. However, in the absence of experimental replicates, it is difficult to determine the significance of this discrepancy.
FIGURE 4.
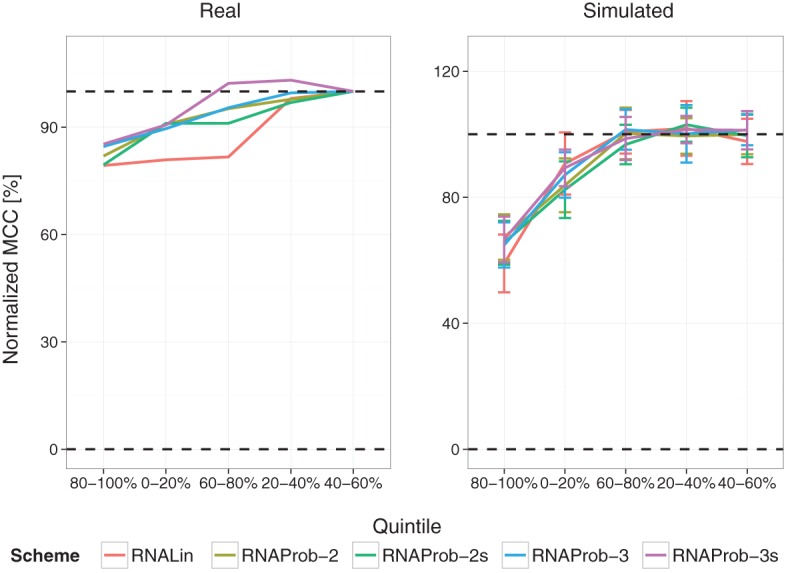
Performances with incremental reconstruction of SHAPE profiles. Left and right panels show normalized MCCs for real data and simulations (N = 10), respectively. The bottom and upper continuous lines represent performances for the no-SHAPE control (0%) and the entire SHAPE profile (100%), respectively. Errors bars represent standard deviations.
Additionally, we evaluated performances with near-perfect information. For this purpose, we assigned zero or 1.66 valued reactivities (97.5 percentile) to respectively paired and unpaired bases (in the reference structure) in a selected quintile, while leaving the remaining reactivities unchanged. As a control, we used a SHAPE profile entirely set to these so-called perfect reactivities and as expected, both RNAlin and RNAprob achieved very high performances (Fig. 5, upper dashed lines). The 60%–80% quintile shows the biggest performance gain followed by the 40%–60% quintile. In contrast, the 0%–20% and 80%–100% quintiles show limited impact on performances. These observations in conjunction with our cross-validation results confirm that increasing the information content of moderate reactivities is key to further improve structure prediction.
FIGURE 5.
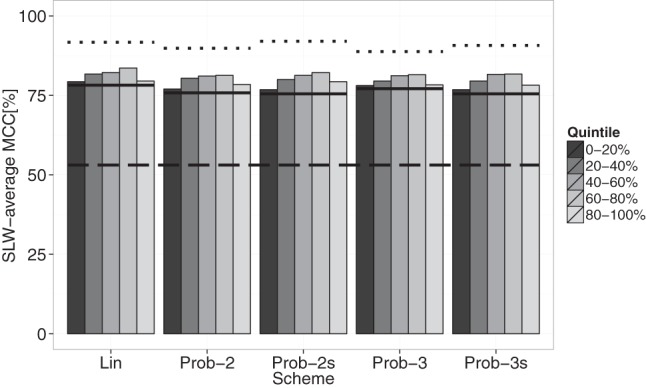
Performances on real data in the presence of perfect information. Bars represent SLW-average MCCs of quintiles when set to perfect information. Upper scheme-specific dashed lines represent the performance with the entire SHAPE-profile set to perfect information. Solid lines indicate the performance with the original SHAPE profile and the bottom dashed line corresponds to the no-SHAPE control.
Information content within quintiles may be better understood from a statistical standpoint. While probing data measure local structural constraints, they only indirectly report base-pairing probabilities (Ochsenreiter 2015; Sloma and Mathews 2015). High reactivities tend to have greater free energy contributions compared to lower reactivities and they generally signify greater discriminatory power as can also be seen from prior data-driven likelihood ratio analysis (Bindewald et al. 2011; Eddy 2014). We calculated posterior probabilities (P(πi|αi) of a structural context given a reactivity value using Bayesian statistics (see Supplemental Material). As expected, high reactivities (>1.66) tend to have high probabilities of unpairing (>80%) and inversely for zero reactivities where paired probabilities were ∼80% (Fig. 6). Moderate reactivities are nearly equiprobable between paired and unpaired, which makes it challenging for folding algorithms to make informed decisions of structural contexts from values in this range. Notably, compared to stacked, helix-end bases tend to be more reactive, i.e., flexible, as indicated by a less sharp decreasing slope and a maximum probability peak found at reactivity values around 0.24–0.26 rather than zero.
FIGURE 6.
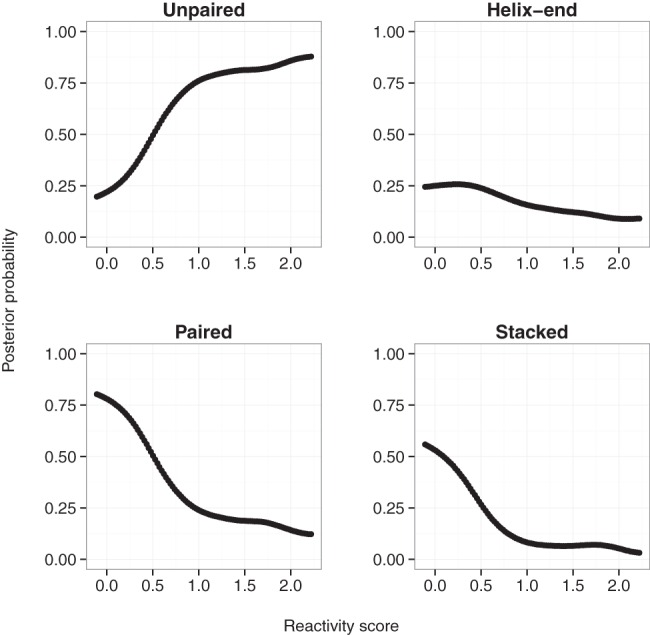
Bayesian posterior probabilities of structural contexts as a function of reactivities. Posterior probabilities are shown for each possible structural context, namely unpaired, helix-end, and stacked paired.
Exploring scheme universality: case studies using mock probes
The recent developments in probing technologies promise to deliver a wealth of data that encompass a range of probes, conditions, and types of probed transcripts (e.g., coding versus noncoding). We therefore anticipate facing a diversity of statistical data properties as well as more complex scenarios, e.g., when one wishes to combine data sets. With such opportunities comes a need for a general and robust framework that self-adapts to the data at hand. RNAlin was designed based on in vitro SHAPE data (Deigan et al. 2009) and it assumes a linear–log relationship between reactivities and pairing-state likelihood ratios (Eddy 2014). However, there is no guarantee that this is universally true. In contrast, the probabilistic nature of RNAprob affords full flexibility to adjust the model to data statistics. To demonstrate this point, we simulated two mock probes whose generated data deviate from RNAlin's linear–log model.
In scenario 1, we randomly drew unpaired and stacked reactivities from SHAPE data distributions (Fig. 2, top panel), while helix-end reactivities were sampled from the unpaired distribution. This emulates a mock probe that can easily access a base which is either unpaired or neighboring to an unpaired base. It diverges from SHAPE, where helix-ends produce a distribution in between stacked and unpaired (Fig. 2). In scenario 2, inspired by DMS modification, a mock probe modifies A and U at a different efficiency compared to G and C. This hypothetical probe generates normally distributed reactivities, centered at zero, 0.25, and 0.5 for stacked, helix-end, and unpaired bases, respectively. For each structural context, we fixed the mean but used different dispersions around it for A/U (σA=σU=0.1) versus G/C (σG=σC=1), resulting in smaller dispersion for unpaired reactivities than for paired ones (Supplemental Fig. S7). This is because folding thermodynamics imply that G/C are more likely to form base pairs than A/U, hence the paired group is enriched in G/C and vice versa for the unpaired group. Consequently, paired bases could generate reactivities that are higher, on average, than their SHAPE counterparts, leading to a nonlinear–log relationship between reactivities and pairing-state likelihood ratios.
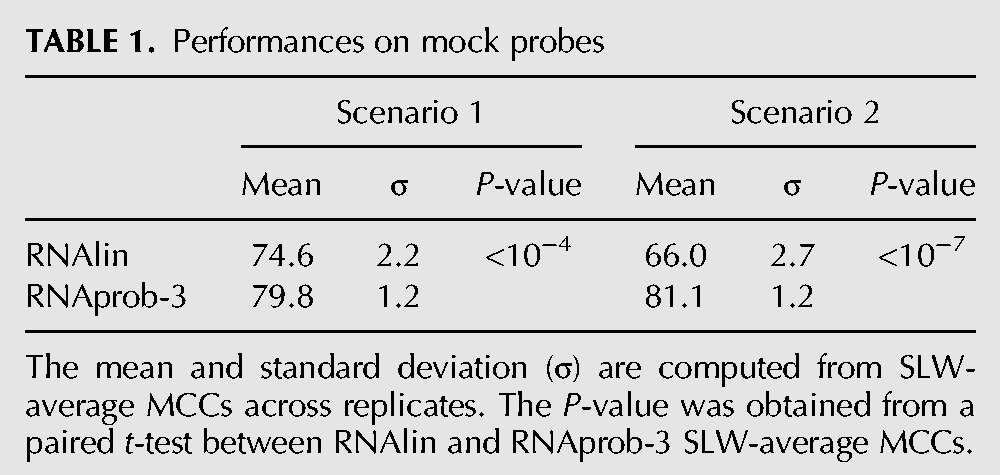
In brief, for each scenario, we simulated 10 replicates per RNA. To cross-validate the results, we divided the RNA in our data set into a training (N = 16) and a test set (N = 7), following the way RNAlin was originally trained (Hajdin et al. 2013). The training set was used to optimize m and b parameters for RNAlin and to learn empirical distributions for RNAprob (see Supplemental Material for details). In both scenarios, RNAprob outperforms RNAlin in a statistically significant way (Table 1) and this is consistently true across all 10 replicates (Supplemental Table S5). These results reveal the limitation of RNAlin's model and provide evidence of RNAprob's adaptive capacity and universality.
TABLE 1.
Performances on mock probes
Evaluating scheme robustness to noise
When comparing different schemes, it is informative to assess their robustness to technical and biological variations. In the absence of biological replicates, we resorted to simulations. Our previous analysis of a different, yet related, probing data set (Loughrey et al. 2014) revealed heteroskedasticity, which we modeled to capture this additional complexity (K Choudhary, NP Shih, F Deng, M Ledda, B Li, S Aviran, in prep.). We used this model to relate reactivity values to corresponding variances by scaling a standard Gaussian noise term for each reactivity. Five noise levels were applied to the data with variances monotonically increased from 1 to 10,000 by factors of 10, starting at values previously observed in experimental data (Loughrey et al. 2014).
Interestingly, all schemes are robust to noise up to a factor of 100 (Supplemental Fig. S4). The first three noise levels show performances comparable to baseline (P > 0.05 in one-tailed two-sample t-tests). As expected, at higher noise levels, performances decrease significantly to the point (10,000-fold) where accuracy is lower compared to the no-SHAPE control. This is likely due to reactivity values being misleading to schemes.
Effect of data transformation
RNAlin integrates a linear–log term, thereby implicitly log-transforming reactivities and inducing Gaussianity as shown in Figure 2 (Ln panel). SHAPE experiments can result in negative reactivities, which exclude direct log-transformation. Negative reactivities, which arise from a stronger readout in the (−) channel compared to (+) channel, are a product of noise in the system (Aviran et al. 2011a). In theory, these should be set to zero. Converting negatives to zero, as done in RNAlin, is therefore legitimate, yet it precludes log-transformation. Under an assumption that the random noise is symmetric and centered at zero, one could directly take absolute values. Often, however, SHAPE data are released with these assigned zeros, eliminating the option of recovering their original readout. As this is the case with a subset of our data, we reassigned both negatives and zeros to values sampled from a distribution, which we fit to negative values (see Materials and Methods). This routine allowed us to generate strictly positive SHAPE reactivities amenable to log transformation.
In the absence of context-based classification, log-transformation produces nearly Gaussian reactivities. A closer look at the category level shows that distributions within unpaired and helix-end bases are left-skewed (Fig. 2, Ln panel). To correct for this skewness, we used a Box–Cox transform function, also known as a power transform. It can be viewed as a parametrizable transform that allows us to simultaneously log transform and correct for skewness. This produced distributions closer to normality, with helix-end reactivities passing a formal statistical test for normality (P = 0.14 in a Lillifors test). Overall, performances on new data are comparable to their original data counterparts (Supplemental Fig. S5).
DISCUSSION
In this study, we implemented, extended, and investigated a probabilistic framework for data-directed RNA secondary structure prediction. Performance evaluations on real and simulated SHAPE data sets showed that it performs comparably to the widely used RNAlin. The most appealing feature of this probabilistic framework is its flexibility and generality. While RNAlin has been developed and optimized for SHAPE, yielding remarkable performance enhancements (Hajdin et al. 2013), it is a daunting but essential task to reoptimize its parameters when used with other data types. This is because there is no guarantee that default values are universally optimal and furthermore, it is unclear if RNAlin's linear–log model fits other data with sufficient accuracy. In fact, using mock-probe simulations, we showed that RNAprob outperforms RNAlin when data deviate from RNAlin's model. Of course, a straightforward workaround would be to modify RNAlin's model to better characterize these probes. This, although feasible, is a nontrivial task because there is no principled way to choose an optimal formula. Moreover, if one tries to combine information sources, such as data from different probes, RNAlin would either require multiple linear models or a more complex model, thus increasing the number of parameters (Rice et al. 2014; Wu et al. 2015). This would not only pose extra computational challenges for parameter optimization, but would also carry the risk of converging to local optima that are not globally optimal, as the multidimensional search space is not guaranteed to be convex.
RNAprob, on the other hand, relies on a more direct and explicit statistical model of the data, which eliminates the need for parameter optimization and the concern for the applicability of the linear–log model. Consequently, it is readily adaptable to any type of probing data and has the potential to account for more complex data sets and data interpretations. Such flexibility renders RNAprob an appealing choice, especially in light of the unprecedented diversity and rapid growth in available probing methods along with recent expansion in their capabilities and scope. Note that although we focused on MFE predictions, RNAprob could be extended into partition function calculations in the same manner as RNAlin. The difference between them is how pseudo-energy terms are derived from reactivities, but once we obtain a structure's free-energy and pseudo-energy, further calculations simply use the total score in the same way as they use RNAlin's score.
RNAlin implicitly accounts for three structural contexts, i.e., unpaired, helix-end, and stacked. However, extending it to accommodate more elaborate contexts is also not straightforward. As aforementioned, it warrants the introduction of additional parameters and more complex formulas. We showed that RNAprob can also account for similar single-nucleotide contexts, but its principled approach allows for easier extension to more complex structural motifs (Eddy 2014). Our work sets the foundation for such future explorations. Importantly, by comparing variants that accommodate two versus three contexts (RNAprob-2 and 3), we demonstrated that proper and sufficiently refined modeling of structural information has the potential to improve prediction accuracy. As more data become available, we will be able to refine models by considering more proper context dependencies, such as entire loops (Ochsenreiter 2015) or simply NNTM stacks.
Our performance analysis made use of both real data and simulations, revealing statistically significant discrepancies between the two benchmarks. This gap raises several issues that warrant further study. The model-based simulations we used rely on simplified interpretation of structural information, which may not be powerful enough to capture all aspects of a probing experiment. For example, this model does not account for putative correlations between nucleotides that reside within the same motif. Better-defined models are necessary but require deeper understanding of probing data. As an example, we showed that kernel density estimation closely models real reactivities. On the other hand, by attempting to capture subtle local variations in reactivity distributions, one faces the risk of over-fitting (i.e., fitting of the noise).
A potential workaround is to fit models upstream of reactivity computations, such as at the readout level. For example, given that adduct formation on RNA nucleotides during probing likely follows a Poisson process, the resulting distribution could be approximated from the readouts of experimental channels (Aviran et al. 2011a; Siegfried et al. 2014). Final reactivity distributions could then be mathematically derived or numerically approximated based on these prior distributions (Aviran et al. 2011b). Models that rely on mechanistic understanding of molecular dynamics and of measurement platforms are more descriptive and potentially more meaningful. They may thus result in more faithful representation of the data. From a statistical analysis perspective, multiple replicates for each probed RNA are essential components toward obtaining better characterization of the data. This makes it possible to accommodate natural stochasticity into analysis, for example, by quantifying variation in structure prediction accuracies for each RNA. Additionally, replicates can help evaluate the validity of simulation models and ultimately facilitate further improvements. Unfortunately, multiple replicates were not available for the RNAs in our data set. We anticipate that in the near future such data will become publicly available.
Probing data have been shown to greatly improve structure prediction, but their relative contribution remains poorly understood. In this study, we showed that the top 20% of reactivities remarkably account for ∼80% of the performance gain against a no-SHAPE control. Of particular interest are moderate reactivities, as these are not substantially informative to the prediction and act as a major bottleneck to further improvements in data-directed performance gains. This highlights a need for future work on probing techniques, to enhance their discriminative power, along with the development of better approaches to data analysis, so as to judiciously convert raw data into meaningful reactivities (Aviran and Pachter 2014). Overall, our analysis pipeline can serve as a general framework for future tests on various types of probing data.
An appealing aspect of RNAprob is its generalizability. In that context, it could be useful to also standardize the way data are interpreted and input to prediction algorithms. A natural choice would be to consider normally distributed values. Here, we proposed a novel approach to log-transform SHAPE reactivities in the presence of zeros and negatives. There are two rationales behind this transformation. First, it induces Gaussianity for each structural context we considered, obviating the need for fitting distinct density functions on a per-context basis (Sükösd et al. 2013). Second, it increases homoskedasticity as a consequence of the log–log relationship between reactivities and associated variances as shown by (K Choudhary, NP Shih, F Deng, M Ledda, B Li, S Aviran, in prep.). Normality and homoskedasticity are common assumptions for many statistical tests, hence they broaden the spectrum of statistical analysis applicable to log-transformed data.
In conclusion, we presented a statistical framework for RNA secondary structure prediction, which can be readily generalized to various probes. Furthermore, we outlined methods to systematically quantify the information content of probing data. Finally, we highlighted the potential for better probabilistic data modeling to improve structure prediction.
MATERIALS AND METHODS
Data-directed predictions
At the core of the free energy minimization paradigm is a dynamic programming algorithm that incorporates NNTM parameters and recursively finds an MFE structure (Zuker and Stiegler 1981; Mathews et al. 1999). To incorporate SHAPE data, Deigan et al. (2009) introduced a pseudo-energy term for each base i, ΔG′i, based on the linear–log formula:
| (1) |
where αi is the ith SHAPE reactivity and m and b are parameters set to m = 1.8 and b = −0.6 kcal/mol by default (Hajdin et al. 2013). This term is added to the NNTM free energy of a structure each time base i is involved in a nearest-neighbor stack. Consequently, the pseudo-energy term is counted once for a base involved in a helix-end pair, while it is counted twice for a stacked pair (Low and Weeks 2010; Sloma and Mathews 2015). This is because a helix-end pair is involved in one stack, while a stacked pair is involved in two stacks. To optimize m and b, Deigan et al. (2009) evaluated structure prediction performance over a grid with respect to known reference structures. We refer to this scheme as RNAlin hereafter.
The probabilistic framework outlined by Eddy (2014), hereafter called RNAprob, derives explicitly from a statistical model of probing data. Under the assumption that αi is independent of the input sequence and depends only on i’s structural context, one can compute ΔG′i as follows:
| (2) |
where R and T are thermodynamics constants and P(αi|πi) is the likelihood of reactivity αi given structural context πi. For brevity, we use to denote the pseudo-energy term with respect to πi. Here, πi can be as simple as paired versus unpaired, as pointed out by Eddy (2014). However, with increasing availability of data, it becomes feasible to incorporate more refined contexts with different statistical properties, which may improve prediction accuracy. For example, bases at helix ends tend to be more reactive than those in stacked pairs (Sükösd et al. 2013).
Unlike RNAlin, where pseudo-energy terms are only applied to paired bases, in RNAprob, they are applied exactly once for each base. While RNAprob explicitly assigns pseudo-energy terms based on the structural contexts considered, RNAlin assigns 0×, 1×, and 2× ΔG′i to unpaired, helix-end, and stacked bases, respectively, in an implicit way. The way RNAprob derives and applies pseudo-energies offers full flexibility in modeling and accounting for these three contexts. Despite differences in how pseudo-energy terms are obtained and applied, Eddy observed that the two approaches share a common idea—that a pseudo-energy term implies a particular paired/unpaired likelihood ratio (Eddy 2014).
It is worth mentioning that in Cordero et al. (2012), Das and colleagues proposed the first approach that converts a reactivity into pseudo-energy by taking the log-likelihood ratio of the base being paired versus unpaired. It can be viewed as an intermediate between RNAlin and RNAprob. Similarly to RNAprob, paired and unpaired distributions are used to derive pseudo-energies. On the other hand, pseudo-energies are plugged into RNAstructure in the exact same way as in RNAlin, i.e., they are applied 0, 1, and 2 times to unpaired, helix-end, and stacked bases, respectively. The Das scheme provides more flexibility to model diverse probing data as compared to RNAlin. However, unlike RNAprob, it cannot readily account for structural contexts beyond paired/unpaired.
Computing likelihood
One can approach the calculation of P(αi|πi) in Equation 2 in two ways, which both start with an empirical distribution of SHAPE reactivities per structural context πi, generated from a set of RNAs with known reference structures (Supplemental Table S1). In one approach, we used a histogram of reactivities to calculate P(αi|πi) with a bin size fixed at 0.1. Alternatively, the data were fit to a known parametric density, from which P(αi|πi) was calculated. In this study, we followed previous work (Sükösd et al. 2013), where unpaired data were fit to an exponential distribution, and data of helix-end and stacked bases were each fit to a generalized extreme value (GEV) distribution (Fig. 2, upper panel). We use RNAprob and RNAprob-s to differentiate between the two approaches. For RNAlin, we used default parameters (m = 1.8 and b = −0.6), which indirectly translate into a likelihood ratio (Eddy 2014).
Quantifying information content by cross validation
To better understand how SHAPE data direct structure prediction, we separated data into quintiles (five equally populated subsets). We then quantified the information content in each quintile by combining two cross-validation strategies: (i) leave-one-out: removing a selected subset from input; and (ii) leave-one-in: restricting input to a selected subset. To quantify relative contributions of quintiles, we incrementally reconstructed SHAPE profiles by sequentially feeding them in a defined order. Quintiles were added in descending order of information content (i.e., from most to least informative), guided by the results from our cross-validation analysis.
Data transformation
A logarithmic transformation is not applicable to SHAPE data due to zero and negative reactivities. To generate a closely related data set amenable to such a transformation, we reassigned such values to produce strictly positive reactivities. In brief, we first fit a Pearson distribution to absolute values of negative reactivities and then used random samples from this distribution to replace all zeros and negatives (see Supplemental Material for details). To induce Gaussianity, we subsequently applied two types of transformations on the resulting data: a natural logarithm and a Box–Cox function x′=(xλ−1)λ (Box and Cox 1964) with λ=0.1.
Performance measures
Performance was measured with three widely used metrics: sensitivity, positive predictive value (PPV), and Mathews correlation coefficient (MCC) (Gardner and Giegerich 2004). Sensitivity is the fraction of correctly predicted base pairs in the reference structure, whereas PPV considers base pairs in the predicted structure. MCC summarizes both sensitivity and PPV (see Supplemental Material for formal definitions).
Studies often report average performance over a set of RNAs. This metric is heavily biased by the numerous short RNAs in our data set, for which performances largely vary as a result of small differences in predicted structures. We thus also calculated a “sequence-length-weighted (SLW) average” (Supplemental Material), which we used as a default performance metric. Note that “slipped” base pairs were not allowed when scoring. That is, a base pair between i and j (denoted i–j) is said to be correctly predicted if it occurs in both predicted and reference structures.
Availability
The source code, which is available for download from http://bme.ucdavis.edu/aviranlab/rnaprob_software, is freely available for noncommercial use.
SUPPLEMENTAL MATERIAL
Supplemental material is available for this article.
Supplementary Material
ACKNOWLEDGMENTS
We thank Christine Heitsch for discussions at the 2015 Benasque meeting on Computational Analysis of RNA Structure and Function. This work was supported by National Institutes of Health (NIH) grants: HG006860 from the National Human Genome Research Institute (NHGRI)-NIH and T32-GM008799 from The National Institute of General Medical Sciences (NIGMS)-NIH.
Footnotes
Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.055756.115.
REFERENCES
- Aviran S, Pachter L. 2014. Rational experiment design for sequencing-based RNA structure mapping. RNA 20: 1864–1877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aviran S, Trapnell C, Lucks JB, Mortimere SA, Luo S, Schroth GP, Doudna JA, Arkin AP, Pachter L. 2011a. Modeling and automation of sequencing-based characterization of RNA structure. Proc Natl Acad Sci 108: 11069–11074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aviran S, Lucks JB, Pachter L. 2011b. RNA structure characterization from chemical mapping experiments. In Proceedings of the 49th Allerton conference on communication, control and computing, pp. 1743–1750, University of Illinois, Monticello, IL. [Google Scholar]
- Bindewald E, Wendeler M, Legiewicz M, Bona MK, Wang Y, Pritt MJ, Le Grice SFJ, Shapiro BA. 2011. Correlating SHAPE signatures with three-dimensional RNA structures. RNA 17: 1688–1696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Box GE, Cox DR. 1964. An analysis of transformations. J R Stat Soc Series B (Methodological) 211–252. [Google Scholar]
- Cheng CY, Chou F-C, Kladwang W, Tian S, Cordero P, Das R. 2015. Consistent global structures of complex RNA states through multidimensional chemical mapping. eLife 4: e07600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordero P, Kladwang W, VanLang CC, Das R. 2012. Quantitative dimethyl sulfate mapping for automated RNA secondary structure inference. Biochemistry 51: 7037–7039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cover TM, Thomas JA. 2012. Elements of information theory. Wiley, New York. [Google Scholar]
- Deigan KE, Li TW, Mathews DH, Weeks KM. 2009. Accurate SHAPE-directed RNA structure determination. Proc Natl Acad Sci 106: 97–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Y, Lawrence CE. 2003. A statistical sampling algorithm for RNA secondary structure prediction. Nucleic Acids Res 31: 7280–7301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Y, Tang Y, Kwok CK, Zhang Y, Bevilacqua PC, Assmann SM. 2014. In vivo genome-wide profiling of RNA secondary structure reveals novel regulatory features. Nature 505: 696–700. [DOI] [PubMed] [Google Scholar]
- Eddy SR. 2014. Computational analysis of conserved RNA secondary structure in transcriptomes and genomes. Annu Rev Biophys 43: 433–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehresmann C, Baudin F, Mougel M, Romby P, Ebel J-P, Ehresmann B. 1987. Probing the structure of RNAs in solution. Nucleic Acids Res 15: 9109–9128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner PP, Giegerich R. 2004. A comprehensive comparison of comparative RNA structure prediction approaches. BMC Bioinformatics 5: 140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutell RR, Lee JC, Cannone JJ. 2002. The accuracy of ribosomal RNA comparative structure models. Curr Opin Struct Biol 12: 301–310. [DOI] [PubMed] [Google Scholar]
- Hajdin CE, Bellaousov S, Huggins W, Leonard CW, Mathews DH, Weeks KM. 2013. Accurate SHAPE-directed RNA secondary structure modeling, including pseudoknots. Proc Natl Acad Sci 110: 5498–5503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hector RD, Burlacu E, Aitken S, Le Bihan T, Tuijtel M, Zaplatina A, Cook AG, Granneman S. 2014. Snapshots of pre-rRNA structural flexibility reveal eukaryotic 40S assembly dynamics at nucleotide resolution. Nucleic Acids Res 42: 12138–12154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kertesz M, Wan Y, Mazor E, Rinn JL, Nutter RC, Chang HY, Segal E. 2010. Genome-wide measurement of RNA secondary structure in yeast. Nature 467: 103–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kielpinski LJ, Vinther J. 2014. Massive parallel-sequencing-based hydroxyl radical probing of RNA accessibility. Nucleic Acids Res 42: e70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavender CA, Lorenz R, Zhang G, Tamayo R, Hofacker IL, Weeks KM. 2015. Model-free RNA sequence and structure alignment informed by SHAPE probing reveals a conserved alternate secondary structure for 16s rRNA. PLoS Comput Biol 11: 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenz R, Bernhart SH, Zu Siederdissen CH, Tafer H, Flamm C, Stadler PF, Hofacker IL. 2011. ViennaRNA package 2.0. Algorithms Mol Biol 6: 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loughrey D, Watters KE, Settle AH, Lucks JB. 2014. SHAPE-Seq 2.0: systematic optimization and extension of high-throughput chemical probing of RNA secondary structure with next generation sequencing. Nucleic Acids Res 42: e165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Low JT, Weeks KM. 2010. SHAPE-directed RNA secondary structure prediction. Methods 52: 150–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu ZJ, Gloor JW, Mathews DH. 2009. Improved RNA secondary structure prediction by maximizing expected pair accuracy. RNA 15: 1805–1813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucks JB, Mortimer SA, Trapnell C, Luo S, Aviran S, Schroth GP, Pachter L, Doudna JA, Arkin AP. 2011. Multiplexed RNA structure characterization with selective 2′-hydroxyl acylation analyzed by primer extension sequencing (SHAPE-Seq). Proc Natl Acad Sci 108: 11063–11068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luntzer D, Lorenz R, Hofacker IL, Stadler PF, Wolfinger MT. 2015. SHAPE directed RNA folding. Bioinformatics 32: 145–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markham NR, Zuker M. 2008. UNAFold: software for nucleic acid folding and hybridization. In Bioinformatics: structure, function, and applications. Methods in molecular biology (ed. Keith JM), Vol. 453, pp. 3–31. Humana Press, Totowa, NJ. [DOI] [PubMed] [Google Scholar]
- Mathews DH, Sabina J, Zuker M, Turner DH. 1999. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J Mol Biol 288: 911–940. [DOI] [PubMed] [Google Scholar]
- Mathews DH, Disney MD, Childs JL, Schroeder SJ, Zuker M, Turner DH. 2004. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc Natl Acad Sci 101: 7287–7292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGinnis JL, Liu Q, Lavender CA, Devaraj A, McClory SP, Fredrick K, Weeks KM. 2015. In-cell SHAPE reveals that free 30S ribosome subunits are in the inactive state. Proc Natl Acad Sci 112: 2425–2430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mortimer SA, Kidwell MA, Doudna JA. 2014. Insights into RNA structure and function from genome-wide studies. Nat Rev Genet 15: 469–479. [DOI] [PubMed] [Google Scholar]
- Ochsenreiter RW. 2015. “Computational refinement of SHAPE-RNA probing experiments.” Master thesis, University of Vienna, Austria. [Google Scholar]
- Ouyang Z, Snyder MP, Chang HY. 2013. SeqFold: genome-scale reconstruction of RNA secondary structure integrating high-throughput sequencing data. Genome Res 23: 377–387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pace NR, Thomas BC, Woese CR. 1999. Probing RNA structure, function, and history by comparative analysis. In The RNA world, 2nd ed. (ed. Gesterland RF, et al. ), pp.113–141, Cold Spring Harbor Laboratory Press, Cold Spring Harbor, New York. [Google Scholar]
- Poulsen LD, Kielpinski LJ, Salama SR, Krogh A, Vinther J. 2015. SHAPE Selection (SHAPES) enrich for RNA structure signal in SHAPE sequencing-based probing data. RNA 21: 1042–1052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Proakis JG, Salehi M. 2007. Digital Communications. McGraw-Hill Education, New York. [Google Scholar]
- Regulski EE, Breaker RR. 2008. In-line probing analysis of riboswitches. Methods Mol Biol 419: 53–67. [DOI] [PubMed] [Google Scholar]
- Reuter JS, Mathews DH. 2010. RNAstructure: software for RNA secondary structure prediction and analysis. BMC Bioinf 11: 129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice G, Leonard C, Weeks K. 2014. RNA secondary structure modeling at consistent high accuracy using differential SHAPE. RNA 20: 846–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouskin S, Zubradt M, Washietl S, Kellis M, Weissman JS. 2014. Genome-wide probing of RNA structure reveals active unfolding of mRNA structures in vivo. Nature 505: 701–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp PA. 2009. The centrality of RNA. Cell 136: 577–580. [DOI] [PubMed] [Google Scholar]
- Siegfried NA, Busan S, Rice GM, Nelson JA, Weeks KM. 2014. RNA motif discovery by SHAPE and mutational profiling (SHAPE-MaP). Nat Methods 11: 959–965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sloma MF, Mathews DH. 2015. Improving RNA secondary structure prediction with structure mapping data. Methods Enzymol 553: 91–114. [DOI] [PubMed] [Google Scholar]
- Spitale RC, Crisalli P, Flynn RA, Torre EA, Kool ET, Chang HY. 2013. RNA SHAPE analysis in living cells. Nat Chem Biol 9: 18–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sükösd Z, Knudsen B, Kjems J, Pedersen CN. 2012. PPfold 3.0: fast RNA secondary structure prediction using phylogeny and auxiliary data. Bioinformatics 28: 2691–2692. [DOI] [PubMed] [Google Scholar]
- Sükösd Z, Swenson MS, Kjems J, Heitsch CE. 2013. Evaluating the accuracy of SHAPE-directed RNA secondary structure predictions. Nucleic Acids Res 41: 2807–2816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talkish J, May G, Lin Y, Woolford JL, McManus CJ. 2014. Mod-seq: high-throughput sequencing for chemical probing of RNA structure. RNA 20: 713–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tullius TD, Greenbaum JA. 2005. Mapping nucleic acid structure by hydroxyl radical cleavage. Curr Opin Chem Biol 9: 127–134. [DOI] [PubMed] [Google Scholar]
- Underwood JG, Uzilov AV, Katzman S, Onodera CS, Mainzer JE, Mathews DH, Lowe TM, Salama SR, Haussler D. 2010. FragSeq: transcriptome-wide RNA structure probing using high-throughput sequencing. Nat Methods 7: 995–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Washietl S, Hofacker IL, Stadler PF, Kellis M. 2012. RNA folding with soft constraints: reconciliation of probing data and thermodynamic secondary structure prediction. Nucleic Acids Res 40: 4261–4272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weeks KM. 2010. Advances in RNA structure analysis by chemical probing. Curr Opin Struct Biol 20: 295–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkinson KA, Merino EJ, Weeks KM. 2006. Selective 2′-hydroxyl acylation analyzed by primer extension (SHAPE): quantitative RNA structure analysis at single nucleotide resolution. Nat Protoc 1: 1610–1616. [DOI] [PubMed] [Google Scholar]
- Wu Y, Shi B, Ding X, Liu T, Hu X, Yip KY, Yang ZR, Mathews DH, Lu ZJ. 2015. Improved prediction of RNA secondary structure by integrating the free energy model with restraints derived from experimental probing data. Nucleic Acids Res 43: 7247–7259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarringhalam K, Meyer MM, Dotu I, Chuang JH, Clote P. 2012. Integrating chemical footprinting data into RNA secondary structure prediction. PLoS One 7: e45160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuker M, Stiegler P. 1981. Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res 9: 133–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


