Developing miRNA signatures: a multivariate prospective

The identification of molecular biomarkers that can be detected with non-invasive techniques in serum and plasma has attracted growing interest (Chen et al, 2008). In this research area many researchers have identified miRNAs as potential biomarkers, especially for the (early) diagnosis of different types of cancer (Calin and Croce, 2006; Cortez et al, 2011).

Several techniques are currently available for assessing miRNA levels in body fluids, such as miRNA microarrays, quantitative real-time PCR (qRT-PCR) and deep sequencing. Among these approaches, the most frequently used is qRT-PCR-based assays, in which miRNA expression data are usually provided on a continuous scale in terms of relative quantification (Livak and Schmittgen, 2001; Cortez et al, 2011; Deo et al, 2011).

However, data might be still not sufficient to establish the clinical utility of miRNA signatures, as most published studies present contradictory findings even within the same cancer type. This can be due to a lack of shared methods for both the pre-analytical and analytical phase of miRNA detection, as well as due to the variety of statistical analysis techniques employed.

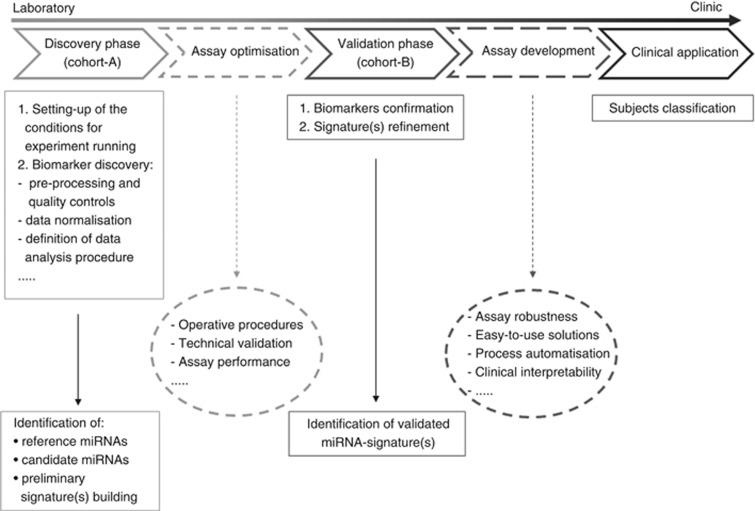
Figure 1 shows some of the most essential steps in the development of cancer biomarker signature, from laboratory to clinical practice. The process begins with the discovery, and is followed by a validation phase and, finally, the clinical application of the identified biomarker signature (Verderio et al, 2010). Two additional assay set-up steps could be included in the workflow, before (assay optimisation) and/or after (assay development) the validation phase (Verderio et al, 2015). Independent cohorts of patients from the same target population should be considered for the discovery and validation phases.

Figure 1.

Workflow for cancer biomarker-signature development, from laboratory to clinical practice. This figure reports the most important phases of biomarker identification and the signature development.

From a statistical-methodological point of view, one of the main difficulties in translating results from laboratory into clinical practice seems to be in the multivariate analysis stage that, ideally, should lead to an optimal combination of miRNAs to obtain a stronger composite score (Yan et al, 2015). Thus, from this perspective the question is ‘how to combine miRNAs appropriately?' To answer this question, it is useful to evoke the multivariate regression model theory and address some key topics related to multivariate model development.

First of all, when in the multivariate model we consider a number of explanatory variables that is larger than the number of outcome events, model overfitting can occur, a situation where the model fits the original data but fails to predict disease in an independent data set (Harrell, 2001; Verderio et al, 2010). As a consequence, the concept of number of events-per-variable (EPV) becomes crucial in the development of multivariate model, and, as a rule of thumb, it is advisable to have at least 10 EPV in order to obtain reliable estimates (Peduzzi et al, 1996; Verderio, 2012). When EPV is <10 the use of penalised regression strategies may represent a useful tool to reduce overfitting as much as possible (Pavlou et al, 2015; Verderio et al, 2016). The two most popular penalised approaches are ridge (Cessie and HouweLingen, 1992) and LASSO (least absolute shrinkage and selection operator) (Tibshirani, 1996), both shrinking the regression coefficients towards zero by introducing a penalty. Penalised maximum likelihood estimation (PMLE) has been proposed as an extension of the ridge regression technique (Harrell, 2001; Moons et al, 2004), together with other methods such as elastic-net, adaptive LASSO and the smoothly clipped absolute deviation recently discussed by Pavlou et al (2015).

Another important feature that needs to be taken into consideration while developing the multivariate model process is that, according to the principle of parsimony, a reduced model - involving less predictors - could be identified without a substantial loss of performance (Verderio et al, 2016). To develop this process, several well-established approaches for standard regression are available, such as backward elimination, a method that starts from a full multivariate model, including all the considered variables (initial multivariate model), and identifies a reduced one (final multivariate model) (Moons et al, 2015). Similarly, model-reduction strategies have been proposed for penalised models: for PMLE, a backward reduction method based on the R square coefficient has been reported by Moons et al (2004), whereas for LASSO shrinking of some coefficients to exactly zero intrinsically allows model reduction (Tibshirani, 1996). The above backward-oriented approaches are suitable strategies when no a priori knowledge about the actual value of the biomarkers is available, like in the context of biomarker discovery. An alternative strategy could consist in performing all possible combinations of the candidate miRNAs included in the initial model (i.e. all-subsets analysis) and selecting the best one (Miller, 1984).

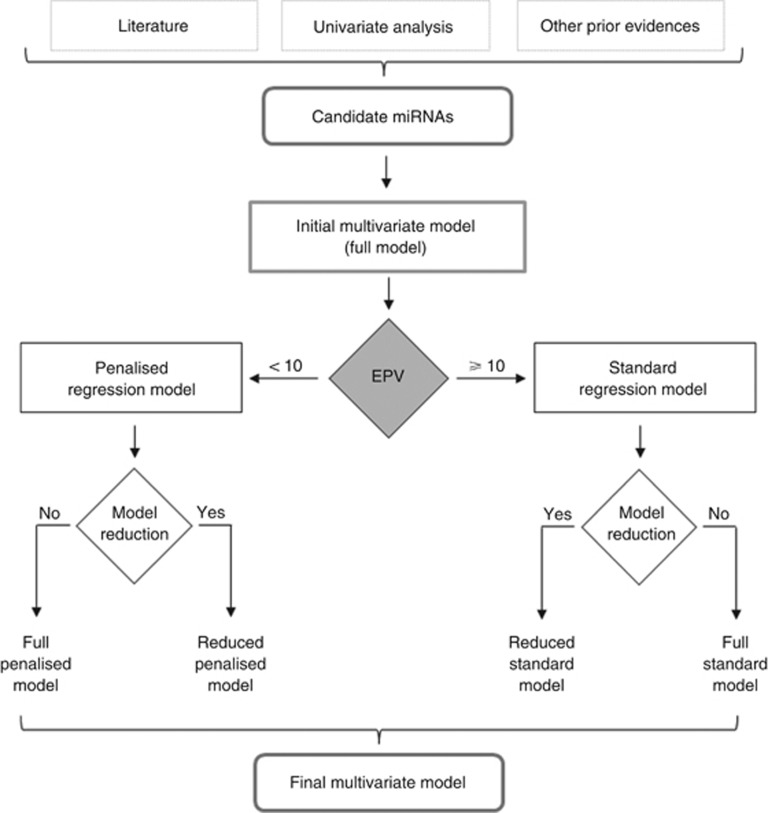
Figure 2 depicts some of the most important steps of the workflow for statistical analysis applied to the development of miRNA signatures. The starting point consists in defining the initial model(s) so as to include all relevant miRNAs, such as those selected as significant by (prior) univariate analysis, identified in the literature or by other evidence. The choice between standard and penalised regression model is based on the EPV value: for <10 EPV, the use of penalised regression strategies is recommended, whereas for higher EPV values standard regression methods can be used. Regardless of the EPV value, the analysis can be performed by looking for a more parsimonious reduced model: for both the standard and the penalised regression model the selection procedure described above should be used. Although the principle of parsimony is essential for discriminating the structural part of empirical data from noise (Verderio et al, 2016), it remains to be established how far one should go with model reduction, especially in the context of miRNA signature discovery, where the structural component of the model is not clearly separated from the idiosyncratic one.

Figure 2.

Statistical analysis flowchart for miRNA signature development. The figure reports the key steps of the entire process, from candidate miRNAs to signature identification.

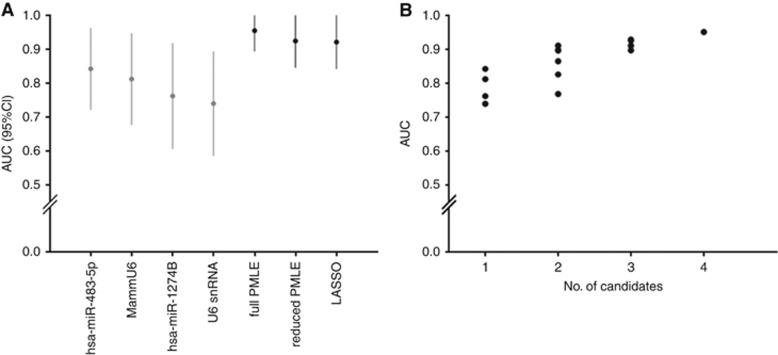
In our letter (Verderio et al, 2016), we have reported an application of the statistical workflow discussed here to the data on plasma circulating miRNAs from 20 hepatocellular carcinoma patients and 20 healthy donors, based on information from the Gene Expression Omnibus database (http://www.ncbi.nlm.nih.gov/gds) (GSE50013). Briefly, following the workflow illustrated in Figure 2, an initial multivariate model including the four candidate biomarkers identified by univariate analysis was fitted, leading to an EPV value <10. Accordingly, we constructed the following multivariate models: (i) full penalised regression model (full PMLE), (ii) a reduced penalised model (reduced PMLE) and (iii) a LASSO model. Figure 3A shows the estimated Area Under the ROC Curve (AUC) values with their 95% Confidence Interval (CI) for each candidate, as well as those for the full PMLE, reduced PMLE and LASSO models. In addition, Figure 3B reports the AUC values of the all-subsets analysis we performed for a total of 14 models. Again, it emerges that an increase in the predictive capability can be obtained by appropriately combining the candidate miRNAs (multivariate fashion) instead of evaluating each single candidate (univariate fashion).

Figure 3.

AUC values for the candidate biomarkers. (A) In gray are reported the AUC (95% CI) of the univariate analysis; in black those of the penalised regression models (full PMLE, reduced PMLE, LASSO). (B) AUC values corresponding to the all-subsets analysis including those from univariate analysis.

In conclusion, although it was acknowledged that availability of standardised operative procedures (SOPs) for both the pre-analytical and analytical phase is fundamental for miRNA reliability (Verderio et al, 2010, 2015), SOPs are not sufficient to address clinical utility. An additional requirement for developing multivariate prediction models based on miRNAs is the optimisation of the statistical analysis workflow, involving the complete procedure, from the generation of the initial multivariate model to the final one. This often implies resorting to advanced statistical methodology in order to use as much of the information provided by these biomarkers as possible and thus to retain its complexity. Accordingly, similar methodological considerations should be taken into account for many other formal aspects of the implementation of prediction models based on miRNAs. For example, one issue that we have not discussed here is the choice of the measurement scale. Various researchers have cautioned against the categorisation of continuous explanatory variables, especially when developing predictive models; according to Moons et al (2015), a categorisation ‘should be done on the basis of the model's predicted probabilities or risks' only to classify people in distinct groups in the final stage.

The authors declare no conflict of interest.