Meta-analysis with missing study-level sample variance data

Abstract

We consider a study-level meta-analysis with a normally distributed outcome variable and possibly unequal study-level variances, where the object of inference is the difference in means between a treatment and control group. A common complication in such an analysis is missing sample variances for some studies. A frequently-used approach is to impute the weighted (by sample size) mean of the observed variances (mean imputation). Another approach is to include only those studies with variances reported (complete case analysis). Both mean imputation and complete case analysis are only valid under the missing-completely-at-random assumption (MCAR), and even then the inverse variance weights produced are not necessarily optimal. We propose a multiple imputation method employing gamma meta-regression to impute the missing sample variances. Our method takes advantage of study-level covariates that may be used to provide information about the missing data. Through simulation studies, we show that multiple imputation, when the imputation model is correctly specified, is superior to competing methods in terms of confidence interval coverage probability and type I error probability when testing a specified group difference. Finally, we describe a similar approach to handling missing variances in cross-over studies.

1. Introduction

1.1. Background

In evidence-based medicine, the highest level of evidence is considered to be a systematic review of well-conducted clinical trials [1]. Meta-analysis is often an essential part of systematic review. Comprehensive discussion of statistical methods for classical meta-analysis can be found in Whitehead [2], Hedges and Olkin [3], and Borenstein et al. [4]. For meta-analysis of a continuous variable, methods based on the asymptotic normality of the estimator of the parameter of interest are commonly performed. This paper focuses on the case where one is interested in the difference in mean response (θ) between the independent treatment and control groups of a collection of clinical trials. The standard meta-analytic estimate is the weighted average of the study-level sample mean differences, where the weights are the inverses of the variances of the study-level estimators [5]. For a study-level meta-analysis, the sample variance information is collected for the outcome variables of interest and used to compute the variance of the estimated treatment effect for each study.

A common situation that arises in this context is that study-level sample variances are missing and cannot be calculated given the data reported in the original papers. One should obtain the missing data from the original authors, but it is not always possible. An approach to dealing with this issue is to impute the missing data using a weighted or unweighted average of the observed sample variances. However, this approach, like any single imputation method, does not take into account the variability due to estimating the missing sample variances.

1.2. Motivating Example

The data for our application come from a meta-analysis performed using a large database of neuropathic pain clinical trials (n=200), which was originally analyzed using meta-regression in Dworkin et al. [6]. The primary goal of that research was to identify patient, study, and site factors associated with the magnitude of the treatment effect among randomized, double-blind, placebo-controlled trials of pharmacologic treatments established to be effective in treating various neuropathic pain conditions. In this and similar data sets [7], a sizable portion of the sample variance data were missing. Therefore, a method that handles the missing sample variance data efficiently is of interest.

To illustrate our methods, we focus on the estimation of the average treatment effect in the 84 parallel group trials that used either the visual analog scale (VAS) or the numerical rating scale (NRS) as the outcome variable. The VAS is a pain measure where subjects rate their pain by indicating a spot on a 100 mm line with the ends labeled ‘no pain’ and ‘worst possible pain’ or similar wording. The NRS is a pain measure where subjects rate their pain by selecting a number, most often 0 to 10 in increments of 1, with 0 labeled ‘no pain’ and 10 labeled ‘worst possible pain’ or similar wording. The VAS was transformed to the same scale as the NRS by dividing the means and standard deviations by 10. We treat the two measures equivalently, since they are highly correlated and there is no evidence to suggest that they measure treatment effect differently [6]. For trials involving multiple active dosages of a treatment in a study, we chose the largest dosage. Sample variance data could not be extracted from 16 (19%) of the studies.

1.3. Missingness Assumptions

There are three different possible assumptions that can be made about missing data [8]. Under the missing completely at random (MCAR) assumption, there is no dependence of the missingness on any of the data (observed or unobserved). A less restrictive assumption is the missing-at-random (MAR) assumption, under which the missingness, conditional on the observed data, is independent of the data that would have been observed had they not been missing. Finally, the least restrictive assumption is the missing-not-at-random (MNAR) assumption, under which the missingness may be dependent on the value that would have been observed, even conditional on the observed data. In practice, analyses under the MNAR assumption are typically reserved for sensitivity analyses, as they rely on untestable assumptions about the dependence of the missingness on the unobserved values. In this paper, we focus on analyses that are valid under the MAR assumption.

1.4. Prior Work on Missing Variances

Wiebe et al. surveyed the meta-analysis literature for approaches to handling missing sample variances and other quantities and identified 153 studies that addressed the issue of missing variances, including 112 systematic reviews/meta-analyses and 41 methods papers [9]. The most common method used (aside from algebraic recalculation based on other information presented) was “direct substitution with a baseline or other treatment SD, another included study’s SD, or the maximum thereof, or an SD from another literature source.” This method was found in 13% of the studies in their sample. The simplest method for handling missing sample variance data is to exclude studies with missing data from the analysis, known as complete case analysis (done by 9% of studies in Wiebe et al. [9]). Another approach involves taking an average of the sample variances observed (either weighted or unweighted), and imputing the value obtained [10]; Wiebe et al. found that 10% of studies in their survey used this approach [9]. They concluded that there is no standardized methodology for handling missing variance data. Marinho [11] proposed using simple linear regression of the log-transformed standard deviation on study-level covariates, such as the sample mean, and imputing the exponentiated predicted values for the missing standard deviations. Robertson, Idris, and Boyle [12] proposed multiply imputing missing sample variances using a gamma distribution with parameters for this distribution estimated using the method of moments (the first and second moments of the sample variance), under the equal variance and MCAR assumption.

Idris and Robertson [13] proposed a multiple imputation model that assumes equal variances across studies, using a hot-deck approach to imputation. Stevens [14] proposed a fully-Bayesian multiple imputation model for missing standard errors in meta-analysis that is valid under the equal variance and MCAR assumptions.

The above previously proposed methodology has assumed a common sample variance across studies, or has not properly accounted for the uncertainty associated with the impuation model. In this paper, we propose using a meta-regression-based imputation model that includes study-level covariates to impute the missing data. This approach incorporates the uncertainty associated with the imputation model. Linear fixed effects meta-regression was first described by Greenland [15] and linear mixed effects meta-regression was introduced by Berkey et al. [16]. We extend these methods for the gamma distribution, using a generalized linear mixed model, to multiply impute missing gamma-distributed sample variances. We also consider the problem of missing sample variances in cross-over trials, which may require a different type of imputation model depending on the available information. For a comprehensive overview of multiple imputation, see Rubin [17], Schafer [18], and Carpenter and Kenward [19].

2. Methods

2.1. Meta-Analysis Statistical Methodology for Parallel Group Trials

We focus on the situation where we have summary data from the treatment and control groups from a number of clinical trials. The study-level observations are ${\overline{Y}}_{j,\mathit{treat}}~N({\theta }_j,{\sigma }_j^2/n_{j,\mathit{treat}}),{\overline{Y}}_{j,\mathit{control}}~N(0,{\sigma }_j^2/n_{j,\mathit{control}})$, and $s_j^2=((n_{j,\mathit{treat}}-1)s_{j,\mathit{treat}}^2+(n_{j,\mathit{control}}-1)s_{j,\mathit{control}}^2)/(N_j-2)~\mathrm{\Gamma }\left(\frac{N_j-2}{2},\frac{N_j-2}{2{\sigma }_j^2}\right)$, where N_j = n_j,treat + n_j,control and j denotes study (j = 1, …, J). The expected value of the treatment effect for each study is θ_j (j = 1, …, J). In a meta-analysis with a fixed-effects model, θ_j may be assumed to be constant (equal to θ); alternatively, it may be assumed to follow a particular distribution, such as the normal distribution, under a random effects model (θ_j ~ N(θ, τ²)). We consider both cases. It’s also important to note that while we assume a common variance for the treatment and control groups for the purposes of this manuscript, this assumption is not required. This is discussed further in Section 6.

We are interested in estimating θ = E[Ȳ_j,treat] − E[Ȳ_j,control] (fixed effects model) or θ = E_θj[E_{Ȳj,treat|θj}[Ȳ_j,treat] − E_{Ȳj,control|θj}[Ȳ_j,control]] (random effects model), the expected difference in mean response between the treatment and control groups. As described in Whitehead [2], the inverse variance estimator in meta-analysis is as follows:

$$\widehat{\theta }=\frac{{\sum }_{j=1}^J{w}_j{\widehat{\theta }}_j}{{\sum }_{j=1}^J{w}_j}.$$ (1)

For the fixed effects meta-analysis model, $w_j=1/\widehat{\mathit{var}}({\widehat{\theta }}_j)=1/{\widehat{v}}_j$ and for the random effects model, w_j = (v̂_j + τ̂²)⁻¹, j = 1, …, J. The quantity v̂_j is an estimator for the variance of the estimator θ̂_j for each study (within-study variance), and τ² is the between-study variance. In this paper, τ² is estimated using the DerSimonian-Laird estimator [5], as there can be convergence issues with other methods such as restricted maximum likelihood estimation [20].

2.2. Meta-Analysis Statistical Methodology for Cross-Over Trials

We now consider the meta-analysis of a collection of two-treatment, two-period cross-over trials comparing a treatment (A) and a control (B), with n_ABj subjects randomly assigned to sequence AB and n_BAj subjects assigned to sequence BA in the jth study, j = 1, …, J. The study-level observations are ${\overline{Y}}_{\mathit{ABj}}~N({\theta }_j,{\sigma }_j^2/n_{\mathit{ABj}}),{\overline{Y}}_{\mathit{BAj}}~N({\theta }_j,{\sigma }_j^2/n_{\mathit{BAj}})$, and $S_{xj}^2=\frac{(n_{\mathit{ABj}}-1)s_{\mathit{ABj}}^2+(n_{\mathit{BAj}}-1)s_{\mathit{BAj}}^2}{n_{\mathit{ABj}}+n_{\mathit{BAj}}-2}~\mathrm{\Gamma }\left(\frac{N_j-2}{2},\frac{N_j-2}{2{\sigma }_j^2}\right)$, where Ȳ_ABj (Ȳ_BAj) is the mean within-subject difference in response (A – B) in sequence AB (BA), and N_j = n_ABj + n_BAj, j = 1, …, J. It is of interest to estimate θ = E[Ȳ_j,A] − E[Ȳ_j,B] (fixed effects model) or θ = E_θj[E_Ȳj,A|θj[Ȳ_j,A] − E_Ȳj,B|θj[Ȳ_j,B]] (random effects model), the expected difference in mean response between treatments A and B. It is assumed here that there is no treatment-by-period interaction present.

An estimate of the treatment effect in study j that adjusts for period effects is given by ${\widehat{\theta }}_j=\frac{{\overline{Y}}_{\mathit{ABj}}+{\overline{Y}}_{\mathit{BAj}}}{2}$, j = 1, …, J. The variance of θ̂_j is given by ${\widehat{v}}_j=\frac{1}{4}\frac{n_{\mathit{ABj}}+n_{\mathit{BAj}}}{n_{\mathit{ABj}}{n}_{\mathit{BAj}}}{s}_{xj}^2$. Sometimes, the treatment effect is estimated by the mean of all N_j within-subject A – B differences with corresponding variance $s_{dj}^2/N_j$, j = 1, …, J. In the absence of prominent period effects, $s_{xj}^2$ and $s_{dj}^2$ are very similar. The inverse variance estimator for θ given in (1) above can be applied to the study-level data on estimated treatment effects and their corresponding variances. Curtin et al. [21] and Elbourne et al. [22] describe a simple method for combining the results of parallel group trials and cross-over trials in a meta-analysis.

2.3. Proposed Methodology

For parallel group trials, we propose to use a gamma meta-regression model to impute the missing sample variances, and then use multiple imputation to perform inference about the overall treatment effect (θ) across studies. We fit the meta-regression model based on the observed data in the meta-analysis. Our approach uses the fact that when the outcome variable is normally distributed, the sample variance follows a gamma distribution. Furthermore, we assume for this paper that the study-level covariates have linear relationships with the log of the study-level variance, but this assumption can be modified to fit the application. Considerations for missing variances in cross-over trials are addressed in Section 5.

2.4. Imputation Model for Parallel Group Trials

When the outcome variable of interest is normally distributed, the distribution of the sample variance for each study is

$$s_j^2\mid {\sigma }_j^2~\mathrm{\Gamma }\left(\frac{N_j-2}{2},\frac{N_j-2}{2{\sigma }_j^2}\right),$$ (2)

where ${\sigma }_j^2$ is the population variance. We initially propose the following gamma meta-regression model for the sample variance, in conjunction with Equation 2 above:

$$g({\sigma }_j^2)={\mathbf{x}}_j^T\beta ,$$ (3)

where x_j represents the vector of study-level covariates (j = 1, …, J) and g(·) is a link function, for example the log(·) function. This is a gamma generalized linear model [23], and it can be fit using PROC NLMIXED in SAS. This fixed effects meta-regression model assumes that all of the variation in the sample variances is due to sampling error and the covariates.

Thompson and Higgins [24] argue that for conventional meta-regression analyses of studies, one should use a mixed effects meta-regression model, for it would be impossible to measure all possible sources of variation in a meta-regression. In order to address the heterogeneity among the studies not explained by the covariates, it is necessary to include a random effect. We therefore propose the following mixed effects meta-regression model for the sample variance, in conjunction with Equation 2 above:

$$g({\sigma }_j^2)={\mathbf{x}}_j^T\beta +b_j,$$ (4)

where $b_j~N(0,{\tau }_b^2)$ is the random effect for the variance for the jth study, j = 1, …, J, with ${\tau }_b^2$ being a measure of the between-study variation in the sample variance not explained by covariates. This is a generalized linear mixed effects model, as described in McCulloch and Searle [25]. The parameters and their respective standard errors can be estimated by the method of maximum likelihood, for example using PROC NLMIXED in SAS.

This method is valid under the MAR assumption, takes into account covariate information, and properly accounts for the uncertainty associated with the imputation model. Current methods such as mean imputation and complete case analysis are only valid under more restrictive assumptions. Complete case analysis is only valid under MCAR, while mean imputation assumes equal variances, implying MCAR. Moreover, mean imputation and regression-based single imputation methods do not take into account the uncertainty of imputation of the sample variance. Finally, aside from regression-based single imputation methods, no other methods account for unequal variances. Therefore, these methods, and similar competing methods, do not satisfactorily address the problem of missing sample variances.

2.5. Imputation Procedure

We propose the following procedure for imputing the missing sample variance data.

1. Estimate parameters for a either a fixed effects or mixed effects gamma meta-regression model, using the study sample variance as the outcome, with known dispersion parameter (N_j − 2)/2.

2. For the mixed effects model case, impute ${\tau }_b^2$ using a random draw ${\tau }_b^{2\ast }$ from the inverse gamma distribution. The parameters λ and κ of the inverse gamma distribution are estimated using ${\widehat{{\tau }_b}}^2$ and its estimated variance, V, so that $\widehat{\kappa }={\widehat{\tau }}_b^4/V+2$ and $\widehat{\lambda }={\widehat{{\tau }_b}}^2(\widehat{{\tau }_b^4}/V+1)$, where $f({\widehat{\tau }}_b^2;\kappa ,\lambda )=\frac{{\lambda }^{\kappa }}{\mathrm{\Gamma }(\kappa )}{({\widehat{\tau }}_b^2)}^{-(\kappa +1)}exp\left(\frac{-\lambda }{{\widehat{\tau }}_b^2}\right)$.

3. Obtain a random draw β^* from a N(β̂, var(β̂)) distribution; for the mixed effects model case, also obtain a random draw $b_j^{\ast }$ from a $N(0,{\tau }_b^{2\ast })$ distribution, j = 1, …, J.

4. For each study j = 1, …, J, use the sampled values of the parameters to compute the variance parameters ${\sigma }_j^{2\ast }$ using equation $g({\sigma }_j^{2\ast })={\mathbf{x}}_j^T{\beta }^{\ast }$ or $g({\sigma }_j^{2\ast })={\mathbf{x}}_j^T{\beta }^{\ast }+b_j^{\ast }$ depending on whether one is using a fixed or mixed effects model for the variance, respectively.

5. Sample $s_j^{2\ast }$ from the $\mathrm{\Gamma }\left(\frac{N_j-2}{2},\frac{N_j-2}{2{\sigma }_j^{2\ast }}\right)$ distribution to impute the missing sample variances.

6. Compute a meta-analytic estimate of the mean treatment difference using standard meta-analysis methodology (either a fixed effects or random effects method).

7. Repeat steps 2–6 100 times, each time storing the estimated mean treatment difference and its variance from the analysis.

8. Combine estimates and draw inferences concerning the mean treatment difference using Rubin’s rules for multiple imputation [17].

3. Simulation Studies

3.1. Data Generation

We performed simulation studies to evaluate the proposed approach in terms of power, type I error probability, confidence interval width, confidence interval coverage probability, bias, estimated standard error, and empirical standard error under a variety of scenarios. The object of interest is the difference in the mean of the outcome variable between the treatment and control groups. We consider both a fixed effects model and a mixed effects model for the treatment effects and variances.

We simulated the number of subjects per treatment group once using n_j/5 ~ Poisson(20) to achieve a mean sample size of 100 per treatment group, and kept study sizes constant across all simulations. We included an intercept in the simulation and imputation model, thus making x_j = (x_j,0, x_j,1)^T and β = (β₀, β₁)^T two dimensional vectors, with x_j,0 = 1, j = 1, …, 50. We randomly generated one set of covariates, x_j,1 ~ N(2, 0.81), held constant for all simulations. For the fixed effects model, θ_j = θ = 0.1, and $log({\sigma }_j^2)={\mathbf{x}}_j^T\beta$, with β₀ = 0.5 and β₁ being either 0, 0.75, or 1.5, depending on the simulation. For each subject i and study j, we generated $Y_{ij,\mathit{treat}}~N({\theta }_j,{\sigma }_j^2)$ and $Y_{ij,\mathit{control}}~N(0,{\sigma }_j^2)$, with i = 1, … n_j, n_j = n_j,treat = n_j,control, and j = 1, …, 50.

For the mixed effects model, we independently generated θ_j ~ N(θ, τ²) and $b_j~N(0,{\tau }_b^2)$, with θ = 0.4, $log({\sigma }_j^2)={\mathbf{x}}_j^T\beta +b_j$, and β as above, j = 1, …, 50. The variance components τ² and ${\tau }_b^2$ were each examined for values of 1 and 2.

Power was estimated as the proportion of times that the null hypothesis, H₀ : θ = 0, was rejected under the alternatives θ = 0.1 (fixed effects model) and θ = 0.4 (mixed effects model). To estimate the type I error probability, the simulation studies were repeated with θ = 0. The empirical standard error was computed as the standard deviation of the estimates of θ among the 10,000 simulations, and the estimated standard error was calculated based on the formula for the estimated standard error of θ̂ for each missing data method, averaged across simulations. The missingness model was as follows: π_j, the probability of a study having a missing sample variance, was used to randomly generate missingness (r_j) for each study from a Bernoulli(π_j) distribution, with $\mathit{logit}({\pi }_j)={\mathbf{x}}_j^T\gamma$, j = 1, …, 50. The parameter vector γ = (γ₀, γ₁)^T, with γ₀ = 3 for all simulations and γ₁ being either 0.3584, 0.83475, or 1.1811, to generate 10%, 25%, and 40% missingness, respectively. The number of replications of each simulation was 10,000. The upper bound of the Monte Carlo simulation standard error for probabilities (assuming a true probability of 0.50) for all simulations is 0.005. For Type I error probabilities, a more appropriate estimate of the Monte Carlo simulation standard error (assuming a true Type I error probability of 0.05) is 0.002.

The data were analyzed with the following competing methods for handling missing data: the proposed multiple imputation method, mean imputation (using a sample-size weighted average of the sample variances), single imputation using fixed-effects gamma meta-regression with log-link (using equations 2 and 3 above), single imputation using simple linear regression of the log of the sample variance, and complete case analysis. The data were also analyzed without any missingness (i.e., they were analyzed before any observations were deleted), as a gold standard comparison.

3.2. Simulation Results for Fixed Effects Model

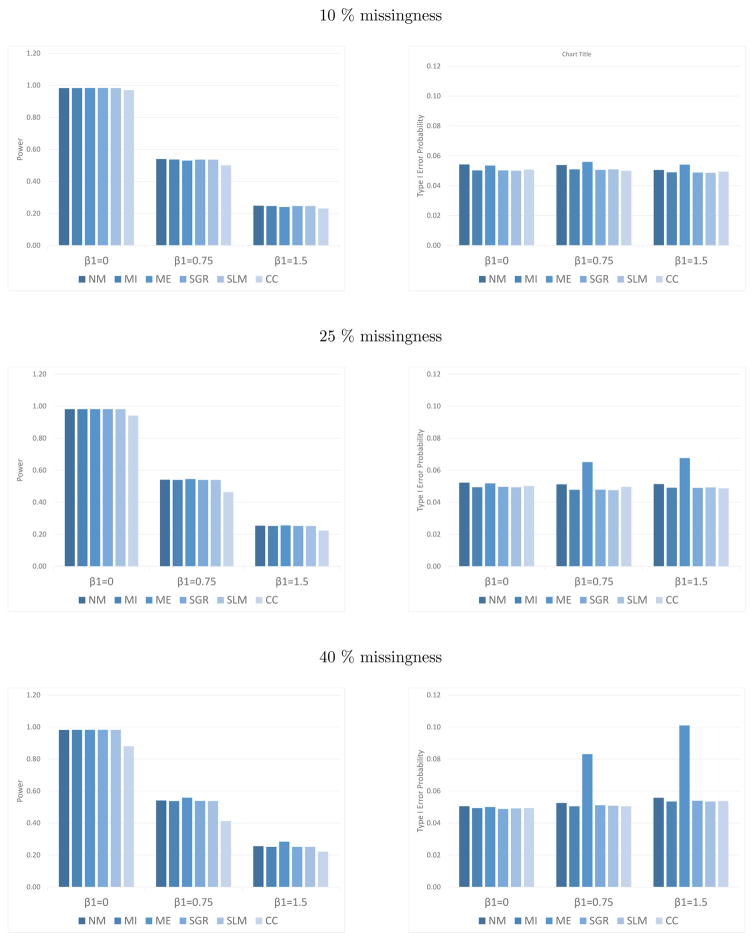
As seen in Figure 1 and Web Appendix A, Tables 1–4, under the MCAR assumption and equal variance assumption (β₁ = 0), all methods except complete case analysis perform comparably. As is well established in other settings, complete case analysis suffers from lower power, wider confidence intervals, and larger estimated standard errors than other methods. It is important to note that if one has prior information that β₁ = 0, it is better not to include the covariate in the imputation model.

Figure 1.

Power and type I error probability (α) for fixed effects analysis, with 10%, 25%, and 40% missingness. The target significance level is 0.05. NM is no missingness, MI is multiple imputation using gamma meta-regression, ME is mean imputation, SGR is single imputation using gamma meta-regression, SLM is single imputation using linear regression based on the log-variance, and CC is complete case analysis.

Under the MAR assumption (β₁ ≠ 0), both complete case analysis and mean imputation perform poorly. Complete case analysis suffers from lower power than other methods, and mean imputation suffers from higher type I error and poorer coverage probabilities (Figure 1). As the amount of missingness increases, the performance of mean imputation and complete case analysis declines. No major differences are seen between single and multiple imputation regression methods. The reason for this will be addressed in the next subsection.

In general, mean imputation results in a larger power than the other methods examined. When the dependence between the sample variance and the predictor is strong (β₁ = 1.5), however, the type I error probability for mean imputation is greater than those for all other methods. Specifically, there is a 0.10 type I error probability for mean imputation, compared with a type I error probability of 0.05–0.06 for all other methods. Similarly as seen in Table 1, the standard error for mean imputation, for 40% missingness and β₁ = 1.5, is substantially underestimated, as compared with the empirical standard error.

Table 1.

Confidence interval width, coverage probability, estimated standard error (SE), and empirical SE for fixed effects analysis, with 40% missingness in sample variances and β₁ = 1.5. NM is no missingness, MI is multiple imputation using gamma meta-regression, ME is mean imputation, SGR is single imputation using gamma meta-regression, SLM is single imputation using linear regression based on the log-variance, and CC is complete case analysis.

β1 = 1.5	Width	Coverage	Estimated SE	Empirical SE
NM	0.303	0.944	0.077	0.079
MI	0.304	0.947	0.078	0.079
ME	0.309	0.899	0.079	0.094
SGR	0.304	0.946	0.078	0.079
SLM	0.304	0.947	0.078	0.079
CC	0.335	0.946	0.086	0.087

Bias is close to 0 for all simulations, as seen in Web Appendix A, Tables 2–4.

3.3. Simulation Results for Mixed Effects Model

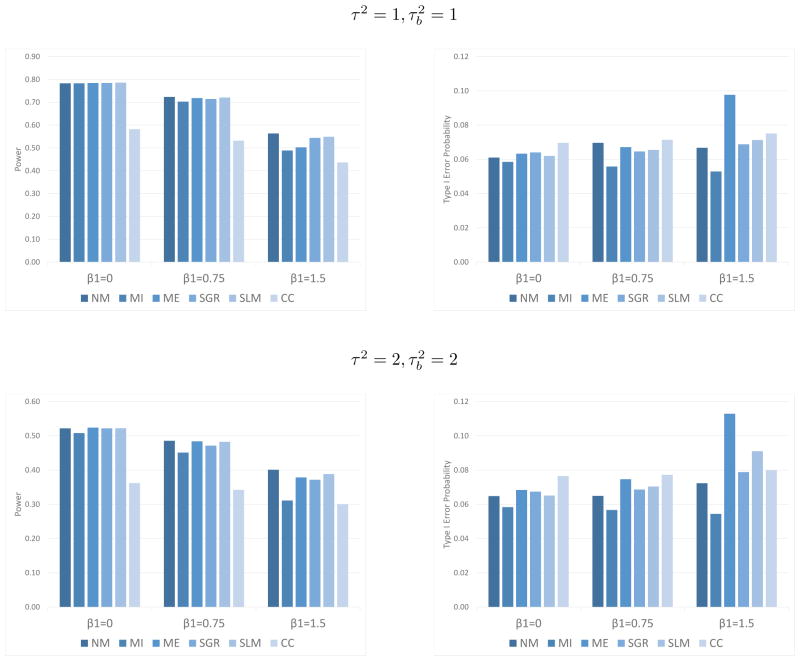
Generally, when β₁ ≠ 0, mean imputation results in a greater inflation of type I error probability than when no data are missing, particularly as β₁ increases. As seen in Figure 2 and Web Appendix A, Tables 5–7, these differences, though found at all amounts of missingness examined, are larger when the degree of missingness is greater. The power and type I error probability from the simulations with 40% missing data when τ² = 1, ${\tau }_b^2=1$ and τ² = 2, ${\tau }_b^2=2$ are shown in Figure 2. The mixed effects multiple imputation model provides stronger control of the type I error probability than the other methods examined. However, the power for multiple imputation is less than or equal to the power for other imputation methods. This is expected, as the estimated standard error is increased to account for the uncertainty involved in imputing $s_j^2$ based on the meta-regression model, rather than treating the imputed value as observed data. Though the power may appear to be higher with single imputation methods, this is misleading since the type I error probability is also significantly inflated with those methods.

Figure 2.

Power and type I error probability (α) for mixed effects analysis, and 40% missingness in sample variances when τ² = 1, ${\tau }_b^2=1$ and τ² = 2, ${\tau }_b^2=2$. The target significance level is 0.05. NM is no missingness, MI is multiple imputation using gamma meta-regression, ME is mean imputation, SGR is single imputation using gamma meta-regression, SLM is single imputation using linear regression based on the log-variance, and CC is complete case analysis.

When β₁ = 1.5, τ² = 1, and ${\tau }_b^2=1$, the confidence interval width and coverage probability combination is better with the mixed effects multiple imputation model than with mean imputation and complete case analysis (Table 2). This pattern is seen in most other cases examined (see Web Appendix A, Tables 8–16). The advantage of using multiple imputation rather than regression-based single imputation is most apparent when β₁ = 1.5, τ² = 2, and ${\tau }_b^2=2$. This is a case where there is a large amount of both explained and unexplained heterogeneity in the sample variances, as well as unexplained heterogeneity in the mean. As can be seen in Figure 2, multiple imputation provides good control of the type I error probability, while regression-based single imputation methods provide poor control.

Table 2.

Confidence interval width, coverage probability, estimated standard error (SE), and empirical SE for mixed effects analysis, with 40% missingness in sample variances, β₁ = 1.5, τ² = 2, and ${\tau }_b^2=2$. NM is no missingness, MI is multiple imputation using gamma meta-regression, ME is mean imputation, SGR is single imputation using gamma meta-regression, SLM is single imputation using linear regression based on the log-variance, and CC is complete case analysis.

β1 = 1.5	Width	Coverage	Estimated SE	Empirical SE
NM	0.952	0.928	0.243	0.250
MI	1.104	0.946	0.282	0.279
ME	1.024	0.887	0.261	0.320
SGR	1.002	0.921	0.256	0.269
SLM	0.978	0.909	0.250	0.277
CC	1.165	0.920	0.297	0.307

Unlike in the simulations for the fixed effects model, differences are seen between regression-based single imputation and multiple imputation methods in the simulations for the mixed effects model, particularly for larger levels of missingness. The likely reason for no difference being observed in the fixed effects model is that the total number of patients is large relative to the number of studies, so the missing variances are imputed with a high degree of precision, and thus there is little between-imputation variability. In the mixed effects model, when the unexplained between-study heterogeneity in the variances ( ${\tau }_b^2$) increases, the ability of the regression model to precisely predict the sample variance declines, and single regression imputation performs poorly relative to multiple imputation in terms of confidence interval coverage probability and control of Type I error probability due to the fact that it does not properly account for the larger between-imputation variability.

The reason why the Type I error probability is above 0.05 in the case of no missing data is that the standard meta-analysis methodology is based on asymptotic results and does not take into account the uncertainty due to the estimation of the sample variance. Our imputation model, on the other hand, takes into account the uncertainty due to the estimation of the variance. A feature of our simulation study is that larger variances are more likely to be missing (through dependence on a known predictor). Also, the standard error of the sample variance is larger when the variance is larger (since the standard error of the sample variance depends on the value of the population variance). We conjecture that the type I error probability is smaller for MI than when there are no missing data because MI takes into account the uncertainty due to estimation of the sample variances. This effect may be more striking in our case in which larger variances have a higher probability of being missing.

As with the fixed effects simulations, bias is close to 0 for all simulations, as reported in Web Appendix A, Tables 8–16.

4. Application

We used the study-level data described in Section 1.2 to estimate the average treatment effect of the interventions established as being effective for neuropathic pain. To perform multiple imputation for the missing sample variances, we selected an imputation model from among 16 variables included in the meta-regression analyses in Dworkin et al. [6]. Two variables, minimum baseline pain required for entry and titration period (days), were included in the model because they were associated with pain score (p<0.20) in univariate meta-regression analyses. Minimum baseline pain represents the smallest level of pain such that a patient can be included in a given study. Titration period (days) represents the total number of days of titration included in the trial; if different treatment groups had different titration period lengths, the largest number of days was used. Minimum baseline pain was trichotomized (30,40,50–60), so it was coded as two binary variables (with parameters β₁ for minimum baseline pain of 40 and β₂ for minimum baseline pain of 50–60, with 30 being the referent group). Therefore, the parameter vector for the imputation model is β = (β₀, β₁, β₂, β₃)^T, with β₀ being the intercept and β₃ being the slope for titration period (days).

The parameter estimates for the imputation model were ${\widehat{\tau }}_b^2=0.32(95\%\text{CI}[0.18,0.46])$, β̂₀ = 1.05 (95% CI [0.48, 1.62]), β̂₁ = 0.44 (95% CI [−0.19, 1.07)]), β̂₂ = 0.71 (95% CI [−0.08, 1.51)]), and β̂₃ = −0.00021 (95% CI [−0.00894, 0.00852)]). The results of the meta-analyses using the different ways to handle the missing sample variance data are presented in Table 3. As with most of our simulations, complete case analysis yielded a wider confidence interval and a larger estimated standard error than other methods. Furthermore, we observed slightly shorter confidence interval width with multiple imputation than with mean imputation and complete case analysis. That there are not large differences between the methods is not surprising, since only 19% of the studies had missing sample variances. As seen in our simulations, larger differences between methods are apparent at higher levels of missing data (≥ 25%). Moreover, we might have seen a greater difference between methods if the estimated elements of β were larger, or if their standard errors were smaller.

Table 3.

Analysis of neuropathic pain data using a mixed effects model, with 19% missingness in sample variances. TE denotes treatment effect and SE denotes standard error. NM is no missingness, MI is multiple imputation using gamma meta-regression, ME is mean imputation, SGR is single imputation using gamma meta-regression, SLM is single imputation using linear regression based on the log-variance, and CC is complete case analysis.

	Estimated TE	Estimated SE	95% CI	CI Width
MI	−0.7512	0.07342	(−0.8951, −0.6073)	0.2878
ME	−0.7521	0.07366	(−0.8965, −0.6078)	0.2888
SGR	−0.7525	0.07335	(−0.8963, −0.6088)	0.2875
SLM	−0.7541	0.07296	(−0.8971, −0.6111)	0.2860
CC	−0.7521	0.08150	(−0.9118, −0.5923)	0.3195

5. Imputation Model for Cross-Over Trials

The meta-analysis of cross-over trials requires an estimate of the variance of the estimated treatment effect, ${\widehat{v}}_j=\frac{1}{4}\frac{n_{\mathit{ABj}}+n_{\mathit{BAj}}}{n_{\mathit{ABj}}{n}_{\mathit{BAj}}}{s}_{xj}^2$. It is sometimes the case that neither v̂_j nor $s_{xj}^2(\text{or}{s}_{dj}^2)$ is reported and this information cannot be recovered through other means (e.g., reported p-values or confidence intervals for treatment effects). If information on variance is available for each treatment condition separately, i.e., $s_{Aj}^2$ and $s_{Bj}^2$, then one can use the formula $s_{xj}^2\approx s_{dj}^2=s_{Aj}^2+s_{Bj}^2-2{\widehat{\rho }}_j{s}_{Aj}{s}_{Bj}$ so that imputation of the required variance only involves imputation of the correlation ρ_j between the within-subject measurements. Of course, this correlation can be estimated from studies that report $s_{xj}^2(\text{or}{s}_{dj}^2),s_{Aj}^2$, and $s_{Bj}^2$.

One solution is to singly impute arbitrary values of the correlation for studies that do not report $s_{xj}^2$, such as 0.5 or 0 [9]. Imputing a value of 0 is conservative in the sense that it over-estimates the variance of the treatment difference, so it reduces power. Other approaches include imputing the minimum correlation from the studies, using correlations from external data sources, or performing a sensitivity analysis using various plausible values for the missing correlations [9]. We propose a meta-regression-based multiple imputation method employing known covariates to impute the missing correlations. The method is as follows:

1. Apply the Fisher transformation to all sample correlations, ${\widehat{z}}_j({\widehat{\rho }}_j)=\frac{1}{2}log\left(\frac{1+{\widehat{\rho }}_j}{1-{\widehat{\rho }}_j}\right)$, in trials in which these can be estimated.

2. Estimate parameters for a either a fixed effects or mixed effects linear meta-regression, using the transformed correlation, ẑ_j, as the outcome, with known variance 1/(N_j − 3).

3. For the mixed effects model case, impute ${\tau }_b^2$ using a random draw ${\tau }_b^{2\ast }$ from the inverse gamma distribution. The parameters of the inverse gamma distribution are estimated using ${\widehat{{\tau }_b}}^2$ and its estimated variance, V, so that $\widehat{\kappa }={\widehat{{\tau }_b}}^2/V+2$ and $\widehat{\lambda }={\widehat{{\tau }_b}}^2(\widehat{{\tau }_b^4}/V+1)$, where $f({\widehat{\tau }}_b^2)=\frac{{\lambda }^{\kappa }}{\mathrm{\Gamma }(\kappa )}{({\widehat{\tau }}_b^2)}^{-(\kappa +1)}exp\left(\frac{-\lambda }{{\widehat{\tau }}_b^2}\right)$.

4. Obtain a random draw β^* from a N(β̂, var(β̂)) distribution; for the mixed effects model case, also obtain a random draw $b_j^{\ast }$ from a $N(0,{\tau }_b^{2\ast })$ distribution, j = 1, …, J.

5. For each study j = 1, …, J, use the sampled values of the parameters to compute the correlations, ${\rho }_j^{\ast }$, using the equation $z_j^{\ast }=x_j^T{\beta }^{\ast }$ or $z_j^{\ast }=x_j^T{\beta }^{\ast }+b_j^{\ast }$ depending on whether one is using a fixed or mixed effects model for the transformed correlation, respectively.

6. Sample $z_j^{\ast }$ from the $N\left(log\left(\frac{1+{\rho }_j^{\ast }}{1-{\rho }_j^{\ast }}\right),\frac{1}{n_j-3}\right)$ distribution to impute the missing sample correlations as ${\widehat{\rho }}_j^{\ast }=\frac{exp(2z_j^{\ast })-1}{exp(2z_j^{\ast })+1}$.

7. Compute a meta-analytic estimate of mean treatment difference using standard meta-analysis methodology (either a fixed effects or random effects method).

8. Repeat steps 2–6 100 times, each time storing the estimated mean treatment difference and its variance from the analysis.

9. Combine estimates and draw inferences concerning the mean treatment difference using Rubin’s rules for multiple imputation [17].

In cases where $s_{Aj}^2$ and $s_{Bj}^2$ are missing as well, one can impute $s_{xj}^2$ by adapting the algorithm presented in Section 2.5.

6. Conclusion

Under the MAR assumption and the unequal variance assumption implied by MAR, mean imputation can yield poor control of the type I error probability, poor coverage probability, and in some instances wider intervals than can be achieved with other methods. Regression-based single imputation methods perform well in fixed effects meta-analysis, where most of the heterogeneity in the variance can be explained by known predictors, but do not perform as well when there is heterogeneity in the variance unexplained by known predictors, particularly when this heterogeneity is large. One may have expected larger improvements with MI relative to competing methods. The likely reason for the relatively modest improvements seen with MI is that the missing data contribute to the estimator only through the weights w_j, j = 1, …, J.

Studies within a meta-analysis may vary in several respects, including patient populations, eligibility criteria, and study design. These differences may lead to heterogeneity of variances between studies. Much as a random effects meta-analysis is performed to allow for heterogeneity in the mean between studies, our method allows for heterogeneity in the variance between studies.

While we assumed a common variance between the treatment and control groups in parallel group trials for the purposes of this manuscript, this assumption is not necessary to apply this general approach. To allow for unequal group variances, one needs to fit separate imputation models for the treatment and control group variances. Furthermore, the distribution of $s_{j,\mathit{treat}}^2\mid {\sigma }_j^2$ is $\mathrm{\Gamma }\left(\frac{n_{j,\mathit{treat}}-1}{2}\frac{n_{j,\mathit{treat}}-1}{2{\sigma }_j^2}\right)$; an analogous result holds for the control group.

We considered the situation where the sample variances are MCAR or MAR. It is also possible that the missingness depends on the true value of the missing variance, that is, the data are missing-not-at-random (MNAR). Our model can be adapted using a pattern mixture model to perform a sensitivity analysis. For example, one can modify the imputation model to be $g({\sigma }_j^2)={\mathbf{x}}_j^T(\beta +\delta )+b_j$, where δ is a vector that is varied. While this model is conceptually simple, it may not be clear how to choose a range of plausible values of δ to explore, particularly when the dimension of β is large. Therefore, more work is needed in this area.

We note that the multiple imputation procedure for missing correlations in cross-over studies can also be applied to the commonly-encountered situation in parallel group studies where a change from baseline is the outcome variable of interest, and some studies only report the sample variance at baseline and at the time point of interest, but not the sample variance of the difference.

Our results also emphasize that even when the missing quantity is itself not of primary interest (e.g., when the missing quantity estimates a nuisance parameter), principled methods such as multiple imputation can provide a benefit over naive methods. The proposed multiple imputation methods yield type I error and coverage probabilities as good as an analysis of the full data with no missingness. Complete case analysis has poor properties and, although often used, is generally not recommended.