DEMARCATE: Density-based magnetic resonance image clustering for assessing tumor heterogeneity in cancer

Abstract

Tumor heterogeneity is a crucial area of cancer research wherein inter- and intra-tumor differences are investigated to assess and monitor disease development and progression, especially in cancer. The proliferation of imaging and linked genomic data has enabled us to evaluate tumor heterogeneity on multiple levels. In this work, we examine magnetic resonance imaging (MRI) in patients with brain cancer to assess image-based tumor heterogeneity. Standard approaches to this problem use scalar summary measures (e.g., intensity-based histogram statistics) that do not adequately capture the complete and finer scale information in the voxel-level data. In this paper, we introduce a novel technique, DEMARCATE (DEnsity-based MAgnetic Resonance image Clustering for Assessing Tumor hEterogeneity) to explore the entire tumor heterogeneity density profiles (THDPs) obtained from the full tumor voxel space. THDPs are smoothed representations of the probability density function of the tumor images. We develop tools for analyzing such objects under the Fisher–Rao Riemannian framework that allows us to construct metrics for THDP comparisons across patients, which can be used in conjunction with standard clustering approaches. Our analyses of The Cancer Genome Atlas (TCGA) based Glioblastoma dataset reveal two significant clusters of patients with marked differences in tumor morphology, genomic characteristics and prognostic clinical outcomes. In addition, we see enrichment of image-based clusters with known molecular subtypes of glioblastoma multiforme, which further validates our representation of tumor heterogeneity and subsequent clustering techniques.

Highlights

• •Tumor heterogeneity in glioblastoma is represented by a probability density function.
• •A technique for clustering, based on these density functions is introduced.
• •Geometry of the space on which these density functions lie is utilized.
• •Clusters show difference in tumor characteristics and prognostic clinical outcomes.
• •Clusters also show enrichment with subtypes of tumor and genomic covariates.

1. Introduction

Glioblastoma multiforme (GBM), also known as grade IV glioma, is a morphologically heterogeneous disease that is the most common malignant brain tumor in adults (Holland, 2000). Despite recent advancements in treatments and discoveries of molecular signatures which can be effectively used in diagnosis, the prognosis for most patients with GBM is extremely poor (Tutt, 2011, McNamara et al., 2013). In the United States alone, twelve thousand new cases are diagnosed every year (www.abta.org/about-us/news/brain-tumor-statistics), among which less than 10% of individuals survive 5 years after diagnosis (Tutt, 2011). The median survival time for patients diagnosed with GBM is approximately 12 months (McLendon et al., 2008). Biological features that differentiate GBM from any other grade of brain tumor include the presence of dead cells (tissue necrosis) and an increased formation of blood vessels near the tumor. Originating from a single cell, a tumor invariably exhibits heterogeneity in physiological and morphological features as it progresses (Marusyk et al., 2012). This presents a considerable challenge for predicting the impact of standard cancer treatments such as chemotherapy and radiation therapy. Thus, exploring tumor heterogeneity is critical in cancer research as inter- and intra-tumor differences have stymied the systematic development of targeted cancer therapies (Felipe De Sousa et al., 2013). However, studies that integrate molecular data (genomics), clinical data and morphological tumor characteristics such as appearance, size, shape and location, have the potential to provide improved and more systematic quantification of tumor heterogeneity (McLendon et al., 2008). Using quantitative imaging features along with clinical features has been shown to be effective in prediction of survival time, which is beneficial for treating patients with GBM (Mazurowski et al., 2013, Gevaert et al., 2014). Colen et al. (Colen et al., 2014) showed that biomarker signatures can be used to identify distinct GBM phenotypes associated with highly significant differences in survival and specific molecular pathways. Thus, data integration can significantly impact the development of personalized therapeutic strategies for cancer, and for GBM in particular.

Modern medical imaging techniques have been extensively used to investigate tumor development in various contexts, including computed tomography (CT), positron emission tomography (PET) and magnetic resonance imaging (MRI) (Held et al., 1997, Tesa et al., 2008, Cheng et al., 2013). In particular, MRI is frequently chosen over other imaging modalities because it furnishes a wide range of image contrasts at high resolution (Nyúl and Udupa, 1999). These images are primarily used to exhibit and evaluate the location, growth and progression of tumors, which serve as indicators for clinical decision making for patients with GBM (McLendon et al., 2008). Recent technological advancements have improved the resolution of MRI, allowing investigators to study distributions of numerous tumor features like permeability in dynamic contrast-enhanced MRI (DCE-MRI), vessel size index (VSI) and apparent diffusion coefficient (ADC) in diffusion MRI, etc. (Just, 2014).

The increasing availability of imaging data through digitalization has spawned substantial computational efforts to quantify and extract features from these routine diagnostic images – providing additional information about the physiology of the tumors. Numerous physiological features have been studied by using the (more detailed) voxel-level data to visualize the progression (or regression) of tumors. However, in almost all of these studies, some ‘summary’ parameters/metrics for the entire regions of interest are evaluated. Baek et al. (Baek et al., 2012) used skewness, kurtosis, histographic pattern, range and mode of the MRI-based voxel intensity histograms. Song et al. (Song et al., 2013) utilized the extreme percentiles (5th and 95th) as features for histogram analysis to study GBM progression. Analogously, Just (Just, 2011) used the 25th and 75th percentiles in the context of gliomas. While these metrics have shown some utility in assessing tumor heterogeneity, they have two major drawbacks. First, the choice of the number and location of summary features (e.g., quantiles or percentiles) is somewhat subjective. Second, and more importantly, these summary features fail to capture the entire information in a histogram (or corresponding density) and thus cannot detect small-scale and sensitive changes in the tumor due to treatment effects (Just, 2014). Thus, using a few statistical features to summarize the entire tumor image leads to significant loss in statistical information, which potentially results in low prediction and correlative power. Alternatively, one can exploit the entire histogram, or its corresponding smoothed density profile for a tumor, which contains more detailed and refined information about the voxel-level tumor characteristics. By utilizing the entire density obtained from various medical imaging modalities, more effective tools for assessing and analyzing tumor heterogeneity can be developed, which leads to improved methods to detect associations with clinical and genomic data.

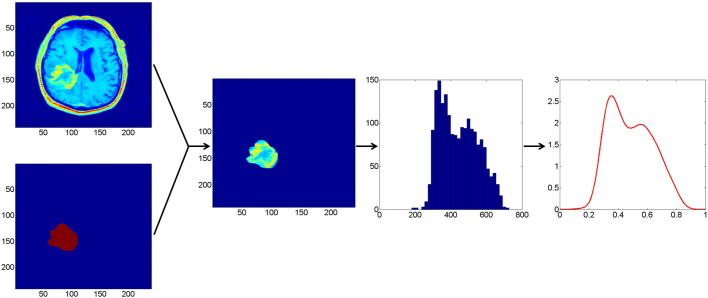
To address these limitations and challenges, we have developed a novel method for the statistical analysis of tumor heterogeneity: DEMARCATE (DEnsity-based MAgnetic Resonance image Clustering for Assessing Tumor hEterogeneity). For each patient, we generate a density profile of voxel intensities that correspond to the segmented tumor region, and use the space of probability density functions (PDFs) for building an appropriate framework for metric-based clustering. In particular, we utilize the geometry of this space for the purpose of comparing and clustering patients based on these density profiles. To achieve this, we utilize the Fisher–Rao Riemannian framework and construct a metric that quantifies the similarity (or dissimilarity) between the densities, which can then be used in conjunction with standard clustering approaches. The main innovation of this approach is the use of the entire distribution of tumor intensities as a representation of tumor heterogeneity, which is in contrast to existing methods based on histogram summaries. Fig. 1 shows the schematic analysis pipeline for DEMARCATE. Applying our methodology to The Cancer Genome Atlas (TCGA) dataset for GBM, our analyses revealed significant patient clusters that correspond to different anatomical features of the tumor, which suggested varying levels of disease aggressiveness. We validated our established cluster memberships to known molecular subtypes, genomic signatures and prognostic clinical outcomes using imaging biomarkers, which revealed new findings and confirmed several previous findings.

Fig. 1.

Brief outline of DEMARCATE.

The rest of this paper is organized as follows. In Section 2, we provide a detailed description of the data used in this study. Section 3 focuses on the statistical framework for DEMARCATE by analyzing tumor heterogeneity under the Fisher–Rao Riemannian-geometric framework. In Section 4, we describe the experimental results. In particular, we study the association between tumor heterogeneity, patient survival, clinical covariates, and the subtypes and genomic signatures of the tumors. We close with a brief discussion and some directions for future work in Section 5.

2. GBM dataset

We collated radiologic images along with linked genomic and clinical data from 64 patient samples for which the patients consented under TCGA protocols (cancergenome.nih.gov). The imaging data consist of a series of pre-surgical T1-weighted post contrast and T2-weighted fluid-attenuated inversion recovery (FLAIR) magnetic resonance (MR) sequences from The Cancer Imaging Archive (www.cancerimagingarchive.net). The acquisition sequences for both imaging modalities are presented in Table B4 in the Appendix. The dataset comprising survival times, clinical and genomic data for these patients was obtained from cBioPortal (www.cbioportal.org).

2.1. Image pre-processing

The pre-surgical MR sequences (T1-weighted post contrast and T2-weighted FLAIR) were processed before extracting the density profiles of tumor intensities, which were then used to derive appropriate representations of tumor heterogeneity. The image pre-processing steps are as follows:

• •Registration of T2-weighted FLAIR MR image to T1-weighted post contrast image;
• •Inhomogeneity correction on the registered T2-weighted FLAIR and original T1-weighted post contrast images: Registration and inhomogeneity correction were performed using Medical Image Processing and Visualization software (mipav.cit.nih.gov), an open-source medical image processing program developed at the National Institutes of Health. Inhomogeneity correction, also known as nonparametric, nonuniform intensity normalization (N3) correction, was performed to remove the shading artifacts in MRI scans;
• •Semi-automated 3D/volumetric segmentation of tumors: Tumors were segmented semi-automatically in 3D using the Medical Image Interaction Toolkit MITK3M3 Image Analysis (v 1.1.0) (mitk.org/wiki/MIT), which has been validated as a method to segment tumors in various organ systems. The segmentation tools were used by the clinician to contour the relevant area on multiple slices. These contours were then interpolated to obtain the 3D volumetric tumor mask. The segmented region corresponds to the contrast enhancing tumor on the T1-weighted post contrast image. On the T2-weighted FLAIR image, the segmented region corresponds to the solid tumor as well as regions of infiltrating tumor and edema that are delineated by increased intensity. Images and their 3D tumor masks were subsequently resliced for isotropic pixel resolution using the NIFTI toolbox in MATLAB. From these resliced images, the slice with the largest tumor area in the T1-weighted post contrast image and the corresponding slice in the T2-weighted FLAIR image were selected as the regions of interest (ROI) for analysis.

2.2. Clinical and genomic data/annotation

The imaging dataset is a subset of a larger patient dataset that contains information on the linked clinical and genomic variables. For clinical variables, we used survival times of the patients. The demographic variables that correspond to the clinical covariates in this dataset are presented in Table 1. Recent investigations have identified four subtypes of GBM: classical, mesenchymal, neural and proneural, each of which is characterized by different molecular alterations (Verhaak et al., 2010). Note that a GBM tumor can be classified as simultaneously belonging to two subtypes. We also curated the information about these GBM subtypes (see Table B2 in the Appendix) and some well-characterized driver genes (see Table B3 in the Appendix) that are considered significant in GBM (Frattini et al., 2013): DDIT3, EGFR, KIT, MDM4, PDGFRA, PIK3CA and PTEN. Biologically, a gene is known as a driver gene when it has a mutation along with DNA-level changes (amplifications or deletions).

Table 1.

Patient demographics for the GBM dataset. Numbers in parentheses represent percentages. Patient age and survival time are represented by the mean ± standard deviation.

Characteristic
Sex
Male (%)	43 (67.19)
Female (%)	21 (32.81)
Age (in years)	56.53 ± 15.40
Survival (in months)	17.53 ± 14.15

3. DEMARCATE statistical framework

In this section, we provide details of the statistical framework for DEMARCATE. As introduced in Section 1, our analytic pipeline consists of three sequential components: (1) Extraction of the tumor voxel intensities from MR images to construct the PDFs – referred to as tumor heterogeneity density profiles (THDPs) – that serve as data objects for this study (Section 3.1), (2) Transformation of the THDPs, which allows for the comparison and modeling of such data objects using a comprehensive Riemannian–geometric framework in the statistical analysis (Section 3.2), (3) Clustering of the subjects based on the geometry of the space of THDPs using the Fisher–Rao Riemannian metric (Section 3.3). We also provide methods for visualizing the clusters, as well as cluster validation (Section 3.4). Although the methods discussed in the following sections are motivated by and described in the context of the specific MRI-based GBM study, they can be applied to any imaging modality that generates voxel-level intensity data structures.

3.1. Extraction of tumor heterogeneity density profiles (THDPs) from MRI data

In the first step of DEMARCATE, we extract the image intensity values associated with the segmented tumors. This process is schematically depicted in Fig. 2 for a T1-weighted post contrast MR image of a typical patient. For all the patients, a similar (analogous) procedure is used for the T2-weighted FLAIR MR image. We begin with a 2D slice of an MR image and a binary mask delineating the tumor (left) as described in Section 2.1. By fusing these two sources of information, we are able to extract the image intensity values that correspond to the tumor only. A histogram of the intensity values that correspond to the extracted tumor region is shown in the third panel of Fig. 2. This is subsequently used to generate a THDP without assuming a specific form for the underlying distribution of the intensity values, i.e., a nonparametric representation. We use the kernel density estimation technique (Rosenblatt, 1956) to determine the density profile directly from the MR image for a given patient. We choose the standard Gaussian kernel as the smoothing function, with the default bandwidth that is theoretically optimal for the Gaussian kernel (Silverman, 1986). The right panel of Fig. 2 displays the kernel density estimate based on the tumor intensity value histogram. Note that after the density estimate is computed, we normalize its domain to [0, 1]. This is done to remove the relative variability in MRI pixel intensities across patients, which is a common phenomenon in MRI data (Nyúl and Udupa, 1999). We repeat this procedure for both modalities and across all 64 patients. As a result, our data objects for the downstream analyses consist of these T1-weighted post contrast and T2-weighted FLAIR THDPs. The DEMARCATE framework is readily adapted to bivariate THDPs estimated using both (or more) imaging modalities (we use the intersection of the T1-weighted post contrast and T2-weighted FLAIR binary tumor masks to extract the respective image intensity values). While the description of the framework focuses on the univariate case for simplicity, we present results of univariate and bivariate THDP analysis in Section 4. Since the THDP data objects are actually bonafide PDFs (i.e., they integrate to 1), we require tools for statistical analysis on the space of PDFs, which we discuss in the next section.

Fig. 2.

Extraction of a THDP. Leftmost two panels: T1-weighted post contrast MR image of a tumor (top) and the corresponding tumor mask (bottom). Second panel: Mask overlaid on the tumor. Third panel: Histogram of pixel intensities corresponding to the tumor. Right: Estimated probability density function representation of tumor heterogeneity (THDP).

3.2. Space of probability density functions and the Fisher–Rao Riemannian metric

In the following steps of DEMARCATE, we exploit the differential geometry of the nonlinear space on which the THDPs lie. We begin with the definition of the nonlinear representation space, which we restrict to the case of univariate densities on [0, 1]. Let $\mathcal{P}$ denote the Banach manifold of THDPs: $\mathcal{P}=\left\{f:\left[0,1\right]\to {\mathrm{ℝ}}_{\ge 0}\left|{\displaystyle {\int }_0^{1}f\left(t\right)\mathit{dt}=1}\right)\right\}$. We note that $\mathcal{P}$ has a boundary, which contains all THDPs for which normalized pixel values become 0 anywhere on the domain. Next, we consider a vector space that contains the set of tangent vectors at a point in $\mathcal{P}$. Intuitively, this space contains all possible perturbations of a THDP f. For any point $f\mathcal{\in }\mathcal{P}$, the tangent space at that point is defined as $T_f\left(\mathcal{P}\right)=\left\{\mathit{\delta f}:\left[0,1\right]\to \mathrm{ℝ}\left|{\displaystyle {\int }_0^1\mathit{\delta f}\left(t\right)f\left(t\right)\mathit{dt}}=0\right)\right\}$. This tangent space will be used to define a suitable metric between two THDPs on the manifold.

Since our final objective is to cluster the patients using their THDPs, we need an appropriate metric to compute distances on $\mathcal{P}$. One intrinsic Riemannian metric that can be used for this purpose is the Fisher–Rao (FR) Riemannian metric. For any two tangent vectors $\delta f_1,\delta f_2\in T_f\left(\mathcal{P}\right)$, the nonparametric version of the FR metric is defined by the following inner-product (Rao, 1945, Kass and Vos, 2011):

$$〈〈\delta f_1,\delta f_2〉〉={\displaystyle {\int }_0^1\delta f_1\left(t\right)\delta f_2\left(t\right)}\frac{1}{f\left(t\right)}\mathit{dt}.$$ (1)

The FR metric has been used in various applications in computer vision (Srivastava et al., 2007). Additionally, metrics related to the FR metric have been widely used for statistical shape analysis (Peter and Rangarajan, 2006, Srivastava et al., 2011, Kurtek et al., 2012). A crucial property of this metric, making it very appealing for statistical analysis, is that it is invariant to re-parameterizations (smooth one-to-one transformations of the domain) of PDFs (Cencov, 2000). Since the FR metric changes from point to point on the space of THDPs, the computation of geodesic paths (locally distance minimizing paths on $\mathcal{P}$) and the distances between these THDPs is very cumbersome, requiring numerical methods to approximate the metric on $\mathcal{P}$. Thus, instead of working on the Banach manifold $\mathcal{P}$ directly, it is useful to select a suitable representation of the space for which the calculations become much easier. In particular, we want to use a transformation on the THDPs such that the nonlinear space changes to a simpler space and computation of the FR metric becomes more convenient.

A convenient choice of representation for THDPs, which helps us overcome the aforementioned computational issue, is its square root representation introduced by Bhattacharyya (Bhattacharyya, 1943). We define a continuous mapping $\varphi :\mathcal{P}\to \mathrm{\Psi }$, where the square root transform (SRT) of a THDP f is given by $\varphi \left(f\right)=\psi =+\sqrt{f}$. The inverse mapping is simply ϕ^− 1(ψ) = f = ψ² (Kurtek and Bharath, 2015). The space of SRT representations of THDPs is given by $\Psi =\left\{\psi :\left[0,1\right]\to {\mathrm{ℝ}}_{\ge 0}\left|{\displaystyle {\int }_0^1{\psi }^2\left(t\right)\mathit{dt}=1}\right)\right\}$ and represents the positive orthant of the unit Hilbert sphere (Lang, 2012). Furthermore, let T_ψ(Ψ) = {δψ | < δψ ,ψ > = 0} denote the tangent space at ψ (for elements not lying on the boundary). With the choice of SRT representation, for any two vectors δψ₁ , δψ₂ ∈ T_ψ(Ψ), the FR metric defined in Eq. (1) becomes the standard ${\mathbb{L}}^2$ Riemannian metric:

$$〈\delta {\psi }_1,\delta {\psi }_2〉={\displaystyle {\int }_0^1\delta {\psi }_1\left(t\right)\delta {\psi }_2\left(t\right)}\mathit{dt}.$$ (2)

To summarize, the SRT representation of PDFs provides two important simplifications: (1) the nonlinear space of THDPs becomes the positive orthant of the unit Hilbert sphere, and (2) the complicated FR metric reduces to the standard ${\mathbb{L}}^2$ metric. Because the ${\mathbb{L}}^2$ Riemannian geometry of the unit sphere is well known, quantities of interest such as geodesic paths and distances between THDPs can be calculated analytically, and thus, in a computationally efficient manner.

3.3. Statistical analysis of the transformed THDPs

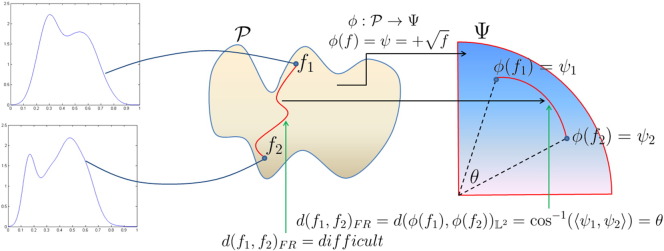
We begin with the definition of the FR distance using the geometry of ψ, i.e., the space of the square root transformed THDPs. This metric will be used to cluster patients with GBM based on their THDPs. The geodesic distance between two THDPs f₁ , f₂ ∈ $\mathcal{P}$, represented by their SRTs ψ₁ , ψ₂ ∈ $\mathrm{\Psi }$, is defined as the shortest arc connecting them on $\mathrm{\Psi }$: cos^− 1(ψ₁, ψ₂) = θ, where the inner product is given by Eq. (2). We denote this distance as d(f₁, f₂)_FR. This is also the standard ${\mathbb{L}}^2$ distance between ψ₁ and ψ₂ on $\mathrm{\Psi }$, denoted by $d{\left({\psi }_1,{\psi }_2\right)}_{{\mathbb{L}}^2}$ or $d{\left(\varphi \left(f_1\right),\varphi \left(f_2\right)\right)}_{{\mathbb{L}}^2}$. Since we are restricted to the positive orthant of the unit sphere, the geodesic distance θ between two THDPs is bounded above by π/2. Fig. 3 provides a description of these ideas. We start with two THDPs, f₁ and f₂, which are points on the Banach manifold $\mathcal{P}$. The FR distance between f₁ and f₂ is given by the length of the shortest geodesic path between them; unfortunately, this quantity is difficult to compute. We use the SRT mapping to simplify the geometry of $\mathcal{P}$ to $\mathrm{\Psi }$, the positive orthant of the Hilbert sphere, where the FR metric becomes the standard ${\mathbb{L}}^2$ metric. Now, the FR distance between f₁ and f₂ on $\mathcal{P}$ is simply the shortest arc between their SRT representations ψ₁ and ψ₂ on $\mathrm{\Psi }$.

Fig. 3.

Graphical representation of the square root transform (SRT) from $\mathcal{P}$ to the positive orthant of the unit Hilbert sphere $\mathrm{\Psi }$, where f₁ , f₂ represent two THDPs and θ is the FR geodesic distance between them.

The final step of DEMARCATE, which consists of grouping patients on the basis of their tumor heterogeneity profiles, uses k-means clustering of THDPs. To proceed, we must specify two important tools from differential geometry required for implementing such an algorithm on this space: the exponential and inverse-exponential maps. For ψ ∈ $\mathrm{\Psi }$ and δψ ∈ T_ψ($\mathrm{\Psi }$), the exponential map at ψ, exp : T_ψ($\mathrm{\Psi }$) → $\mathrm{\Psi }$ is defined as

$${exp}_{\psi }\left(\mathit{\delta \psi }\right)=cos\left(‖\mathit{\delta \psi }‖\right)\psi +sin\left(‖\mathit{\delta \psi }‖\right)\frac{\mathit{\delta \psi }}{‖\mathit{\delta \psi }‖}.$$ (3)

Similarly for ψ₁ , ψ₂ ∈ $\mathrm{\Psi }$, the inverse-exponential map denoted by exp_ψ^− 1 : $\mathrm{\Psi }$ → T_ψ($\mathrm{\Psi }$) is given by

$${exp}_{{\psi }_1}^{-1}\left({\psi }_2\right)=\frac{\theta }{sin\left(\theta \right)}\left({\psi }_2-cos\left(\theta \right){\psi }_1\right),$$ (4)

where θ = cos^− 1(〈ψ₁, ψ₂〉). With the help of these two expressions, we can map points from the representation space $\mathrm{\Psi }$ that contain all the SRTs of THDPs to the tangent space of $\mathrm{\Psi }$ (T_ψ($\mathrm{\Psi }$)), and vice versa.

We are now in a position to exploit the geometry of $\mathrm{\Psi }$ to define an average THDP. The average (or mean) THDP is a representative density profile of the tumor intensity values across multiple patients, which allows us to efficiently summarize and visualize different GBM groups using their THDPs. A generalized version of the mean on a metric space that can be used to compute the average THDP is the Karcher mean (Karcher, 1977). The sample Karcher mean $\bar{\psi }$ on Ψ is the minimizer of the Karcher variance $\rho \left(\bar{\psi }\right)={\displaystyle \sum _{i=1}^{n}d{\left(\bar{\psi },{\psi }_i\right)}_{{\mathbb{L}}^2}^2}$, i.e., $\bar{\psi }=\mathrm{a}\text{rgmi}{\mathrm{n}}_{\psi \in \mathrm{\Psi }}{\displaystyle {\sum }_{i=1}^{n}d{\left(\psi ,{\psi }_i\right)}_{{\mathbb{L}}^2}^2}$. An algorithm for calculating this mean is presented in the Appendix (see Algorithm A1). Note that the sample THDP Karcher mean is an intrinsic average that is computed directly on $\mathrm{\Psi }$ (or equivalently $\mathcal{P}$). We are thus equipped with a mean that is an actual THDP (Karcher mean) and a distance function (FR metric) that we can effectively use to specify a clustering algorithm directly on the space of THDPs.

3.4. Cluster analysis

There are many possible choices of clustering methods that can be used in the current problem. Specifically, we want to utilize an intrinsic version of the k-means clustering technique on $\mathrm{\Psi }$. This approach partitions the space by minimizing the within-cluster sum of squared distances (using the FR metric) to the assigned cluster center. The k-means clustering algorithm for THDPs is provided in the Appendix (see Algorithm A2). This algorithm has two main constraints:

• (i)The number of clusters k must be specified beforehand;
• (ii)The solution depends on the initialization of the cluster means.

We address these two issues in the current problem as follows. The first constraint is application dependent and context-specific – governed by both sample size and interpretability of the clusters. In our setting, we fix the number of clusters at k = 2. This is natural since our primary objective is to find two groups of GBM patients with a high difference in survival time (long versus short survival times). Further, the tumor driver gene covariates are binary, which makes it natural to study whether the two clusters effectively capture the presence versus absence of driver gene mutations. In other contexts, different cluster configurations could be run in parallel as well. In the next section, we address the second issue listed above.

3.4.1. Cluster initialization

There are various choices for initializing the two cluster means in the k-means clustering algorithm. Since we have the ability to quickly compute the pairwise distances for all THDPs using the FR metric, we look at clustering methods that can be implemented using a distance matrix, i.e., hierarchical clustering with complete linkage, hierarchical clustering with average linkage, and partitioning around medoids (PAM) (Theodoridis and Koutroumbas, 2006). For each of these methods, we calculate the cluster membership for each patient. Accordingly, we evaluate the Karcher means and Karcher variances for each cluster.

Let ${\rho }_1\left({\bar{\psi }}_1\right)$ and ${\rho }_2\left({\bar{\psi }}_2\right)$ be the sample Karcher variances (Section 3.3) for clusters 1 and 2 of sizes n₁ and n₂, respectively. To initialize the k-means clustering algorithm, we select the method that minimizes the pooled Karcher variance: $\frac{n_1{\rho }_1\left({\bar{\psi }}_1\right)+n_2{\rho }_2\left({\bar{\psi }}_2\right)}{n_1+n_2}$, i.e., the method that produces the smallest weighted average of cluster-wise sample Karcher variances. It must be noted that the initialization of the cluster means is data-dependent. There is no unique method for initializing the cluster means; rather, it can vary from dataset to dataset. Once we select the ‘optimal’ initialization technique, we can use it to specify the two unique functions (see Algorithm A2 in the Appendix) to initialize the k-means algorithm.

3.4.2. Cluster visualization

In standard settings, it is difficult to intuitively visualize THDPs for different imaging modalities, especially in higher dimensions. Thus, we explore the variability in the THDPs using principal component analysis (PCA), which is an effective method for visualizing the primary modes of variation in data. Note that this visualization is possible because of the FR-geometric framework. Since the tangent space is a vector space (Euclidean), PCA can be implemented, as in standard problems.

Suppose there are n MR images leading to n THDPs. To suitably implement PCA on the space generated by these THDPs, we perform the following steps:

• (i)Compute ψ₁ , … , ψ_n using the SRT of the THDPs.
• (ii)Compute $\bar{\psi }$, the Karcher mean of ψ₁ , … , ψ_n using Algorithm A1.
• (iii)For i = 1 , … , n, compute $v_i={exp}_{\bar{\psi }}^{-1}\left({\psi }_i\right)$ using the inverse-exponential map.
• (iv)Compute the sample covariance matrix. At the implementation stage, THDPs are typically sampled using N points, resulting in an N × N covariance matrix given by $K=\frac{1}{n-1}{\displaystyle \sum _{i=1}^n{v}_i{v}_i^T}$. In practice, v_i’s are N-dimensional vectors that represent the density values at N points on its domain.
• (v)Perform singular value decomposition (SVD) of K. Since K is symmetric, SVD of K is given by K = UΣU^T.

Σ is a diagonal matrix containing the principal component variances ordered from largest to smallest. The columns of U represent the corresponding principal modes of variation in the given data. The principal components computed using these steps can also be used to visualize the THDPs in a lower dimensional space.

3.4.3. Cluster validation

We provide a general Bayesian strategy for cluster validation – wherein we investigate the association between cluster partitions and external information (i.e., covariates) on the cluster-specific subjects. To concretize the discussions, we describe this approach in the context of our GBM MRI example, where we study association between the computed clusters and various covariates that include information about tumor subtypes and genomic mutation status of driver genes (as described in Section 2.2).

To do so, we consider the notion of ‘cluster enrichment’ – specific clusters will exhibit higher rates of enrichment for specific covariate values. To estimate the enrichment, we use a Bayesian model-based approach under a beta-binomial sampling model. We begin with a contingency table that displays the frequency distribution of a particular dichotomous covariate in each cluster. An illustration of such a contingency table is given in Table 2. We want to compare the relative occurrence of a specific covariate across clusters. We recast the problem in terms of a binomial probability model. Let θ₁ ∈ [0, 1] denote the true proportion of A in cluster 1. Similarly, let θ₂ ∈ [0, 1] denote the true proportion of A′ in cluster 1. Accordingly, y₁₁ ~ Binomial(n₁, θ₁) and y₂₁ ~ Binomial(n₂, θ₂). Consider a uniform prior (Uniform(0, 1)) on the true proportions θ₁ and θ₂, which is equivalent to a Beta(1, 1) prior. Since the Beta distribution is conjugate for the binomial, the posterior distribution is of the same family as the prior. The resulting posterior distributions for θ₁ and θ₂ are given by

$$\begin{array}{ll}{\pi }_{{\theta }_1}\left({\theta }_1|y_{11},n_1\right)\hfill & ~\mathit{Beta}\left(y_{11}+1,n_1-y_{11}+1\right)\hfill \\ {\pi }_{{\theta }_2}\left({\theta }_2|y_{21},n_2\right)\hfill & ~\mathit{Beta}\left(y_{21}+1,n_2-y_{21}+1\right).\hfill \end{array}$$

Table 2.

Contingency table showing frequency distribution of a categorical covariate in both clusters for any image modality. A symbolizes the presence of a molecular tumor subtype or a driver gene mutation, whereas A′ represents the absence of such a subtype or mutation.

	Cluster 1	Cluster 2	Total
A	y11	y12	n1 = y11 + y12
A′	y21	y22	n2 = y21 + y22
Total	y11 + y21	y12 + y22	n = n1 + n2

We generate a large number m of samples from the two posteriors π_θ1 and π_θ2, resulting in a set of pairs {(θ₁⁽¹⁾, θ₂⁽¹⁾), … , (θ₁^(m), θ₂^(m))}. Then, we can approximate the true probability P(θ₁ > θ₂) using a Monte Carlo estimate as follows: $P\left({\theta }_1>{\theta }_2\right)\approx \widehat{E}=\frac{1}{m}{\displaystyle {\sum }_{i=1}^{m}I\left({\theta }_1^{\left(i\right)}>{\theta }_2^{\left(i\right)}\right)}$, where I is the indicator function that equals 1 if θ₁⁽ⁱ⁾ > θ₂⁽ⁱ⁾ , i = 1 , … , m, and 0 otherwise. The intuition behind this approach is as follows. If the computed cluster 1 is not associated with the dichotomous covariate of interest, the values of y₁₁ and y₂₁ should be similar, resulting in essentially the same posteriors for θ₁ and θ₂. This in turn would result in a Monte Carlo estimate of P(θ₁ > θ₂) close to 0.5, or no enrichment of that covariate in cluster 1. On the other hand, if y₁₁ and y₂₁ are drastically different, this manifests itself in the posterior distribution, and the Monte Carlo estimate of P(θ₁ > θ₂) would be either very close to 1 (if y₁₁ is much larger than y₂₁), or 0 (if y₁₁ is much smaller than y₂₁). These two scenarios constitute high enrichment of the covariate in one of the clusters (cluster 1 if P(θ₁ > θ₂) is close to 1 and cluster 2 if P(θ₁ > θ₂) is close to 0).

We represent enrichment probabilities (EP) for each covariate (i.e., tumor subtype and mutation status of driver genes) in each cluster using an enrichment matrix in which each row in the matrix corresponds to the aforementioned covariates, and the columns contain enrichment values for the appropriate cluster (ranging between 0 and 1). Thus, an individual cell represents the posterior probability of a molecular tumor subtype or driver gene being enriched in that specific cluster. Graphically, this enrichment probability is represented by a grayscale heat map in which dark gray or black cells indicate greater enrichment of a covariate in that cluster.

4. Application to GBM MRI data

In this section, we use DEMARCATE to study the MRI-based tumor heterogeneities for each patient and for each imaging modality (T1-weighted post contrast and T2-weighted FLAIR). We exploit the full tumor voxel space and generate univariate and bivariate THDPs to study tumor heterogeneity. We cluster the patients based on their respective THDPs (Section 4.1) and then visualize the clusters on a lower dimensional space (Section 4.2). In the following section (Section 4.3), we relate the clusters to prognostic clinical outcomes. We also compare the clustering performance of DEMARCATE to that of popular scalar histogram summary measures such as skewness, kurtosis, percentiles, etc. (Section 4.4). Finally, we validate the clusters using known linked clinical outcomes and radiogenomic covariates, i.e., tumor subtypes and genomic signatures (Section 4.5).

4.1. Clustering results

For the TCGA dataset, we consider estimation of three different THDPs based on the MRI modalities:

• •Univariate THDP for T1-weighted post contrast,
• •Univariate THDP for T2-weighted FLAIR,
• •Bivariate THDP for joint analysis of T1-weighted post contrast and T2-weighted FLAIR.

As discussed in Section 3.4, to implement the intrinsic k-means clustering algorithm, we need to select an appropriate cluster initialization method. We choose the method based on the minimum pooled Karcher variance criterion. The pooled Karcher variances for the three initialization methods we considered are provided in the Appendix (see Table B1). For all three cases, the PAM method produces the minimum value for the pooled variance and is thus chosen for initializing the k-means clustering algorithm.

The number of subjects for the two clusters computed using DEMARCATE are given below:

• •For the T1-weighted post contrast MRI modality, cluster 1 contains 24 subjects and cluster 2 contains 40 subjects.
• •For the T2-weighted FLAIR MRI modality, cluster 1 contains 30 subjects and cluster 2 contains 34 subjects.
• •For the bivariate modality, cluster 1 contains 19 subjects and cluster 2 contains 45 subjects.

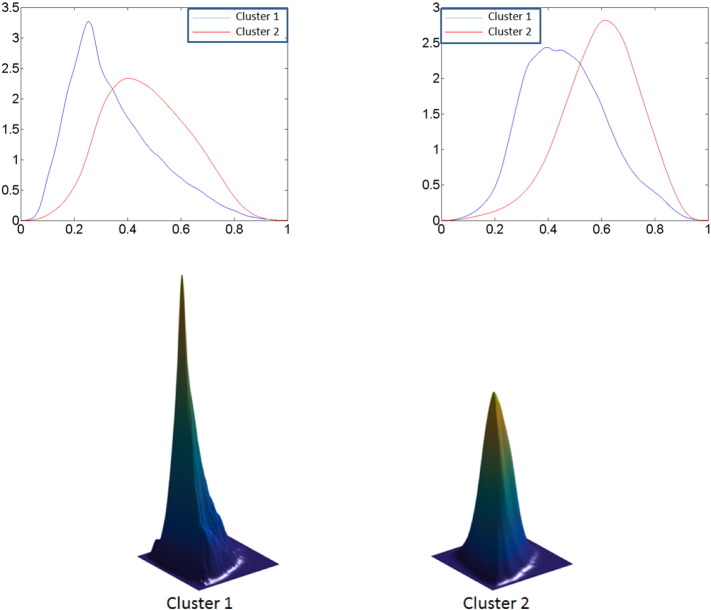
The number of subjects in the T2-weighted FLAIR clusters are almost comparable whereas the T1-weighted post contrast clusters are slightly unbalanced; the clusters computed for the bivariate modality are also unbalanced. The average THDPs for the T1-weighted post contrast clusters are shown in the top left panel of Fig. 4; the average THDPs for the T2-weighted FLAIR clusters are shown in the top right panel of Fig. 4. In both cases, the cluster 1 THDP is displayed in blue, and the cluster 2 THDP is shown in red. The cluster-wise average THDPs for both modalities are considerably different with respect to the mean and spread, with the red THDP (cluster 2) always having much higher average tumor intensity values. We note that the modes for THDPs in each cluster are quite different. The cluster-wise average bivariate THDPs are shown in the bottom panel of Fig. 4. The average THDP for cluster 1 has a much higher and tighter peak, as can be seen in the left panel, than the average THDP for cluster 2 (right panel). Note that each bivariate THDP is plotted on the same scale and thus can be compared visually. In each case, the average THDPs represent the entire set of features for a cluster, which cannot be captured by the often-used histogram summaries like skewness, kurtosis, mode and percentiles.

Fig. 4.

Top: Average cluster THDPs for T1-weighted post contrast MR images (left) and T2-weighted FLAIR MR images (right). Cluster 1 is depicted in blue and cluster 2 in red. Bottom: Average bivariate THDPs for cluster 1 (left) and cluster 2 (right). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

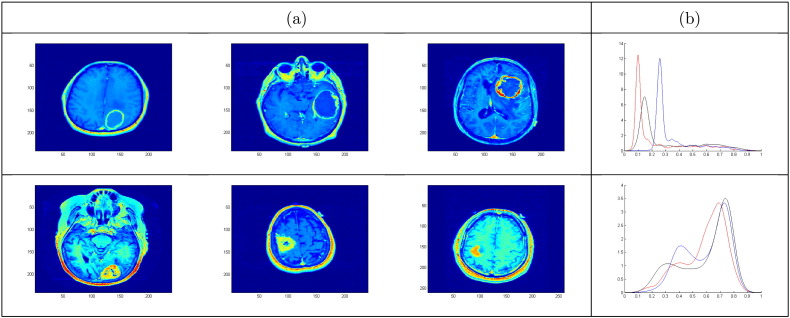
To aid visualization in the original voxel space, we plot a few examples of the actual tumor images in Fig. 5. We find that typical patients in each T1-weighted post contrast cluster display marked phenotypic tumor differences. For patients in cluster 1, we observe an explicit ‘ring-like’ boundary of the tumor (panel (a)), which is characterized by the sharp mode of the THDP, as shown in panel (b). THDPs in this cluster are mostly unimodal, with a sharp peak representing pixel values in the interior tumor region. In cluster 2, we note bimodal THDPs, where the distribution of pixel intensity values in the corresponding tumor regions is more heterogeneous. Also, the mode for THDPs in cluster 2 shifts to the right as compared to cluster 1, which represents higher pixel values being present in greater number for tumors in cluster 2. Thus, based on the T1-weighted post contrast imaging modality, we find two markedly distinct image-based clusters with differences in tumor attributes. Similarly, cluster 2 is hyperintense based on the T2-weighted FLAIR signal, which corresponds to edema and infiltrated tumor cells (Hawkins-Daarud et al., 2013, Zinn et al., 2011). We emphasize that THDP cluster visualization is a difficult task. In this section, we have provided crude summaries of the clusters via average THDPs and a few cluster representatives. In order to capture the complex structure of clusters, it is better to study and visualize the cluster-wise variability, which is better at capturing the inter- and intra-tumor heterogeneity.

Fig. 5.

(a) T1-weighted post contrast MR images for three typical patients in cluster 1 (top) and cluster 2 (bottom). (b) Corresponding THDPs for cluster 1 (top) and cluster 2 (bottom).

4.2. Cluster visualization using PCA

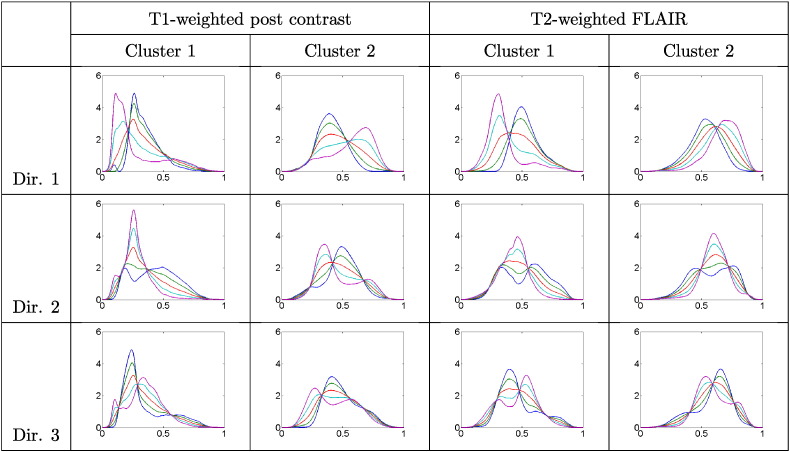
Utilizing the algorithm for PCA discussed in Section 3.4.2, we display the computed clusters (for the univariate case only) using a lower dimensional representation of the tangent space $T_{\bar{\psi }}\left(\mathrm{\Psi }\right)$. We investigate the cluster-wise principal directions of variation in each modality using $t\sqrt{{\mathrm{\Sigma }}_{\mathit{ii}}}{U}_i$ for t ranging from − 2 to + 2, with t = 0 corresponding to the mean. The value $\sqrt{{\mathrm{\Sigma }}_{\mathit{ii}}}$ refers to the square root of the ith element of the diagonal matrix Σ (variance of the ith principal component), and U_i refers to the ith column of U (ith principal direction of variation). Fig. 6 shows the three principal directions of cluster-wise variability (i = 1 , 2 , 3) for the T1-weighted post contrast and the T2-weighted FLAIR modalities. For each imaging modality, the dominant (first) direction of variability shows significant changes in the mode as we differ from the mean, i.e., as we vary t. Such transformations reflect natural differences in relative proportions of the different tumor tissue compartments. When examining the second and third principal directions of variability, we notice more complex structure where THDPs change in shape and the number of modes. This suggests that the computed clusters capture both, simple THDP mode differences (shifts shown in the first direction) and finer changes in shape and multimodality (the second and third directions). As mentioned earlier, such complex cluster structure is difficult to capture using histogram summary statistics. A display of the projection of the THDPs onto the two-dimensional principal subspace as well as the dominant direction of variability in each modality are provided in Fig. 9 in the Appendix.

Fig. 6.

First three principal directions (top to bottom) of cluster-wise variability (left to right) in THDPs for each modality. Blue = − 2 standard deviations (sd); green = − 1 sd; red = mean; cyan = + 1 sd; magenta = + 2 sd. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

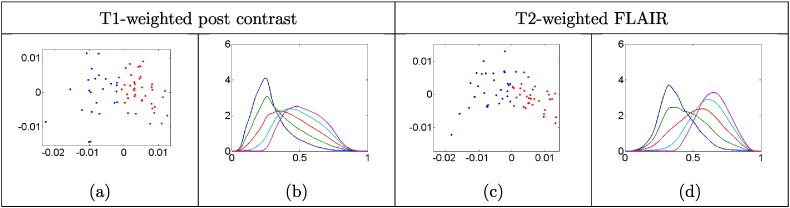
Fig. 9.

Graphs (a) and (c) show a two-dimensional plot of the first two principal component scores. Cluster 1 is represented in blue and cluster 2 in red; (b) and (d) show the first principal direction of variability. Blue = − 2 standard deviations (sd); green = − 1 sd; red = mean; cyan = + 1 sd; magenta = + 2 sd. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4.3. Cluster association with linked prognostic clinical outcomes

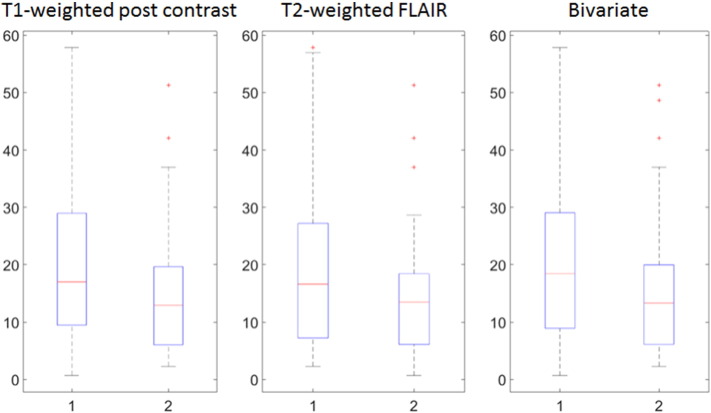
Next, we relate the computed cluster membership from all the estimated THDPs to their survival time and other clinical prognostic indicators. We note a marked cluster difference between the distributions of survival times. In particular, cluster 1 with the ring-like structures has a higher mean and median survival time compared to cluster 2 (Fig. 7) for all three modalities.

Fig. 7.

Boxplots of cluster-wise survival times (in months) for the T1-weighted post contrast MRI modality (left), T2-weighted FLAIR MRI modality (center) and bivariate modality (right).

The results for survival times are summarized in Table 3. These results are consistent with our finding that the mean of the average THDP in cluster 1 is always lower than that in cluster 2, as can be clearly seen from Fig. 4. This suggests that the heterogeneity of pixel intensities captured through the density representation of a tumor may be related to a patient's survival prognosis. The altered hyperintensity between the clusters derived from T2-weighted FLAIR MR images suggests a clear survival difference based on varying infiltrative characteristics of the tumor. We emphasize that the mean (and median) survival differences across the two clusters found using the THDPs are quite large (3–7 months), especially in the context of GBM – considering that the overall median survival in GBM is only around 12 months, as indicated in Section 1.

Table 3.

Summary statistics for cluster-wise survival times (in months) for each modality. The survival time differences are highlighted in bold.

	Mean			Median
Cluster 1	Cluster 2	Difference	Cluster 1	Cluster 2	Difference
T1-weighted post contrast	22.06	14.81	7.25	17.00	12.95	4.05
T2-weighted FLAIR	20.28	15.11	5.17	16.60	13.45	3.15
Bivariate	22.37	15.49	6.88	18.40	13.30	5.10

4.4. Performance of clustering algorithms based on standard summary features

Table 4 provides statistics for the histogram summary features proposed in Section 1. The left column lists the features considered for histogram analysis in previous clinical studies. We do not use the bivariate THDP representation in this case since, to the best of our knowledge, extracting statistical summary features from bivariate histograms has not been previously considered in any GBM study. We apply k-means clustering using the univariate features and note the difference in mean and median survival times for each method. To implement the clustering algorithm, we choose 100 different initializations to calculate the clusters. For each imaging modality, the average difference in mean and median survival times, along with their standard deviations are reported. We note that for both imaging modalities, DEMARCATE generally performs better. We always obtain a greater difference in mean survival time (Table 3) using DEMARCATE, which validates our representsation of tumor heterogeneity and geometry-based clustering.

Table 4.

Comparison of various clustering methods based on histogram summary measures. The numbers represent the average difference in cluster-wise mean and median survival times (in months) for each modality obtained using k-means clustering. Numbers in parentheses represent standard deviation of the differences based on 100 different initializations of the clustering algorithm.

		T1-weighted post contrast	T2-weighted FLAIR
Difference	Difference
Skew., Kurt., Range, Mode (Baek et al., 2012)	Mean	0.08 (0)	1.01 (0.55)
Median	0.05 (0)	1.81 (0.04)
5th and 95th percentile (Song et al., 2013)	Mean	6.85 (0.55)	2.64 (2.30)
Median	6.92 (0.26)	1.38 (1.05)
25th and 75th percentile (Just, 2011)	Mean	4.94 (≈ 0)	2.96 (1.03)
Median	5.10 (≈ 0)	2.36 (0.88)

4.5. Cluster validation using radiogenomic associations

Certain molecular and genomic signatures related to the growth and progression of GBM provide useful information for the clinical management of the disease. In a secondary analysis, we aim to validate whether the clusters are characterized by salient features based on tumor subtypes (see Table B2 in the Appendix) and to verify the mutation status of driver genes (see Table B3 in the Appendix). This helps us to biologically relate each cluster to the differently expressed driver genes. The GBM genes that are used to validate our clustering technique are genes targeted by somatic mutations and copy number variations (Frattini et al., 2013). In primary GBM, EGFR amplification is the most frequently amplified and over expressed gene (30%–70%) (McNamara et al., 2013). Similarly, a tumor suppressor gene, PTEN, is deleted in 50%–70% of cases and mutated in 14%–47% cases of primary GBM (Simpson and Parsons, 2001). Thus, a study of these emerging biomarkers that reveal molecular and metabolic alterations in GBM can guide patient-specific therapies.

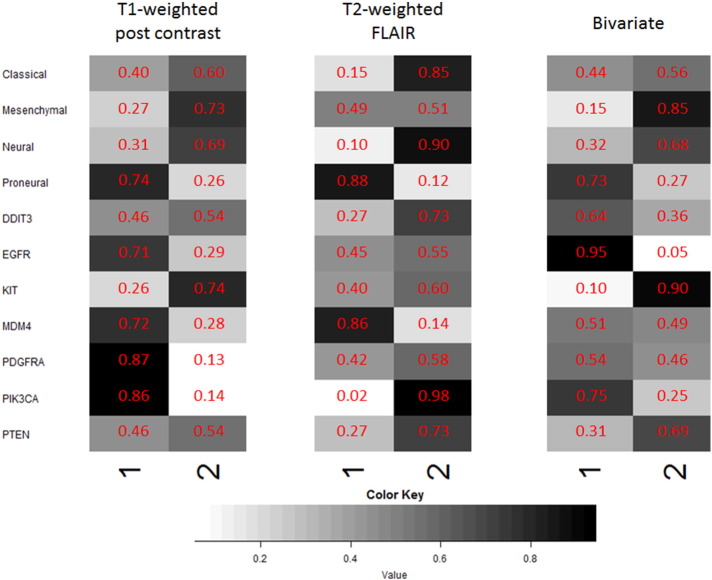
For each imaging modality (including bivariate), enrichment for the different covariates in each cluster is calculated using the methodology described in Section 3.4.3. The enrichment plots (overlayed with enrichment probabilities) in Fig. 8 display results consistent with some of the well-characterized genomic signatures in GBM. In each case, we found associations between tumor subtypes and driver gene mutations that are in concordance with prior studies and corroborate their findings. Below, we present our findings and cite the relevant references where these associations have been studied before. For the T1-weighted post contrast MRI modality:

• •Proneural subtype (EP = 0.74) and PDGFRA (EP = 0.87) are enriched in the same cluster (cluster 1) (Verhaak et al., 2010);
• •Mesenchymal subtype (EP = 0.73) and PTEN (EP = 0.54) are enriched in the same cluster (cluster 2) (McNamara et al., 2013).

Fig. 8.

Enrichment plots for tumor subtype and genomic covariates for the T1-weighted post contrast MRI (left) and the T2-weighted FLAIR MRI (right). The color key is provided below the enrichment plots.

For the T2-weighted FLAIR MRI modality, we found the following associations:

• •Classical subtype (EP = 0.85) and EGFR (EP = 0.55) are enriched in the same cluster (cluster 2) (Verhaak et al., 2010);
• •Neural subtype (EP = 0.90) and many of the driver genes including DDIT3 (EP = 0.73), EGFR (EP = 0.55), KIT (EP = 0.60), PDGFRA (EP = 0.58), PIK3CA (EP = 0.98), PTEN (EP = 0.73) are enriched in the same (cluster 2). For the neural subtype, McNamara et al. (McNamara et al., 2013) described mutations in many of the same genes as the other three subgroups, which can be seen from our enrichment plot.

Similarly, for the bivariate clusters based on joint analysis of T1-weighted post contrast and T2-weighted FLAIR, we find the following associations:

• •Proneural subtype (EP = 0.73) and PDGFRA (EP = 0.54) are enriched in the same cluster (cluster 1) (Verhaak et al., 2010);
• •Mesenchymal subtype (EP = 0.85) and PTEN (EP = 0.69) are enriched in the same cluster (cluster 2) (McNamara et al., 2013).

The most assertive clinical association is the inclusion of younger patients in the proneural subtype (Verhaak et al., 2010). For the T1-weighted post contrast MRI, the average age of a patient in cluster 1 is 52.5 years as opposed to 59 years in cluster 2. Similarly, for the T2-weighted FLAIR MRI, the average age of a patient belonging to cluster 1 is 51.3 years, which is distinctly lower than the average age of 61.1 years in cluster 2. For the bivariate modality, we note a slight difference in the average age of a patient in each cluster: 54.16 years for cluster 1 and 57.53 years in cluster 2. For all of the modalities, the classical, mesenchymal and neural tumor subtypes are enriched in cluster 2 whereas the proneural subtype is highly enriched in cluster 1. The proneural tumor subtype is associated with a longer overall survival time and better prognosis than that for the classical tumor subtype (Lin et al., 2014) and mesenchymal tumor subtype, which has the worst patient prognosis (Naeini et al., 2013). For all modalities, the proneural subtype is highly enriched in the cluster with higher mean and median survival while the classical and mesenchymal subtypes are enriched in the cluster with lower mean and median survival survival times.

5. Discussion and future work

We have defined a novel representation of tumor heterogeneity based on T1-weighted post contrast and T2-weighted FLAIR MRI modalities that is a probability density function estimated from tumor intensity histograms. While most methods have used summary statistics of the intensity histograms to study tumor heterogeneity, we proposed to study the full THDPs under the Fisher–Rao Riemannian-geometric framework through our method DEMARCATE. For each patient and each MRI modality, we apply the DEMARCATE pipeline: (1) extract pixel intensity values corresponding to the tumor, (2) estimate the THDP from the intensity histogram using kernel density estimation, (3) transform the estimated THDP to its SRT representation, and (4) apply k-means clustering on the space of THDPs to separate the patients into two groups. This framework allows for intrinsic summarization and clustering of the patients based on their respective THDPs. We have shown through multiple analyses that the computed cluster memberships are associated with distinct clinical characteristics, molecular tumor subtypes and driver gene mutations. This shows promise for DEMARCATE in further radiogenomic studies of GBM. Although applied to a specific imaging modality (MRI) in GBM, the proposed technique can be used for any voxel-level data and is not confined to MRI data alone.

In spite of recent advancements in the field of radiogenomics, clinical diagnosis of the affected tissue region is still required to differentiate between primary and metastatic brain tumors. For large populations of patients, validation and standardization of the proposed density-based clustering approach to analyze MRI data in GBM is a demanding challenge. If validated in a suitably matched large clinical cohort, DEMARCATE can be reliably used for any imaging modality to segregate and inspect tumor heterogeneity through noninvasive means. Future directions of study include exploring phenotypic characteristics in each cluster identified from the two MRI modalities.

Although the current framework for clustering patients with GBM using their THDPs extracted from 2D MRI modalities is showing promise, there is clear room for improvement. In particular, one could use the full 3D tumor information to form the THDPs for clustering purposes. This presents a way to suitably leverage all the intensity information in the tumor rather than just the information contained in the largest slice. Secondly, important spatial information is discarded during the construction of THDPs. We are currently working on extending the THDP representation to include spatial information in addition to pixel/voxel intensities. Finally, the versatility of the proposed representation of tumor heterogeneity allows for simultaneous analysis of multiple THDPs corresponding to relevant tumor compartments. This extension would allow for a more in-depth analysis of intra-tumor heterogeneity.

Appendix A

A gradient-based algorithm for computing the Karcher mean on Ψ (Dryden and Mardia, 1998, Kurtek, 2016) is presented below for convenience. This algorithm can be initialized using either one of the THPDs in the given sample or the extrinsic average.

The k-means algorithm on $\mathrm{\Psi }$ minimizes the within-cluster Karcher variance if we choose the cluster center to be the Karcher mean and the distance to be the FR distance. Let f₁ , … , f_n denote a sample of THDPs, and ψ₁ , … , ψ_n be their respective square root representations. The k-means clustering algorithm (MacQueen, 1967) on $\mathrm{\Psi }$ is given as follows.

Appendix B

Table B1.

The following table contains pooled Karcher variances for the three initialization strategies: (1) hierarchical clustering with complete linkage, (2) hierarchical clustering with average linkage, and (3) partitioning around medoids (PAM).

MRI modality	Hierarchical (complete)	Hierarachical (average)	PAM
T1-weighted post contrast	2.6663	5.5457	2.4446
T2-weighted FLAIR	5.0315	5.7524	2.3261
Bivariate	14.7683	17.4325	9.3037

Table B2.

The following table shows the frequency of different tumor subtypes in the dataset. Note that a GBM tumor may simultaneously belong to two different tumor subtypes.

Tumor subtype	Classical	Mesenchymal	Neural	Proneural
Frequency	28	30	13	11

Table B3.

The following table shows the frequency of driver gene alterations in the dataset. The numbers in parentheses represent percentages.

Driver gene with alterations	DDIT3	EGFR	KIT	MDM4	PDGFRA	PIK3CA	PTEN
Frequency (%)	6 (9.4)	24 (37.5)	5 (7.8)	4 (6.3)	7 (10.9)	5 (7.8)	5 (9.4)

Table B4.

The acquisition sequences for the T1-weighted post contrast and T2-weighted FLAIR imaging modalities are given in the following table for the relevant dataset.

T1-weighted post contrast	T2-weighted FLAIR
TE: 2.1–20 ms	TE: 14–155 ms
TR: 4.944–3256.24 ms	TR: 400–11,000 ms
Slice thickness: 1.4–5 mm	Slice thickness: 2.5–5 mm
Spacing between the slices: 0.7–6.5 mm	Spacing between the slices: 2.5–7.5 mm
Matrix size: 256 × 256 or 512 × 512	Matrix size: 256 × 256 or 512 × 512
Pixel spacing: 0.468–1.016 mm	Pixel spacing: 0.429–0.938 mm

Appendix C

In Fig. 9, we plot each THDP using its first two principal component scores, which are found by PCA (Section 3.4.2) of the entire dataset (not cluter-wise). We do this separately for each modality (univariate THDPs only) and plot the two clusters using different colors; additionally, we investigate the principal direction of variation. The clusters for each modality are well separated along the principal direction of variability (right side of each panel in Fig. 7).