Differential Multiphoton Laser Scanning Microscopy

Abstract

Multifocal multiphoton microscopy (MMM) in the biological and medical sciences has become an important tool for obtaining high resolution images at video rates. While current implementations of MMM achieve very high frame rates, they are limited in their applicability to essentially those biological samples that exhibit little or no scattering. In this paper, we report on a method for MMM in which imaging detection is not necessary (single element point detection is implemented), and is therefore fully compatible for use in imaging through scattering media. Further, we demonstrate that this method leads to a new type of MMM wherein it is possible to simultaneously obtain multiple images and view differences in excitation parameters in a single shot.

1 Introduction

Owing to its numerous advantages over confocal microscopy, multiphoton microscopy (MPM) has become a vital tool for obtaining high resolution images of biological tissues in a relatively non-invasive manner. Due to the nature of the nonlinear excitation process, MPM has proven especially useful for imaging deep into highly scattering biological tissues [1, 2]. Furthermore, MPM can be performed with several contrast mechanisms, including nonlinear absorption [3] and nonlinear fluorescence [1], harmonic generation [4–7] and nonlinear scattering processes [8, 9]. Each of these mechanisms allows one to gain insight into the structure and function of the sample under study via the localization of nonlinear response.

Since it was first introduced in 1998 [10, 11], multifocal multiphoton microscopy (MMM) has been a useful extension of MPM for high speed image acquisition. By separating a single excitation focus into several foci, the area each focus must scan may be decreased, thereby increasing the speed with which successive frames may be acquired. Unfortunately, multifocal systems suffer from several disadvantages often associated with confocal and wide-field microscopes, thereby reducing or eliminating the advantages gained by MPM. The largest restriction in MMM setups is the need to use imaging detectors to accurately map the nonlinear signal generated by each focus [12], resulting in a reduction in resolution in scattering samples, and negating other advantages of MPM for highly scattering media.

In this paper we report on a system for imaging with multiple foci that does not require an imaging detector. Instead, a single-element detector (e.g. a photomultiplier tube (PMT)) is used to collect the nonlinear signal generated by each focus inside the sample. The signal measured by the PMT is electronically demultiplexed to attribute photons to the appropriate focus. This allows one to collect images from multiple foci while maintaining the whole-field detection typical of MPM, making it possible to image through highly scattering media for the first time. Further, we show that the nature of the optical system used leads to a new type of microscopy, dubbed differential multiphoton microscopy (DMM), which makes it possible to simultaneously obtain multiple images and view differences in excitation parameters in a single shot. In the DMM setup presented here, the beams which generate each foci are spatially separated, making it possible to modify each focus individually. The result is a set of simultaneous images which highlight the differences resulting from varied excitation parameters, a tremendous advantage for imaging in dynamic biological specimens.

Another great advantage of the DMM system outlined herein is the ability to perform multimodal whole field detection with multiple foci. This has yet to be done in a multifocal system without the use of imaging detectors such as CCD cameras, and has the advantage that spatial resolution does not degrade any more than in a standard MPM apparatus. This is especially useful for multiply tagged samples, as in the case of imaging deep into living brain tissue with multiple fluorophores [13], or in the case where multiple nonlinear modalities such as harmonic generation and nonlinear fluorescence are of interest [14]. Since shorter wavelengths are subject to more scattering, this is extremely beneficial for biological microscopy, especially for imaging without exogenic fluorophores.

This paper presents several new imaging results made possible by the DMM system, including:

• First demonstration of simultaneous DMM by optical multiplexing and electronic demultiplexing.

• First simultaneous multi-color excitation DMM.

• First video-rate DMM with simultaneous acquisition. Each of these imaging modalities is highly beneficial for numerous assays in biological microscopy, and thus the ability to apply them to in highly scattering media for the first time has great potential for a myriad of experiments.

2 Multifocal Multiphoton Microscopy (MMM)

Multifocal multiphoton microscopy has been implemented in a number of configurations for biological imaging applications. In all cases, a single femtosecond laser pulse is split into multiple pulses, each of which is then relayed to the sample plane in the microscope. By careful design of the image relay optics, each focus is spatially, and in some cases temporally, offset from the others far enough to prevent interference and preserve spatial resolution. Thus instead of a single focus in the specimen plane of the microscope, an array of foci is generated, each of which has sufficient energy to generate nonlinear contrast. While the methods used to generate multiple foci in a microscope can vary, the purpose of MMM is typically related to two major shortcomings of standard MPM systems.

First, a typical MPM setup is extremely inefficient. The femtosecond laser source must be driven by an optical pump beam and operates at somewhere around 20–30% efficiency. In the case of most commercial titanium-doped sapphire (Ti:Al₂O₃) oscillators, for example, 2 W of power in the femtosecond beam requires the cavity to be pumped with green laser light at ~10 W. The efficiency is further degraded by the fact that 2 W of power is far too high for most biological imaging applications. Several published accounts have indicated that the peak intensity that can be tolerated by most biological tissues is roughly 200 GW/cm² for pulses 200 fs in duration [15, 16], so only a small portion of the available pulse energy may be used for imaging. For example, if one assumes laser pulses 200 fs in duration (measured at the FWHM of an assumed Gaussian intensity profile) occurring at a repetition rate of 80 MHz, 2 W of average power results in a peak power of 83 kW. If the excitation objective used for imaging focuses the laser to 1 µm² in the specimen, an average power of just 48 mW is needed to generate 200 GW/cm² in the sample plane (cf. Appendix A), meaning that only about 2.4% of the oscillator power may be used to image. This assumes that the relay optics from the laser cavity to the microscope are perfectly efficient, which is of course not possible in practice. If a more reasonable throughput efficiency of 50% is assumed from laser cavity to sample plane, then 4.8% of the laser power available at the focal plane may be used. Clearly, this is a waste of very expensive excitation photons, and in a typical MPM setup this extra energy is simply discarded.

MMM circumnavigates this issue by taking some of that discarded energy and using it to generate multiple focal points in the sample plane. Available laser power may be more efficiently used by splitting a single focus into multiple foci, thereby placing the maximum average power into N beams. If, for example, one images with 16 foci, then the average power incident on the sample may be increased 16-fold, resulting in 768 mW of average power in the sample plane. As long as this amount of average power does not adversely affect the specimen by heating in the sample plane, excitation photons may be used much more efficiently, 76.8% of the 1 W throughput in this case instead of 4.8%.

While efficiency of power use is important, it is not the most common reason for implementing an MMM system. In fact, the inefficient use of power makes it possible to use low throughput devices such as spatial filters and pulse shapers between the laser oscillator and the microscope. A more common reason for switching to an MMM setup from a standard MPM setup is to improve image acquisition speeds.

Biological samples are inherently four-dimensional (4D), requiring that a three dimensional (3D) data stack be obtained within an acceptable time frame. In the case of imaging fixed specimens, the temporal component is not critical and the problem effectively becomes 3D. In the ideal case however, image acquisition would collect data from a specimen in 3D with high spatial resolution, and with enough temporal resolution to resolve dynamic processes occurring within the sample. This is the ultimate goal of MPM in the biological sciences – to study the 4D behavior of a specimen with high spatial and temporal resolution, all without damaging the sample.

All laser-scanning microscopes are limited in their image acquisition time by the read time of the detector, the scan rate of the beam-rastering mechanisms, and the photon yield of the nonlinearity used to generate image contrast. To acquire a 3D image in a typical MPM apparatus, the focal volume must be rastered across the sample in a two-dimensional (2D) plane, and then either the sample or the excitation objective is translated and another 2D image is acquired. This process is continued until the desired volume within the sample has been imaged. In a common imaging scheme with galvonometric scan mirrors for example, frame rates of 0.5–10 Hz can be achieved. While this may be adequate temporal resolution for certain applications, it is only in a 2D plane within the sample that is being scanned. Typical translation times in the axial direction take milliseconds, greatly increasing total data collection time, and making it difficult to resolve dynamic processes in living tissues.

Many examples of solutions to this fundamental limit in acquisition speed have been proposed, such as nonlinear holographic microscopy (NHM), and nonlinear wide-field microscopy [17]. While these methods improve the 3D acquisition rate by either imaging a 3D field of view (FOV) or by negating the need for 2D scanning in the lateral plane, they suffer from some disadvantages that are circumnavigated by MPM with single point excitation.

Until recently, all MMM setups reported on have generated a laterally dispersed 2D array in the focal plane of a multiphoton microscope. While this is a very effective means of greatly reducing the scan time required in the lateral plane, and thus improving total volume image acquisition times, these setups are still limited by the speed at which the specimen or excitation objective may be translated to achieve axial scanning.

Recently, we reported on several variations of a simple optical multiplexing scheme using a single beam splitter to generate two foci for MMM [14, 18–20]. However, instead of spatially orienting our foci in the lateral plane, we make the two foci collinear and offset them axially to achieve volumetric imaging. The unique photon-counting and electronic demultiplexing used to attribute signal photons to their proper point of origin in the sample make it possible to simultaneously collect images from multiple planes. While this system was developed with the intent of performing MMM in volumetric imaging modality by generalizing to N foci, the two-foci system has the distinct advantage that the various excitation parameters of each focus, such as polarization, spectral content, etc., may be varied independently. Combining this fact with the simultaneous image acquisition capability of our apparatus makes it possible to view differences in excitation properties in a single shot, opening the door to DMM and many new experimental assays.

The greatest advantage of the DMM system outlined in this paper is its ability to characterize these differences in a single scan of the beam rastering mechanism. While it is possible to, for example, image with varying polarization states by taking one image, changing the polarization state and imaging again, this is an impractical method in dynamic specimens. By allowing for these differences to be visualized simultaneously, DMM makes it possible to observe such differences in vivo, or as a sample undergoes a phase or conformational change.

To understand why DMM is such a tremendous advantage for MPM in the biological sciences, it is instructive to examine the antecedents of MMM in biological microscopy.

2.1 Antecedents to Multifocal Multiphoton Microscopy

One of the first methods demonstrated for improving the 2D image acquisition time in MPM was line scanning (in contrast with point scanning) [21], in which the excitation source is focused with cylindrical optics to create a line-focus within the sample, negating the need for scanning in one lateral direction. This allows one to achieve scanning rates above video rate in the sample with typical scanning mechanisms. Although this greatly reduces the 2D image acquisition time, the axial resolution suffers due to the fact that fewer high-spatial-frequency components are included in the cone of focused light [11, 22]. So while it is possible to attain diffraction limited resolution in the laterally focused direction, the axial resolution is worse than could be obtained with spherical focusing optics.

One method to get around this problem and bring back the inherent optical sectioning capability of MPM is to simultaneously focus the excitation source in both space and time [23]. This is accomplished by spatially dispersing the spectral content of the beam prior to the focusing objective such that the duration of the pulse is shortest only in the spatial focus of the laser. Since the intensity of the focused beam strongly depends on the pulse duration, appreciable nonlinear absorption or scattering occurs only where the pulse is short, reducing the axial extent of the nonlinear interaction. This method has been demonstrated to result in axial resolutions of 1.5 µm, with image acquisition time of approximately 100 ms [24]. However, another problem arises with this scheme because the excitation objective cannot be overfilled in one lateral direction at its back aperture. Thus axial resolution is gained at the expense of lateral resolution, and the images obtained are essentially wide-field MPM images.

Wide-field MPM is another method for solving the image acquisition time problem by negating the need for scanning in the lateral dimension. By underfilling the excitation objective in both lateral directions to obtain a large focus within the specimen plane, Fittinghoff and coworkers demonstrated wide-field MPM [17]. By negating the need for scanning in the lateral dimensions, image acquisition at video rates (30 Hz) were attained.

Finally, MPM by multi-point excitation was proposed and demonstrated by two separate groups in 1998 [11, 22]. Since that time, MMM has developed steadily and is becoming a standard tool for high-speed image acquisition.

2.2 MMM: The Current State of the Art

As stated previously, MMM is most often implemented to reduce scan times and improve image acquisition speeds. By scanning an array of foci in the specimen, the area that an individual focus must scan in order to obtain an image of the same FOV as a single focus is drastically reduced. As a consequence the scanning mechanism, such as galvonometric scan mirrors, must map out only a fraction of the area that they do with a single focus, FOV/N where N is the number of foci, and the time required to image the same FOV is decreased.

In the first demonstration of MMM by Bewersdorf and coworkers [10, 15], a spinning disk containing an array of microlenses was used to rapidly scan the specimen at 225 Hz. While the authors were able to scan the FOV at this rate, they were limited by the readout time of the CCD camera used to image the nonlinear signal to 32 Hz for a 480×640 pixel image, and 67 Hz for a 384×384 pixel image. Both of these acquisition rates are greater than the video rate of 30 Hz, and consequently a real-time image could be viewed either on the CCD, or in the eyepiece of their multiphoton microscope [10]. Soon after the demonstration, another use of microlens arrays was reported in which real-time image acquisition under TPEF was observed. This strategy involved using a stationary microlens array instead of an array on a rotating disc, and rapidly scanning the 2D array of foci generated by the lens array with a pair of galvonometric scan mirrors [11]. Again, a CCD was used for imaging detection making it possible to view an image of the specimen under study in real-time.

Due to interference between adjacent pulses, the spatial resolution of many MMM setups is degraded [11]. This is due to the fact that in the region of overlap between the pulses, interference enhances off-axis components of the electric field, leading to reduced axial sectioning capability. Since MPM is performed with femtosecond-duration pulses, a small temporal delay between pulses that overlap spatially mitigates this effect, allowing for diffraction limited MMM to be performed. In one such implementation, picosecond delays were generated between adjacent pulses in the scanning disc microlens array method by addition of small delay plates on each lens of the disc [25]. Another solution generated delays between pulses by use of cascaded beamsplitters, thereby using the optical path length difference of each pulse to generate delay [26–28]. Both methods were successful in achieving diffraction limited MMM at or above video-rates. An additional advantage of the beamsplitter setup however, is the ability to easily adjust the spacing between adjacent foci within the sample. In fact, it is possible to place the temporally delayed pulses so close to one another spatially that scanning becomes unnecessary, allowing for wide field detection by multipoint excitation [28]. While advantageous for continual spacing adjustment, the beamsplitter system is much more cumbersome to implement in practice than a simple microlens array.

Another solution for optical multiplexing MMM was to use diffractive optical elements (DOE) to generate multiple foci in the sample plane [29, 30]. This method has the tremendous advantage of adjustable focal densities by simply modifying the period of the diffractive mask, which can be accomplished electronically with various DOEs. This method produces unequal intensities in the array of foci, resulting from the variation in the spatial intensity profile of the incident excitation beam, and thus differences in signal intensity must be numerically or electronically corrected to obtain a homogenous response in the sample plane.

Despite the advantages of these MMM setups for image acquisition speed, an inherent disadvantage is the need to optically image the nonlinear signal to a multipoint detector such as a CCD camera for spatial registration.

2.3 Drawbacks to MMM in Biological Tissues

One of the main advantages of MPM over conventional linear microscopy in the biological sciences is its ability to produce high resolution images through highly scattering media [1, 2, 12]. While it is often sufficient to image in vitro samples by histologically constructing a 3D data set of the specimen, for many applications this method is unacceptable. An example of such a case is in vivo imaging of blood flow restoration following a targeted insult to the vasculature of cortical tissue in live rodents [31]. By imaging deep within the tissue, one has the ability to view more of the brain to study how blood flow is redirected during stroke or aneurism, a highly beneficial application to the study of so-called silent strokes and adult dementia [31].

Currently, imaging depths are limited to approximately 600 µm with conventional femtosecond oscillator sources (i.e., Ti:Al₂O₃ oscillators at 800–950 nm), although depths of up to 1 mm have been achieved with amplified systems [32], and by use of sources with wavelengths further into the nIR spectrum [33].

Several aspects of scattering limit the imaging depth in biological samples. First, the only photons from the excitation source that are able to contribute to nonlinear excitation are the so-called ballistic photons [2], that is, the photons that undergo no scattering between the objective lens and the geometric focus of the laser beam. Thus any excitation light that is scattered reduces the amount of nonlinear signal generated by reducing the intensity of the excitation source at focus. The decay in power reaching the focus decreases exponentially with penetration depth in a scattering sample [2]. Given the nonlinear dependence of the generated contrast signal on the intensity of the excitation source, this can cause a significant reduction in the number of signal photons generated deep within scattering media.

Furthermore, the signal photons are subject to scattering as well. Due to conservation of energy in both TPEF and harmonic generation, the wavelength of signal photons is always shorter than that of the excitation light in MPM. (Note that in linear fluorescence microscopy, the Stokes shift results in fluorescence photons of longer wavelength than the excitation source.) Since the mean scattering length, that is the average length a photon travels in a medium before it is scattered, is reduced with decreasing wavelength, signal photons in highly scatting tissues are subject to significant amounts of scattering, degrading the measured signal further.

The advantage of MPM for deep tissue imaging is a result of the nonlinear dependence on the excitation intensity as the laser pulse goes through the focus of the microscope. In TPEF for example, the nearly simultaneous (~10⁻¹⁶ s) absorption of two photons depends quadratically on the intensity excitation source. Using the results of Zipfel, et al. [34] to approximate the volume in which TPE occurs, one can calculate that for an excitation wavelength of 800 nm focused with a water immersion objective lens of 0.8 NA, the volume in which TPA occurs is 0.467 µm³, or 467 attoliters (cf. Appendix A). Since this volume is so small, any signal photons measured are known to originate from a point-like volume within the specimen. This makes it possible to spatially register signal photons by the clock signal on the scanning mechanism, and hence signal photons do not suffer from scattering ambiguity inherent in spatial registration by optical imaging.

In all of the MMM implementations discussed in the previous section, imaging detection is required to map the origin of a signal photon to the region of origin within the sample plane. This is done by simple relaying optics to image the specimen to a two-dimensional detector such as a CCD camera or to the eye [10, 15]. While this method is very straightforward and has the advantage that very fast frame rates can be achieved, the ability to attain high-spatial-resolution images deep within scattering tissues is greatly reduced [35–37]. In highly scattering media, signal photons that are scattered appear to originate from a position other than that of the focal volume, and thus appear out of focus [2, 12]. This is not, however, an issue in weakly scattering tissue, or at shallow depths within strongly scattering specimens. Several published reports have demonstrated that as one images deeply into strongly scattering media, the resulting image begins to blur [35–37]. While there are methods such as confocal detection arrays to reduce this affect, it is still an undesirable method for imaging deep in biological tissues.

One solution to the spatial mapping problem in scattering media is to use multiple-anode PMT (MAPMT) detectors with the number of anodes matched to the number of foci [37]. By descanning the nonlinear signal, each focus is essentially treated like a single focus MPM system would be, each anode integrating signal from a large field of view. While this study demonstrated that blurring due to scattered photons is indeed greatly reduced, this method is still limited by image blurring due to cross-talk between anodes from scattered photons. While this can be effectively removed to achieve deep imaging within brain tissue, it requires post processing deconvolution techniques [37].

By approaching the problem of MMM in a different manner, we have demonstrated that it is possible to collect nonlinear signal photons from multiple foci by electronically demultiplexing the signal from single-element detectors such as a single-element PMT or avalanche photodiode (APD), negating the need to spatially register each signal photon by image relay optics. Using this method, we have shown for the first time that it is possible not only to achieve MMM with an MPM detection scheme, but that post processing is no more necessary in our MMM system than in a typical MPM system. Furthermore, by negating the need for imaging optics or descanning, we are able to simultaneously measure multiple modalities other than TPEF [14, 20]. Although multimodal MMM has been performed by imaging SHG in the transmissive direction and TPEF in the epi-direction [38], no other method of MMM has achieved MPM detection in multimodal experiments. Given the shorter wavelength of harmonic generation, the signal photons in such an experiment are subject to more scattering, and therefore blurring, than the fluorescence photons. Thus this system is capable of not only collecting images from multiple foci in a single shot, but from multiple modalities as well while maintaining the whole-field detection inherent in MPM.

3 Differential Multiphoton Microscopy: A New Approach to MMM

We view the problem of data acquisition in MPM from a different perspective, and consequently have developed an MMM scheme that not only improves imaging rates, but opens the door for direct comparisons of varying excitation parameters to be visualized in a single shot. Instead of approaching the problem of MMM in the classic way by generating an array of foci in the lateral focal plane, we generate multiple foci in the axial plane. By then extending the delay between adjacent pulses to nanosecond durations instead of picosecond durations, and employing photon-counting detection, we are able to electronically demultiplex the nonlinear contrast signal from the specimen to obtain multiple images simultaneously. The concept of the DMM system is straightforward, and may be readily applied to existing MPM setups. The DMM concept is based on optical multiplexing prior to the MPM setup, and electronic demultiplexing of the detection signal.

3.1 Optical Multiplexing

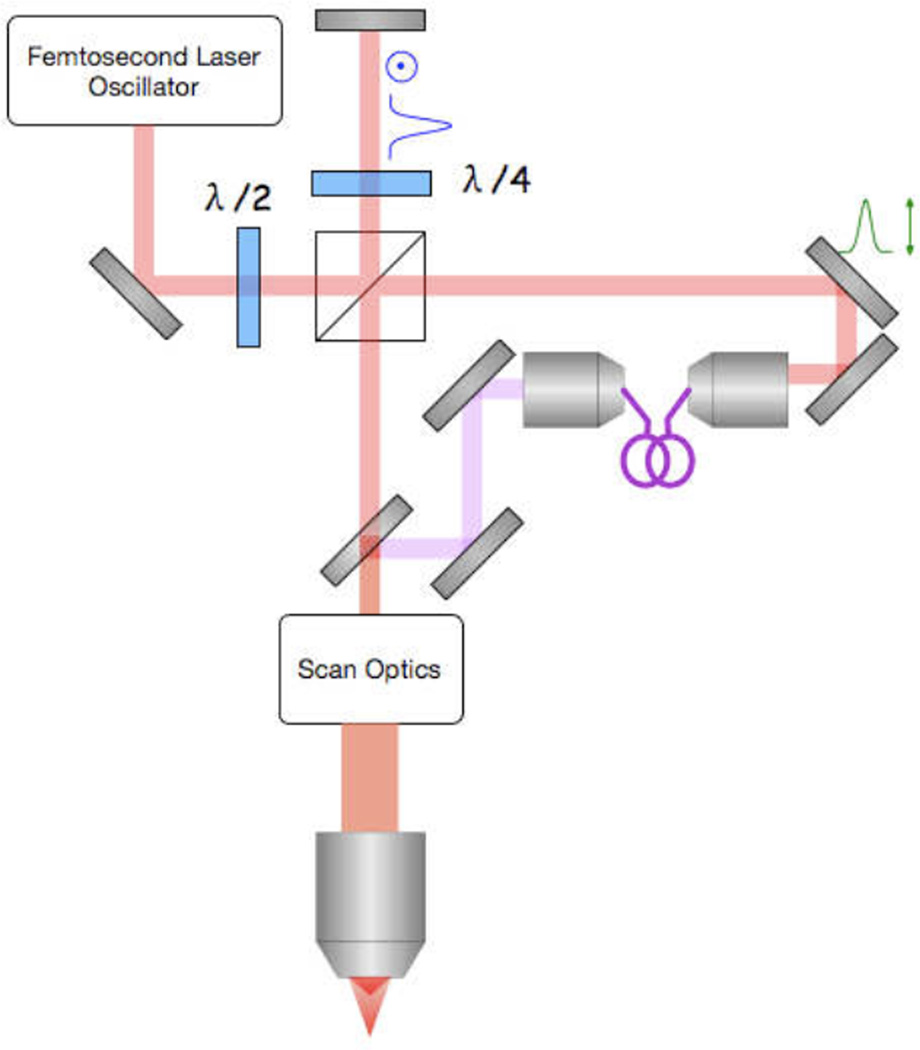
There are several methods for generating multiple foci in an MMM system. In our implementation we generate two foci that are spatially collinear, but we temporally delay one pulse by one half of the period of the oscillator. This is accomplished by constructing an interferometer-like setup with a polarizing beam splitter (PBS) and two retro-reflecting mirrors (Fig. 1b). By careful alignment of these elements, it is possible to achieve collinear laser pulse trains. For comparison, the corresponding diagram for a typical single-point MPM system is represented in Fig. 1a. In both diagrams in Fig. 1 the scan optics include a beam rastering mechanism, and can contain beam expanding telescopes or other optics for proper telecentric scanning.

Figure 1.

Comparison of (a) a traditional MPM imaging system, and (b) the optical demultiplexing used for the DMM system. Generating two collinear beams to achieve two orthogonally polarized foci in the sample plane is done with straightforward optical components, and optical delay by path length modification is used to achieve interlacing of pulse trains.

Because a single pulse is split into two using a PBS, a λ/4 waveplate is inserted into each beam path such that the polarization state of the beam is rotated by 90° upon double passing the waveplate. This ensures that each pulse with be transmitted through the PBS towards that scan optics. By using polarization state to split our single beam into two, the pulse train in the scan optics consists of an interlaced train of pulses from each arm of the interferometer, every pulse being orthogonally polarized with respect to those adjacent to it. This pulse train is focused into a specimen as though it were a single-focus MPM system.

To date, we have used two sources for this method, one an extended cavity Ti:Al₂O₃ oscillator with a repetition rate of 21.7 MHz [14, 18], and the other a Yb:KGd(WO₄)₂ oscillator with a repetition rate of 56 MHz [20]. The delay between pulses directly out of these oscillators is 46 ns and 18 ns respectively, so one pulse from the beamsplitter is delayed with respect to the other by either 23 ns or 9 ns, depending on the excitation source. Due to the additional path length experienced by one of the two beam paths, which is one full cavity length, each beam focuses to a slightly different depth within the specimen. This is due to the additional divergence experienced by the beam with a longer optical path length. While this can be overcome by the addition of a simple telescope to the longer arm, we have found it more useful to insert user-defined divergence control into one arm of the interferometer as shown in Fig. 1b. This can be done in any number of ways, such as a deformable mirror (DM) [14, 18, 20] or image relaying with objective lenses [39]. This allows for programmable control of the axial spacing between the two foci in the specimen plane.

Altogether, the foci in the specimen are separated in time by tens of nanoseconds, have orthogonal polarization states, and can be separated axially by a user-defined amount. Due to the temporal separation and orthogonal polarization states, it is possible to spatially overlap the foci within the sample without interference. Because the beams are collinear, the same 2D plane is scanned in the specimen by each focus. Furthermore, due to the spatial separation in the interferometer setup, we are able to modify other properties of each pulse separately. As we will demonstrate later, this can be greatly advantageous for many assays in biological MPM.

3.2 Electronic Demultiplexing

In order to avoid the limitations of most MMM setups due to imaging detection, we take advantage of the nanosecond separations between pulses to electronically demultiplex the nonlinear signal measured by a single-element detector. Detailed electronic layouts and demultiplexing procedures are discussed at length in Ref. 20, and we urge the interested reader to consult the description therein. Here, we only give a brief description of the principles behind the detection scheme to make it clear how the system is able to obtain simultaneous images in a single scan using whole field detection.

As shown schematically in Fig. 2a, the laser pulse train is incident on a dichroic mirror which transmits the excitation light, and reflects the nonlinear signal towards the PMT in the epi-direction. At some point in the system, before the scan mirrors in practice, a glass slide is inserted into the pulse train to reflect a small portion of the laser intensity to a photodiode detector. The analog signal from the photodiode is known as the laser clock (LC) and acts as the clock signal for demultiplexing. Since we may safely assume that at most we generate one signal photon per laser pulse, there is no need to consider multiple signal photons under a single TTL pulse of the LC. (We can easily check to ensure that we are in a photon-counting regime. If not, the excitation intensity is simply reduced.) This allows us to use the interlaced pulse train as a clock signal for an electronic demultiplexer.

Figure 2.

Explicit schematic of (a) the optical multiplexing and (b) the electronic demultiplexing used in the dual-focus DMM system.

Both the LC and PMT signals are thresholded, and converted to TTL logic pulses (Fig. 2b), which are then fed into a field-programmable gate array (FPGA). The FPGA is programmed to contain two counters, one for each focus. As each signal photon occurs under the envelope of a LC pulse, it is possible to rapidly switch between counters to attribute signal photons from each focus to their appropriate position in the sample. For every pixel in the image, the counters are set to zero, and signal photons are incrementally counted for each focus in the specimen. Once the dwell time has been reached, both counters are reset to zero and the scan mirrors move to the next position in the sample. During scanning the count for each pixel of each image is stored in the memory of the FPGA, and is downloaded to the computer after each frame is scanned.

By electronically demultiplexing the nonlinear signal out of a single-element PMT, we are able to simultaneously acquire two images from a single scan. This is the heart of DMM, as it allows us to vary the excitation parameters of each foci to visualize the difference in specimen response simultaneously.

This detection scheme is easily scalable to multimodal detection by additional detection pathways in the microscope and additional FPGAs for each detector. Thanks to the low cost of FPGAs (~$300 for Altera DE-2 models used in this work), it is economically feasible to introduce multimodal detection with multipoint excitation.

While multimodal detection in MMM is possible by imaging detection in the forward direction and descanning in the backward direction, this configuration makes possible multimodal detection in the nature of MPM detection. That is, multimodal MMM is possible while using whole field detection as in MPM. This is a tremendous advantage for direct comparisons of biological structure deep within highly scattering tissues.

3.3 Photon-Counting Detection

At the heart of our demultiplexing technique is photon counting detection. Photon counting is used for several reasons.

First, because we are electronically demultiplexing and converting an analog signal from the PMT into a train of TTL electronic pulses, it is a natural method of detection. Second, photon counting detection improves the signal to noise ratio (SNR) of obtained images by the use of discrimination electronics. Since only a small portion of the noisy background signal occurs at an amplitude comparable to the signal due to a photon, discrimination of background pulses below a certain threshold greatly reduces the number of noise pulses that are attributed to signal photons. As a result, we have obtained noise levels on the order of 10–50 counts in a 1 second image. For a 512×512 pixel image, this amount of noise per pixel is nearly negligible, resulting in a very good signal-to-noise ratio (SNR).

Finally, photon counting allows for quantitative imaging assays with MMM to be performed. As we will soon demonstrate, this is especially useful for DMM in which we directly compare the number of signal photons measured with one focus to the number measured with the other.

4 DMM Results

Having described the underlying principles of the DMM system, several results obtained with this setup will now be discussed. These results are not meant to be an exhaustive collection of the capabilities of the system, rather a brief window into what is possible. The purpose of this section is to show that by using the DMM system, acquiring images with varied excitation parameters is no longer a limitation in image acquisition time. For example, if one wishes to examine the differences in response to orthogonal polarizations with a traditional MPM system, a half waveplate would be necessary to rotate the polarization state of the excitation light, and images obtained with the two orthogonal polarization states would be temporally separated by the time necessary to rotate the waveplate and scan the sample a second time. While this is not a problem for fixed samples, in vivo studies can be hindered by this delay as the morphology can change in this time span. The DMM system is not hindered by such problems, and in vivo DMM imaging assays can be performed without changes in chemical environment or morphology occurring between differential images.

4.1 Depth DMM

Perhaps the most obvious DMM imaging application is to image multiple depths simultaneously. Since biology is three-dimensional, the morphology of various depths in the sample are crucial for understanding the structure and function of a specimen. Moreover, it is desirable to resolve dynamic data within such a 3D structure to understand a variety of complex phenomena. While forming a 2D array of foci in a single lateral plane of the sample can help to drastically reduce scan times in that area, the sample must still be scanned in the axial dimension to acquire 3D data. Despite the decrease of scan times in the lateral plane, the axial scan time is slow due to the inertia of relatively massive objective lenses and piezo scan stages. Therefore, in typical MMM, conformational changes or chemical changes can occur faster than the temporal resolution between adjacent axial planes, resulting in a very complex set of data that must be deconvolved temporally and/or spatially.

In DMM, we are able to simultaneously extract two planes (and have demonstrated up to six [19]). This allows for volumetric imaging in the whole-field MPM detection scheme for the first time by obtaining data from a three-dimensional volume in a single scan. This is demonstrated for two foci in Fig. 3 where two planes in a transgenic maize plant expressing enhanced yellow fluorescent protein (eYFP) were acquired simultaneously. Not only does depth DMM allow for the sample to be viewed in multiple axial planes simultaneously, but it also makes it possible to perform rudimentary particle tracking measurements in 3D, both of which are useful for many biological assays.

Figure 3.

Simultaneous images separated by 8 µm axially in the epidermis of a maize leaf transgenically modified to express eYFP. Circles indicate the location of a feature within the specimen that moves over time, which can be seen in both depths simultaneously. Scale bar is 10 µm.

This is the first example of volumetric imaging with the DMM system, and although it is limited to two planes in the dual focus configuration, extension beyond multiple foci is trivial electronically.

In order to obtain depth DMM, the two foci must be offset axially with some method of divergence control. While several methods have been used to adjust the focal depth of one focus, including passive telescopes [20] and deformable mirrors [14, 18], we have recently constructed a setup based on relaying an image of the focus from an external objective to the excitation objective [39]. By placing an objective lens in the short arm of the DMM setup and image relaying the back aperture of that lens to the back aperture of the excitation objective, a piezo mirror in the short arm of the DMM setup can be used to control the axial position of the focal plane of the short arm in the specimen. A schematic of this system is shown in Fig. 4. This allows us to quickly control the spacing between the two foci.

Figure 4.

Schematic of system used for depth scanning with a piezo actuated mirror. The two lenses image relay the back aperture of the first objective to the back aperture of the excitation objective (dashed lines).

To test the axial scanning capability of this system, we measured the THG signal from two cover slips separated by 90 µm of wax film. The axial response for THG from cover slips has been well characterized [6, 7], so we may use this sample to perform a characterization of the axial scanning capabilities of this system. The THG response shows us not only how far the system can scan, but allows us to see if the excitation point spread function (PSF) degrades as the axial position is changed. Figure 5 shows the results of this axial scan, and demonstrates that we are able to maintain tight focusing as the axial position is scanned over a range of 120 µm.

Figure 5.

THG response measured from the glass/air interfaces of two cover slips separated by 90 µm. The axial THG response demonstrates that it is possible to maintain tight focusing over the 120 µm scan range.

Figure 6 compares two 3D data sets acquired with specimen scanning and by scanning the piezo mirror. Clearly there is very good agreement between the two data sets, indicating that we are capable of scanning a large area axially in scattering media. Moreover, the resolution of the data set is nearly identical for both methods when imaging deeper in the tissue, confirming that one can maintain tight focusing with this scheme. One important point to note when comparing the image series in Fig. 6 is that the piezo scanning and specimen scanning do not necessarily scan the same axial planes in the specimen. We can correlate the maximum and minimum depths in the specimen, but the axial spacing in the piezo-scanning data set differs from those in the specimen-scanning set. However, we still note that tight focusing is maintained over a total axial range of 42 µm in this image set.

Figure 6.

Direct comparison of axial scanning with (a) the piezo mirror and (b) the specimen stage. Total axial scan range is 42 µm in transgenic maize epidermis expressing eYFP. Intensity maps represent TPEF intensity. Notice that the spatial resolution with the piezo scanning mechanism is as good at the specimen scanning results, indicating that tight focusing is maintained throughout the scan range. Scale bars are 10 µm.

Finally, this method could easily be extended to achieve arbitrary scan planes in the specimen by coupling the scan mirrors for the lateral plane with the piezo mirror in the appropriate manner to achieve the desired pattern. This would allow one to rotate the 2D scan plane in a specimen by simply programming the scanning electronics for all three degrees of freedom, a capability that could be greatly advantageous in a myriad of biological MPM applications.

4.2 Polarization DMM

Many processes in nonlinear optics are highly dependent upon the polarization state of the excitation source. For harmonic generation, this is a result of the phase matching conditions necessary to give an appreciable signal. Phase matching in MPM can be a very valuable tool for determining orientation of structures within biological specimens without the need for an exogenous fluorophore. SHG from fibrous structures such as rat tail tendon [34] and crystalline cellulose strands [20, 40, 41] have been shown to not only have a strong dependence upon the orientation of excitation polarization, but have been used to show that the harmonic signal generated in the forward- and backwards-propagating directions are dependent on factors such as sample density, mean scattering length, and structural size and orientation. This allows one to not only visualize intensity maps of the specimen to gain insight into the structure of a sample, but to understand phase matching conditions within the structure by collecting images with varying polarization states.

One example of such a sample is simple corn starch [14]. Amylopectin chains in corn starch grains, the molecule responsible for SHG, are arranged azimuthally along the grain. Since only those molecules that are parallel to the input polarization state satisfy the phase matching conditions necessary to generate SHG, one does not see the entire grain in an SHG image of corn starch. Moreover, the central portion of the grain is centrosymmetric, meaning that SHG cannot occur from this region regardless of the polarization state of the excitation source. Consequently, when images are taken with orthogonal linearly polarized beams, two different sets of lobes of each starch grain are activated. This is demonstrated in Fig. 7, in which the SHG response of corn starch gains is demonstrated by generating composite images resulting from each polarization. Fig. 7a was taken in the transmissive direction, while Fig. 7b was taken in the epi-direction. Note that both panels are composites of two images acquired simultaneously, and thus each panel is a polarization DMM image.

Figure 7.

Polarization DMM in SHG for both the (a) transmission and (b) epi-directions. Purple and green arrows indicate the orientation of the polarization state corresponding to the region of the sample that is visible in the image. Regions in white appear where the response from each polarization overlaps with the same intensity. Note that each figure is composed of two images taken at orthogonal polarizations. All four images comprising this figure were taken in a single shot with a Ti:Al₂O₃ oscillator, focused by a 0.75 NA/40× objective (Olympus, UPlanFL). Scale bars are 10 µm.

The usefulness of polarization sensitive DMM for quantitative biological applications is demonstrated in Fig. 8. Here images of fixed murine neocortical tissue are imaged in TPEF and SHG simultaneously. TPEF in these images is due to green fluorescent protein (GFP), and owing to the random orientation of the dipole moment of each fluorophore, the TPEF response is nominally polarization independent. The SHG response however is strongly dependent on the amount of coupling between the incident laser polarization and fiber orientation. Thus when activated with two differing polarizations, different structures within the sample can be visualized. This is highlighted in Fig. 8d where the SHG response from each polarization state has been displayed in a composite image. The false color intensity applied to each image was chosen such that when the response from each polarization was the same, the resulting color is white.

Figure 8.

Polarization DMM of the trigeminal nerve in murine neocortical tissue, with SHG measured in transmission and TPEF of endogenous fluorophores collected in the epi-direction. Panels (a) and (c) contain composite TPEF and SHG images for orthogonal polarization states, while (c) contains a bright-field image of the sample. Panel (d) represents the DMM image for SHG, showing a composite of the SHG response from each polarization state. All four images comprising this figure were taken in a single shot with a Ti:Al₂O₃ oscillator, focused by a 0.75 NA/40× objective (Olympus, UPlanFL). Scale bars are 10 µm.

4.3 Excitation Wavelengths

Another parameter that is useful to have control over in an multiphoton microscope is the central wavelength of the excitation pulse.

To fully observe the behavior of complex biological systems, multiple fluorophores can be introduced, each tagging to a different feature of interest within a cell. The different fluorophores often have widely varying cross-sections centered at a given wavelength, and thus may not be efficiently excited by a single source. TPEF further restricts the sources available, as the high peak intensity required to activate this process necessitates pulsed laser sources. One option is to direct multiple lasers into the microscope, using dichroics to select which wavelength to image with at a given time [42]. Not only is this expensive, but the difficulty of precisely matching laser repetition rates prevents interlacing two pulse trains for simultaneous imaging. Thus images must be acquired by use of multiple sets of scan mirrors in different imaging ports of the microscope [42]. Anecdotal experience has proven that attempting to change laser sources by switching the dichroic mirror in the microscope not only makes it difficult to ensure the same features in the specimen are scanned, but that the scan areas of each source can vary in size and be skewed with respect to one another. This makes post-processing of the images cumbersome. However, the most undesirable result of this method is that DMM cannot be performed due to the time delay associated with dichroic alignment.

A more elegant solution is to utilize a photonic crystal fiber (PCF) to generate the bandwidth needed to activate multiple fluorophores, filtering out different portions of the resulting spectrum to be used in a two focus DMM apparatus. PCFs can generate bandwidths of 500 nm or greater with modest input pulse energies (1–10 nJ) [43, 44]. PCFs have been used in many imaging applications, including optical coherence tomography (OCT) [45, 46] and coherent anti-Stokes Raman scattering (CARS) spectroscopy [47–50]. Additionally, the output of a PCF can directly be used as a source for multiphoton imaging without post-fiber compression [51–55].

We have modified our DMM system to include a photonic-crystal fiber (PCF), as shown in Fig. 9. By interlacing the broadband pulse train with our 1040 nm pulse train, we enable simultaneous dual-color imaging for the first time. The 1040nm pulse train from one arm is redirected into a 0.45 NA aspheric lens (New Focus), which focuses the pulse train into a 6cm length of PCF (955-3.7-NL, Crystal Fibre). The output of the PCF is then collected with a matching aspheric lens, which is on a translation stage to allow the collimation of a chosen wavelength of light. With the PCF, we are able to generate a pulsed supercontinuum with sufficient energy in wavelengths from 760–1200 nm to activate SHG.

Figure 9.

Schematic of the DMM system with a PCF inserted into the long arm of the interferometer. By carefully adjusting the delay of this arm, the timing is maintained to allow for electronic demultiplexing to be performed in the typical manner. Interference filters placed after the PCF allow for certain portions of the spectrum to be selected.

To determine the imaging viability of the light generated from the PCF (without compression), we directed the pulse train from the PCF into our IX-71 microscope, and imaged corn starch granules, which are known to strongly generate second-harmonic light [56]. We detected SHG from 380 nm to 600 nm, with scans at select wavelengths shown in Fig. 10.

Figure 10.

SHG images of corn starch taken with various portions of the PCF spectrum. SHG was detected at (a) 380 nm, (b) 450 nm, (c) 520 nm, (d) 600 nm. All images are 512×512 pixels, with a pixel dwell time of 183 µs. Scale bar is 10 µm.

Whereas the SHG images of corn starch shown previously (cf. Fig. 7) showed only two lobes lighting up from the linear polarization, we note that the corn starch images obtained with the PCF result in annular images from the starch. This is because the PCF does not maintain the linear input polarization, so the resulting images are obtained with randomly polarized light, activating all portions of the corn starch except the central portion of the grain in which the harmoniphores are centrosymmetric.

Another complication that arose with this PCF was shot noise in the pulse train, i.e., significant variations in the peak intensities of adjacent pulses. While this could cause problems in some experiments, we are able to obtain images with this modulation because the dwell times on each pixel (183 µs) result in 10,250 pulses per pixel, effectively averaging over the variation in peak intensity.

4.4 Spatial profile

Spatial resolution in MPM has become an area of great interest in recent years, and several methods have demonstrated so-called super-resolution [57–61], i.e., resolution beyond that defined by the diffraction-limited focusing of light. While many of these methods have been demonstrated in TPEF, only one method to date has been reported for improving the spatial resolution in harmonic microscopy [61], and in that case only for a particular case in THG microscopy. Since MPM inherently allows for several nonlinear contrast mechanisms to be viewed simultaneously, it would be advantageous to have a method for enhancing resolution for any contrast mechanism.

One simple method for achieving such resolution enhancement is spatial filtering of the excitation beam by annular pupils [62–64]. Annular pupil filters have been used previously in confocal microscopy to enhance the lateral spatial resolution. Essentially, the annular filter can be viewed as a high-pass filter, as only the highest spatial frequency components are allowed to pass the objective lens. Consequently, the lateral resolution is enhanced. Since spatial resolution in MPM is determined only by the spatial extent of the excitation point spread function (PSF), this simple method may be used to gain lateral resolution in any nonlinear contrast modality. An example of such improvement is shown in Fig. 11, in which crystalline cellulose fibers were sequentially imaged in epi-SHG with one arm of the DMM system. Figure 11a shows the fibers imaged with the beam filling the full NA of the excitation beam, while Fig. 11b shows the result when an annular pupil filter is applied. Clearly there is an improvement in the lateral resolution of the resulting images.

Figure 11.

Lateral resolution enhancement in SHG images of crystalline cellulose fibers. Images taken with (a) full-beam (FB) and (b) annular aperture (AA) excitation. Normalized plots of the intensity at the lineouts are shown in (c) where it is easy to see that the resolution has been greatly enhanced.

Improvement in lateral resolution, however, comes at the cost of axial resolution. The axial component of the PSF is dramatically increased in annular aperture focusing because fewer k-vectors are included in the focusing cone, resulting in less cancellation of out-of-focus components. One can imagine the limiting case in which only two k-vectors are focused at NA=1 in air, corresponding to a semi-aperture angle of 90°. In such a case, the PSF is defined by the interference of two counter-propagating plane waves, causing the axial extent of the PSF to extend to infinity. This decrease in axial resolution is not an issue in confocal microscopy, as the confocal pinhole in the detection arm samples only a small region near the focus. However, in the wide-field detection inherent in MPM, the axial resolution is severely degraded. Often this is advertised as increased depth of focus, since one can detect features from a large 3D volume, but for most applications of biological microscopy it is imperative that the axial resolution be maintained.

Because the beams in the interferometric setup shown in Fig. 1b are spatially separated, it is possible to modify the spatial profile of one beam while leaving the other unaffected, similar to the axial scanning method already presented. However, instead of modifying the divergence of only one beam by image relaying the focal spot, it is easy to imagine applying an annular pupil filter to one beam while leaving the other beam unaffected. Thus a 3D data set may be acquired with enhanced lateral resolution offered by the annular-aperture beam, while the axial sectioning capability can be maintained by the full-aperture beam. The simultaneous imaging capability offered by the DMM system would allow one to obtain both data sets simultaneously, making it possible to perform a deconvolution of the data to obtain a single high-resolution 3D data set.

5 DMM Beyond Two Foci

So far, all of the DMM results we have demonstrated were obtained by two foci in the specimen plane. One of the great advantages of the DMM concept presented above (i.e. optical multiplexing and electronic demultiplexing) is the ability to extend the concept beyond two foci. In principle, the shortest duration that may be generated between two pulses in the laser clock is ~2 ns. As long as the temporal separation between adjacent pulses in the pulse train is at or above this threshold, electronic demultiplexing with the FPGAs is attainable. This sets an upper limit on the number of foci that may be used with a single FPGA, but it is feasible that multiple FPGAs be used to extend the capabilities of this method to any number of foci desired.

5.1 Six-foci Yb:KGd(WO₄)₂ System

To demonstrate the use of more than two foci, we constructed a unique Yb:KGd(WO₄)₂ which puts out six femtosecond laser beams, each appropriately time-delayed, from a single extended cavity [19]. The net output of the laser is six spatially and temporally separated beams. Temporal offset is generated purely by the round-trip time in the cavity, since each pulse is output from the cavity as it bounces off of the output coupler. Thus the pulse train that is output from the cavity is a burst of six pulses, each separated by 6 ns, occurring at a repetition rate of 18.6 MHz. The pulses are 250 fs in duration and contain 19 nJ of energy per pulse.

The principle of our DMM system as described in section 3 above is directly extended to this novel laser, only now the FPGA is programmed to contain six counters instead of two. In this system, each scan of the galvonometric scan mirrors results in six simultaneously acquired images. Again, we can use multimodal detection to achieve twelve or eighteen images per scan for bi- and tri-modal detection respectively.

Multimodal imaging with the six-beam Yb:KGd(WO₄)₂ system was demonstrated in Ref. 19, where twelve images of the trigeminal nerve in murine neocortical tissue were obtained in a single scan of the galvonometric mirrors..

5.2 Video-Rate Imaging

One clear advantage of the six-foci system is the ability to acquire images at least six times faster than a traditional MPM system without increasing the scan speed. However, it is desirable to acquire images in any MPM system at video rates (≥30 Hz), and therefore scan times must be significantly reduced. As mentioned in the introductory material, MMM systems easily reach video rate imaging capacities, typically at the cost of imaging deep within scattering tissues. The Yb:KGd(WO₄)₂ system presented here has the ability to image at well above video rates by acquiring multiple images per scan.

To that end, we replaced one of the galvonometric mirrors in our six-beam system with a rotating polygonal mirror to image at video rates for each focus in the system, as shown schematically in Fig. 12. We imaged non-fluorescent polystyrene beads flowing in a microfluidic channel in a solution of Rhodamine 6G (Rh6G) dye. Since the foci in the six-beam system are arranged in a linear pattern within the sample, we arranged the system such that the linear array was parallel to the direction of flow in the specimen, and oriented the polygonal mirror such that we scanned the array of foci perpendicular to the direction of flow. By scanning the polygonal mirror as the beads flowed in the channel, we were able to obtain six simultaneous images of the channel (cf. Fig. 13). Since the foci are separated in the direction of flow, each image has the spatial coordinate along the horizontal axis, while the vertical axis represents time. We scanned the sample and acquired data at 30 Hz, resulting in pixel dwell times of 0.9 µs. Note that this rate is for each of the six foci, such that the true acquisition rate of the electronics is 180 Hz. With this method we were able to determine the flow rate of the beads in the microfluidic channel to be approximately 2.5 µm/ms. This is the first demonstration of video-rate DMM.

Figure 12.

Configuration of six-foci DMM system using a polygonal scan mirror for imaging the flow in a microfluidic channel.

Figure 13.

Simultaneous images of non-fluorescent polystyrene beads and Rhodamine 6G flowing in a microfluidic channel. Note that the vertical axis of each image represents time since each focus only scans in the horizontal direction.

5.3 Lifetime Detection

Since the laser clock is formed by this temporal pulse train, a disadvantage of this system is that signal photons for fluorophores with lifetimes longer than ~6 ns are not completely binned into their proper channel. This is illustrated schematically in Fig. 14, where two hypothetical fluorophores with varying lifetimes are shown along with one cycle of the laser clock. Clearly, some fluorescence photons from the long-lived fluorophore will appear in the counter adjacent to the beam that actually excited it. Therefore, bleedthrough of fluorescence into adjacent images is an issue with this system.

Figure 14.

Schematic depiction of the bleedthrough process. The gray pulses represent the laser pulses that form the laser clock, while the solid and dashed black lines represent the fluorescence lifetime of two different fluorophores. Since both fluorophores are excited with the first pulse, it is clear that the fluorophore with a short lifetime (dashed) will be properly counted by the FPGA, and no bleedthrough will be measured. In contrast, the longer-lived fluorophore (solid) will bleed into adjacent channels at a steadily decreasing intensity, thereby making it possible to measure a change in the lifetime between these fluorophores.

Although this appears to be a disadvantage for imaging purposes, it enables rudimentary lifetime imaging to be performed. We show two examples of lifetime sensitive imaging. By allowing only the beam responsible for the first pulse in the line clock to be incident on the sample, but counting six images as we typically would, we have performed basic lifetime detection imaging.

First, we placed fluorescent polystyrene beads in a solution of quantum dots (QDs; Invitrogen) and allowed the samples to dry before imaging. Since QDs are known to have long lifetimes due to their high photostability [65], we expected that the lifetime of the fluorescent bead would be significantly shorter than that of the background signal from the QDs. Figure 15 shows that this was indeed the case, and demonstrates the ability to view lifetime changes in real time with the six-beam DMM setup. Note that the curves fit to the data points assume single exponential decay, but that the functional form of the decay may not follow the same functional form. The small number of data points is a shortcoming of this method for lifetime detection.

Figure 15.

Variation in the fluorescent lifetime of a fluorescent polystyrene bead and QDs in solution. Note that the small number of data points makes accurate determination of a fluorescent lifetime difficult as the functional form is difficult to infer.

Note that while we are able to detect lifetimes with this scheme, this method is not a good choice for determining the quantitative value of the lifetimes. This is simply due to the fact that we only measure six data points over a 36 ns time window, making it impossible to determine with the decay is a single-exponential, multiple-exponential, etc., and thus making it difficult to assign a lifetime.

6 Conclusions

We have presented a simple scheme for simultaneous image acquisition in multiphoton microscopy with whole field detection by a single-element detector based on optical multiplexing and electronic demultiplexing. The simultaneous imaging capability allows us to perform differential multiphoton microscopy measurements in a single shot for the first time, an advantage for in vivo DMM assays in dynamic samples. Moreover, the spatially separated beam paths in our optical multiplexing scheme allow for various parameters to be varied independent of the other beam(s). This has allowed us to perform simultaneous imaging with two pulses of varying spectral content for the first time. Due to the widely varied two-photon absorption spectra of fluorophores and fluorescent proteins commonly used in MPM, the ability to vary the central wavelength of one excitation pulse with respect to the other allows for a wide array of fluorophores to be used with the same excitation source.

The orthogonal polarization states of each beam in the two-foci DMM system also make it possible to perform polarization DMM simultaneously for the first time. By performing polarization DMM in this manner, it is possible to visualize not only the structure under study, but infer the phase-matching conditions within the specimen. Furthermore, exciting fluorescent specimens with orthogonal linearly-polarized beams should make it possible to perform anisotropy measurements in a single shot as well, thereby extending the polarization capabilities of the system.

We have also demonstrated simultaneous DMM beyond two foci with a novel six-beam Yb:KGd(WO₄)₂ oscillator, and showed that this system is capable of video-rate multimodal imaging. Another advantage of this system is the possibility of performing stereo imaging with this microscope. Since the six foci are laterally offset from one another, it should be possible to obtain up to 3 stereographic images in a single shot by proper orientation of the foci in the specimen plane.

We anticipate that simultaneous image acquisition for DMM imaging will have great impact on biological imaging experiments.

Appendix A: Calculating TPE Volume and Peak Intensity in Focus

The full vectorial calculation for the PSF near the focus of a lens has been rigorously derived by Richards & Wolf [66]. According to Ref. 34, fitting a Gaussian intensity envelope to the resulting PSF results in the following expressions for the e⁻¹ point in the intensity envelope for a Gaussian spheroid:

$${\omega }_{xy}=\{\begin{array}{cc}\frac{0.320\lambda }{\sqrt{2}\mathrm{N}\mathrm{A}}\hfill & \mathrm{N}\mathrm{A}\le 0.7\hfill \\ \frac{0.325\lambda }{\sqrt{2}\mathrm{N}{\mathrm{A}}^{0.91}}\hfill & \mathrm{N}\mathrm{A}>0.7\hfill \end{array}$$ (1)

$${\omega }_z=\frac{0.532\lambda }{\sqrt{2}}\left[\frac{1}{n-\sqrt{n^2-\mathrm{N}{\mathrm{A}}^2}}\right]$$ (2)

where λ is the wavelength of incident light, NA is the numerical aperture of the lens, and n is the index of refraction of the surrounding medium. By integrating the PSF for TPEF, the authors of Ref. 34 show that the volume in which TPE occurs can be approximated as

$$V_{\mathrm{T}\mathrm{P}\mathrm{E}}=\frac{{\pi }^{3/2}}{0.68}{\omega }_{xy}^2{\omega }_z.$$ (3)

The peak power of a pulsed laser source can be calculated from the average power, pulse duration τ, repetition rate f, and shape factor g_p according to the relation

$$P_{\text{peak}}=g{P}_{\text{ave}}\frac{g_{\mathrm{p}}}{\tau f}{P}_{\text{ave}}.$$ (4)

The factor g is known as the second-order temporal coherence of the pulse [67], defined as

$$g=\frac{\int \mathrm{d}tf{I}^2(t)}{{[\int \mathrm{d}tfI(t)]}^2}=\frac{g_{\mathrm{p}}}{\tau f}$$ (5)

where I(t) is the intensity of the pulse. The shape factor g_p for a Gaussian pulse is 0.664, which is what we assume throughout this manuscript. Of course, the shape factor can be calculated for any pulse shape.

Since intensity is defined as power per area, the peak power of the pulse and the radius of the spot size can be used to estimate the peak intensity in the focal plane of the microscope with the expression

$$I_{\text{peak}}=\frac{P_{\text{peak}}}{A_{xy}}=\frac{P_{\text{peak}}}{\pi {\omega }_{xy}^2}=g{P}_{\text{ave}}=\frac{g_{\mathrm{p}}}{\tau f\pi {\omega }_{xy}^2}{P}_{\text{ave}}.$$ (6)

We use the area in the lateral dimension because this is where the intensity of the pulse is maximal. Note also that it is straightforward to convert from the area at the 1/e point to other points along the Gaussian intensity by multiplicative factors. If, for example, we wished to calculate the area using the FWHM of the intensity envelope, we simply multiply the radius at e⁻¹ by $\sqrt{2\text{ln}2}$, resulting in a factor of (2ln2)⁻¹ in front of the preceding expression.