Scaling identity connects human mobility and social interactions

Significance

Both our mobility and communication patterns obey spatial constraints: Most of the time, our trips or communications occur over a short distance, and occasionally, we take longer trips or call a friend who lives far away. These spatial dependencies, best described as power laws, play a consequential role in broad areas ranging from how an epidemic spreads to diffusion of ideas and information. Here we established the first formal link, to our knowledge, between mobility and communication patterns by deriving a scaling relationship connecting them. The uncovered scaling theory not only allows us to derive human movements from communication volumes, or vice versa, but it also documents a new degree of regularity that helps deepen our quantitative understanding of human behavior.

Abstract

Massive datasets that capture human movements and social interactions have catalyzed rapid advances in our quantitative understanding of human behavior during the past years. One important aspect affecting both areas is the critical role space plays. Indeed, growing evidence suggests both our movements and communication patterns are associated with spatial costs that follow reproducible scaling laws, each characterized by its specific critical exponents. Although human mobility and social networks develop concomitantly as two prolific yet largely separated fields, we lack any known relationships between the critical exponents explored by them, despite the fact that they often study the same datasets. Here, by exploiting three different mobile phone datasets that capture simultaneously these two aspects, we discovered a new scaling relationship, mediated by a universal flux distribution, which links the critical exponents characterizing the spatial dependencies in human mobility and social networks. Therefore, the widely studied scaling laws uncovered in these two areas are not independent but connected through a deeper underlying reality.

Over the past few years, we have witnessed tremendous progress in uncovering patterns behind human mobility (1–7) and social networks (8–10), owing partly to the increasing availability of large-scale datasets capturing human behavior in a new level of detail, resolution, and scale (11, 12). Building on rich, fundamental literature from the social sciences (13–19), these data offer a huge opportunity for research, fueling concomitant advances in areas of both human mobility and social networks with profound consequences in broad domains. One important aspect affecting both areas is the critical role space plays. Indeed, growing evidence suggests both our movements and communication patterns are associated with spatial costs that follow reproducible scaling laws. Indeed, previous studies have shown that human travels adhere to spatial constraints (20), characterized by levy flights and continuous time random walk models (1, 2, 4), a scaling law that has proven to be critical in various phenomena driven by human mobility, from spread of viruses (21–23) to migrations (2, 6) and emergency response (24–26). In another related yet distinct area, there has been much empirical evidence about the geographic effect on communication patterns (20), documenting that the probability for two individuals to communicate decays with distance, following power law distributions (20, 27–30). This robust pattern plays an important role in navigating the social network (31), from routing (32, 33) to search of experts (34, 35) to spread of information (27, 36) and innovations (37). Although human movements and social interactions bear high-level similarities in the role spatial distance plays, and are often referred to as two prominent examples of spatial networks (20), they remain as largely separate lines of inquiry, lacking any known connections between their critical exponents. This is particularly perplexing given the fact that they often exploit the same datasets (5, 20, 38–40) and are treated similarly in most modeling frameworks (6, 41).

In this paper, we test the hypothesis that previously observed spatial dependency captures a convolution of geographical propensity and a popularity-based heterogeneity among locations, by exploiting three large-scale mobile phone datasets from different countries across two continents (see Datasets for more details). By separating these two factors, we discovered a scaling relationship linking the critical exponents associated with the spatial effect on movement and communication patterns, effectively reducing the number of independent parameters characterizing human behavior. The uncovered scaling theory not only allows us to derive human movements from communication volumes, or vice versa, it also hints for a deeper connection that may exist among all networked systems where space plays a role, from transportations (2, 6, 42) and communications (27, 29, 30) to the internet (32, 33) and human brains (43).

Results

Mobile communication records, cataloged by mobile phone carriers for billing purposes, provide an extensive proxy of human movements and social interactions at a societal scale. Indeed, by keeping track of each phone call between two users and the spatiotemporal information about the user who initiated the call, mobile phone data offer information on both human mobility and social communication patterns at the same time. In this study, we compiled a uniquely rich database consisting of three different datasets that are of a similar level of detail yet with different demographics, economic status, and scales. The resulting data corpus includes D1, which contains 1.3 million users in Portugal and covers a period of 1 mo; D2, which is a dataset from an unnamed western European country that covers a 1-y period for about 6 million users; and D3, which is collected by the largest mobile phone carrier in Africa, covering a period of 4 y in Rwanda.

To quantify the spatial effect on social communication patterns, we measure the distance distribution of communications using two frequently used distance metrics.

Communication Distance Distribution.

The distance r characterizing social communications is the geodesic distance between two individuals u and v, who communicate via phone calls or short message service (SMS). Previous studies suggested that the probability for two individuals to communicate decreases with distance, following a power law distribution (20, 29, 44). Here we recovered previous results (Fig. 1A), finding that the distance distribution of each studied system, ${\mathit{P}}^{\mathit{S}}\left(\mathit{r}\right)$, can be approximated by a power law tail:

$$P^S\left(r\right)\mathrm{\sim }{r}^{\mathrm{-}{\beta }_i^r}.$$ [1]

We find the exponents ${\mathit{\beta }}_i^r$ to be similar for $D1$ and $D3$ (${\beta }_i^r\mathrm{\approx }1.5$) and slightly different for $D2$ (${\beta }_i^r\mathrm{\approx }1.35$) (Fig. 1A and Table 1).

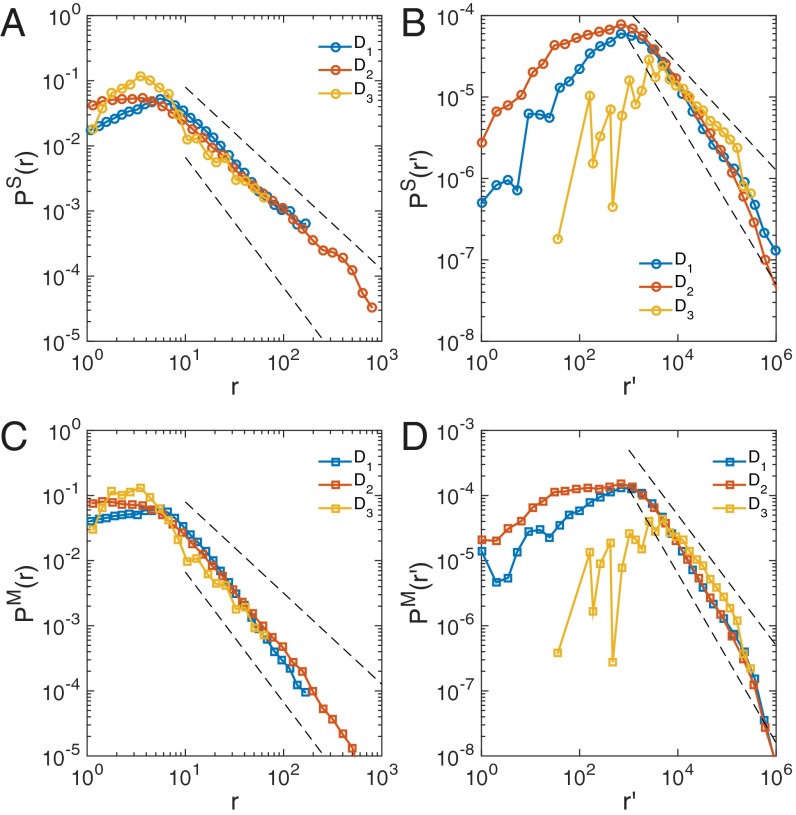
Fig. 1.

Communication and jump size distance distributions. (A) Communication distance distributions measured in geodesic distance r, $P^S\left(r\right)$, for all three datasets. Here, r measures the distance between two users when they communicate with each other via either phone calls or SMS. r is measured in the unit of kilometers. (B) Rank distributions $P^S(r\prime )$ for the three datasets follow a power law tail with exponents ${\beta }^{r\prime }=0.89$ for $D1$, ${\beta }^{r\prime }=1.00$ for $D2$, and ${\beta }^{r\prime }=0.64$ for $D3$. (C) Jump size distribution $P^M\left(r\right)$ measured in geodesic distance r follows a power law distribution. (D) Rank jump size distribution $P^M(r\prime )$ for rank $r\prime$ follows a power law distribution with exponent ${\alpha }^{r\prime }$ between 1.2 and 1.3 for $D1$ and $D2$ and ${\alpha }^{r\prime }\approx 1$ for $D3$. Here we mainly focus on large r (or $r\prime$) regime, fitting the tail part of the distributions. For fat-tailed distributions such as power law distributions, the tail part is the most important, determining the convergence/divergence of moments of distributions. The small r (or $r\prime$) regime before the peak is often referred to as small value saturations. Dashed lines serve as guide to the eye.

Table 1.

Critical exponents

Dataset	${\alpha }_{r\prime }$	${\beta }_{r\prime }$	${\theta }_{r\prime }$	${\delta }_{r\prime }$	$\widetilde{{\beta }_{r\prime }}$	${\alpha }_r$	${\beta }_r$	${\theta }_r$	${\delta }_r$	$\widetilde{{\beta }_r}$
$\mathit{D}1$	${1.22}_{\pm 0.03}$	${0.89}_{\pm 0.04}$	${0.89}_{\pm 0.02}$	${0.15}_{\pm 0.02}$	${0.94}_{\pm 0.04}$	${2.02}_{\pm 0.08}$	${1.50}_{\pm 0.06}$	${0.88}_{\pm 0.02}$	${0.16}_{\pm 0.04}$	${1.61}_{\pm 0.09}$
$D2$	${1.28}_{\pm 0.07}$	${1.00}_{\pm 0.07}$	${0.94}_{\pm 0.02}$	${0.16}_{\pm 0.02}$	${1.04}_{\pm 0.08}$	${1.75}_{\pm 0.05}$	${1.35}_{\pm 0.03}$	${0.92}_{\pm 0.02}$	${0.17}_{\pm 0.03}$	${1.44}_{\pm 0.07}$
$D3$	${1.00}_{\pm 0.07}$	${0.64}_{\pm 0.03}$	${0.67}_{\pm 0.03}$	$-{0.07}_{\pm 0.15}$	${0.70}_{\pm 0.16}$	${1.80}_{\pm 0.14}$	${1.57}_{\pm 0.18}$	${0.83}_{\pm 0.04}$	${0.24}_{\pm 0.08}$	${1.25}_{\pm 0.16}$

We measured ${\alpha }_{r\prime }$, ${\beta }_{r\prime }$, ${\theta }_{r\prime }$, and ${\delta }_{r\prime }$ independently for each dataset by using rank as distance metric. We estimate the errors in our measurements based on 95% confidence level. We then compute $\widetilde{{\beta }_{r\prime }}={\alpha }_{r\prime }{\theta }_{r\prime }-{\delta }_{r\prime }$ using Eq. 8. The error of $\widetilde{{\beta }_{r\prime }}$, $\sigma \left(\widetilde{{\beta }_{r\prime }}\right)$, is calculated using error propagations $\sigma \left(\widetilde{{\beta }_{r\prime }}\right)=\sqrt{{\theta }_{r\prime }^2{\sigma }^2\left({\alpha }_{r\prime }\right)+{\alpha }_{r\prime }^2{\sigma }^2\left({\theta }_{r\prime }\right)+{\sigma }^2\left({\delta }_{r\prime }\right)}$. We find that $\widetilde{{\beta }_{r\prime }}$ largely agrees with ${\beta }_{r\prime }$ within uncertainties across all datasets. Similarly, we repeated the same measurements by using geodesic distance, obtaining ${\alpha }_r$, ${\beta }_r$, ${\theta }_r$, ${\delta }_r$, and their corresponding errors, allowing us to compute $\widetilde{{\beta }_r}$ and its error $\sigma \left(\widetilde{{\beta }_r}\right)$. We find $\widetilde{{\beta }_r}$ also well approximates ${\beta }_r$. The largest deviations are observed in $D3$, which is characterized by much larger uncertainties in estimations of all exponents. This is due to its much smaller data size. Because both our data size and noninteger nature of distance metrics prevent us from using standard fitting algorithms for power laws (57), we computed all our exponents by using the least-square method.

Rank Distribution.

Within a country, the populations are not distributed uniformly in space. To account for such inhomogeneity, previous studies proposed the rank measure as an alternative to quantifying the effective distance between two individuals (27). The rank between two users u and v is the number of people closer to u than v, formally defined as $r\prime \mathrm{=}\left|w:r\left(u,w\right)\mathrm{<}r\left(u,v\right)\right|$. We measure the rank distributions for our three datasets (Fig. 1B), finding $P^S(r\prime )$ is characterized by a power law tail, consistent with previous studies (20, 27):

$$P^S(r\prime )\sim {r\prime }^{-{\beta }_i^{r\prime }}.$$ [2]

The exponents ${\beta }_i^{r\prime }$ for our three datasets are shown in Table 1.

Similarly, for mobility patterns, the jump size distribution is most commonly used to quantify spatial constraints in human movements. Here we measure this quantity in different distance metrics.

Jump Size Distribution.

Jump size measures the displacement in the unit of kilometers between two consecutive sightings of an individual. A fundamental property of human mobility is that the aggregated jump size distribution follows a power law (1, 2, 4),

$$P^M\left(r\right)\sim r^{-{\alpha }_i^r},$$ [3]

indicating most of the time people travel over short distances, between home and work for example, whereas they occasionally take longer trips. We measured $P^M\left(r\right)$ in our data corpus (Fig. 1C), finding few variations in ${\alpha }_i^r$ between datasets $D2$ and $D3$ (${\alpha }_i^r\mathrm{\approx }1.75$ and 1.8) but slight differences for dataset $D1$ (${\alpha }_i^r\mathrm{\approx }2.02$).

Rank Jump Size Distribution.

To account for biases from population density we measure the rank $r\prime$ of each jump. We find that $P^M(r\prime )$ is also characterized by a power law tail as suggested by previous studies (20, 39),

$$P^M(r\prime )\sim {r\prime }^{-{\alpha }_i^{r\prime }}.$$ [4]

As shown in Fig. 1D, ${\alpha }_i^{r\prime }$ is rather similar for D1 and D2 (${\alpha }_i^{r\prime }\approx 1.22$ and 1.28) but different from D3: ${\alpha }_i^{r\prime }\approx 1$ (Table 1).

Taken together, the spatial scaling of social interactions [$P^S\left(r\right)$ and $P^S(r\prime )$] for dataset i is characterized by exponents ${\beta }_i^r$ and ${\beta }_i^{r\prime }$, respectively, whereas human movements [$P^M\left(r\right)$ and $P^M(r\prime )$] are characterized by exponents ${\alpha }_i^r$ and ${\alpha }_i^{r\prime }$. These quantities were reported previously by independent research groups with different measurement details (1, 2, 29, 44). Here we measure these quantities systematically by using a comprehensive database we compiled. We find that within each of the two categories, the critical exponents (${\alpha }_i$ or ${\beta }_i$) in different countries are rather similar to each other. For example, there is little difference between the three ${\alpha }_i^r$ or ${\beta }_i^r$ exponents. For the rank metrics, D1 and D2 are also very similar to each other, whereas D3 is characterized by slightly different exponents. However, most noticeably, we observed substantial and systematic differences between ${\alpha }_i^{r,r\prime }$ and ${\beta }_i^{r,r\prime }$. Such differences contradict current modeling frameworks from gravity model (45) to radiation model (6) that treat these two classes of problems as similar phenomena given the same population distribution, thus predicting the same scaling exponent within each country. This raises a critical question: What is the origin of the observed differences between exponents ${\alpha }_i$ and ${\beta }_i$?

$P^S(r\prime )$ [or $P^S\left(r\right)$] measures the intensity of social communications as a function of distance, capturing on a population-averaged level the social fluxes between different locations. On the other hand, $P^M(r\prime )$ [or $P^M\left(r\right)$] measures the aggregated jumps between places, corresponding to the mobility fluxes from one location to another. Denoting with $T_{i,j}^S$ the social fluxes from location i to j and with $T_{i,j}^M$ the mobility fluxes representing the total number of communications ($T_{i,j}^S$) and jumps ($T_{i,j}^M$) between two locations, we measure $T_{i,j}^S$ and $T_{i,j}^M$ between any two locations over a 1-mo period. We find that both social and mobility fluxes follow fat-tailed distributions across our three studied datasets (Fig. 2). This is somewhat expected: Indeed, if we view each location as a node and fluxes as links connecting different locations, the fat-tailed distributions of fluxes are consistent with previous results on link weight distributions (46). Hence, Fig. 2 documents an inherent heterogeneity between locations: There are few fluxes between most locations, yet a nonnegligible fraction of location pairs are characterized by a large number of fluxes. The fat-tailed nature of flux distributions raises an important question: Can distance dependencies (Fig. 1) be accounted for by the observed heterogeneity in fluxes alone (Fig. 2)? To this end, we take D1 as an exemplary case and control for spatial effect by choosing location pairs that are of similar distances ($r\prime$) and measuring the distributions for social [$P_T^S\left(T|r\prime \right)$ in Fig. 3A] and mobility fluxes [$P_T^M\left(T|r\prime \right)$ in Fig. 3B], respectively. We find that the fluxes follow a fat-tailed distribution within each group, indicating there still exists much heterogeneity in fluxes even among locations within similar distances. Moreover, locations that are nearby (small $r\prime$) tend to have higher fluxes, corresponding to higher intensity in both communications (Fig. 3A) and movements (Fig. 3B). Indeed, the curves in Fig. 3 A and B shift to the right as $r\prime$ decreases, indicating the probability for two locations to have large fluxes decays with distance. This is consistent with preceding results (Fig. 1 and Eqs. 2 and 4) because most communications and movements are associated with short distances, accounting for the majority of the fluxes. However, as shown in Fig. 3 A and B, not all pairs of nearby locations have large fluxes. To the contrary, most of them have very small fluxes. Rather, it is a small fraction of location pairs in each distance groups, i.e., the tails of $P_T^S\left(T|r\prime \right)$ and $P_T^M\left(T|r\prime \right)$, that are responsible for generating the majority of fluxes. Most surprisingly, once we rescale the flux distributions with the average fluxes, $\langle T^S(r\prime )\rangle$ or $\langle T^M(r\prime )\rangle$, all curves shown in both Fig. 3 A and B (10 curves in total) collapse into one single curve, suggesting that a single universal flux distribution characterizes both social interactions and human movements, independent of distance (Fig. 3C). To be specific, this data collapse indicates that

$$P_T^{S,M}\left(T|r\prime \right)={\langle T^{S,M}(r\prime )\rangle }^{-1}\mathrm{ℱ}\left(T^{S,M}/\langle T^{S,M}(r\prime )\rangle \right),$$ [5]

where $\mathrm{ℱ}\left(x\right)$ is a distance-independent function. The data collapse in Fig. 3C is rather remarkable. It indicates that the observed localization in social communications and human movements can be decomposed into two independent factors: one is the universal distribution $\mathrm{ℱ}\left(x\right)$, which is distance independent, characterizing the inherent popularity-based heterogeneity among different locations. All of the distance dependencies are now encoded in the average fluxes at a given distance, i.e., $\langle T^S(r\prime )\rangle$ for social and $\langle T^M(r\prime )\rangle$ for mobility fluxes. We repeated our measurements using r as the distance metric, finding again an excellent data collapse (Fig. 3 D–F).

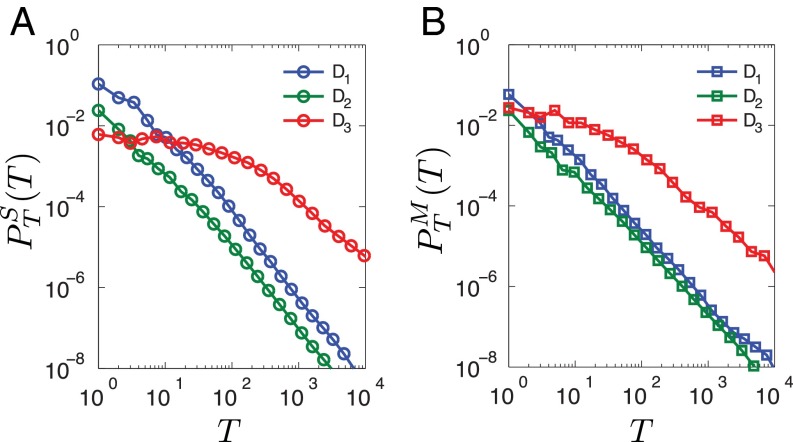
Fig. 2.

Flux distributions. Fat-tailed distributions of (A) social fluxes $T^S$ and (B) mobility fluxes $T^M$ for all three datasets. The fluxes $T_{i,j}^S$ (or $T_{i,j}^M$) are defined as the total number of communications (or jumps) between two locations i and j. The term fat-tailed refers to distributions $p\left(x\right)$ whose decay at large x is slower than exponential.

Fig. 3.

Flux distributions for different rank and distance groups. (A) Flux distributions of social communications for different rank groups, $P^S\left(T|r\prime \right)$. (B) Same distributions as A for mobility fluxes, $P^M\left(T|r\prime \right)$. (C) Mobility and communication fluxes (ten curves), denoted by circles and squares, respectively, collapse into one single curve after rescaled by the average fluxes in each group $\langle T\rangle$. (D) Flux distributions of communications for different distance groups, $P^S\left(T|r\right)$ (same as A but measured in geodesic distance r). (E) Same distributions as D for mobility fluxes, $P^M\left(T|r\prime \right)$. (F) Mobility and communication fluxes measured in geodesic distance (ten curves), denoted by circles and squares, respectively, again collapse into one single curve after rescaled by $\langle T\rangle$ for the different geodesic distance groups.

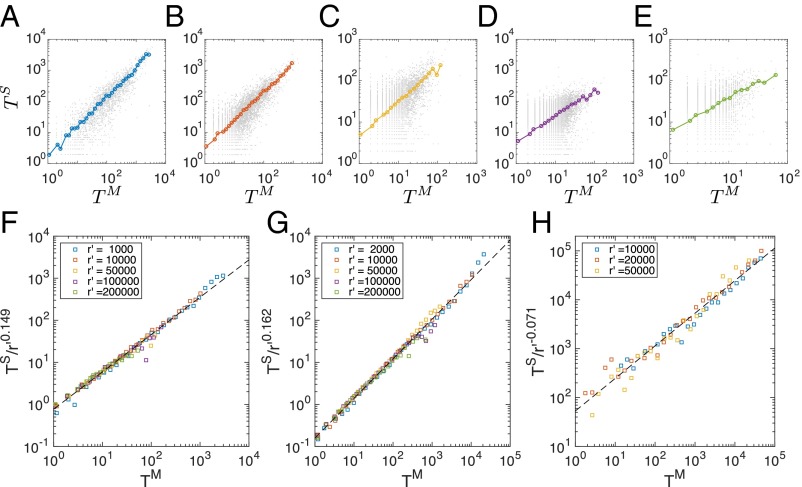
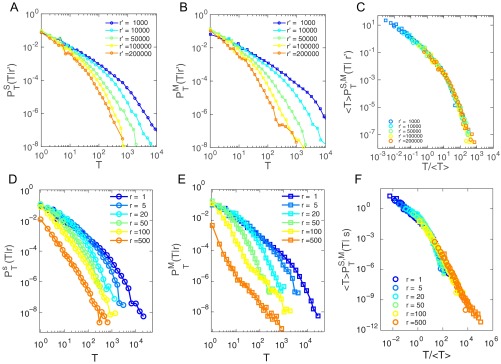
The uncovered universal function in Eq. 5 indicates that the social and mobility fluxes are important factors to characterize communication and mobility patterns, prompting us to measure correlations between the two quantities. We group location pairs (i and j) based on their distance and measure the relationship between $T_{i\mathrm{\to }j}^S(r\prime )$ and $T_{i\to j}^M(r\prime )$ for each group ($\mathit{r}\prime \mathrm{=}1e3$, $r\prime =1e4$, $r\prime \mathrm{=}5e5$, $r\prime =1e6$, and $r\prime =2e6$ in Fig. 4 A–E). In these scatterplots, each gray dot represents a pair of locations, and its x–y coordinates correspond to the mobility [$T_{i\to j}^M(r\prime )$] and social [$T_{i\to j}^S(r\prime )$] fluxes from i to j. We find strong correlations between these two quantities regardless of the separation between these locations. To quantify this correlation, we measure the average social fluxes given the mobility fluxes at a certain distance, $\overline{T^S}\left(T^M|r\prime \right)$ (colored symbols in Fig. 4 A–E), which is formally defined as

$$\overline{T^S}\left(T^M|r\prime \right)\mathrm{\equiv }\frac{{{\displaystyle \sum }}_{i\to j}{T}_{i\to j}^S\delta \left(T-T_{i\to j}^M\right)\delta \left(r\prime -r_{ij}\prime \right)}{{{\displaystyle \sum }}_{i\to j}\delta \left(T-T_{i\to j}^M\right)\delta \left(r\prime -r_{ij}\prime \right)},$$ [6]

where $\delta \left(x\right)$ is the delta function [$\delta \left(x\right)=1$ when $x=0$, and $\delta \left(x\right)=0$ otherwise]. We find that the average social fluxes $\overline{T^S}\left(T^M|r\prime \right)$ follow a power law scaling relationship with $T^M$, i.e.

$$\overline{T^S}\left(T^M|r\prime \right)=A(r\prime )T^M{(r\prime )}^{{\theta }_{r\prime }},$$ [7]

where the scaling exponents for different $r\prime$, ${\theta }_{r\prime }<1$, indicating social fluxes scale sublinearly with mobility fluxes, independent of distance. The prefactor in Eq. 7, $A(r\prime )$, corresponds to the shift along the y axis through Fig. 4 A–E. We find that as distance increases, the average social fluxes increase given the same volume of mobility fluxes. Hence, $A(r\prime )$ characterizes the cost tradeoff between phone communications and human movement. Rescaling $\overline{T^S}$ by $r^{\prime {\delta }_{r\prime }}$, we find all curves collapse into a straight line (Fig. 4F), indicating that $A(r\prime )\mathrm{\sim }{r}^{\prime {\delta }_{r\prime }}$, where ${\delta }_{r\prime }\mathrm{=}0.15$. We repeated the same measurement for D2 and D3, finding that although each dataset is characterized by a different set of ${\theta }_{r\prime }$ and ${\delta }_{r\prime }$, Eq. 7 holds consistently well across different datasets (Fig. 4 G and H). We also repeated our analysis by replacing $r\prime$ with other distance metrics (geodesic distance r), finding again consistent results with Eq. 7. Indeed, each dataset is well described by its characteristic set of ${\theta }_r$ and ${\delta }_r$ exponents, demonstrating the robustness of our findings (Correlation Between Social and Mobility Fluxes with Geodesic Distance).

Fig. 4.

Correlations between social and mobility fluxes. Correlations between $T_{i\to j}^S(r\prime )$ and $T_{i\to j}^M(r\prime )$ for location pairs (gray dots) separated by a distance of (A) $r\prime =1e3$, (B) $r\prime =1e4$, (C) $r\prime =5e5$, (D) $r\prime =1e6$, and (E) $r\prime =2e6$. We find all curves collapse into a straight line when $\overline{T^S}$ is rescaled by $r^{\prime {\delta }_{r\prime }}$ for (F) $D1$, (G) $D2$, and (H) $D3$.

Most important, Eq. 7 together with the data collapses in Fig. 3 C and F (Eq. 5) allows us to derive a new scaling relationship,

$${\beta }_{r\prime }={\alpha }_{r\prime }{\theta }_{r\prime }-{\delta }_{r\prime },$$ [8]

connecting the exponent that characterizes social communications (${\beta }_{r\prime }$) with the exponent characterizing human movements (${\alpha }_{r\prime }$) (see Derivation of the Scaling Relationship Between Exponents for details). Similarly, for geodesic distance metric r, we obtain

$${\beta }_r={\alpha }_r{\theta }_r-{\delta }_r.$$ [9]

We measure each exponent in Eqs. 8 and 9 independently for each dataset, finding excellent agreement between the empirical measurements and our theoretical predictions (Table 1). Hence, Eqs. 8 and 9 offer an explicit link between critical exponents characterizing spatial dependencies in human movements and social interactions, showing that the social exponent (β) can be expressed in terms of the mobility exponents (α), a consistently robust result that is independent of the distance metrics used. The uncovered scaling relationship between these two classes of exponents is mediated by a universal flux distribution [$\mathrm{ℱ}\left(\mathit{x}\right)$] we uncovered in this study. This scaling relationship bridges two fields that are traditionally disjoint (12, 20), showing that they represent different facets of a deeper underlying reality, effectively reducing the number of independent parameters characterizing human behavior.

The uncovered relationship offers a powerful framework to derive quantities pertaining to one field from those of the other. Next, we show one practical application in public health domain as an exemplary case. Over the past few years, many computational studies highlighted the importance of social data to tackle public health challenges (10, 47). Among them, epidemic spreading is perhaps one of the most prominent (48–51). To this end, we simulate a virus spreading process using D1 to demonstrate how our findings can be used to connect human mobility and social interactions. Of the many ingredients in computational modeling of virus spreading, human mobility is among the most critical (1, 22, 23, 51, 52, 53). To understand how human movements catalyze societal-wide spreading processes, we infect a few randomly selected individuals with some hypothetical germ in a random location at time $t=0$. Denoting with μ the infection rate of this germ, we assume, at each time step, that an infected individual could spread the disease to others within his/her vicinity, i.e., individuals within the same mobile tower. At the same time, any infected individual can recover from the disease at rate ν. This process is known as the susceptible–infectious–susceptible (SIS) model, commonly used in modeling disease spreading (54, 55).

Choosing any set of μ and ν, we can simulate a spatial SIS model by following the real mobility fluxes between locations ($T_{i,j}^M$) measured from our dataset (see Supporting Information for modeling details). This raises an interesting question: had we not had access to mobility information, how well could we have approximated the observed spreading pattern using social fluxes rescaled by the predicted scaling (Eq. 8)?

Following Eq. 7 and using the exponents from Eq. 8, mobility fluxes between a location i and j can be approximated by rescaled social fluxes, ${\tilde{T}}_{i,j}^S$, defined as ${\tilde{T}}_{i,j}^S={\left(r_{i,j}^{\prime -{\delta }_{r\prime }}{T}_{i,j}^S\right)}^{-{\theta }_{r\prime }}$, where ${\delta }_{r\prime }=0.15$ and ${\theta }_{r\prime }=0.89$ for D1 (Table 1) and $r_{i,j}\prime$ is the distance between the two locations. We simulate a spreading process in Portugal using the real mobility fluxes $T^M$ and the rescaled social fluxes ${\tilde{T}}^S$ as well as the mobility fluxes $T_{GM}^M$, approximated by the widely used gravity model (20, 45) (see Determination of Gravity Law’s Parameters for more details). To compare these results, we started from the same initial conditions ($\mu =0.9$, $\nu =0.3$) and initial infected users located in a major city (Lisbon) for all simulations in this example.

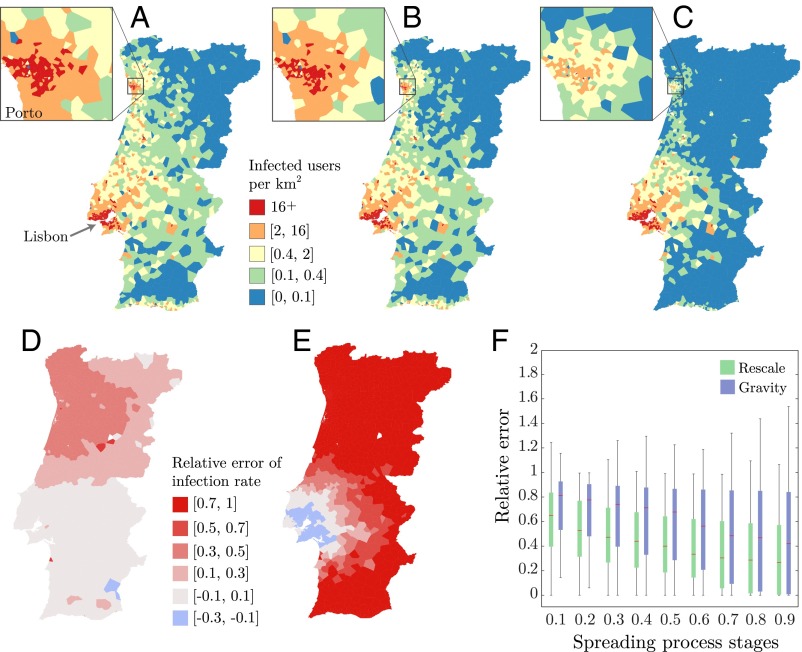
We measure the density of infected users estimated in each location i for the three cases (Fig. 5 A–C), finding a remarkable agreement between our simulation and the real spreading patterns. Moreover, close up on the city of Porto reveals a superior accuracy of our model comparing with predictions from gravity model. We quantify the differences between the two methods (Fig. 5 D and E). The drastic difference between Fig. 5 D and E highlights the superior predictive power of our model.

Fig. 5.

Epidemic spreading simulations in Portugal. Densities of infected users at time $\mathit{t}\mathrm{=}17$ following a simulation of an SIS spreading process ($\mu =0.9$, $\mathit{\nu }\mathrm{=}0.3$) originated from Lisbon by using (A) real mobility fluxes $T^M$, (B) the rescaled social fluxes ${\tilde{T}}^S$, and (C) the mobility fluxes approximated by gravity model $T_{gm}^M$. (D) Relative errors of infection rate ${\tilde{e}}_i\left(t\right)$ (Eq. S19) and (E) ${\tilde{e}}_i^{gm}\left(t\right)$ (Eq. S20) at each location i at time $t=17$. (F) Distributions of mean relative error $\overline{\tilde{e}}\left(t\right)$ (green) and $\overline{e^{gm}}\left(t\right)$ (blue) over 500 SIS simulations at different stages before reaching the steady state, documenting the superior predictive power of our method comparing with gravity model at all stages of the spreading processes.

To systematically assess and compare the accuracy of our results, we simulated 500 independent spreading processes following the same procedure described above but choosing randomly μ and ν parameters as well as the initial infected location and the number of infected users. We find that errors obtained from the 500 simulations are systematically lower than estimations from gravity model across all stages of the spreading processes (Fig. 5F), demonstrating the practical relevance of our scaling relationship, effectively predicting mobility patterns using social communication records.

The practical applications are most useful when only one of the two facets of information is available. For example, companies that provide social networking functionalities or services have exploded over the past few years. For many of them, mobility information is essential but difficult to collect. Conversely, companies providing location services such as global positioning system (GPS) have many mobility records yet typically lack social information. For both cases, our method may provide a reasonable estimate to fill the void, which is particularly promising given the fact that it outperforms gravity model, the prevailing framework to predict movements. Therefore, in many cases, our method may serve as a viable alternative, working in unison with or in certain cases even replacing model-based approaches, improving the predictive accuracy of most of the phenomena affected by mobility and transport processes. It could be particularly useful for developing countries where many people still live in data-scarce environments.

Taken together, by analyzing three large-scale mobile phone datasets from three different countries, we uncovered a new scaling relationship between the critical exponents that characterize spatial dependencies in human mobility and social interactions. This scaling relationship is mediated by a universal flux distribution for both movement and communication patterns, indicating the previously observed distance dependencies capture a convolution of geographical propensity and a popularity-based heterogeneity among locations. Separating these two factors allows us to establish a formal connection between different critical exponents that were perceived as independent. Together, our results document a new order of regularity that helps deepen our quantitative understanding of human behavior. Last, our results may reach far beyond communications and transportations studied in this paper because many networked systems are also subject to spatial costs in establishing connections in a very similar fashion as our quoted examples, from routers linked by physical cables to form globally connected internet to axons that connect different regions of human brains. Hence, our results may provide relevant insights to a diverse set of networked systems where space plays a role (20), opening up a promising direction for future investigation.

Finally, our study is not without limitations. Indeed, although the critical exponents we studied here capture macroscopic patterns of mobility and social interactions, both processes are affected by various sociodemographic factors both within and across countries, resulting in population variations that may not be captured adequately by power law exponents alone. It would be fruitful to analyze the degree to which such information affects mobility and social interactions, when more sociodemographic information becomes available. Among our three datasets, D3 seems to be an outlier, having different critical exponents than D1 and D2. Such information would also help us uncover deeper reasons behind variations across different countries. Furthermore, although our datasets capture people and their interactions, the focus of our paper is on data rather than people. Indeed, the virtue of our results lies in the uncovered statistical regularities revealed by our datasets. As such, our paper focuses on facts that can be measured from the data rather than deeper sociological reasons behind these observations. Last, to what degree are movements and social interactions estimated from mobile phone datasets representative? Although studies that compare self-report surveys and observational data (56) together with results obtained using higher-resolution traces (12) offer additional, convincing assurance that our results are not affected by the peculiarities of call detail records used in our study (Potential Limitations of Mobile Phone Datasets), we need further studies to test these assumptions in a more systematic manner.

Materials and Methods

Details of studied datasets are described in Datasets. Mathematical derivations of the scaling relationships in Eqs. 8 and 9 are summarized in Derivation of the Scaling Relationship Between Exponents. The same measurements as Figs. 2 and 3 obtained by using D2 and D3 are shown in Distribution of Social and Mobility Fluxes for D2 and D3. Data necessary to replicate results of this study (D1, D2, and D3) are available upon request. The use of mobile phone datasets for research purposes was approved by the Northeastern University Institutional Review Board. Informed consent was not necessary because research was based on previously collected anonymous datasets.

Datasets

Mobile communication records, cataloged by mobile phone carriers for billing purposes, provide an extensive proxy of human movements and social interactions at a societal scale. Indeed, by keeping track of each phone call between two users and the spatiotemporal information about the users who initiated and received the call, mobile phone data offer information on both human mobility and social communication patterns at the same time, as we will detail hereunder.

In this project, we compiled a uniquely rich database consisting of three different datasets that are of a similar level of detail yet with different demographics, economic status, and scales:

Dataset D1 contains mobile phone calls between 1.3 million users over a period of 1 mo in 2006 from a European country (Portugal). For each phone call, the caller and the callee, both anonymized with a key (hash code); the time; the date; and the phone towers routing the communication are recorded. Only phone calls between users that called each other at least 5 times over a period of 18 mo are known. Furthermore, only the coordinates of the mobile phone towers are known; hence, the position of a user within the range of an antenna is unknown.

Dataset D2 covers a 6-mo period of mobile phone calls between 6 million anonymized users from a large European country. For each phone call, the caller, the callee, the time, and the towers routing the communication are recorded. Similarly to $D1$, only the coordinates of the mobile towers are known; hence, the position of a user within the range of an antenna is unknown.

Dataset D3 covers a period from 2005 to 2009 and is made of all transaction logs of all mobile phone activity that occurred in an African country (Rwanda) over the 5-y period. The data originate from the largest mobile phone operator in that country and contain about 1.5 million phone calls. The logs include the date, the time, and the mobile phone towers routing the call for each of the phone calls and are again anonymous. Again, only the coordinates of the mobile towers are known; hence, the position of a user within the range of an antenna is unknown.

Inferring Mobility and Social Fluxes

Mobility Fluxes.

For each phone call, the position of the tower routing the call is known for the caller. Because we know the location of each tower, we know the location of the user was within the range of the tower’s service area. By looking at each consecutive phone call made by a user, we can thus reconstruct the user’s jumps between two consecutive locations where his calls were initiated. By aggregating all movements for all users, we can thus obtain the total number of jumps from any tower i to any tower j ($T_{i,j}^M$). All jumps made outside continental territories (i.e., islands) were not taken into account. The jumps do not exceed $\sim \mathrm{1,000}$ km, $\sim 400$ km, and $\sim 100$ km for datasets $D1$, $D2$, and $D3$, respectively, due to national frontiers and coverage limitations driven by geographical constraints in the country. We consider the number of jumps between two locations as the mobility fluxes between them.

Social Fluxes.

For each phone call, the position of the tower routing the call is known for both the caller and the callee. By considering all phone calls, we thus know the total number of calls from a tower i to a tower j ($T_{i,j}^S$). We consider the number of phone calls between two locations as the social fluxes between them.

Jump Size Distribution at Fixed Interevent Time

It is known that the distribution of interevent times between two consecutive calls (locations) from the same user is heterogeneous (2). It is thus important to investigate if the observed displacement statistics (the jumps) are affected by this characteristic.

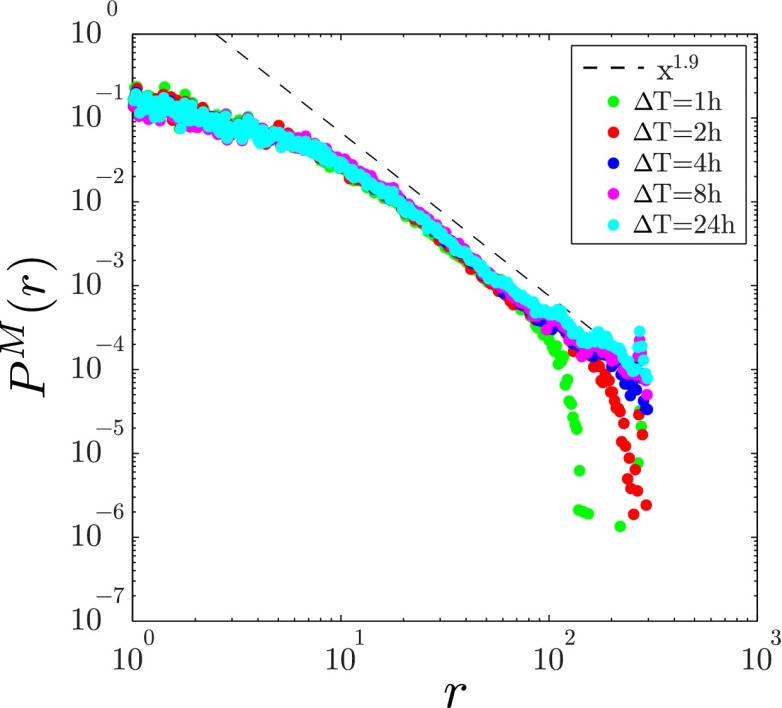
To simulate location traces left by a phone on a regular basis (instead of those due to calls) using data available to us, we calculate location displacement between a fixed time interval instead of two consecutive phone calls. More specifically, we use our dataset D1 and calculate the jump size distribution $P^M\left(r\right)$ for displacements separated by a time $\mathrm{\Delta }T\pm 0.05\mathrm{\Delta }T$. We systematically vary $\mathrm{\Delta }T$ from 1 h to 1 d (Fig. S1). We find the distributions collapse for different choices of $\mathrm{\Delta }T$, suggesting that the use of consecutive calls serves as a good proxy for movements. Also, the curves can be well approximated by a power law consistent with our previous results. Note our results are bounded by the maximum distance a user can travel during $\mathrm{\Delta }T$, thus explaining the differences in the tail part of the distribution.

Fig. S1.

Jump size distribution $P^M\left(r\right)$ for interevent time $\mathrm{\Delta }T=1,\hspace{0.17em}2,\hspace{0.17em}4,\hspace{0.17em}8,\hspace{0.17em}\text{and}\hspace{0.17em}24$ h for the $D1$ dataset. A power law with exponent $r^{-1.9}$ provides a guide to the eye. We observe that the curves are bounded by the maximum distance a user can travel during their corresponding interevent time for $\mathrm{\Delta }T<4\hspace{0.17em}\text{h}$ or the maximum distance enforce by geographical constraints in that country.

Distribution of Social and Mobility Fluxes for D2 and D3

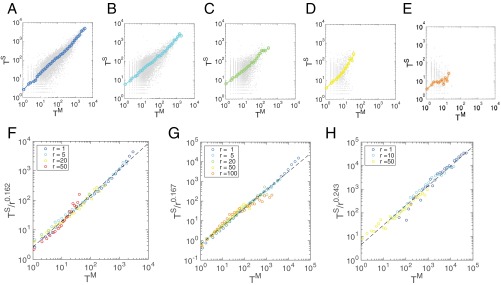
In Figs. S2 and S3, we present results obtained for the datasets $D2$ and $D3$ regarding the distributions of the social fluxes $P_T^S\left(T|r\prime \right)$ and $P_T^S\left(T|r\right)$ (Fig. 3 A and D for $D1$) and mobility fluxes $P_T^M\left(T|r\prime \right)$ and $P_T^M\left(T|r\right)$ (Fig. 3 B and E for $D1$) for pairs of locations that are of similar distances (r and $r\prime$). We also show how flux distributions collapse for both datasets when they are rescaled with their average flux, $\langle T\left(r\right)\rangle$ or $\langle T\left(r\prime \right)\rangle$ (Fig. 3 C and F). The same procedure for the dataset $D1$ is applied to $D2$ (Fig. S2) and $D3$ (Fig. S3). We again find that the fluxes for each group still follow a fat-tailed distribution, indicating there also exists much heterogeneity in fluxes among locations within similar distances for both $D2$ and $D3$. Locations that are nearby (small $r\prime$ or r) tend to have higher fluxes, corresponding to higher intensity in both communications (Figs. S2 A and D and S3 A and D) and movements (Figs. S2 B and E and S3 B and E), corroborating our results for $D1$. Indeed, the curves shift to the right as $r\prime$ (or r) decreases, indicating the probability for faraway location pairs to have large fluxes is much lower. Once we rescale the flux distributions with the average flux, $\langle T(r\prime )\rangle$ or $\langle T\left(r\right)\rangle$, we find all of the curves collapse into a single curve, demonstrating again a single universal flux distribution characterizes both social communication and human movement fluxes, independent of distance (Figs. S2 C and F and S3 C and F).

Fig. S2.

(A) Communication fluxes $P^S\left(T|r\prime \right)$ conditional to the rank $r\prime$ for dataset $D2$. (B) Mobility fluxes $P^M\left(T|r\prime \right)$ conditional to the rank $r\prime$ for dataset $D2$. (C) Mobility and communication fluxes, denoted by circles and squares, respectively, collapse after rescaled by $\langle T\rangle$ for dataset $D2$ for the rank-based distance. (D) Communication fluxes $P^S\left(T|r\prime \right)$ conditional to the distance r for dataset $D2$. (E) Mobility fluxes $P^M\left(T|r\right)$ conditional to the distance r for dataset $D2$. (F) Mobility and communication fluxes, denoted by circles and squares, respectively, collapse after rescaled by $\langle T\rangle$ for dataset $D2$ for the geodesic distance.

Fig. S3.

(A) Communication fluxes $P^S\left(T|r\prime \right)$ conditional to the rank $r\prime$ for dataset $D3$. (B) Mobility fluxes $P^M\left(T|r\prime \right)$ conditional to the rank $r\prime$ for dataset $D3$. (C) Mobility and communication fluxes, denoted by circles and squares, respectively, collapse after rescaled by $\langle T\rangle$ for dataset $D3$ for the rank-based distance. (D) Communication fluxes $P^S\left(T|r\right)$ conditional to the distance r for dataset $D3$. (E) Mobility fluxes $P^M\left(T|r\right)$ conditional to the distance r for dataset $D3$. (F) Mobility and communication fluxes, denoted by circles and squares, respectively, collapse after rescaled by $\langle T\rangle$ for dataset $D3$ for the geodesic distance.

Correlation Between Social and Mobility Fluxes with Geodesic Distance

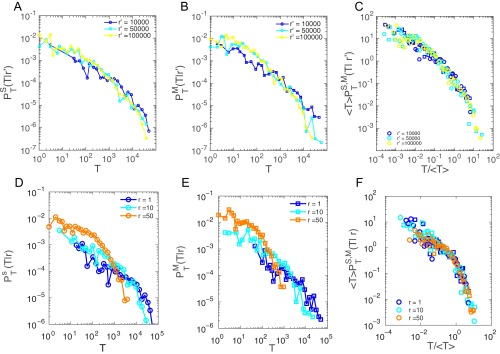
As developed in the manuscript for the rank-based distance, we here analyze the correlations between the social fluxes $T_{i\to j}^S\left(r\right)$ and mobility fluxes $T_{i\to j}^M\left(r\right)$ in the case of the geodesic distance. We group location pairs (i and j) based on their distance and measure the relationship between $T_{i\to j}^S\left(r\right)$ and $T_{i\to j}^M\left(r\right)$ for each group ($r=1$, $r=5$, $r=10$, $r=50$, and $r=100$ in Fig. S4 A–E). In these scatterplots, each gray dot represents a pair of locations, and its x–y coordinates correspond to the mobility [$T_{i\to j}^M\left(r\right)$] and social [$T_{i\to j}^S\left(r\right)$] fluxes from i to j for dataset $D1$.

Fig. S4.

Correlation between $T_{i\to j}^S\left(r\right)$ and $T_{i\to j}^M\left(r\right)$ for pair of locations (gray dots) separated by a distance of (A) $r=1\hspace{0.17em}\text{km}$, (B) $r=5\hspace{0.17em}\text{km}$, (C) $r=20\hspace{0.17em}\text{km}$, (D) $r=50\hspace{0.17em}\text{km}$, and (E) $r=100\hspace{0.17em}\text{km}$ for $D1$. We find all curves collapse into a straight line when $\overline{T^S}$ is rescaled by $r^{{\delta }_r}$ for (F) $D1$, (G) $D2$, and (H) $D3$.

Same as for the rank-based measures, we find again strong correlations between these two quantities regardless of how far away these locations are separated. To quantify this correlation, we measure the average social fluxes given the mobility fluxes at a certain distance, $\overline{T^S}\left(T^M|r\right)$ (colored symbols in Fig. S4 A–E), which is formally defined as

$$\overline{T^S}\left(T^M|r\right)\equiv \frac{{\displaystyle {\sum }_{i\to j}{T}_{i\to j}^S\delta \left(T-T_{i\to j}^M\right)\delta \left(r-r_{ij}\right)}}{{\displaystyle {\sum }_{i\to j}\delta \left(T-T_{i\to j}^M\right)\delta \left(r-r_{ij}\right)}},$$ [S1]

where $\delta \left(x\right)$ is the delta function [$\delta \left(x\right)=1$ when $x=0$, and $\delta \left(x\right)=0$ otherwise]. We find that the average social fluxes $\overline{T^S}\left(T^M|r\right)$ have again a power law scaling relationship with $T^M$, following

$$\overline{T^S}\left(T^M|r\right)=A\left(r\right)T^M{\left(r\right)}^{{\theta }_r},$$ [S2]

where the scaling exponent ${\theta }_r<1$ for different r, indicating social fluxes again scale sublinearly with mobility fluxes. The prefactor in Eq. S2, $A\left(r\right)$, corresponds to the shift along the y axis through Fig. S4 A–E. We find, as distance increases, the average social fluxes increase given the same volume of mobility fluxes. Rescaling $\overline{T^S}$ by $r^{{\delta }_r}$, we find all curves collapse into a straight line (Fig. S4F), indicating $A\left(r\right)\sim r^{{\delta }_r}$.We repeated the same measurement for D2 and D3. We found that although each dataset is again characterized by a different set of ${\theta }_r$ and ${\delta }_r$, Eq. S2 (same as Eq. 7 in the main manuscript) holds consistently well across different datasets (Fig. S4 F–H), demonstrating the robustness of our findings for both the distance r and $r\prime$.

Derivation of the Scaling Relationship Between Exponents

As stated in the main manuscript, we find that the average social fluxes $\overline{T^S}\left(T^M|r\prime \right)$ follow a power law scaling relationship with $T^M$, i.e.,

$$\overline{T^S}\left(T^M|r\right)=A(r\prime )T^M{(r\prime )}^{{\theta }_{r\prime }},$$ [S3]

where ${\theta }_{r\prime }<1$, indicating social fluxes scale sublinearly with mobility fluxes, independent of distance. As described in Correlation Between Social and Mobility Fluxes with Geodesic Distance, a similar result is obtained for geodesic distance metric r (Eq. S2).

The data collapses observed in Fig. 3 C and F, i.e.,

$$P_T^{S,M}\left(T|r\prime \right)={\langle T^{S,M}(r\prime )\rangle }^{-1}\mathrm{ℱ}\left(T^{S,M}/\langle T^{S,M}(r\prime )\rangle \right),$$ [S4]

together with Eq. S3 allow us to derive a new scaling relationship between different critical exponents. Indeed, the average social fluxes at distance $r\prime$, $\overline{T^S}(r\prime )$, can be obtained by integrating $\overline{T^S}\left(T^M,r\prime \right)$ over $T^M$:

$$\overline{T^S}(r\prime )={\displaystyle \int P_T^M\left(T^M|r\prime \right)\overline{T^S}\left(T^M,r\prime \right)d{T}^M.}$$ [S5]

Substituting Eqs. S4 and S3 into Eq. S5, we have

$$\overline{T^S}(r\prime )={\displaystyle \int \mathrm{ℱ}\left(x\right)\overline{T_M^S}\left(\overline{T^M}(r\prime )x,r\prime \right)dx}\sim \overline{T^M}{(r\prime )}^{{\theta }_{r\prime }}{r\prime }^{{\delta }_{r\prime }}{\displaystyle \int x^{{\theta }_{r\prime }}\mathrm{ℱ}\left(x\right)dx,}$$ [S6]

where $x\equiv T^M/\overline{T^M}$ as a change of variable. As $\overline{T^S}(r\prime )\sim {\displaystyle \sum _{i\to j}{T}_{i\to j}^S\delta \left(r\prime -r_{ij}\prime \right)=P^S(r\prime )\sim {r\prime }^{-{\beta }_{r\prime }}}$, and similarly $\overline{T^M}(r\prime )\sim {r\prime }^{-{\alpha }_{r\prime }}$, we have

$${r\prime }^{-{\beta }_{r\prime }}={r\prime }^{-{\alpha }_{r\prime }{\theta }_{r\prime }}{r\prime }^{{\delta }_{r\prime }}{\displaystyle \int x^{{\theta }_{r\prime }}\mathrm{ℱ}\left(x\right)dx}.$$ [S7]

The tail behavior of $\mathrm{ℱ}\left(x\right)$ indicates the integral in Eq. S7 converges. Hence, Eq. S7 leads to a scaling relationship,

$${\beta }_{r\prime }={\alpha }_{r\prime }{\theta }_{r\prime }-{\delta }_{r\prime },$$ [S8]

connecting the exponent that characterizes social communications (${\beta }_{r\prime }$) with the exponent characterizing human movements (${\alpha }_{r\prime }$). Similarly, for geodesic distance metric r, we obtain

$${\beta }_r={\alpha }_r{\theta }_r-{\delta }_r.$$ [S9]

The scaling analyses performed here have their roots in the canonical statistical physics literature, namely, the scaling identities in phase transitions and critical phenomenon. The power law scaling behavior in the vicinity of a continuous transition is captured by a set of critical exponents $\left(\alpha ,\beta ,\gamma ,\delta ,\sigma ,\eta ,\dots \right)$, characterizing various fundamental quantities such as free energy, specific heat, magnetization, susceptibility, etc. In the beginning, these critical exponents were measured independently and found to vary slightly across different materials. Later, we witnessed a burst of results demonstrating that these critical exponents are not independent but are in fact connected through what we now call scaling identities. The famous examples include Rushbrooke’s identity, Widom’s identity, Josephson’s identity, and Fisher’s identity (58).

Determination of Gravity Law’s Parameters

The gravity law assumes that the mobility fluxes between a locations i of origin and a location j of destination can be expressed as a function of the two populations at the two locations ($m_i$ and $m_j$) and the geodesic distance between them ($r_{i,j}$) as

$$T_{GM,i,j}^M=C\frac{m_i^{\mu }{m}_j^{\kappa }}{f\left(r_{i,j}\right)},$$ [S10]

where $f\left(r\right)=r^{\gamma }$ (6, 20, 45, 59). By taking the logarithm on both sides we obtain

$$log\left(T_{GM,i,j}^M\right)=log\left(C\right)+\mu log\left(m_i\right)+\kappa log\left(m_j\right)-\gamma log\left(r_{i,j}\right).$$ [S11]

Using the observed mobility fluxes ($T^M$), we can then estimate the parameters through a least square regression, giving us $\left[log\left(C\right),\mu ,\kappa ,\gamma \right]=\left[-3.42,0.67,0.68,1.32\right]$.

Epidemic Spreading Simulations

To compare the accuracy and usefulness of our rescaling formula, we simulated an SIS process commonly used in modeling disease spreading (54, 55) by following the observed mobility fluxes $T^M$ and the rescaled social fluxes ${\tilde{T}}^S$ but also the mobility fluxes $T_{gm}^M$ approximated by the well-known gravity model (20, 45).

We consider the process where each location i (mobile tower) is characterized by a constant population size $N_i$, equal to the number of distinct users present in the vicinity of the mobile tower over the period covered by the dataset $D1$. The total population in our system is thus given by ${\displaystyle {\sum }_{i=1}^m{N}_i}$, and the system equilibrated as the population is constant. In each location, users are classified according to their infectious state: they can be either infectious (I) or susceptible to be infected (S). The standard generalization of this spatial SIS model is given by

$$S_i+I_i\stackrel{\mu }{\to }{I}_i$$ [S12]

$$I_i\stackrel{\nu }{\to }{S}_i$$ [S13]

$$S_i\stackrel{A_{i,j}}{\to }{S}_j$$ [S14]

$$I_i\stackrel{A_{i,j}}{\to }{I}_j,$$ [S15]

where reaction S5 indicates that susceptible users can become infectious at a rate μ and reaction S6 corresponds to infected users recovering from the disease at a rate ν. In addition to the standard SIS dynamics, susceptible as well as infected users can randomly move between one location i to another location j as described in reactions S7 and S8. The probability rate of these movements from location i to j is governed by the probability rate $A_{i,j}$ defined as

$$A_{i,j}=\frac{{\left(T_{i,j}{T}_{j,i}\right)}^{-2}}{N_i}.$$ [S16]

Because the system is equilibrated, the flux of users from i to j must balance that of j to i (detailed balance condition):

$$A_{i,j}{N}_i=A_{j,i}{N}_j,$$ [S17]

which is fulfilled by Eq. S18.

In this case, the spatial SIS model can be defined as a set of m coupled ordinary differential equations (ODEs) for the infected people in each location (22, 60):

$${\partial }_t{I}_i=\mu \frac{I_i}{N_i}\left(N_i-I_i\right)-\nu I_i+{\displaystyle \sum _{j\ne i}\left[A_{j,i}{I}_j-A_{i,j}{I}_i\right]},$$ [S18]

enabling us to compute the evolution of infected users in each location over time by solving these.

Denoting with $n_i$ the number of users at location i, with $a_i$ the area of location i and $m_i\left(t\right)$, ${\tilde{m}}_i\left(t\right)$, and $m_i^{GM}\left(t\right)$ the number of infected users at time t in location i when using $T^M$, ${\tilde{T}}^S$, and $T_{GM}^M$, respectively, we measure $m_i\left(t\right)/a_i$, ${\tilde{m}}_i\left(t\right)/a_i$, and $m_i^{GM}\left(t\right)/a_i$, i.e., the density of infected users estimated in each location i for the three cases (Fig. 5 A–C for $t=17$). We find a remarkable agreement between our simulation and the real spreading patterns. Moreover, close up on the city of Porto reveals a superior accuracy of our model comparing with predictions from gravity model. To quantify the differences between the two methods, we measure

$${\tilde{e}}_i\left(t\right)=\frac{m_{i,t}-{\tilde{m}}_{i,t}}{m_{i,t}}$$ [S19]

and

$$e_i^{GM}\left(t\right)=\frac{m_{i,t}-m_{i,t}^{GM}}{m_{i,t}},$$ [S20]

corresponding to the relative error of infection rate in each location i at time t for both methods (Fig. 5 D and E at $t=17$). The drastic difference between Fig. 5 D and E highlights the fact that lower ${\tilde{e}}_i\left(t\right)$ are observed comparing with $e_i^{GM}\left(t\right)$ in this particular example, again documenting the superior predictive power of our model.

To systematically assess and compare the accuracy of our results, we simulated 500 independent spreading processes following the same procedure described above but choosing randomly μ and ν parameters as well as the initial infected location and the number of infected users. For each simulation, we compute the mean values $\overline{\tilde{e}}\left(t\right)$ and $\overline{e^{GM}}\left(t\right)$ from Eqs. S19 and S20, respectively, at different stages (time steps). We find that $\overline{\tilde{e}}\left(t\right)$ obtained from the 500 simulations are systematically lower than $\overline{e^{GM}}\left(t\right)$ across all stages of the spreading processes (Fig. 5F), demonstrating the practical relevance of our scaling relationship, effectively predicting mobility patterns using social communication records.

Normalizing the Time Steps of the Spreading Processes

In this section, we describe the procedure we use to compare spatial spreading processes whose initial conditions differs.

As formulated in Eq. S18, each spatial process is characterized by a set of m coupled ODEs. Each ODE corresponds to a spreading subprocess within a location, and each one of them reaches the steady-state after a different number of time steps (61, 62). Here we consider the global process to be at equilibrium when no more changes are observed for any of its subprocesses, i.e., $\underset{i}{\text{max}}\hspace{0.17em}{\partial }_t{I}_i/N_i<{10}^{-5}$.

As described in the main manuscript, we simulated 500 spatial spreading processes, each with parameters μ, ν, initial infected location, and initial number of infected users chosen randomly. Each process i will thus reach the equilibrium at a different time $t_i^c$. To compare their accuracy at different stages of the process, we normalize the time steps $t_i$ of each process i by its time before equilibrium, i.e., $t_i/t_i^c$. As a result, a time step of $t_i/t_i^c=0.5$ for any process i would correspond to half the time it takes to reach the equilibrium. This normalization is used in Fig. 5F to compare processes at similar stages.

Potential Limitations of Mobile Phone Datasets

For studies on mobility and social interactions, the mobile phone dataset is the most relevant dataset that is currently in existence. Indeed, at present, the most detailed information on human mobility across a large segment of the population is collected by mobile phone carriers. Mobile carriers record the closest mobile tower each time the user uses his or her phone. Other possible data sources include dollar bills, GPS, or check-in datasets from location-based social networking services, all of which suffer from well-known limitations that are resolved by mobile phone datasets. Indeed, dollar bills are carried by various individuals; hence, mobility inferred from them captures population-level aggregated movements instead of individual mobility. GPS tracks individual positions on a continuous basis with high precision, but it operates on a much smaller scale (typically hundreds of people) in contrast to millions of individuals’ mobile phone data records. Check-in datasets only record mobility information when users report their positions voluntarily on subset of population who use the service, in contrast to mobile phones that objectively collect mobility information across a societal-scale population. For this reason, research on human mobility has literally exploded following the availability of mobile phone datasets, resulting in a number of rather fundamental papers. Furthermore, mobile phone datasets offer comprehensive information on phone calls and text messages, providing social network information in addition to mobility trajectories of each individual. Therefore, mobile phone datasets are excellent data sources to study simultaneously human mobility and social networks.

However, mobile phone datasets have a number of well-known limitations. Most notably, there are three aspects:

First, as mobile phones approximate a user’s location by the tower that routed the call, the spatial resolution of the dataset is limited by the area covered by each tower, which typically ranges between 1 and 3 km. This is a spatial limitation of the data. Luckily, earlier research has extensively focused on this issue and documented that, at least for results we discussed, the results are not affected by this limitation.

Second, a user’s position is only recorded when he or she makes a call or sends a text. However, human communications follow bursty patterns. This is the temporal limitation of the data. However, there are ample reasons to believe that our results are not affected by it. Mobility studies that compare mobility patterns obtained through mobile phone data and other continuous tracing technologies consistently find that the two are largely indistinguishable (2). These include GPS traces (2) as well as high-resolution mobile phone records (4, 5). Although we do not have direct access to these datasets, using our own datasets, we further calculated location displacement between a fixed time interval instead of two consecutive phone calls, in doing so artificially creating mobility traces that occur on a continuous basis. We find that results are remarkably stable as we vary the time interval systematically from 1 h to 1 d (Jump Size Distribution at Fixed Interevent Time). All these results suggest that although mobility information is obtained from calling patterns in mobile phone datasets, call detailed record (CDR) data offer representative patterns of mobility, offering convincing reassurance that our results are not affected by this limitation.

Third, social network information is inferred based on calling patterns, yet calls using mobile phones can be ambiguous and hence may not represent true social relationships. This is the third limitation of the data. However, results by Eagle et al. (56) compared self-report survey data on mobility and social interactions with observational data obtained using mobile phones, demonstrating a high degree of accuracy (95%) in inferring friendship structures based on observational data alone.

Taken together, mobile phone datasets are the best and largest datasets for the type of study we conducted here. Although they have well-known limitations, extensive studies and results have demonstrated that our study is not affected by these limitations.