Emergent perversions in the buckling of heterogeneous elastic strips

Significance

Perversions in an otherwise uniform helical structure provide the mechanism of helical symmetry breaking. In this work, using a three-dimensional elastomeric bistrip model, we investigate the intrinsic properties of perversions that are independent of specific strip shapes. Besides the fundamental role as generic domain walls that connect states of distinct symmetries, this study reveals richer physics of perversions in the three-dimensional elastic system. The major findings include the condensation of strain energy over perversions, the identification of the repulsive nature of the perversion–perversion interaction, and the coalescence of perversions. These intrinsic properties of perversions may have implications to the understanding of relevant biological motifs and the designing of micromuscles and soft robotics.

Abstract

A perversion in an otherwise uniform helical structure, such as a climbing plant tendril, refers to a kink that connects two helices with opposite chiralities. Such singularity structures are widely seen in natural and artificial mechanical systems, and they provide the fundamental mechanism of helical symmetry breaking. However, it is still not clear how perversions arise in various helical structures and which universal principles govern them. As such, a heterogeneous elastic bistrip system provides an excellent model to address these questions. Here, we investigate intrinsic perversion properties which are independent of strip shapes. This study reveals the rich physics of perversions in the 3D elastic system, including the condensation of strain energy over perversions during their formation, the repulsive nature of the perversion–perversion interaction, and the coalescence of perversions that finally leads to a linear defect structure. This study may have implications for understanding relevant biological motifs and for use of perversions as energy storers in the design of micromuscles and soft robotics.

Spontaneous symmetry breaking provides a unifying conceptual understanding of emergent ordered structures arising in various condensed matters (1). In an elastic medium, which is one of the simplest organizations of matter, symmetry-breaking instabilities via buckling can lead to extraordinarily rich patterns and generate a wealth of shapes at multiple length scales that can be exploited in many scientific disciplines (2). A prototype of elastic buckling is the Euler instability of a homogeneous elastic rod under uniaxial compression at the ends that finally breaks the rotational symmetry (3). Introduction of extra structures in an elastic medium like mechanical heterogeneities (4), nonlinearity of materials (2), geometric asymmetry (5), or intrinsic curvature (6) provides new dimensions that can produce even richer buckling modes, including helices and perversions (6, 7), wavy structures (8), regular networks of ridges (9), and even self-similar fractal patterns (2, 10). Of these emergent symmetry broken structures, the helical shapes are of particular interest due to their ubiquitousness in nature and the strong connection with biological motifs, as noticed by Darwin in his 1875 book describing the curl of plant tendrils (11). Remarkably, biological helical structures permeate over several length scales from the developed helical valve on opening seed pods (12), to the regular chiral structures in the flagella of bacteria (13), the spiral ramps of rough endoplasmic reticulum (14), and the chromosome of Escherichia coli (15, 16).

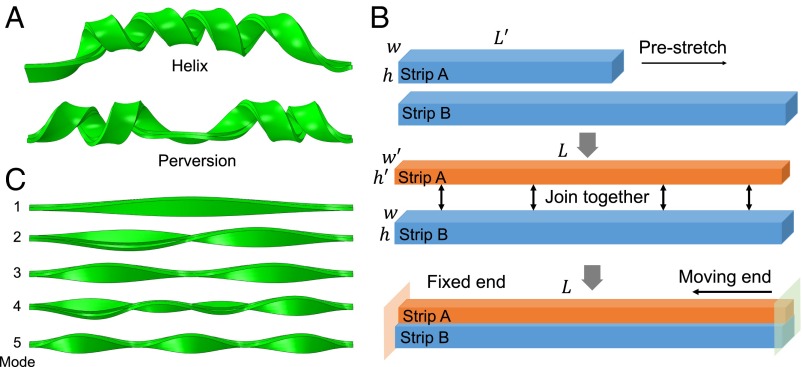
The proliferation of perversions in an otherwise uniform helical structure can further break the helical symmetry (Fig. 1A shows a typical perversion in the helix) (4, 6, 17). Here, a perversion refers to a kink that connects two helices with opposite chiralities. Therefore, perversions belong to a large class of fundamental defects in systems with discrete symmetry which have the names of domain walls, solitons, or kinks depending on the particular context (1). In contrast to domain walls in prototype spin systems, perversions embedded in both natural (6, 17) and artificial (4) helical systems have the unique freedom to wind around themselves in response to mechanical or geometric constraints. This salient feature of perversions accounts for several important observations, including the generation of more helices by a self-winding single perversion (6) and formation of the ripple patterns extensively found in animal guts and leaf edges through multiple perversions (18, 19). Recent studies have further revealed that the perversion in the cucumber tendril, with its variable local stiffness, can unexpectedly overwind under tension rather than unwind (20). Previous theoretical studies using an ideal rod model with intrinsic curvature have qualitatively characterized the perversions (21, 22), yet cannot fully capture the postbuckling deformation or the interactions between perversions. These studies inspire us to have a closer look at the nature of perversions in helical structures, including perversion-driven helical symmetry breaking and interactions between perversions.

Fig. 1.

Illustration of the bistrip model. (A) A typical perversion arising in an otherwise uniform helix (Upper) by controlling the boundary condition. (B) Illustration of the bistrip model we used in the simulation. Strip A has the same cross-section as strip B but shorter length in the initial state. Strip A is stretched and glued to strip B; both strips have the same length. One end of the bistrip system is fixed whereas the other end is allowed to translate but forbidden to rotate. (C) The first five buckling modes from eigenvalue buckling analysis.

The bistrip hyperelastic system provides an ideal model for studying the helical symmetry breaking and the physics of the resulting emergent perversions. The model hyperelastic system consists of two clamped strips with rectangular cross-sections (Fig. 1B); the shorter strip (strip A) is stretched and then attached to the longer one (strip B). With reduction of the strip length, we numerically observe the hierarchical buckling in the sequence of the development of helical shapes and then the spontaneous formation of perversions therein. Systematic simulations using different mesh sizes and initial perturbations show that the bistrip system can be easily trapped in metastable states; it is not guaranteed that the lowest energy conformation found by optimizing the simulation parameters is the true ground state. We therefore focus on the intrinsic features of perversions that are independent of specific shapes. Our study reveals the remarkable condensation of strain energy over perversions during their formation and the repulsive nature of the perversion–perversion interaction. These intrinsic properties of perversions may be exploited in the design of micromuscles (23) and soft robotics (24).

Model

In the bistrip hyperelastic model, the strips have the same rectangular cross-section but different lengths in their free states (Fig. 1B). The upper shorter strip is first longitudinally stretched to the same length as the lower longer one, and then they are “glued” together such that both mutual slide and delamination are forbidden. In simulations, we carefully control the slow approach of the anchored ends of the bistrip whose orientations are fixed. The geometric and mechanical incompatibility of the strips is numerically observed to drive the out-of-plane deformations, including the helical shapes and perversions. The strips are made of the same material. Considering the involved large elastic deformations, we use the neo-Hookean model, the simplest hyperelastic model, which was originally proposed to treat the rubber elasticity and has been incorporated in a great deal of modern finite-element software to analyze the elasticity of extensive elastomeric materials (25). Herein the stress and strain in the neo-Hookean model are related via the following form of the strain energy density U (25):

$$U=C_{10}\left({\overline{I}}_1-3\right)+\frac{K_1}{2}{\left(J-1\right)}^2.$$ [1]

$C_{10}$ and $K_1$ characterize the resistance of the material to shear stress and compression, respectively. $J={\lambda }_1{\lambda }_2{\lambda }_3$, representing the elastic volume ratio of the solid, where ${\lambda }_1,{\lambda }_2,{\lambda }_3$ are the principal stretch ratios. ${\overline{I}}_1=J^{-2/3}\left({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2\right)$. In our simulations, we treat the material as nearly incompressible, a feature of most elastomeric materials. It seems that the appearance of perversions in the buckled helical system does not rely on the hyperelastic nature of materials; in soft elastic materials former finite-element simulations have also revealed the existence of perversion structures (4).

In contrast with Euler’s rod, the rectangular cross-section in the prestretched bistrip system is crucial for the appearance of nontrivial regular structures like the initially developed periodic helical shape and the scattered perversions therein with the reduction of the strip length. We first perform qualitative geometric analysis of helices and perversions in an originally flat strip whose ends are clamped without allowing any movement and rotation (see Fig. S1). By grabbing an arbitrary point of the strip, we can twist the whole strip, thereby generating a perversion and helices. This generated perversion connects two helices with opposite chiralities. The strip-like geometry does not impose a constraint on the allowed number of perversions. Multiple perversions have been found in animal guts (18) and in the bistrip model (4). The specific number of perversions in a helical strip is determined by several factors, such as the materials property and the external constraints (4, 26).

Fig. S1.

Paper experiments to illustrate that the number of perversions on the helical system is not geometrically constrained. By grabbing and rotating a point on the initially straight paper band (A), a perversion can be manually produced as shown in B. Further rotation of the perversion in C can generate more helices.

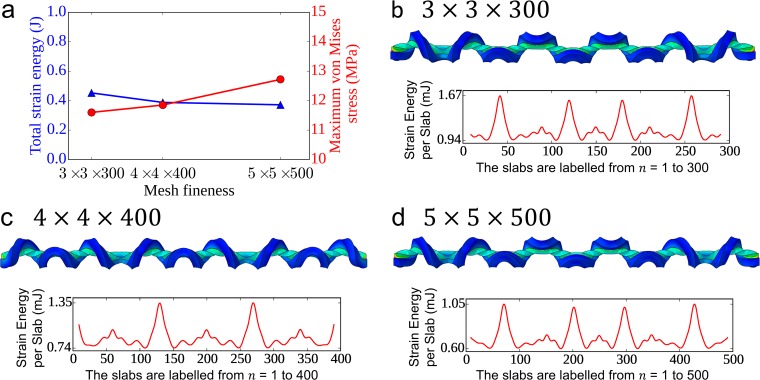
We resort to finite-element analysis to track the shape evolution of the heterogeneous bistrip. Specifically, we first perform an eigenvalue buckling analysis to examine the stability of the bistrip under the constraints in Fig. 1B. The eigenmodes of the bistrip include two types of perturbation shapes depending on the shape symmetry. Among the five modes listed in Fig. 1C, modes 1, 3, and 5 have mirror symmetry, whereas the others do not have apparent symmetry. These eigenmodes are used as initial perturbations for the further explicit dynamical finite-element analysis performed in Abaqus/Explicit. Simulations show that the postbuckling shapes of the bistrip do not appear dependent on the type of these eigenmodes. Our results indicate that the bistrip system can reach multiple metastable states by varying the mesh densities and the loading rate (see Figs. S2 and S3). These states have very close strain energy but different numbers of perversions. Because we are only concerned with the intrinsic properties of perversions, the presence of these metastable states does not influence our major conclusions. In our simulations, initially the long strip (strip B in Fig. 1B) is 30-cm long, whereas the length of the shorter strip (strip A in Fig. 1) is about $8\hspace{0.17em}\text{cm}$. Both of the strips are 3-mm thick, and the width is varied to produce different number of perversions.

Fig. S2.

Influence of the degree of mesh refinement on the final buckled strip shapes. (A) The total strain energy and maximum von Mises stress mostly converged for the three inspected mesh densities. (B–D) Shapes and energy profiles for $3\times 3\times 300$, $4\times 4\times 400$, and $5\times 5\times 500$, respectively. The geometric parameters of the strip are $w=3\hspace{0.5em}\text{mm}$, $h=3\hspace{0.5em}\text{mm}$, $L=30\hspace{0.5em}\text{cm}$, and $L\prime =L/3.5$.

Fig. S3.

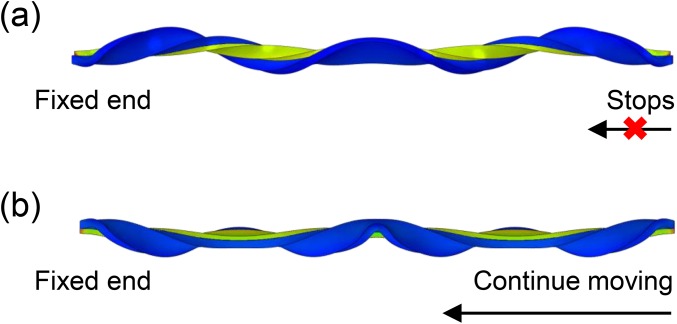
Effect of the displacement loading rate on the buckling shape of the bistrip. The original lengths of the bistrip in A and B are both 30.0 cm. (A) Buckling shape when the moving end stops at 23.3 cm. (B) Buckling shape at 23.3 cm while the end-to-end distance will continue shrinking to 9.0 cm.

Results and Discussion

In the simulations, the ends of the bistrip are carefully controlled to approach each other without allowing any rotation. This constraint ensures that the helices formed near the ends have opposite chiralities and guarantees the appearance of a perversion. Fig. 2A demonstrates the growing of the initially slight out-of-plane deformation and the subsequent development of the single perversion in the helical state. The emergent perversion is located at the center of the strip, breaking the helical symmetry while preserving the mirror symmetry. The perversion is observed to wind around itself to generate more helices, meanwhile suppressing its own size. It has been observed that climbing tendrils also conform to the same winding scheme while growing longer (6). In our case, the winding perversion plays the opposite role; it winds to reduce the pitch of helices in response to the reduction of the end-to-end distance of the bistrip.

Fig. 2.

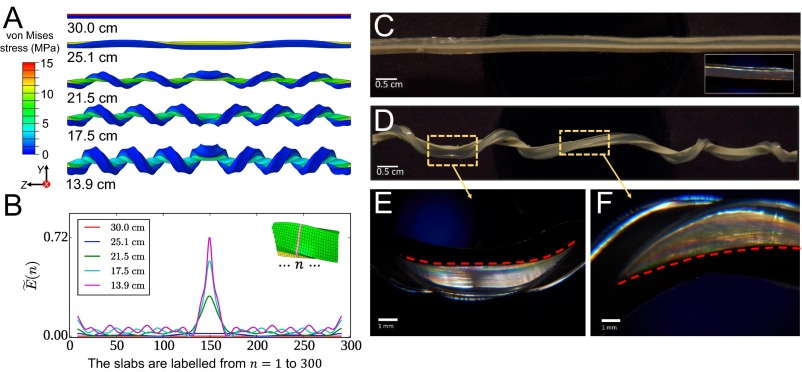
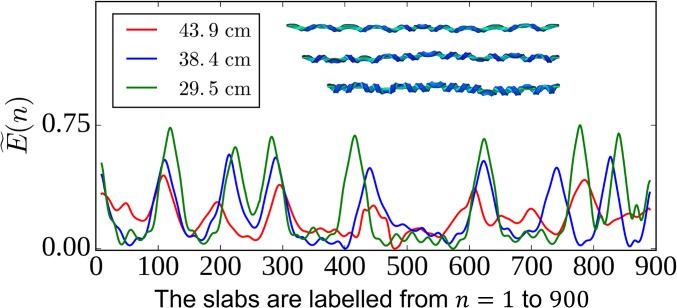
Energy condensation in the perversion of the bistrip system. (A) The formation and evolution of one perversion with the reduction of the strip length L, $w=5\hspace{0.5em}\text{mm}$, $h=3\hspace{0.5em}\text{mm}$, $L=30\hspace{0.5em}\text{cm}$, and $L\prime =L/3.5$ following the notation labeled in Fig. 1B. The stress state of the bistrip is characterized by the distribution of the scalar von Mises stress which is originally proposed to analyze the yielding of materials (30). (B) The scaled strain energy profile of the strips in A. $\tilde{E}\left(n\right)=E\left(n\right)/{\text{min}}_{\left\{n\right\}}\left\{E\left(n\right)\right\}-1$, where n labels the slab of elements as shown (Inset), and $E\left(n\right)$ is the total strain energy of all these elements in the nth slab. (C–F) The designed bistrip system made of polyethylene and prestretched rubber strip to confirm the numerically observed energy condensation over the perversions. (C and D) Shape of the bistrip before and after buckling. (C, Inset) Featureless birefringence pattern of the initial bistrip. The dashed red lines in E and F indicate the interface of the two strips. The different birefringence patterns in the perversion (E) and the helical (F) regions reflect the distinct strain energy distributions.

Simulations show that as the perversion is winding, the strain energy is concentrating. Fig. 2B shows the energy distribution along the strip with the conformations in Fig. 2B. The energy is obtained by dividing the bistrip into n slabs and summing the strain energy across the cross-sectional area of the slab. This quantity is then rescaled to capture the relative energy changes in the perversions and in the helices. The energy condensation in the perversion region is clearly seen in Fig. 2B. The winding of the perversion provides the specific mechanism to focus energy locally in the perversion region. In a more general case where multiple perversions emerge in a very long bistrip, this energy condensation phenomenon can still be identified (see Fig. S4). The amount of energy condensation will eventually saturate if the two ends of the bistrip are sufficiently close, because the perversion and helices under high compression will have contact with each other, and the whole structure may collapse at the position of the perversion. The spontaneous focusing of energy is a rich concept that permeates in fields as diverse as fluid mechanics, electrostatics, and elasticity of 2D materials (9). Similar energy condensation phenomena occur on ridges in 2D elastic medium where the stress is focused (9). Here the revealed strain energy concentration is the demonstration of the energy focusing in 3D elastic medium. The perversions as energy-absorbing singularity structures in helical systems may find applications in the design of micromuscles (23) and soft robotics (24).

Fig. S4.

Energy profile of the bistrip where the two strips have same cross-section but different initial stress. The geometric parameters of the prestretched strip are (before stretching) $w=9\hspace{0.5em}\text{mm}$, $h=3\hspace{0.5em}\text{mm}$, $L=90\hspace{0.5em}\text{cm}$, and $L\prime =L/3.5$ following the notation labeled in Fig. 2 of the main text.

To check the reliability of numerical simulations and to exclude the possibility that the numerically observed energy focusing phenomenon is due to any hidden artifacts in simulations, we perform experiments to substantiate that the perversion structure is indeed energetically distinguishable from helices. The bistrip system is created by carefully casting polyethylene melt onto a prestretched rubber strip; the polyethylene melt becomes an initially stress-free elastic strip once it is cooled. Fig. 2 C–F shows the shapes of the bistrip with the controlled shrinking as in Fig. 2A. The differentials in the energy distribution over the strip are characterized by analyzing the birefringence of the elastic medium. No birefringence occurs in the initially straight strip (Fig. 2C, Inset). Birefringence patterns start to emerge at both the perversion (Fig. 2E) and the helical regions (Fig. 2F). Closer examinations show that in the perversion region the colored pattern only spreads around the edge of the prestretched strip, whereas at the helical region, the pattern distributes smoothly across the strip. To conclude, the distinct optical responses in the perversion and helical regions reflect the energetically distinguishable local states.

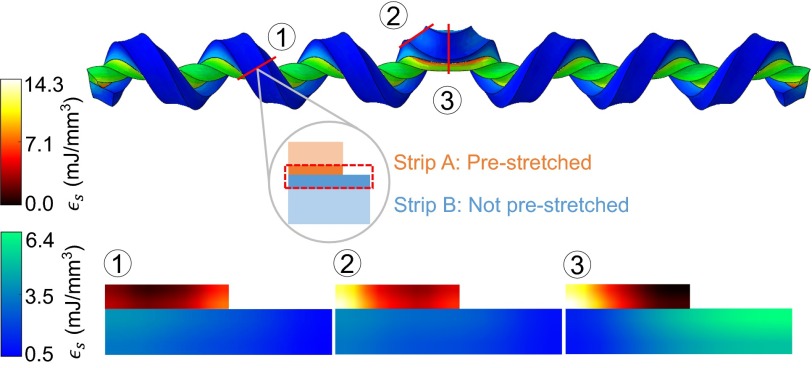
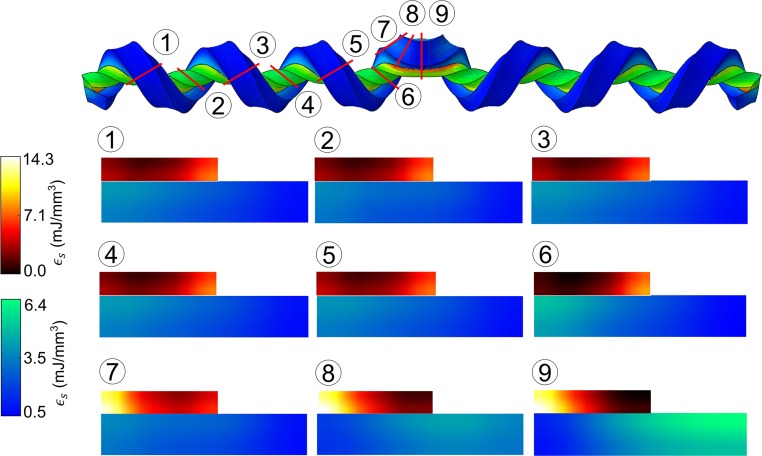
We resort to numerical simulations to perform quantitative analysis of the strain energy distribution over the strip, as the optical patterns in experiments can only reveal limited information. The distinct birefringence patterns in Fig. 2 E and F imply different modes of transferring strain energy over the cross-section from the high-energy prestretched strip to the other one in contact. Fig. 3 illustrates the energy distributions over the cross-sections at typical sites at the bistrip. In the helical region labeled “1” in Fig. 3, the strain energy is evenly distributed along the interface. At the edge of the perversion labeled “2,” the distribution of the energy over the cross-section at the side of the strip B is similar to that in the helical region, whereas in the cross-section of strip A the strain energy mostly concentrates at the lower-left corner attached to strip B. This trend is more pronounced over the cross-section at the center of the perversion labeled “3;” the strain energy in strip A is focused on the left side, whereas at the side of strip B the strain energy is concentrated at the upper-right corner where strip B is highly squeezed. To conclude, the strain energy is transferred highly unevenly within the perversion from strip A to strip B compared with that in the helical region. In other words, in the perversion region the transferred energy distribution in strip B is obviously uneven. Similar patterns are found in more cases in substantiation for this conclusion and the relevant results are presented in Fig. S5. The obvious discontinuity in the strain energy distribution over the thickness of the bistrip system in Fig. 3 suggests that the basic features in the deformation of the bistrip system cannot be fully captured by a 2D elastic model.

Fig. 3.

Analysis of the strain energy distribution over the cross-section at different sites demonstrates distinct energy transfer modes in the perversion and helical regions. The images below show the distribution of strain energy density (${\mathit{ϵ}}_s$) at sites 1, 2, and 3 in the above image, respectively. The cross-sections of strip A and B share different scale bars for the different energy density ranges. The middle inset in the circle depicts the region over the cross-section where we inspect.

Fig. S5.

Analysis of the strain energy distribution over the cross-section at different sites demonstrates the distinct energy transfer modes in the perversion and helical regions. The images below show the distribution of strain energy density (${\mathit{ϵ}}_s$) at the sites 1–9 in the above image, respectively. The cross-sections of strip A and B share different scale bars for the different energy density ranges.

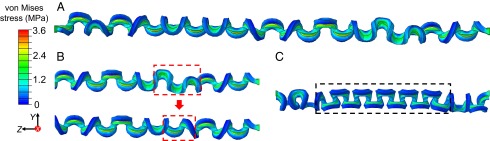
We study the case of multiple perversions on a single bistrip. These can be introduced by adjusting the geometric parameters of the strip and the loading rate. Fig. 4A shows that the mirror symmetry of the system is broken while the three perversions are winding around themselves (see the last two conformations). Specifically, the broken mirror symmetry results from asynchronous rotation of the two perversions at the sides of the central perversion. As in the case of single perversion, all three perversions are observed to wind around themselves to shrink the strip length to fit the boundary condition and to reduce the energy of the system. The longitudinal energy distribution in Fig. 4B reveals the repulsive nature of the perversion–perversion interaction; the elevated energy profile between the perversions 1 and 2 in Fig. 4B is an indicator of repulsive interaction. Although the exact energy–distance relation is difficult to define in this system, the repulsion is expected to be short-ranged because we can only observe the energy elevation when the perversions are closer enough with each other. The shape evolution under quasi-static loading demonstrates the repulsion of perversions: The rightmost perversion rotates approximately $360°$ more than the other two whereas the end-to-end distance of the bistrip is reduced from 23.3 to $13.9\hspace{0.17em}\text{cm}$. This process pushes the central perversion to move toward the leftmost perversion. The energy focusing phenomenon is also observed in the multiperversion systems. The condensation of the strain energy over all of the perversions suggests that the energy focusing feature is an intrinsic property of the perversion structure. The geometric conformation of the central perversion is different from the other two perversions as shown in Fig. 4A. Consequently, the energy peak 1 in the energy profile of Fig. 4B corresponding to the central perversion is more focused and much higher than the other perversions.

Fig. 4.

Formation and evolution of three perversions in a single bistrip. (A and B) Conformations and the corresponding strain energy distribution. A shows that the symmetric bucklings of the perversions are broken by the winding of the rightmost perversion where the strip length is reduced by 35%. In B, the energy peaks labeled as 1, 2, and 3 correspond to the perversions formed in the buckling. The green arrow in the last figure indicates energy elevation and therefore repulsion between perversions. The geometric parameters of the strips are $w=9\hspace{0.5em}\text{mm}$, $h=3\hspace{0.5em}\text{mm}$, $L=30\hspace{0.5em}\text{cm}$, and $L\prime =L/3.5$ following the notation labeled in Fig. 1.

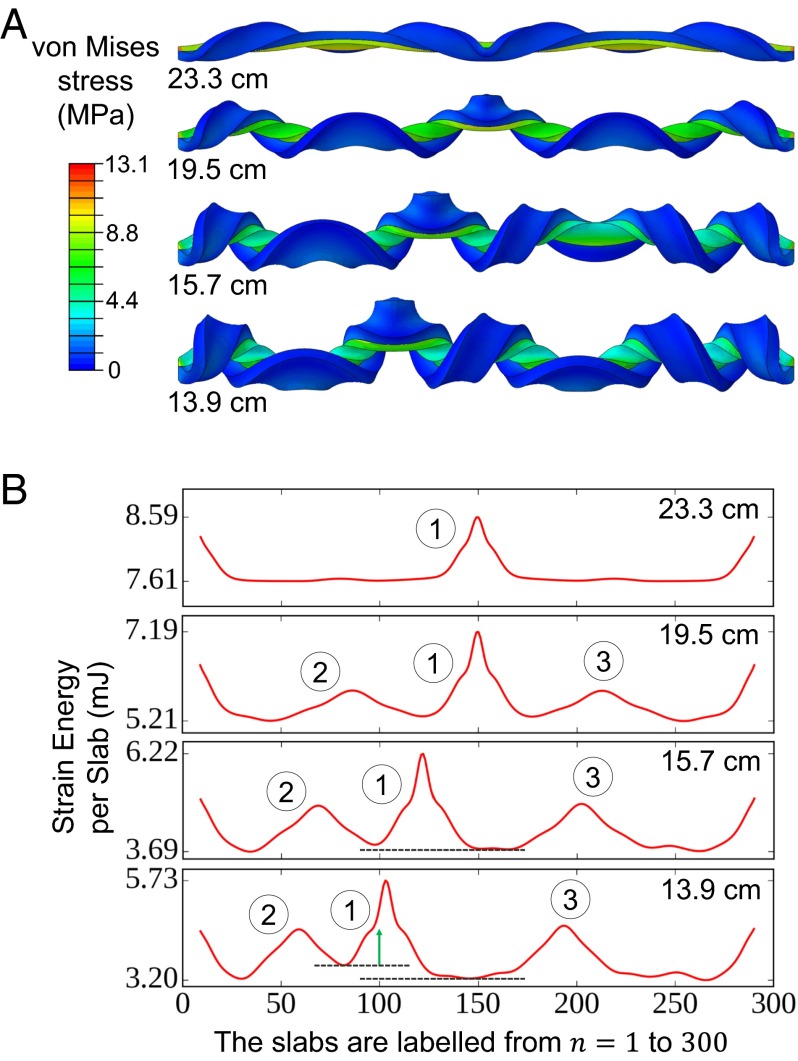
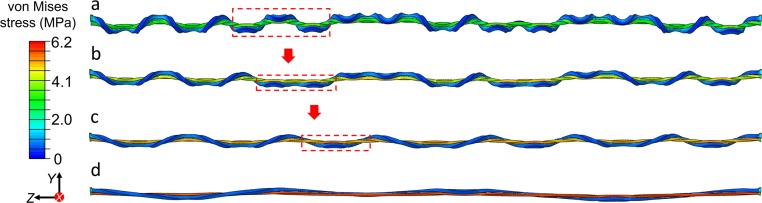
We also explore a distinct routine to introduce the mechanical incompatibility over the bistrip system and observe unexpected behaviors of emergent perversions not found in the prestretched bistrips described above. Specifically, we use a precompressed strip to replace the prestretched one in the bistrip. We find that further compression of the precompressed bistrip introduces perversions; around 20 perversions form when the bistrip length shrinks by only a tiny amount ($\sim 1\text{\%}$), as can be seen in Fig. 5A. During the controlled shrinking of such a bistrip system, we numerically observe the merge of neighboring perversions and the development of an ordered helical section (Fig. 5B). Remarkably, through this perversion annihilation mechanism, combined with the aforementioned winding behavior, perversions over a single bistrip can self-assemble to form some highly ordered linear structure, dubbed “perversion lines” as shown in Fig. 5C.

Fig. 5.

Formation and evolution of the perversions in a bistrip where one of the strips is precompressed. (A) Eighteen perversions emerge when two ends of the bistrip approaches. (B) In the right half of this bistrip, the two perversions in the red dashed boxes annihilate and coalesce into the nearby perversion. (C) Ordered perversion line structure (labeled in the black dashed box) eventually formed when the moving end is close enough with the other one. The geometric parameters of the strip are $w=3\hspace{0.5em}\text{mm}$, $h=3\hspace{0.5em}\text{mm}$, $L=30\hspace{0.5em}\text{cm}$, and $L\prime =75\hspace{0.17em}\text{cm}$ following the notation labeled in Fig. 1.

Perversions are the emergent defects in the helical prestressed bistrip. The spontaneous formation of the perversion line from individual perversions (as shown in Fig. 5C), which are defects themselves in an otherwise uniform helical structure, is strongly analogous to the self-organization of individual disclinations to form ordered compound defects like scars and pleats over curved crystals (27–29). Note that the coalescence of perversions is not observed when their separation exceeds about two helical periods in the surveys of typical bistrip systems. In contrast, by uniformly stretching the precompressed bistrip, we numerically observe a series of dynamical events: the initial reduction of the amplitude of the out-of-plane deformation patterns (Fig. S6 A and B), the coalescence and annihilation of neighboring perversions (Fig. S6 A–C), and the reduction of the number of resulting helical periods (Fig. S6D). Obviously, external stretching significantly facilitates the unknotting of perversions. To conclude, the examination of the precompressed bistrip system reveals physics of perversions not found in the prestretched bistrips, including the coalescence of neighboring perversions that is crucial for the formation of ordered perversion lines.

Fig. S6.

Evolution of the multiple perversions over a precompressed bistrip under stretching. The red dashed boxes in A–C are tracking a typical coalescence and annihilation of perversions. The total number of perversions consequently decreases as shown in C and D. The length of the bistrip is becoming longer from (a) to (d). The geometric parameters of the strips are $w=9\hspace{0.5em}\text{mm}$, $h=3\hspace{0.5em}\text{mm}$, $L=30\hspace{0.5em}\text{cm}$, and $L\prime =L/3.5$ following the notation labeled in Fig. 2 of the main text.

We further investigate the essential material features that are crucial for producing the helical and perversion structures to break the symmetry. It is obvious that the prestretching in one of the strips in the bistrip system provides the driving force for the deformation of the entire system due to the elastic instability. Further simulations show that the geometries of the strips’ cross-sections can also critically control the resulting deformation patterns. In the preceding discussions, we focus on the bistrip system where the two strips in their relaxed states have an identical cross-section profile. The cross-section of the prestretched strip shrinks as schematically shown in Fig. 1B due to the small volume compressibility of the material, leading to the geometric asymmetry. In addition, the prestretched strip breaks the up–down symmetry in the stress state of the bistrip system. It is natural to ask if these preexistent asymmetries are responsible for the out-of-plane deformation of the entire bistrip and the emergence of the helical structure.

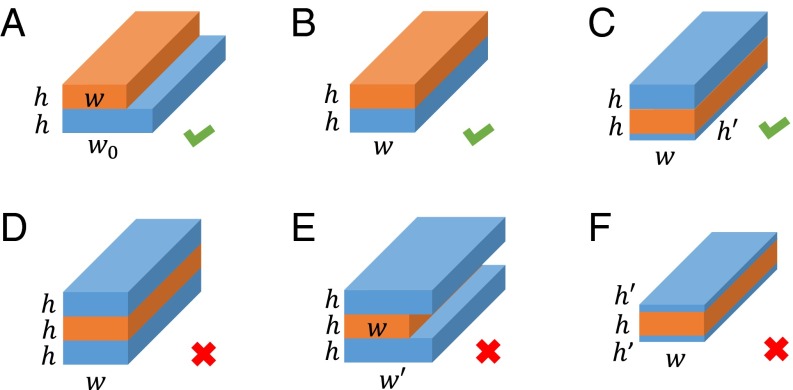
To address this question, we first prepare a bistrip system as illustrated in Fig. 6B. In contrast to Fig. 6A, the upper strip, in its prestretched state, has the same cross-section profile as the lower one. We numerically observe the formation of helical structure over such a bistrip with the reduction of the end-to-end length. Therefore, the asymmetry of the cross-section width in the bistrip system can be excluded to be responsible for the formation of helical structures. Furthermore, we prepare tristrip systems that preserve the up–down symmetry in the initial state (Fig. 6 D and E). In both systems, the tristrips are numerically observed to buckle and form a V-like shape with the reduction of their lengths; no helical shapes are numerically observed. When the thickness of an outer strip in the tristrip system is reduced to be sufficiently small (Fig. 6C; Fig. 6B can be regarded as the case where an outer strip is of zero thickness), helical structures appear again over such a tristrip system with the broken up–down symmetry.

Fig. 6.

Cross-section profiles of the strips inspected. The orange color of the strips indicate prestretching state; blue strips are stress-free in the initial state. As indicated by the ticks and crosses at the lower-right corner of each figure, A–C can produce helices and perversions, whereas D and E only deform to V-like shape. The geometric parameters of the strips are $w_0=9\hspace{0.5em}\text{mm}$, w is the width after prestretching, and $w\prime$ can vary from $5.4\sim 6.3\hspace{0.5em}\text{mm}$, $h=3\hspace{0.5em}\text{mm}$, and $h\prime =0.2\hspace{0.5em}\text{mm}$.

These numerical results are still not sufficient to conclude that the asymmetry of the cross-section thickness controls the formation of helical structures. It is well known that the bending of elastic plates or shells strongly depends on the thickness. To clarify whether it is the total thickness of the tristrip system or the differences between the two outer strips that determines the helical deformation, we simulate the system in Fig. 6F with the up–down symmetry but much thinner outer strips compared with the one in Fig. 6C. Similar to the case of Fig. 6 D and E, no perversions are observed. The strips only buckle to a V-like shape with slight twisting around the center. Therefore, we can conclude that the up–down asymmetry in the strip thickness is more crucial to the emergence of the helices and perversions than the total thickness of the strip system.

Conclusions

This study uncovers several intrinsic properties of perversions that naturally occur to release stress in designed heterogeneous elastic bistrips. Besides playing a fundamental role as a generic domain wall that connects states of distinct symmetries, perversions exhibit richer physics in the 3D elastic system. Specifically, we numerically observe the strain energy condensation over perversions during their formation, which is well confirmed in our designed experiments. We further identify distinct modes of energy transfer from a stretched strip to an initially unstretched one, and the repulsive nature of perversion–perversion interaction. Examination of the precompressed bistrip system reveals the coalescence of neighboring perversions which is crucial for their self-assembly into a highly ordered linear defect structure; it is in strong analogy with the formation of scars and pleats out of the elementary crystallographic defects in curved crystals. These intrinsic properties of perversions may be applicable to understanding and designing micromuscles and soft robotics where perversions can be introduced in relevant helical structures to realize desired functions. Perversions as defects in the helical state may also share the common attributes of defects in generic ordered phases, so there is much room for further exploration, notably regarding their possible coalescence, annihilation, and intriguing interactions in response to various external constraints.

Materials and Methods

The buckling analysis is performed using the Buckle Module in Abaqus/Standard using the 3D linear reduced integration elements (C3D8R). The buckled shapes are then seeded as imperfections in the postbuckling simulations. The explicit dynamical finite-element analysis is performed in Abaqus/Explicit using C3D8R elements. The quasi-static condition is satisfied by carefully controlling the slow approach of the two anchored ends such that the kinetic energy of the system is negligible compared with strain energy. The mesh of the elastic medium is sufficiently refined to ensure that the total strain energy is converged.

The experimental setup mounts the stretched band in the path between the light source and the detector, which are well placed in advance. Two polarizing filters are placed one each on the light source and detector. Polarizing filters are placed facing each other and rotated in plane such that there is a 90° offset in filter direction. This filters out any nonbirefringent light. Each sample is prepared by casting polyethylene melt onto a prestretched rubber band and allowing it to cool to room temperature so that the solidified polyethylene is in a stress-free state. While this bilayer is still in the stretched state, excess polyethylene material is trimmed as quickly as possible with a heated razor to avoid any residual processing artifacts. This procedure produces the initial difference in the stress states over the two strips, which in turn causes formation of helical and perversion structures with the controlled reduction of the bistrip length. Polyethylene is an ideal candidate to use in observing the stress-driven birefringence phenomena. We use the commercially available polyethylene hot glue sticks and rubber bands of the Up & Up brand. A commercially available modified Room Essentials white light-emitting diode lamp provides a polarized, coherent light source for demonstrating the birefringence phenomena. For our detector, we use a SONY alpha 6000 Mirrorless digital single-lens reflex camera, with the key parameters: ISO 400, shutter speed 1/60 s, and F-stop of 32. The F-stop is set to maximum to reduce incoherent light to the fullest possible extent. A macro lens is mounted to obtain close-up images.

Paper Experiments to Demonstrate Perversion Structures

We perform paper experiments to qualitatively understand the possible geometric constraint on the number of perversions in a helical system. In our setup, the two ends of the paper strip are clamped to forbid rotational motion (Fig. S1A). A perversion can be produced by grabbing a point on the strip and rotating the strip (Fig. S1B). Further rotation (from Fig. S1B to Fig. S1C) leads to a reduction of the pitch and an increase of the number of helices in the paper strip. More perversions can be produced by grabbing other points and rotating in the region of helices. Therefore, the allowed number of perversions is not geometrically constrained.

Finite Element Analysis

Mesh Refinement and Metastable States.

A careful mesh refinement study is performed to determine the best mesh size and fineness for the simulations. However, for two different mesh sizes, the final shapes of the bistrip can be very different––even though the maximum von Mises stress and total strain energy are very close (Fig. S2A). In Fig. S2 B and D, the final shapes of the bistrip meshed as $3\times 3\times 300$ and $5\times 5\times 500$ are the same, and five perversions are generated. However, when using $4\times 4\times 400$ mesh, seven perversions are generated accordingly, as shown in Fig. S2C. Therefore, the evolution of the bistrip model is easily trapped in metastable states, depending on the small external perturbations. The energy profiles in Fig. S2 B–D also demonstrate two different types of energy peaks corresponding to the perversions, which essentially result from the different bending directions of the bistrip when the perversions are formed.

In our simulations, the quasi-static equilibrium is obtained by carefully controlling the displacement loading rate of the moving end. The shape evolution of the bistrip system will be perturbed by this displacement loading rate, so changing the total loading time and distance can result in different buckling states of the bistrip even at the same end-to-end distance. For instance, both the bistrip shapes shown in Fig. S3 A and B are obtained by reducing the end-to-end distance from 30 to 23.3 cm. However, the moving end in Fig. S3A will stop exactly at 23.3 cm, whereas in Fig. S3B the end will continue moving until the end-to-end distance reduces to 9.0 cm. Consequently, different numbers of perversions emerge in Fig. S3 A and B.

Energy Profiles of the Bistrip.

We have also analyzed the energy profile of the bistrip where the prestretched strip has the same cross-section as the other strip without initial stress. The energy condensation of the perversions can be clearly identified from Fig. S4.

Energy Condensation over the Cross-Sections of the Bistrip.

Here, we demonstrate more snapshots of the strain energy distributions over the cross-section of the bistrip model (Fig. S5). Consistent with results in the article, the strain energy condensation is also found in the perversion region.

Stretching a Precompressed Bistrip.

We further investigate the evolution of the perversions in a precompressed bistrip under uniform stretching. The bistrip is first slightly compressed such that a series of perversions can spontaneously form (Fig. S6A). One end of the bistrip is then slowly stretched without allowing any rotation. From Fig. S6 A to B, the amplitudes of the three perversions enclosed in the dashed box decrease significantly. Eventually these perversions coalesce into one perversion as shown in Fig. S6C. Similar coalescence phenomena can be found in other places over the bistrip, leading to the reduction of the number of perversions in the end (Fig. S6D).