Electron collisions with atoms, ions, molecules, and surfaces: Fundamental science empowering advances in technology

Abstract

Electron collisions with atoms, ions, molecules, and surfaces are critically important to the understanding and modeling of low-temperature plasmas (LTPs), and so in the development of technologies based on LTPs. Recent progress in obtaining experimental benchmark data and the development of highly sophisticated computational methods is highlighted. With the cesium-based diode-pumped alkali laser and remote plasma etching of Si₃N₄ as examples, we demonstrate how accurate and comprehensive datasets for electron collisions enable complex modeling of plasma-using technologies that empower our high-technology–based society.

Electron collisions with atoms, ions, molecules, and surfaces are critically important to the understanding and the modeling of laboratory plasmas, astrophysical processes, lasers, and planetary atmospheres, to name just a few examples. In addition to the investigation of naturally occurring phenomena, electron collisions form the basis of a vast array of plasma-using technologies, which continue to empower our high-technology–based society (1). Atomic, molecular, and optical (AMO) physics, the field that encompasses electron–atom and electron–molecule collisions, has made tremendous contributions to our fundamental understanding of nature. Despite the field’s longevity, breakthrough developments in atomic collisions continue to be made at the fundamental level of both experiment and theory.

The Need for Atomic and Molecular Data

In low-temperature plasmas (LTPs), electron and ion collisions with otherwise unreactive gas and surfaces activate those atoms and molecules through forming excited states, ions, and radicals. Those activated species are then used in applications ranging from microelectronics fabrication (2) to human healthcare (3). The most basic, necessary, and first step in the development of those technologies is the electron or ion impact with the initially unreactive species to produce the activated species. As a result, fundamental AMO physics is closely and beneficially connected to technology development.

Examples of experimental progress in advancing the knowledge base for LTPs include, but are certainly not limited to, the “magnetic angle changer” (MAC) (4) and the so-called “reaction microscope” (RM) (5). The MAC makes it possible to carry out measurements of electron impact cross sections in angular regimes that were previously inaccessible because of geometric limitations due to the position of the electron gun. Furthermore, taking advantage of dramatic improvements in detector technology and fast electronics, the RM has enabled unparalleled detailed studies of electron–atom and electron–molecule collision processes over a wide range of parameters (energies, angles), and so provided an extensive database to test theory.

At the same time, theoretical and particularly computational advances have made the calculation of data for atomic/molecular structure as well as electron collision processes both reliable and cost-effective, and hence enabled their use in models for technology development. Although the basic equations that describe these quantum-mechanical many-body phenomena are believed to be known with a high degree of confidence, their necessarily approximate solution—with an accuracy that allows for reliable quantitative predictions—remains a formidable challenge. As a result of collaborative efforts between experimentalists and theorists worldwide to produce benchmark data for thoroughly testing the existing and further developing theoretical/computational methods, theory has advanced to a point that there is now confidence in many theoretical predictions of fundamental collision processes for which no experimental data are (and possibly never will become) available, even though these data are required in self-consistent modeling efforts.

These developments and the improvement in our understanding of fundamental atomic collisions have been critical for advances in modeling electron-driven processes in plasmas. These models allow for the study of basic plasma processes, but also enable analysis and optimization of current technologies using plasmas, as well as predicting the performance of as-yet-unbuilt systems for new applications. There is no doubt that the fidelity, depth, and impact of the modeling depends on the quality of fundamental electron and ion scattering data (FSD). Modeling, therefore, is empowered by the availability and robustness of FSD. As mentioned already, of particular importance is the fact that much of the FSD used today are taken from theoretical rather than experimental efforts, a situation dictated by the enormous amount of data needed for these complex models, as well as both the difficulties and the costs associated with experimental investigations. It is therefore crucial that the quality of the FSD be assessed in a reliable way.

This Perspective is organized as follows. Using the examples of the cesium-based diode-pumped alkali laser (DPAL) and remote plasma etching of Si₃N₄, Examples of Modeling Needs illustrates the kind and amount of data that are needed to thoroughly model such systems. One of the many ingredients for a sophisticated model are cross sections for electron collisions with atoms and molecules, as well as atomic and molecular structure, data for atom–atom and atom–molecule collisions, interactions with the boundaries, etc. In this Perspective, we will focus on electron collisions. We devote Selected Recent Advances in Electron Collisions with Atoms and Molecules to highlight some recent experimental progress as well as theoretical developments in this field. Because these are only selected examples from the very large field of charged-particle collisions in AMO physics, references will be given that contain more comprehensive and detailed information. Connecting Fundamental Data with Modeling Applications presents two examples where extensive sets of electron collision data, obtained with highly sophisticated and validated computational models, have enabled the thorough modeling of the systems of interest. We finish with a few conclusions and an outlook regarding the likely future of this field.

Examples of Modeling Needs

Cs-Based DPAL.

DPALs are a class of optically pumped lasers that leverage inexpensive semiconductor diode lasers (DLs) to pump alkali vapor. The generally poor optical quality and the wide bandwidth of a DL is converted into high optical quality, narrow bandwidth from the alkali laser. Laser ionization based on resonance (LIBOR) is an efficient means to produce plasmas in alkali vapor with low laser intensity. Electron heating by superelastic relaxation of laser-produced excited species then rapidly avalanches to nearly full ionization.

In DPALs, large densities of resonant excited states in alkali vapor are produced by laser pumping. With preexisting or laser-generated seed electrons, superelastic electron heating and associative ionization may result in plasma formation through a LIBOR-like process. The resulting plasma has the potential to reduce or quench laser oscillation through electron collision mixing. Hence, a critical question concerns the importance of plasma formation in a given DPAL system.

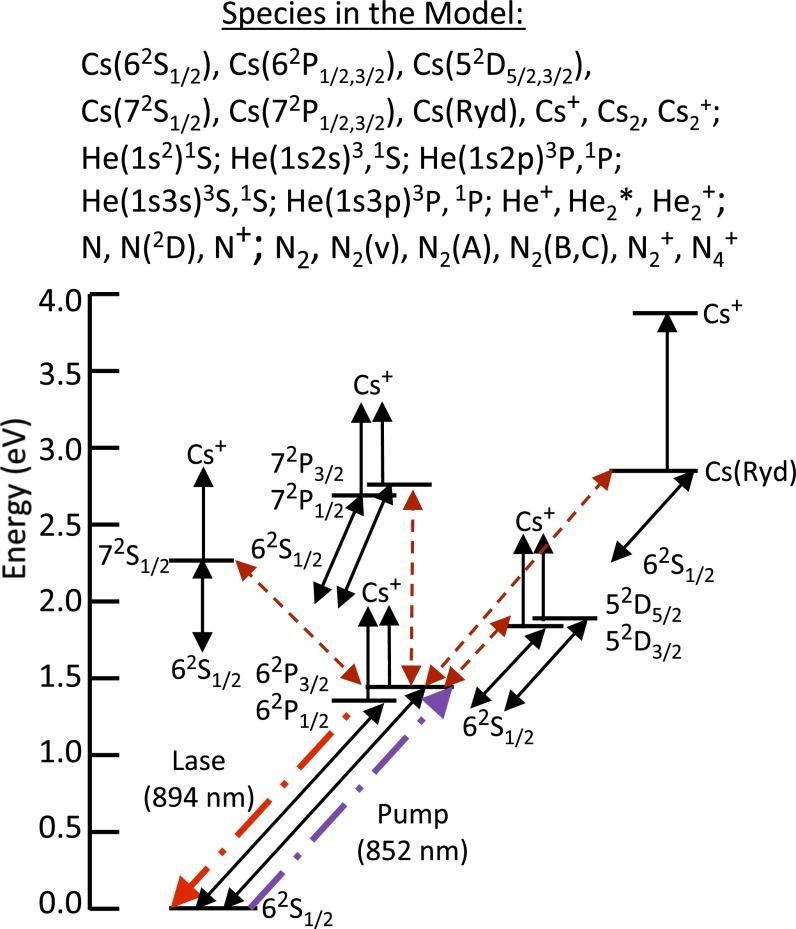
Our specific example concerns the computational investigation of a pulsed DPAL in He/Cs/C₂ H₆ and He/Cs/N₂ mixtures with lasing occurring on the Cs (6p)²${\text{P}}_{1/2}\to$ (6s)²S_1/2 transition with a wavelength of 894 nm. Fig. 1 gives an impression of the species contained in the model and the processes that are accounted for. Data for electron collisions with Cs atoms are by no means the only pieces needed for the puzzle, but they turn out to be a very important ingredient—in addition to data for electron collisions with helium atoms and ions, their dimers, as well as nitrogen atoms, ions, and molecules formed by Cs, He, and N. We also emphasize that cross sections for collisions with Cs atoms in their ground state are not sufficient, but rather data for collisions with atoms in excited states, including short-lived species, are needed. Such data are extremely difficult to obtain experimentally, and hence modelers have to rely on theoretical predictions.

Fig. 1.

Scheme for modeling a Cs-based DPAL. The solid lines denote electron collisions that induce transitions between the ground state and all excited states, and to the ion. The dotted lines are representative of electron impact collisions that produce transitions between all excited states. Additional reactions include collisions between atoms and molecules, and radiative transitions. Also shown (thick dashed-dotted lines) are the pump and lasing transitions.

Remote Plasma Etching of Si₃N₄.

To fabricate modern microprocessors, hundreds of manufacturing steps are required, many of them involving LTPs to etch (remove material), deposit (add material), clean, and passivate surfaces. As feature sizes in microelectronics shrink, the devices become more sensitive to damage from the plasmas being used to fabricate the device. As a result, the plasma is often sustained remotely from the wafer being etched and so protect the wafer from the most damaging reactive species. The less damaging reactive species are then flowed to the wafer for processing. This procedure is called remote plasma etching.

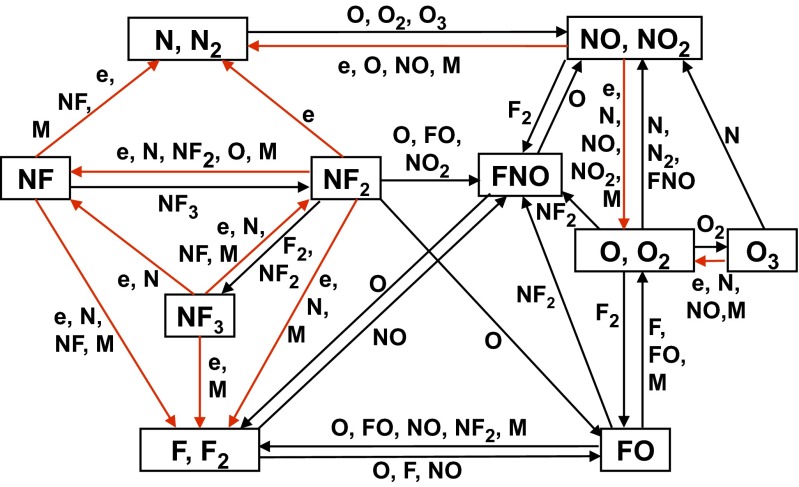
The gas mixtures that may be used for plasma etching, and for remote plasma etching in particular, contain complex molecular feedstocks. The choice of feedstock is based on how electron impact dissociation and ionization can produce the desired activated species. For example, in remove plasma etching of Si₃N₄, mixtures of NF₃ and O₂ may be used to create NF_x, N, and FNO_x (x = 1–3) species that ultimately etch the wafer. In modeling these systems to assist with technology development, a large number of individual species and reactions between those species must be accounted for. A subset of the species and reactions that must be considered in an LTP sustained only in an NF₃/O₂ mixture is shown in Fig. 2. For each of the electron-mediated processes, highlighted in red, FSD are required as a function of electron energy and scattering angle. Here, the reactive process is initiated by electron impact on NF₃ producing NF₂ and F, and with O₂ producing O atoms, and then followed by electron impact with those dissociation products. The availability of FSD for complex molecules such as NF_x and the fragments are rate-limiting steps in developing models for LTP processes.

Fig. 2.

Reaction mechanism in NF₃/O₂ mixtures. “M” denotes a third body.

Selected Recent Advances in Electron Collisions with Atoms and Molecules

We now describe a few advances that have pushed the production of reliable atomic collision data forward significantly during the past two decades. No attempt is being made to be comprehensive, and we will only summarize the basic ideas. Interested readers should consult the references given.

Two Experimental Advances.

The basic workhorse used in a large number of electron-scattering studies is the electron spectrometer. Free electrons are formed into a beam and energy selected by various combinations of electrostatic and magnetic fields. The use of electrostatic fields is most common, because they are more easily controlled and shielded than their magnetic counterparts. This is particularly important when it is essential to preserve the direction of low-energy electrons following the collision process.

Fig. 3 exhibits an example of such a spectrometer (6), which combines the characteristics of a conventional electrostatic device with an important innovation. It can be used for elastic scattering and electron impact excitation studies. The electron gun consists of a source of electrons produced by thermionic emission from a heated filament. The electrons are collimated and focused by an electrostatic lens system onto the input aperture of a double hemispherical energy selector. Those electrons within a narrow band of energies satisfying the criteria for transmission through the selector are then focused on the gas beam produced by a nozzle arrangement. Scattered electrons from the interaction region traveling in the direction of the scattered electron analyzer are similarly focused onto the input aperture of its double hemispherical analyzer, and the transmitted electrons are finally being focused into a single-channel electron multiplier detector.

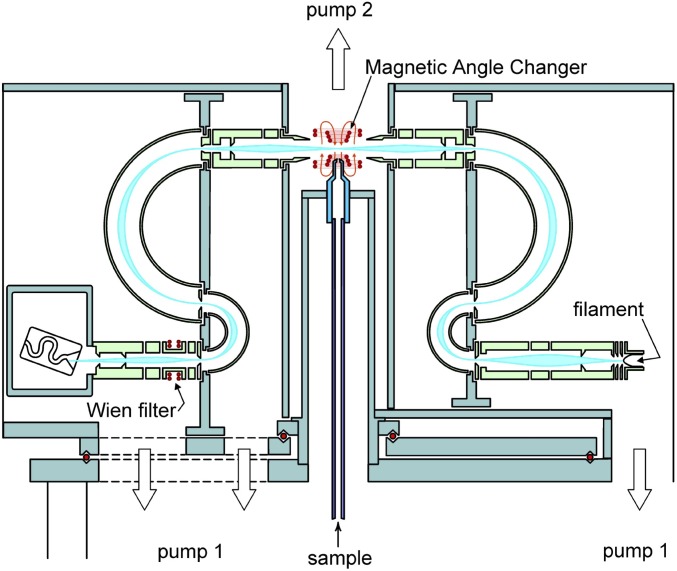
Fig. 3.

The electron spectrometer of Allan (6).

One drawback of conventional electron spectrometers is that the angular range of the electron analyzer is limited by the physical presence of other components of the spectrometer. This limitation was overcome by Read and Channing (4) who applied a localized static magnetic field to the interaction region of a conventional spectrometer. The incident electron beam and the scattered electrons are, respectively, steered to and from the interaction region through angles set by the field (hence, the common name “magnetic angle changer” or “MAC”). This steering means that electrons normally scattered into inaccessible scattering angles are rotated into the accessible angular range of the electron analyzer while the magnetic field design is such that it leaves the angular distribution of the electrons undistorted. The spectrometer shown in Fig. 3 has a MAC fitted, thereby enabling the full angular range 0–180° to be accessed.

Another novel experimental development in electron–atom/molecule scattering (and also heavy-particle collisions) is the reaction microscope described by Ullrich et al. (5). In contrast to conventional electron spectrometers, it uses recoil-ion and electron momentum spectroscopy to measure the vector momenta of outgoing charged particles.

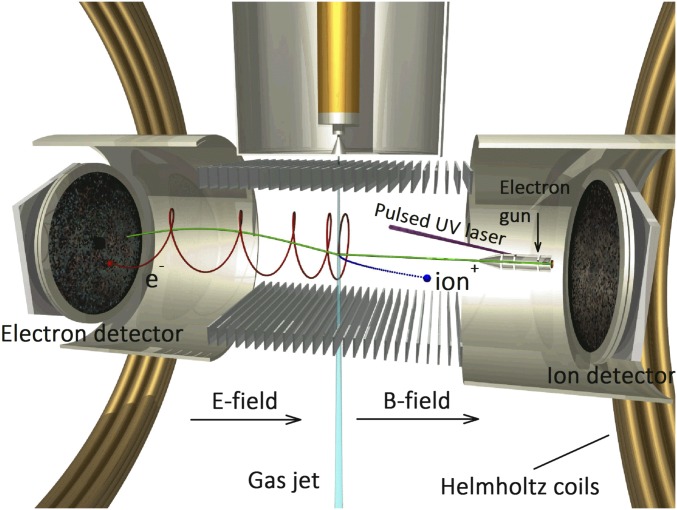
A recent version, developed by Ren et al. (7) to study single ionization processes is shown in Fig. 4. The RM operates on entirely different principles from conventional electron spectrometers. Briefly, a pulsed beam of electrons crosses a supersonic atom beam. The ejected electrons and the recoiling ions are extracted in opposite directions by a weak uniform electric field parallel to the incident electron beam direction. A uniform magnetic field is also applied in this direction to confine electrons emitted perpendicular to the electric field. After passing through field-free drift regions, the slow ejected electrons are detected in two time- and position-sensitive multihit detectors, allowing for the vector momenta of all particles to be calculated. Unlike most conventional coincidence electron spectrometers, which only enable measurements in a single plane at any one time, this technique allows for data to be collected over a large part of the entire 4π solid angle simultaneously.

Fig. 4.

The reaction microscope of Ren et al. (7). The projectile-electron beam is crossed with a supersonic gas beam. The projectile is created by a pulsed UV laser illuminating a photocathode. The outgoing electrons and ions are extracted by a homogeneous electric (E) field, created by a series of parallel electrodes, and detected by 2D position- and time-sensitive multihit detectors. A pair of Helmholtz coils generates a uniform magnetic (B) field, which forces the electrons into cyclotron trajectories and guides them onto the detector. The time of flight for each particle from the collision region to the respective detector is determined by the clock signals from the projectile pulse and the detectors.

Without going into detail, we emphasize the difficulty of obtaining absolute cross sections. Most of the time, some cross-normalization to “known” (or believed to be known) other data, such as cross sections for another target in a mixed-flow setup, data for angle-integrated state-to-state transitions after performing angle-differential measurements, total (summed over all accessible exit channels) cross sections, or even theoretical predictions, is required. Only in exceptional cases, absolute total ionization or recombination cross sections can be obtained directly (after carefully determining many experimental parameters) and fed into plasma models. An example is the crossed-beam apparatus developed by Müller and collaborators (8, 9).

Two Theoretical Advances.

Recent advances in computational power have enabled enormous progress in the treatment of atomic and molecular collisions. Even for electron collisions alone, the number of techniques is so extensive that we are not aware of a single recent comprehensive review on the subject. A broad overview with a summary of the basic ideas behind various methods used today for electron–atom collisions can be found in ref. 10. Even more general, atomic and molecular structure, electron–molecule, and heavy-particle collisions are addressed in ref. 11. In the latter work, particular emphasis is placed on estimating the uncertainty associated with theoretical predictions. Although not easy to quantify, this was recently recognized as a very important issue (12).

Here, we only mention two approaches, the so-called convergent close-coupling (CCC) (13) method and various R-matrix with pseudostates (RMPS) formulations based on the ideas presented in (14). The former is formulated in momentum space and the latter in coordinate space. These different formulations have a number of practical consequences, but both methods are based on the time-independent close-coupling approximation, in which the total wavefunction of the $\left(N+1\right)$-electron collision system is expanded in terms of a set of fully antisymmetrized products built from the N-electron target states and functions that describe the projectile. As described below, CCC and RMPS are fundamentally equivalent and hence should lead to the same result if the same target states are included in the expansion. For complex targets, of course, the atomic or molecular structure itself can be a major challenge, and care must be taken to ensure that correlations as well as relativistic effects are accounted for to sufficient accuracy in order for the subsequent collision calculation to be meaningful.

The close-coupling expansion results in a set of coupled integro-differential equations, either for the transition matrix elements in the CCC momentum–space formulation or for the unknown projectile wavefunction in coordinate space. Interestingly, the CCC equations for the transition matrix simplify for high projectile energies, whereas coordinate-space close coupling has been the method of choice for low-energy collisions for many years. In this context, “high” refers to incident projectile energies of several times the ionization threshold, whereas “low” refers to energies at which at most a few inelastic excitation processes are energetically possible. It is also worth mentioning that the R-matrix approach, as pioneered by Burke and collaborators (see ref. 15 for a comprehensive overview), is basically a numerical method to solve the close-coupling equations very efficiently for a large number of projectile energies. Hence, the method is particularly suitable when resonances change the energy dependence of the results dramatically, something that often happens in the low-energy near-threshold regime.

As one might expect from the description so far, the so-called “intermediate energies,” from about the ionization threshold to several times that energy, are the most difficult to handle. For this energy regime, channel coupling to an infinite (although countable) number of high-lying Rydberg states as well as the infinite (uncountable) target continuum spectrum is known to affect the results even for transitions between low-lying discrete states. To address this issue, so-called “pseudostates” are introduced that approximate these effects by including a large number (often several hundred) of square-integrable states in the close-coupling expansion. These states are not physical, because their wavefunctions are forced to vanish beyond some distance away from the target. Even though the expansion is no longer exact, the use of the pseudostates provides a general, and systematically improvable, way of accounting for this coupling. In addition, it enables the ab-initio calculation of ionization cross sections as the sum of all excitation cross sections to pseudostates with energies above the ionization threshold.

Over the years, enormous efforts have been dedicated to the general formulation, the construction of practical algorithms, and the development of general computer programs, many (although not all) of which are accessible to the general public. Here, we only mention the R-matrix package of the Belfast group (16) and the B-spline R-matrix (BSR) program of Zatsarinny (17). For a review of the BSR approach and a number of its applications, we refer to ref. 18.

In addition to the time-independent CCC and RMPS approaches, we mention the time-dependent close-coupling (TDCC) (19) formulation, as well as “exterior complex scaling” (ECS) (20). Both methods have provided important cross-checks for CCC and RMPS predictions, in particular because they can either avoid or treat in an alternative way the unphysical boundary conditions that must be handled in CCC and RMPS due to the finite range of the pseudostates. Although TDCC has also been used in some production calculations (generally to describe ionization processes), the computational effort required, as well as the quality of the target structure that can be used at this time, have limited the application of both TDCC and ECS regarding the mass production of atomic and molecular collision data. We also note that the current suite of CCC codes is limited to quasi one- and two-electron targets, i.e., at most two active electrons outside of an inert core without orbital or spin angular momentum can be handled. Although the general R-matrix packages may, in principle, be applied to complex targets with multiple open shells, the number of possible configurations and channels leads to practical limitations as well.

It should also be mentioned that the computational treatment relies on both supercomputer hardware such as Stampede (21), on which many of the recent BSR with pseudostates calculations have been performed, and on efficient, fully parallelized linear-algebra packages. For R-matrix approaches in particular, the complete diagonalization (i.e., the determination of all eigenvalues and eigenvectors) of nonsparse matrices is required. Recent calculations involved matrices of rank up to 200,000.

As mentioned earlier, there are many other methods around by which cross sections for electron collisions may be obtained. Variants of the relatively simple distorted-wave Born approximation remain important, especially if results from more sophisticated methods are not available. An example is the interface website to the Atomic Collision Codes (22) of the Los Alamos National Laboratory. Also, results have been collected in many databases. Some information can be found in ref. 23.

Some Illustrative Results.

We now discuss a few examples to show the current state of comparison between experiment and theory. Due to the experimental convenience, many of the benchmark studies have been carried out with noble gases, and hence most of our examples are also for such targets, namely electron-impact excitation of Ar and Kr as well as ionization of He and Ar. In addition, we show selected results for Cs and N targets.

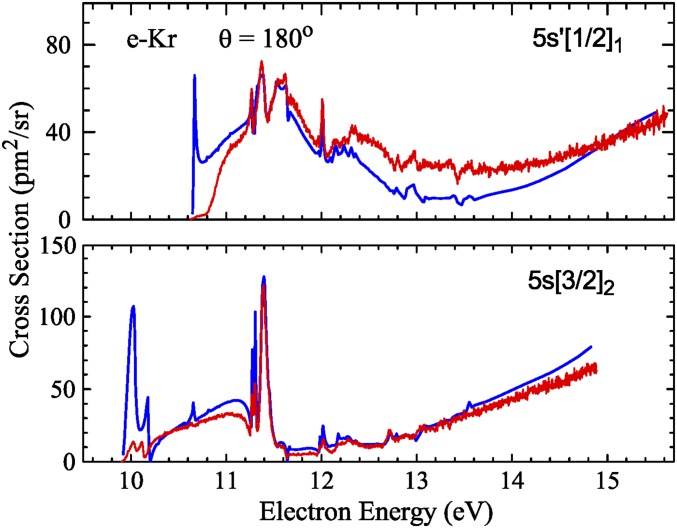
Fig. 5 exhibits the differential cross section as a function of energy for electron-impact excitation of the 5s[3/2]₂ and the 5s′[1/2]₁ states of krypton (24). Both states have the dominant configuration 4p⁵5s. The former is metastable (total electronic angular momentum $J=2$) and couples mainly to the (4p⁵)²P_3/2 ionic core, whereas the latter with $J=1$ couples to the (4p⁵)²P_1/2 core and can optically decay to the (4p⁶)¹S₀ ground state. To indicate that the valence orbital is strongly term dependent, one commonly uses the notations 5s and 5s′, respectively.

Fig. 5.

Differential cross section for electron-impact excitation of Kr at a scattering angle of 180°. The experimental data are compared with predictions from a full-relativistic BSR model (24).

The overall agreement between the measurements and predictions from a full-relativistic 69-state BSR model is very satisfactory, particularly for the optically forbidden transition to the metastable state. Note how well the complex resonance structure in the energy range from about 10.5 to 13 eV is reproduced by the BSR theory. The remaining discrepancies very close to threshold are most likely due to experimental issues, whereas theory apparently has some problems left for the 5s′[1/2]₁ state. Nevertheless, the unprecedented agreement between experiment and theory achieved in this study resolved discrepancies between previous measurements and calculations of angle-integrated cross sections for this collision system, as well as other heavy noble-gas targets (18).

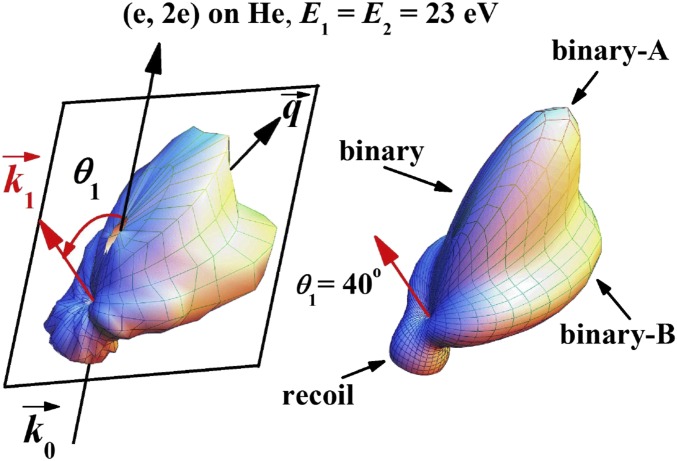
Fig. 6 exhibits the experimental and theoretical fully differential cross section (FDCS) for ionization of helium by 70.6-eV electron impact as 3D polar plots (25). The two outgoing electrons share the excess energy of 46 eV equally. One electron is detected at a fixed angle ${\theta }_1=40°$, whereas the detection angle of the second electron is varied. In this presentation, the FDCS for a particular direction is given as the distance from the origin of the plot to the point on the surface, which is intersected by the ionized electron’s emission direction. For the purpose of the present Perspective, we only note that the agreement between experiment and the CCC prediction is excellent. More details, including a discussion of the physical background, can be found in ref. 25.

Fig. 6.

Three-dimensional representation of the FDCS for ionization of He(1s²) (25). The experimental patterns on the Left are compared with CCC predictions on the Right, for a fixed detection angle ${\theta }_1=40°$ of one electron. The incident projectile energy is 70.6 eV, and both outgoing electrons have an energy of 23.0 eV.

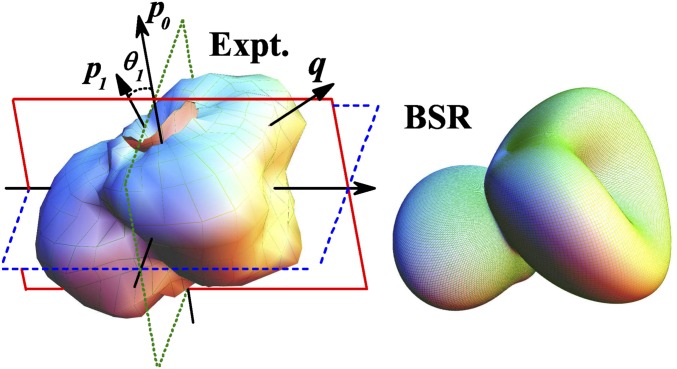
Moving on to a more complex target, Fig. 7 exhibits the FDCSs for ionization of Ar(3p⁶) by 66-eV electron impact. In this case, the excess energy is shared unequally between the two electrons in the final state, with the fast one being detected at ${\theta }_1=15°$ and the emission direction of the slow one with energy $E_2=3$ eV being varied. Although not perfect, the agreement between experiment and BSR is sufficiently good to provide significant confidence in the BSR prediction for this—and many other—electron collision problems involving atomic targets.

Fig. 7.

Three-dimensional representation of the FDCS for ionization of Ar(3p⁶) (26). The experimental patterns on the Left are compared with BRS predictions on the Right, for a fixed detection angle ${\theta }_1=15°$. The incident projectile energy is 66 eV, and the slower of the two outgoing electrons has an energy of 3 eV.

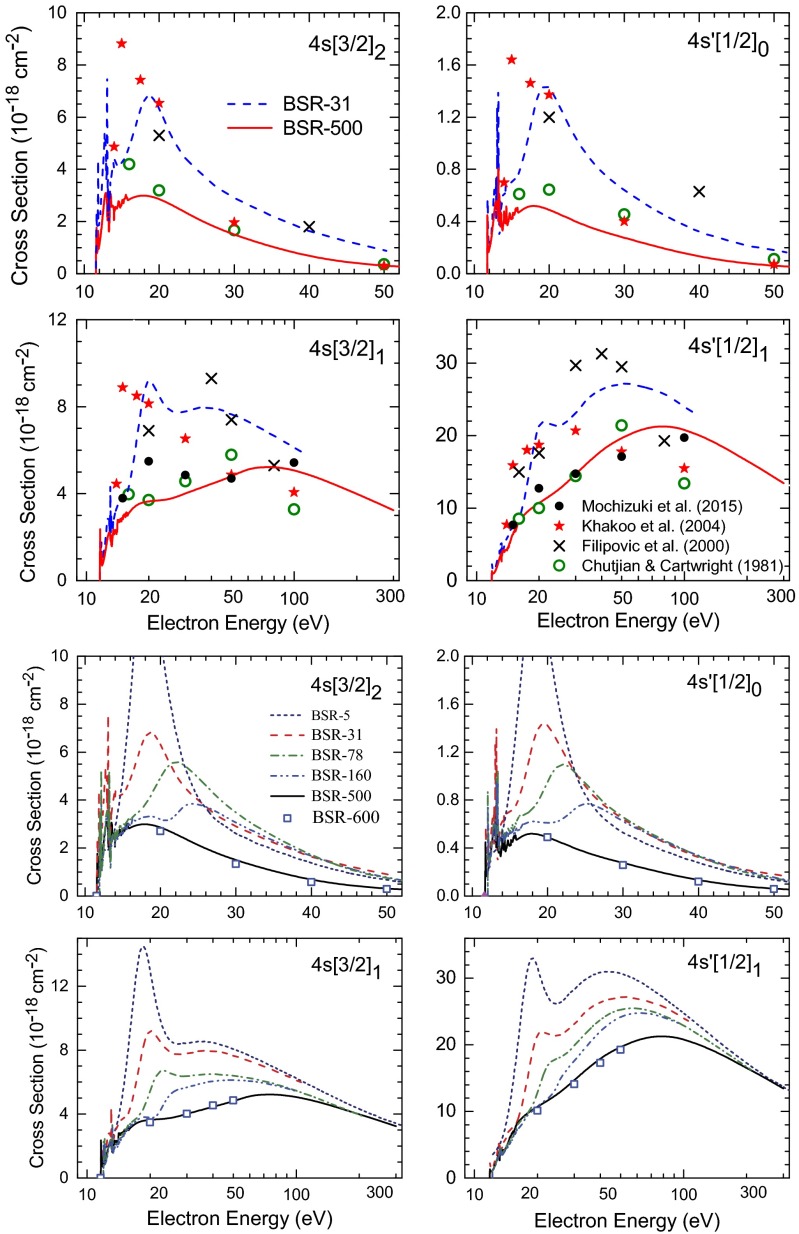
The detailed comparisons mentioned above subsequently had a significant impact on production calculations for angle-integrated cross sections for electron collisions. Two more examples are shown below. The first one concerns electron impact ionization of the four states with dominant configuration 3p⁵4s from the (3p⁶)¹S₀ ground state in argon. Fig. 8 shows results from a detailed study using the BSR approach (27). Looking at the top two rows, we see the enormous effect of accounting for coupling to both high-lying discrete states and the ionization continuum on the results for these transitions from the ground state to the first four excited states. The effect is particularly strong for the metastable 4s[3/2]₂ and 4s′[1/2]₀ states. Somewhat surprisingly, however, the coupling effect also prevails for the excited states with electronic angular momentum $J=1$ for incident energies at least up to 100 eV. This fact suggests that simple models, such as a distorted-wave approach, would not be appropriate until such comparatively high energies. Semiempirical fixes to such models, as suggested by Kim (31) with so-called “BEf-scaling,” may help. However, such methods are limited to particular situations, and success is by no means guaranteed due to the lack of a firm theoretical foundation.

Fig. 8.

Angle-integrated cross sections for electron-impact excitation of the 3p⁵4s states in argon from the (3p⁶)¹S₀ ground state (27). Top two rows: The results from a variety of BSR models (see text) are compared with each other to provide an indication of the convergence pattern in the theoretical predictions. Bottom two rows: The results from the BSR-31 and BSR-500 models are compared with a number of experimental data [28–30 and (Mochizuki Y, Murai H, Kato H, Hoshino M, Tanaka H (2015) Electron impact excitation of the low-lying 4s[3/2]₁ and 4s'[1/2]₁ levels in Ar atom. Proceedings of the XXIX International Conference on Photonic, Electronic, and Atomic Collisions (ICPEAC), Toledo (Spain). Poster MO-115, and private communication.)].

The bottom two rows of Fig. 8 exhibit the results again, this time as a comparison between the predictions from a 31-state model (coupling only the lowest 31 discrete states of Ar) and a 500-state model (including 78 discrete and 422 continuum pseudostates) with experimental data from several groups. Without going into details, we note that energy dependence seen in many of the individual datasets is very scattered, much more than one would expect in reality. Consequently, the experimental data apparently have significant uncertainties, most likely due to a combination of statistical and systematic effects. Based on the careful analysis of trends in the theoretical predictions (11), one would advise modelers to use the very comprehensive BSR-500 dataset (state-to-state transitions between the lowest 31 states plus ionization cross sections are available) rather than any of the few experimental data currently available.

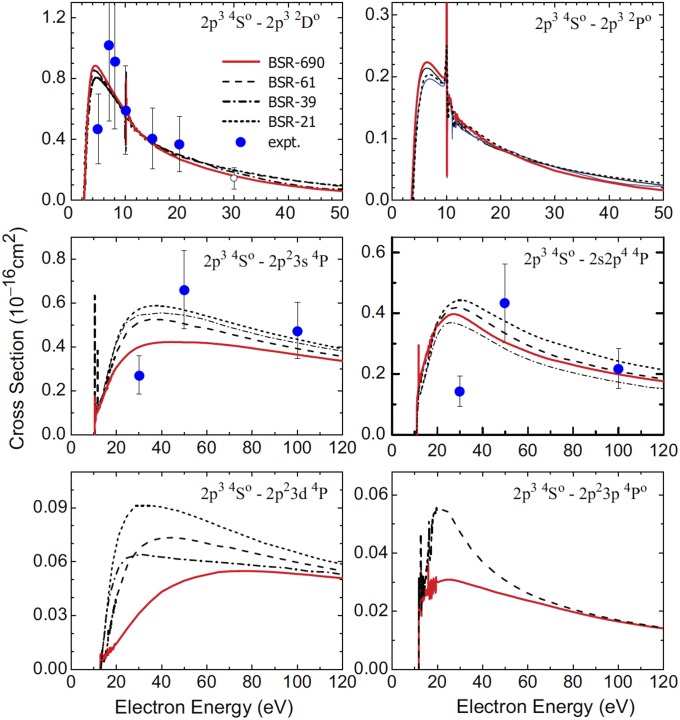
The need for using theoretical rather than experimental data becomes even more apparent for targets that only form atoms under special conditions. An example is shown in Fig. 9, which depicts electron-impact excitation cross sections for a number of transitions in atomic rather than molecular nitrogen. Once again, predictions from a number of BSR models, with up to 690 states included in the close-coupling expansion, are compared with the few experimental data currently available for this collision system. The very large error bars associated with these experimental data, and just the few energy points for which they exist, clearly limits their use in practical applications. In contrast, the best BSR dataset, once again carefully analyzed with respect to the convergence of the close-coupling expansion, is expected to be both sufficiently comprehensive and accurate for most modeling applications.

Fig. 9.

Cross sections, as function of collision energy, for electron-impact excitation of the most important transitions from the (2s²2p³)⁴S^o ground state of atomic nitrogen. The final states are listed in the various panels. Unless listed explicitly as 2s, the inner-shell configuration is 1s²2s². BSR-696 and BSR-61 results from ref. 32 are compared with those from previous BSR-39 and BSR-21 calculations (33). Also shown are various sets of experimental data (34–36).

Space does not allow us to present further examples, in particular for atomic ions. In general, with growing ionic charge, the Coulomb interaction within the target and also between the target and the projectile electron increasingly dominates electron correlation and channel coupling effects. Hence, perturbative methods are likely to be more successful for these cases than for neutral targets, provided only the background cross sections are needed rather than a detailed analysis of resonances. Many of these systems are of tremendous importance in the interpretation of astrophysical observations. Once again, the enormous amount of data needed has made theoretical predictions essential. Nevertheless, carefully selected and planned experimental studies remain important for benchmark comparisons with theory.

Connecting Fundamental Data with Modeling Applications

We now return to the two examples mentioned in The Need for Atomic and Molecular Data, namely the Cs-based DPAL and remote plasma etching of Si₃N₄. To model these systems, a significant number of data for electron collisions with either the Cs atom or NF_x molecules were required.

Cs-Based DPAL.

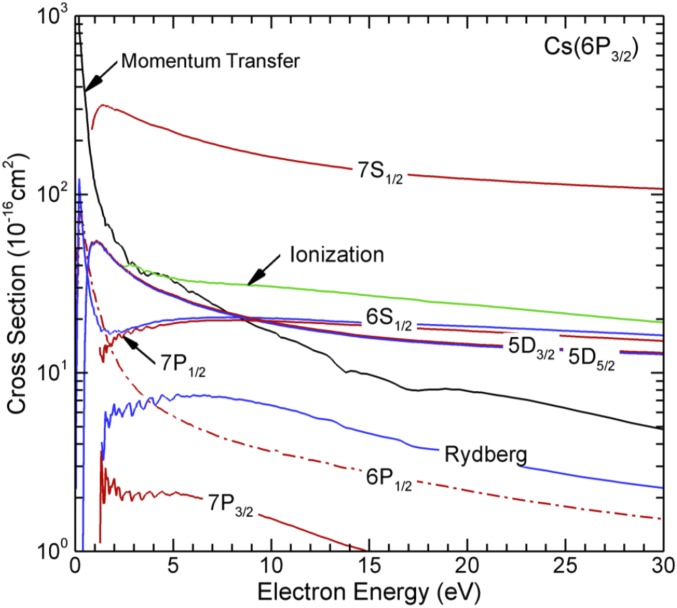
Optical pumping of Cs vapor and possible plasma formation was discussed in detail in a recent paper (37). It is an excellent example of a mutually beneficial collaboration between data producers and data users. As just a small subset of electron collision data needed for the modeling, Fig. 10 exhibits the cross sections for electron collisions with Cs in its excited (6p)²P_3/2 state. Obtaining these cross sections experimentally from beam setups, or possibly from collisions in laser traps, is extremely challenging (39), due to the difficulties of preparing the target. Hence, the cross sections were obtained from full-relativistic BSR calculations based on the work reported in ref. 38 and cross-checked against independently generated results from an earlier, also highly successful semirelativistic model (40). Although one can never be sure, of course, there is every reason to believe that the rate coefficients, which were calculated from the electron collision cross sections, are accurate to better than 10%.

Fig. 10.

Cross sections predicted by the B-spline R-matrix with pseudostates approach for electron collisions with Cs atoms in the (6p)²P_3/2 excited state (38).

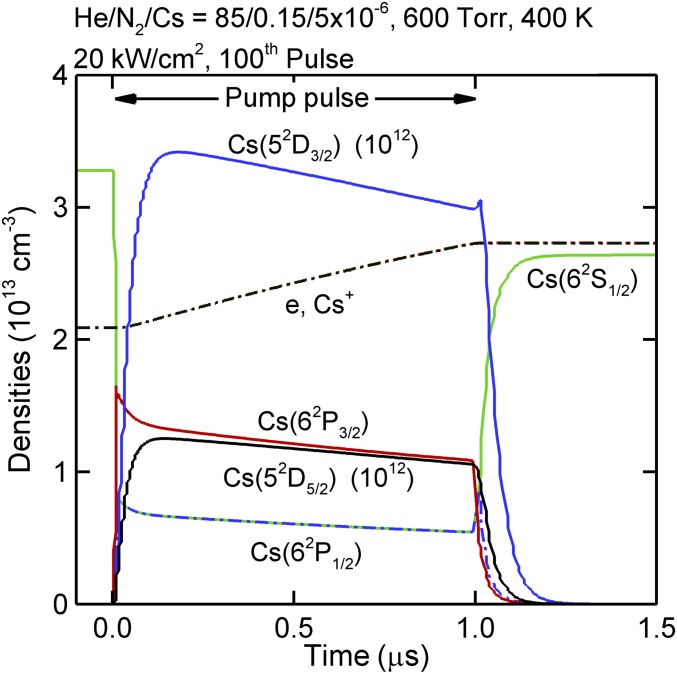
An example of modeling the DPAL with numerically generated FSD is shown in Fig. 11. These results were produced with a global kinetics, collisional-radiative model (41), in which conservation equations for the densities of the charged and neutral species, electron temperature, gas temperature, and laser optical fluxes are integrated in time while accounting for transport in the form of diffusion to surfaces and/or plug flow. Rate and transport coefficients for electron impact processes were obtained from solutions of Boltzmann’s equation for the electron energy distribution with FSD for cross sections as input. A high-power, 20 kW/cm², 1-μs pump pulse excites a 600-torr mixture of He/N₂/Cs = 85/15/5 × 10⁻⁶ gas mixture at 400 K. The Cs density is determined by the metal vapor pressure. Results are shown for the hundredth in a series of pump pulses. Over the series of pulses, a plasma density of 2 × 10¹³ cm⁻³ is formed. During the pump pulse, lasing occurs that saturates the Cs (6s)²S_1/2 and (6p)²P_1/2 states. The higher excited states of Cs (5d)²D_3/2,5/2 are largely produced by electron impact excitation from the Cs (6p)²P_1/2,3/2 states. Note that electron impact cross sections for these excitation processes are particularly large.

Fig. 11.

Densities of Cs species and electrons during high-power DPAL pumping of a He/N₂/Cs gas mixture at 600 torr and 400 K (37).

The above work revealed that heating of electrons by superelastic relaxation of the diode laser-excited Cs ²P_1/2,3/2 resonant states leads to significant plasma formation. This plasma ultimately reduces the laser power by depletion of the ground state through ionization and by electron-collision mixing of the laser levels (37).

Remote Plasma Etching of Si₃N₄.

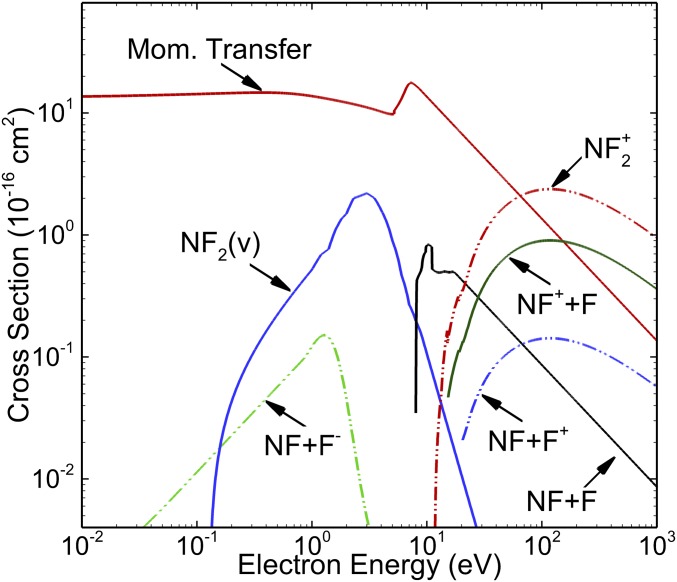
As seen from Fig. 2, modeling this process requires, among many other data, cross sections for electron collisions with NF₃, NF₂, NF, various molecular ions, as well as data for heavy-particle collisions. Fig. 12 shows results for NF₂, for which no experimental data were available. The predictions were generated by Tennyson and collaborators (42) using the UK molecular R-matrix codes (43). After the success achieved by the RMPS and CCC approaches for atoms and atomic ions, the very same ideas were implemented in the molecular codes. As a result, accurate and sufficiently comprehensive datasets can now be generated to serve the modeling community.

Fig. 12.

Some cross sections used for the processes depicted in Fig. 2. The data for electron collisions with NF₂, including momentum transfer, vibrational excitation (v), and dissociation into combinations of various molecular ions were generated by Tennyson and collaborators (42) with the UK molecular R-matrix codes (43).

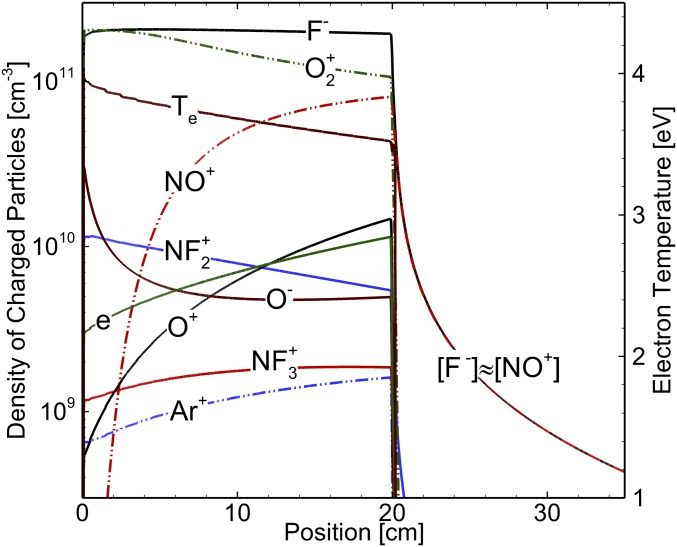
Using these FSD, results from a model for a remote plasma sustained in an Ar/NF₃/O₂ = 5/10/100 gas mixture at 400 mtorr are shown in Fig. 13 for a power deposition of 900 W. The densities of the charged particles and electron temperature are shown as the gas flows through the plasma zone and downstream toward the etching chamber. NF₃ and O₂ rapidly dissociate in the plasma zone, largely due to electron impact dissociative attachment and excitation. The plasma is highly electronegative with a ratio of negative ions to electrons of about 20. The electron density increases during the flow to a maximum of 1.1 × 10¹⁰ cm⁻³. The formation of negative ions is due to dissociative attachment (e + ${\text{NF}}_x\to$ ${\text{NF}}_{x-1}$ + F⁻ and e + ${\mathrm{O}}_2\to$ O + O⁻). In the plasma zone, the electron temperature is 3.5–4.0 eV. This high value is necessary to offset the high rate of electron loss due to attachment. Downstream of the power deposition zone, the plasma rapidly transitions to an ion–ion plasma mainly composed of F⁻ and NO⁺.

Fig. 13.

Charged particle densities during remote plasma etching using an Ar/NF₃/O₂ gas mixture at 400 mtorr. Significant electron impact dissociation of the feedstock gases produce ions composed primarily of the dissociation products and their products through subsequent reactions.

Conclusions and Outlook

In this Perspective, we highlighted a few of the advances that have been made in basic research in the AMO physics field of electron–atom and electron–molecule collisions, from the beginning of quantum mechanics nearly a century ago to the highly sophisticated theoretical, computational, and experimental methods used today. Experimental and theoretical/computational efforts in basic research were coordinated to provide benchmark data for thoroughly testing the reliability of various theoretical approaches. As a result of these collaborative efforts, theory has advanced to a point that there is now confidence in many theoretical predictions of fundamental collision processes for which no experimental data are (and possibly never will become) available. However, these data are required in self-consistent modeling efforts for plasmas, and they have been used successfully in many occasions. The production of fundamental electron-scattering data in this manner is accelerating the development of society benefiting technologies.

Despite the maturity of the field of charged-particle collisions, benchmark comparisons between experiment and theory, as well as between predictions from independent, highly sophisticated approaches such as CCC, RMPS, BSR, TDCC, ECS, etc., remain invaluable for continued progress. Fundamental scattering data, critically evaluated with respect to their likely uncertainties, are essential for the empowerment of plasma modeling and, consequently, to further advance our high-technology–based society. Last, but certainly not least, we emphasize the continued need for experimental benchmark data, especially for complex systems, where theory still needs to be checked carefully.