Abstract
Aim:
Our preliminary results show that huperzine A, an acetylcholinesterase inhibitor used to treat Alzheimer's disease (AD) patients in China, exhibits different pharmacokinetic features in elderly and young healthy subjects. However, its pharmacokinetic data in elderly subjects remains unavailable to date. Thus, we developed a population pharmacokinetic (PPK) model of huperzine A in elderly Chinese people, and identified the covariate affecting its pharmacokinetics for optimal individual administration.
Methods:
A total of 341 serum huperzine A concentration records was obtained from 2 completed clinical trials (14 elderly healthy subjects in a phase I pharmacokinetic study; 35 elderly AD patients in a phase II study). Population pharmacokinetic analysis was performed using the non-linear mixed-effect modeling software Phoenix NLME1.1.1. The effects of age, gender, body weight, height, creatinine, endogenous creatinine clearance rate as well as drugs administered concomitantly were analyzed. Bootstrap and visual predictive checks were used simultaneously to validate the final population pharmacokinetics models.
Results:
The plasma concentration-time profile of huperzine A was best described by a one-compartment model with first-order absorption and elimination. Age was identified as the covariate having significant influence on huperzine A clearance. The final PPK model of huperzine A was: CL (L/h)=2.4649*(age/86)(−3.3856), Ka=0.6750 h−1, V (L)=104.216. The final PPK model was demonstrated to be suitable and effective by the bootstrap and visual predictive checks.
Conclusion:
A PPK model of huperzine A in elderly Chinese subjects is established, which can be used to predict PPK parameters of huperzine A in the treatment of elderly AD patients.
Keywords: huperzine A, Alzheimer's disease, elderly Chinese people, population pharmacokinetics, modeling and simulation, NLME
Introduction
Huperzine A is an alkaloid extract of the Huperzia serrata plant that may be useful as a treatment for AD. During the 1980s, investigators in China determined that huperzine A is a potent inhibitor of acetylcholinesterase, a finding that has been confirmed repeatedly. Based on its 50% inhibitory concentration (IC50), huperzine A is more potent than tacrine, physostigmine, and galantamine with respect to inhibition of AChE activity1. Hence, it is presumed that huperzine A would exert its clinical efficacy in AD via this mechanism.
Clinical trials in Chinese subjects have shown that huperzine A can improve memory function with MMSE, MQ, ADAS-COG, and ADL tests2,3,4. Zhang et al5 conducted a large-scale, multicenter, randomized, double-blind, placebo-controlled study in China in 2002. This study included 202 patients given either huperzine A at graduated doses and vitamin E or a placebo and vitamin E for 12 weeks. The huperzine A graduated doses were 0.1 mg twice daily for 1 week, then 0.15 mg twice daily for 2 weeks and 0.2 mg twice daily for 9 weeks. The two groups were studied for a total of 12 weeks and were evaluated using numerous memory-function tests. The results of the MMSE, ADAS-COG, ADAS-non-COG, CIBIC-plus, and ADL tests indicated a significant increase in memory function in the huperzine A-treated group. Zhang et al6 conducted a study in 2006 in China. In this 24-week, placebo-controlled study, 120 participants received either 0.5 mg/d of huperzine A or placebo. The ADAS-COG test revealed a significant improvement in the scores of those treated with huperzine A compared with the placebo group.
Rafii et al7 reported a phase II multicenter, randomized, double-blind, placebo-controlled clinical trial in the United States. In this study, 210 patients with mild to moderate AD were given either a placebo, 0.2 mg twice daily or 0.4 mg twice daily of huperzine A for 16 weeks. A total of 177 subjects completed the treatment phase. The ADAS-COG test indicated cognitive enhancement at the 0.4-mg twice-daily dose, but no improvement at the 0.2-mg twice-daily dose.
In several clinical trials in China, the effective doses of huperzine A were markedly different from those in other countries. The differences in the pharmacodynamics may be due to many factors, including ethnic or physiological differences in clinical trial subjects. To investigate the differences in the pharmacodynamics, we aimed to identify the pharmacokinetic factors that influence the drug concentration of huperzine A, including physiological factors such as weight, age, height, gender and creatinine clearance rate as well as drug combination.
Li et al8 and Qiang et al9 reported that pharmacokinetic studies were conducted in young healthy volunteers after taking 0.4 mg8 or 0.99 mg9 of huperzine A, which are higher than the commonly used clinical dose in Chinese subjects. Li et al10 conducted a pharmacokinetic study in healthy subjects who received a single 0.2-mg dose huperzine A. After the dose was normalized, the AUCs of the two tests were similar; both were approximately 50% lower than that in our pretest in elderly subjects. Only animal pharmacokinetic parameters were listed in the manufacturer's instructions for huperzine A, which showed a large gap with the international general requirements.
To date, a pharmacokinetic study of huperzine A in elderly subjects has not been reported. The results of our pretest revealed differences in the pharmacokinetic features of huperzine A between elderly and young healthy subjects. These may be due to the degradation of body function and co-administration of other drugs in the elderly individuals. Given that huperzine A is used mainly in elderly patients, pharmacokinetic studies should be conducted in elderly populations to ensure the drug's safe use in these individuals. The objectives of our study were to develop a model that described the disposition characteristics of huperzine A, to estimate the inter-individual variability (IIV) of the main PK parameters and the random residual error, and to explore possible covariates influencing the population PK parameters based on PK data collected in aged subjects with or without AD. However, because the reported information (eg, therapeutic range and PK/PD relationship) for huperzine A is incomplete, it is very difficult to design dosage regimens based on the current population pharmacokinetic (PPK) model. The primary aim of the current study was to investigate the PK profile in elderly individuals and screen potential covariates in order to obtain useful information for further studies.
Materials and methods
Subjects and study design
Plasma concentration-time data for huperzine A were obtained from two studies (phase I and phase II) evaluating the drug's safety, tolerability, pharmacokinetics, and pharmacodynamics in elderly subjects with or without AD. Both studies were conducted at the Xuhui Center Hospital, Shanghai, China, and performed according to the Ethical Principles Set forth in the Declaration of Helsinki, the International Conference on Harmonisation (ICH) for Good Clinical Practice and all other applicable regulatory requirements.
The first study was an open-label, single-dose phase I pharmacokinetic study in 14 elderly male and female subjects without AD. Safety evaluations were conducted over the course of the study, including physical examinations, monitoring of vital signs, twelve-lead ECGs, and clinical laboratory tests (ie, biochemistry, hematology and urinalysis). The subjects were screened within 28 days before the study. In the study, the 14 subjects were confined to the phase I wards for at least 12 h (d 1) prior to treatment. The following morning, each was given a single 0.1-mg huperzine A tablet with 200 mL drinking water. Afterward, blood samples were collected through an intravenous catheter at the following time: 0 (pre-dose), 0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 2.0, 3.0, 4.0, 6.0, 8.0, 12, 24, 36, and 48 h. The collected blood samples were immediately centrifuged at 3000 rpm for 10 min at 4 °C before being aliquoted into polypropylene tubes. The aliquots were stored at -20 °C until chromatographic analysis.
The second study was a single-center, open-label, self-controlled multiple-dose phase II study in patients with AD. A total of 35 patients with mild to serious AD were recruited. An initial treatment regimen of 0.1 mg of huperzine A twice a day for 4 weeks was prescribed. Then, the dosage was increased to 0.2 mg twice a day for 4 weeks. The daily dose was adjusted depending on the response and tolerability of the treatment in the eighth week. The treatment duration was 24 weeks. Multiple-concentration samples of huperzine A were collected before and at 1 to 3 h after drug administration, near the trough and peak concentrations, at weeks 4, 8 and 24. Each subject submitted three to six blood samples. The time of the last dose and the exact time of collection were available for each of the samples.
The following data were collected from the subjects' medical charts: body weight, height, age, sex, concomitant medications, severity of AD, results of liver function tests, and serum creatinine level.
Bioanalytical methods
The concentrations of huperzine A in the plasma were determined by a validated liquid chromatography–tandem mass spectrometric (LC-MS/MS) method described by Liu et al11. All samples were assayed in the same laboratory. The plasma samples were processed by direct protein precipitation with acetonitrile. Analysis was performed via positive-ion electrospray tandem mass spectrometry on an AB Sciex QTRAP® 5500 (Foster City, AB SCIEX, USA). The standard curves for huperzine A ranged from 0.05 to 10 ng/mL. In plasma analysis, the precision (%CV) and accuracy (%bias) of the QC samples at the four concentrations were ≤10% and between -5% and 15%. The LC-MS/MS method was selective for huperzine A, and the lower limit of quantification was 0.05 ng/mL.
PPK model development
The PPK of huperzine A was analyzed using the nonlinear mixed-effect modeling software Phoenix NLME, version 1.1.1 (Pharsight, USA). The initial model development focused on a base model structure with PK parameter assessment.
Model selection was guided by the plausibility of the estimates and minimum objective function value (OFV), which was equal to minus twice the log-likelihood function (Δ-2LL). In the initial stage of model building, one- and two-compartment models with first-order absorption and elimination were tested. Population PK analyses used the first-order conditional estimation LAPLACIAN method. Inter-individual variability (IIV) for PK parameters was evaluated using the exponential model Pi=PTV×eηP, where Pi is the parameter estimate for the ith individual and PTV is the typical value for the parameter at the population level. The variability between the ith individual and the population parameter values was described by ηP, which followed a normal distribution and has a mean of 0 and a variance of ω2 (ie, ηP ∼N[0, ω2]). Different residual error models included exponential, additive, proportional, and combined additive models. The combined additive and proportional residual modes were defined as Cij=C (1+ɛpij)+ɛaij, where Cij is the jth measured observation for the ith subject and ɛpij and ɛaij are the proportional and additive residual random errors, respectively, for an individual i and measurement j. Each measurement was assumed to be independently normally distributed, for example, ɛpij ∼N(0, σ12) and ɛaij ∼N(0, σ22), where σ1 and σ2 represent the standard deviations for the proportional and additive residual error, respectively.
After construction of the optimal model for huperzine A, covariate analysis was carried out to assess additional variables as possible determinants of the variability observed in the pharmacokinetic estimates. Covariates examined include total body weight, height, age, gender, creatinine level, endogenous creatinine clearance rate (CLcr) and co-administration. Table 1 summarizes the categorical and continuous covariates evaluated. The potential covariates were then tested using a stepwise forward addition approach followed by stepwise backward elimination. The influence of the covariates was tested by adding a covariate to the model at a time in the forward addition step and then removing a covariate from the model at a time in the backward elimination step. Next, the changes in Δ-2LL between the “full” and the “reduced” models were calculated. The difference in the Δ-2LL between the two nested models was approximated by a χ² distribution. A Δ-2LL change of 6.64 (corresponding to a significant level of 0.01 and one degree of freedom) was used as the cut-off to include a covariate in the stepwise addition. When no more covariates could be included, the stepwise backward elimination was carried out. For a covariate to remain in the model, a change in the Δ-2LL of at least 10.83 (corresponding to a significance level of 0.001 and one degree of freedom) was needed.
Table 1. Summary statistics of subjects covariates (n=49).
| Continuous covariate | Total | Healthy elders | AD patients |
|---|---|---|---|
| Median (Min–Max, RSD%) | Median (Min–Max, RSD%) | Median (Min–Max, RSD%) | |
| Age (year) | 86 (63–96, 11.57%) | 68 (63–79, 7.55%) | 88 (75–96, 4.94%) |
| Body weight (kg) | 60.0 (34.0–82.9, 17.63%) | 65.8 (53.1–82.9, 15.10%) | 60.0 (34.0–80.0, 18.05%) |
| Height (cm) | 161.0 (147.1–185.0, 5.54%) | 157.8 (147.1–175.4, 5.65%) | 165.0 (150.0–185.0, 5.22%) |
| Scr (μmol/L) | 76 (44–152, 33.87%) | 61 (44–79, 22.18%) | 88 (44–152, 31.32%) |
| CLcr (mL/min) | 52.64 (17.67–106.66, 44.65%) | 87.88 (65.40–106.66, 14.78%) | 40.01 (17.67–79.07, 35.91%) |
| Categorical covariate | Numbers (%) | Numbers (%) | Numbers (%) |
|---|---|---|---|
| Gender | |||
| 1: Male | 23 (46.94) | ||
| 0: Female | 26 (53.06) | ||
| Co-administration | |||
| Isosorbide mononitrate | 26 (53.06) | 0 (0) | 26 (53.06) |
| Clopidogrel | 14 (28.57) | 0 (0) | 14 (28.57) |
| Mosapride | 14 (28.57) | 0 (0) | 14 (28.57) |
| Metoprolol | 11 (22.45) | 0 (0) | 11 (22.45) |
| Finasteride | 11 (22.45) | 1 (2.04) | 10 (20.41) |
| Valsartan | 10 (20.41) | 0 (0) | 10 (20.41) |
| Aspirin | 10 (20.41) | 2 (4.08) | 8 (16.33) |
| Rabeprazole | 10 (20.41) | 0 (0) | 10 (20.41) |
| Trimetazidine | 9 (18.37) | 0 (0) | 9 (18.37) |
| Atorvastatin calcium | 9 (18.37) | 1 (2.04) | 8 (16.33) |
| Rosuvastatin calcium | 9 (18.37) | 0 (0) | 9 (18.37) |
Model evaluation
A non-parametric bootstrap procedure was employed to evaluate the precision of the parameter estimates and the robustness of the final model. One thousand bootstrap datasets were generated by repeated random sampling with replacement from an NLME input data file, and the final NLME model was fitted to the bootstrap datasets. Bootstrap parameter estimates, standard errors and 95% confidence intervals were obtained and compared with the parameter estimates from the original dataset.
To evaluate the predictive ability of the final model, 1000 virtual observations at each sampling time point were simulated using the final model and its parameter estimates. The observed data were then plotted with the 5th, 50th, and 95th percentiles of the simulated data, which were above the limit of quantification. The percentage of observations outside the 90% prediction interval was also calculated.
Results
Demographic data
Table 2 shows the demographic characteristics of the subjects in the two clinical trials. The huperzine A dataset consisted of 49 subjects, contributing a total of 341 huperzine A plasma concentration records that were used to develop the model. In total, 180 observations were from the 14 subjects in the phase I study and 161 observations were from the 35 subjects in the phase II study. Huperzine A concentration observations that were below the analytical assay quantification limit and any missing values were excluded from the analysis. Most of the subjects were taking a combination of drugs, including isosorbide mononitrate, clopidogrel, mosapride, metoprolol, and/or finasteride.
Table 2. Demographic characteristics of subjects in the phase I & II study. n, number of subjects; BMI, body mass index; SD, standard deviation.
| Characteristics | Phase I study |
Phase II study |
||
|---|---|---|---|---|
| Mean (SD) | Median (range) | Mean (SD) | Median (range) | |
| Subject number | 14 | 35 | ||
| Male, n (%) | 7 (50%) | 16 (46%) | ||
| Female, n (%) | 7 (50%) | 19 (54%) | ||
| Age (year) | 69.4 (5.24) | 68 (63–79) | 87.8 (4.34) | 88 (75–96) |
| Height (cm) | 158.6 (8.96) | 157.8 (147.1–175.4) | 164.5 (8.59) | 165.0 (150.0–185.0) |
| Body weight (kg) | 65.7 (9.93) | 65.8 (53.1–82.9) | 59.4 (10.73) | 60.0 (34.0–80.0) |
| BMI (kg/m2) | 26.03 (2.06) | 26.41 (21.02–28.92) | 22.04 (3.38) | 22.24 (13.97–29.38) |
| Scr (μmol/L) | 61.6 (13.66) | 61 (44–79) | 88.8 (27.82) | 88 (44–152) |
| CLcr (mL/min) | 86.73 (12.82) | 87.88 (65.40–106.66) | 42.91 (15.41) | 40.01 (17.67–79.07) |
PPK model
A one-compartment model with first-order absorption and elimination best described the huperzine A data. When a two-compartment model was fitted to the data, the AIC (Akaike information criterion) was mildly increased, from 394.27 in the one-compartment model to 399.48. In accordance with the AIC minimization principle, we chose the one-compartment model to fit the huperzine A data.
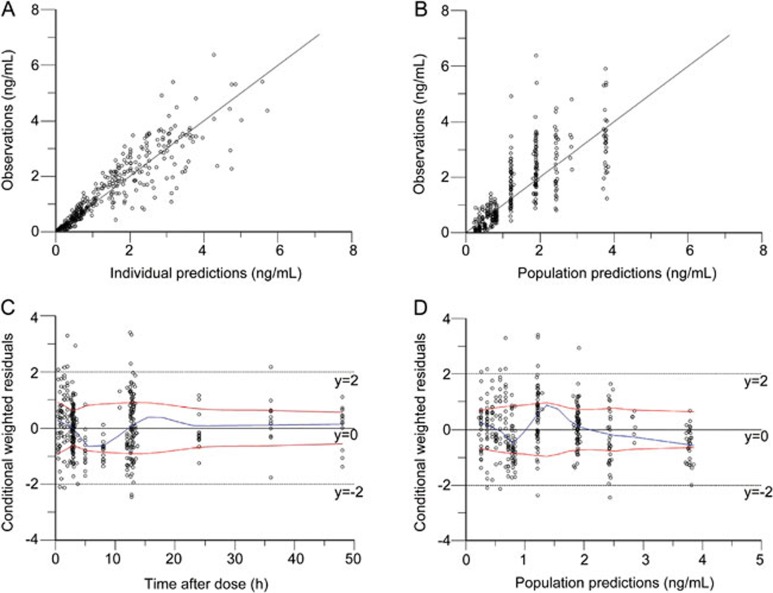
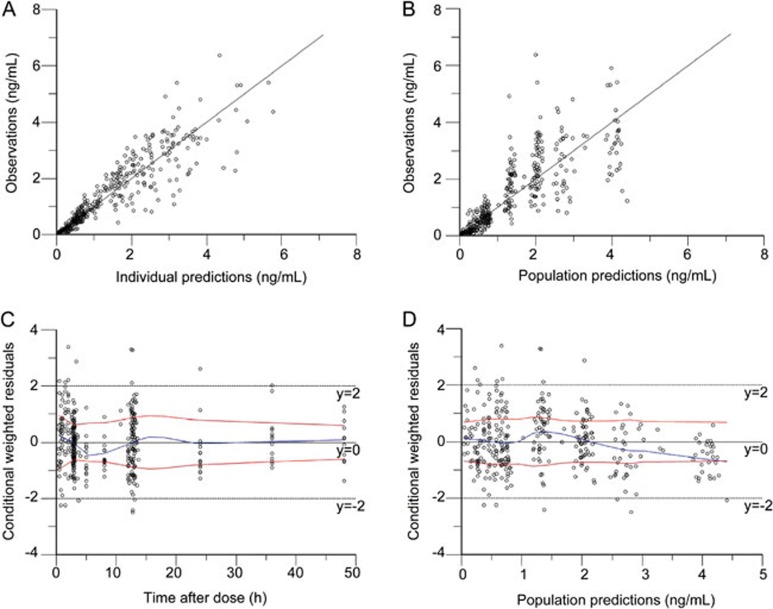
Several residual error models were tested, and the proportional residual error model (normal distribution) was found to best describe the data. Diagnostic plots for the base model showed a reasonable fit with no apparent trends of residuals over time or model predictions. Following the identification of the base model, the effects of covariates on the principal PK parameters (CL, Ka, and V) were investigated. Continuous and categorical covariates included age, gender, body weight, height, Scr, CLcr and treatment (co-administration of huperzine A). Table 1 lists the summary statistics of the subjects' covariates during the PPK model development. Goodness-of-fit (GOF) plots for huperzine A for the base mode and final model are shown in Figures 1 and 2, respectively. The information criteria for the selection of the final huperzine A model are listed in Table 3. The final estimates of the parameters are shown in Table 4. The fixed effects and random variance parameter estimates were estimated with good precision (NLME derived % relative standard error [%RSE]). The following is the final PPK model for huperzine A: CL(L/h)=2.4649*(age/86)(−3.3856)*exp(ηnCl), V(L)=104.216*exp(ηnV), Ka(h−1)=0.6750*exp(ηnKa).
Figure 1.
Goodness-of-fit plots of huperzine A for the base model. Observed plasma concentrations of huperzine A versus individual predictions (A) and versus population predictions (B), conditional weighted residuals versus time (C) and versus population predictions (D).
Figure 2.
Goodness-of-fit plots of huperzine A for the final model. Observed plasma concentrations of huperzine A versus individual predictions (A) and versus population predictions (B), conditional weighted residuals versus time (C) and versus population predictions (D).
Table 3. Information criteria for the selection of the final model for huperzine A. Ka, absorption rate constant (1/h); Cl/f, apparent clearance (L/h); V/f, apparent volume of distribution (L).
| Model number | Model short description | Statistic criteriona |
|
|---|---|---|---|
| −2LL | AIC | ||
| 1 | 1-compartment, Covariate: None | 380.27 | 394.27 |
| 2 | 2-compartment, Covariate: None | 377.48 | 399.48 |
| 3 | 1-compartment, Covariate: gender as covariate on Ka, V/f, CL/f | 374.05 | 394.05 |
| 4 | 1-compartment, Covariate: Body weight as covariate on Ka | 377.97 | 393.97 |
| 5 | 1-compartment, Covariate: Body weight as covariate on V/f | 375.29 | 391.28 |
| 6 | 1-compartment, Covariate: Body weight as covariate on CL/f | 378.27 | 394.27 |
| 7 | 1-compartment, Covariate: Height as covariate on V/f, CL/f | 376.51 | 394.51 |
| 8 | 1-compartment, Covariate: Height as covariate on Ka | 376.43 | 392.43 |
| 9 | 1-compartment, Covariate: age as covariate on Ka, V/f, CL/f | 346.54 | 366.54 |
| 10 | 1-compartment, Covariate: age as covariate on CL/f | 349.34 | 365.34 |
| 11 | 1-compartment, Covariate: age as covariate on CL/f and Cr as covariate on Ka, V/f, CL/f | 346.64 | 368.64 |
| 12b | 1-compartment, Covariate: age as covariate on CL/f and Ccr as covariate on Ka, V/f, CL/f | 341.35 | 363.35 |
| 13 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related | 339.12 | 357.12 |
| 14 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and isosorbide mononitrate as covariate on CL/f | 334.44 | 354.44 |
| 15 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and isosorbide mononitrate as covariate on Ka | 335.01 | 355.01 |
| 16 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and isosorbide mononitrate as covariate on V/f | 338.02 | 358.02 |
| 17 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and finateride, clopidogrel as covariate on Ka, V/f, CL/f | 333.59 | 363.59 |
| 18 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and mosapride as covariate on Ka, V/f, CL/f | 338.44 | 362.44 |
| 19 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and metoprolol as covariate on CL/f | 336.25 | 356.25 |
| 20 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and metoprolol as covariate on Ka, V/f | 334.96 | 356.96 |
| 21 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and valsartan, aspirin as covariate on CL/f, Ka, V/f | 332.42 | 362.42 |
| 22 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and rabeprazole as covariate on CL/f | 335.03 | 355.03 |
| 23 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and rabeprazole as covariate on Ka, V/f | 333.84 | 355.84 |
| 24 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and trimetazidine as covariate on CL/f, Ka, V/f | 336.41 | 360.41 |
| 25 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and atorvastatin calcium as covariate on CL/f, Ka, V/f | 336.13 | 360.13 |
| 26 | 1-compartment, Covariate: age as covariate on CL/f, CL and V related, and rosuvastatin calcium as covariate on CL/f, Ka, V/f | 338.62 | 362.62 |
a The terms -2LL and AIC refer to -2 Log-Likelihood function and Akaike information criterion, respectively.
b The formula of endogenous creatinine clearance(Ccr) of male is Ccr=[(140-age)*weight (kg)]/[0.818*Scr(μmol/L)]. Endogenous creatinine clearance is related to age and weight. When age had been considered as a covariate, the effect of Ccr on population pharmacokinetic effect was the same as the body weight.
Table 4. Parameter estimates of the final covariate model for huperzine Aa.
| Parameters (Units) | Description | Final model estimate | %RSE | Bootstrap median (95% CI) |
|---|---|---|---|---|
| Primary parameters | ||||
| CL/f (L/h) | Population mean apparent clearance | 2.4649 | 17.45 | 2.4621 (1.4821, 3.2727) |
| V/f (L) | Population mean apparent volume of distribution | 104.216 | 7.18 | 103.768 (88.552, 120.271) |
| Ka (1/h) | Population mean absorption rate constant | 0.6750 | 19.57 | 0.7142 (0.4610, 1.1088) |
| θage | Exponent for effect of age on CL | −3.3856 | 28.39 | −3.5132 (−6.5322, −1.8559) |
| R (CL∼V) | Correlation coefficient of CL and V | 0.8831 | 0.9164 | |
| Random effect (Between subject variability, BSV%) | ||||
| ΩCl (%) | BSV% of clearance | 40.75 | 60.90 | 38.98 (22.55, 54.97) |
| ΩV (%) | BSV% of apparent volume of distribution | 26.55 | 59.62 | 26.20 (16.90, 35.68) |
| ΩKa (%) | BSV% of absorption rate constant | 61.48 | 66.96 | 57.26 (5.46, 100.35) |
| Residual variability | ||||
| σ (%) | Proportional error of RV | 0.3359 | 4.79 | 0.3347 (.2956, 0.3727) |
a The final PPK model of huperzine A was: CL (L/h)=2.4649*(age/86)(−3.3856)*exp(ηnCl), V (L)=104.216*exp(ηnV), Ka (h−1)=0.6750*exp(ηnKa)
Model evaluation
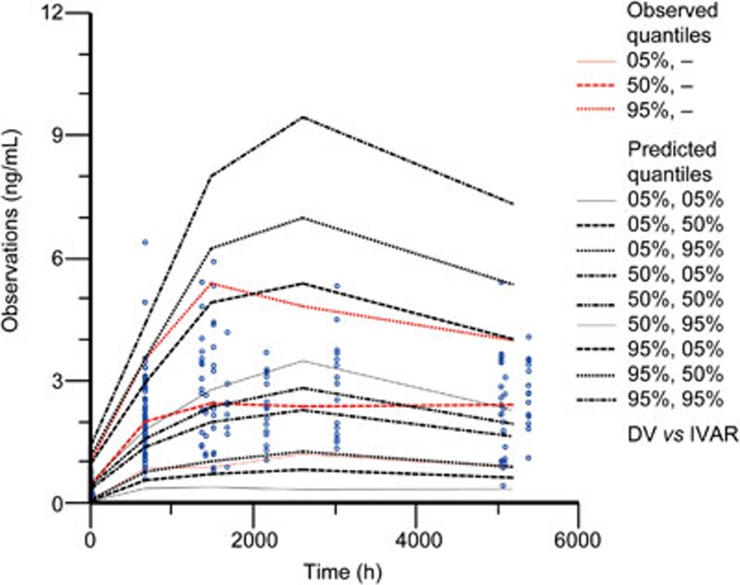
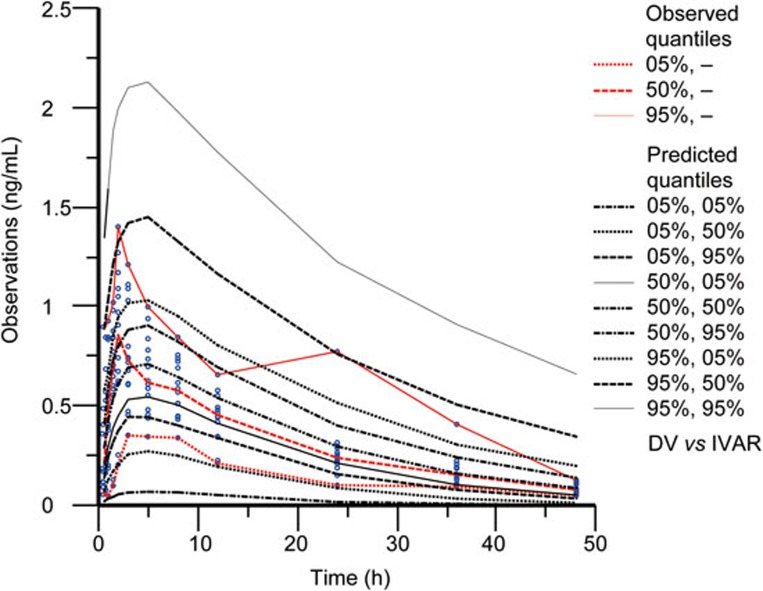
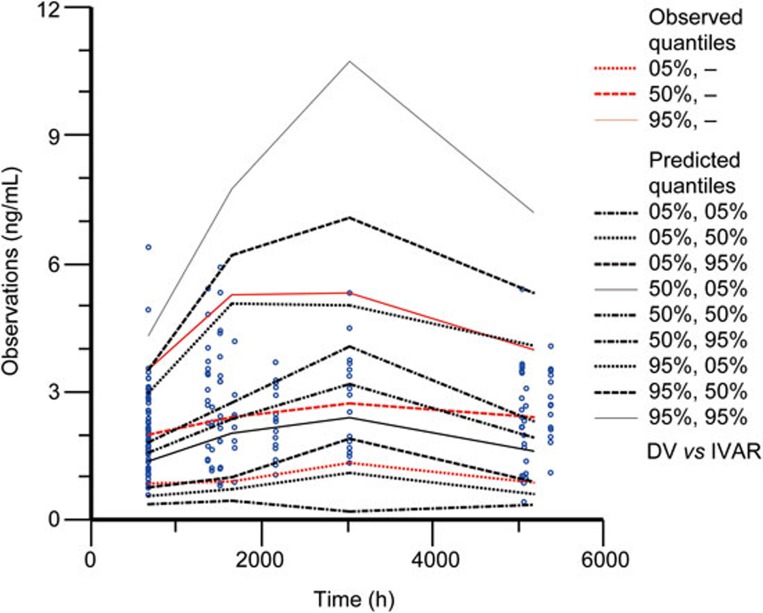
In total, 100% of the 1000 bootstrap runs converged successfully. The parameter estimates and 95% confidence interval for the parameters were calculated from the converged runs and are presented in Table 4. The parameter distributions were generally symmetrical. All the estimates obtained from the final model were comparable to the bootstrap estimates and were contained within the 95% bootstrap confidence intervals. Figure 3 shows the results of the visual predictive checks for huperzine A. Overall, the final model adequately described the observed concentrations. Approximately 0.59% of the 341 huperzine A observations were not contained within the 90% confidence interval. The visual graphic checks in the healthy elderly subjects and patients in Figures 4 and 5 evaluated the robustness of the model built, respectively. All of the huperzine A observations in healthy elderly subjects and approximately 98.76% of the observations in AD patients were contained within the 90% confidence interval.
Figure 3.
Visual predictive check of the final model for huperzine A observations.
Figure 4.
Visual predictive check of the final model in healthy elderly subjects for huperzine A observations.
Figure 5.
Visual predictive check of the final model in elderly patients with AD for huperzine A observations.
Discussion
Although some pharmacokinetic studies concerning huperzine A in young healthy subjects have been reported8,9,10,11, there are still no reports on the pharmacokinetic study of huperzine A in elderly subjects. Our preliminary experiments with huperzine A in elderly people showed that drug exposure AUC increased by 75% compared with that in young healthy individuals8,9. One factor may be the degraded physiological functions in elderly people compared with young people. Furthermore, AD itself may affect the pharmacokinetic profiles of huperzine A. Therefore, data for huperzine A in young people cannot be used to guide AD patients. The results from the PPK model of huperzine A indicated that the older subjects had lower clearance; therefore, the drug exposure of huperzine A was higher in the elderly people than in the young people. The causes are the decline in kidney function and the reduction of endogenous creatinine clearance in elderly people and possibly other, as-yet-unknown reasons.
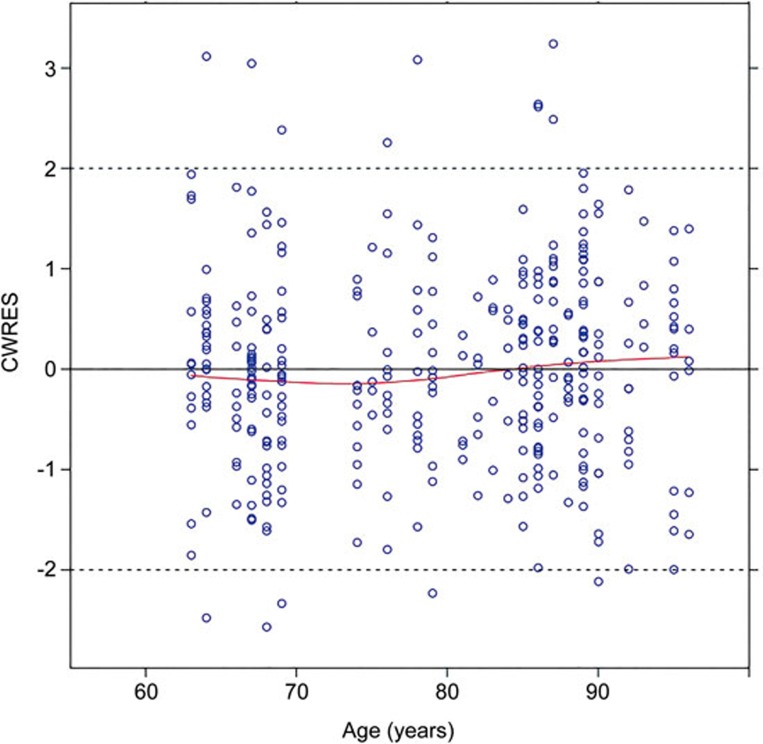
The development of a huperzine A PPK model was divided into two steps. In the first step, we used the data from a pharmacokinetic study after administration of a single dose of huperzine A to elderly subjects without AD to establish the base PPK model. In the second step, we merged the data from elderly subjects with and without AD to establish the final model. In the first step, the typical values for CL/f and V/f were 6.078 L/h and 120.436 L, respectively, which were similar to the 5.968 L/h and 123.374 L calculated by the non-compartmental analysis method. The deviations were both less than 2.50%, which showed that the population base model was reliable. In the second step, the typical values for CL/f and V/f were 2.4649 L/h and 104.216 L, respectively. The apparent difference in the CL/f between the first and second steps was that the median age of AD patients enrolled was 86 years, which is much higher than the median age of elderly subjects without AD, which was 68. If we assign the age of 68 years into the PPK model equation, CL/f would be 5.459 L/h, which deviates by 9.6% compared with the typical CL/f value calculated in the first step and by 8.0% compared with the CL/f calculated by the non-compartment analysis. The results showed that it was feasible to merge the data from the two studies. Additionally, the prediction error of the concentration for the age groups of 63–70, 71–80, 81–90, and 91–96 years were low, suggesting that conditional weighted residuals did not have a trend with age (Figure 6).
Figure 6.
Conditional weighted residuals vs age.
During the process of selecting covariates, when age had been selected as a covariate for CL/f, CLcr was also chosen as a covariate, and the minus twice the log-likelihood (Δ-2LL) of the model fell by 7.99, which was more than the criteria (P=0.01). However, the formula for endogenous creatinine clearance (Ccr) in males is Ccr=[(140-age)*weight (kg)]/[0.818*Scr(μmol/L)]. Ccr is related to age, weight and Scr. When age was considered a covariate, the effect of Ccr on PPK was the same as body weight and Scr. Therefore, CLcr was not chosen as a covariate when the final PPK model was established.
Essentially, the sample size, the size of the covariate effect, the distribution of the covariate across the study population, the complexity of the structural model (both PK and covariate), and other factors will influence findings of covariate screening. Although Table 3 showed neither significant impact on the clearance (CL/f) nor apparent volume variation for the distribution (V/f) of huperzine A after co-administration of the drugs, the sample size of the study was insufficient. However, the old AD cases are difficult to collect. The study yielded only partial information for subsequent research. It was unknown whether the effect of age on CL/f contributed to the degradation of body function or to disease.
In conclusion, a PPK model for huperzine A in Chinese elderly subjects was established. This population analysis of huperzine A indicated that age is the most important factor in huperzine A clearance. PPK parameters for huperzine A could be predicted accurately with this model. This study provides information for future research.
Author contribution
Hong-rong XU designed the study and drafted of the manuscript; Lei SHENG discussed the study and drafted the manuscript; Yi QU, Gang-yi LIU, Wei-liang WANG, Yi-jun WANG, Hong-yi WANG, Meng-qi ZHANG, Chuan LU, Yun LIU, Jingyin JIA, Chao-ying HU, and Chen YU performed the study; Jing YAN participated in data analysis; and Xue-ning LI revised this manuscript.
Acknowledgments
We gratefully thank Jun-jie DING at Children's Hospital of Fudan University for technical assistance in PPK model building.
References
- Lunardi P, Nardin P, Guerra MC, Abib R, Leite MC, Goncalves CA. Huperzine A, but not tacrine, stimulates S100B secretion in astrocyte cultures. Life Sci 2013; 92: 701–7. [DOI] [PubMed] [Google Scholar]
- Hu NH, Shi H, Chen GS. Clinical effect of huperzine A microemulsion cataplasm to Alzheimer patients by Governor vessel acu-points. Clin J Mod Appl Pharm 2014; 31: 581–3. [Google Scholar]
- Shi CC, Yu F. Meta-analysis of efficacy and safety of huperzine A for treatment of Alzheimer's disease. Chin J New Drugs Clin Rem 2012; 31: 737–42. [Google Scholar]
- Clinical study of huperzine A on patients with mild and moderate Alzheimer disease. Practical Pharmacy and Clinical Remedies 2013; 16: 2. [Google Scholar]
- Zhang Z, Wang X, Chen Q, Shu L, Wang J, Shan G. Clinical efficacy and safety of huperzine Alpha in treatment of mild to moderate Alzheimer disease, a placebo-controlled, double-blind, randomized trial. Zhonghua Yi Xue Za Zhi 2002; 82: 941–4. [PubMed] [Google Scholar]
- Zhang ML, Yao JJ, Bi P, Ni SQ. Evaluation of clinical effect and safety of huperzine A in treating 52 Alzheimer's disease. Chin J New Drugs Clin Rem 2006; 25: 693–5. [Google Scholar]
- Rafii MS, Walsh S, Little JT, Behan K, Reynolds B, Ward C, et al. A phase II trial of huperzine A in mild to moderate Alzheimer disease. Neurology 2011; 76: 1389–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li YX, Zhang RQ, Li CR, Jiang XH. Pharmacokinetics of huperzine A following oral administration to human volunteers. Eur J Drug Metab Pharmacokinet 2007; 32: 183–7. [DOI] [PubMed] [Google Scholar]
- Qian BC, Wang M, Zhou ZF, Chen K, Zhou RR, Chen GS. Pharmacokinetics of tablet huperzine A in six volunteers. Acta Pharmacol Sin 1995; 16: 396–8. [PubMed] [Google Scholar]
- Li W, Li J, Hu Q. Determination of huperzine A in human plasma by liquid chromatography-electrospray tandem mass spectrometry: application to a bioequivalence study on Chinese volunteers. Biomed Chromatogr 2008; 22: 354–60. [DOI] [PubMed] [Google Scholar]
- Liu GY, Wang W, MQ Z. Quantitation of huperzine A in human plasma by LC-MS/MS for elderly population. Clin J New Drugs Clin Remedies 2012; 31: 728–31. [Google Scholar]