Abstract
Aim:
Combined therapy of EGFR TKI and VEGFR TKI may produce a greater therapeutic benefit and overcome EGFR TKI-induced resistance. However, a previous study shows that a combination of EGFR TKI erlotinib (ER) with VEGFR TKI sunitinib (SU) did not improve the overall survival in patients with non-small-cell lung cancer (NSCLC). In this study we examined the anticancer effect of ER, SU and their combination in the treatment of A549 human NSCLC xenograft mice, and conducted PK/PD modeling and simulations to optimize the dose regimen.
Methods:
ER (20, 50 mg·kg−1·d−1) or SU (5, 10, 20 mg·kg−1·d−1) alone, or their combination were administered to BALB/c nude mice bearing A549 tumors for 22 days. The tumor size and body weight were recorded daily. The experimental data were used to develop PK/PD models describing the quantitative relationship between the plasma concentrations and tumor suppression in different dose regimens. The models were further evaluated and validated, and used to predict the efficacy of different combination regimens and to select the optimal regimen.
Results:
The in vivo anticancer efficacy of the combination groups was much stronger than that of either drug administered alone. A PK/PD model was developed with a combination index (φ) of 4.4, revealing a strong synergistic effect between ER and SU. The model simulation predicted the tumor growth in different dosage regimens, and showed that the dose of SU played a decisive role in the combination treatment, and suggested that a lower dose of ER (≤5 mg·kg−1·d−1) and adjusting the dose of SU might yield a better dosage regimen for clinical research.
Conclusion:
The experimental data and modeling confirm synergistic anticancer effect of ER and SU in the treatment of A549 xenograft mice. The optimal dosage regimen determined by the PK/PD modeling and simulation can be used in future preclinical study and provide a reference for clinical application.
Keywords: erlotinib, sunitinib, EGFR, VEGFR, synergistic effect, non-small-cell lung cancer, PK/PD model, simulation
Introduction
Lung cancer is the leading cause of cancer-associated death worldwide, and non-small-cell lung cancer (NSCLC) accounts for approximately 85% of all cases1,2. Erlotinib (ER) is an orally active, small-molecule tyrosine kinase inhibitor (TKI) and was first approved by the Food and Drug Administration in 2004 for the treatment of locally advanced and metastatic NSCLC after the failure of at least one prior chemotherapy regimen; erlotinib was only approved for EGFR mutations in NSCLC patients1. Erlotinib is able to reversibly bind to the intracellular tyrosine kinase domain of epidermal growth factor receptor (EGFR) and inhibits EGFR autophosphorylation, which then inhibits cell proliferation. Several clinical trials have proven that erlotinib could prolong survival with a promising objective response rate in patients with non-small-cell lung cancer after the failure of first-line or second-line chemotherapy2,3. Sunitinib is a promising multi-targeted receptor tyrosine kinase (RTK) inhibitor with activity against the vascular endothelial growth factor receptors VEGFR-1 and -2, the platelet-derived growth factor receptors PDGFR-α and -β, and the stem-cell factor receptor KIT in many types of cancer4,5. Among these RTKs, VEGFR is associated with signaling pathways that regulate the process of angiogenesis and the growth of tumor endothelial cells6.
A known challenge to the use of EGFR TKIs in clinics is their resistance, including primary resistance and acquired resistance7. Because the EGFR and VEGFR pathways play a pivotal role in tumor progression and there are many complex functional relationships and crosstalk between these two pathways8, it is reasonable to consider simultaneously targeting EGFR and VEGFR to achieve a greater therapeutic benefit and to overcome EGFR TKI-induced resistance. Several preclinical studies have demonstrated promising results for this combination therapeutic strategy. Vandetanib, a multitargeted TKI that inhibits the EGFR and VEGFR pathways, shows significant tumor growth inhibition activity and is effective in overcoming EGFR inhibitor resistance in xenograft models9. In addition, the combination of vargatef (VEGFR TKI) and afatinib (EGFR TKI) shows synergistic activity in colorectal cancer models better than the combination of bevacizumab (VEGF monoclonal antibody) and cetuximab (EGFR monoclonal antibody), which provided a rationale for the use of the two TKIs together10. In a global, randomized, phase III trial in patients with NSCLC that were previously treated with chemotherapy, cotreatment with erlotinib and sunitinib did not improve the overall survival, although there were increased rates of progression-free survival (PFS) and objective response rate (ORR) compared with erlotinib alone11. Based on the inconsistent results between the preclinical and clinical experiments, our aim was to understand the reason for the unsatisfactory outcome of the above clinical trial using a pharmacokinetic/pharmacodynamics (PK/PD) modeling approach and further provide more reasonable dose regimens based on our model simulation, which might provide a reference for the design of clinical trials.
With the increasing risks and costs of drug development, model-based drug development has been widely used. Using mathematical and statistical methods, PK/PD modeling is able to describe the quantitative relationship between the drug concentration and the drug effect. Based on the estimated parameters from a PK/PD model, different types of dose regimens and experimental designs could be tested and optimized by modeling and simulations without conducting trials, which saves time and cost and also helps with making decisions concerning the details of further trials12. Some preclinical and clinical studies concerning the trial design optimization of the combination therapy for cancer treatments have applied PK/PD modeling, which provides new thinking regarding predicting outcomes, making decisions and optimizing dosage regimens13,14,15. For example, Wang et al15 found that a change in tumor size at week 8 is meaningful for the early prediction of the clinical outcome of NSCLC, and a modeling simulation in the work from Li et al14 indicates that an interval schedule of erlotinib and gemcitabine could achieve synergistic anti-tumor effects and is superior to simultaneous treatment.
The purpose of our study is to investigate the anti-tumor efficacy of the cotreatment of erlotinib and sunitinib in vitro and in an A549 xenograft model and to further develop and test a PK/PD model of erlotinib, sunitinib and combination therapy to describe the relationship between the plasma concentration and tumor size and to quantitatively investigate the PD interaction of ER and SU. Based on the PK/PD model and the estimated parameters, a model simulation was performed to optimize the dose regimens and to further provide reasonable suggestions for the clinical application of EGFR TKIs.
Materials and methods
Drugs and reagents
ER and SU were purchased from Melone Pharmaceutical Co, Ltd (Dalian, China). SU12662 was obtained from MCE (Neodesha, KS, USA). Pazopanib (purity>99%) was purchased from Melone Pharmaceutical Co, Ltd (Dalian, China) and used as an internal standard (IS) in the pharmacokinetics study. RPMI-1640 medium and fetal bovine serum were purchased from Macgene Biotech Co, Ltd (Beijing, China) and Gibco (Grand Island, USA), respectively.
Cell culture
Primary resistant A549 human non-small cell lung cancer (NSCLC) cells were purchased from the Chinese Academy of Medical Sciences Cancer Hospital (Beijing, China) and were grown in RPMI-1640 medium containing 10% fetal bovine serum. The cells were maintained at 37 °C under 5% CO2 and 95% atmosphere.
Animals
Female BALB/c nude mice (16–18 g) were purchased from the Animal Service of Health Science Center, Peking University. All the animals were kept in individual ventilated cages (IVC) at a humidity of 50%–60% and 25–28 °C and were controlled under 12 h light/dark cycles. All the animal studies were approved by the Institutional Animal Care and Use Committee of Peking University and were conducted under the Principles of Laboratory Animal Care (NIH publication No 85–23, revised 1996).
Pharmacokinetic study
A LC-MS/MS method to determine the plasma concentration of ER in BALB/c nude mice was developed in our previous work16. A two-compartment model was used to describe the pharmacokinetic behavior of ER in BALB/c nude mice after the oral administration of 12.5 mg/kg ER. The LC-MS/MS method to measure the plasma concentration of SU and its active metabolite SU12662 simultaneously in BALB/c nude mice was established in another previous study by our group17. SU was administered by gavage at 20 mg/kg to BALB/c nude mice, and two- and one-compartment models of SU and SU12662 were included in the pharmacokinetic model of SU. The pharmacokinetic parameters of ER and SU were extracted from the above PK studies.
Pharmacodynamic study in vivo
A total of 5×106 A549 cells, which are primarily resistant to ER9, were suspended in 200 μL RPMI-1640 with no fetal bovine serum and inoculated subcutaneously in the right flank of the mice. An electronic Vernier caliper was used to measure the length and width of the tumors, and the tumor volumes (TV) were calculated according to the following formula: TV (cm3)=length×width2/218. When the tumor size reached 0.7–0.9 cm3, the animals were randomly divided into 9 groups, and each group contained 5 nude mice. These 9 groups of nude mice received different treatments according to the following groups: a vehicle control group, ER monotherapy groups (20 or 50 mg/kg), SU monotherapy groups (5, 10, and 20 mg/kg), and ER and SU combination groups (ER 10 mg/kg and SU 5 mg/kg, ER 10 mg/kg and SU 10 mg/kg, ER 20 mg/kg and SU 20 mg/kg). ER was dissolved in a 4% SBE-β-CD Captisol solution, and SU was prepared with 1,2-propanediol. The 4% SBE-β-CD Captisol solution, 1,2-propanediol, and the different doses of ER and SU were orally administered once daily according to the different groups for 22 d, and the nude mice of all the groups were euthanized afterwards to collect tumor samples. The tumor size and body weight were recorded every day during the study.
PK/PD models
The tumor natural growth model used in this study was suggested by Simeoni et al19. The model describes the two different phases of the vehicle control group: an initial exponential growth followed by a linear growth. The assumed tumor growth switches from exponential to linear growth at a threshold tumor mass (wth). The differential equations used (Eqs 1,2,3) are as follows:
where λ0 and λ1 represent the rates of exponential and linear growth, respectively, and w0 represents the tumor size at time 0 is 0. wth could be expressed using λ0 and λ1 as follows:
For a more convenient computational method, Eqs 1,2,3 could be expressed in a single differentiable function as Eq 5:
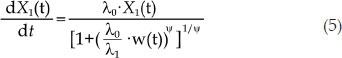 |
where ψ is an adjustment factor. When ψ is large, Eq 5 is a good approximation for Eqs 1,2,3. In this transformation, when the tumor size is smaller than wth, {(λ0/λ1)·w(t)}ψ could be ignored, and Eq 5 represents the exponential growth phase of tumor growth. If the tumor size is larger than wth, 1 is negligible, and Eq 5 describes the linear growth phase. In this study, we fixed ψ to 20 according to a previously published study19.
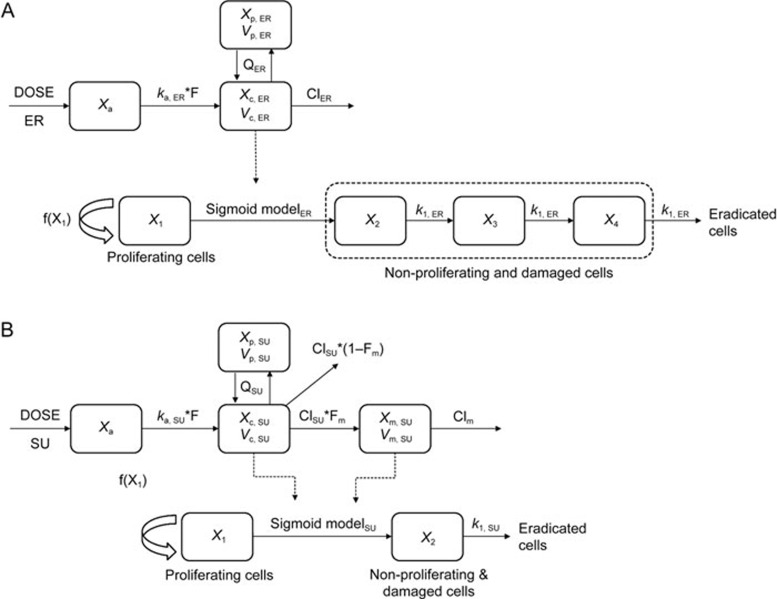
The drug effect on tumor growth could be established based on the tumor natural growth model. The PK/PD model structures of ER and SU monotherapy, which were suggested by Simeoni et al, are represented in Figure 119. The tumor natural growth model assumes that all cells are proliferating (X1) in the control group. The single agent model assumes that some cells became damaged by the anticancer drug and transfer to the nonproliferation state (X2, X3, X4) and further became dead cells through a mortality chain. The hysteresis phenomenon between the anticancer drug concentration and the inhibition of tumor growth could be described by this model. Based on the attempts of one to three transit compartments in both ER and SU monotherapy, three transit compartments in the ER PK/PD model and one transit compartment in the SU PK/PD model were applied in this study.
Figure 1.
The PK/PD model structure of erlotinib (A) and sunitinib (B).
The differential equations of the PK/PD model of ER are as follows:
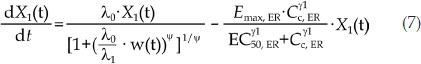 |
where Cc, ER is the ER concentration of the central compartment, Emax, ER is the maximal potency factor of ER, EC50, ER is the plasma concentration of ER when the potency reaches 50% of Emax, ER, γ1 is the shape factor, and k1, ER is the transit-rate constant in the nonproliferation compartments. λ0 and λ1 were fixed according to the results of the tumor natural growth model parameters.
Similar to ER, the differential equations of the PK/PD model of SU are as follows:
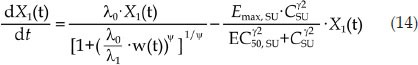 |
where CSU is the effective plasma concentration of SU, which is the total plasma concentration of SU and its active metabolite SU12662 because both compounds have similar potency and molecular weight. Emax, SU is the maximal potency factor of SU, EC50, SU is the plasma concentration of SU when the potency reaches 50% of Emax, SU, γ2 is the shape factor, and k1, SU is the transit-rate constant in the nonproliferation compartments. λ0 and λ1 were also fixed according to the tumor natural growth model established above.
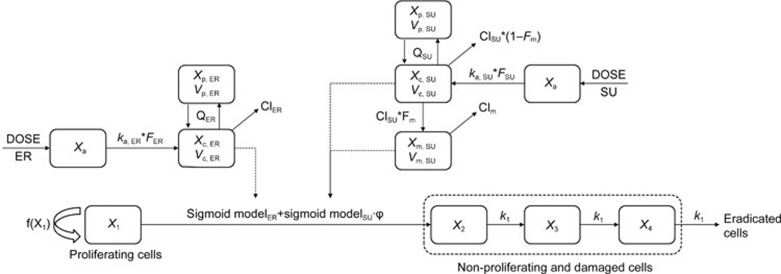
In the combination groups, the combination index (φ) was introduced into the PK/PD model to explain the effect of the interaction of the two drugs on the drug potency20, and the model structure is shown in Figure 2. If there was no interaction between the two drugs, φ would equal 1, which indicates that the combinatorial effect of the two drugs is additive. If φ is larger or smaller than 1, the total influence of the combination therapy on tumor growth was greater or less than either one drug alone, which indicates that there is a synergistic effect or an antagonistic effect between the two drugs. All the drug potency parameters were fixed according to the monotherapy PK/PD model, including the parameters Emax, ER, EC50, ER, Emax, SU, EC50, SU and the shape factors of ER and SU. The differential equations of the PK/PD model of the combination group are as follows:
Figure 2.
The PK/PD model structure of the combination model.
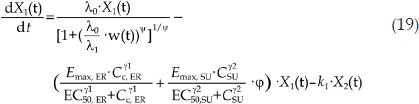 |
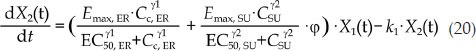 |
where k1 denotes the transit rate in the combination model. λ0 and λ1 were also fixed according to the tumor natural growth model, and the other parameters were as defined above.
Modeling construction, validation and simulation
All modeling and simulations were conducted using NONMEM 7.1.2 (ICON Development Solutions, Ellicott City, MD, USA) and Perl-speaks-NONMEM (PsN, Version 3.5.3) with the first order conditional estimation (FOCE) method. An exponential model was used to characterize the inter-individual variability, and the relative standard errors (RSE) were provided to evaluate the precision and reliability of the parameters. Proportional, additive or the mixed error models were chosen according to the situation. The model selection and evaluation depended mainly on the comprehensive analysis of the reasonability of the parameters, the change in the objective function value (OFV), and a visual inspection of the visual predictive check (VPC) plots and the diagnostic plots. The low dose data of both SU monotherapy (5 mg/kg SU) and the combination therapy (5 mg/kg SU and 10 mg/kg ER) were used for the external validation of the PK/PD models, and the data from the vehicle control group and other treatment groups were used for model development. The VPC was conducted using 1000 simulations, and the 5th, 50th, and 95th percentiles of the simulations were compared with the observed value. The simulations of different dose regimens were performed by fixing all parameters obtained from the PK/PD models developed above. In the simulation of monotherapy treatments, 5, 20, 50, 80, and 100 mg/kg of ER and 10, 15, 20, 40, and 60 mg/kg of SU were considered. ER at 5 mg/kg with different doses of SU (10, 15, and 20 mg/kg) was considered, with the two compounds being given simultaneously. ER and SU were administered every day in all schedules.
Statistical analysis
The PD results are presented as the mean±SD, and the statistical analysis was completed using GraphPad Prism 5.0 software (GraphPad Software, Inc, USA). A one-way analysis of variance (ANOVA) was used to determine the significance among groups, followed by post hoc tests with Bonferroni's correction. A difference at a level of P<0.05 was considered statistically significant.
Results
Tumor growth inhibition of ER, SU and combination therapy
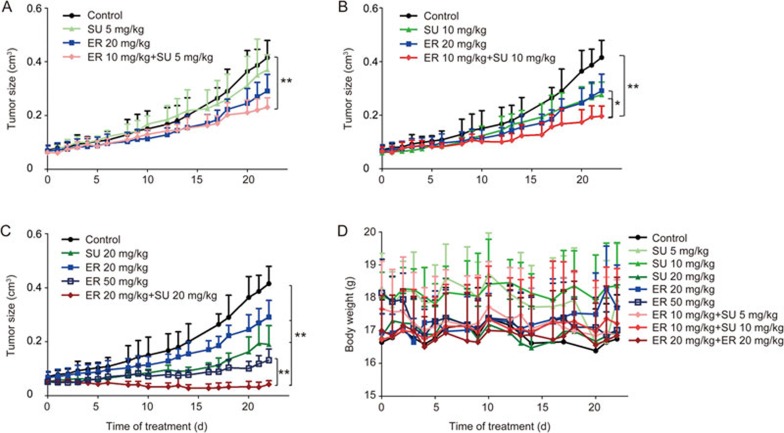
The anti-tumor effect and a photo of the excised tumor of different dose regimens of ER and SU given separately or simultaneously, as well as the body weight, are shown in Figure 3. The combination of ER and SU was associated with a possible synergistic effect compared with the control and monotherapy groups at all 3 dose levels. In addition, the inhibitory effect in the combination group was even stronger than that of a double dose of ER alone. The mouse weights did not show notable reduction in any treatment groups, suggesting little systemic toxicity. The PD data profiles of the different dose regimens, except that of 5 mg/kg SU alone and that of 5 mg/kg SU and 10 mg/kg ER, were applied to develop the PK/PD models in the next steps.
Figure 3.
The anti-tumor efficacy after 3 different doses of the single or combination oral therapy of ER and SU in an A549 xenograft model in female BALB/c nude mice. (A–C) represent the tumor growth curves after 22 d of treatment at a low dose, middle dose and high dose for the combination therapy (mean±SD, n=5). *P<0.05, **P<0.01. (D) represents the body weight change in BALB/c nude mice bearing an A549 xenograft after different treatment regimens (mean±SD, n=5).
PK/PD model
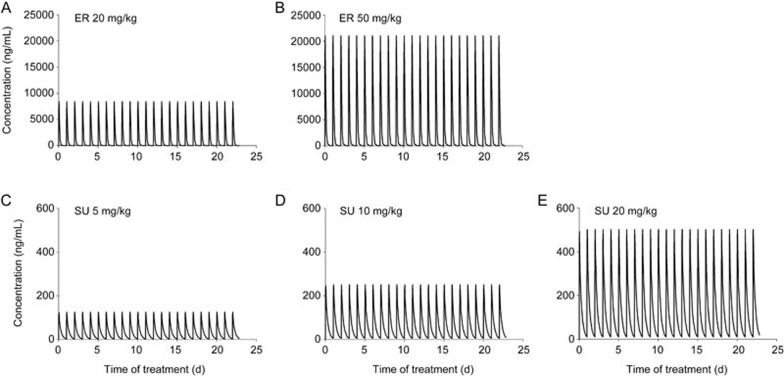
The PK models were developed based on the administration of the two compounds given alone. The PK models of SU, its metabolite SU12662, and ER were developed by previous work by our group and are well verified16,17. The xenograft model used in this report was identical to those for both PK studies, and the doses of both drugs in this PD study are within the range of their linear PK. This simulation method has been widely used to obtain plasma concentrations of different doses when the PK parameters are well known. The PK characteristics of ER and SU were both linear under our treatment conditions. Therefore, we used the PK parameters of both drugs to simulate their plasma concentration-time profiles. The PK parameters extracted from our previous work on ER and SU are summarized in Table 1, and the concentration-time curves simulated from the PK model according to the PD study are shown in Figure 4.
Table 1. Pharmacokinetic parameters obtained from literatures.
| ER | SU | ||
|---|---|---|---|
| CLER/F (mL·kg−1·d−1) | 19 000 | CLSU/F (mL·kg−1·d−1) | 254 000 |
| Vc, ER/F (mL/kg) | 885 | Vc, SU/F (mL/kg) | 323 00 |
| QER/F (mL·kg−1·d−1) | 763 | QSU/F (mL·kg−1·d−1) | 708 000 |
| Vp, ER/F (mL/kg) | 168 | Vp, SU/F (mL/kg) | 284 00 |
| ka, ER (d−1) | 22.6 | ka, SU (d−1) | 50.9 |
| – | – | Fm, SU | 0.583 |
| – | – | Vm, SU/F (mL/kg) | 1 710 |
| – | – | CLm, SU/F (mL·kg−1·d−1) | 247 000 |
Figure 4.
The simulation results of the drug plasma concentration according to the PD experiment: ER at 20 mg/kg (A) and 50 mg/kg (B); SU at 5 mg/kg (C), 10 mg/kg (D), and 20 mg/kg (E).
We developed a PD model for the vehicle control group and PK/PD models for the treated groups. First, the tumor natural growth model was established, and the parameters of the control group are shown in Table 2. Based on the hypothesis that an anticancer agent only influences the rate of the transition from the proliferating compartment to the non-proliferating compartment and has no effect on proliferating cells, we fixed λ0 and λ1 in the drug-perturbed group to the same value of the unperturbed group. The parameters of the groups treated with different dose regimes are summarized in Table 2. Sigmoid models were used to describe the potency of different doses of both drugs, and the parameters from a single agent were fixed in the combination groups. The EC50, ER was larger than the EC50, SU, implying that SU was more potent than ER in the A549 xenograft model. By comparing the average transit time (n/k1, which was 3/1.35, 1/8.3, and 3/4.26 d for the ER, SU and combination treatments, respectively. n is the number of transit compartments)19, we found that the hysteresis phenomenon is stronger in the ER group than the SU group, and the combination group was between the two monotherapies. The combination index φ was introduced in the model to describe the interaction of the two drugs, and the typical value of φ was 4.4, suggesting that a strong synergistic effect existed between ER and SU. The RSE of all the model parameters were small, indicating reliable and precise parameters.
Table 2. Pharmacodynamic parameters estimated from PK/PD models.
| Parameters | Vehicle (RSE%) (CV%) | ER (RSE%) (CV%) | SU (RSE%) (CV%) | Combination (RSE%) (CV%) |
|---|---|---|---|---|
| w0 (cm3) | 0.0662 (12) (28.27) | 0.054 (5) (31.40) | 0.0549 (1) (15.78) | 0.0557(7) (24.68) |
| λ0 (d−1) | 0.0799 (7) (16.09) | 0.0799 FIX | 0.0799 FIX | 0.0799 FIX |
| λ1 (d−1·cm3) | 0.0354 (2) (0 FIX) | 0.0354 FIX | 0.0354 FIX | 0.0354 FIX |
| ψ | 20 FIX | 20 FIX | 20 FIX | 20 FIX |
| EC50, ER (μg/mL) | – | 8.74 (9) (0 FIX) | – | 8.74 FIX |
| Emax, ER (d−1) | – | 0.474 (4) (115.8) | – | 0.474 FIX |
| γ1 | – (7) (0 FIX) | 7.19 | – | 7.19 FIX |
| k1, ER (d−1) | – | 1.35 (5) (140.4) | – | 1.35 FIX |
| EC50, SU (μg/mL) | – | – (14) (0 FIX) | 0.355 | 0.355 FIX |
| Emax, SU (d−1) | – | – (20) (0 FIX) | 0.275 | 0.275 FIX |
| γ2 | – | – (14) (74.50) | 3.77 | 3.77 FIX |
| k1, SU (d−1) | – | – (28) (20.59) | 8.3 | 8.3 FIX |
| φ | – | – | – | 4.4 (14) (53.38) |
| k1 (d−1) | – | – | – | 4.26 (6) (96.75) |
| Residual error (RSE%) | ||||
| σ12 (Proportional) | 0.0175 (38) | 0.018 (4) | 0.0145 (2.91) | 0.0158 (8) |
| σ22 (Additive) | 0.00016 (46) | 0 FIX | 0 FIX | 0.00003 (19) |
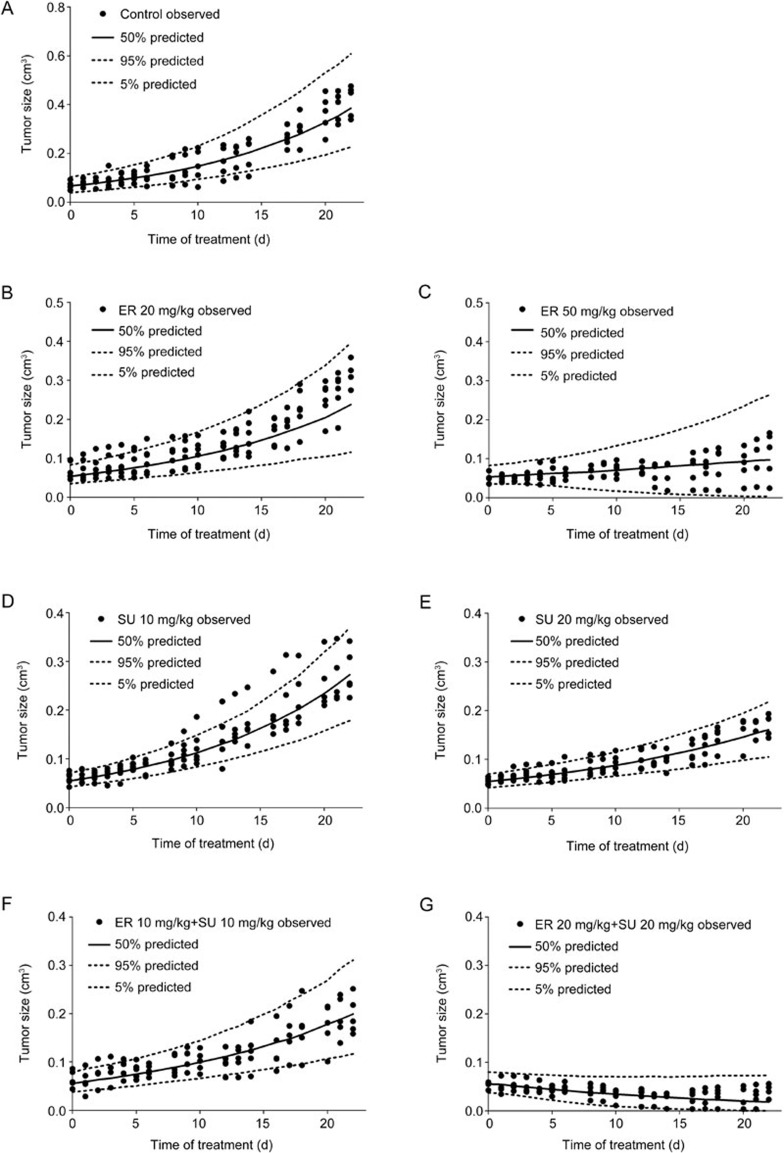
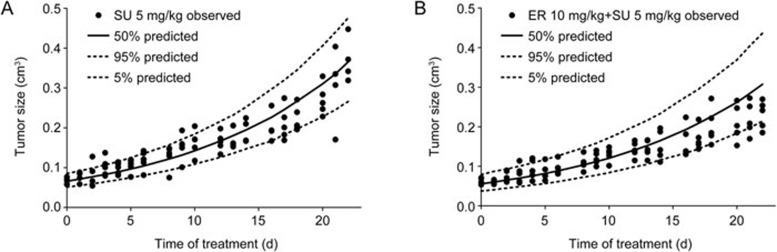
The VPC results of the different treatment groups are shown in Figure 5. The 50th percentiles of the predictions nearly pass through the middle of observed value, and the most observed values were within the 90% confidence interval of the predictions, suggesting that the model could fit the current PD data very well and also had a high predictability. To further understand the extrapolation ability of the models, the tumor growth data of 5 mg/kg SU and 5 mg/kg SU with 10 mg/kg ER were used to perform an external validation of the PK/PD models of the SU monotherapy and the combination therapy, respectively. Figure 6 shows the external validation results, which indicated that both models had satisfactory extrapolation ability within a certain dose level. The goodness-of-fit plots provided in Supplementary Figure S1 also demonstrate the fitness of the models.
Figure 5.
The VPC results of the PK/PD models in BALB/c nude mice bearing an A549 xenograft using a simulation that was conducted 1000 times. (A) Control group, (B) 20 mg/kg ER, (C) 50 mg/kg ER, (D) 10 mg/kg SU, (E) 20 mg/kg SU, (F) 10 mg/kg ER and 10 mg/kg SU, and (G) 20 mg/kg ER and 20 mg/kg SU. The range between the dashed lines represents the 90% confidence intervals, the solid lines are the medians of the simulated data, and the solid dots are the observed data.
Figure 6.
The external validation of the VPC results of the PK/PD models using a simulation that was conducted 1000 times. (A) 5 mg/kg SU, (B) 10 mg/kg ER and 5 mg/kg SU.
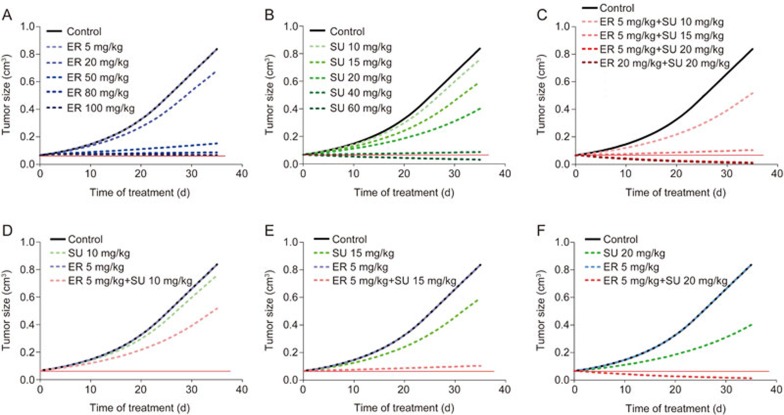
Model simulations
To optimize the therapeutic regimen of the combination of ER and SU for the treatment of primary resistant NSCLC and to investigate the characteristics of the coadministration of two anticancer drugs, a simulation of the tumor volume-time profiles for a series of different dosage regimens was performed by fixing the PK and PD parameters. The simulation results are shown in Figure 7. The dose-dependent efficacy was found for both of the drugs and the combination group; 100 mg/kg ER, 60 mg/kg SU and 5 mg/kg ER with 15 mg/kg SU could all stop the tumor growth (the red solid line). Furthermore, 60 mg/kg SU and 5 mg/kg ER with 20 mg/kg SU could shrink the tumor size (below the red solid line). The total dose of the combination group was smaller than one single agent alone to achieve the same standard of tumor growth inhibition. When ER was fixed at 5 mg/kg, the anticancer efficacy was significantly strengthened as the dose of SU increased, and the tumor growth curve of 5 mg/kg ER with 20 mg/kg SU was almost the same as that of the high dose group (20 mg/kg ER with 20 mg/kg SU) in the nude mouse experiment.
Figure 7.
The simulation results of different dose regimens of ER and SU in single or combination therapy. A, B, and C represent different dosages of ER alone, SU alone, and their combination treatment, respectively. D, E, and F represent the comparison of 5 mg/kg ER combined with SU at 10 mg/kg, 15 mg/kg and 20 mg/kg, respectively.
Discussion
The anticancer efficacy of the coadministration of ER and SU did not have the expected effect in a phase III trial with NSCLC patients previously treated with chemotherapy11. To further understand the reason for this unsatisfactory clinical outcome, we hypothesized that different dose regimens might markedly influence the effects of the treatment, and a change in the dose regimen might lead to a satisfactory response. Therefore, PK/PD modeling and simulation based on preclinical data were used in this study to test our assumption. First, an A549 xenograft model was established to conduct an in vivo experiment to investigate the tumor growth inhibition of ER and SU alone and the combination therapy. The results showed that the combination therapy exerted much stronger efficacy compared with the vehicle and single agents. In addition, based on the PK parameters from our previous work and the PD data from the in vivo experiment, PK/PD models of the vehicle and treated groups were developed. Finally, based on the parameters of the PK/PD models, simulations were performed to optimize the dose regimen for the combination therapy and to elucidate the possible reason for the failure of the above clinical trial.
In the PK profile, it is necessary to consider the PK interactions between the two drugs because ER and SU are both metabolized by the CYP34A pathway21. Clinical research has indicated that the treatment of SU with ER does not affect the pharmacokinetics of ER but might result in an increase in the catabolism of SU, which results in decreased exposure to the parent drug and increased exposure to the metabolite22. Because SU12662 (N-desethyl-sunitinib), the main active metabolite, has equipotent competence, similar protein binding capacity and molecular weight to its parent drug23,24, we assume that the coadministration of ER and SU did not influence the total anticancer effect of SU. Therefore, the PK interactions between ER and SU might be ignored. For the same reason mentioned above, the total concentration of SU and SU12662 was taken as the effective concentration to link the PD model. The PK/PD model could be simplified with a lesser number of parameters. The PK profiles of the combination model were derived from the simulation based on the PK parameters obtained from the previous study in which the PK/PD models were established.
In regard to natural tumor growth, several models were used in an attempt to fit the available data. Although Gilbert Koch's model20 described tumor growth as a smooth curve between the two growth phases, the linear growth parameter λ1 could not be obtained in our model development. A semi-mechanistic model suggested by Simeoni19 was eventually adopted in this study, with φ fixed at 20, with the assumption of a threshold tumor mass (wth) existing between the exponential growth and linear growth phases. We did not try the Gompartz model or the Logistic model because the shape of the tumor growth curve of the vehicle group did not have the typical S-shape.
We tried various commonly used model structures to fit both the monotherapy and combination data many times during the development of the PK/PD models. The models attempted include the linear PK/PD model, the Emax model and the sigmoid model. We found that the Emax model allowed a better adherence to the observed data. In addition, we tried to model individual arms to examine the single arm-specific drug parameters. However, the linear model could hardly fit two dose levels and confirm the external validation at the same time. Additionally, the parameter k1 was unstable when the classic Emax model was applied during the fitting process. The sigmoid model was used last with a satisfactory predictability and promising extrapolation ability. In the treatment of cancer, there is always a delay between the drug efficacy and drug concentration. To describe this phenomenon in this study, some transit compartments with the same first-order transit rate k1 were applied, as recommended by Jusko and Savic25,26. The number of transit compartments was always 3 in the previous study27,28, and we used different transit compartment numbers from 0 to 4 to investigate model fitting. Ultimately, the PK/PD model of the ER group and the combination group included 3 compartments, and the model of the SU group contained one compartment.
As for the PK/PD model of the combination group, the combination index φ was introduced in the model to further understand the drug interaction between the two drugs20. ER and SU are both TKIs, and their anticancer efficacy is exerted via inhibiting tyrosine kinase phosphorylation. We tried to add φ to either ER or SU, and instability was exhibited when adding φ to ER. Therefore, φ was added to SU in the final PK/PD model. Based on the PK/PD model developed above, the typical value of φ is 4.4, which indicates that the anticancer efficacy of ER was strengthened greatly by SU when it was simultaneously given with SU. To further understand the characteristics of the coadministration of the two anticancer drugs and to provide a better reference dose combination for clinical trials, the tumor growth of a series of different dosage regimens was predicted by a model simulation according to the model developed above. As shown in the simulation results, the anticancer efficacy of SU alone was more potent than that of ER alone, which agrees with the finding that A549 cells are primarily resistant to ER, and SU has a smaller EC50 value (0.355 μg/mL) compared with that of ER (8.74 μg/mL). In addition, the simulation results indicated that the anticancer efficacy was more sensitive to a change in the SU dose level when coadministered. We conducted a simulation in which SU was fixed and ER was changed to different dose levels in the combination treatment. However, the tumor size changed little compared to SU used alone under this condition. Therefore, the dose level of ER could be kept at very low level, such as 5 mg/kg or lower, and the risk of toxicity could be reduced. From our simulation results, we found that the treatment of 5 mg/kg ER with 20 mg/kg SU completely inhibited the tumor growth. The mass ratio of ER to SU was 1/4, suggesting that more SU in the combination therapy is required. However, in the combination therapy that was mentioned above in the phase III clinical trial, the dose ratio of ER to SU was 4/1 (the dosage of ER and SU were 150 mg/kg and 37.5 mg/kg, respectively)11. This dosing was the complete opposite to our simulated optimal regimen, with the ratio of 1/4, which indicates one possible reason for the unpromising results of the clinical study. Therefore, the PK/PD model established in our study could predict the characteristics of tumor growth in different treatment groups and could offer insights for clinical dose guidance of the coadministration of ER and SU.
Conclusion
For the first time, our study developed a PK/PD model of the combination treatment of ER and SU in female BALB/c nude mice with NSCLC. This model quantitatively described the relationship between the plasma concentration and the anticancer efficacy and the PD interaction of the two drugs, and the model predicted the tumor growth characteristics of different dose regimens. The value of the combination index φ (4.4) indicated a strong synergistic effect of ER and SU in the treatment of primary resistant NSCLC, and the anticancer efficacy of ER was greatly strengthened when administered with SU. The SU dose was found to play a decisive role in the combination treatment, indicating that a lower dose of ER and adjusting the dose of SU might yield a better dosage regimen for clinical research. The outcome of this study suggests an interesting hypothesis to be tested in the clinic, and the preclinical PK/PD models developed in our study might provide a reference for the dose selection of the combination therapy of ER and SU in cancer treatment.
Author contribution
Tian-yan ZHOU and Jing-yun LI designed the research; Jing-yun LI, Yu-peng REN, Yin YUAN, Shuang-min JI, Ye YAO, Liang LI, and Shu-pei ZHOU performed the research; Jing-yun LI, Tian-yan ZHOU, Li-jie WANG, and Wei LU analyzed the data; Jing-yun LI and Tian-yan ZHOU wrote the manuscript.
Abbreviations
ER, erlotinib; SU, sunitinib; NSCLC, non-small-cell lung cancer; PK/PD, pharmacokinetic/pharmacodynamics; TKI, tyrosine kinase inhibitor; EGFR, epidermal growth factor receptor; VEGFR, vascular endothelial growth factor receptor; FOCE, first order conditional estimation; RSE, relative standard errors; OFV, object function value; VPC, visual predictive check.
Acknowledgments
This study was supported by the National Natural Science Foundation of China (Grant No 81473277).
Footnotes
Supplementary information is available at the Acta Pharmacologica Sinica's website.
Supplementary Information
Goodness-of-fit plots of PK/PD model in BALB/c nude mice bearing A549 xenograft.
References
- Lee CC, Shiao HY, Wang WC, Hsieh HP. Small-molecule EGFR tyrosine kinase inhibitors for the treatment of cancer. Expert Opin Investig Drugs 2014; 23: 1333–48. [DOI] [PubMed] [Google Scholar]
- Shepherd FA, Rodrigues Pereira J, Ciuleanu T, Tan EH, Hirsh V, Thongprasert S, et al. Erlotinib in previously treated non-small-cell lung cancer. N Engl J Med 2005; 353: 123–32. [DOI] [PubMed] [Google Scholar]
- Perez-Soler R, Chachoua A, Hammond LA, Rowinsky EK, Huberman M, Karp D, et al. Determinants of tumor response and survival with erlotinib in patients with non-small-cell lung cancer. J Clin Oncol 2004; 22: 3238–47. [DOI] [PubMed] [Google Scholar]
- Mendel DB, Laird AD, Xin X, Louie SG, Christensen JG, Li G, et al. In vivo antitumor activity of SU11248, a novel tyrosine kinase inhibitor targeting vascular endothelial growth factor and platelet-derived growth factor receptors: determination of a pharmacokinetic/pharmacodynamic relationship. Clin Cancer Res 2003; 9: 327–37. [PubMed] [Google Scholar]
- Abrams TJ, Lee LB, Murray LJ, Pryer NK, Cherrington JM. SU11248 inhibits KIT and platelet-derived growth factor receptor beta in preclinical models of human small cell lung cancer. Mol Cancer Ther 2003; 2: 471–8. [PubMed] [Google Scholar]
- Ferrara N, Gerber HP, LeCouter J. The biology of VEGF and its receptors. Nat Med 2003; 9: 669–76. [DOI] [PubMed] [Google Scholar]
- Lin L, Bivona TG. Mechanisms of resistance to epidermal growth factor receptor inhibitors and novel therapeutic strategies to overcome resistance in NSCLC patients. Chemother Res Pract 2012; 2012: 817297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tortora G, Ciardiello F, Gasparini G. Combined targeting of EGFR-dependent and VEGF-dependent pathways: rationale, preclinical studies and clinical applications. Nat Clin Pract Oncol 2008; 5: 521–30. [DOI] [PubMed] [Google Scholar]
- Naumov GN, Nilsson MB, Cascone T, Briggs A, Straume O, Akslen LA, et al. Combined vascular endothelial growth factor receptor and epidermal growth factor receptor (EGFR) blockade inhibits tumor growth in xenograft models of EGFR inhibitor resistance. Clin Cancer Res 2009; 15: 3484–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poindessous V, Ouaret D, El Ouadrani K, Battistella A, Megalophonos VF, Kamsu-Kom N, et al. EGFR- and VEGF(R)-targeted small molecules show synergistic activity in colorectal cancer models refractory to combinations of monoclonal antibodies. Clin Cancer Res 2011; 17: 6522–30. [DOI] [PubMed] [Google Scholar]
- Scagliotti GV, Krzakowski M, Szczesna A, Strausz J, Makhson A, Reck M, et al. Sunitinib plus erlotinib versus placebo plus erlotinib in patients with previously treated advanced non-small-cell lung cancer: a phase III trial. J Clin Oncol 2012; 30: 2070–8. [DOI] [PubMed] [Google Scholar]
- Suleiman AA, Nogova L, Fuhr U. Modeling NSCLC progression: recent advances and opportunities available. AAPS J 2013; 15: 542–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tham LS, Wang L, Soo RA, Lee SC, Lee HS, Yong WP, et al. A pharmacodynamic model for the time course of tumor shrinkage by gemcitabine + carboplatin in non-small cell lung cancer patients. Clin Cancer Res 2008; 14: 4213–8. [DOI] [PubMed] [Google Scholar]
- Li M, Li H, Cheng X, Wang X, Li L, Zhou T, et al. Preclinical pharmacokinetic/pharmacodynamic models to predict schedule-dependent interaction between erlotinib and gemcitabine. Pharm Res 2013; 30: 1400–8. [DOI] [PubMed] [Google Scholar]
- Wang Y, Sung C, Dartois C, Ramchandani R, Booth BP, Rock E, et al. Elucidation of relationship between tumor size and survival in non-small-cell lung cancer patients can aid early decision making in clinical drug development. Clin Pharmacol Ther 2009; 86: 167–74. [DOI] [PubMed] [Google Scholar]
- Li M, Wu Q, Li H, Ning M, Chen Y, Li L, et al. Sensitive LCMS/ MS method to determine the concentrations of erlotinib and its active metabolite OSI420 in BALB/c nude mice plasma simultaneously and its application to a pharmacokinetic study. J Chin Pharm Sci 2012; 21: 296–303. [Google Scholar]
- Li J, Li J, Wang S, Yuan Y, Su Q, Lu W, et al. Simultaneous determination of sunitinib and its active metabolites N-desethylsunitinib (SU12662) in nude mice plasma by liquid chromatography tandem mass spectrometry and its application to a pharmacokinetic study. J Chin Pharm Sci 2015; 24: 217–24. [Google Scholar]
- Salphati L, Wong H, Belvin M, Bradford D, Edgar KA, Prior WW, et al. Pharmacokinetic-pharmacodynamic modeling of tumor growth inhibition and biomarker modulation by the novel phosphatidylinositol 3-kinase inhibitor GDC-0941. Drug Metab Dispos 2010; 38: 1436–42. [DOI] [PubMed] [Google Scholar]
- Simeoni M, Magni P, Cammia C, De Nicolao G, Croci V, Pesenti E, et al. Predictive pharmacokinetic-pharmacodynamic modeling of tumor growth kinetics in xenograft models after administration of anticancer agents. Cancer Res 2004; 64: 1094–101. [DOI] [PubMed] [Google Scholar]
- Koch G, Walz A, Lahu G, Schropp J. Modeling of tumor growth and anticancer effects of combination therapy. J Pharmacokinet Pharmacodyn 2009; 36: 179–97. [DOI] [PubMed] [Google Scholar]
- van Erp NP, Gelderblom H, Guchelaar HJ. Clinical pharmacokinetics of tyrosine kinase inhibitors. Cancer Treat Rev 2009; 35: 692–706. [DOI] [PubMed] [Google Scholar]
- Blumenschein GR Jr, Ciuleanu T, Robert F, Groen HJ, Usari T, Ruiz-Garcia A, et al. Sunitinib plus erlotinib for the treatment of advanced/metastatic non-small-cell lung cancer: a lead-in study. J Thorac Oncol 2012; 7: 1406–16. [DOI] [PubMed] [Google Scholar]
- Faivre S, Delbaldo C, Vera K, Robert C, Lozahic S, Lassau N, et al. Safety, pharmacokinetic, and antitumor activity of SU11248, a novel oral multitarget tyrosine kinase inhibitor, in patients with cancer. J Clin Oncol 2006; 24: 25–35. [DOI] [PubMed] [Google Scholar]
- Haznedar JO, Patyna S, Bello CL, Peng GW, Speed W, Yu X, et al. Single- and multiple-dose disposition kinetics of sunitinib malate, a multitargeted receptor tyrosine kinase inhibitor: comparative plasma kinetics in non-clinical species. Cancer Chemother Pharmacol 2009; 64: 691–706. [DOI] [PubMed] [Google Scholar]
- Jusko WJ. Pharmacodynamics of chemotherapeutic effects: dose-time-response relationships for phase-nonspecific agents. J Pharm Sci 1971; 60: 892–5. [DOI] [PubMed] [Google Scholar]
- Savic RM, Jonker DM, Kerbusch T, Karlsson MO. Implementation of a transit compartment model for describing drug absorption in pharmacokinetic studies. J Pharmacokinet Pharmacodyn 2007; 34: 711–26. [DOI] [PubMed] [Google Scholar]
- Rocchetti M, Simeoni M, Pesenti E, De Nicolao G, Poggesi I. Predicting the active doses in humans from animal studies: a novel approach in oncology. Eur J Cancer 2007; 43: 1862–8. [DOI] [PubMed] [Google Scholar]
- Karlsson MO, Anehall T, Friberg LE, Henningsson A, Kloft C, Sandstrom M, et al. Pharmacokinetic/pharmacodynamic modelling in oncological drug development. Basic Clin Pharmacol Toxicol 2005; 96: 206–11. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Goodness-of-fit plots of PK/PD model in BALB/c nude mice bearing A549 xenograft.