The Greatly Misunderstood Erythropoietin Resistance Index and the Case for a New Responsiveness Measure

Abstract

Background

The optimal use of erythropoiesis stimulating agents (ESAs) to treat anemia in end stage renal disease (ESRD) remains controversial due to reported associations with adverse events. In analyzing these associations, studies often utilize ESA resistance indices (ERIs), to characterize a patient’s response to ESA. In this study, we examine whether ERI is an adequate measure of ESA resistance.

Methods

We used retrospective data from a non-concurrent cohort study of incident hemodialysis patients in the United States (n=9386). ERI is defined as average weekly erythropoietin (EPO) dose per kg body weight (wt) per average hemoglobin (Hgb), over a 3-month period (ERI = (EPO/wt)/Hgb). Linear regression was used to demonstrate the relationship between ERI and weight-adjusted EPO. The coefficient of variation (CV) was used to compare the variability of Hgb with that of weight-adjusted EPO in order to explain this relationship. This analysis was done for each quarter during the first year of dialysis.

Results

ERI is strongly linearly related with weight-adjusted EPO dose in each of the 4 quarters by the equation ERI = 0.0899*(EPO/wt) (range of R² = 0.97–0.98) and weakly linearly related to 1/Hgb (range of R² = 0.06–0.16). These correlations hold independent of age, sex, hgb level, ERI level, and epo-naïve stratifications.

Conclusions

ERI is strongly linearly related to weight-adjusted (and non-weight-adjusted) EPO dose by a “universal”, not patient-specific formula, and thus is a surrogate of EPO dose. Therefore, associations between ERI and clinical outcomes are associations between a confounded EPO dose and those outcomes.

INTRODUCTION

In healthy humans, the homeostatic mechanisms associated with erythropoiesis maintain physiological Hgb levels. In end-stage renal disease (ESRD) and chronic kidney disease (CKD), these mechanisms are impaired, often leading to anemia, which is associated with decreased quality of life, increased morbidity, and mortality.¹ Some of these impairments involve decreased erythropoietin (EPO) production, acute blood loss, reduced red blood cell (RBC) lifespan, bone marrow diseases and ESA resistance factors such as inflammation.²

The administration of erythropoiesis stimulating agents (ESAs) in the treatment of anemia of ESRD has been the single most important aspect of anemia protocols for over three decades. However, current ESA dosing guidelines do not appear to provide information about optimal ESA therapies. Two large randomized controlled trials addressed the hypothesis that a higher Hgb goal might benefit CKD patients.^3,4 In 2011, because of evidence of increased cardiovascular risks in patients assigned to a higher Hgb goal (with higher doses of ESA) in these trials, the FDA warned that: “No trial has identified a hemoglobin target level, ESA dose, or dosing strategy that does not increase these risks”.⁵ The FDA currently recommends minimizing ESA dosing to a level sufficient to reduce the need for red blood cell transfusions, but does not mention what Hgb level is optimal to achieve this goal.⁵ Hence, there is an increasing interest in developing measures that relate ESA dose level with the resulting change in Hgb level in the hope of maximizing the effect while minimizing adverse outcomes.

The relationship between the Hgb response and ESA is complex, nonlinear, and dynamic, and may be affected by several confounders including acute or chronic infection and inflammation, iron availability or deficiency, and bleeding. Borrowing from pharmacology, a responsiveness measure is concerned with the degree of Hgb change from baseline in response to a constant ESA dose, whereas a resistance measure, the inverse of responsiveness, is concerned with the amount of ESA needed to achieve a specific Hgb change. Either way, individualized dose-response curves must take time into account by using sufficiently long study periods for the full drug effect to be realized, and must also be evaluated over a wide range of drug dose levels and confounding factors.

The measurement of ESA responsiveness in incident and maintenance ESRD patients is confounded by medical indication since typical anemia protocols escalate ESA doses at lower Hgb levels, so that patients with worse health status receive larger ESA doses.^6–8 Another type of confounding occurs when clinical practice guidelines or anemia protocols change during the study period, resulting in time-dependent confounding.⁸ Confounding can result in a bias of the estimated effect of the confounded variable on the outcome of interest.⁸

Control of confounding can be done at the study design stage. For example, Solomon et al⁹ used TREAT³ trial data, in which ESA doses were decoupled from prior ESA levels and/or anemia status, to define a responsiveness measure as percent change in hemoglobin level after the first 4 weeks of therapy. A somewhat similar responsiveness measure based on initial response was derived from the NCHT study¹⁰, although ESA doses were not fully decoupled from previous levels.¹¹ Control of confounding can also be done at the analysis stage. A linear mixed-effects model was used to separate the (confounded) population ESA response from the ESA responsiveness of individual patients in a retrospective cohort of long-term HD patients.⁶ Cotter et al⁷ used marginal structural models to estimate the dose-response relationship in ESA-naïve incident patients. The vast majority of ESA association studies have defined resistance using the ESA resistance index (ERI), which is the simple ratio (ESA/weight)/Hgb, based on weekly, monthly or multi-month averages.^13–22 The motivation for using multi-month averaging is to smooth out the longitudinal variability in ESA and Hgb. Given the complexity of the Hgb response to ESA stimulation one can appreciate why investigators seeking to correlate ESA response with adverse outcomes have turned to ERIs: “It is easy to calculate and is highly useful in the bedside evaluation of the patient’s clinical status.” ¹⁵ Unfortunately, such simplicity can lead to a great misunderstanding of what ERI truly represents, and therefore its actual meaning in association studies.

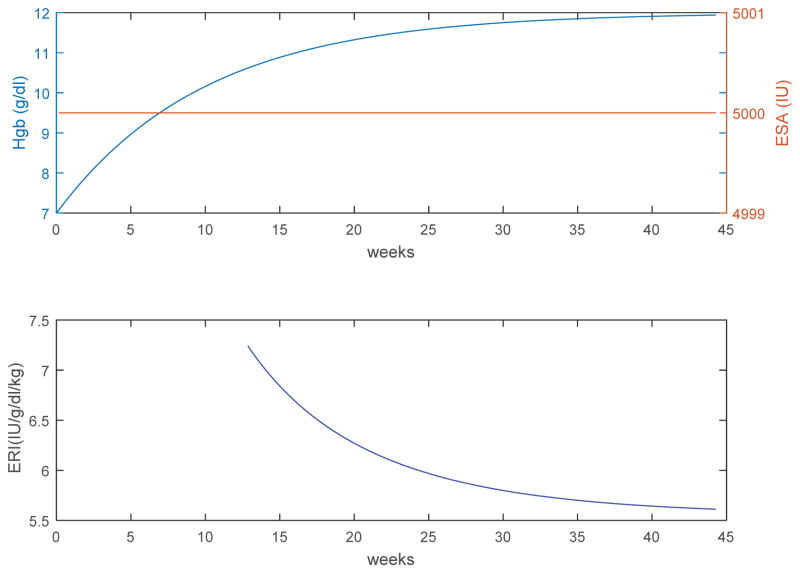
To illustrate this point, consider the Hgb response (Figure 1) of a hypothetical subject to a constant ESA dose computed using a model of erythropoiesis¹² (75 kg ESRD subject, 7 g/dl endogenous Hgb, mean red blood cell lifespan of 70 days, dose-response Hgb/EPO sensitivity of 0.001 g/dl/IU at a weekly EPO dose of 5000 IU). From Figure 1 we observe that in a moving 3-month window, ERI varies over time as Hgb increases in response to the constant ESA dose. The decrease in ERI makes it appear as though the patient’s actual resistance is decreasing over time, whereas, in fact, the subject is merely going through the transient phase of the physiological response to ESA, which can take several months until Hgb stabilizes at its new level. It is only the ratio of ESA to change in Hgb from baseline (not total Hgb) at steady state that corresponds to the dose-response curve.

Figure 1.

Hypothetical response of a subject to constant ESA dosing. Physiological Hgb response (top) from an endogenous Hgb level of 7 g/dL to a constant weekly ESA dose of 5000 IU (top), and the corresponding ERI (bottom) defined as average weekly ESA per kg body weight per hemoglobin over a moving 3-month window. It appears that ESA resistance is decreasing over time from an initial value of 7.24 (IU/g/dl/kg) to 5.61 (IU/g/dl/kg) at steady state, whereas in fact is that the subject is merely going through the transient phase of its physiological response to ESA, which can take several months until a new steady state is reached.

Given the prevalent and increasing use of ERIs in studying the association of ESA resistance with clinical outcomes, the present study examines whether ERI is an adequate independent measure of ESA resistance.

MATERIALS AND METHODS

Patients

The Accelerated Mortality on Renal Replacement (ArMORR) study is a prospective cohort study of 10,044 incident hemodialysis patients in 1056 US centers operated by Fresenius Medical Care North America (FMC) between June 2004 and August 2005.^18–19 Most participants underwent 1 year of follow-up, except for those who died (15.2%), voluntarily discontinued dialysis (5%), underwent kidney transplantation (3%), recovered renal function (4%), transferred to a dialysis unit outside the FMC system before completing 1 year of hemodialysis (12%), or enrolled late in the study period. Clinical data were prospectively collected by physicians at the point of care and included demographic information, coexisting conditions, results of studies performed by a central laboratory (Spectra East, Northvale, NJ), medication administration, and outcomes. To be included in analysis in a particular quarter, a patient must have survived that quarter.

Responsiveness Measure

ERI was defined as average weekly erythropoietin dose [IU] per kg body weight per hemoglobin [g/dl]) in each quarter during the first year following dialysis initiation (3-month period). A total of 9386, 7925, 6403, 4415 patients had sufficient data to compute their ERI value in the first, second, third, and fourth quarters, respectively.

Statistical analysis

Linear regression with zero intercept was used to establish the linear relationship between ERI and weight-adjusted EPO. Variability of Hgb and weight-adjusted EPO was measured by the coefficient of variation (CV). The ratio of the CV of weight-adjusted EPO to the CV of Hgb was used to explain why Hgb in the relation between ERI and weight-adjusted EPO can be replaced with a population constant resulting in a linear relation between ERI and weight-adjusted EPO.

All statistical analyses were performed using MATLAB’s Statistics and Machine Learning Toolbox (v10.0; the MathWorks, Inc., Natick, MA) and R (v3.2.0, Foundation for Statistical Computing, Vienna, Austria).

RESULTS

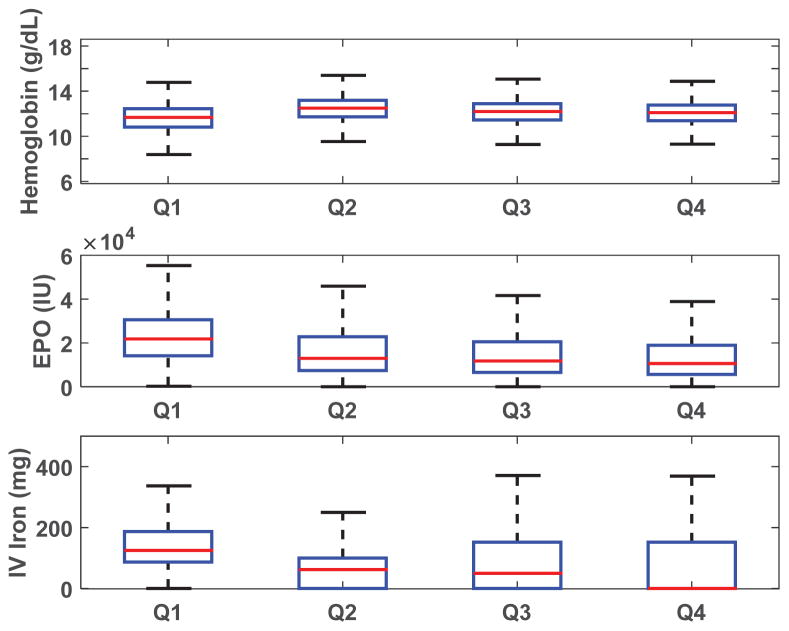
The baseline characteristics of the study population are summarized in Table 1. Study participants were predominantly Caucasian (60.3%), and 26.7% had a catheter as the initial vascular access. Relevant laboratory values included median ferritin of 200 ng/ml (interquartile range [IQR] = 97–392), median albumin of 3.5 g/dl (IQR = 3.2–3.8), transferrin saturation of 18% (IQR =1 4–24), and parathyroid hormone of 209 pg/ml (IQR=113–355). Box plots of quarterly values of hemoglobin, EPO doses, and iron doses are shown in Figure 2.

Table 1.

Baseline characteristics for the study population

Variable	All subjects (n=9386)
Age, yr	62.2 ± 15.5
Women	4268 (45.5)
White race	5663 (60.3)
Comorbidities:
Coronary artery disease/myocardial infarction	929 (9.9)
Diabetes mellitus	2192 (23.4)
Vascular access: catheter	5564 (26.7)
Weight (kg)	77.2 ± 21.9
Body mass index (kg/m2)	27.6 ± 8.4
Systolic BP (mmHg)	145 (131–159)
Diastolic BP (mmHg)	74 (65–83)
Urea reduction ratio	70 (63–76)
Laboratory data
Hemoglobin (g/dl)	10.3 (9.4–11.2)
Albumin (g/dl)	3.5 (3.2–3.8)
Ferritin (ng/ml)	200 (97–392)
Transferrin saturation (%)	18 (14–24)
Phosphorus (mg/dl)	4.5 (3.7–5.6)
Parathyroid hormone (pg/ml)	209 (113–355)

Categorical data are n (%). Continuous measures are mean ± SD. Laboratory values are median (quartile 1 to quartile 3). Some variables had <10% missing values) with the exception of urea reduction ratio (22% missing) and parathyroid hormone (13.3%),.

Figure 2.

Boxplots of quarterly averages. Hemoglobin (top), EPO (middle), and IV iron (bottom) in quarter 1 (Q1=weeks 1–13), quarter 2 (Q2 = weeks 14–26), quarter 3 (Q3 = weeks 27–39), and quarter 4 (Q4 = weeks 40–52). Outliers are not shown. IV iron includes Venofer, Ferrlecit, and Infed. Number of patients in Q1, Q2, Q3, and Q4, were 9386, 7925, 6403, 4415, respectively.

Table 2 lists quarterly correlations between ERI = (EPO/wt)/Hgb and the corresponding quarterly mean weekly weight-adjusted EPO (range of R² = 0.97–0.98), 1/Hgb (range of R² = 0.06–0.16), and EPO (range of R² = 0.57–0.89).

Table 2.

Correlations between ERI and several covariates in Quarters 1–4

	Q1	Q2	Q3	Q4
n	9386	7925	6403	4415
R2: ERI and (EPO/wt)	0.97	0.97	0.98	0.98
R2: ERI and 0.0899*(EPO/wt)	0.97	0.97	0.98	0.98
R2: ERI and 1/Hgb	0.06	0.16	0.11	0.12
R2: ERI and EPO	0.57	0.79	0.71	0.89

Each quarter is 13-weeks long

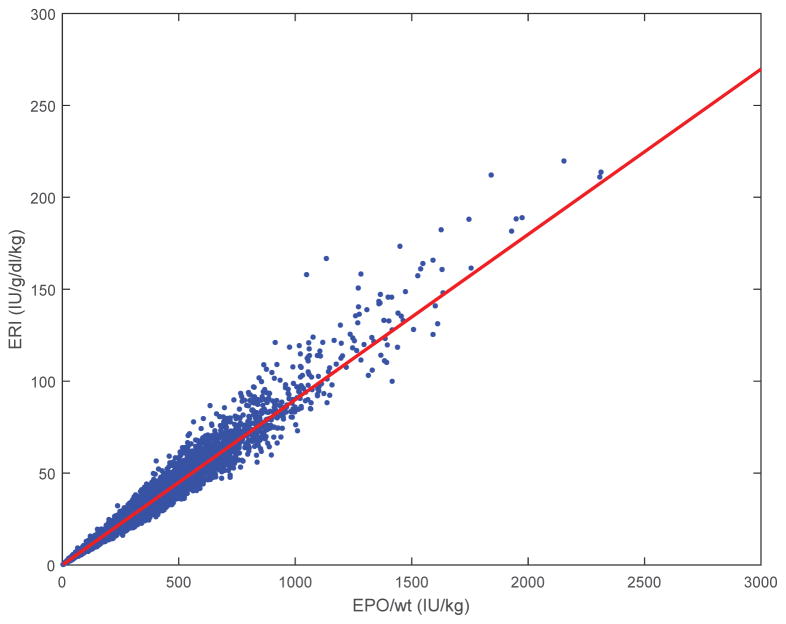
Scatter plots of ERI vs. EPO/wt and ERI vs. 1/Hgb for the 4^th quarter are shown in Figure 3. We focused on the 4^th quarter because EPO protocols in the early quarters of HD initiation were strongly influenced by patient weight, and the 4^th quarter can be assumed to closely resemble maintenance conditions. 4^th) A linear regression of ERI vs. EPO/wt with intercept forced to = 0 gave a regression line ERI = 0.0899*(EPO/wt) when data from all 4 quarters were combined (R² = 0.98). In order to test for differences in the established associations between ERI and mortality and the association with only EPO and mortality we ran cox proportional hazard models. Cox proportional hazard ratios (HR) for all-cause mortality were the same with either covariate ERI (1.0036, P<0.0001) or universal ERI = 0.0899*(EPO/wt) (1.0035, P<0.0001).

Figure 3.

Scatterplot of first-quarter (weeks 1–13) ERI for all patients (n = 9386) shows strong correlation with EPO dose (R² = 0.98). The line is ERI = 0.0899*(EPO/wt).

Subgroup analysis stratifying from lowest to highest quartiles of ERI respectively, using 4^th quarter data, gave the following correlations between ERI and EPO/wt (R² = 0.97, 0.83, 0.76, 0.97) and ERI and 1/Hgb (R² = 0.045, 0.005, 0.014, 0.08). Subgroup analysis stratifying by Hgb, again using 4^th quarter data, gave the following correlations between ERI and EPO/wt (R² = 0.99, 0.99, 0.99, 0.99) and ERI and 1/Hgb (R² = 0.08, 0.002, 0.002, 0.003).

Subgroup analysis stratifying by age, again using 4^th quarter data, gave the following correlations between ERI and EPO/wt (R² = 0.96, 0.98, 0.98, 0.98) and ERI and 1/Hgb (R² = 0.15, 0.11, 0.10, 0.14).

Subgroup analysis stratifying by sex, again using 4^th quarter data, gave the following correlations between ERI and EPO/wt (R² = 0.98, 0.97) and ERI and 1/Hgb (R² = 0.10, 0.13).

Subgroup analysis stratifying by EPO-naïve status (initial catheter access, no prior dialysis treatment, and initial Hgb<12 g/dl), again using 4^th quarter data, gave the following correlations between ERI and EPO/wt (R² = 0.98) and ERI and 1/Hgb (R² = 0.12).

Coefficients of variation of Hgb and EPO/wt were (0.10,0.95), (0.10,10.7), (0.10, 1.30), and (0.09,1.27), in each quarter, respectively, and the ratios CV(EPO/wt)/CV(Hgb) were 9.12, 10.96, 13.58, and 13.39, respectively.

DISCUSSION

ERIs often exhibit significant longitudinal variability, which is strongly correlated with ESA dosing patterns²⁵ and may not reflect actual variability in patients’ underlying ESA resistance. Thus, ERIs strongly depend on the particular time frame during which they were computed. In our study, we found a linear relation between ERI and weight-adjusted EPO (range of R² = 0.97–0.98), which was equally applicable to each quarter, implying that ERI is essentially equivalent to weight-adjusted EPO.

To establish the generality of our result, we performed subgroup regression analyses of 4^th quarter data. The choice of 4^th quarter is motivated by the fact that at the time, EPO protocols in the early quarters of HD initiation were strongly influenced by patient weight, and the 4^th quarter can be assumed to closely resemble maintenance conditions. Stratification was carried out based on ERI, Hgb, and age quartiles, and based on sex and EPO-naïve groups. Because the correlation between ERI and EPO/wt and between ERI and 1/Hgb remains strong and that between ERI and 1/Hgb remains weak, across all subgroups, it appears our results are generalizable. To explain the linear relation between ERI and EPO/wt in spite of Hgb variability, we compared the coefficients of variation of CV(EPO/wt) and CV(Hgb). The range of the ratio CV(EPO/wt)/CV(Hgb) over the 4 quarters was 9.12–13.58, indicating that weight-adjusted EPO doses are roughly 9–13-fold more variable than Hgb values. Thus, the term 1/Hgb in ERI = (EPO/wt)/Hgb is approximately constant by comparison with weight-adjusted EPO, and this leads to the “universal” linear approximation ERI = 0.0899*(EPO/wt). We note that the slope 0.0899, which was obtained by linear regression forced to have zero intercept, is very close to the population mean of 1/Hgb (= 0.083); indeed, using the relation ERI = 0.083*(EPO/wt) gives essentially the same results.

To further explain these correlations, consider that whereas typical quarterly mean Hgb levels range at most between 9 and 12 g/dl or a range of ±15% around 10.5, mean EPO doses typically exhibit a significantly larger range of 1000–10000 IU or ±81% around 5500 independent of how stable either Hgb or EPO are over the period. This is precisely the reason why Hgb in the ERI relation can be replaced by a constant over the entire population.

The exception would be when mean EPO doses are globally within a very narrow range, for example 2000–3000 IU (very few clinics can boast this); however, even then ERI could be a poor measure of resistance. For example, consider two similar patients of the same 70 kg weight, same mean Hgb of 10 g/dl and mean EPO of 2800 IU, and therefore same ERI value of 4 IU/kg/(g/dl). If one patient has an endogenous Hgb level of 7 g/dl and the other of 8.25 g/dl, accounting for endogenous Hgb in ERI by taking ERI = (EPO/wt)/(Hgb-endogenous_Hgb), results in ERI values of 22.9 and 13.3, respectively. That is a difference of 72%, indicating a huge difference in ESA resistance.

Is it possible to derive measures of responsiveness that can inform clinicians about optimal Hgb target levels and safe ESA dose levels at the individual level? A key obstacle to achieving this goal is the inherent confounding of ESA doses by medical indication.^6–8 This can be overcome at the study design stage; however, randomized controlled trials may not offer a practical approach. The notion of responsiveness proposed by Kalantar-Zadeh et al⁶ addresses confounding by employing a linear mixed-effects model to separate the population-level ESA effect from the individual ESA responsiveness. This analysis resulted in a subset of individual ESA responsiveness measures being negative, suggesting that this approach may not correctly represent the physiological individual responsiveness for at least a subset of the population. Pharmacokinetic/pharmacodynamic modelling of erythropoiesis^12,26–28 could be used for deriving dose-response curves, however, relative standard errors of 50% are not uncommon in PKPD model parameter estimates.²⁹

A limitation of our study is its observational, retrospective nature, and its focus on incident patients. It is also possible that anemia management practices at dialysis facilities other than Fresenius, over different time periods, or in prevalent hemodialysis populations, may result in different CV(EPO/wt)/CV(Hgb) ratios. However, two larger studies, one with a cohort in another large dialysis provider in 2001–2002³⁰, and the other including Medicare prevalent hemodialysis patients in 2008³¹, reported that analysis results using ERI were similar to results obtained when ESA dose was used. These results are not surprising in view of our results above.

The clinical relevance of our study is in the demonstration that associations found between ERI and adverse events such as mortality are in fact associations between weight-adjusted or non-weight-adjusted EPO, a highly confounded covariate, and the adverse events. For example, the Cox proportional hazard ratio (HR) for all-cause mortality is the same with either ERI or universal ERI = 0.0899*(EPO/wt). Moreover, without appropriate adjustment for confounding, which often required sophisticated modelling, the estimated effect of the confounded variable may be biased and cannot be trusted. For example, an instrumental variable analysis markedly attenuated the strong association between high EPO doses and greater mortality risk found using conventional multivariable analysis.³² Hence, contrary to the intuitive presumption about the meaning of ERI, because it is a surrogate of ESA, ERI does not offer additional information regarding responsiveness. The derivation of responsiveness measures that can inform clinicians about individualized optimal Hgb target levels and safe and optimal ESA use remains elusive.