Cortical Sulcal Atlas Construction Using a Diffeomorphic Mapping Approach

Abstract

We present a geometric approach for constructing shape atlases of sulcal curves on the human cortex. Sulci and gyri are represented as continuous open curves in ${\mathbb{R}}^3$, and their shapes are studied as elements of an infinite-dimensional sphere. This shape manifold has some nice properties – it is equipped with a Riemannian ${\mathbb{L}}^2$ metric on the tangent space and facilitates computational analyses and correspondences between sulcal shapes. Sulcal mapping is achieved by computing geodesics in the quotient space of shapes modulo rigid rotations and reparameterizations. The resulting sulcal shape atlas is shown to preserve important local geometry inherently present in the sample population. This is demonstrated in our experimental results for deep brain sulci, where we integrate the elastic shape model into surface registration framework for a population of 69 healthy young adult subjects.

1 Introduction

A surface-based morphometric analysis of the cortex has been shown to have wide reaching applicability for the purpose of mental disease detection, progression, as well as prediction and understanding of normal and abnormal developmental behaviors. Cortical morphometry has three major ingredients: i) surface representation, ii) registration and alignment for construction of atlases, and iii) statistical analysis of deformations or warps explaining the variability of surface features in a given population. Surface registration aims at determining point-to-point correspondences between a pair of surfaces by aligning several homologous features on the two cortical surfaces. Theses correspondences can be achieved either automatically by using both local and global features as in the case of Dale et al. [2], or in a semi-automated manner, using expertly delineated sulcal and gyral landmarks as in the case of Thompson et al. [10,4]. The underlying idea in both approaches is modeling (either explicitly or indirectly) the sulcal and gyral patterns exclusively based on local geometric features. These features are usually 3D continuous space curves corresponding to the deepest regions of the valleys for sulci, and topmost regions of the ridges for the gyri. The main advantage of using explicit landmarks is the incorporationof expert anatomical knowledge that improvesthe consistency in matching of homologous features. This in turn potentially improves statistical power in the neighborhood of the landmarks. Additionally, increasing the number of consistent landmarks also improves the alignment accuracy, thereby allowing more control in the registration process. Previously, landmark curves have mostly been used as boundary conditions for various cortical alignment approaches. Various researchers have modeled the sulci and gyri using different representations. Tao et al. [9] represent sulci using landmark points on curves, and build a statistical model using a Procrustes alignment of sulcal shapes. Vaillant et al. [11] represent cortical sulci by medial surfaces of cortical folds. Although, the advantage of this model is that it represents entire cortical folds, a limitation of this method is the use of unit speed parameterizations of active contours for constructing Procrustes shape averages for sulci. Furthermore, for the two approaches, the shapes are represented by finite features or landmarks, and thus are limited in the characterization of rich geometric detail that manifests in the cortical folds giving the sulci their shapes. Recently, there have been several interesting approaches using continuous representations for sulci [8,1,3]. For e.g. Auzias et al. [1] model whole sulci using distributions of point sets and use a LDDMM framework for registering not only the surfaces but full MRI volumes. Durrleman et al. [3] use currents for modeling curves and surfaces.

In our work, we represent sulci and gyri by parameterized three-dimensional curves. However, unlike previous approaches, we construct a shape space of such sulcal and gyral curves and build a statistical model of sulci and gyri intrinsically on the shape space. Our approach models the whole curve without the use of landmarks or discrete parametric representations and deals with functional mappings of curve instances on the shape manifold. The main contributions of this paper are as follows: i) an inverse-consistent diffeomorphic framework for matching sulcal shapes, ii) An intrinsic sulcal shape atlas based on the Riemannian metric on the shape manifold, and iii) integration of sulcal curve diffeomorphisms in driving cortical surface registrations. To our knowledge, the proposed framework of direct diffeomorphic three-dimensional sulcal curve mappings have not been used in cortical registration before. This paper is organized as follows. Section 2 outlines the shape modeling scheme for sulci and gyri. It also outlines the procedure for computing statistical shape averages for sulci and gyri for a given population. Section 3 incorporates the sulcal shape model in cortical surface registration, followed by results and conclusion.

2 Diffeomorphic Shape Analysis of Sulci and Gyri

In this section, we describe the modeling scheme used to represent sulcal and gyral shape features. We represent the cortical valleys (sulci), and the ridges (gyri) by open curves. However unlike previous approaches which have used landmarks for representing the sulcal and gyral features, we will use continuous functions of curves for representing shapes.

2.1 Shape Representation

Let β be a 3D, arbitrarily parameterized [5], open curve, such that $\beta :[0,2\pi ]\to {\mathbb{R}}^3$. We represent the shape of the curve β by the function $q:[0,2\pi ]\to {\mathbb{R}}^3$ as follows,

$$q\left(s\right)=\frac{\stackrel{.}{\beta }\left(s\right)}{\sqrt{\Vert \stackrel{.}{\beta }\left(s\right)\Vert }}\in {\mathbb{R}}^3.$$ (1)

Here, $s\in [0,2\pi ]$, $\Vert \cdot \Vert \equiv \sqrt{{(\cdot ,\cdot )}_{{\mathbb{R}}^3}}$, and ${(\cdot ,\cdot )}_{{\mathbb{R}}^3}$ is the standard Euclidean inner product in ${\mathbb{R}}^3$. The quantity ∥q(s)∥ is the square-root of the instantaneous speed, and the ratio $\frac{q\left(s\right)}{\Vert q\left(s\right)\Vert }$ is the instantaneous direction along the curve. The original curve β can be recovered upto a translation, using $\beta \left(s\right)={\int }_0^s\Vert q\left(t\right)\Vert q\left(t\right)dt$. In order to make the representation scale invariant, we will normalize the function q as $\mathbf{q}=\frac{q}{\sqrt{{(q,q)}_{{\mathbb{R}}^3}}}$. We now denote ${\mathbb{S}}^q\equiv \{q\mid q\left(s\right):[0,2\pi ]\to {\mathbb{R}}^3\mid {\int }_0^{2\pi }{(q\left(s\right),q\left(s\right))}_{{\mathbb{R}}^3}ds=1\}$ as the space of all unitlength, elastic curves. On account of scale invariance, the space ${\mathbb{S}}^q$ becomes an infinite-dimensional unit-sphere and represents all open elastic curves invariant to translation and uniform scaling. The tangent space of ${\mathbb{S}}^q$ is easy to define and is given as $T_q\left({\mathbb{S}}^q\right)=\{w=(w_1,w_2,\dots ,w_n)\mid w\left(s\right):I\to {\mathbb{R}}^3\forall s\in [0,2\pi )\mid {\int }_0^{2\pi }{(w\left(s\right),q\left(s\right))}_{{\mathbb{R}}^3}ds=0\}$. Here each w_i represents a tangent vector in the tangent space of ${\mathbb{S}}^q$. Due to the spherical nature of the shape space, any vector on the shape space can be transformed to a tangent vector by simply subtracting its normal component. We define a metric on the tangent space as follows. Given a curve $q\in {\mathbb{S}}^q$, and the first order perturbations of q given by u, $v\in T_q\left({\mathbb{S}}^q\right)$, respectively, the inner product between the tangent vectors u, v to ${\mathbb{S}}^q$ at q is defined as, $\langle u,v\rangle ={\int }_0^{2\pi }{(u\left(s\right),v\left(s\right))}_{{\mathbb{R}}^3}ds$. Now given two shapes q₁ and q₂, the translation and scale invariant shape distance between them is simply found by measuring the length of the geodesic connecting them on the sphere. We know that geodesics on a sphere are great circles and can be specified analytically. Thus given a tangent vector $f\in T_{q1}\left({\mathbb{S}}^q\right)$, the geodesic on ${\mathbb{S}}^q$ between the two points q₁, q₂ $q_2\in {\mathbb{S}}^q$ along f, for a time t is given by χ_t(q₁; f) = cos (t cos⁻¹ 〈q₁, q₂〉) q₁ + sin (t cos⁻ 〈q₁, q₂〉) f where t is a subscript for time. Then the geodesic distance between the two shapes q₁ and q₂ is given by $d(q_1,q_2)={\int }_0^1\sqrt{\langle {\stackrel{.}{\chi }}_t,{\stackrel{.}{\chi }}_t\rangle }dt$. The quantify ${\stackrel{.}{\chi }}_t$ is also referred to as the velocity vector field on the geodesic path χ_t So far, we have constructed geodesics between a pair of curves directly on the sphere $\left({\mathbb{S}}^q\right)$. In doing so, we implicitly assumed that the curves were rotationally aligned, as well as the parameterization of the curves was fixed. However the shape of a curve remains unchanged under rotations as well as different parameterizations of the curve. Thus in order to register shapes accurately, the matching should be invariant to rotations as well as reparameterizations. This matching is achieved by constructing the space of elastic shapes, and measuring the “elastic” distance between curves under certain well-defined shape-preserving transformations as explained in the next section.

2.2 Geodesics between Elastic Shapes

In order to match curves elastically, in addition to translation and scaling, we consider the following reparameterizations and group actions on the curve that preserve its shape. A rigid rotation of a curve is considered as a group action by a 3 × 3 rotation matrix O₃ ∈ SO(3) on q, and is defined as O₃ · q(s) = O₃q(s), ∀s ∈ [0, 2π]. A curve traveled at arbitrary speeds is said to be reparameterized by a non-linear differentiable map γ (with a differentiable inverse) also referred to as a diffeomorphism. We define $\mathcal{D}=\{\gamma :{\mathbb{S}}^1\to {\mathbb{S}}^1\}$ as the space of all orientation-preserving diffeomorphisms. Then the resulting variable speed parameterizations of the curve can be thought of as diffeomorphic group actions of γ ∈ D on the curve q. This group action is derived as follows. Let q be the representation of a curve β. Let α = β(γ) be a reparameterization of β by γ. Then the respective velocity vectors can be written as $\stackrel{.}{\alpha }=\stackrel{.}{\gamma }\stackrel{.}{\beta }\left(\gamma \right)=\stackrel{.}{\gamma }q\left(\gamma \right)\Vert q\left(\gamma \right)\Vert =\Vert \sqrt{\stackrel{.}{\gamma }}q\left(\gamma \right)\Vert \sqrt{\stackrel{.}{\gamma }}q\left(\gamma \right)$. The reparameterization q by γ is defined as a right action of the group D on the set C and written as $q\cdot \gamma =\sqrt{\stackrel{.}{\gamma }}(q\circ \gamma )$. Thus are interested in constructing the shape space as a quotient space of ${\mathbb{S}}^q$, modulo shape preserving transformations such as rigid rotations and reparameterizations.

Altogether, the set of curves affected by the group actions above, partition the space ${\mathbb{S}}^q$ into equivalence classes. We now define the elastic shape space as the quotient space $\mathcal{S}={\mathbb{S}}^q∕(SO\left(3\right)\times \mathcal{D})$. The problem of finding a geodesic between two shapes in S is same as finding the shortest path between the equivalent classes of the given pair of shapes. Since the actions of the re-parametrization groups on C constitute actions by isometries, this problem also amounts to minimizing the length of the geodesic path, such that

$$d_e(q_1,q_2)=\underset{O_3\in SO\left(3\right),\gamma \in \mathcal{D}}{\min }d(q_1,\left(O_3{q}_2\right)\cdot \gamma ),$$ (2)

where d is given by the geodesic distance. In order to optimize Eq. 2, we recognize that for a fixed rotation O₃, the distance d_e can be obtained by finding the optimal reparameterization $\widehat{\gamma }$ between q₁ and q₂, whereas for a fixed γ, the distance d_e is calculated by finding the optimal rotation Ô₃. Thus in order to minimize the distance in Eq. 2, we alternate between optimizing over O₃ and γ repeatedly until the process converges. At each step, the optimal rotation Ô₃ is given by Ô₃ = USV^T, where, all $U,S,V\in {\mathbb{R}}^{3\times 3}$, and given by the singular decomposition of Ô₃. Furthermore this decomposition is approximated using the ${\mathbb{L}}^2$ function given by $US{V}^T={\int }_0^{2\pi }{q}_1\left(s\right)q_2{\left(s\right)}^{T}ds$. Also, at each iteration, we compute a geodesic path between the starting shape q₁ and the target shape O₃q₂ · γ. Upon convergence of this procedure, we also obtain the tangent vector $\stackrel{.}{\chi }$ along the geodesic path connecting the two shapes.

2.3 Construction of a Statistical Sulcal Atlas

In order to construct a sulcal atlas of a large population of curves in the shape space, we need the notion of a shape average based on the sulcal and gyral curves. Owing to the nonlinearity of the shape space, the computation of an average shape is not straightforward. There are two well known approaches of computing statistical averages in such spaces. The extrinsic shape average is computed by projecting the elements of the shape space in the ambient linear space, where an Euclidean average is computed, and subsequently projected back to the shape space. On the other hand, the intrinsic average, also known as the Karcher mean ([6]) is computed directly on the shape space, and makes use of distances and lengths that are defined strictly on the manifold. It uses the geodesics defined via the exponential map, and iteratively minimizes the average geodesic variance of the collection of shapes. We will adopt the intrinsic approach by computing the Karcher mean for a given set of shapes. The Karcher mean is computed by minimizing the geodesic variance for a given collection of shapes. In other words, given a set of shapes {q_i}, i = 1, . . . , N, the Karcher mean is given by $\mu ={\mathrm{argmin}}_{q_{\mu }}{\sum }_{i=1}^N{d}_e{(q_{\mu },q_i)}^2,i=1,\dots ,N$. This mean is computed by an optimization procedure that involves repeated computations of geodesics from each of the shapes of the population to the current estimate of the mean. Next, we describe the procedure of combining the nonlinear sulcal atlas along with cortical surface registration for mapping brains across populations.

3 Integrating Sulcal Shapes with Cortical Surface Registration

In this section, we introduce our scheme for registering cortical surfaces. There have been several prominent approaches [10,4,1] for cortical registration in the neuroimaging community. Our method, although based on the same conceptual framework of elastic registration, provides a slightly different model for computing the deformation, with certain improvements in the implementation that increase flexibility and efficiency. A general outline of the process is as follows. The first stage is to establish homology of the curve data, which is accomplished by matching the shapes in a Riemannian shape space framework. Next, the surfaces and curves are conformally mapped to the sphere, establishing a common space where deformation will be defined. Following this, there is a rotational alignment of the surfaces and curves to account for the differences in spherical mapping orientations. Next, the spherical mean of the curves is found to define the atlas curves for the domain of the deformation. Finally, the elastic deformation of the atlas on the sphere is found, which constrained to map the atlas curves to each case's set of curves. The surfaces are reparameterized by this elastic deformation. The resulting surfaces then have homologous coordinate systems, allowing local comparisons across the group. We define a set of N surfaces, {M₁ , ...,M_N} where $M_i\subset {\mathbb{R}}^3$. We represent their mesh geometry using a set of simplicial complexes, {(K₁, f₁), ..., (K_N, f_N)} where K_i is a simplicial complex and $f_i:K\mapsto M_i$. For each surface i, we have a set of M landmarks represented by continuous open curve {β_i1,..., β_iM} where ${\beta }_{ij}:[0,2\pi ]\mapsto M_i$, and the set of curves $\{{\beta }_{ij}:i\in [1,N]\}$ represent homologous regions on the set of surfaces. Additionally, the curves are discretized, where the j-th curve has k_j vertices. The first step of the process is to establish correspondence between the homologus landmark curves by computing mappings ${\widehat{\gamma }}_{ij}:[0,2\pi ]\mapsto [0,2\pi ]$ such that for curve j and parameter t, the set $\{{\beta }_{ij}\left({\gamma }_{ij}\left(t\right)\right):i\in [1,N]\}$ is a set of homologous points on the surfaces. This is accomplished by mapping the curves to a Riemannian manifold shape space, where reparameterizations are defined by geodesics to the Karcher mean of the curves in the shape space.

3.1 Spherical Mapping and Alignment

Next, the meshes are simplified using a QEM-based method, and a set of conformal mappings is found from each surface to the unit sphere, $\{{\varphi }_1,\dots ,{\varphi }_N\}$ where ${\varphi }_i:M_i\mapsto S^2$ S². The spherical mapping of the matched curves is then $\widetilde{{\beta }_{ij}}={\varphi }_i\circ {\beta }_{ij}\circ {\gamma }_{ij}$, which is found using the barycentric coordinates of each curve vertex. A bounded interval hierarchy is used to efficiently search for the coincident face of each curve vertex. Once the data are mapped to the sphere, they are rotationally aligned to enforce a consistent orientation of the spherical mappings. Given an arbitrarily chosen target, each set of curves is aligned to the target by computing the rotation and reflection that minimizes the least-squared difference between the discretized curve coordinates. This is accomplished by solving the unconstrained orthogonal Procrustes problem using singular value decomposition, allowing reflections to account for the inversion between the hemispheres. For an arbitrary $T\in \{\widetilde{{\beta }_{ij}}:i\in [1,N]\}$, we find an optimal alignment $R_i\in {\mathbb{R}}^{3\times 3}$ and then optimally rotate the data as, ${\widehat{\varphi }}_i=R_i\circ {\varphi }_i$, and $\widehat{{\beta }_{ij}}=R_i\circ \widetilde{{\beta }_{ij}}$.

3.2 Spherical Curve Atlas

Once the data have been aligned on the sphere, the mean curves are computed to serve as the atlas curves in the surface warping. The Karcher mean on the sphere is found for each vertex of each curve. In this method, an initial guess is found by the normalized average of the points. For this point, the tangent space is defined by the gnomonic projection. A new mean is computed in the tangent space and then is mapped back to the sphere, repeating this process until convergence. We can express the curve atlas as the set $\{\overline{{\beta }_j}:j\in [1,M]\}$, where $\overline{{\beta }_j}$ is the karcher mean of $\{\widehat{{\beta }_{ij}}:i\in [1,N]\}$.

3.3 Elastic Surface Warping

For surface i, the deformation of the atlas is ${\varphi }_i:S^2\mapsto S^2$, where ${\varphi }_i\left(\overline{{\beta }_j}\left(t\right)\right)=\widehat{{\beta }_{ij}}\left(t\right)$ for t ∈ [0, 2π], j ∈ [1, M]. Six flattenings of the sphere are defined $\{{\phi }_n:S^2\mapsto {[0,1]}^2:n\in 1,2,3,4,5,6\}$. For a point on the sphere, p ∈ S², the optimal flattening is chosen as ${\phi }_p=\arg {\min }_{{\phi }_n}\Vert {\phi }_n\left(p\right)-(\frac{1}{2},\frac{1}{2})\Vert$. The displacement field $u_p:S_2\mapsto {\mathbb{R}}^2$ is then $u_p\left(x\right)={\phi }_p\left({\varphi }_i\left(x\right)\right)-{\phi }_p\left(x\right)$. At non-landmark points, i.e. $x\in S^2,x\notin {\cup }_j\{\widehat{{\beta }_{ij}}\left(t\right):t\in [0,2\pi ]\}$, the mapping is constrained to satisfy a small deformation elastic proposed by Thompson et al. [10], and is given by

$$\mu {\nabla }^2{u}_p\left(x\right)+(\lambda +\mu )\nabla (\nabla \cdot u_p\left(x\right))=0$$ (3)

The atlas mesh is defined on the sphere by tessellating the sphere with a subdivided octahedron [7]. This representation is advantageous for its multiscale processing and flattening. The flattening can be imagined as follows. First, choose one of the vertices of the octahedron to map the center of the grid. Then, cut the four far edges that do not contain the center vertex. These edges are duplicated and define the boundary of the grid, and the opposite vertex maps to the four corners of the grid. The deformation is computed iteratively using multigrid finite differences, where the octahedral subdivisions and flattenings are used for prolongation and restriction operations. The solver accounts for the spherical topology of the domain by solving the above nonlinear model and resampling the deformed atlas by establishing vertex homology between the meshes.

4 Experimental Results

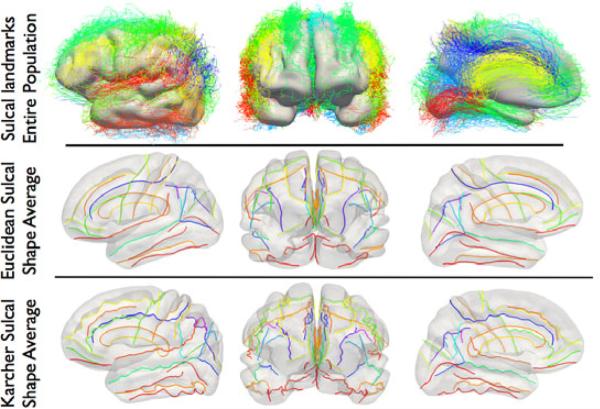
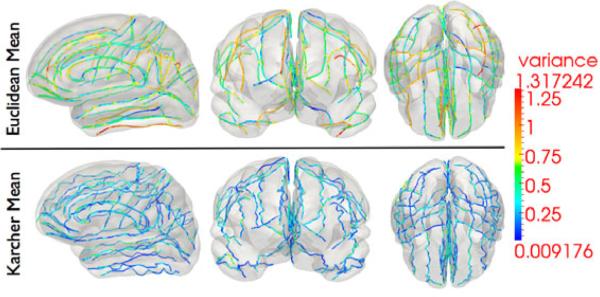
Our experimental data consisted of 3T MRI acquisitions (GE) for a population of 69 healthy, Chinese, right-handed volunteers (30 men, 39 women; 18-33 yr) using a transverse 3D T1-weighted fast spoiled gradient-echo (FSPGR) sequence (TR/TE = 6.8 cm; ms/2.9 ms; voxel size = 0.47 mm × 0.47 mm × 0.70 mm; FOV = 24.0 × 24.0 cm; matrix size = 512 × 512; flip angle = 10°, slice thickness = 1.4 mm, and slice gap = 0.7 mm). After preprocessing the raw data, and registering it stereotaxically to a standard atlas space, the cortical surfaces for these subjects were extracted using an automated algorithm [2]. For each of these subjects, a total of 27 landmark curves were manually traced. Figure 1 shows the original 27 landmark curves for each of the 69 subjects for both hemispheres overlaid together. Additionally, Figure 1 also shows the intrinsic sulcal shape averages of the 27 landmark curves, as well as the respective extrinsic Euclidean averages for the same. While computing the extrinsic average, each curve for the same landmark type was mapped to its q representation, thus making it scale and translation invariant. The Euclidean average of all the q functions was then computed after a pairwise rotational alignment. Both the Karcher mean shapes as well as the Euclidean averages were then mapped back to the native space in order to visualize them. It is observed that the intrinsic averages although smooth, have preserved important features along the landmarks, thus representing the average local shape geometry along the sulci and gyri. This also implies that the shape average has not only captured the salient geometric features, but has also reduced the shape variability in the population. In order to demonstrate this property, we plot the variance of the shape deformation for each landmark type as captured by the velocity vector along the geodesic path, both for Euclidean extrinsic, and Riemannian intrinsic averages. This quantity measures the invariant deformation between a pair of shapes, and only depends upon the intrinsic geometry of the shapes. For both of these averages, the tangent vectors were computed using the procedure outline in Section 2.2 and the computations were done using the elastic geodesic method for consistent comparisons. Figure 2 shows a comparison of the plots of $\frac{1}{69}{\sum }_1^{69}{\left(\langle \stackrel{.}{\chi }\left(i\right),\stackrel{.}{\chi }\left(i\right)\rangle \right)}^2$ for each of the landmarks, taken along the length of the curve, for both Euclidean shape averages, as well as intrinsic shape averages. Here the $\stackrel{.}{\chi }\left(i\right)$ is the tangent vector from the mean shape to i^th shape. From the color-coded map, it is observed that the intrinsic average has reduced the variance in terms of shape geometry deformation, and thus is a better representative of the population.

Fig. 1.

Lateral, frontal, and medial views of, top row: 27 landmark sulci and gyri for 69 subjects, middle row: Euclidean sulcal shape averages, bottom row: Karcher shape average for each landmark type

Fig. 2.

Comparison of the geodesic variance for the entire sulcal population for each of the 27 landmarks, both for Euclidean shape averages, as well as elastic shape averages, along the length of the curves

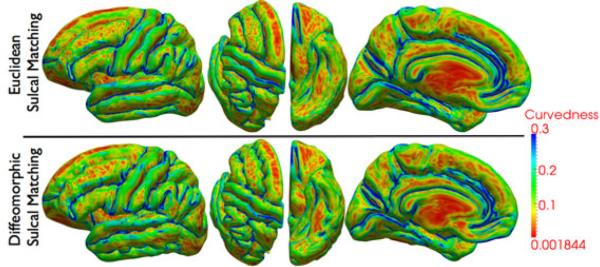
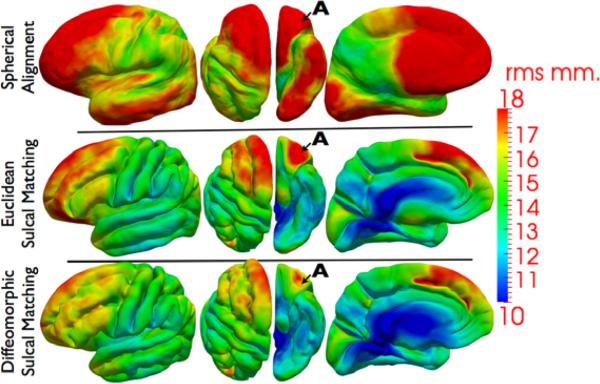
Next, we demonstrate results of cortical surface registration with and without the incorporation of the above diffeomorphic sulcal atlas in Figure 1. As an initial step, we compute geodesics between the average shape of the landmark, and the set of all sulci belonging to that landmark type, and reparameterize the set of sulci according to inverses of the resulting diffeomorphisms. We then follow the steps outlined in Sec. 3 in order to warp all the surfaces meshes to the atlas. Figure 3 shows three the lateral, axial, ventral, and medial views of the reconstructed cortical surface averages from the flattened representations. The surface is colored by its curvedness in order to highlight the fundi of the sulci as well as the ridges of the gyri. It is observed that the surface with diffeomorphic sulcal mapping shows richer geometric detail than the traditional Euclidean reconstruction. As another measure of distortion, we also computed the root mean square (r.m.s.) error of the distance from each sample surface to the average reconstructed cortical surface with and without diffeomorphic sulcal matching. It is observed that the diffeomorphic method yields lower errors throughout the surface as compared to the Euclidean matching. Interesting, the diffeomorphic mapping approach has also shown considerable improvement in the frontal lob (Labeled as A in Figure 4) even in the absence of sulcal landmarks. The results from spherical alignment are also shown for comparison.

Fig. 3.

Lateral, axial, ventral, and medial views of the reconstructed cortical surface with Euclidean sulcal matching (top), and diffeomorphic sulcal matching (bottom). The surfaces are colored according to shape curvedness.

Fig. 4.

R.M.S error of the distance from each sample surface to the average reconstructed cortical surface with and without diffeomorphic sulcal matching shown for left hemisphere. There is considerable improvement in registration even where there is an absence of landmarks (labeled as A).

5 Conclusion

We have presented a direct diffeomorphic approach for shape analysis of sulcal and gyral features and demonstrated its application in cortical surface registration. We emphasize that the use of the sulcal atlas is not limited to registration alone, and can be also used to study cortical patterns for developmental, diseased or even normative patterns. The success of our method on deep brain sulci also demonstrates the effectiveness in capturing the intrinsic shape variability of the sulci and gyri. In the future, we intend to perform extensive validation studies for large populations as well as apply the sulcal models for neuroimaging population studies.