Identification of neutral tumor evolution across cancer types

Abstract

Despite extraordinary efforts to profile cancer genomes, interpreting the vast amount of genomic data in the light of cancer evolution remains challenging. Here we demonstrate that neutral tumor evolution results in a power-law distribution of the mutant allele frequencies reported by next-generation sequencing of tumor bulk samples. We find that the neutral power-law fits with high precision 323 of 904 cancers from 14 types, selected from different cohorts. In malignancies identified as neutral, all clonal selection occurred prior to the onset of cancer growth and not in later-arising subclones, resulting in numerous passenger mutations that are responsible for intra-tumor heterogeneity. Reanalyzing cancer sequencing data within the neutral framework allowed the measurement, in each patient, of both the in vivo mutation rate and the order and timing of mutations. This result provides a new way to interpret existing cancer genomic data and to discriminate between functional and non-functional intra-tumor heterogeneity.

Introduction

Unraveling the evolutionary history of a tumor is clinically valuable, as prognosis depends on the future course of the evolutionary process, and therapeutic response is determined by the evolution of resistant subpopulations^1,2. In humans, the details of tumor evolution have remained largely uncharacterized as longitudinal measurements are impractical, and studies are complicated by inter-patient variation³ and intra-tumor heterogeneity (ITH)^4,5. Several recent studies have begun tackling this complexity⁶, revealing patterns of convergent evolution⁷, punctuated dynamics⁸, and intricate interactions between cancer cell populations⁹. However, the lack of a rigorous theoretical framework able to make predictions on existing data¹⁰ means that results from cancer genomic profiling studies are often difficult to interpret. For example, how much of the detected intra-tumor heterogeneity is actually functional is largely unknown, also because a rigorous ‘null model’ of genomic heterogeneity is lacking. In particular, interpreting the mutant allele frequency distribution reported by next-generation sequencing (NGS) is problematic because of the absence of a formal model linking tumor evolution to the observed data. Therefore, making sense of the wealth of available sequencing data in cancer remains challenging.

Here we show that the subclonal mutant allele frequencies of a significant proportion of cancers of different types and from different cohorts precisely follow a simple power-law distribution predicted by neutral growth. In those neutral cancers, all tumor-driving alterations responsible for cancer expansion were present in the first malignant cell and subsequent tumor evolution was effectively neutral. We demonstrate that under neutral growth, the fundamental parameters describing cancer evolution that have been so far inaccessible in human tumors, such as the mutation rate and the mutational timeline, become measurable. Importantly, this approach allows identifying also non-neutral malignancies, in which ongoing clonal selection and adaption to microenvironmental niches may play a strong role during cancer growth.

Results

Neutral cancer growth

Recently, we showed that colorectal cancers (CRC) often grow as a single expansion, populated by a large number of intermixed subclones¹¹. Consequently, we expect that after malignant transformation, individual subclones with distinct mutational patterns grow at similar rates, coexisting within the tumor for long periods of time without overtaking one another. Moreover, only a handful of recurrent driver alterations have been identified in CRC¹², and those are reported to be ubiquitous in multi-region sampling¹¹ and stable during cancer progression¹³, indicating that they all occurred in the “first” cancer cell and that subsequent clonal outgrowths are relatively rare. Consequently, we hypothesized that cancer evolution may often be dominated by neutral evolutionary dynamics.

The dynamics of neutral evolutionary processes have been widely studied in the context of molecular evolution and population genetics^14–16 as well as in mouse models of cancer¹⁷. However, the widely held presumption that subclone dynamics in human cancers are dominated by strong selection has meant these ideas have been neglected in current studies of cancer evolution.

Motivated by this, here we present a theoretical model describing the expected pattern of subclonal mutations within a tumor that is evolving according to neutral evolutionary dynamics. The model postulates that, after the accumulation of a “full house” of genomic changes that initiates tumor growth, some tumors expand neutrally, generating a large number of passenger mutations that are responsible for the extensive and common ITH. The parameter-free model is applicable to NGS data from any solid cancer. Here we present the model, and by applying it to large pre-existing cancer genomics datasets, determine which tumors are consistent with neutral growth. When the model applies, we measure new tumor characteristics directly from the patient’s data.

Model derivation

A cancer is founded by a single cell that has already acquired a significant mutation burden³: these “pre-cancer” mutations will be borne by every cell in the growing tumor, and so become “public” or clonal. Mutations that occur within different cell lineages remain “private” or subclonal in an expanding malignancy under the absence of strong selection. Here we focus on subclonal mutations as they contain information on the dynamics of the cancer growth. We denote the number of tumor cells at time t as N(t), with cells dividing at rate λ per unit time. During a cell division, somatic mutations occur at rate μ. If we consider an average number of π chromosome sets in a cancer cell (e.g. the ploidy of the cell), we can calculate the expected number of new mutations per time interval as:

$$\frac{dM}{dt}=\mu \pi \lambda N(t)$$ [1]

Solving this requires integrating over the growth function N(t) in some time interval [t₀,t]:

$$M(t)=\mu \pi \lambda {\displaystyle \underset{t_0}{\overset{t}{\int }}N(t)dt}$$ [2]

Since not all cell divisions may be successful in generating two surviving lineages due to cell death or differentiation, we introduce the fraction β of “effective” cell divisions in which both resulting lineages survive. In the case of exponential growth, the mean number of tumor cells as a function of time is therefore:

$$N(t)=e^{\lambda \beta t}$$ [3]

Substituting into equation [2] gives the explicit solution:

$$M(t)=\frac{\mu \pi }{\beta }\left(e^{\lambda \beta t}-e^{\lambda \beta t_0}\right)$$ [4]

This equation describes the total number of subclonal mutations that accumulate within a growing tumor in the time interval [t₀, t] . We note that for t₀=0 equation [4] corresponds to the Luria-Delbrück model, which describes mutation accumulation in bacteria¹⁸. In our case, this equation is of limited use as none of the parameters μ, λ, β or the age of the tumor t can be measured directly in humans. However, we do know that for a new mutation occurring at any time t, its allelic frequency (the relative fraction) f must be the inverse of the number of alleles in the population:

$$f=\frac{1}{\pi N(t)}=\frac{1}{\pi e^{\lambda \beta t}}$$ [5]

For example, if a new mutation arises in a tumor of 100 cells, it will comprise a fraction of 1/100. In the absence of clonal selection (or indeed significant genetic drift), the allelic frequency of a mutation will remain constant during the expansion, as all cells, with and without this mutation, grow at the same rate. In the previous example, after one generation has elapsed, we will have 2 cells with that particular mutation, but a total of 200 tumor cells, again a fraction of 1/100. This implies that in the neutral case, tumor age t and mutation frequency f are interchangeable. For example, t₀=0 in a diploid tumor (π=2), corresponds to f_max=0.5 (the expected allelic frequency of clonal variants):

$$f_{\max }=\frac{1}{\pi e^{\lambda \beta t_0}}$$ [6]

Substituting t for f in equation [4] gives an expression for the cumulative number of mutations in the tumor per frequency M(f):

$$M(f)=\frac{\mu }{\beta }\left(\frac{1}{f}-\frac{1}{f_{\max }}\right)$$ [7]

thus converging to the solution for expanding populations under neutrality obtained using other approaches^19–22. Critically, the distribution M(f) is naturally provided by NGS data from bulk sequencing of tumor biopsies and resections, against which the model can be tested. The model predicts that mutations arising during a neutral expansion of a cancer accumulate following a 1/f power-law distribution. In other words, when neutral evolution occurs in a tumor, the number of mutations detected should accumulate linearly with the inverse of their frequency. The 1/f noise or pink noise is common in nature and found in several physical, biological and economic systems²³.

Importantly, the coefficient μ_e=μ/β is the mutation rate per effective cell division, and corresponds to the easily measureable slope of M(f). This model therefore provides a straightforward parameter-free method to measure the in vivo mutation rate in a patient’s tumor using a single NGS sample. We note that the results do not depend on the identity of the alterations considered, since any genomic alteration (mutations, copy number changes or epigenetic modifications) anywhere in the genome that changes the dynamics of tumor growth (e.g. any alteration that is clonally selected) would result in deviation from the neutral 1/f power-law by causing an over- or under-representation of the alleles in that clone. Hence, here we use single nucleotide variants as ‘barcodes’ to follow clone growth. Stochastic simulations of neutral tumor growth confirm the analytical solution in equation [7] (see Online Methods).

Identification of neutrality in colorectal cancer evolution

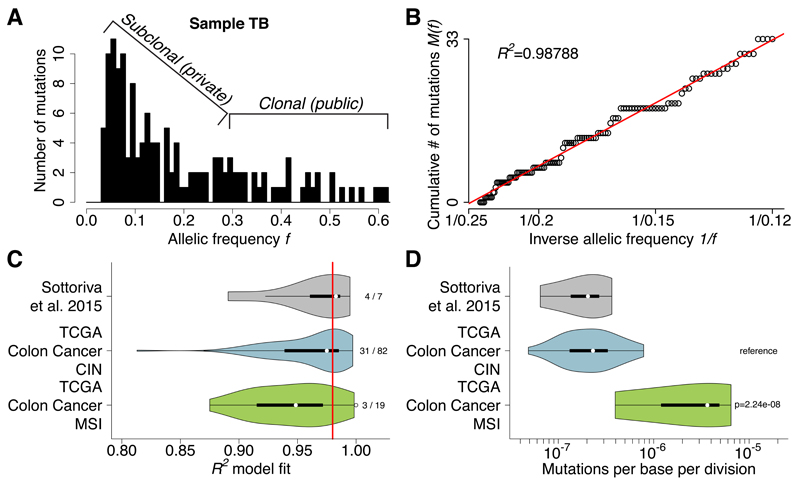
A typical allelic frequency distribution of mutations in a tumor measured by NGS whole-exome sequencing is shown in Figure 1A (data from ref11). Considering tumor purity and aneuploidy, mutations with high allelic frequency (>0.25) are likely to be public (clonal) while all others are likely subclonal. The same data can be represented as the cumulative distribution M(f) of subclonal mutations as in equation [7] (Figure 1B). Remarkably, as reported by the high goodness-of-fit measure R², these data precisely follow the distribution predicted by the model, indicating that this tumor grew under neutral evolutionary dynamics.

Figure 1. Neutral evolution is common in colon cancer and allows the measurement of mutation rates in each tumor.

(A) The output of NGS data, such as whole-exome sequencing, can be summarized as a histogram of mutant allele frequencies, here for sample TB. Considering purity and ploidy, mutations with relatively high frequency (>0.25) are likely to be clonal (public), whereas low frequency mutations capture the tumor subclonal architecture. (B) The same data can be represented as the cumulative distribution M(f) of subclonal mutations. This was found to be linear with 1/f, precisely as predicted by the neutral model. (C) R² goodness of fit of our CRC cohort (n=7) and the TCGA colon cancer cohort (n=101) grouped by CIN versus MSI confirmed that neutral evolution is common (38/108, 35.1% with R²≥0.98). (D) Measurements of the mutation rate showed that the CIN groups had median mutation rate of µ_e=2.31×10^-7, whereas MSI tumors reported a 15-fold higher rate (median: µ_e=3.65×10^-6, F-test: p=2.24×10^-8), as predicted due to their DNA mismatch repair deficiency.

We next considered our cohort of 7 multi-sampling CRCs¹¹ and 101 TCGA colon adenocarcinomas¹² selected for high tumor purity (≥70%) that underwent whole-exome sequencing (see Online Methods). The latter were separated between tumors characterized by chromosomal instability (CIN) versus microsatellite instability (MSI). The power-law is remarkably well supported in both these cohorts, with 38/108 (35.1%) of the cases reporting a high R²≥0.98 (Figure 1C). These results confirm that in a large proportion of colon cancers, intra-tumor clonal dynamics are not dominated by strong selection but rather follow neutral evolution. In particular, a larger proportion of CIN cancers evolved neutrally (31/82, 37.8%) with respect to MSI cancers (3/19, 15.7%) (Figure 1C), possibly because the latter acquired so many new mutations that some are likely under strong selection. Since M(f) is a monotonic growing function, this stringent threshold of R²≥0.98 was chosen to prevent over-calling neutrality, but we note that we may have therefore misclassified some tumors as non-neutral due to limited sequencing depth or low mutation burden. R² values were independent from the mean coverage of mutations, the total number of mutations in the sample or the number of mutations within the model range (see Online Methods). See Supplementary Data Set 1 for summary of TCGA data used.

Measurement of the mutation rate in colorectal cancer

Estimating the per-base mutation rate μ per division in human malignancies is challenging since direct measurements are not possible. Previous estimates critically depend on assumptions about the cell cycle time and the growth rate λ, as well as on the total mutational burden of the cancer^24–26. However, accurate measurement of all mutations within a cancer, including heterogeneous subclonal variants, is technically unfeasible since most mutations are present in very small numbers of cells⁴. With our approach it is possible to circumvent this issue by measuring the rate of accumulation of subclonal mutations represented by the slope of M(f). In the case of neutral evolution, this can be done in principle within any (subclonal) frequency range, without the need of detecting extremely rare mutations. We estimated the mutation rate in all samples with R²≥0.98 (Figure 1D) and found that it was more than 15-fold higher in the MSI group (median: μ_e=3.65×10^-6) with respect to the CIN group (median: μ_e=2.31×10^-7; F-test: p=2.24×10^-8) and our cohort of CRCs (median: μ_e=2.07×10^-7), which was comprised of all but one CIN tumors¹¹. Different mutational types (e.g. transitions or transversions) are caused by particular mutational processes²⁷, and so likely occur at different rates and accordingly we found that C>T mutations occurred at median μ_e,C>T=2.19×10^-7, a rate nearly 10-fold higher than any other type of mutation (F-test: p=3.13×10^-3; Supplementary Figure 1A). We stratified according to CIN versus MSI and found that the mutation rate of each mutational type reflected the overall mutation rate for the group (Supplementary Figure 1B). The variation in mutation rates within and between subgroups was remarkably in line with the variation in estimates of mutational burden in colon cancer³. We note the mutation rate estimate is scaled by the (unknown) effective division rate β, which means for example that if only 1 in 100 cell divisions leads to two surviving offspring (β=0.01), then the mutation rate μ is 100 times lower than the effective rate μ_e reported. Importantly, mutation rates of non-neutral cases (R²<0.98) cannot be estimated, as the model does not fit the dynamics of these tumors.

We examined the effect of copy-number changes in the model by performing the analysis using only mutations in diploid regions and found highly similar proportions of neutral tumors and mutation rates (see Online Methods and Supplementary Figure 2). The validity of the variant calls was also corroborated by the consistency of the underlying mutational signature across a range of allelic frequencies; hence the results are unlikely to be influenced by sequencing errors (Supplementary Figure 3).

Frequent selection events should induce a higher number of missense and nonsense mutations than expected by chance whereas under neutrality we expect the same rate of silent and non-silent mutations. To test this, we contrasted the estimated rate of synonymous mutations (unlikely to ever be under selection) versus the rate of missense and nonsense mutations (liable to experience selection). Although the latter are more common than the former, after adjustment for the number of potential synonymous and nonsynonymous sites in the exome, the two rates were equivalent (Supplementary Figure 4), consistently with neutral evolution.

Neutral evolution in coding and non-coding regions

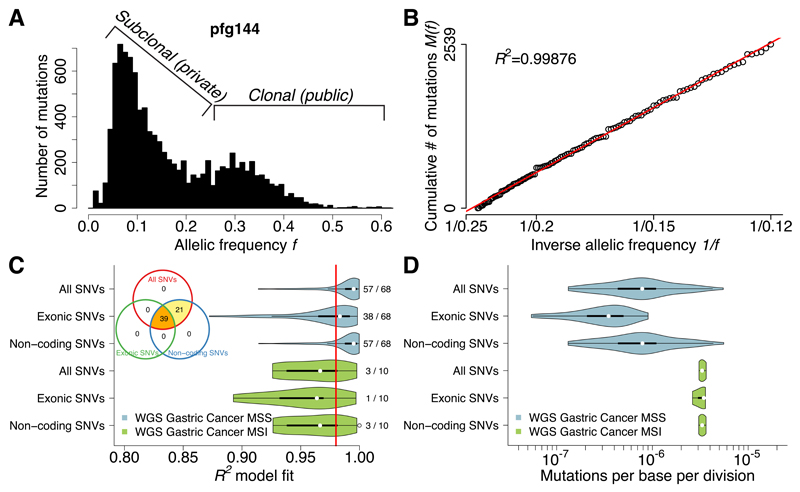
We next tested whether the signature of neutral evolution could be detected across the entire genome, not just in coding regions. To do this, we analyzed 78 gastric cancers from a recent study²⁸ subjected to high depth whole-genome sequencing. The large number of mutations detected by WGS accumulated precisely as predicted by the model (example in Figure 2A,B), revealing neutral evolution in 60/78 (76.9%) cases (Figure 2C). A smaller proportion of MSI tumors were neutral (3/10, 30%) than microsatellite stable (MSS) tumors (57/68, 83.8%), in line with the observation in CRC. A tumor was consistently classified as neutral independently of whether all SNVs or only non-coding SNVs were used to perform the classification (Figure 2C, Venn diagram), whereas due to the limited number of mutations available in the exome alone, fewer tumors were identified as neutral. Importantly, every case was verified as neutral by at least two different variant sets. These results confirm that neutral evolution can be robustly assessed from mutations anywhere in the genome.

Figure 2. Neutral evolution across the whole-genome of gastric cancers.

(A) Large number of coding and non-coding mutations can be identified using WGS. (B) All detected mutations precisely accumulate as 1/f following the neutral model in this example. (C) Neutral evolution is very common in gastric cancer, with 60/78 (76.9%) samples showing goodness of fit of the neutral model R²≥0.98. This was consistent using all, exonic or non-coding subclonal mutations. The same tumors were identified as neutral by all three methods, although limitations in detecting neutrality were present when considering exonic mutations due to the limited number of variants. (D) Mutation rates were more than 4 times higher in MSI (µ_e=3.30×10^-6) versus MSS (µ_e=7.82×10^-7; F-test: p=1.35×10^-4) cancers, consistently with the underlying biology.

Mutation rate analysis of the neutrally evolved gastric cancers showed that cancers with MSI had a more than fourfold higher mutation rate (μ_e=3.30×10^-6) with respect to MSS (μ_e=7.82×10^-7; F-test: p=1.35×10^-4) (Figure 2D). Results were robust to copy number changes when the analysis was performed only using variants in diploid regions (Supplementary Figure 5). The mutational signature of the variant calls for this cohort was also consistent across the frequency spectrum (Supplementary Figure 6). Synonymous versus nonsynonymous mutation rates were also consistent with neutral evolution (Supplementary Figure 7). See Supplementary Data Set 2 for summary of Wang et al. data used.

Neutral evolution across cancer types

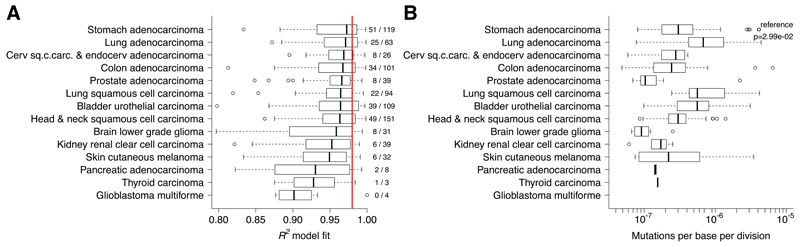
We then applied the neutral model to a large pan-cancer cohort of 819 exome-sequenced cancers from 14 tumor types from the TCGA consortium (which included the 101 colon cancers previously examined). All of these samples had been pre-selected for high tumor purity (≥70%). The fit of the model was remarkably good across types (Figure 3A) with 259/819 (31.6%) cases showing R²≥0.98. We found that neutral evolution was more prominent in some tumor types, such as stomach (validating the WGS analysis), lung, bladder, cervical, and colon. Others showed a consistently poorer fit, indicating that the clonal dynamics in these malignancies were typically not neutral, such as in renal, melanoma, pancreatic, thyroid, and glioblastoma. Consistent with these results, “non-neutral” renal carcinoma has been shown to display convergent evolution in spatially disparate tumor regions driven by strong selective forces⁷, whereas the same phenomenon was not found in more “neutral” lung cancer^29,30. Other types displayed mixed dynamics, with some cases that were characterized by neutral evolution and some that were not. We note that a proportion of melanoma samples in this cohort are derived from regional metastases and not primary lesions, and this could potentially explain the lack of neutral dynamics observed.

Figure 3. Neutral evolution and mutation rates across cancer types.

(A) R² values from 819 cancers of 14 different types supported neutral evolution in a large proportion of cases (259/819, 31.6% of R²≥0.98) and across different cancer types, particularly in stomach (validating the WGS analysis), lung, bladder, cervical and colon. On the contrary, renal, melanoma, pancreatic, thyroid, and glioblastoma were characterized by non-neutral evolution. The other types displayed a mixed dynamics. (B) The highest mutation rates were found in lung cancer. Lower rates were found in thyroid, low grade glioma and prostate.

Mutation rate analysis on the neutral cases showed differences of more than an order of magnitude between types (Figure 3B). The highest mutation rates were observed in lung adenocarcinoma (median μ_e=6.79×10^-7) and in lung squamous cell carcinoma (median μ_e=5.61×10^-7) and the lowest rates in low grade glioma (median μ_e=9.22×10^-8) and in prostate (median μ_e=1.04×10^-7). We stratified the mutation rates into different mutational types (Supplementary Figure 8) and found that C>A mutations occurred at a significantly higher rate in lung cancers, consistent with their causation by tobacco smoke²⁷. C>T mutation rates were most consistent across cancer types, likely because of their association with replicative errors, as opposed to being caused by a particular stochastically-arising defect in DNA replication or repair²⁷.

These results demonstrate that within-tumor clonal dynamics can be neutral, and the classification of tumors based on neutral versus non-neutral growth dynamics leads to new measurements of fundamental tumor biology. See See Supplementary Data Set 1 for summary of TCGA data used.

In silico validation of the neutral model

To assess the different inherent sources of noise in NGS data (normal contamination, limited sequencing depth, tumor sampling), we designed a stochastic simulation of neutral growth that produced synthetic NGS data from bulk samples (see Online Methods). The simulations produced realistic synthetic NGS data (Supplementary Figure 9) with minimal assumptions and under a range of different scenarios for tumor growth dynamics (variable low mutation rate, variable number of clonal mutations) and sources of assay noise (normal contamination in the sample, sequencing depth, detection limit). For each of these potentially confounding factors, we were able to fit our neutral model to the synthetic NGS data and accurately recover both the underlying neutral dynamics and the mutation rate (Supplementary Figure 10). We also validated the prediction that M(f) would deviate from the neutral power-law in the presence of emerging subclones with a higher fitness advantage (Supplementary Figure 11A,B), as well as in the case of a mixture of subclones (as observed in ref.31) emerging either by means of clonal expansions triggered by selection, or by segregating microenvironmental niches (Supplementary Figure 11C-F). Variation of mutation rate between subclones also causes a deviation from neutrality (Supplementary Figure 11G,H). These results confirm the reliability of the conservatively high R² threshold used to call neutrality.

Mutational timelines

Under neutral evolution, it is possible to estimate the size of the tumor when a mutation with frequency f arose from equation [5]:

$$N(t)=\frac{1}{\pi f}$$ [8]

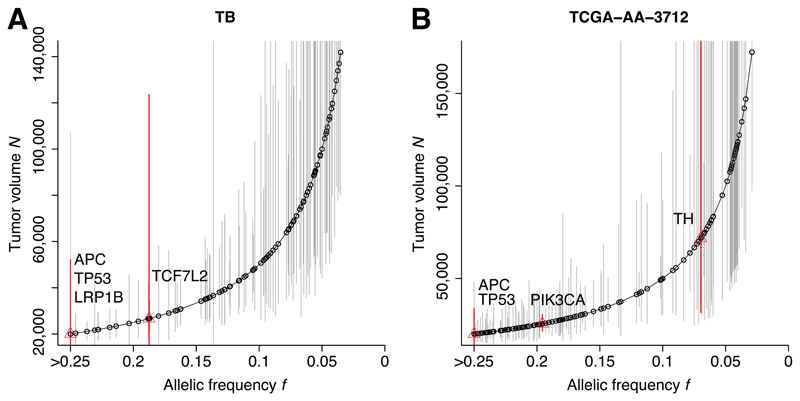
Figure 4A,B shows the decomposition of the mutational timeline for two illustrative cases: sample TB from¹¹ and sample TCGA-AA-3712 from¹². Previous estimates of mutational timelines relied on cross-sectional data^32–35, which are compromised by the extensive heterogeneity, whereas multi-region profiling approaches are instead more accurate but expensive and laborious^7,36,37. Using our formal model of cancer evolution, the timeline information becomes accessible from routinely available genomic data. We found that classical CRC driver alterations, such as in the APC, KRAS and TP53 genes, were indeed present in the first malignant cell (likely because they accumulated during previous neoplastic stages). This confirms what we previously reported using single-gland mutational profiling where all these drivers, when present, were found in all glands¹¹. However, we also found that when we considered a more extended list of putative drivers, many occurred during the neutral phase of tumor growth, suggesting that the selective advantage conferred by a putative driver alteration may be context-dependent, as demonstrated in a p53 murine model³⁸.

Figure 4. Reconstruction of the mutational timeline in each patient.

The allelic frequency of a mutation within the tumor predicts the size of the tumor when the mutation occurred. (A,B) The deconvolution of the mutational timeline is illustrated for samples TB and TCGA-AA-3712 respectively. Whereas established CRC drivers (APC, KRAS, TP53) were found to be present from the first malignant cell, several recurrent putative drivers not yet validated were mutated after malignant seeding, despite the underlying neutral dynamics. This suggests that some of these candidate alterations may not be fundamental drivers of growth in all cases. Confidence intervals are calculated using a binomial test on the number of variant reads versus the depth of coverage for each mutation.

Discussion

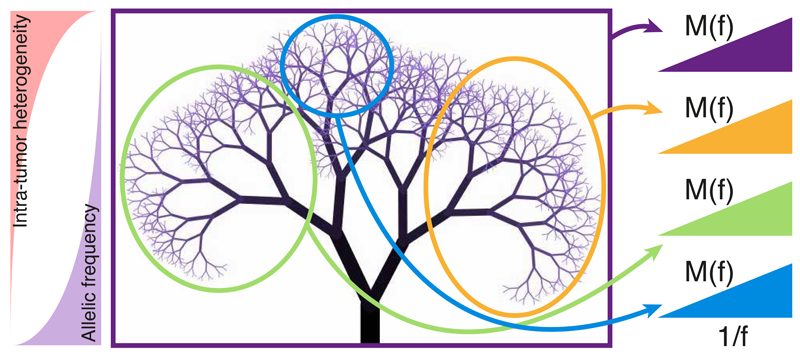
Understanding the evolutionary dynamics of subclones within human cancers is challenging because longitudinal observations are unfeasible and the genetic landscape of cancer is highly dynamic, leading to genomic data that are hard to interpret³⁹. In particular, complex non-linear evolutionary trajectories have been observed, such as punctuated evolution and karyotypic chaos^8,39,40. Here we have presented a formal law that predicts mutational patterns routinely reported in NGS of bulk cancer specimens. Our analysis of large independent cohorts using this framework shows that cancer growth is often dominated by neutral evolutionary dynamics, an observation that is consistent across 14 cancer types. Under neutrality, the clonal structure of a tumor is expected to have a fractal topology characterized by self-similarity (Figure 5). As the tumor grows, a large number of cell lineages are generated and therefore ITH rapidly increases while the allele frequency of the new heterogeneous mutations quickly decreases due to the expansion. This implies that sampling in different parts of the tree leads to the detection of distinct mutations which all show the same 1/f distribution. Clonal mutations found in a sample (not considered in the model) belong to the most recent common ancestor in the tree.

Figure 5. Neutral evolution and tumor phylogeny.

After the accumulation of key genomic alterations, in neutral malignancies the cancer expansion is likely triggered by a single critical genomic event (the accumulation of a “full house” of genomic changes) followed by neutral evolution that generates a large number of new mutations in ever-smaller subclones. While the tumor heterogeneity rapidly increases, the allele frequency of heterogeneous mutations decreases. In this context, the accumulation of mutations M(f) follows a characteristic 1/f distribution. Moreover, the tumor phylogeny displays a characteristic fractal topology that is self-similar. Sampling in different regions of the phylogenetic tree exposes distinct mutations that however show the same 1/f distribution. Clonal mutations in a sample (not considered in the model) arose in to the most recent common ancestor of the sampled cells. Due to the large population of cells sampled using bulk sequencing, the majority of detected clonal mutations belongs to the trunk of the tree and therefore is found in the first cancer cell. Deviations from the 1/f law indicate different dynamics from neutral growth.

We note that some cancers were dominated by neutral evolution whereas others were not. In non-neutral tumors, strong selection, microenvironmental constrains and non-cell autonomous effects⁴¹ may play a key role. Importantly, this formalization represents the ‘null model’ of cancer intra-clone heterogeneity that can be used to identify those cases in which complex non-neutral dynamics occur, and to discriminate between functional and non-functional intra-tumor heterogeneity. Furthermore, we speculate that neutral evolutionary dynamics may be favored by the cellular architecture of the tumor (e.g. glandular structures that limit the effects of selection) and/or the anatomical location of the malignancy (e.g. growing in a lumen versus growing in a highly confined space), as well as the presence of potentially selective microenvironmental features of the tumor such as hypoxic regions. Despite the evidence for lack of natural selection during malignant growth, eventual treatment is likely to “change the rules of the game” and strongly select for treatment resistant clones⁴². Treatment-resistance driver alterations that were not under selection during growth may expand due to new selective pressures introduced by therapy. The same may happen in the context of the purported evolutionary bottleneck preceding metastatic dissemination. Importantly, this reasoning highlights how ‘drivers’ can only be defined within a context, and so the same ‘driver’ alteration can be neutral in a certain microenvironmental context (e.g. absence of treatment), and not neutral in another (e.g. during treatment). Moreover, we predict that if a tumor is characterized by different microenvironmental niches but still presents as neutral, it is likely that adaptation will be driven by cancer cell plasticity, rather than clonal selection. Cell plasticity is hard to study in cancer because it implies a change in the cell phenotype that is not caused by any inheritable variation (genomic or epigenomic). This means that this phenomenon has been so far largely neglected in cancer. As neutrality can be used as the ‘null model’ with which to identify clonal selection, this facilitates the study of adaptation through plasticity directly in human malignancies. Furthermore, it is important to note that due to the intrinsic detection limits of sequencing technologies, it is possible to explore only the early expansion of cancer clones (Figure 5) and the dynamics of extremely small clones may remain undetected.

Importantly, the realization that the within-tumor clonal dynamics are neutral means that the in vivo mutation rate per division and the mutational timeline, factors that play a key role in cancer evolution, progression and treatment resistance can be inferred without the need to assume cell division rates. These measurements can be performed in a patient-specific manner and so may be useful for prognostication and the personalization of therapy. Recognizing that the growth of a neoplasm is dominated by neutral dynamics provides an analytically tractable and rigorous method to study cancer evolution and gain clinically relevant insight from commonly available genomic data.

Online Methods

Data analysis

The processing of exome-sequencing data from¹ and TCGA² involved variant calling on matched-normal pairs using Mutect³. A mutation was considered if the depth of coverage was ≥10 and at least 3 reads supported the variant. Mutations that aligned to a more than one genomic location were discarded. The WGS gastric cancers⁴ were processed using VarScan2⁵, with minimum depth of coverage for a mutation being 10x and at least 3 reads supporting the variant. Non-CRCs in the TCGA had mutations called using Mutect according to the pipeline described in ref6. Microsatellite instability in the TCGA colon cancer samples was called using MSIsensor⁷. Annotation was performed with ANNOVAR⁸.

To fit the neutral model to allele frequency data we considered only variants with allele frequency in the range [f_max,f_min] corresponding to [t₀,t] in equation [2]. The low boundary f_min reflects the limit for the reliable detectability of low-frequency mutations in NGS data, which is in the order of 10%³. The high boundary f_max is necessary to filter out public mutations that were present in the first transformed cell. In the case of diploid tumors, clonal mutations are expected at f_max=0.5 (mutations with 50% allelic frequency are heterozygous public or clonal), in the case of triploid tumors, this threshold drops to 0.33 and in the case of tetraploid neoplasms, it drops to 0.25. For all samples we used a boundary of [0.12-0.24] to account only for reliably called subclonal mutations and tumor purity in the samples. All the samples considered in this study were reported to have tumor purity ≥70% and a minimum of 12 reliably called private mutations within the fit boundary. Once these conditions were met in a sample, equation [7] was used to perform the fit as illustrated in Figure 1B and 2B. In particular, for x=1/f, equation [7] becomes a linear model with slope μ/β and intercept –μ/(β f_max). We exploited the intercept constraint to perform a more restrictive fit using the model y=m(x-1/f_max)+0.

Copy-number changes (allelic deletion or duplication) can alter the frequency of a variant in a manner that is not described by equation [7]. We assessed the impact of copy-number alterations (CNAs) on our estimates of the mutation rate within the TCGA colorectal cancer samples by using the paired publically available segmented SNP-array data to exclude somatic mutations that fell within regions of CNA. CNAs were identified having an absolute log-R-ratio>0.5, and the model fitting was performed only on diploid regions of the genome. In the gastric cancer cohort, regions with copy number changes were identified using Sequenza⁹ and removed from the analysis. Mutation rates were adjusted to the size of the resulting diploid genome. Supplementary Figures 2 and 5 demonstrate the robustness of our analysis to copy number changes. R² values were independent from the mean coverage of mutations (p=0.32), the total number of mutations in the sample (p=0.40), the mutation rate (p=0.11), or the number of mutations within the model range (p=0.65).

Stochastic Simulation of Tumor Growth

To further validate our analytical model and to test the robustness to the noise in NGS data, we developed a stochastic simulation of tumor growth and accumulation of mutations that allowed us to generate synthetic datasets. The model was written and analyzed in the Julia programming language (http://julialang.org/). We then applied the analytical model to the simulated data to confirm that sources of noise in NGS data do not considerably impact our results. In particular, we verified that we could reliably extract input parameters of the simulation (namely the mutation rate) from “noisy” synthetic data. Confounding factors in the data include normal contamination, sampling effects, the detection limit of NGS mutation calling, and variable read depth. We simulate a tumor using a branching process with discrete generations, beginning with a single “transformed” cancer cell that gives rise to the malignancy. Under exponential growth, the population at time t will be given by:

$$N(t)=R^t=e^{\ln (R)t}$$ [9]

Where R is the average number of offspring per cell and the time t is in units of generations. We will consider primarily the case when R=2 (a cell always divides into 2), but we will also consider values <2, noting that R must be greater than 1 to have growth. At each division, cells acquire new mutations at a rate µ and we assume every new mutation is unique (infinite sites approximation). The number of mutations acquired by a newborn cell at division is a random number drawn from a Poisson distribution. Each cell in the population is defined by its mutations and its ancestral history (by recording it’s parent cell). Using this information we can then reconstruct the history of the whole tumor and crucially, calculate the variant allele frequency of all mutations in the population. To relate the discrete simulation to the continuous analytical model we will now re-derive equation [7] within the context of our model. As we simulate a growing tumor using discrete generations, both the mutation rate µ and per capita growth rate λ=ln(R) are in units of generations. For an offspring probability distribution P=(p₀,p₁,p₂) where p_k=P(# of OFFSPRING = k) where, the average number of offspring R is simply given by the expected value of P:

$$R=E[P]=p_1+2p_2$$ [10]

For example, for R=2 we have P=(p₀=0,p₁=0,p₂=1). By choosing different offspring probability distributions we can easily modulate the growth rate. We note that we are now expressing both μ and λ as rates per generation rather than probabilities (all rates are scaled by units of generation). This allows us to write the growth function as N(t)=exp(λt) with λ=ln(R). Proceeding as in the main text, our cumulative number of mutations with an allelic frequency f is therefore:

$$M(f)=\frac{\mu }{\lambda }\left(\frac{1}{f}-\frac{1}{f_{\max }}\right)$$ [11]

Therefore, when fitting the model to our stochastic simulation we extract μ/λ from the linear fit, making it straightforward to compare the simulation with the analytical model.

NGS data only captures a small fraction of the variability in a tumor, as the resolution is often limited to alleles with frequency >10% due to sequencing depth and limitations in mutation calling. To account for this, we employ a multistage sampling scheme in our simulations. For all simulations reported here we grow the tumor to size 1,024 cells, which gives a minimum allele frequency of ~0.1%, considerably smaller than the 10% attainable in next generation sequencing data. After growing the tumor and calculating the VAF for all alleles, we take a sample of the alleles in the population, noting that we are assuming the population is well mixed and has no spatial structure. We can vary the percentage of alleles we sample, thus allowing us to investigate the effect of the depth of sequencing on our results. As we know the true allelic frequency in the simulated population, we can use the multinomial distribution to produce a sample of the “sequenced” alleles, where the probability of sampling allele i is proportional to its frequency. The probability mass function is given by:

$$f(x;n,p)=\frac{n!}{x_1!\dots x_k!}{\displaystyle {\prod }_{i=1}^k{p}_i^{x_i}}\hspace{0.17em},\hspace{0.17em}{x}_1+\dots +x_k=n$$ [12]

where x_i is the sampled frequency of allele i, n is the number of trials (the chosen percentage of alleles sampled) and p_i is the probability of sampling allele i (which has frequency ρ_i in the original population):

$$p_i=\frac{{\rho }_i}{{\displaystyle {\sum }_{j=1}^k{\rho }_j}}$$ [13]

The variant allele frequency VAF is therefore given by:

$$VAF=\frac{x_i}{N_i}$$ [14]

Where N_i is the total number of sampled cells from which every sampled allele is derived. As we are assuming a constant mutation rate μ, we can assume that the percentage of alleles sampled comes from an equivalent percentage of cells. However, to include an additional element of noise that resembles the variability of read depth, we calculate a new N_i for each allele i, which approximates the read depth. For a desired “sequencing” depth D we calculate the corresponding percentage of the population we need to sample that will give us our desired depth. For example, for a desired depth of 100X from a population of 1,000 cells, we would need to sample 10% of the population. To include some variability in depth across all alleles we use Binomial sampling so that N_i is a distribution with mean D.

Contamination from non-tumor cells in NGS results in variant allele frequencies being underestimated. To include this effect in our simulation we can modify our N_i by an additional fraction ε, the percentage of normal contamination. Our VAF calculation thus becomes:

$$VAF=\frac{x_i}{N_i\left(1+\epsilon \right)}$$

We also include a detection limit in our sampling scheme, we only include alleles that have an allelic frequency greater than a specified limit in the original tumor population.

To include the effects of selection in the simulation we introduce a second population, where on average each cell has a greater number of offspring than the first population. To model this, our second population has a modified offspring probability distribution: the previous offspring probability distribution was P=(p₀,p₁,p₂), and the offspring probability distribution of our second fitter population is defined as Q=(q₀,q₁,q₂), where q₂>p₂. The selective advantage of a population – s, will be given by the ratio of the expected number of offspring:

$$1+s=\frac{E[Q]}{E[P]}=\frac{q_1+2q_2}{p_1+2p_2}$$

Therefore given P, and a desired selective advantage s we can easily calculate the offspring probability distribution of a fitter clone – Q.

Previous studies have detected the presence of mixtures of subclones in breast cancer samples that emerged by means of clonal expansions, thus generating multiple subclonal clusters in the data¹⁰. We also used our computational model of NGS data to produce similar synthetic data by means of mixing of different clonal clusters and verified that in this scenario (a model of differential selective pressure across subclones), the power law does not hold. The simulation code is available at https://github.com/andreasottoriva/neutral-tumor-evolution.

Simulation Results

From the simulated data we produced histograms of the allelic frequency and calculated M(f) in order to fit the analytical model. We used the same frequency range as applied to empirical data [f_max,f_min] = [0.12,0.24]. Supplementary Figure 9A and B shows equivalent plots to Figures 1A and B but with simulated data. These demonstrate that we are able to accurately model the allelic distribution of NGS data with our simple neutral model of tumor growth. We also show the effect of a low mutation rate (Supplementary Figure 9C), a large number of clonal mutations (Supplementary Figure 9D), 30% contamination in the sample (Supplementary Figure 9E) and a low detection limit (Supplementary Figure 9F). Importantly, by fitting the analytical model to the simulated data, we can recover the input mutation rate with high accuracy (Supplementary Figure 9G, 10,000 equivalent simulations). The mean percentage error from the fit is 1.1%. We also see uniformly high R² values across all simulations (Supplementary Figure 9H).

To test the robustness of the model to the number of clonal mutations, the detection limit and the amount of normal contamination we ran 10,000 simulations across the spectrum of these parameters. Supplementary Figures 10A-B show that we accurately recover (to within 15%) the mutation rate for 95% of simulations across different numbers of clonal mutations and different detection limits. Differently, we found that levels of normal contamination above 30% considerably impact the parameter estimations of the model, hence our decision of only considering samples with ≥70% of tumor content (Supplementary Figure 10C). Indeed, when normal contamination is above 30%, the clonal peak in the allelic frequency distribution interferes significantly with our chosen cumulative sum limit (f_max = 0.24), thus impacting our results. Nevertheless, the estimates are within a factor 2 for normal contamination of up to 50%, which we consider an acceptable level of accuracy. When we consider normal contamination ε directly within our analytical model, the allelic fraction of a new mutation becomes:

$$f=\frac{1}{\pi N(t)}=\frac{1}{\pi e^{\lambda \beta t}(1+\epsilon )}$$ [15]

And consequently, M(f) is:

$$M(f)=\frac{\mu }{\beta (1+\epsilon )}\left(\frac{1}{f}-\frac{1}{f_{\max }}\right)$$ [16]

Showing that normal contamination alters the measurement of mutation by a factor of 1/(1+ε): much lower than one order of magnitude. Furthermore, if normal contamination can be estimated accurately from histopathological scoring or from reliable bioinformatics tools, we would be able to correct the frequency of variants in the data and thus rescue our ability to correctly estimate parameters with up to 40-45% normal contamination (Supplementary Figure 10D). We also tested the model with varying read depths and mutation rates. We find that either a low mutation rate or low read depth resulted in a higher proportion of poor model fits (R²<0.98) and inaccurate or higher variance in mutation estimates (Supplementary Figures 10E-H). It is therefore possible that due to our stringent neutrality criteria that the true proportion of tumors that are dominated by neutral dynamics is higher than reported, and relatedly our gastric cancer cohort covers the whole genome (greater mutation rate per division) and has mean depth of coverage >90X which may explain in part why we see a greater proportion of gastric cancers classified as neutral.

Additionally, we tested the model with simulations using a range of different probability distributions for the number of surviving offspring at each cell division. We simulated a growing tumor 10,000 times with 5 different offspring probability distributions and then reported the distributions of the fitted parameters. Supplementary Figures 10I-J show that as λ decreases the distribution of mutation estimates becomes wider and we see an increase in poorly fitted models (larger number of R²<0.98). Again this suggests that tumor growth may still be neutral even when we classify a tumor as non-neutral due to a poor R² value. Hence our underestimation of the number of neutral cases may be largely due to a low proportion of cells that successfully produce 2 viable offspring (the β term in equation [7]), rather than the presence of selection.

By introducing a second fitter population early during tumor growth we show that the fitter clone causes an overrepresentation of variants at high frequency compared to what we would expect from our “null” model of neutral tumor growth. This causes the cumulative distribution to bend and deviate from the linear relationship predicted by neutral growth, as shown in Supplementary Figures 11A-B. This is because an overrepresentation of variants at high frequency, as compared to what we would expect from our “null” model, is caused by the clonal selection of the fitter clone, but we note that we do not know what caused this increase (it could be a point mutation, chromosomal aberration or a change in environmental pressures for example). In other words, some passenger mutations are just in the “right clone at the right time” and become overrepresented in the tumour when that “right” clone expands.

We also show that having multiple subclones that arose by means of clonal expansion, thus producing multiple clonal ‘clusters’, produces a deviation from the linear relationship we predict (Supplementary Figures 11C-F), as does having a marked increase in the mutation rate early in tumour growth (Supplementary Figures 11G,H).