A correlation study of the American Shoulder and Elbow Society Score and the Oxford Shoulder Score with the use of regression analysis to predict one score from the other in patients undergoing reverse shoulder joint arthroplasty for cuff tear arthropathy

Abstract

Background

More than 30 different scoring systems are available for evaluating outcomes of shoulder surgery. Unfortunately, given the multitude of scoring systems, there is no objective method to compare results between studies when different scoring systems are utilized.

Methods

We compared the American Shoulder and Elbow Society score (ASES) and the Oxford Shoulder Score (OSS) in patients undergoing reverse shoulder arthroplasty for cuff tear arthropathy. Twenty-nine patients had the ASES and OSS recorded pre-operatively, and at 6 and 12 months follow-up. The paired scores were assessed for their degree of correlation and sensitivity to change over time. Linear regression analysis was used to formulate a regression equation to predict one score from the other.

Results

The ASES and OSS correlated well with a Pearson’s correlation coefficient of 0.91 (p < 0.0001, n = 87). Both scores were sensitive to change. Regression analysis yielded a formula to predict the ASES from the OSS and vice versa with good accuracy (r²= 0.83, F_1,85 = 422.6, p < 0.0001).

Conclusions

Where good correlation exists, regression formulae can be used to accurately predict one score from the other in a specific population that it has been validated for. This can be of benefit when objectively comparing outcomes between studies using these two scoring systems.

Introduction

Scoring systems are widely used in orthopaedic surgery to give an objective measure of outcome after surgery. This is especially true of shoulder surgery, with more than 30 shoulder outcome measures being described [1]. Unfortunately, it can be difficult to objectively compare results between studies when different scoring systems are utilized.

The Constant Score (CS) developed in the UK is the official scoring instrument as mandated by The European Society of Shoulder and Elbow Surgeons. As a result, the CS is the most widely used scoring tool in Europe [2]. Similarly, the American Shoulder and Elbow Society Score (ASES), developed and endorsed by the research committee of the American Shoulder and Elbow Surgeons, is one of the most widely used scoring tools in the USA and Canada. In New Zealand, the New Zealand Joint Registry uses the Oxford Shoulder Score (OSS) as its official scoring tool for all shoulder joint arthroplasty. With so many different scoring tools being used worldwide, it can be difficult to compare outcomes between studies.

In 2007, Baker et al. compared the CS and the OSS in 103 patients who were treated conservatively for proximal humeral fractures [3]. In their study, they described the formulation of a regression equation to accurately predict the CS from the OSS within their population group. Although it was not their intent for use in clinical practice, their findings have shown an objective method for being able to predict one score directly from another. With this knowledge, their regression equation can be used to calculate and compare scores in studies of a similar population where either the CS or OSS is used. A similar method has not been devised to compare scores between the ASES and OSS. This was the aim of the present study.

Methods and materials

We used our institution’s shoulder joint arthroplasty database where we had the ASES and OSS recorded prospectively for 69 consecutive patients with cuff tear arthropathy presenting for reverse shoulder joint arthroplasty. Patients had their ASES and OSS recorded pre-operatively and postoperatively at 6 months and 1 year by a dedicated research nurse specialist. All patients had their surgery performed by one of three consultant upper limb specialists, all of whom are experienced orthopaedic surgeons.

Patients who incorrectly completed the questionnaires or failed to answer all questions were removed from the study. Both the ASES and OSS were available for all 69 patients pre-operatively. At the 6-month follow-up, 37 patients had both scores recorded and, similarly, at 1 year, 37 patients had both scores recorded. Twenty-nine patients in total had both scores recorded at all three time intervals, giving 87 sets of scores. These 29 patients were included in the final statistical analysis. Forty patients with 56 sets of scores were excluded in the derivation of the regression model because they did not have scores recorded at all three time intervals. However, these scores were used to test the internal validity of the regression equations.

The ASES consists of a medical professional assessment section and a patient self-evaluation section [4]. The medical professional assessment portion includes a physical examination and documentation of range of motion, strength and instability, as well as demonstration of specific physical signs. No score is derived for this section of the instrument. The self-evaluation section consists of a pain component and functional component. The pain component is addressed with a single question using a visual analogue scale of 0 to 10. The functional component consists of 10 questions rated on a four-point ordinal scale addressing activities of daily living. The pain score and function composite score are weighted equally and combined for a total score out of a possible 100 points, with 0 being the worst score and 100 being the best.

The OSS [5] is a questionnaire that is completed by the patient and consists of 12 questions. Each has five categories of response, which are scored from 0 to 4. Four questions relate to pain and the remaining eight questions relate to activities of daily living. Scores are added to give a single score ranging from 0 to 48, with 0 being the worst score and 48 being the best.

Statistical analysis

The ASES was plotted against the OSS in a scatter plot and Pearson’s correlation coefficient was calculated to measure the strength of correlation. A linear regression analysis was then performed to calculate the best-fit line for the correlation between the ASES and OSS and its algebraic formula was derived such that one score can be predicted from the other. The coefficient of determination was calculated to measure the strength of fit of the regression model. The appropriateness of the linear regression model was tested by residual analysis to assess the agreement between the actual and the predicted scores obtained from the regression analysis. Sensitivity to change over time for the ASES and OSS was assessed by comparing the mean scores, the 95% confidence intervals and calculating the effect sizes, as well as performing t-tests for the paired scores between pre-operatively and 6 months, pre-operatively and 1 year, and 6 months and 1 year. The internal validity of the regression equations were tested using the 56 excluded sets of scores by assessing the strength of fit of the model and the agreement between the actual and predicted scores by performing a residuals plot.

results

Eighty-seven sets of scores were collected in 29 patients who had complete scores recorded for the ASES and the OSS pre-operatively and postoperatively at 6 months and 1 year. The male to female ratio was 1 : 2.6 and the mean age was 78.9 years (Table 1).

Table 1.

Breakdown of patient demographics by sex, age and handedness.

Demographics	Age				Dominant hand	Nondominant hand
	n	Mean	SD	Range
Male	8	77.0	8.4	63.3 to 87.6	2	6
Female	21	79.6	4.9	69.3 to 87.6	13	8
Total	29	78.9	6.0	63.3 to 87.6	15	14

The mean (SD) ASES was 54.5 (25.1) with a range of scores from 5 to 100. The mean (SD) OSS was 31.1 (11.8) with a range of scores from 4 to 48. The breakdown of scores pre-operatively and postoperatively at 6 months and 1 year is shown in Table 2

Table 2.

Summary of the mean score with Standard Deviation (SD) and range for the American Shoulder and Elbow Society Score (ASES) and Oxford Shoulder score (OSS) recorded preoperatively and postoperatively at 6 months and 1 year.

	n	ASES			OSS
		Mean	SD	Range	Mean	SD	Range
Pre-operative	29	28.2	13.6	5 to 51.7	18.3	6.8	4 to 32
6 months	29	64.8	17.3	28.3 to 100	36.0	7.8	20 to 48
1 year	29	70.4	18.8	25 to 100	38.9	7.8	22 to 48
All	87	54.5	25.1	5 to 100	31.1	11.8	4 to 48

Both the ASES and the OSS showed sensitivity to change over all three time intervals from pre-operatively to 6 months, pre-operatively to 1 year and postoperatively 6 months to 1 year, as demonstrated in Table 3 (p < 0.001, p < 0.001 and p < 0.05, respectively).

Table 3.

Sensitivity to change over time for the American Shoulder and Elbow Society Score (ASES) and Oxford Shoulder Score (OSS) pre-operatively, and at 6 months and 1 year.

	Effect size	p-value	Pre-operative		6 months		1 year
			Mean	95% CI	Mean	95% CI	Mean	95% CI
ASES
Pre-operative and 6 months	2.37	p < 0.001	28.2	23.2 to 33.1	64.8	58.5 to 71.1	70.4	63.6 to 77.3
6 months to 1 year	0.31	p < 0.05
Pre-operative to 1 year	2.60	p < 0.001
OSS
Pre-operative and 6 months	2.41	p < 0.001	18.3	15.8 to 20.8	36.0	33.1 to 38.9	38.9	36.1 to 41.8
6 months to 1 year	0.38	p < 0.05
Pre-operative to 1 year	2.82	p < 0.001

CI, confidence interval.

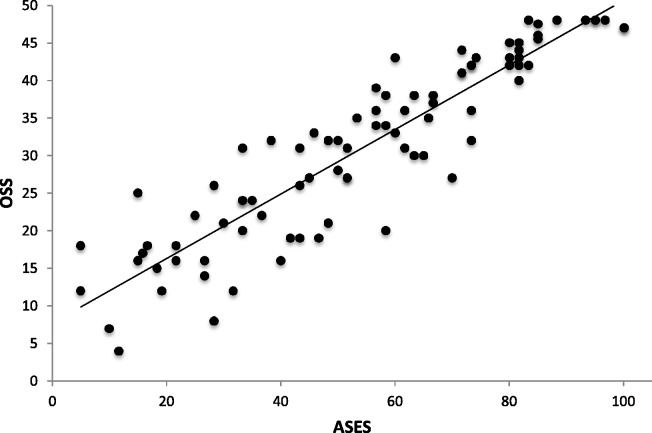
Figure 1 shows the scatter plot of the ASES plotted against the OSS with its trend line. Visually, a good correlation can be seen with all the data points being clustered around the trend line. Pearson’s correlation coefficient, which is a statistical measure of the degree of correlation, was calculated to be 0.91 (p < 0.0001; n = 87). This clearly demonstrates a strong relationship between the two scoring systems.

Fig. 1.

Scatter plot of the American Shoulder and Elbow Society Score (ASES) versus the Oxford Shoulder Score (OSS) for all patients recorded pre-operatively and postoperatively at 6 months and 1 year.

Because of such a good correlation between the two scores, we were able to calculate the best-fit line for this correlation and its algebraic formula using regression analysis. The derived formula is:

$$\text{OSS}=0.4288\times \text{ASES}+7.7199$$

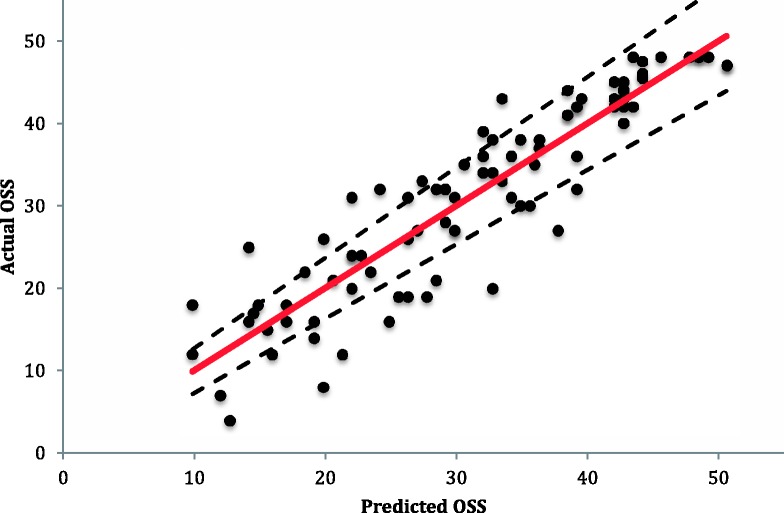
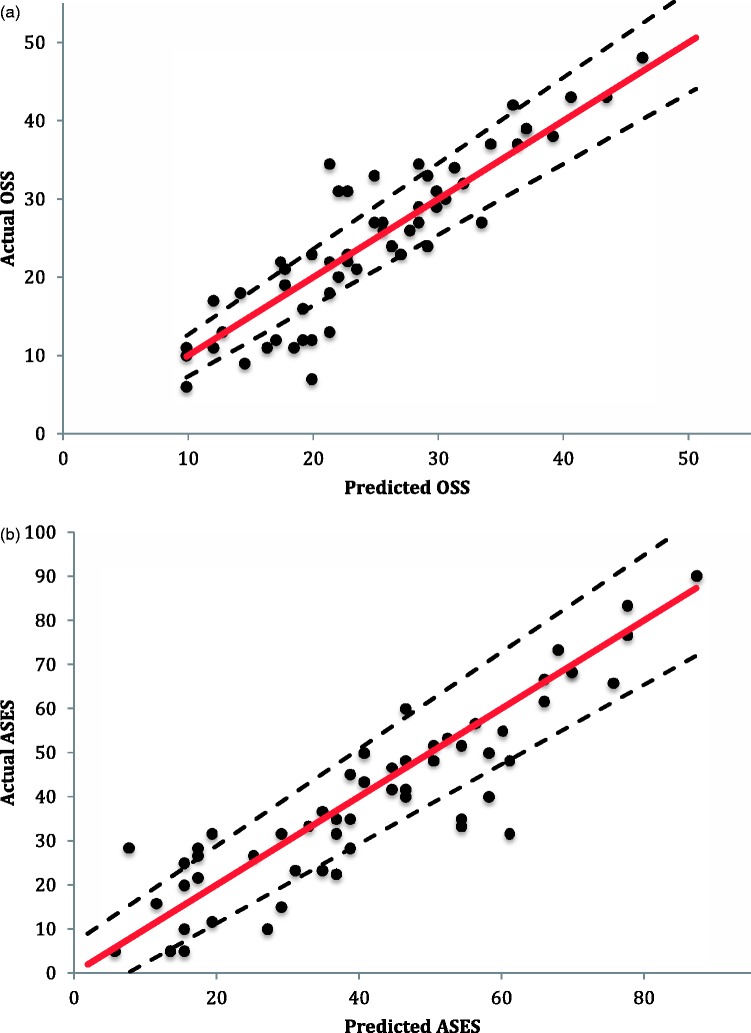
Using this formula, any ASES score can be inputted into the equation to calculate the equivalent predicted OSS. The coefficient of determination, which is a statistical measure of the strength of fit of the regression model, was calculated to be 0.83. This indicates that 83% of the variation of the predicted OSS can be explained by the ASES. This level of model fit was statistically significant (F_1,85 = 422.63, p < 0.0001), indicating that the model can predict the OSS from the ASES with good accuracy. The fit of the model with 95% confidence intervals is shown in Fig. 2, where the actual OSS is plotted against the predicted OSS using the regression equation and recorded ASES. If the model were able to predict the OSS perfectly from the ASES, all the data points would be expected to lie along the red line. Table 4 shows the predicted OSS for each ASES using the regression model described above.

Fig. 2.

The actual Oxford Shoulder Score (OSS) plotted against the predicted OSS calculated from the regression equation OSS =0.4288 × American Shoulder and Elbow Society Score +7.7199 (the dotted line representing the 95% confidence interval and the red line representing perfect prediction).

Table 4.

Predicted Oxford Shoulder Score (OSS) calculated from the American Shoulder and Elbow Society Score (ASES) using the regression equation OSS =0.4288 × ASES + 7.7199 (rounded to the nearest whole score).

ASES	OSS	ASES	OSS	ASES	OSS	ASES	OSS	ASES	OSS	ASES	OSS	ASES	OSS	ASES	OSS
0	8	13	13	26	19	39	24	52	30	65	36	78	41	91	47
1	8	14	14	27	19	40	25	53	30	66	36	79	42	92	47
2	9	15	14	28	20	41	25	54	31	67	36	80	42	93	48
3	9	16	15	29	20	42	26	55	31	68	37	81	42	94	48
4	9	17	15	30	21	43	26	56	32	69	37	82	43	95	48
5	10	18	15	31	21	44	27	57	32	70	38	83	43	96	48
6	10	19	16	32	21	45	27	58	33	71	38	84	44	97	48
7	11	20	16	33	22	46	27	59	33	72	39	85	44	98	48
8	11	21	17	34	22	47	28	60	33	73	39	86	45	99	48
9	12	22	17	35	23	48	28	61	34	74	39	87	45	100	48
10	12	23	18	36	23	49	29	62	34	75	40	88	45
11	12	24	18	37	24	50	29	63	35	76	40	89	46
12	13	25	18	38	24	51	30	64	35	77	41	90	46

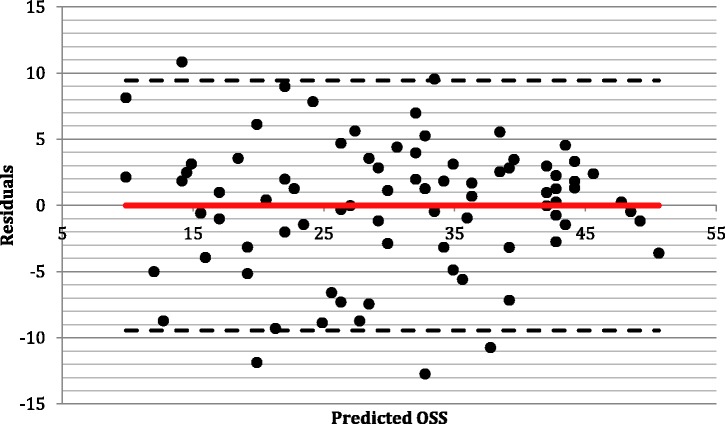
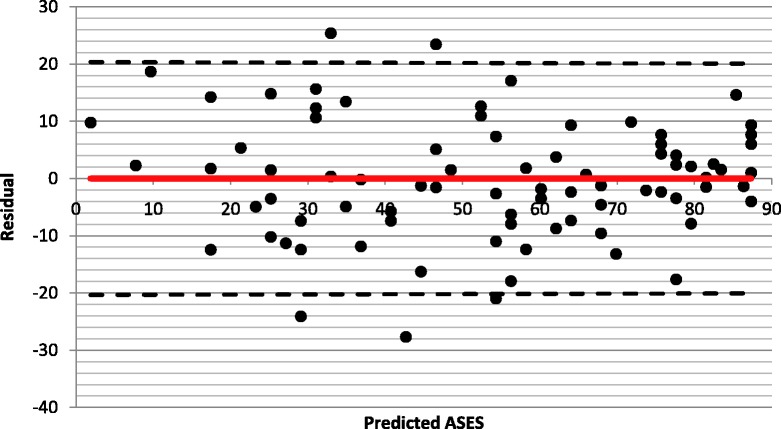
The appropriateness of the regression analysis was assessed with a residuals plot of the predicted OSS, as shown in Fig. 3. If there were perfect agreement between the scores, a straight line along the x-axis would be seen. The plot shows the scores to be scattered around the x-axis in random, with no clustering and no discrepancy between the scores at either end of the scales, therefore indicating a linear relationship between the scores. The mean of the residuals was −7.76 × 10⁻¹⁶, which is very close to zero and indicates the regression equation did not over-predict nor under-predict the OSS. The majority of scores lie within 1.96 SD of the mean and are therefore within the 95% limits of agreement of these two scores.

Fig. 3.

Residuals plot of the difference between the observed Oxford Shoulder Score (OSS) and predicted OSS to assess agreement between the scores (the dotted line representing the 95% confidence interval and the red line representing perfect prediction).

Similarly, regression analysis was also used to predict the ASES from the OSS. The derived algebraic equation for predicting the ASES is:

$$\text{ASES}=1.9414\times \text{OSS}-5.8661$$

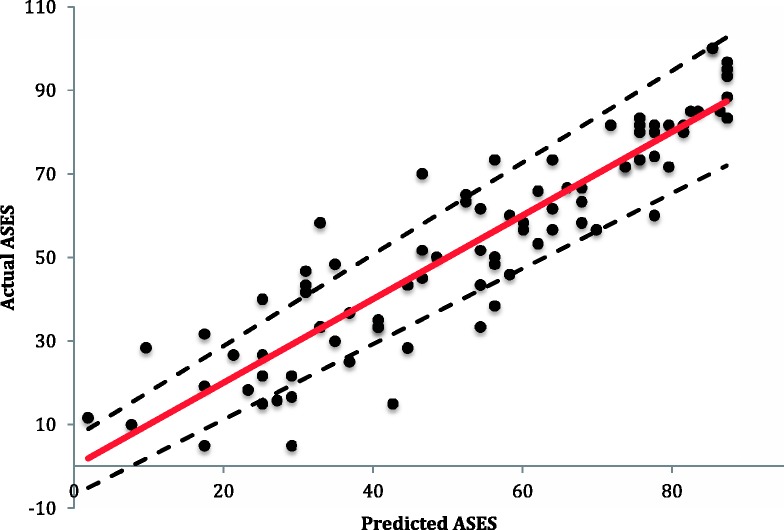
The level of fit of this model was also statistically significant (F_1,85 = 422.63, p < 0.0001) with a coefficient of determination of 0.83. The fit of this model with 95% confidence intervals is shown in Fig. 4, where the actual ASES is plotted against the predicted ASES. Table 5 shows the predicted ASES for each OSS using the regression model described above. The residuals plot of the predicted ASES is shown in Fig. 5 and also shows a linear relationship, indicating the appropriateness of the linear regression analysis. The mean of the residuals was −3.92 × 10⁻¹⁵, which also indicates the regression equation did not over-predict, nor under-predict the ASES.

Fig. 4.

The actual American Shoulder and Elbow Society Score (ASES) plotted against the predicted ASES calculated from the regression equation ASES = 1.9414 ×Oxford Shoulder Score – 5.8661 (the dotted line representing the 95% confidence interval and the red line representing perfect prediction).

Table 5.

Predicted Oxford Shoulder Score (OSS) calculated from the American Shoulder and Elbow Society Score (ASES) using the regression equation ASES = 1.9414 × OSS – 5.8661.

OSS	ASES	OSS	ASES	OSS	ASES	OSS	ASES	OSS	ASES
9	12	19	31	29	50	39	70
0	0	10	14	20	33	30	52	40	72
1	0	11	16	21	35	31	54	41	74
2	0	12	17	22	37	32	56	42	76
3	0	13	19	23	39	33	58	43	78
4	2	14	21	24	41	34	60	44	80
5	4	15	23	25	43	35	62	45	82
6	6	16	25	26	45	36	64	46	83
7	8	17	27	27	47	37	66	47	85
8	10	18	29	28	49	38	68	48	87

Fig. 5.

Residuals plot of the difference between the observed American Shoulder and Elbow Society Score (ASES) and predicted ASES to assess agreement between the scores (the dotted line representing the 95% confidence interval and the red line representing perfect prediction).

To confirm the internal validity of the regression equations, the 56 sets of scores from the 40 patients excluded for not having scores recorded at all three time intervals were used. These scores were used to test the level fit of the model, which was found to be statistically significant in predicting the OSS from the ASES and vice versa (F_1,54 = 283.07, p < 0.0001 and F_1,54 = 332.97, p < 0.0001, respectively) (Fig. 6). The residuals plots for the predicted OSS and the predicted ASES of these patients also showed good agreement, with the majority of scores lying within 1.96 SD of the mean, and therefore being within the 95% limits of agreement of these two scores (Fig. 7). On average, these patients were 2.1 years younger, with a higher proportion having surgery on their dominant arm and there was a slightly decreased male to female ratio compared to those patients included in the regression model. However, none of these baseline characteristics showed statistical significance, nor did the mean scores across the ASES and OSS at all three time intervals (Table 6).

Fig. 6.

Internal validation using the excluded sets of scores. (a) The actual Oxford Shoulder Score (OSS) plotted against the predicted OSS calculated from the regression equation OSS =0.4288 ×American Shoulder and Elbow Society Score (ASES) +7.7199. (b) The actual ASES plotted against the predicted ASES calculated from the regression equation ASES = 1.9414 × OSS − 5.8661(the dotted line representing the 95% confidence interval and the red line representing perfect prediction).

Fig. 7.

Internal validation using the excluded sets of scores to assess agreement between the scores. (a) Residuals plot of the difference between the observed Oxford Shoulder Score (OSS) and predicted OSS. (b) Residuals plot of the difference between the observed American Shoulder and Elbow Society Score (ASES) and predicted ASES (the dotted line representing the 95% confidence interval).

Table 6.

Breakdown of patient characteristics between those included in the derivation of the regression equation versus those excluded.

Included	Excluded	p-value
Male/female	8/21	9/31	0.63
Age	78.9	76.8	0.19
Dominant/nondominant limb	15/14	25/15	0.37
ASES
Pre-operative	28.2	30.1	0.57
6 months	66.2	59.8	0.42
1 year	71.5	66.4	0.51
OSS
Pre-operative	18.3	20.5	0.25
6 months	36.0	34.0	0.39
1 year	38.9	36.0	0.40

Discussion

The use of scoring tools and patient-reported outcomes gives an objective measure of outcome after surgery and represents a valuable source of feedback. A surgeon designing a study to measure a predetermined outcome will be influenced in choosing a suitable scoring instrument not only by the appropriateness of that instrument in measuring the particular outcome of interest, but also by the surgeon’s geographical location and familiarity of the scoring tool in that region, as well as the endorsement of the scoring instrument by their local expert committee. Therefore, different clinicians studying the same outcome in different geographical locations may choose different scoring systems simply as a result of their regional biases.

The present study is the first to explore an objective method for predicting one score from another between the ASES and OSS. To our knowledge, this is the only study where the ASES and OSS have been correlated following reverse shoulder joint arthroplasty. Where a good correlation exists between two scoring systems, linear regression analysis can be used to accurately predict one score from another [3]. Our results showed a good correlation between the ASES and OSS, with a Pearson’s correlation coefficient of 0.91 (p < 0.0001; n = 87), which is comparable to other studies correlating these two scoring tools [6]. The level of model fit of our regression equations were statistically significant (F_1,85 = 422.63, p < 0.0001) for predicting the OSS from the ASES and for predicting the ASES from the OSS, indicating that the models accurately predict either score from the other in this population of patients.

A limitation of the present study is its small size, with the regression model being based on 29 out of 69 potentially eligible patients. However, our regression equations were able to show a strong correlation and a level of model fit that reached well above statistical significance. Although 40 patients were excluded from the formulation of the regression model, these patients did not have any significant difference in their baseline characteristics or scores compared to those included in the regression model. Furthermore, the internal validation using these patients showed good agreement in the residuals plots across the score range and the level of model fit achieved was also well above statistical significance, indicating the accuracy of the regression model. These all indicate there would be no selection bias or strong influences had these patients been included in the model.

Because our study population was very specific to patients with cuff tear arthropathy undergoing reverse shoulder joint arthroplasty, the regression equations that we postulate would be most suited to this specific population. Intercepts and slopes obtained by correlating scoring instruments may vary across populations with different spectrum of disease and different procedures. Therefore, we would recommend its external validation before its use in other patient populations.

Similarly, the regression equation postulated by Baker et al. to predict the equivalent CS from the OSS was also based on a specific study population with patients treated non-operatively following fracture of the proximal humerus [3]. Therefore, external validation will also be required prior to the use of their equation in other patient populations.

However, if the regression equation of Baker et al. [3] can also be validated for use in a patient population similar to ours undergoing reverse shoulder joint arthroplasty, the OSS can be used to predict the equivalent scores of both the CS and AESES. Therefore, outcome studies utilizing the OSS can be objectively compared with other similar studies utilizing the CS and ASES. With the CS and ASES in popular use in Europe and North America, respectively, and with the use of the OSS as the official scoring tool in the New Zealand Joint Registry for all shoulder joint arthroplasty, New Zealand shoulder joint arthroplasty data can be objectively compared with the literature for both North America and Europe. Similarly, European and North American literature can also be compared directly and objectively with each other by converting the CS and ASES to the OSS. Although our intent is not to use this method in clinical practice, it does highlight the advantage of being able to accurately predict one score from the other. Not only will it allow direct comparison of outcome, but also it may be used in power calculations for study design.

Conclusions

Based on our findings, linear regression analysis can be used to make an accurate prediction of the equivalent OSS directly from the ASES and vice versa. It is the strength of the correlation that will determine the level fit of the regression analysis, with stronger correlations yielding more accurate predictions. With the appropriate validation in the correct patient populations, this concept can be applicable to other scoring systems not only of the shoulder, but also of the hip, knee and more global assessments of function.

Conflicts of Interest

None declared