Directed Acyclic Graphs for Oral Disease Research

Abstract

Directed acyclic graphs (DAGs) are nonparametric graphical tools used to depict causal relations in the epidemiologic assessment of exposure-outcome associations. Although their use in dental research was first advocated in 2002, DAGs have yet to be widely adopted in this field. DAGs help identify threats to causal inference such as confounders, bias due to subject selection, and inappropriate handling of missing data. DAGs can also inform the data analysis strategy based on relations among variables depicted on it. This article uses the example of a study of temporomandibular disorders (TMDs), investigating causal effects of facial injury on subsequent risk of TMD. We illustrate how DAGs can be used to identify 1) potential confounders, 2) mediators and the consequences of attempt to estimate direct causal effects, 3) colliders and the consequences of conditioning on colliders, and 4) variables that are simultaneously mediators and confounders and the consequences of adjustment for such variables. For example, one DAG shows that statistical adjustment for the pressure pain threshold would necessarily bias the causal relation between facial injury and TMD. Finally, we discuss the usefulness of DAGs during study design, subject selection, and choosing variables to be measured in a study.

Introduction

The primary goal of epidemiologic studies is to produce unbiased estimates of exposure-outcome associations. “Exposure” refers to any characteristic of a person or his or her environment, and “outcome” refers to a health-related factor of interest. A person-level characteristic includes factors such as genes, biomarkers, behaviors, or clinical findings, whereas environmental factors could be toxic substances, injury, or the weather. Unbiased estimation can be challenging because of confounding, defined as a mixing of effects from extraneous variables related to both exposure and outcome. When confounders are correctly identified, bias can be corrected (e.g., through subject selection, study design, or statistical adjustment). However, not all extraneous variables are confounders, and “correction” with a nonconfounder can increase instead of reduce bias.

Directed acyclic graphs (DAGs) are diagrams depicting causal structure thought to underlie a given exposure and outcome. In addition to the effect of exposure on outcome, DAGs specify relationships among other variables that influence the exposure or outcome. DAGs can also incorporate mediator variables—a consequence of the exposure and a cause of the outcome—and variables (measured or not) that are common causes of other variables on the DAG.

DAGs aid in streamlining study questions and identifying appropriate adjustment variables without sacrificing bias and precision. During study design, DAGs are useful when considering selection criteria for study participants, whether to match study participants, which variables to collect and when, and procedures for statistical adjustment during data analysis. DAGs are thus helpful in identifying subtle but common mistakes inherent in confounder selection and their management (Greenland et al. 1999).

Because DAGs are nonparametric diagrams (Greenland et al. 1999), they make no parametric assumptions like normality or linearity among variables depicted on it. They also do not depict magnitude or strength of causal associations. In other words, DAGs are powerful and intuitive tools based on qualitative assumptions used in causal modeling (Greenland and Brumback 2002) that allow nonmathematicians to draw logically sound conclusions about certain types of statistical relations (Rothman et al. 2008). For every hypothesized exposure-outcome relationship, a DAG underlying the true causal structure exists; however, this DAG is not necessarily known. Instead, there are usually several potentially plausible causal DAGs, as determined by the hypothesis. Importantly, to be plausible, a given DAG must be based on a priori knowledge of the exposure-outcome associations. This, in turn, relies on subject matter expertise (Robins 2001), preferably from across the range of scientific disciplines needed to fully evaluate the causal question at hand. Indeed, drawing a DAG before data collection and/or analysis ensures that any underlying assumptions guiding the research question are made explicit.

DAGs were introduced to epidemiologic research by Greenland et al. (1999) after having been developed in computer science (Pearl 1988) and formalized for research purposes (Pearl 1995). Although DAGs have been advocated for dental research (Merchant and Pitiphat 2002), they have yet to be widely adopted. In this article, we provide an expanded discussion of DAGs for dental research, focusing on their use to identify and minimize bias due to confounding and identifying nonconfounders (Hernán et al. 2004; Daniel et al. 2012; Westreich 2012). Using the example of a study of temporomandibular disorders (TMDs), this article illustrates 4 uses of DAGS: 1) identify confounders, 2) identify mediators and the consequences of attempts to estimate direct causal effects, 3) identify variables that are the effect of 2 other variables (colliders) and the consequences of adjustment for such variables, and 4) identify variables that are simultaneously confounders and mediators and the consequences of adjustment for such variables. We focus on the structural relations among variables and, for clarity of illustration, we assume that measurement and random errors are not a concern. We also draw on previous work in which DAGs have been applied to epidemiologic research (Greenland et al. 1999; Hernán et al. 2002, 2004; Merchant and Pitiphat 2002; Cole et al. 2010).

Definitions and Uses of Directed Acyclic Graphs (DAGs)

Conventions and Terminology Used in DAGs

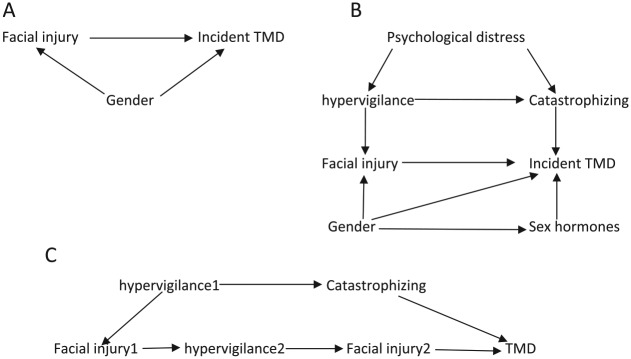
For a study of the relationship between facial injury and TMD onset, the DAGs depicted in Fig. 1A and B provide useful starting points to illustrate the putative causal relationships. In addition to the primary exposure (facial injury) and the outcome (incident TMD), we also consider individual factors such as gender and its associated sex hormones. Other factors include overall psychological distress, hypervigilance, and catastrophizing. Pronounced gender differences in the rate of facial injury are observed even in childhood (Locker 2005), probably because males are more likely than females to engage in activities that result in facial injury. In contrast, TMD occurs more frequently in women than men (Mundt et al. 2011; Slade et al. 2011), as some of the effect appears to be mediated through sex hormones. Likewise, elevated hypervigilance (increased and sustained attention to a bodily process or symptom) and catastrophizing (situation-triggered active beliefs of a negative outcome) likely contribute to an individual’s perception that certain aspects of jaw function are injurious. For example, prolonged mouth opening may result in an alteration of sensation, and hypervigilance could contribute to a perception of jaw injury as a result of the prolonged opening. Furthermore, catastrophizing may amplify that perception (McDermid et al. 1996; Hollins et al. 2009). Both hypervigilance and catastrophizing may contribute directly to TMD onset, and both may be the consequence of psychological distress. In DAG terminology, these variables are called nodes and the arrows are called edges. The edges are directed and acyclical, meaning that a series of arrows emanating from 1 node cannot terminate at the same node (i.e., a variable cannot cause itself). In Figure 1A, gender is a parent of both facial injury and incident TMD (both of which are children) (Greenland et al. 1999).

Figure 1.

Illustrating confounders with a directed acyclic graph. (A) Simple confounding by gender on the association between facial injury and temporomandibular disorders (TMDs). (B) Confounding by multiple variables. (C) Time-dependent confounding by hypervigilance.

A path between an exposure and outcome is any noncrossing, nonrepeating series of arrows starting at the exposure and ending with the outcome irrespective of direction of the arrowheads (Pearl 1998; Rothman et al. 2008). In Figure 1A, [facial injury → incident TMD] is a path and [facial injury ← gender → incident TMD] is another path. A given exposure and outcome could have ≥1 paths connecting them. Paths are classified as front door and backdoor, and they can be open or closed. Front door paths have arrowheads pointing from the exposure toward the outcome and consequently represent causal paths. These front door paths can either be open (i.e., all arrows on such paths flow in the same direction) or closed (i.e., there is a change in direction of at least 1 arrow on such paths). In Figure 2B, [facial injury → inflammatory response → incident TMD] is an open front door path, whereas [facial injury → inflammatory response ← psychological distress → incident TMD] is a closed front door path. Any variable on an open causal path from exposure to outcome is a mediator. In the open front door path [facial injury → inflammatory response → incident TMD] of Figure 2B, inflammatory response is a mediator. In contrast, backdoor paths are biasing paths (i.e., noncausal paths) because ≥1 arrowhead point toward the exposure instead of away from it, whereas other arrows on such paths point in any direction. Similar to front door paths, backdoor paths can be open or closed. With the exception of the necessary arrowhead(s) pointing to the exposure and that pointing to the outcome, all other arrows on open backdoor paths flow in the same direction. In contrast, all other arrows on closed backdoor paths include at least one arrow that exhibits a change in direction (i.e., the path is blocked, or closed). In Figure 3D, [facial injury ← contact sports → hypervigilance → incident TMD] is an open backdoor path, whereas the path [facial injury ← gender → contact sports ← hypervigilance → incident TMD] is a closed backdoor path. A variable that is a common effect of 2 other variables on a given path is called a collider because 2 arrowheads from the parents “collide” at the child (Cole et al. 2010). In essence, paths (front door or backdoor) containing ≥1 colliders are by definition naturally closed, because there is no flow of association from the exposure to the outcome on such paths. Colliders are path specific (Rothman et al. 2008); therefore, on a given DAG, a variable can be a collider on one path and a mediator or confounder on another path.

Figure 2.

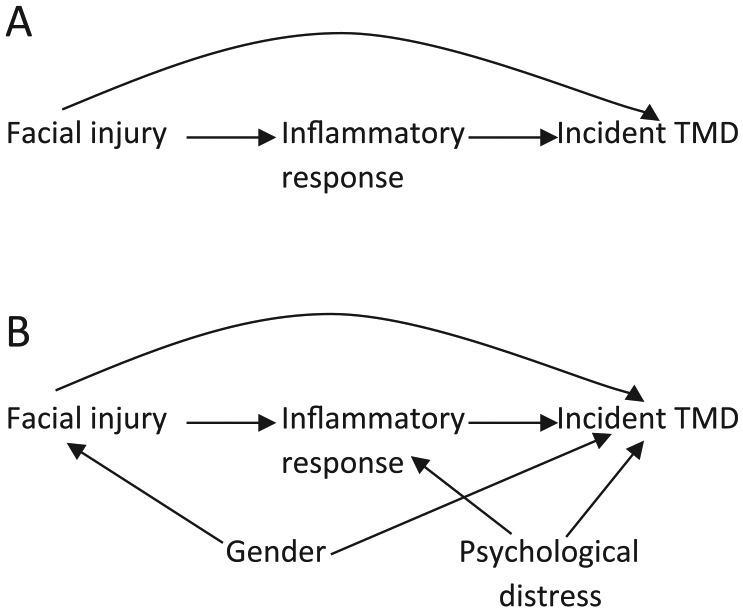
Illustrating confounders and mediators with a directed acyclic graph and the unintended consequences of estimating direct causal effects by adjusting for mediators. (A) The path from facial injury to an incident temporomandibular disorder (TMD) indicates a direct effect. (B) The path from facial injury to incident TMD through inflammatory response indicates a mediated effect.

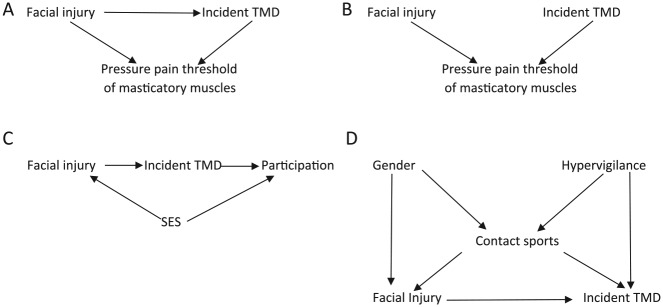
Figure 3.

Illustrating colliders with a directed acyclic graph and the unintended consequences of adjusting for colliders. (A) A scenario is shown in which there is direct effect of facial injury on an incident temporomandibular disorder (TMD) and pressure pain threshold is depicted as a collider. (B) A scenario is shown in which there is no direct effect of facial injury on incident TMD and pressure pain threshold is a collider. (C) Study participation is depicted as a collider. (D) Contact sport is a collider as well as a confounder of the association between facial injury and TMD. SES, socioeconomic status.

To identify a sufficient set of variables to estimate an unbiased causal effect of facial injury on incident TMD, we follow the recommendations given by Greenland et al. (1999): 1) erase all arrows pointing from facial injury toward incident TMD (i.e., all front door paths), and 2) assess whether there are any backdoor paths from facial injury to TMD not blocked by a collider.

Using DAGs to Identify Confounding Variables

Following the steps outlined above, Figure 1A contains 1 open backdoor path: [facial injury ← gender → incident TMD]. Hence, controlling for gender during study design (by restriction or matching) or during data analysis (by regression adjustment, stratification, or restriction) is sufficient to estimate, without bias, the causal effect of facial injury on incident TMD, assuming this DAG correctly depicts the true underlying causal relationship and omits no variables.

Similarly, Figure 1B contains 4 backdoor paths: 1) [facial injury ← hypervigilance ← psychological distress → catastrophizing → incident TMD], 2) [facial injury ← hypervigilance → catastrophizing → incident TMD], 3) [facial injury ← gender → incident TMD], and 4) [facial injury ← gender → sex hormones → incident TMD]. Adjusting for gender as described above only blocks the backdoor paths that include gender (i.e., 2 of the 4 backdoor paths). Therefore, to block the 2 remaining biasing (backdoor) paths, we need to additionally control for either hypervigilance or catastrophizing. It is important to note at this point that irrespective of the direction of the arrow between hypervigilance and catastrophizing, adjusting for either of these variables is sufficient to close the 2 remaining biasing paths because they are present on both paths. In Figure 1B, we therefore identified 1 sufficient set of confounders (hypervigilance, gender, sex hormones, catastrophizing) and 2 minimally sufficient (Greenland et al. 1999) adjustment sets ([hypervigilance, gender] or [catastrophizing, gender]). A minimally sufficient adjustment set of confounders blocks all open noncausal paths but is not necessarily the set with the fewest number of covariates (Greenland et al. 1999). The choice between these 2 minimally sufficient adjustment sets depends on study factors such as completeness of data, accuracy in measurement, and effects on statistical precision.

In the preceding example, hypervigilance resulting from psychological distress was depicted as a cause of perceived facial injury. However, it is also plausible that facial injury contributes to hypervigilance in a recursive or positive feedback manner. For instance, a trait characteristic of hypervigilance might contribute to the initial perception that facial injury occurred, whereas a given injury might contribute to subsequent hypervigilance. Although both constructs of hypervigilance are measured in perhaps the same manner, they represent different aspects of a process measured at different time points. Given that DAGs are by definition acyclical, this reality can be depicted by indexing hypervigilance with time, thus denoting separability across time. For example, Figure 1C uses subscript numbers indexing assessments at times 1 and 2 (i.e., facial injury and hypervigilance measured at time 1 and time 2). In other words, facial injury 1 is the initial event, whereas facial injury 2 is the exacerbation of the injury due to poorly adaptive mechanisms. To this DAG, other variables that are either time invariant or time varying can also be added. The steps to identifying confounders in these circumstances are the same as described above but a little more complicated and are discussed below (see the section on using DAGs to identify variables that are simultaneously confounders and mediators and bias resulting from incorrect adjustment for such variables).

Using DAGs to Identify Mediators and the Unintended Consequences of Estimating Direct Causal Effects by Conditioning on a Mediator

Figure 2 adds a biological element to the DAG, depicting inflammatory response as a mediator of the facial injury and incident TMD relationship. One aim is to estimate the effect of facial injury on TMD not mediated through an inflammatory response (i.e., the direct causal effect). Traditionally, adjusting simultaneously for mediators on the causal pathway (i.e., inflammatory response) and any confounder(s) of the exposure-outcome association will accomplish this. For example, in Figure 2A, we can estimate the direct effect by adjusting only for inflammatory response, because there are no confounders. This is sufficient under the assumption that this DAG (Fig. 2A) is correct and omits no variables. However, Figure 2A is rather simplistic because it ignores factors like gender and psychological distress and other relevant variables that may be unmeasured. Therefore, estimating a direct causal effect is not as simple as indicated above because of confounders of the mediator-outcome association (Cole and Hernán 2002).

To estimate the total (direct and indirect) effect of facial injury on TMD given the DAG depicted in Figure 2B, we identify gender as a confounder, so we will adjust for it. However, we do not adjust for psychological distress because the path [facial injury → inflammatory response ← psychological distress → TMD] is blocked (i.e., closed) at inflammatory response. In other words, inflammatory response is a common effect (i.e., a collider) of both facial injury and psychological distress on this path. Given that colliders are path specific, inflammatory response, although a collider on the path [facial injury → inflammatory response ← psychological distress → TMD] is not a collider on the indirect path [facial injury → inflammatory response → TMD] from facial injury to TMD. Therefore, if we decide to estimate a direct causal effect and, in addition to gender, also adjust or stratify by inflammatory response, we open up the path [facial injury → inflammatory response ← psychological distress → TMD] which was blocked at inflammatory response preadjustment. By opening the latter path, we bias the estimate of the direct causal effect. This is because psychological distress, which prior to adjustment was a nonconfounder of the facial injury-incident TMD association (based solely on the causal structure depicted in Fig. 2B), becomes a confounder of the direct effect when we adjust for inflammatory response. By adjusting for inflammatory response, we inadvertently induce an association between psychological distress and facial injury within groups defined by inflammatory response. As can be imagined, estimating a direct causal effect becomes even more complicated if psychological distress was not measured or if there are other unmeasured confounders of the mediator-outcome association. This example illustrates the use of DAGs in depicting causal relations as well how traditional regression adjustment methods (without additional assumptions) and stratification are unable to estimate direct causal effects without bias. For more, refer to Robins and Greenland (1992), Pearl (2012, 2014), and VanderWeele (2009, 2015).

Using DAGs to Identify Variables That Are Nonconfounders and the Unintended Consequences of Adjustment for Such Variables

To estimate the association between facial injury and incident TMD, we identified pressure pain threshold of masticatory muscles as an important factor, with recent evidence suggesting that lowered pain thresholds occur as a consequence of TMD (Slade et al. 2014). The DAG corresponding to the causal relation between these variables is shown in Figure 3A. Pain accompanying both facial injury and TMD will result in a lower pressure pain threshold. In Figure 3A, the pressure pain threshold is thus a common effect of both facial injury and incident TMD (i.e., a collider along the path [facial injury → pressure pain threshold ← TMD]). Therefore, the unadjusted relationship between facial injury and incident TMD based solely on Figure 3A is unbiased, assuming that this DAG is correct and omits no variables. However, if we inadvertently adjust, condition, or stratify by pressure pain threshold of masticatory muscles, we open up this blocked path (i.e., collider conditioning bias) (Merchant and Pitiphat 2002; Greenland 2003; Cole et al. 2010), thus producing an effect different from the unadjusted effect, albeit a biased one.

A similar causal structure is shown in Figure 3B. In this instance, we have removed the arrow between facial injury and incident TMD, implying that there is no causal relationship between facial injury and incident TMD. In other words, facial injury and TMD are considered marginally (i.e., unconditionally) independent. As a consequence, the unadjusted association will be null in expectation. By adjusting, conditioning, or stratifying by pressure pain threshold, the marginally independent relationship between facial injury and incident TMD becomes conditionally dependent on pressure pain threshold. In other words, knowing that an individual with a low pressure pain threshold of masticatory muscles does not have facial injury automatically tells us that they likely have TMD because in the absence of facial injury, it follows that another cause of the low pressure pain threshold of masticatory muscles (i.e., TMD) is present. See Pearl (1998) for further explanation.

In general, bias from conditioning on a collider arises not only by conditioning on a common effect of 2 variables but also by conditioning on a common cause of exposure and a cause of the outcome. To illustrate this, refer to the DAG depicted in Figure 3C. In this example, our interest is still the causal effect of facial injury on incident TMD. However, by necessity, the study was restricted to those who agree to participate. Although facial injury does not directly affect study participation, its effects on study participation are through its parent socioeconomic status (SES), assuming that SES is associated with willingness to participate, whereas the presence of TMD directly affects study participation. Therefore, if we have a complete census of the population, we can estimate the causal question without bias. However, if we instead condition on participation by restricting our study to those who agree to participate, we induce a type of bias called selection bias (Greenland et al. 1999; Hernán et al. 2004). Another example of this type of restriction can occur during data analysis when conducting a complete participant analysis, which is synonymous with restricting data analysis to nonmissing data points (by default, nonparticipants have missing data points). For more on the use of DAGs to depict the structure of missing data and how to handle them, refer to Daniel et al. (2012) and Westreich (2012). For general approaches to handling selection bias using inverse probability weights, refer to Hernán et al. (2004). In Figure 3D, contact sports is a confounder as well as a collider. To estimate the effect of facial injury on incident TMD, contact sports is a confounder on the path [facial injury ← contact sports → incident TMD], so by necessity, we adjust for it. However, it is also a collider on the path [facial injury ← gender → contact sports ← hypervigilance → incident TMD]. Thus, by adjusting for it, we open up this closed backdoor path. To remove the bias resulting from adjusting for contact sports, we need to also adjust for either gender or hypervigilance.

Using DAGs to Identify Variables That Are Simultaneously Confounders and Mediators and Bias Resulting from Incorrect Adjustment for Such Variables

DAGs can identify variables that are simultaneously confounders and mediators, which is useful when determining bias that can result from adjustment for such variables. If we are interested in estimating the cumulative effects of facial injury (at time 1 and time 2) on incident TMD, the hypothesized causal relations may look like the one shown in Figure 4. Previous facial injury (i.e., at time 1) may cause reactive guarding behavior (jaw parafunction), whereas jaw parafunction may, in turn, increase the perception of another facial injury (i.e., at time 2) and likewise TMD. Therefore, jaw parafunction is a mediator on path [facial injury 1 → jaw parafunction → incident TMD] and a confounder on path [facial injury 2 ← jaw parafunction → incident TMD].

Figure 4.

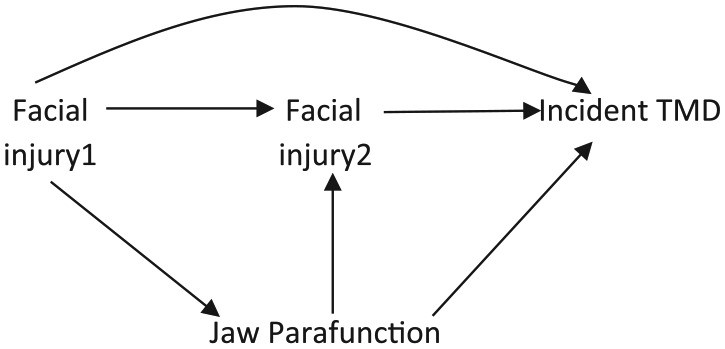
Illustrating with a directed acyclic graph, variables that are simultaneously confounders and mediators and the unintended consequences of adjusting for such variables. Jaw parafunction is both a mediator and a confounder. TMD, temporomandibular disorder.

Given that our goal is to estimate the cumulative effect of facial injury (at times 1 and 2) on incident TMD, we will adjust for jaw parafunction because it is a confounder of the facial injury 2–TMD association. However, this adjustment blocks part of the indirect effect of facial injury that we set out to estimate—specifically, the path from facial injury 1 to TMD mediated through jaw parafunction. Therefore, adjusting for jaw parafunction estimates the direct effect of facial injury at time 2 and part of the indirect effect of facial injury at time 1 on incident TMD (i.e., effects mediated through facial injury at time 2) but blocks the effects of facial injury at time 1 mediated through jaw parafunction. Thus, standard regression adjustment or stratification is unable to estimate without bias the intended effect. However, newer methods like inverse probability weighted marginal structural models (Robins et al. 2000; Cole and Hernán 2008) or Robins’ g-estimation methods (Westreich et al. 2012) can estimate the intended effects without bias.

Applied Example

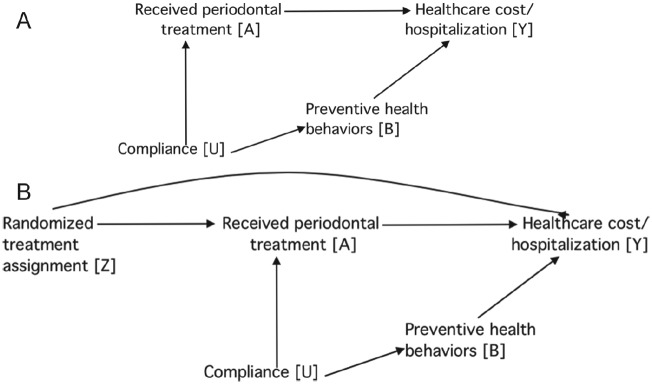
Causal interpretation of treatment effects is controversial when based on findings from observational studies. For example, a recent study analyzed health insurance claims for patients with periodontitis who also experienced ≥1 of 5 major health conditions, comparing total health care costs for those who received ≥4 periodontal treatments (optimal treatment) with those who received fewer (Jeffcoat et al. 2014). The authors’ conclusion that periodontal treatment significantly reduced health care costs was challenged in 1 letter and 1 review, each of which cited the potential for bias due to a greater tendency for compliance with health care recommendations in the optimally treated group compared with the suboptimally treatment group (DeRouen 2015; Sheiham 2015). This is depicted in Figure 5A, in which compliant individuals are likely to receive recommended periodontal treatments and adopt healthy behaviors likely to minimize the need for health care. It is therefore necessary to adjust for the confounding effect of compliance to obtain unbiased estimates. However, this was not possible, as the original authors noted that the health care claims database contained only “rudimentary demographic variables” that could be used for statistical adjustment (Jeffcoat et al. 2014).

Figure 5.

The causal effect of received treatment on health care cost is confounded by compliance. (A) Confounding bias could be removed by preventive health behaviors. (B) The causal relationship between randomized treatment and health care cost is unbiased.

In the ensuing debate, the original author stated that “no study—even the best-designed RCT—can hope to capture, let alone control for all the parameters that have the potential to influence the chosen outcomes” (Jeffcoat 2015). This statement holds true only in limited situations that can be clarified using a DAG. Specifically, in Figure 5B, received periodontal treatment differs from randomly assigned treatment due to noncompliance. This represents a special case of treatment misclassification that occurs in randomized experiments (Hernán and Robins 2016). If the goal is to estimate the causal effect of received periodontal treatment on health care costs (called “per-protocol analysis”), the effect is confounded by compliance.

However, the statement is misleading under other circumstances. For instance, if measurements are made of variables affected by compliance (e.g., preventive health behaviors) which themselves affect health care costs, adjusting for these variables is sufficient to estimate without bias the causal effect of received periodontal treatment on health care costs, assuming that the DAG in Figure 5B is correct and omits no variables. Meanwhile, the statement does not hold in intent-to-treat analysis, in which the goal is to evaluate the causal effect of treatment assignment on health care costs. This is because randomized treatment allocation is not associated with compliance or any other covariate, as indicated by the lack of arrows pointing into Z.

In conclusion, DAGs are useful tools in study planning because they inform which variables to be collected and how they should be analyzed in order to evaluate causal associations. In situations where data have already been collected, the process of creating DAGs motivates the investigator to consider causal relations among variables. When constructed, DAGs help identify situations in which standard regression methods will fail and alternative methods are required. Although the DAGs presented in this article were simplified for the purpose of illustration, all of the relevant variables can, and should, be included on a single DAG. This requires that critical consideration be given to drawing and identifying confounders from such DAGs. Even in situations where the true causal DAG is unknown, one nevertheless exists. Failure to draw a DAG allows for chance to guide the study, as opposed to logical discussion and consideration of underlying biology to settle on one or more plausible DAGs. We reiterate that DAGs are nonparametric and qualitative tools that must be combined with a quantitative tool such as regression modeling when estimating the effect of an exposure on an outcome. In other words, DAGs act as an adjunct as opposed to an alternative to causal modeling (Greenland and Pearl 2006). Finally, there are several software packages available for analyzing DAGs; one that we find particularly helpful is DAGitty (Textor et al. 2011).

Author Contributions

A.A. Akinkugbe, G.D. Slade, contributed to conception and design, drafted and critically revised the manuscript; S. Sharma, R. Ohrbach, contributed to design, drafted and critically revised the manuscript; C. Poole, contributed to conception, drafted and critically revised the manuscript. All authors gave final approval and agree to be accountable for all aspects of the work.