Difference-in-Differences Method in Comparative Effectiveness Research: Utility with Unbalanced Groups

Abstract

Background

Comparative effectiveness research (CER) often includes observational studies utilizing administrative data. Multiple conditioning methods can be used for CER to adjust for group differences, including difference-in-differences (DiD) estimation.

Objective

This study presents DiD and demonstrates how to apply this conditioning method to estimate treatment outcomes in the CER setting by utilizing the MarketScan® Databases for multiple sclerosis (MS) patients receiving different therapies.

Methods

The sample included 6762 patients, with 363 in the Test Cohort [glatiramer acetate (GA) switched to fingolimod (FTY)] and 6399 in the Control Cohort (GA only, no switch) from a US administrative claims database. A trend analysis was conducted to rule out concerns regarding regression to the mean and to compare relapse rates among treatment cohorts. DiD analysis was used to enable comparisons among the Test and Control Cohorts. Logistic regression was used to estimate the probability of relapse after switching from GA to FTY, and to compare group differences in the pre- and post-index periods.

Results

Crude DiD analysis showed that in the pre-index period more patients in the Test Cohort experienced an MS relapse and had a higher mean number of relapses than in the Control Cohort. During the pre-index period, numeric and relative data for MS relapses in patients in the Test Cohort were significantly higher than in the Control Cohort, while no significant between-group differences emerged during the post-index period. Generalized linear modeling with DiD regression estimation showed that the mean number of MS relapses decreased significantly in the post-index period among patients in the Test Cohort compared with patients in the Control Cohort.

Conclusion

In this study, an MS population was utilized to demonstrate how DiD can be applied to estimate treatment effects in a heterogeneous population, where the Test and Control Cohorts varied greatly. The results show that DiD offers a robust method for comparing diverse cohorts when other risk-adjustment methods may not be adequate.

Key Points for Decision Makers

Difference-in-differences (DiD) permits the comparison of differences in outcomes, before and after an intervention, between groups by controlling for bias from unobserved variables that remain fixed over time.

The current study demonstrated the application of the DiD methodology in CER settings to estimate treatment effects in a heterogeneous MS population, where the Test and Control Cohorts varied greatly.

This study has shown that DiD offers a robust comparison of groups, when propensity score matching and other risk-adjustment methods are not suitable. One potential issue is a jump in health outcomes immediately prior to switching the drug.

Introduction

Comparative effectiveness research (CER) has become a cornerstone methodology for health-care decision making, particularly for informing therapeutic options [1]. While randomized controlled trials are the gold standard of CER, observational studies utilizing administrative data are increasingly being conducted to estimate treatment effects between groups [2]. In order to evaluate treatment effects, comparable groups should be established that are well-balanced on multiple factors which may influence outcomes [3, 4].

Although propensity score matching (PSM) is commonly used in CER to create comparable groups, PSM does not apply to studies where treatment and control groups are highly skewed. Applying PSM may result in a small sample size because unmatched patients are dropped from the final sample [2, 4–8]. Furthermore, King and Nielsen [9] argue that PSM should not be used as it “increases imbalance, inefficiency, model dependence, research discretion, and statistical bias at some point in both real data and in data generated to meet the requirements of PSM theory”. Inverse probability of treatment weighting (IPTW) can be applied to balance treatment groups regarding factors that may bias the treatment effect estimates, without losing any patients from the sample [3, 4]. However, treatment effect estimates may be impacted by propensity scores that have very large weights [2]. In addition, approximates of PSM are subject to the completeness of measures related to the differences in patient and clinical characteristics; however, in observational studies, a complete composite of all these differences is not easy to capture because of the lack of related measures. Therefore, these characteristics may not be balanced between different groups, and this may bias the estimate of treatment effects.

Due to the limitations of PSM and IPTW, the difference-in-differences (DiD) method may be an alternative methodology [10]. Historically, DiD has been used in the evaluation of health-care policy, as it allows the researcher to control for background changes in outcomes [10]. DiD estimation permits the comparison of differences in outcomes before and after an intervention (e.g. treatment or health-care policy change) between groups affected and unaffected by the intervention [10, 11]. This methodology is appropriate to use when the interventions involved are “as good as random, conditional on time and group fixed effects” [11]. This means that DiD has the advantage of allowing researchers to estimate treatment effect, while accounting for unobserved variables that are assumed to remain fixed over time [12].

Study Objective

This retrospective administrative claims database study demonstrates how to apply the DiD method to estimate treatment outcomes in the CER setting. Specifically, this study applied DiD for analyzing treatment effects related to multiple sclerosis (MS) relapses. MS is a unique population, which is characterized by heterogeneity in clinical features and responsiveness to treatment [13]. Using DiD, this study focused on specific methods used to obtain the results regarding treatment effects in patients switching from glatiramer acetate (GA) to fingolimod (FTY) compared with those remaining on GA.

Difference-in-Differences (DiD) Methodology

Review of DiD Methodology

Simple pre- and post-treatment comparisons may be impacted by temporal trends in the outcome variable, or by other events that occurred between the two periods [14]. To overcome this issue, using a quasi-experimental design, DiD can be used when two periods of data are available for the treatment and comparison groups. The DiD estimator measures the treatment effect by looking at the difference between the average outcome in the control and treatment groups, before and after treatment [14].

DiD Assumptions

A key assumption of DiD is known as the ‘parallel trend’ assumption, which supposes that in the absence of treatment, the average outcomes of the treatment group and the comparison group would follow parallel paths over time [14]. This allows DiD to account for unobserved variables, which are assumed to remain fixed over time [12].

DiD Approach

In an evaluation of a treatment effect, a sample of patients are observed before and after a treatment. In the simplest case, if two periods of data (0 and 1) are analyzed and treatment begins in between the two periods of time, the treatment effect can be identified by simply looking at outcomes before and after the treatment, and classify the effect as:

$${\overline{Y}}_1-{\overline{Y}}_0$$

Herein, ${\overline{Y}}_1$ is the mean outcome in the period following the treatment and ${\overline{Y}}_0$ is the mean outcome in the period prior to the commencement of the treatment. At this point, this can be called or thought of as a matching estimator where these actions match a member of the treatment group to him/herself prior to receiving the treatment. For covariates that do not change over time, perfect balance is present whether or not those variables are included in the dataset.

The problem with this approach is that ‘things’ do change over time. Moreover, the effects of any other event that happened between the two periods are attributed to the treatment. Therefore, in order to account for changes over time, a second group is required. Assume one group, Group A, is administered the treatment between periods 0 and 1 (Let ${\overline{Y}}_{\text{A1}}-{\overline{Y}}_{\text{A0}}$ be the change in the outcome for this group), while a second group, Group B, does not receive the treatment at all (Let ${\overline{Y}}_{\text{B1}}-{\overline{Y}}_{\text{B0}}$ be the difference in outcome for that group).

Under the assumption that ${\overline{Y}}_{\text{B1}}-{\overline{Y}}_{B0}$ provides a good estimate of what would have happened to Group A had they not received the treatment, the treatment effect can be estimated using the DiD estimate:

$$\widehat{\mathit{\alpha }}=({\overline{Y}}_{\text{A1}}-{\overline{Y}}_{\text{A0}})-({\overline{Y}}_{\text{B1}}-{\overline{Y}}_{\text{B0}}).$$

This approach can be formally justified with a fixed effects model.

Let $Y_{it}={\mathit{\beta }}_0+\mathit{\alpha }{T}_{it}+\mathit{\delta }t+{\mathit{\theta }}_i+{\mathit{\epsilon }}_{it}$ where $Y_{it}$is the outcome for person i at time t, $T_{it}$ indicates whether person i received the treatment at time t, t is time period (0 or 1) and ${\mathit{\theta }}_i$ is a person fixed effect. As long as $E({\mathit{\epsilon }}_{it}|G_i,t)=0$ where $G_i$ indicates the group type (either A or B). Then:

$$\begin{array}{cc}\hfill \widehat{\mathit{\alpha }}& \approx (E(Y_{it}|G_i=A,t=1)-E(Y_{it}|G_i=A,t=0))\hfill \\ \hfill & -(E(Y_{it}|G_i=B,t=1)-E(Y_{it}|G_i=B,t=0))\hfill \\ \hfill & =([{\mathit{\beta }}_0+\mathit{\alpha }+\mathit{\delta }+E({\mathit{\theta }}_{it}|G_i=A)]-[{\mathit{\beta }}_0+E({\mathit{\theta }}_{it}|G_i=A)])\hfill \\ \hfill & -([{\mathit{\beta }}_0+\mathit{\delta }+E({\mathit{\theta }}_{it}|G_i=B)]-[{\mathit{\beta }}_0+E({\mathit{\theta }}_{it}|G_i=B)])\hfill \\ \hfill & =(\mathit{\alpha }+\mathit{\delta })-(\mathit{\delta })\hfill \\ \hfill & =\mathit{\alpha }\hfill \\ \hfill \end{array}$$

In addition, this approach makes clear what key assumption justifies DiD. The sample analogue of the equation above yields:

$$\widehat{\mathit{\alpha }}=\mathit{\alpha }+({\overline{\mathit{\epsilon }}}_{\text{A1}}-{\overline{\mathit{\epsilon }}}_{\text{A0}})-({\overline{\mathit{\epsilon }}}_{\text{B1}}-{\overline{\mathit{\epsilon }}}_{\text{B0}})$$

Therefore, for consistency we need that:

$$E[({\overline{\mathit{\epsilon }}}_{\text{A1}}-{\overline{\mathit{\epsilon }}}_{\text{A0}})-({\overline{\mathit{\epsilon }}}_{\text{B1}}-{\overline{\mathit{\epsilon }}}_{\text{B0}})]=0$$

In practice, the DiD estimate can be obtained either as a simple DiD, by running the fixed effect regression above, or by running a regression of $Y_{it}$on $T_{it}$, t, and a dummy variable to belonging to Group A. This can be further generalized to include more time periods (T), more groups (G), and additional covariates as one can run the regression

$$Y_{it}=X_{it}^{\prime }\mathit{\beta }+\mathit{\alpha }{T}_{it}+D_t^{\prime }\mathit{\delta }+G_i^{\prime }\mathit{\theta }+{\mathit{\epsilon }}_{it}$$

where $X_{it}$ represents additional covariates, $D_t$ is a $T\times 1$ vector of dummy variables indicating the time period and $G_i$ is a $G\times 1$ vector of dummy variables indicating the group to which individual i belongs. That is $D_t$ consists of a one in row t and zeros in all other rows while $G_i$consists of a one in the row corresponding to the group in which individual i belongs, and zeros in all other rows. Expanding this notion to nonlinear models of a linear index such as a logit or a negative binomial is straight forward.

Limitations of Difference-in-Differences Method

The limitations of DiD relate to the need to find similar study groups, as ideally, the only difference should be exposure to the intervention. For instance, according to the common shocks assumption, any event that occurs during or following the intervention, should equally affect each group. Likewise, the parallel trends assumption, outlined above, can be evaluated using a regression model; if the trends between the two groups are significantly different, the analysis may be biased [10]. Therefore, a limitation of this method is in finding treatment and control groups which meet these assumptions [10]. While this approach accounts for unobservable variables that are fixed over time, the biggest issue is that it does not account for unobservable variables that are not fixed over time [15].

Application of Difference-in-Differences Method

MS Study Sample

The sample was obtained from the Truven Health MarketScan^® Commercial Claims and Encounters and Medicare Supplemental Databases, one of the largest administrative claims databases in the USA with employer-sponsored and Medicare population with supplemental insurance [16]. Data were de-identified according to the US Insurance Portability and Accountability Act (HIPAA). The study did not involve collection, use, or transmission of individually identifiable data; thus, no Institutional Review Board approval was required.

Patient Cohorts and Study Design

In this study, two treatment cohorts were evaluated: (1) the Test Cohort (patients who had switched from GA to FTY and 2) the Control Cohort (patients who remained on GA) (see Fig. 1 for details on patient selection). The Test Cohort were patients who switched to FTY in the identification period and the Control Cohort were patients who received GA only during the identification period (October 1, 2010 to September 30, 2012). The index date was defined as the first FTY claim in the Test Cohort, or first GA claim in the Control Cohort. The pre-index period, or baseline period, was defined as the 12 months before the index date, while the post-index period was defined as the 12 months following the index date.

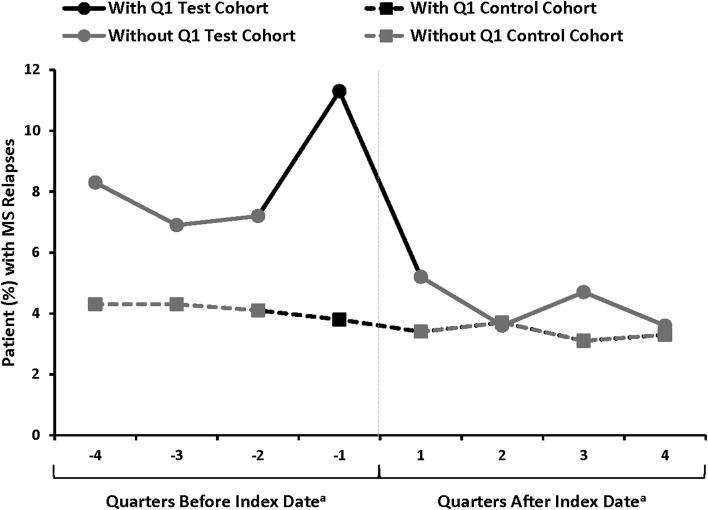
Fig. 1.

Patient selection flowchart. ^aFor patients in the Test Cohort, the date of the first FTY claim is the index date; for patients in the Control Cohort, the date of the first GA claim is the index date. ^bFor patients in the Test Cohort, this excludes other MS drugs that are not FTY; for patients in the Control Cohort, this excludes other MS drugs that are not GA. FTY fingolimod, GA glatiramer acetate, MS multiple sclerosis

The primary outcome was relapse rate during the post-index period. In this study, an MS relapse was defined using the claims-based algorithm validated by Chastek et al. [17], which involves meeting one of two criteria: a claim with an MS diagnosis code in the primary position at any time during an inpatient hospitalization, or a claim with an MS diagnosis code in the primary or secondary position in an outpatient setting plus a pharmacy or medical claim for a qualifying corticosteroid on the day of, or within 7 days, after the visit [17]. Additionally, the ‘clean period’ between initiation of relapses must be at least 30 days [17].

The study included eight quarters, representing the pre-index and post-index periods; the pre-index period included four quarters of data (4th quarter prior to index, 3rd quarter prior to index, 2nd quarter prior to index, 1st quarter prior to index; labeled as: −4, −3, −2, −1, respectively in Fig. 2), likewise, the four quarters of data in the post-index period were the 1st quarter post index, 2nd quarter post index, 3rd quarter post index and the 4th quarter post the index. These quarters are labeled as: 1, 2, 3, and 4, respectively in Fig. 2.

Fig. 2.

Patients (%) with MS relapses during the pre- and post-index period by quarter. ^aThe index date was defined as the first claim for FTY in the Test Cohort and as the date of first claim for the Control Cohort. FTY fingolimod, GA glatiramer acetate, MS multiple sclerosis

In the first phase of this study, IPTW analyses were applied (see Appendix Table 4. Balance Check Propensity Score Weighted Baseline Measures in appendices). The preliminary analysis revealed that the patient populations varied greatly across the two treatment cohorts; therefore, PSM and other risk-adjustment methods would not have been suitable for further analysis. DiD analysis was used to enable robust comparison of the Test and Control Cohorts.

Table 4.

Balance check propensity score weighted baseline measures

Variable	Test cohort	Control cohort	Odds ratio (difference) (test vs. control)
	(GA to FTY)	(GA only)	Mean	95 % CI	p value
Age group, years (%)					0.2228
18–34	7.1	8.7
35–44	19.3	22.8
45–54	36.2	34.7
55+	37.4	33.8
Female gender (%)	80.7	76.8			0.09
Plan type (%)					0.23
Fee for service	80.5	83.0
HMO and POS capitation	19.5	17.0
Region (%)					0.87
Northeast	19.3	19.1
North central	26.3	28.1
South	31.2	31.0
West	23.2	21.8
Medication burden, meana	7.90	7.35	0.54	0.01, 1.08	0.05
Patients with MRI service (%)	50.7	48.8	1.08	0.87, 1.33	0.49
Patients with relapse (%)	14.4	14.9	0.97	0.71, 1.30	0.82
MS symptoms (%)
Pain	49.4	43.2	1.28	1.04, 1.59	0.02
Depression	15.3	14.4	1.07	0.80, 1.44	0.64
Fatigue	12.5	13.0	0.95	0.69, 1.31	0.78
Walking (gait), balance, coordination problems	12.5	10.9	1.17	0.85, 1.61	0.34
Headache	9.7	10.2	0.95	0.66, 1.35	0.76
Bladder dysfunction	9.2	9.7	0.94	0.65, 1.35	0.73
Other emotional changes	10.7	9.4	1.16	0.83, 1.64	0.39
Numbness	11.0	9.0	1.25	0.89, 1.75	0.20
Others	36.4	33.7	1.12	0.90, 1.40	0.29
Modified PDC groupb
<50 %	10.7	9.9			0.84
50 to ≤80 %	17.6	18.4
≥80 %	71.8	71.7

PDC proportion of days covered, MS multiple sclerosis, MRI magnetic resonance imaging, HMO Health Maintenance Organization, POS point of service, GA glatiramer acetate, FTY fingolimod, PDC proportion of days covered

^aExcluding DMTs

^bModified PDC is calculated by [total Rx days of supply – max (0, (estimated next Tx date - study end date))] / (index date – date of first GA in baseline period)

MS Study Patient Baseline Characteristics

The analysis included data from 6762 patients, including 363 (5.4 %) in the Test Cohort, 6399 (94.6 %) in Control Cohort. For reasons we will discuss later, we eliminated data from −1Q prior to switching drugs, the quarter immediately prior to the index date, as described in the section below (see Sect. 2.3).

Baseline demographic and clinical characteristics varied between the Test Cohort and the Control Cohort (Table 1). While no significant differences in gender or type of insurance plan were reported, on average, patients in the Test Cohort were significantly younger than those in the Control Cohort (p = 0.0000; Table 1). Patients in the Test Cohort had a significantly higher mean (SD) number of medications than those in the Control Cohort [8.0 (5.1) vs. 7.3 (5.5), p = 0.0099, respectively]. Furthermore, a significantly larger percentage of patients in the Test Cohort had MRI scans than the Control Cohort (71.9 vs. 47.5 %, p = 0.0000), and patients in the Test Cohort had significantly more MRI scans than those in the Control Cohort [1.0 (0.9) vs. 0.6 (0.8), p = 0.0000; Table 1]. Overall, the Test Cohort had a higher percentage of patients with MS symptoms (78.8 %) compared to the Control Cohort (69.5 %; p = 0.0002). Specifically, compared to the Control Cohort, a significantly higher percentage of patients in the Test Cohort experienced pain (p = 0.0206), fatigue (p = 0.0051), gait, balance and coordination (p = 0.0140), other emotional changes (p = 0.0159) and other symptoms (p = 0.0000; Table 1). For both continuous and categorical measures of medication adherence, values for patients in the Test Cohort were significantly lower than were those for patients in the Control Cohort (Table 1).

Table 1.

Summary of pre-index period (baseline) demographics and clinical characteristics for Test Cohort and Control Cohort

Characteristic	Test cohort (n = 363)d	Control cohort (n = 6399)e	Between-group OR/difference
			Mean	95 % CI	p valuea
Including −1Q before index date
Mean (SD) age, y	47.3 (10.1)	49.7 (10.5)	−2.37	−3.44, −1.30	0.0000
Age group, n (%)
18–34	43 (11.8)	541 (8.5)			0.0000
35–44	95 (26.2)	1446 (22.6)
45–54	143 (39.4)	2205 (34.5)
≥55	82 (22.6)	2207 (34.5)
Female gender, n (%)	283 (78.0)	4905 (76.7)			0.5660
Plan type, n (%)					0.3334
Fee for service	308 (84.8)	5304 (82.9)
HMO and POS capitation	55 (15.2)	1095 (17.1)
Region, n (%)					0.0227
Northeast	51 (14.0)	1241 (19.4)
North central	101 (27.8)	1800 (28.1)
South	134 (36.9)	1961 (30.6)
West	77 (21.2)	1397 (21.8)
Mean (SD) medications	8.0 (5.1)	7.3 (5.5)	0.71	0.17, 1.25	0.0099
Patients w/MRI services, n (%)	261 (71.9)	3038 (47.5)	2.83	2.24, 3.58	0.0000
Mean (SD) MRI services	1.0 (0.9)	0.6 (0.8)	0.40	0.31, 0.50	0.0000
Patients w/MS symptoms, n (%)	286 (78.8)	4447 (69.5)	1.63	1.26, 2.11	0.0002
Pain	178 (49.0)	2742 (42.9)	1.28	1.04, 1.59	0.0206
Depression	52 (14.3)	924 (14.4)	0.99	0.73, 1.34	0.9518
Fatigue	65 (17.9)	820 (12.8)	1.48	1.12, 1.96	0.0051
Gait, balance and coordination	54 (14.9)	687 (10.7)	1.45	1.08, 1.96	0.0140
Headache	44 (12.1)	648 (10.1)	1.22	0.88, 1.70	0.2226
Bladder dysfunction	34 (9.4)	626 (9.8)	0.95	0.66, 1.37	0.7948
Other emotional change	47 (12.9)	586 (9.2)	1.48	1.07, 2.03	0.0159
Numbness	41 (11.3)	566 (8.8)	1.31	0.94, 1.84	0.1122
Othersb	165 (45.5)	2113 (33.0)	1.69	1.37, 2.09	0.0000
Mean (SD) compliance (modified)c	0.68 (0.28)	0.84 (0.21)	−0.16	−0.19, −0.13	0.0000
Modified compliancec group, n (%)					0.0000
<50 %	93 (25.6)	577 (9.0)
50–80 %	104 (28.7)	1139 (17.8)
≥80 %	166 (45.7)	4683 (73.2)

CI confidence interval, GA glatiramer acetate, FTY fingolimod, HMO Health Maintenance Organization, MRI magnetic resonance imaging, Max maximum, MS multiple sclerosis OR odds ratio, POS point-of-service, Q quarter, Rx prescription, SD standard deviation, Tx treatment, w with, y year

^aChi-square test (Fisher’s exact test is employed when ≥20 % of the cells have an expected value <5) for categorical/dummy variables and 2-sided 2-sample t test with unequal variance for continuous variables

^bOther includes bowel dysfunction, visual symptoms, sexual dysfunction, dizziness and vertigo, muscle weakness/spasm/spasticity, cognitive function, speech disorders, swallowing problems, hearing loss, seizures, tremor, itching

^cCalculated as: [total Rx days of supply − Max (0, (estimated next Tx date − study end date))]/(index date − date of first GA in baseline period)

^dThe Test Cohort included patients who switched from GA to FTY

^eControl Cohort included patients who remained on GA

Trend Analysis

Before conducting the DiD analyses, a trend analysis was conducted to investigate the parallel trends assumption, the key assumption of DiD.

Ideally, in the absence of treatment, the trends in outcomes would be parallel between the treatment and control groups. While it is impossible to test this assumption after the treatment has been administered, it is feasible to test it in the prior periods. The common practice is to examine the outcomes of interest graphically with multiple points of time to see whether the common trend assumption remains in the periods before the treatment is administered. As shown in Fig. 2, we see MS relapses, either measured by the mean number of MS relapses or proportion of patients who experienced an MS relapse, were close to parallel between the Test Cohort and the Control Cohort during the pre-index period, except in the quarter immediately prior to the switch, labeled as −1Q in Fig. 2.

In −1Q, we observed a peak in relapse rates, an issue referred to as the Ashenfelter’s Dip in the economics literature [18, 19]. We suspect that the MS relapse may be a major driver for patients to switch medications, which relates to our model above. This suggests an issue to be addressed. To explore this issue mathematically, we have four quarters before and four quarters after the treatment has been implemented so we can write the DiD estimator as:

$$\begin{array}{cc}\hfill \widehat{\mathit{\alpha }}& =([{\overline{Y}}_{\text{A1}}+{\overline{Y}}_{\text{A2}}+{\overline{Y}}_{\text{A3}}+{\overline{Y}}_{\text{A4}}]-[{\overline{Y}}_{\text{A}-4}-{\overline{Y}}_{\text{A}-3}-{\overline{Y}}_{\text{A}-2}-{\overline{Y}}_{\text{A}-1}])\hfill \\ \hfill & -([{\overline{Y}}_{\text{B}1}+{\overline{Y}}_{\text{B2}}+{\overline{Y}}_{\text{B3}}+{\overline{Y}}_{\text{B4}}]-[{\overline{Y}}_{\text{B}-4}-{\overline{Y}}_{\text{B}-3}-{\overline{Y}}_{\text{B}-2}-{\overline{Y}}_{\text{B}-1}])\hfill \\ \hfill & =\mathit{\alpha }+([{\overline{\mathit{\epsilon }}}_{\text{A}1}+{\overline{\mathit{\epsilon }}}_{\text{A}2}+{\overline{\mathit{\epsilon }}}_{\text{A}3}+{\overline{\mathit{\epsilon }}}_{\text{A}4}]-[{\overline{\mathit{\epsilon }}}_{\text{A}-4}+{\overline{\mathit{\epsilon }}}_{\text{A}-3}+{\overline{\mathit{\epsilon }}}_{\text{A}-2}+{\overline{\mathit{\epsilon }}}_{\text{A}-1}])\hfill \\ \hfill & -([{\overline{\mathit{\epsilon }}}_{\text{B}1}+{\overline{\mathit{\epsilon }}}_{\text{B}2}+{\overline{\mathit{\epsilon }}}_{\text{B}3}+{\overline{\mathit{\epsilon }}}_{\text{B}4}]-[{\overline{\mathit{\epsilon }}}_{\text{B}-4}+{\overline{\mathit{\epsilon }}}_{\text{B}-3}+{\overline{\mathit{\epsilon }}}_{\text{B}-2}+{\overline{\mathit{\epsilon }}}_{\text{B}-1}])\hfill \\ \hfill \end{array}$$

For consistency, we need the expected value of the $\overline{\mathit{\epsilon }}$ terms to be zero; however, in Fig. 2 it looks like ${\overline{\mathit{\epsilon }}}_{A-1}$ is a large number. It suggests that timing of MS relapse may be related to switching to FTY. Doctors do not switch their patients at random times, they are likely to switch them following a relapse. The problem is if a high value of ${\overline{\mathit{\epsilon }}}_{A-1}$ induces the doctor to switch drugs then we would expect that ${\overline{\mathit{\epsilon }}}_{\text{A}-1}-{\overline{\mathit{\epsilon }}}_{\text{B}-1}>0$ which would lead us to overstate the effect of the drug.

There is no perfect way to address this problem. On the one hand, if the switch to FTY was only related to ${\overline{\mathit{\epsilon }}}_{\text{A}-1}$ and not any of the other error terms, then by throwing out data from −1Q we can get a consistent estimate of $\mathit{\alpha }$. On the other hand, if there is positive serial correlation in ${\overline{\mathit{\epsilon }}}_{\text{AQ}}$ then we would expect some of the shock to persist. If this is the case, then excluding data from period −1Q likely leads us to understate the effect of the drug. In this instance, we can think of the two specifications (excluding and including data from −1Q) as providing upper and lower bounds on the effect.

Results

Crude DiD Estimate

First, a crude DiD estimate was applied to estimate treatment effects. As shown in Table 2, when including data from −1Q, in the pre-index period 109 (30.0 %) of the patients in the Test Cohort had an MS relapse, compared to 898 (14.0 %) in the Control Cohort. Overall, in the post-index period, 50 patients (13.8 %) in the Test Cohort experienced an MS Relapse, compared to 739 patients (11.5 %) in the Control Cohort (Table 2). In terms of the frequency of MS relapses, the mean (SD) number of relapses in the pre-index period was 0.34 (0.58) and 0.17 (0.47), for the Test and Control Cohorts, respectively, while in the post-index period, the mean (SD) was 0.18 (0.52) and 0.14 (0.43) in the Test and Control Cohorts, respectively (data not shown). Similarly, when excluding data from −1Q, a higher number of patients in the Test Cohort experienced an MS relapse than in the Control Cohort in the pre-index period (Table 2).

Table 2.

Crude DiD outcomes and odds ratio by logistic regression

	Test cohorta	Control cohortb	Between-group odds ratio/difference
	(n = 363)	(n = 6399)	Mean	95 % CI	p Valuec	–2 Log Ld
Including −1Q before index date
Patients with MS relapse, n (%)
Overall in pre-period	109 (30.0)	898 (14.0)	2.63	2.08, 3.33	0.0000	5634
Overall in post-period	50 (13.8)	739 (11.5)	1.22	0.90, 1.67	0.1994	4870
Excluding −1Q before index date
Patients with MS relapse, n (%)
Overall in pre-period	76 (20.9)	736 (11.5)	2.04	1.56, 2.65	0.0000	4939
Overall in post-period	50 (13.8)	739 (11.5)	1.22	0.90, 1.67	0.1994	4870

CI confidence interval, DiD difference-in-differences, FTY fingolimod, GA glatiramer acetate, MS multiple sclerosis; Q quarter, OR odds ratio, SD standard deviation

^aThe Test Cohort included patients who switched from GA to FTY

^bControl Cohort included patients who remained on GA

^cChi-square test (Fisher’s exact test is employed when ≥20 % of the cells have an expected value <5) for categorical/dummy variables and 2-sided 2-sample t test with unequal variance for continuous variables

^dThere were two subpopulations and two model parameters in each logistic regression model and residual degrees of freedom is zero. Therefore, the Pearson and deviance goodness-of-fit tests cannot be obtained

Logistic Regression Models

Following the trend and crude DiD analyses, logistic regression was utilized to statistically test the parameters relating to group differences in the pre- and post-index periods to understand whether treatment can reduce relapse rates. Using the number of relapses while taking the medication (herein, presented by the proportion of patients experiencing a relapse) as the dependent variable, logistic regression was used to estimate the probability of experiencing a relapse while taking FTY or GA, and group differences in the pre- and post-index periods between the Test and Control Cohorts were compared.

Including data from −1Q, during the pre-index period, the overall risk of MS relapse was significantly higher in patients in the Test Cohort than for the Control Cohort (OR = 2.63, 95 % CI: 2.08, 3.33, p = 0.0000). However, after switching, the overall risk of MS relapse was not significantly different between the Test and Control Cohorts (OR = 1.22, 95 % CI: 0.90, 1.67, p = 0.1994) (Table 2). Likewise, when excluding data from −1Q, the overall risk of an MS relapse was significantly higher among patients in the Test Cohort than for the Control Cohort in the pre-index period (OR = 2.04, 95 % CI: 1.56, 2.65, p = 0.0000).

DiD Regression Estimation

Finally, using DiD regression estimation by including an interaction between time (pre-index vs. post-index period) and cohorts (Test vs. Control Cohort) into explanatory variables and the count of number of patients with MS relapse as dependent variables, treatment effects by switching from GA to FTY were estimated while controlling for time effects. The purpose of this analysis was two-fold: first, it was used to estimate the magnitude of treatment effects, by controlling for the time period to see how much treatment contributes to the outcomes; and secondly, it was used to test if these differences were statistically significant. The results showed that the mean number of MS relapses decreased significantly from the pre- to the post-index period for Test Cohort, compared with the Control Cohort. As mentioned previously, the MS relapse rate made a significant jump in the quarter prior to switching to FTY for the Test Cohort, implicating Ashenfelter’s Dip. To handle this issue, two separate analyses were conducted, one including data from −1Q and another excluding data from –1Q. The analysis showed that the MS relapse rate decreased by 36 % [1 − exp (−0.44)] in the Test Cohort from the pre- to post-index period (p = 0.0007, Table 3) when including data from −1Q while the MS relapse rate decreased by 25 % [1 − exp (−0.29); p = 0.0276, Table 3] when excluding data from −1Q. Thus applying our bounding argument, we conclude that the MS relapse rate decreased by between 25 and 36 %.

Table 3.

Negative binomial DID model for the number of MS relapses

Parameter	Estimate	SE	95% CI	p value
Test Cohorta vs Control Cohortb (including –1Q before index date)
Intercept	−1.78	0.02	−1.82, −1.73	<0.0001
Cohort: GA → FTY (reference = Control Cohort)	0.71	0.08	0.55, 0.87	<0.0001
Time: post-period (reference = pre-index period)	−0.19	0.04	−0.26, −0.12	<0.0001
Cohort × time	−0.44	0.13	−0.69, −0.18	0.0007
Test Cohorta vs. Control Cohortb (excluding –1Q before index date)
Intercept	−2.04	0.03	−2.09, −1.99	<0.0001
Test Cohort (reference = control cohort)	0.56	0.09	0.39, 0.74	<0.0001
Time: post-period (reference = pre-index period)	0.08	0.04	0.01, 0.15	0.0303
Cohort × time	−0.29	0.13	−0.55, −0.03	0.0276

CI confidence interval, DiD difference-in-differences, FTY fingolimod, GA glatiramer acetate, MS multiple sclerosis; Q quarter, S standard error

^aThe Test Cohort included patients who switched from GA to FTY

^bControl Cohort included patients who remained on GA

Discussion

To the best of our knowledge, the DiD method has not previously been used in a CER setting to examine treatment effects on health outcomes. The current study provides a unique example to demonstrate the application of DiD, evaluating treatment effects of two MS therapies on the number of relapses experienced in two patient cohorts: the Test Cohort and the Control Cohort. The preliminary analysis of the Test and Control Cohorts showed that the patient populations varied significantly on several demographic and clinical characteristics; therefore, PSM and other risk-adjustment methods would not have been adequate.

A trend analysis was conducted to rule out concerns regarding regression to the mean and to compare the relapse rates among the Test and Control Cohorts. The trend analysis showed that the mean number of MS relapses, and the proportion of patients experiencing an MS relapse, were significantly higher in the Test Cohort compared to the Control Cohort during the pre-index period. This change represents a problem known as Ashenfelter’s Dip. In the economics literature, the Ashenfelter’s Dip refers to the decline in mean earnings among participants in government training programs just prior to program entry (e.g. adult education programs), which may bias before-after estimates in program evaluation, where pre- and post-program earnings are compared [18, 19]. In the current study, the Ashenfelter’s Dip may have important consequences in measuring treatment effects, as before-after comparisons may overstate or understate the impact of treatment [19]. Evidence of the Ashenfelter’s Dip among the Test Cohort is not surprising, as it suggests that a switch in medication may be due to the timing of an MS relapse. In order to provide an estimate of the upper and lower bounds of the treatment effect, analyses were conducted including and excluding data from −1Q.

Including data from −1Q, the crude DiD analysis showed that a higher percentage of patients in the Test Cohort had experienced an MS relapse than in the Control Cohort in the pre-index period, as well as a higher mean number of relapses. Logistic regression was used to estimate the probability of experiencing a relapse while taking FTY or GA, and to compare group differences in the pre- and post-index periods. Overall, for the duration of the pre-index period, both numeric and relative data for MS relapse in patients in the Test Cohort were significantly higher than in the Control Cohort, while no significant between-group differences emerged during the post-index period. Finally, differences in the number of relapses while on FTY or GA were estimated using generalized linear modeling with a DiD regression model, which showed that while patients in the Test Cohort experienced significantly more MS relapses, the interaction term for time × treatment cohort showed that the mean number of MS relapses decreased significantly in the post-index period and compared with patients in the Control Cohort.

As an alternative to other methods (e.g. PSM or IPTW), DiD allows the researcher to control bias from unobserved variables that remain fixed over time and which are correlated with outcomes [12]. DiD is most often used to look at interventions, programs, or health-care policy changes. In one review [11], the most commonly used variables include employment/wages, other market variables, and health outcomes. Several papers utilizing DiD have examined health-care policy and health outcomes [20–27]. For example, Dimick and Ryan [10] highlighted two articles [28, 29] utilizing DiD to evaluate changes following the 2011 Accreditation Council for Graduate Medical Education duty hour reforms. From the pharmacology perspective, DiD has been used to evaluate patterns of oral hypoglycemic agents (e.g. discontinuation) following the publication of a meta-analyses on adverse events with specific medications [30].

Limitations

There are limitations associated with the utilization of administrative data, as these databases are created to manage health-care transactions rather than for research purposes. Variation in patient characteristics covered by different types of health insurance plans may be present; therefore, the findings of this study may not be generalizable outside of MS patients covered by commercial health insurance in the USA.

Conclusion

The current study demonstrated the application of DiD methodology in CER settings to estimate treatment effects in a heterogeneous MS population, where the Test and Control Cohorts varied greatly. Our study has shown that DiD offers a more appropriate comparison when PSM and other risk-adjustment methods are not deemed to be adequate

Appendix

See Table 4.

Compliance with Ethical Standards

H Zhou is an Analyst at KMK Consulting Inc. and works as a consultant for Novartis Pharmaceuticals Corporation. Y. Li and S. Arcona are employees of Novartis Pharmaceuticals Corporation. C. Taber is an Economist at the Department of Economics, University of Wisconsin, and received consulting fees for his expertise from Novartis Pharmaceuticals Corporation. Funding for this project was provided by Novartis Pharmaceuticals Corporation, East Hanover, NJ. Publication of the study results was not contingent upon sponsor’s approval and operated independently of funders.