Abstract
Motivation: Finding genes which are directly perturbed or targeted by drugs is of great interest and importance in drug discovery. Several network filtering methods have been created to predict the gene targets of drugs from gene expression data based on an ordinary differential equation model of the gene regulatory network (GRN). A critical step in these methods involves inferring the GRN from the expression data, which is a very challenging problem on its own. In addition, existing network filtering methods require computationally intensive parameter tuning or expression data from experiments with known genetic perturbations or both.
Results: We developed a method called DeltaNet for the identification of drug targets from gene expression data. Here, the gene target predictions were directly inferred from the data without a separate step of GRN inference. DeltaNet formulation led to solving an underdetermined linear regression problem, for which we employed least angle regression (DeltaNet-LAR) or LASSO regularization (DeltaNet-LASSO). The predictions using DeltaNet for expression data of Escherichia coli, yeast, fruit fly and human were significantly more accurate than those using network filtering methods, namely mode of action by network identification (MNI) and sparse simultaneous equation model (SSEM). Furthermore, DeltaNet using LAR did not require any parameter tuning and could provide computational speed-up over existing methods.
Conclusion: DeltaNet is a robust and numerically efficient tool for identifying gene perturbations from gene expression data. Importantly, the method requires little to no expert supervision, while providing accurate gene target predictions.
Availability and implementation: DeltaNet is available on http://www.cabsel.ethz.ch/tools/DeltaNet.
Contact: rudi.gunawan@chem.ethz.ch
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Knowing the molecular targets of a drug or chemical compound is crucial in the drug discovery research for, among other things, identifying therapeutic properties and side effects, understanding the mechanism of action of a drug, finding alternative compounds with similar or greater efficacy and exploring new applications of a drug for treatment of other diseases (drug repositioning). In this regard, advances in high-throughput omics technology have been playing a crucial role in providing the data for elucidating cellular entities which interact with drug and chemical compounds. Cellular-wide response such as whole-genome gene expression profile, to genetic perturbations and chemical compounds can now be measured easily and cheaply. Furthermore, large amount of omics data are available from the ever-growing public biological databases. Because such data are typically of high dimensionality, the use of computational methods has become necessary in their analysis, for example in the inference of gene regulatory networks (Hurley et al., 2012).
Computational systems biology has provided many tools to analyze gene expression profiles for drug target predictions. A summary of different methods in this topic can be found in a review article (Chua and Roth, 2011). Briefly, there exist two main strategies: comparative analysis and network analysis. In comparative analysis, the gene targets are determined by comparing the gene expression profiles under drug treatments of interest with those from experiments with known genetic perturbations. This strategy generally involves gathering a compendium of expression profiles from genetic perturbations and chemical compound treatments with known mechanisms, followed by an association analysis of the expression profiles from drugs (e.g. using clustering, distance or connectivity score) (Hughes et al., 2000; Lamb et al., 2006; Iorio et al., 2010). A strong degree of association suggests a high similarity between the molecular targets of a drug of interest and the known perturbations.
In network analysis strategy, a model of the GRN is employed to predict GRN perturbations caused by drugs. The perturbation analysis requires constructing a network model of gene transcriptional regulation. One class of network analysis called network filtering is based on an ordinary differential equation (ODE) model of the gene transcription process. By taking the steady state assumption, the inference of GRN and drug targets reduces to solving a multivariate linear regression problem (see Methods and Materials for more details). Algorithms from this class of network analysis include network identification by multiple regression (NIR) (Gardner et al., 2003), mode of action by network identification (MNI) (di Bernardo et al., 2005) and sparse simultaneous equation model (SSEM) (Cosgrove et al., 2008). Here, the gene target predictions are obtained by first inferring the GRN using a library of gene expression data from the same species or cell line. Subsequently, the inferred GRN is used to filter the expression data of drug treatments. More precisely, genes with expressions which could not be explained by the transcriptional activity of their regulators are scored more likely to be direct targets of the drug.
Another type of network analysis methods rely on statistical test or enrichment analysis of the gene expression profiles to identify drug targets. One strategy called reverse causal reasoning uses literature-mined gene regulatory networks to generate hypotheses, which are subsequently scored against the gene expression profile (Belcastro et al., 2013; Chindelevitch et al., 2012; Martin et al., 2012). Another set of methods employ a transcription factor (TF) enrichment analysis followed by an upstream analysis, which involves a search for proteins that are highly connected to enriched TFs in signal transduction or protein-protein interaction networks (Chen et al., 2012; Koschmann et al., 2015; Lachmann and Ma’ayan, 2009; Laenen et al., 2015). Meanwhile, a method called Master Regulatory Inference algorithm (MARINa) applies gene set enrichment analysis using a transcriptional regulatory network to identify TFs whose regulons are enriched for differentially expressed genes (Lefebvre et al., 2010). Finally, a recent algorithm named Detecting Mechanism of Action by Network Dysregulation (DeMAND) uses an input GRN and expression data from control and drug treatments to identify target genes based on dysregulated gene interactions (Woo et al., 2015). Despite the differences in how GRNs are used in network analysis methods, the accuracy of the target predictions naturally depend on the fidelity of the GRN model. Unfortunately, the inference of GRN is known to be very challenging as the problem has been shown to be underdetermined (Szederkényi et al., 2011; Ud-Dean and Gunawan, 2014).
In this work, we developed a network analysis method called DeltaNet for predicting the genetic perturbations caused by a drug or chemical compound using gene expression profiles. DeltaNet is also based on an ODE model of the GRN, but does not require a separate step of GRN inference. Instead, the target predictions are obtained directly from the data, while the GRN is only inferred implicitly. DeltaNet relies on the least angle regression (LAR) (Efron et al., 2004) and the LASSO regularization (Tibshirani, 1996) to tackle the curse of dimensionality of the underlying regression problem. We demonstrated the advantages of DeltaNet over z-scores and other network filtering methods, namely MNI and SSEM, using compendia of gene expression data from Escherichia coli, Saccharomyces cerevisiae, Drosophila melanogaster and Homo sapiens.
2 Methods and materials
2.1 DeltaNet formulation
DeltaNet is based on the following ODE model of gene transcriptional process (Liao et al., 2003):
| (1) |
where rk denotes the mRNA concentration of gene k, and denote the mRNA transcription and degradation rate constants of gene k, respectively, denotes the regulatory control of gene j on gene k, and n denotes the total number of genes. The sign of describes the nature of the regulatory control, where a positive (negative) value represents activation (inhibition). Meanwhile, the magnitude of corresponds to the strength of the regulation. We assume that , i.e. there exists no direct self-regulatory loop. While this assumption may appear limiting, the case studies showed that DeltaNet could accurately predict network perturbations across different species. Under the steady state assumption, the concentration change of mRNA over time can be set to 0, which simplifies the model above into
| (2) |
where is the ratio between mRNA transcriptional and degradation rate constants.
Gene expression data of a treatment are typically reported as ratios with respect to readings from the corresponding control experiments. One can rewrite the model above for gene expression ratios (dividing both sides of Eq. (2) by the mRNA level in the control experiment), as follows:
| (3) |
where and denote the mRNA levels of gene k in treatment sample i and in the corresponding control experiment , respectively. The model formulation in Eq. (3) relies on the implicit assumption that the drug treatment affects only mRNA transcriptional and/or degradation rate constants without causing any changes in the GRN. Therefore, some care should be taken when applying DeltaNet and related methods such as MNI and SSEM to any treatments that may rewire the GRN.
Taking the logarithm of both sides of Eq. (3) leads to the following linear expression:
| (4) |
where denotes the log-fold change (logFC) of mRNA level of gene k and denotes the effects of treatment in sample i. Typically, a base-2 logarithm is employed in the analysis of gene expression data (Tarca et al., 2006). According to Eq. (4), the logFC of gene transcript k in a given sample comes from a contribution of two factors: (i) changes in the expression of genes that regulate gene k and (ii) a direct perturbation on the effective transcription (i.e. the ratio between transcription and degradation) of gene k by the treatment. A positive (negative) perturbation variable indicates that the effective transcription of gene k is increased (decreased) by the treatment.
Several network filtering methods have been formulated based on Eq. (4), such as NIR, MNI and SSEM (Cosgrove et al., 2008; di Bernardo et al., 2005; Gardner et al., 2003). In these methods, the inference of gene targets of a treatment is performed in two steps. The first step involves the identification of GRN, i.e. the coefficients , using gene expression data from experiments with known genetic perturbations (e.g. gene knock-out or silencing) and/or data compiled from publicly available database. In the second step, the perturbations are calculated for the treatment samples of interest by network filtering using the GRN identified in the first step. Consequently, the predictions of gene targets depend on the GRN inference, a problem that is known to be severely underdetermined (Szederkényi et al., 2011; Ud-Dean and Gunawan, 2014).
In contrast, DeltaNet generates the target prediction in a single step based on rewriting Eq. (4) in a matrix-vector format, as follows:
| (5) |
where C is the matrix of logFC gene expression data of n transcripts from m samples, A is the matrix of the coefficients (with zero diagonal entries), P is the matrix of treatment effects or perturbations , and is the identity matrix. Here, we estimate the coefficients of the matrices A and P simultaneously by solving the linear regression problem:
| (6) |
Since the dimension of the unknowns is larger than the number of samples, the regression problem above is underdetermined. We employ two different strategies for solving Eq. (6). The first involves least angle regression, which is a particularly efficacious model variable selection algorithm for low-sample high-dimensional data (Efron et al., 2004). In the second implementation, we use LASSO regularization by constraining the L1-norm of the solution (Tibshirani, 1996). The details of DeltaNet implementations are given in the next section.
2.2 DeltaNet implementation
In the implementation of DeltaNet, we treat Eq. (6) as a general linear regression problem:
| (7) |
where , and . The columns of X and Y are further centered to have zero mean, while those of X are also normalized to have a unit Eucledian norm. The matrix B could be solved one column at a time, i.e. the matrices A and P are obtained one gene at a time. Thereby, DeltaNet involves solving multiple independent linear regression problems of the type , which can be easily parallelized for computational speed-up. In order to enforce akk = 0, we set the (kth) row of the data matrix C corresponding to gene k to zero when solving The matrix A, if desired, can be computed by rescaling the appropriate submatrix of B. Meanwhile, the matrix P is taken from the solution for B without rescaling.
Two versions of DeltaNet are available: DeltaNet-LAR and DeltaNet-LASSO. As the name suggests, DeltaNet-LAR uses the LAR algorithm to solve the underdetermined regression problem above. LAR is an algorithm developed for creating sparse linear models (Efron et al., 2004). Like the traditional forward selection method, LAR starts with a zero vector as the initial solution (i.e. no active variables), and adds a new predictor variable (i.e. an active variable) at every step. LAR employs a less greedy algorithm than the forward selection method in calculating the coefficients of the active variables. Briefly, in the first iteration, we choose the predictor that correlates most with the data (i.e. one that forms the least angle with the residual vector) and add this variable to the active set. The solution is updated along the direction of equal angles with respect to all variables in the active set, until the residuals become equally correlated with another predictor which is outside the active set. In the next iteration, this predictor is added to the active set, and the process is repeated until completion or until a desired number of active variables is reached.
We employ the LAR algorithm from the MATLAB toolbox SpaSM (Sparse Statistical Modeling) (http://www2.imm.dtu.dk/projects/spasm/). In a typical scenario, LAR terminates after m or fewer steps, since the number of samples m is far fewer than the number of genes in the dataset. The output of LAR consists of a series of solution vectors , , where I is the total number of steps. In DeltaNet-LAR, the steps are carried out until the relative norm error falls below a user-defined stopping criterion δr. Setting δr higher would lead to fewer steps taken in LAR and thus fewer non-zero coefficients in the solution vector The case studies below showed that the accuracy of DeltaNet predictions does not depend strongly on δr in the range of 1% ≤ δr ≤ 10%. A higher δr has the benefit of reducing computational time at the trade-off of slightly reduced prediction accuracy (see Section 3).
In DeltaNet-LASSO, we solve the following penalized minimization problem:
where ak is the kth row vector of the A matrix. Here, we employ GLMNET (Friedman et al., 2010) to generate a regularization path for the LASSO problem above. Briefly, GLMNET uses the cyclical coordinate descent algorithm, which successively minimizes the objective function one-parameter-at-a-time and cycles over the parameters until convergence. While LAR could also be modified to generate the regularization path for LASSO (Efron et al., 2004), our experience showed that GLMNET could reduce the computational times by several folds. For DeltaNet-LASSO, we implemented GLMNET subroutines for MATLAB (http://www.stanford.edu/∼hastie/glmnet_matlab/).
We perform a k-fold cross validation (CV) method to determine the optimal T value. Briefly, we randomly divide the data into k equal-sample parts. For each CV trial, we assign k – 1 parts as the training set and the remaining part as the test set. We then generate the regularization path using GLMNET and evaluate the errors of predicting the test set data as a function of T by rescaling the appropriate subvector of to ak. The optimal T corresponds to the minimum average test errors over k number of CV trials.
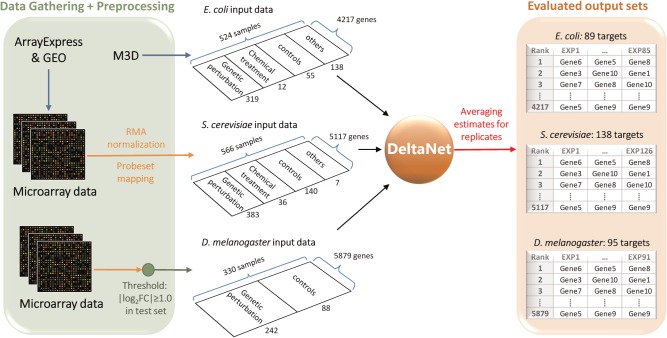
Figure 1 illustrates the general workflow of DeltaNet. In the first case study, we evaluated the performance of DeltaNet in predicting known gene perturbations in Escherichia coli, Saccharomyces cerevisiae (yeast) and Drosophila melanogaster (fruit fly). In the second case study, we assessed enriched transcription factors among the top gene target predictions from chemical treatment samples in yeast and Homo sapiens (MCF7 human cell line) datasets. We compared the performance of DeltaNet with z-score analysis and two network filtering methods, MNI and SSEM.
Fig. 1.
Workflow of gene target prediction using DeltaNet. The performance of DeltaNet in predicting known gene perturbations was evaluated using gene expression data of E.coli, S.cerevisiae and D.melanogaster
2.3 Gene expression data
For the case studies, we gathered gene expression data from public databases. For E.coli, we retrieved microarray data from Many Microbe Microarrays Database (M3D, as of 29th October 2007) (http://m3d.mssm.edu) (Faith et al., 2008). More specifically, we obtained the robust multi-array average (RMA)-normalized dataset from the file E_coli_v4_Build_3_chips524probes4217.tab. As summarized in Figure 1, the data comprised 4217 genes and 524 samples with 319 samples from gene perturbation experiments, 12 samples from chemical treatments, 55 samples from wild-type control experiments and 138 samples from other conditions (e.g. different growth phases, nutrient feeding strategies). The logFC expression data were computed by subtracting the average of wild-type control experiments from the log-2 RMA intensity data.
For S.cerevisiae, we compiled gene expression data from ArrayExpress (Parkinson et al., 2007) and Gene Expression Omnibus (GEO) (Barrett et al., 2013). In order to avoid cross-platform variability, we only used data from Affymetrix GeneChip Yeast Genome S98. Among 9335 probe sets, we could match 5117 probe sets to gene symbols using ygs98.db package in Bioconductor (Saccharomyces Genome database as of 9th March 2014). As shown in Figure 1, the yeast dataset consisted of 566 samples, among which 383 samples were from gene perturbation experiments, 36 samples from chemical treatments, 140 samples from wild-type control experiments and 7 samples from other conditions. The raw data were RMA-normalized using justRMA function in the affy package of Bioconductor (Gentleman et al., 2004), which provided log-2 normalized intensity. The logFC expression data were again calculated by subtracting the average of all wild-type control samples from the log-2 RMA intensity.
For multicellular organisms, like Drosophila and human, the gene expression data should ideally come from the same cell lineage, as the GRN can vary across cell lines. For D.melanogaster, we compiled 330 microarray samples of Affymetrix GeneChip Drosophila Genome 2.0 from ArrayExpress and GEO, of which 80% came from experiments using Schneider 2 (S2) cells and the remaining came from whole-body homogenates. These data originated from five studies involving gene knock-down (KD) and overexpression experiments. In particular, 242 samples came from genetic perturbations and 88 samples were from wild-type control experiments. We mapped the probe sets to GenBank accession number using drosophila2.db in Bioconductor (Entrez Gene database as of 17th March 2015). The expression data were again pre-processed using justRMA to give log-2 normalized intensity. We noted that the RMA intensities of the controls differed significantly among publications. Therefore, we computed the logFC by subtracting the control data for each publication separately. In order to reduce computational complexity, we only used 6165 probe sets which showed significant differential expression (logFC ≥ 1). By using the median values for multiple probe sets that mapped to one gene, we further reduce the dimension to 5879 genes.
Finally, for human dataset, we compiled 2537 samples of MCF-7 human breast cancer cells from the Connectivity Map (C-Map version 2) (Lamb et al., 2006). The expression data were first pre-processed by using justRMA, based on which we computed the logFC expression using mean-centering within batches, as recommended in a previous study (Iskar et al., 2010). We then selected a subset of 569 samples corresponding to 142 different compound treatments with three or more replicates. The final dataset corresponded to the median logFC expressions among the respective replicates. We mapped 19 846 probe sets from Affymetrix GeneChip HT Human Genome U133 to GenBank accession number using hthgu133a.db in Bioconductor (Entrez Gene database as of 17th March 2015). For computational speed-up, we performed the gene target analysis using only 3153 genes that showed significant differential expressions (|median logFC| ≥ 1) in at least one of the treatments.
3 Results
3.1 Predicting network perturbations
In the first application, we used DeltaNet, MNI, SSEM and z-scores to predict the targets of gene perturbation experiments in E.coli, yeast, and Drosophila datasets. The experiments involved known gene knockouts, over-expression and mutations, which provided the gold standard data for comparing the methods.
The z-scores were computed according to:
| (8) |
where is the logFC for gene transcript k in sample i, and are the average and standard deviation of transcript k across all samples, respectively. For DeltaNet-LASSO and SSEM, we employed a 10-fold cross validation to determine the optimal T as discussed in Methods and Materials. Meanwhile, for DeltaNet-LAR, we used a threshold criterion δr of 10%. In the case of MNI, we performed a grid search optimization for each compendium to determine the parameters Q and thP, which we found to influence the target predictions strongly. Here, we selected the parameter combination giving the minimum average rank error for samples with known perturbations by employing a 5-fold CV. Meanwhile, the parameter KEEPFRAC was set such that we retained >200 genes after the last round of tournament (0.37 for E.coli, 0.35 for yeast and 0.33 for Drosophila) following the published protocol (Xing and Gardner, 2006). The remaining parameters (NROUNDS and ITER) were set to their default values. Finally, we used a unit standard deviation for all samples, as this setting gave much better performance than using the recommended sample standard deviation.
The test samples of E.coli came from 85 experiments with known perturbations, while the test samples of yeast comprised 109 experiments (see Supplementary Data). For Drosophila, the test set came from the study of cell cycle regulators using S2 cells (Bonke et al., 2013), comprising 91 different perturbation experiments. Figure 1 gives the numbers of the combined gene targets in the test samples of E.coli, yeast, and Drosophila test samples, which were slightly higher than the number of samples since a few experiments involved more than one gene perturbation. Except for MNI, we analyzed each sample of experimental replications separately, and used the median value as the final prediction. In the analysis using MNI, we followed the published protocol and used the average gene expression values over replicates as the input data (Xing and Gardner, 2006).
From each method and each test dataset, we obtained a rank list of genes where we sorted the genes in decreasing magnitudes of the perturbation variables (see Supplementary Data). The ranking reflects the confidence level that a gene is directly perturbed in the corresponding experiment, while the sign of indicates the nature of the perturbation. In evaluating the performance of the methods, except for MNI, a true positive (TP) requires not only a high confidence prediction (i.e. large magnitude in ), but also the correct sign of perturbations (a positive sign for gene induction and a negative sign for gene repression). As MNI did not provide the sign of the perturbations, we only use the gene ranking in evaluating its performance.
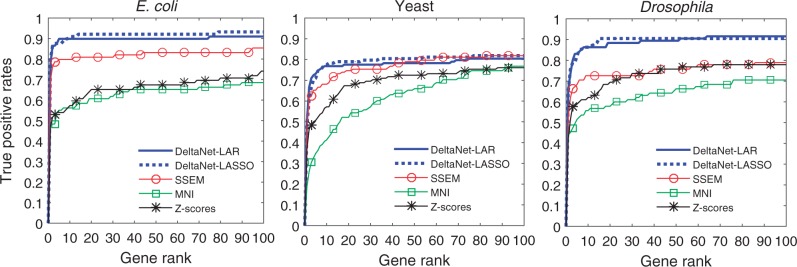
Figure 2 compares the true positive rate (TPR) as a function of the gene rank according to DeltaNet, SSEM, MNI and z-scores. The TPR was computed as the fraction of the known gene perturbations that appear above a given rank (shown in the x-axis). Figure 2 shows that DeltaNet significantly outperformed SSEM, MNI and z-scores for all three test datasets. DeltaNet-LAR and DeltaNet-LASSO gave relatively the same TPR. The top 10 genes from DeltaNet had on average 14% and as large as 19% (for D.melanogaster) higher TPR than the next best method SSEM. MNI gave the worst TPRs among the methods considered, which could be caused by suboptimal tuning of the parameters. The need to optimize the method parameters for different datasets is a known drawback of MNI, since the tuning of these parameters can be computationally demanding (Cosgrove et al., 2008).
Fig. 2.
True positive rates of gene target predictions from DeltaNet, SSEM, MNI and z-scores. The results of DeltaNet-LAR came from analyses using a threshold δr = 10%
As shown in Table 1, DeltaNet-LAR finished faster than DeltaNet-LASSO and SSEM. The computational time of DeltaNet-LAR decreased with increasing δr, as expected. Meanwhile the TPR of DeltaNet-LAR did not vary significantly for δr between 1 to 10% (see Supplementary Fig. S1). DeltaNet-LASSO and SSEM had similar computational times since both methods used the same LASSO regularization with 10-fold CV. If the optimal method parameters were known beforehand, then MNI finished quicker than DeltaNet and SSEM. But, as mentioned above, the parameter tuning could lead to a high total computational requirement (see Table 1). Finally, Table 2 gives the area under precision-recall (AUPR) and receiver operating characteristic curve (AUROC) for each method, which further confirms the higher accuracy of DeltaNet predictions over those from the other strategies.
Table 1.
. Computational times of DeltaNet, SSEM and MNI
| Computational timesa (h) |
E.coli | Yeast | Drosophila | |
|---|---|---|---|---|
| DeltaNet-LAR | δr= 20% | 4.34 | 9.6 | 5.7 |
| δr= 10% | 9.77 | 18.8 | 9.2 | |
| δr = 5% | 13.76 | 24.6 | 11.4 | |
| δr = 1% | 17.20 | 29.1 | 12.9 | |
| completion | 17.90 | 29.9 | 13.2 | |
| DeltaNet-LASSO | 30.5 | 43.8 | 42.9 | |
| SSEM | 33.8 | 48.6 | 43.1 | |
| MNI | Single run | 0.16 | 0.19 | 0.14 |
| Parameter tuningb | 15.58 | 15.55 | 11.83 | |
aComputational times were determined based on a single CPU run in a workstation with AMD Opteron 6282 SE processor and 256 GB RAM.
bThe parameter tuning for E.coli, yeast and Drosophila was performed by a grid search using 99, 96 and 89 grid points, respectively.
Table 2.
AUROC and AUPR of DeltaNet, SSEM, MNI and z-scores
| AUROC | AUPR | |
|---|---|---|
| E.coli | ||
| DeltaNet-LARa | 0.951 | 0.694 |
| DeltaNet-LASSO | 0.942 | 0.717 |
| SSEM | 0.921 | 0.558 |
| MNI | 0.906 | 0.252 |
| Z-scores | 0.860 | 0.262 |
| Yeast | ||
| DeltaNet-LARa | 0.890 | 0.432 |
| DeltaNet-LASSO | 0.903 | 0.402 |
| SSEM | 0.893 | 0.360 |
| MNI | 0.876 | 0.085 |
| Z-scores | 0.897 | 0.233 |
| Drosophila | ||
| DeltaNet-LARa | 0.966 | 0.534 |
| DeltaNet-LASSO | 0.957 | 0.527 |
| SSEM | 0.882 | 0.352 |
| MNI | 0.846 | 0.224 |
| Z-scores | 0.95 | 0.243 |
aDeltaNet-LAR result was obtained using δr = 10%.
3.2 Predicting transcription factor targets of chemical compounds
In the second application, we employed the predicted gene targets to identify transcription factors (TFs) which interact with drug and chemical compounds. We used the subset of yeast dataset corresponding to chemical treatments and the human MCF-7 dataset.
For yeast dataset, we employed DeltaNet, SSEM, MNI and z-scores analysis to rank gene targets. For DeltaNet-LAR, we used δr = 1% in order to keep enough non-zero coefficients. We performed a TF enrichment analysis using the top 100 genes for each chemical treatment sample using Yeastract (Teixeira et al., 2014), and obtained the adjusted p-values of the enriched TFs. We ranked the enriched TFs in increasing p-values (i.e. TFs with lower p-values are ranked higher).
For evaluating the accuracy of the TF prediction, we used protein-chemical interaction database in Search Tool for Interactions of Chemicals (STITCH) (http://stitch.embl.de) (Kuhn et al., 2014) as a reference. STITCH uses experiments, public database and literature mining as evidence to establish links between chemicals and proteins. In addition, we also used two publications to establish links between TFs and acetate (Giannattasio et al., 2013), and between TFs and rapamycin (Jacinto and Hall, 2003). Among the chemical treatment experiments in the yeast compendium, only five compounds have TF interactions in STITCH (with a confidence score > 0.7). Figure 3a compares the rankings of known TF targets of these five chemical compounds, according to the adjusted p-values from Yeastract for DeltaNet, SSEM, MNI and z-scores predictions (see Supplementary Table S1 for more details). Here, DeltaNet gave the best median ranking (69.5), followed by SSEM (85), MNI (92.5), and lastly z-scores (127). However, differences among the methods were not statistically significant (see Supplementary Table S2).
Fig. 3.
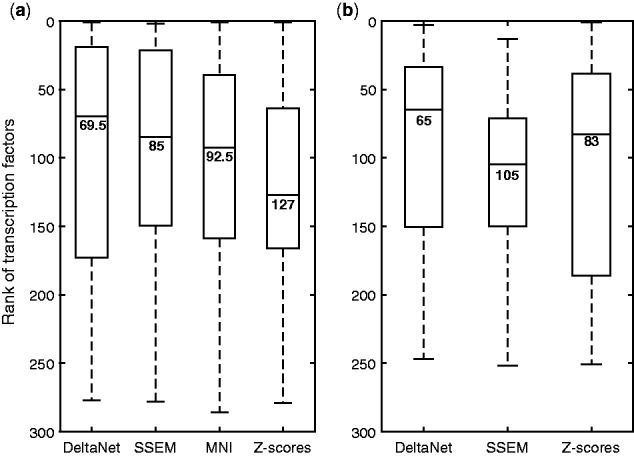
Rankings of known TF targets of chemical compounds based on TF enrichment analysis of DeltaNet, SSEM, MNI and z-scores predictions. The TFs are ranked according to (a) the adjusted p-values of Yeastract for yeast dataset and (b) the combined enrichment scores of Enrichr for human MCF-7 dataset
For MCF7 dataset, we applied DeltaNet, SSEM and z-scores to generate the gene target predictions. We could not perform MNI analysis as we had no known perturbations in the MCF7 dataset for parameter tuning. For the TF enrichment analysis, we employed Enrichr (Chen et al., 2013) with the option of position weight matrices using the top 100 predicted gene targets in each sample. Among the drugs in the dataset, only 21 compounds have at least one reported TF target in DrugBank (Wishart et al., 2006) and STITCH, which is also in Enrichr. Figure 3b compares the rankings of the known TF targets of these 21 compounds according to the combined enrichment scores from Enrichr for DeltaNet, SSEM and z-scores predictions (see Supplementary Table S3 for more details). Again, DeltaNet gave the best median ranking (65), followed by z-scores (83) and SSEM (105). Here, the difference in the median rankings between DeltaNet and SSEM was statistically significant (see Supplementary Table S2). Taken together, the outcomes of TF enrichment analyses above demonstrated that DeltaNet could provide gene target predictions which agreed better with previously reported TFs, than the other methods.
Unfortunately, we could not assess the gene target predictions for the chemical treatment samples from E.coli because the chemical compounds, namely ampicillin, kanamycin, norfloxacin and spectinomycin, do not have any TF interactions with high confidence (score > 0.7) in STITCH.
4 Discussion
We developed a method called DeltaNet for predicting the molecular targets of drugs or chemical compounds from gene expression data. Many applications of great interest and importance in drug discovery research, including elucidating the mode of action (MoA) of drugs and the mechanisms of diseases, fall within the problem that is addressed by this work. DeltaNet formulation uses an ODE model of gene transcription process under steady state condition. We employed two strategies for solving the resulting underdetermined linear regression problem: least angle regression (DeltaNet-LAR) and LASSO regularization (DeltaNet-LASSO). One can relax the assumption in DeltaNet which sets to zero, by treating the predicted as the sum between the self-regulatory feedback and the perturbations caused by the treatment. In such a case, instead of using the magnitude of the perturbation coefficients to rank genes, we could use the q-values of (Storey, 2002). However, for the case studies above, we did not observe any improvement in the prediction accuracy when using gene ranking according to the q-values (see Supplementary Material and Supplementary Fig. S2).
The output of DeltaNet comprises a ranked list of gene target predictions. Such a list is amenable for further enrichment analysis to identify other type of molecular targets, such as TFs in the second case study above. An upstream analysis can also be applied to find protein partners of enriched TFs, for example by using Expression2Kinase (Chen et al., 2012) and Enrichr (Chen et al., 2013). Beyond TF and protein targets, one can also apply functional enrichment analysis to obtain the functional relevance of the gene target predictions. Several web-server tools exist for such a purpose, notably ToppCluster analysis (Kaimal et al., 2010) which provides 17 categories of human-ortholog gene annotations such as gene ontology, pathways, microRNAs and human phenotype.
DeltaNet uses the same ODE model of the gene transcription process as the methods MNI and SSEM, but with a key difference in the manner by which the target predictions are inferred from the data. The first phase of MNI and SSEM involve the identification of the GRN matrix A using a compendium of gene expression data. The perturbation matrix P is subsequently obtained for the treatment samples of interest by network filtering, which in essence uses the difference In MNI, the matrix A is estimated from training data together with the unknown matrix P, using a procedure that resembles Expectation Maximization algorithm (di Bernardo et al., 2005). The convergence of this procedure is however not guaranteed and the solution often varies with the initial starting guess. Also, the performance of MNI is known to sensitively depend on the tuning of method parameters which often leads to numerically intensive optimization (Bevilacqua and Pannarale, 2013). Not to mention, MNI also requires data from known genetic perturbations for parameter tuning.
In contrast, SSEM uses LASSO regularization to identify the matrix A using the complete gene expression data, where the perturbation matrix P is initially set to zero. By doing so, SSEM ignores the treatment or perturbation effects when inferring the GRNs. The matrix P is subsequently obtained from the residuals of the regression above. The LASSO regularization enforces a limit on the model complexity, an assumption which is based on the observed sparsity of GRNs (Gardner et al., 2003; Luscombe et al., 2004; Tegner et al., 2003). The implementation of LASSO requires selecting the appropriate constraint parameter T for model complexity. As the optimal value is not known a priori and is also problem dependent, a cross-validation is often used for setting T. As shown in Table 1, analyses using LASSO, including DeltaNet-LASSO and SSEM, were the slowest among the methods considered. Here, the majority of the computational time was contributed by the cross validation step.
One can view DeltaNet as a hybrid between MNI and SSEM. The inference of the matrices A and P in DeltaNet is performed simultaneously, which resembles the first step of MNI. But, like SSEM, we employed a GRN sparsity assumption by way of LAR and LASSO regularization to tackle the underdetermined problem. Nevertheless, DeltaNet does not involve an explicit network filtering step. Instead, the perturbation matrix P for the treatment samples is obtained together with the other samples in the compendium. We could therefore fully use the information contained in the available data (training and treatment sets) in predicting the effects of a treatment. As demonstrated in the case studies, DeltaNet offers a significant improvement in the accuracy of target prediction over MNI and SSEM. Furthermore, DeltaNet-LAR has better numerical efficiency and robustness with respect to parameter tuning over DeltaNet-LASSO, MNI and SSEM. We therefore recommend DeltaNet-LAR using a threshold parameter δr of 10%, since in our experience, this setting provides a good balance between target prediction accuracy and computational performance.
While the difference between DeltaNet and the existing network filtering methods may appear slight, this deviation is nevertheless important and fundamental. There were two key factors motivating the single-step inference in DeltaNet. First, the inference of GRNs from the typical gene expression has been shown to be underdetermined (Szederkényi et al., 2011; Ud-Dean and Gunawan, 2014). Thus, any method relying on the solution of such an inference problem could be sensitive to the associated uncertainty. Second, despite the underdetermined issue, it is often possible to predict the effects of a network perturbations from existing gene expression data with reasonable accuracy (Maathuis et al., 2010). We formulated DeltaNet based on the premise that the available gene expression data, while lacking information for the accurate inference of GRN, have enough information to identify the network perturbations caused by a treatment.
The differences between the gene target predictions from DeltaNet-LASSO and SSEM are quite interesting, considering that both methods employ the same LASSO regularization. In the first case study, we noted that for yeast and E.coli datasets, DeltaNet-LASSO produced sparser GRNs than SSEM (see Supplementary Fig. S3a). This trend is expected since in comparison to SSEM, DeltaNet formulation has additional degrees of freedom that come from the perturbation vector. However, the network sparsity between DeltaNet and SSEM in the Drosophila dataset did not differ significantly. We further looked at the set of known gene targets among the top 10 predictions from DeltaNet-LASSO, but not from SSEM. For these gene targets (n = 10, 15 and 13 for E.coli, yeast and Drosophila, respectively), DeltaNet-LASSO clearly produced fewer non-zero coefficients than SSEM for all three datasets (see Supplementary Fig. S3b). The observations above indicated a possibility of overfitting in SSEM as the regression problem did not consider perturbations on the genes.
Finally, time-series expression data have become routine and increasingly available in public databases. Applying DeltaNet and similar methods such as SSEM and MNI to time series data should be done with caution because of the underlying steady state assumption in the method formulation. In the case studies, we included time-series data as a part of the training dataset. Excluding time-series data however did not affect the accuracy of DeltaNet predictions significantly (see Supplementary Fig. S4). An extension of DeltaNet to take advantage of time-series data is currently being developed, the results of which will be reported in a separate publication.
Supplementary Material
Acknowledgements
We thank S.M. Minhaz Ud-Dean for useful discussions and suggestions, and Dr. L.N. Lakshmanan for his assistance on DeltaNet website.
Funding
This work was supported by ETH Zurich Research Grant.
Conflict of Interest: none declared.
References
- Barrett T. et al. (2013) NCBI GEO: archive for functional genomics data sets–update. Nucleic Acids Res., 41, D991–D995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belcastro V. et al. (2013) Systematic verification of upstream regulators of a computable cellular proliferation network model on non-diseased lung cells using a dedicated dataset. Bioinf. Biol. Insights, 7, 217–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bevilacqua V., Pannarale P. (2013) Scalable high-throughput identification of genetic targets by network filtering. BMC Bioinformatics, 14, S5.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonke M. et al. (2013) Transcriptional networks controlling the cell cycle. G3 (Bethesda), 3, 75–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen E.Y. et al. (2012) Expression2Kinases: mRNA profiling linked to multiple upstream regulatory layers. Bioinformatics, 28, 105–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen E.Y. et al. (2013) Enrichr: interactive and collaborative HTML5 gene list enrichment analysis tool. BMC Bioinformatics, 14, 128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chindelevitch L. et al. (2012) Causal reasoning on biological networks: interpreting transcriptional changes. Bioinformatics, 28, 1114–1121. [DOI] [PubMed] [Google Scholar]
- Chua H.N., Roth F.P. (2011) Discovering the targets of drugs via computational systems biology. J. Biol. Chem., 286, 23653–23658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cosgrove E.J. et al. (2008) Predicting gene targets of perturbations via network-based filtering of mRNA expression compendia. Bioinformatics, 24, 2482–2490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Bernardo D. et al. (2005) Chemogenomic profiling on a genome-wide scale using reverse-engineered gene networks. Nat. Biotechnol., 23, 377–383. [DOI] [PubMed] [Google Scholar]
- Efron B.B. et al. (2004) Least angle regression. Ann. Stat., 32, 407–499. [Google Scholar]
- Faith J.J. et al. (2008) Many microbe microarrays database: uniformly normalized Affymetrix compendia with structured experimental metadata. Nucleic Acids Res., 36, D866–D870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J. et al. (2010) Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw., 33, 1–22. [PMC free article] [PubMed] [Google Scholar]
- Gardner T. et al. (2003) Inferring genetic networks and identifying compound mode of action via expression profiling. Science, 301, 102–106. [DOI] [PubMed] [Google Scholar]
- Gentleman R.C. et al. (2004) Bioconductor: open software development for computational biology and bioinformatics. Genome Biol., 5, R80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giannattasio S. et al. (2013) Molecular mechanisms of Saccharomyces cerevisiae stress adaptation and programmed cell death in response to acetic acid. Front. Microbiol., 4, 33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes T.R. et al. (2000) Functional discovery via a compendium of expression profiles. Cell, 102, 109–126. [DOI] [PubMed] [Google Scholar]
- Hurley D. et al. (2012) Gene network inference and visualization tools for biologists: application to new human transcriptome datasets. Nucleic Acids Res., 40, 2377–2398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iorio F. et al. (2010) Discovery of drug mode of action and drug repositioning from transcriptional responses. Proc. Natl. Acad. Sci. U. S. A., 107, 14621–14626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iskar M. et al. (2010) Drug-induced regulation of target expression. PLoS Comput. Biol., 6, e1000925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacinto E., Hall M.N. (2003) TOR signalling in bugs, brain and brawn. Nat. Rev. Mol. Cell Biol., 4, 117–126. [DOI] [PubMed] [Google Scholar]
- Kaimal V. et al. (2010) ToppCluster: a multiple gene list feature analyzer for comparative enrichment clustering and networkbased dissection of biological systems. Nucleic Acids Res., 38, 96–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koschmann J. et al. (2015) ‘Upstream Analysis’: an integrated promoter-pathway analysis approach to causal interpretation of microarray data. Microarrays, 4, 270–286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn M. et al. (2014) STITCH 4: integration of protein-chemical interactions with user data. Nucleic Acids Res., 42, D401–D407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lachmann A., Ma’ayan A. (2009) KEA: kinase enrichment analysis. Bioinformatics, 25, 684–686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laenen G. et al. (2015) Galahad: a web server for drug effect analysis from gene expression. Nucleic Acids Res., 43, W208–W212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamb J. et al. (2006) The Connectivity Map: using gene-expression signatures to connect small molecules, genes, and disease. Science, 313, 1929–1936. [DOI] [PubMed] [Google Scholar]
- Lefebvre C. et al. (2010) A human B-cell interactome identifies MYB and FOXM1 as master regulators of proliferation in germinal centers. Mol. Syst. Biol., 6, 377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao J.C. et al. (2003) Network component analysis: reconstruction of regulatory signals in biological systems. Proc. Natl. Acad. Sci. U. S. A., 100, 15522–15527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luscombe N. et al. (2004) Genomic analysis of regulatory network dynamics reveals large topological changes. Nature, 431, 308–312. [DOI] [PubMed] [Google Scholar]
- Maathuis M.H. et al. (2010) Predicting causal effects in large-scale systems from observational data. Nat. Methods, 7, 247–248. [DOI] [PubMed] [Google Scholar]
- Martin F. et al. (2012) Assessment of network perturbation amplitudes by applying high-throughput data to causal biological networks. BMC Syst. Biol., 6, 54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parkinson H. et al. (2007) ArrayExpress – a public database of microarray experiments and gene expression profiles. Nucleic Acids Res., 35, D747–D750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey J.D. (2002) A direct approach to false discovery rates. J. R. Stat. Soc. Ser. B, 64, 479–498. [Google Scholar]
- Szederkényi G. et al. (2011) Inference of complex biological networks: distinguishability issues and optimization-based solutions. BMC Syst. Biol., 5, 177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarca A. et al. (2006) Analysis of microarray experiments of gene expression profiling. Am. J. Obstet. Gynecol., 195, 373–388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tegner J. et al. (2003) Reverse engineering gene networks: integrating genetic perturbations with dynamical modeling. Proc. Natl. Acad. Sci. U. S. A., 100, 5944–5949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teixeira M.C. et al. (2014) The YEASTRACT database: an upgraded information system for the analysis of gene and genomic transcription regulation in Saccharomyces cerevisiae. Nucleic Acids Res., 42, D161–D166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. (1996) Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B, 58, 267–288. [Google Scholar]
- Ud-Dean S.M.M., Gunawan R. (2014) Ensemble inference and inferability of gene regulatory networks. PLoS One, 9, e103812.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wishart D.S. et al. (2006) DrugBank: a comprehensive resource for in silico drug discovery and exploration. Nucleic Acids Res., 34, D668–D672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woo J.H. et al. (2015) Elucidating compound mechanism of action by network perturbation analysis. Cell, 162, 441–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xing H., Gardner T.S. (2006) The mode-of-action by network identification (MNI) algorithm: a network biology approach for molecular target identification. Nat. Protoc., 1, 2551–2554. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.