Abstract
Summary: We present a new R package for training gapped-kmer SVM classifiers for DNA and protein sequences. We describe an improved algorithm for kernel matrix calculation that speeds run time by about 2 to 5-fold over our original gkmSVM algorithm. This package supports several sequence kernels, including: gkmSVM, kmer-SVM, mismatch kernel and wildcard kernel.
Availability and Implementation: gkmSVM package is freely available through the Comprehensive R Archive Network (CRAN), for Linux, Mac OS and Windows platforms. The C ++ implementation is available at www.beerlab.org/gkmsvm
Contact: mghandi@gmail.com or mbeer@jhu.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
We recently introduced a gapped-kmer-SVM classifier (gkmSVM) (Ghandi et al., 2014a) to detect functional sequence elements in regulatory DNA which has been applied to interpret a wide range of genomic datasets (Gorkin et al., 2012; Lee et al., 2015; Pimkin et al., 2014; Mo et al., 2016; Svetlichnyy et al., 2015). While we released a version of our earlier kmer-SVM (Lee et al., 2011) as a webserver (Fletez-Brant et al., 2013), gkmSVM was only released as C ++ source code. Here, we present an R package, gkmSVM-R, with several improvements to facilitate easier implementation and broader use. Our original gkmSVM-1.3 implementation used a tree algorithm to compute the kernel matrix (Ghandi, 2012; Ghandi et al., 2014a, b). In this paper, we describe a new algorithm, iDL-bound, that speeds up kernel matrix computation. We have implemented the algorithm in C ++ and our R package is easily accessible on different platforms. Our package also includes fast implementations of other kernels (Leslie and Kuang, 2004; Leslie et al., 2004). We refer the C ++ code implementing the faster iDL kernel calculation as gkmSVM-2.0.
2 Usage
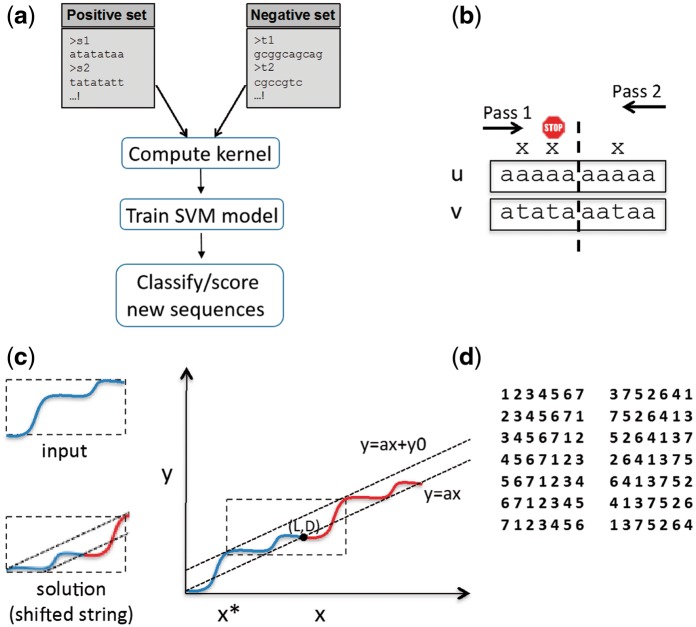
Figure 1 shows an overview of the gkmSVM analysis pipeline. Given two sets of sequences, the goal is to build a predictive model to classify the two sets. For example, in (Lee et al., 2015) a gkmSVM is trained to detect regulatory DNA elements active in a cell type by using chromatin accessible DNA sequences as the positive set and a set of GC matched inaccessible DNA sequences as negative set. The model then can score and predict the accessibility of any DNA sequence. The first step is to build the kernel matrix (the pairwise similarity scores for all the sequences in the positive and negative sets). This is done using gkmsvm_kernel function:
gkmsvm_kernel(posfn, negfn, kernelfn);
where posfn and negfn are the input file names for the positive and negative sets (FASTA format) and kernelfn is the output file name for the kernel matrix. The second step is to train the SVM model, using:
gkmsvm_train(kernelfn, posfn, negfn, svmfnprfx);
where svmfnprfx is the output file name prefix for the SVM model (support vectors). Finally to classify/score a sequence, gkmsvm_classify is used:
gkmsvm_classify(testfn, svmfnprfx, outfn);
where testfn is the sequence input file and outfn is the output. We have also included new functions genNullSeqs to sample the genome to generate a GC, length and repeat fraction matched negative sequence set and extract FASTA sequences, and gkmsvm_delta to score the impact of a variant (Lee et al., 2015) as described in the tutorial (Supplementary Data).
Fig. 1.
(a) gkmSVM pipeline overview. (b) Example of a two-pass string comparison. Input strings are compared in two passes: first from left to right and then from right to left. The search stops when more than one mismatch is found in the first half of the search from each side. (c) Graphical proof for lemma 1. (d) Example of 14 passes used for L = 7, D = 3
3 IDL-bound algorithm
The original algorithm in (Ghandi et al., 2014a), calculated the mismatch profile for all pairs of k-mers with up to D mismatches using a single depth first search (DFS) traversal of the k-mer tree. This is fast for small values of D, but search time exponentially grows with D. Here, we implement an alternative approach that divides the search into n independent passes. Each pass can be truncated, speeding the overall search. To elaborate, Figure 1b shows an example of two strings of length L = 10, denoted by u = u1,…,uLand v = v1,…,vL. We want to check if they differ in at most D = 3 places. One approach is to start from the left and compare the two strings in a left to right order. We stop the search when we observe 4 mismatches or reach the end of the string. Alternatively, we can make the comparison in two passes, from left to right and right to left. If the strings have at most 3 mismatches, then in one of the two passes there is at most 1 mismatch in the first half of the search. So we can stop when we observe more than 1 mismatch, which can greatly reduce search time.
Lemma 1
Given string length L, and maximum mismatch D, there exists L predetermined passes (each pass is a permutation of 1,…,L) where for any pair of strings with at most D mismatches, the number of mismatches in the first i comparisons is bounded by in at least one of the passes. The L passes can be generated by circular shifting of 1,…,L.
To compare two strings, we compare them in L different passes (orders of letters), and at each pass stop the search if the number of mismatches exceeds at the ith step. Lemma 1 guarantees that if the two strings have D or fewer mismatches, at least one of the passes will reach the end, which we here prove graphically, similar to Raney’s problem in (Graham et al., 1994). Given two strings u and v, we plot the mismatch curve by starting from the origin, and for each position i, if ui and vi match, we move one unit in x, and if they do not we move one unit in x and one unit in y. If u and v have D mismatches, the mismatch curve will end at point (L,D), and the line segment between the two ends has slope a = D/L (Fig. 1c). Now if we repeat u and v and continue the mismatch curve it will also pass (2L,2D) as shown. If we shift the y = a⋅x line in y so that the mismatch curve lies entirely below it, the corresponding shift (x*) gives the cyclic shift that satisfies the iDL-bound.
In gkmSVM-2.0, we divide the search into n = 2L passes, L of them given by the L circular shifts of 1.L, and the other given by L circular shifts of the reverse of the scrambled permutation defined as follows: and where if or and otherwise, , . Figure 2d shows the 2L permutations used for L = 7 and D = 3 as an example. In practice, we generate all the possible patterns of mismatches (all the binary strings of length L with at most D ones) and assign each mismatch pattern to the pass that gives the minimum cost:
Here, is the square of the number of nodes at depth i in the k-mer tree, and p = 1/b, where b is the size of the alphabet (e.g. b = 4 for DNA). This equation generally assigns each mismatch pattern to the pass that visits most of the match positions first and mismatch positions toward the end of the search. We then build a k-mer tree using all the mismatch patterns assigned to each pass and use that to prune the DFS search in that pass. Since this new algorithm involves independent passes, we can easily multithread by running each pass on a separate thread, following (Lee, 2016).
Fig. 2.
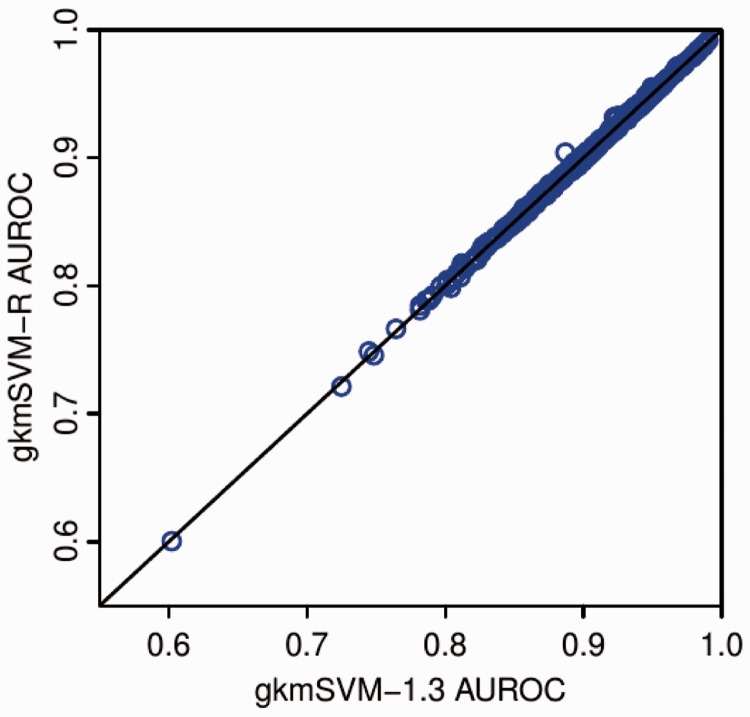
Comparison of AUC on 467 ENCODE ChIP-seq datasets. gkmSVM-R reproduces gkmSVM-1.3 (Ghandi et al., 2014a) when C = 1. Our faster algorithm allowed optimizing over C (shown), but this yields insignificant improvement in AUC
4 Results
To evaluate the algorithm performance, we applied it to CTCF and EP300 datasets described in (Ghandi et al., 2014a). Table 1 shows running times for different values of L and D. We observe an average improvement of two fold using a single thread and up to 20-fold using 8 threads. LS-GKM (Lee, 2016), designed for training on very large datasets, is typically two times slower. With the faster iDL algorithm we were also able optimize the SVM C parameter for the 467 Chip-seq datasets analyzed in (Ghandi et al., 2014a). We reproduce the results of gkmSVM-1.3 with gkmSVM-R when C = 1, and when C is optimized, as shown in Figure 2, there is minimal improvement. We therefore recommend running with C = 1.
Table 1.
Comparison of running times (min)
|
EP300, L=10, k=6 |
CTCF, L=10, k=6 |
CTCF, L=12, k=6 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| nthread | D = 3 | D = 4 | D = 3 | D = 4 | D = 3 | D = 4 | D = 5 | D = 6 | |
| gkmSVM1.3 | 1 | 15.7 | 50.3 | 18.1 | 67.1 | 21.3 | 115.0 | 447.8 | 1237 |
| gkmSVM2.0 | 1 | 9.0 | 33.9 | 13.6 | 49.8 | 7.3 | 34.2 | 136.8 | 570.7 |
| gkmSVM2.0 | 4 | 2.4 | 11.4 | 3.6 | 18.3 | 2.2 | 10.4 | 53.2 | 140.7 |
| gkmSVM2.0 | 8 | 1.4 | 6.1 | 2.2 | 8.6 | 1.4 | 5.7 | 30.2 | 77.1 |
| Lsgkm | 1 | 21.5 | 65.2 | 28.0 | 82.6 | 57.4 | 176.8 | 473.1 | 1167 |
Supplementary Material
Funding
M.A.B. was supported by NIH grant R01 HG0007348. M. M-N and N. G. were supported by grants from IPM (No. CS1391-4-02 and No. 94050016).
Conflict of Interest: none declared.
References
- Fletez-Brant C. et al. (2013) kmer-SVM: a web server for identifying predictive regulatory sequence features in genomic data sets. Nucleic Acids Res., 41, W544–W556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghandi M. (2012) A sequence based model for nucleosome positioning in yeast. (Doctoral dissertation). Proquest/UMI 3537355.
- Ghandi M. et al. (2014a) Enhanced regulatory sequence prediction using gapped k-mer features. PLoS Comput. Biol., 10, e1003711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghandi M. et al. (2014b) Robust k-mer frequency estimation using gapped k-mers. J. Math. Biol., 69, 469–500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorkin D.U. et al. (2012) Integration of ChIP-seq and machine learning reveals enhancers and a predictive regulatory sequence vocabulary in melanocytes. Genome Res., 22, 2290–2301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graham R.L. et al. (1994) Concrete Mathematics: A Foundation for Computer Science 2nd ed. Addison & Wesley, Boston. [Google Scholar]
- Lee D. et al. (2011) Discriminative prediction of mammalian enhancers from DNA sequence. Genome Res., 21, 2167–2180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D. et al. (2015) A method to predict the impact of regulatory variants from DNA sequence. Nat. Genet., 47, 955–961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D. (2016) LS-GKM: a new gkm-SVM for large-scale datasets. Bioinformatics, inpress. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leslie C. et al. (2004) Mismatch string kernels for discriminative protein classification. Bioinformatics, 20, 467–476. [DOI] [PubMed] [Google Scholar]
- Leslie C., Kuang R. (2004) Fast String kernels using inexact matching for protein sequences. J. Mach. Learn. Res., 5, 1435–1455. [Google Scholar]
- Mo A. et al. (2016) Epigenomic landscapes of retinal rods and cones. eLife, 5, e11613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pimkin M. et al. (2014) Divergent functions of hematopoietic transcription factors in lineage priming and differentiation during erythro-megakaryopoiesis. Genome Res., 24, 1932–1944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svetlichnyy D. et al. (2015) Identification of high-impact cis-regulatory mutations using transcription factor specific random forest models. PLoS Comput. Biol., 11, e1004590. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.