A fast and powerful W-test for pairwise epistasis testing

Abstract

Epistasis plays an essential role in the development of complex diseases. Interaction methods face common challenge of seeking a balance between persistent power, model complexity, computation efficiency, and validity of identified bio-markers. We introduce a novel W-test to identify pairwise epistasis effect, which measures the distributional difference between cases and controls through a combined log odds ratio. The test is model-free, fast, and inherits a Chi-squared distribution with data adaptive degrees of freedom. No permutation is needed to obtain the P-values. Simulation studies demonstrated that the W-test is more powerful in low frequency variants environment than alternative methods, which are the Chi-squared test, logistic regression and multifactor-dimensionality reduction (MDR). In two independent real bipolar disorder genome-wide associations (GWAS) datasets, the W-test identified significant interactions pairs that can be replicated, including SLIT3-CENPN, SLIT3-TMEM132D, CNTNAP2-NDST4 and CNTCAP2-RTN4R. The genes in the pairs play central roles in neurotransmission and synapse formation. A majority of the identified loci are undiscoverable by main effect and are low frequency variants. The proposed method offers a powerful alternative tool for mapping the genetic puzzle underlying complex disorders.

INTRODUCTION

Genetic association studies have identified a repertoire of susceptible loci that are associated with common diseases. However, they have collectively explained only a small fraction of disease heritability (1–3). It was widely accepted that epistasis, or gene-gene interactions, plays an essential role in the development of complex disorders (4,5). Past epistasis studies mainly focused on the genomic region in which the minor allele frequency (MAF) is >5%, while rare variant analysis focused on main effect in the exome region where MAF is <1%. The low frequency variants, in which MAF is between 1% and 5%, remain largely understudied. Available tools to calculate genome-wide epistasis can be broadly grouped into three categories: the parametric methods represented by logistic regression, non-parametric methods represented by the classic Pearson's Chi-squared test and the machine learning method by the multifactor dimensionality reduction (MDR) (6). Logistic regression assumes a linear relationship between phenotype and genotypic combinations. It has the unique property of providing an odds ratio interpretation, which allows it to give prospective inferences from retrospective case–control datasets (7). The Pearson's Chi-squared test is fast and non-parametric. However, it requires some minimum cell counts for the test statistic to follow a Chi-squared distribution. The MDR is a very powerful machine learning approach that first pools the genotype combinations into a low risk and a high risk group to achieve dimensionality reduction, evaluates the multi-locus model through cross-validations, and then estimates the model P-values through permutations. Despite the specialties of various methods, the detection of interaction effects faces the common challenges of bringing persistent power in intricate genetic architectures, varying sample sizes, computing efficiency, and reproducibility of results toward mapping clinically relevant biomarkers.

Bipolar disorder (BD) is a serious mental disorder that is characterized by episodes of mania and deep depression. Family studies suggest that the heritability of BD is 80–85% (8–10). Overwhelming evidence shows that genetics play a fundamental role in the onset of BD besides the influence of environmental factors. However, in past decades, genetic association studies had difficulty in identifying suspect genes relating to BD with large effect sizes, and the explained heritability is <5% (11,12). Interplay of multiple genetic markers is crucial for the etiology of bipolar disorder; therefore, we hypothesized that we would have interesting findings when epistasis effects were considered in BD datasets.

In this paper, we introduce a W-test for pairwise epistasis testing that has robust power covering the genome where MAF > 1%. The W-statistic tests the null hypothesis that the joint distribution of a set of single nucleotide polymorphisms (SNPs) is different in the cases from that in the control group. The distributional differences are measured by a combined log odds ratio from the contingency table, with two scalars estimated from the null hypothesis. The method is advantageous in several respects. First, it is model-free, such that it makes no assumption about genotypic effect model. Second, it is very fast; it only uses a subset of bootstrap samples to estimate two distribution parameters and calculate P-values, and genome-wide screening can be performed efficiently. Third, the W-test incorporates a statistical distribution that is data-adaptive, such that the association measurement is robust for various genetic scenarios. In principle, the W-test takes the form of Chi-squared distribution, and its degrees of freedom are estimated from the covariance structure of a contingency table formed by the interaction set. The data-dependent degrees of freedom allow the method to cope with low frequency genotypes, which, for classic tests, will result in low power from imperfect statistical distributions. The W-test showed robust power and reasonable type I error in various genetic environments; when the variants frequency is low, it outperforms all alternative methods.

The remainder of the article is organized as follows. In the next section, we describe the proposed method, including its formulation and distribution. We then will test the power and type I error of the proposed methods and alternative methods under different genetic models and genetic architectures, using simulated phenotype generated from real data. The method will then be applied to an American Caucasian's bipolar GWAS data and an independent European Caucasian's data. We identified a number of genes that are highly relevant to neuronal function and depressive disorders, which can be replicated by the two datasets. To our knowledge, this is also the first report of successful replication of the genes with significant epistasis effect in GWAS. The method proposed also has general application values for identifying disease-susceptible interactions in other types of data.

MATERIALS AND METHODS

The W-test formulation

The basic hypothesis of the W-test is that the statistical distributions of a set of disease-associated markers are different in the case group from that in the control group. Under a co-dominant model, the genotype data X can be coded by minor allele count to take values (0, 1, 2). The phenotype Y is binary for the case and control dataset. To test the association of a pair of SNPs (X₁, X₂), a 2 × 9 contingency table can be formed. Let k denote the number of columns of the table. The cell distribution of (X₁, X₂) in the case and control group can be written as:

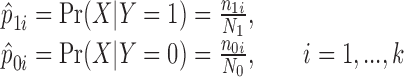where n_1i is the number of case subjects in the ith cell, N₁ is the total number of cases, n_0i is the number of control subjects in the ith cell, and N₀ is the total number of controls. For pair-wise interactions, k = 9. The method can also accommodate main effect testing. When a single SNP is considered, k = 3. For both case and control samples, we have:

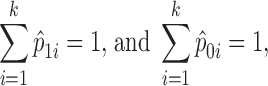To measure the discordance between the two distributions, we first use the following measure to combine the normalized log odds ratios of the cell probability distributions:

(1)

where

Diagram 1 shows the decomposition of X². Since the contingency table's margins are fixed, the cell probabilities are not entirely independent. If they are independent, the X² would follow a k degrees of freedom Chi-squared distribution. The mutual dependency among the cells decreases as k becomes large. The distribution of the X² can be estimated by matching its first two moments to the moments of the following variable R of a known Chi-squared distribution with f degrees of freedom (13):

Diagram 1.

Decomposition of the W-test. The W-test measures the distributional differences between cases and controls using a combined log odds ratio. The dependency among the cells is handled by the data-dependent scalars h and f, estimated from the null hypothesis. The overall test statistic follows a Chi-squared distribution with f degrees of freedom.

The first two moments of X² are:

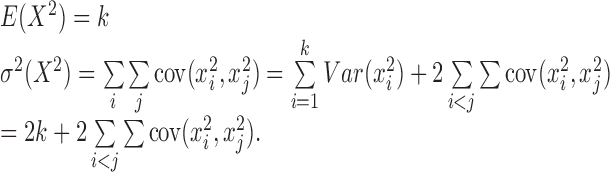x_i and x_j are the components in the summation sign in Equation (1), which are the single cell's normalized log of odds ratio. And the first two moments of R are:

The c and f can be obtained accordingly:

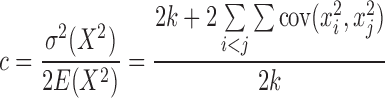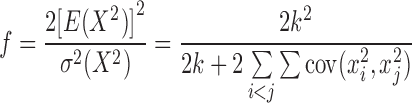Let h = 1/c, we define the W-test, with a scalar h before the X², as:

(2)

Thus the W-test follows a Chi-squared distribution with f degrees of freedom. The approximation is shown to give accurate probability by numerical studies (14). Theoretical justification for the validity of the approximation is given by Chuang and Shih (15). In real data analysis, it might be difficult to obtain the covariance matrix for X². Large sample theory can be used to estimate the covariance from smaller bootstrap samples under the null hypothesis. Each bootstrap sample consists of the real genotype data and permutated Y. Suppose total number of subjects is N, and total number of pairs is P. Converging estimates for h and f can be achieved by setting bootstrap times B > 200, subjects number N_B = min (1000, N), and number of pairs P_B= min (1000, P) (Supplementary Information S1). Empirical studies give h ≈ (k − 1)/k and f ≈ k − 1. A table of estimated h and f in real data is provided in the Supplementary Information S2. Frequently, the degrees of freedom f are non-integer. Then the Chi-squared distribution is in fact a Gamma (f /2, 2) distribution. The covariance of X² is dataset dependent, so for every set of new genotypes, h and f need to be estimated. When there is an empty cell, a continuity correction is applied by adding 0.5 to all cells.

The W-test is a combined log of odds ratio test based on maximum likelihood probabilities conditioned on disease status. It is equivalent to testing the following null hypothesis:

The test is model-free, and does not assume the form of interactions. Because of its odds ratio form, it is suitable to be applied to retrospective case-control datasets, which is how data are collected in most of the genome studies. If a W-value is large and the null hypothesis is rejected, we would conclude that the joint probability distribution has a significant difference between cases and controls, which indicates the interactive set (X₁, X₂) has association effect. The classic odds ratio test is a special case of W-test for a single marker with two levels. The W-test can be extended to higher order interactions mapping. In this paper, we mainly focus on pair-wise interactions tests in simulation studies. Simulation study of main effect is provided in Supplementary Materials S3.

Application on simulated datasets

Simulated datasets are composed of genotypes from real GWAS datasets and simulated phenotypes. Different genetic architectures considered include minor allele frequency (MAF) in the common range (MAF > 5%) and in the low frequency range (1% < MAF < 5%); linkage disequilibrium (LD) in the high range (r² > 80%), medium range (20% < r² < 80%), and low range (r² < 20%) (16,17). In each of the six genetic architecture combinations, 50 SNPs and 1000 subjects are randomly drawn from real GWAS datasets. The original phenotype label is removed, and binary response variables are simulated using two types of model, specified as follows.

Model 1. A linear regression model with interaction effect. A linear model can be prescribed by the following logistic regression (18):

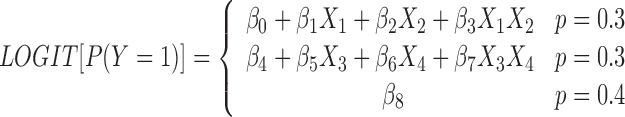The logit has 30% probability to be equal to the first equation, 30% probability to take the second equation, and 40% chance of equaling β₈, which is a random real number. The coefficients are chosen such that the case and control ratio is balanced. This model contains both the main and the interaction effect terms, and the coefficients of the cross-product β₃ and β₇ terms are tested for interaction effects. The genotype takes values of 0, 1 or 2, under a co-dominant genetic model assumption.

Model 2. A non-linear interaction model. The Y has a non-linear association to (X₁, X₂) and (X₃, X₄) (19,20):

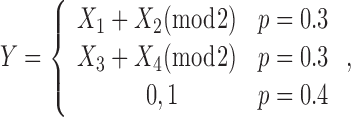where the Ys are (X₁ + X₂) mod 2 or (X₃ + X₄) mod 2 with 30% probability, and are randomly assigned to be 0 or 1 with 40% probability. Only pure interaction effect is present in this model. The null hypothesis is that none of the X predictor is associated with Y.

Power and type I error rate calculation using simulated datasets

For power calculation, simulated dataset using Model 1 or Model 2 for each genetic architecture block is generated 1,000 times. Pairwise interactions are calculated exhaustively by the W-test and alternative methods. For 50 SNPs, 1,225 pairs are evaluated. An interaction set is significant if its P-value is smaller than 4.1 × 10⁻⁵, which is the Bonferroni corrected P-value at a family-wise error rate (FWER) of 0.05. Methods that result significant P-values of all interaction effect variables are said to have successfully identified the causal markers. Power is the averaged true positive proportion in 1000 simulated datasets. For type I error estimation, Y is permutated 10⁶ times, and type I error rate is the average false positive proportion in one million permutated datasets.

Application to real GWAS datasets

Datasets

The W-test is then applied to two real bipolar GWAS datasets. The first dataset is from the Wellcome Trust Case Control Consortium (WTCCC), comprising 2000 bipolar cases and 3000 controls of European Caucasians (21). The dataset includes 500 568 SNPs genotyped with GeneChip 500K Mapping Array Set (Affymetrix Chip). The second dataset is from the Genetic Association Information Network (GAIN) project (22). The GAIN data is composed of an American ancestry population with a bipolar phenotype, which contains 653 cases and 1767 controls. The data includes 906 600 SNPs genotyped with Affymetrix 6.0 platform. Quality control is performed: SNPs with high missing rates (>5%), MAF < 1%, and which depart from the Hardy–Weinberg equilibrium are excluded (23). After the quality control, the WTCCC dataset includes 414 682 SNPs and the GAIN data contains 729 304 SNPs.

Pair-wise interaction search

A three-step procedure is used to search for pair-wise interaction, described as follows.

Step 1. Main effect search The main effects are evaluated exhaustively on the whole genome by the W-test. The SNPs with P-value that is <0.01 are passed to the next step SNP–SNP interaction test. The P-value < 0.01 compared to the genome-wide significance 10⁻⁸ is trivial (24). Thus this filtering can include the weak effect markers that are potentially influential in an interaction setting, while downsizing the candidate sets.

Step 2. Two-way interaction search The epistasis test is performed on the candidate markers. A pair of SNPs will be selected if its P-value passes the Bonferroni corrected alpha at FWER 5%. The P-value of the pair should be more significant than component SNPs’ P-value.

Step 3. Map SNP-SNP to gene-gene interaction pair The SNP-pairs are matched to corresponding genes using web-based databases (25,26); interaction networks are created by linking significant pairs (27,28). Steps 1–3 are performed on the WTCCC and the GAIN data sets respectively, and interactions that are replicated by the two data sets are reported.

RESULTS

Simulation study statistical power and type I error rate

Linear interaction model with main effect

The W-test is compared to the logistic regression, Chi-squared test, and MDR under different genetic architectures (Table 1). Under the common variant (MAF > 5%) and high LD environment, the power for logistic regression is 83.3%, Chi-squared test is 74.5%, MDR is 96.5% and W-test is 86.7%. However, the nominal type I error of the MDR is >1; while W-test's nominal type I error is 5.5% (Table 1). When MAF is low (1% <MAF< 5%), the W-test has the highest power for all LD scenarios. Specifically, in the mid LD range, the power of W is 79.5%, compared to the MDR's 67.1%, Chi-square's 65.2% and logistic regression's 62.5%. The nominal type I errors of the MDR and the W-test are 5.8% and 5.1%, respectively. Interestingly, the model-free W-test outperforms the logistic regression even when the underlying model is linear. In general, the power of all methods improves when the variables are in high LD, and drop as their mutual correlation diminish (Figure 1A). This is likely due to the presence of main effect terms in the linear model, such that a causal marker can pair with another one due to high LD, which makes it easier to be identified.

Table 1. Power and type I error rates of alternative methods on pairwise epistasis effect.

		MAF > 5%			1%< MAF <5%
Model	Methods	LD			LD
		Low	Medium	High	Low	Medium	High
Power (linear model)	Logistic	68.5%	76.9%	83.3%	47.1%	62.5%	71.1%
	Chi-squared	60.0%	67.2%	74.5%	42.2%	65.2%	74.0%
	MDR	88.5%	90.0%	96.5%	42.6%	67.1%	71.6%
	W	71.1%	81.0%	86.7%	49.8%	79.5%	83.8%
Power (nonlinear model)	Logistic	5.9%	1.7%	0.6%	61.7%	31.8%	43.7%
	Chi-squared	72.6%	69.4%	62.8%	67.4%	43.9%	49.1%
	MDR	95.5%	91.5%	83.5%	88.6%	70.8%	70.3%
	W	88.0%	86.6%	79.4%	95.6%	83.3%	83.9%
Type I Error Ratea	Logistic	3.2E−05	4.8E−05	3.2E−05	3.7E−05	4.3E−05	4.6E−05
	Chi-squared	2.3E−05	1.4E−05	2.5E−05	3.0E−06	2.0E−06	2.0E−06
	MDR	7.2E−04	8.6E−04	9.3E−04	3.6E−05	4.7E−05	4.9E−05
	W	4.4E−05	4.9E−05	4.5E−05	3.3E−05	4.2E−05	5.5E−05

^aNominal type I error rate = type I error rate × 1225 pairs.

Figure 1.

Power of alternative methods in low frequency variant environment. In the low frequency variant environment (1% < MAF < 5%),the W-test outperforms alternative methods for both linear and non-linear models.

Non-linear interaction model without main effect

In the common MAF environment, though the average power of MDR is 90.2%, higher than W-test's average power of 84.7%, the nominal type I error of the MDR is around 1, while for the W-test the type I error is around 5% (Table 1, Figure 1B). In the low frequency variant environment (1% < MAF < 5%), the average power of W-test is 87.6%, 14.4% greater than the MDR's. The average nominal type I error of W-test is 5.3%, and the average type I error for the MDR is 5.4%. Specifically, when LD is medium, the power of W is 83.3%, compared to the MDR 70.8%, Chi-squared 43.9% and the logistic regression 31.8%. The nominal type I errors for the W-test and MDR are 5.1% and 5.8%, respectively. The results show that the W-test has robust power and reasonable type I errors in both the common and low frequency variant environment and various LD scenarios. When necessary, the type I error of the W-test can be refined using permutation method for selected markers. Now we briefly describe how LD pattern affects performance for the non-linear two-locus model. Model 2 does not contain any main effect terms, so a high LD environment will not form many strong signal-noise combinations as by Model 1. When the LD is low, the signal-signal pairs could be easier to be distinguished against a low noise background, thus all methods showed higher power in this scenario.

Power and type I error as sample size changes

We reduce the sample size from 1000 to 300 subjects, and compare the different methods’ power and type I error performances under the non-linear model and low frequency variants scenario. When the sample size decreases, the W-test still demonstrates the highest and most robust power (Figure 2, Table 2). At N = 800, the performance of W is 82.2%, which drops 2% compared to the power at N = 1000; while the MDR's power goes down to 63.3%, dropped 13% compared to N = 1000. The Chi-squared test and the logistic regression's power drop to 37.8% and 17.7%, respectively (Table 2). A sample size ranging from 300 to 500 is common for small scale biomedical studies. At N = 400, the W-test's power is 28.8%, while the alternative methods’ power falls <7%. Furthermore, the type I errors of the W are very stable, averaging 4.6 × 10⁻⁵ with standard deviation of 4.5 × 10⁻⁶ (Table 2), while the alternative methods display stringent type I errors that could have affected their power. When N is smaller than 700, the Chi-squared test and MDR have type I errors below 3.0 × 10⁻⁵, which are conservative compared to the multiple testing error rate at 4.1 × 10⁻⁵.

Figure 2.

Power comparison of alternative methods at different sample sizes. As the sample size reduces, the W-test shows a robust power compared to alternative methods. The power is calculated under the genetic environment of 1% < MAF < 5% and LD 20% < r²< 80%, using a non-linear model.

Table 2. Power and type I error rates of alternative methods at different sample sizes.

	Sample size	300	400	500	600	700	800	900	1000
Power	Logistic	2.5%	4.0%	8.6%	12.4%	14.0%	17.7%	21.5%	29.1%
	Chi-squared	1.7%	2.2%	5.7%	18.9%	25.0%	37.8%	42.1%	44.7%
	MDR	2.1%	6.3%	14.5%	36.0%	47.1%	63.3%	67.9%	71.8%
	W	16.0%	28.8%	38.5%	67.8%	72.8%	82.2%	83.2%	83.8%
Type I Error Rate	Logistic	4.1E−05	4.9E−05	3.9E−05	5.0E−05	4.4E−05	4.3E−05	4.6E−05	4.7E−05
	Chi-squared	2.0E−06	2.0E−06	1.0E−06	0	3.0E−06	4.0E−06	0	2.0E−06
	MDR	0	7.0E−06	1.4E−05	2.0E−05	2.8E−05	3.4E−05	6.5E−05	6.1E−05
	W	5.5E−05	4.9E−05	4.6E−05	4.6E−05	4.1E−05	4.4E−05	4.3E−05	4.2E−05

The simulation study is performed using a non-linear genetic model, 1%< MAF < 5%, and medium LD genetic architectures. As the sample size decreases, the W-test showed persistent better power and reasonable type I error rates.

Computing time

On a laptop computer with 2.4 GHz CPU and 8GB memory, for the W-test, the time elapsed for computing one simulation study of 1225 SNP-pairs and 1,000 subjects is 7.4 s; the Chi-squared took 7.7 s; the logistic regression took 45.7 s and the MDR took 77.7 s. The W-test is approximately 10 times faster than the original version of the MDR. For real data analysis, the W-test takes 3.4 h for genome-wide main effect evaluation, and takes about the same time for the stage-wise interaction effects.

Real datasets applications

SNP–SNP interaction has identified a number of replicated genes from the two independent GWAS datasets (Table 3). The Q–Q plot of pair-wise interactions shows no inflation of spurious association (Figure 3). Interestingly, a majority of these replicated genes are marginally insignificant, which means that they are undiscoverable through main effect screening. Furthermore, these markers show a highly relevant biological function to autism spectrum disorder. The replicated and significant gene-gene interactions can be summarized in two networks (Figure 4 and Supplementary Information S6). The first network (Figure 4A) consists of eight genes, in which only one gene, RTN4R, has significant main effect. It encodes a Nogo receptor that mediates axonal growth inhibition and may play a role in regulating axonal regeneration and plasticity in the central nervous system. Studies reported that the deletion of the gene would cause microstructural anomalies in brain white matters (29); human and mouse genetic studies suggested the gene to be a candidate marker for schizophrenia (30). The gene SLIT3 is coupled with CENPN and TMEM132D, forming two significant interaction pairs. Experiments showed that the gene SLIT3 (5q35) decreases neurogenesis and may play a role in regulating neuron-vessel interactions (31). The gene DPP10 is marginally insignificant but is replicated by significant interactions in both datasets. DPP10 facilitates neuronal excitability and its aberrant distribution is associated with Alzheimer's disease as revealed by immunohistochemistry (32). Other genes in the network are also highly related to autism and neurodegenerative disorders. For example, NRXN3 encodes a protein that functions as a synaptic adhesion protein; TMEM132D is a transmembrane protein expressed in white matter in the spinal cord and optic nerve (33); PTPRT is a receptor-type protein tyrosine phosphatase for signal transduction and neurite extension, which promotes synapse formation and is reported to be highly expressed in the central nervous system (34). Chromosome position, MAF and P-value of the replicated genes are reported in Table 3.

Table 3. Replicated bipolar disorder susceptible genes from two datasets.

SNP	Gene	Position	MAFa	P-value of paira
rs6741692	DPP10	2q14	0.303	5.8E−38
rs2407594	CSMD1	8p23	0.029	9.8E−36
rs1864952	SLIT3	5q35	0.046	1.9E−35
rs2849605	PARK2	6q5.2	0.021	3.3E−29
rs3867492	TMEM132D	12q24.33	0.030	1.0E−27
rs11222695	HNT	11q25	0.012	2.7E−25
rs1494451	CNTNAP2	7q35	0.025	1.3E−21
rs2785061	ACCN1	17q12	0.028	9.8E−19
rs17135053	A2BP1	16p13.3	0.025	3.9E−18
rs17170832	ELMO1	7p14.1	0.017	3.9E−18
rs9559408	MYO16	13q33.3	0.035	4.8E−17

^aMAF and P-value are presented using the WTCCC data. Detailed pair information can be found in Supplementary Information S6.

Figure 3.

Q–Q Plot of W-test on real genome-wide data. The W-test is computed on real genome-wide data with permuted phenotype for SNP–SNP interactions. No inflation of spurious association is observed.

Figure 4.

Gene-gene Interaction Networks. The solid lines represent significant epistasis effect. Blue color indicates pairs found in the GAIN dataset and red color indicates that they are identified in the WTCCC dataset. Purple circles represent genes replicated by the two independent data; all of which play important roles in brain and neuronal function.

In the second network (Figure 4B), the well-known autism spectrum disorder-associated loci PARK2 (rs2849605, 6q5.2) has been identified. The pair ELMO1-A2BP1 has significant epistasis effect (P-value = 3.9E−18), while the component SNPs are non-significant with P-values of 3.0 × 10⁻⁶ and 4.0 × 10⁻³, respectively (Supplementary Information S6). Both SNPs are replicated in the GAIN dataset through significant interactions with RTN4R. ELMO1 encodes a protein that interacts with DOCK180 to promote phagocytosis and cell migration. The A2BP1, other name RBFOX1, is an RNA-binding protein that regulates alternative splicing in neurons and plays a key role in the development of human neurons reported in RNA-sequencing, cytogenetic, and molecular characterization studies (35,36). The gene CNTNPA2 has weak main effects in both datasets, yet the gene is replicated through its significant interactions with NDST4 and RTN4R. The product of this gene functions in the vertebrate nervous system as cell adhesion molecules and receptor.

DISCUSSION

We propose the W-test as a general measure for epistasis testing. It is fast, model-free, and powerful. We have demonstrated that the W-test has robust power for linear and non-linear genetic models over a range of genetic environments. The method is especially advantageous for low frequency variants and has persistent power when the sample size is small. The advantages of the W-test are explained through the following characteristics.

The proposed method aims to test the distributional differences between cases and controls, using the sum of squared log odds ratio over the complete cell distribution in a contingency table. The cell distribution that is formed by a pair of markers has the overall probability to be one, in the control group and the case group, respectively. This constraint keeps the cell proportions to reflect distributional differences, which are tested cell by cell using the odds ratio. The W-test is different from the Chi-squared test in three aspects: first, the W tests the case–control distributional differences, while the Chi-squared tests the observed distribution against the joint distribution under an independence assumption. Second, the W-test does not depend on the total sample size, but is a function of the cell proportions; the Pearson Chi-squared test is a function of both the cell proportions and total sample size, such that it can measure the association significance but not the association magnitude (37,38). Third, the Pearson's Chi-squared test has a more stringent requirement on cell sample size. It is well known that the minimum expected cell counts should be no <5 for good approximation to a Chi-squared distribution. For the W-test, at extreme cell count, the distribution approximation is corrected through the implementation of h and f that are estimated from the sample covariance.

The odds ratio has a unique property for drawing prospective inference from a retrospective data set. The GWAS case-and-control dataset has a retrospective nature, so the W-test with an odds ratio interpretation is especially advantageous. The logistic regression also has an odds ratio interpretation. However, it assumes that the logit has a linear relationship with the interaction term x₁x₂. Under a co-dominant genetic model, the heterozygous Aa genotype may correspond to an over-expression of the phenotype, while the homozygous aa and AA genotype may associate with suppressed phenotypes. This non-linear relationship will be missed by logistic regression unless indicator variables for genotypes are specified. On the other hand, the W-test takes a sum of squared form, such that the genotypic combinations can have opposite effect directions; and no genetic model is assumed. In the simulation studies, all the non-parametric tests performed better than the logistic regression when the underlying model is non-linear.

The W-test inherits a statistical distribution that is adaptive to the data. A direct benefit is having a built-in distribution that saves the computational cost for permutations to calculate P-values, although a small proportion of time is needed for estimating the h and f from bootstrapped samples. The original purpose of employing the parameters is to handle correlation among the odds ratios in W, and the implementation has several bonuses. First, deviation from an ideal distribution caused by sparse data can be corrected by h and f. The accurately approximated distribution leads the W-test to have persistent power at small sample size. The second bonus is that the adjustment has the spirit and effect of performing the genomic control (39). The covariance used to calculate the parameters is estimated from bootstrapped subjects and permuted Y, under the hypothesis of no disease association and sample independence, which is similar to the genomic control procedure. Consequently, the h and f absorb the extra variance caused by population stratification. The effect of this correction is evident from the Q–Q plots of W-test on the real GWAS dataset (Figure 3), which showed perfect null distributions. This property can make the W-test robust against false positives arising from population structure, and can assist the replication of genetic markers using other independent datasets. The W-test takes a statistical approach to test for association, which is different from the machine learning approach of the MDR. The MDR incorporates an internal 10- fold cross-validation (CV) to select a model that has the best CV accuracy and consistency; it then uses permutations to calculate model significance. In low frequency variable environment, the subjects with minor alleles may be unevenly distributed in the CV splits, and the CV consistency may be lower than that in the common variant environment. Since the MDR's P-value is calculated using the averaged cross-validation consistency from the observed data comparing to null hypothesis from permutations (6), lower consistency may cause less significant P-values, which might affect its power in the low frequency variables scenario.

Therefore, the proposed method showed better power in the low frequency variables environment. In fact, in the two real datasets applications, 76.4% of the identified significant main effect SNPs have MAF <5%, which explains the large number of SNPs passing the genome-wide significant level compared to previous GWAS studies of Bipolar Disorder (21–22,40). In the two significant interaction networks, 10 out of the 11 replicated genes are identified by SNPs with MAF in the 1% to 5% range (Table 3). Another interesting observation from the real data analysis is that we have identified a number of genes that are highly relevant to neuron disorder but have not been found by previous GWAS studies, even when the SNPs are common variants. The standing example is SNP A-84299018 of gene RTN4R in the GAIN dataset. The SNP has a large MAF 12.2%, and P-value is 5.9E−18. The RTN4R acts as a hub gene connecting to all important genes in the GAIN dataset (Figure 4B). Furthermore, there are converging evidences of this Nogo receptor gene's association with schizophrenia through brain cell, animal and candidate gene studies (41–43). Nevertheless, so far we have not seen a GWAS study to report its significant association with autism related diseases. Similar to the RTN4R, SLIT3 (SNP_A-2229791, MAF = 0.22, P-value = 3.7E−03) has been identified from copy-number variations analysis by whole genome sequencing (44) and mRNA expression studies (31). TMEM132D (SNP_A-8630842, MAF = 0.14, P-value = 5.9E−03) is found to associate with anxiety co-morbidity in depression and panic disorder by brain mRNA analysis (45); the NRXN3 (rs17108944, MAF = 0.03, P-value = 5.1E−3) has been reported to have a strong association with schizophrenia via studies of gene expression (46), DNA-pooling (47), and candidate genes.

To conclude, we proposed the W-test as a model-free and dataset adaptive method for detecting epistasis in genotype dataset. It is fast, robust, and possesses statistical distributions. Real data analysis replicated important genes with epistasis effect, which were undiscoverable through main effect evaluations. These results showed that the W-test is a very powerful and practical tool for detecting functional variants thereby helping to solve the genetic puzzle underlying complex diseases.

AVAILABILITY

The W-test software is available at: http://www2.ccrb.cuhk.edu.hk/wtest/download.html

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Chinese University of Hong Kong Direct Grant [4054169 to M.H.W.]; Research Grant Council – General Research Fund [476013 to M.H.W.]; National Science Foundation of China [81473035, 31401124 to M.H.W.]. Funding for open access charge: National Science Foundation of China [31401124].

Conflict of interest statement. None declared.