Two-Locus Likelihoods Under Variable Population Size and Fine-Scale Recombination Rate Estimation

Abstract

Two-locus sampling probabilities have played a central role in devising an efficient composite-likelihood method for estimating fine-scale recombination rates. Due to mathematical and computational challenges, these sampling probabilities are typically computed under the unrealistic assumption of a constant population size, and simulation studies have shown that resulting recombination rate estimates can be severely biased in certain cases of historical population size changes. To alleviate this problem, we develop here new methods to compute the sampling probability for variable population size functions that are piecewise constant. Our main theoretical result, implemented in a new software package called LDpop, is a novel formula for the sampling probability that can be evaluated by numerically exponentiating a large but sparse matrix. This formula can handle moderate sample sizes ($n\le 50$) and demographic size histories with a large number of epochs ($\mathcal{D}\ge 64$). In addition, LDpop implements an approximate formula for the sampling probability that is reasonably accurate and scales to hundreds in sample size ($n\ge 256$). Finally, LDpop includes an importance sampler for the posterior distribution of two-locus genealogies, based on a new result for the optimal proposal distribution in the variable-size setting. Using our methods, we study how a sharp population bottleneck followed by rapid growth affects the correlation between partially linked sites. Then, through an extensive simulation study, we show that accounting for population size changes under such a demographic model leads to substantial improvements in fine-scale recombination rate estimation.

THE coalescent with recombination (Griffiths and Marjoram 1997) provides a basic population genetic model for recombination. For a very small number of loci and a constant population size, the likelihood (or sampling probability) can be computed via a recursion (Golding 1984; Ethier and Griffiths 1990; Hudson 2001) or importance sampling (Fearnhead and Donnelly 2001), allowing for maximum-likelihood and Bayesian estimates of recombination rates (Fearnhead and Donnelly 2001; Hudson 2001; McVean et al. 2002; Fearnhead et al. 2004; Fearnhead and Smith 2005; Fearnhead 2006).

Jenkins and Song (2009, 2010) recently introduced a new framework based on asymptotic series (in inverse powers of the recombination rate ρ) to approximate the two-locus sampling probability under a constant population size and developed an algorithm for finding the expansion to an arbitrary order (Jenkins and Song 2012). They also proved that only a finite number of terms in the expansion are needed to obtain the exact two-locus sampling probability as an analytic function of ρ. Bhaskar and Song (2012) partially extended this approach to an arbitrary number of loci and found closed-form formulas for the first two terms in an asymptotic expansion of the multilocus sampling distribution.

When there are more than a handful of loci, computing the sampling probability becomes intractable. A popular and tractable alternative has been to construct composite likelihoods by multiplying the two-locus likelihoods for pairs of SNPs; this pairwise composite likelihood has been used to estimate fine-scale recombination rates in humans (International HapMap Consortium 2007; 1000 Genomes Project Consortium 2010), Drosophila (Chan et al. 2012), chimpanzees (Auton et al. 2012), microbes (Johnson and Slatkin 2009), dogs (Auton et al. 2013), and more and was used in the discovery of a DNA motif associated with recombination hotspots in some organisms, including humans (Myers et al. 2008), subsequently identified as a binding site of the protein PRDM9 (Baudat et al. 2010; Berg et al. 2010; Myers et al. 2010).

The pairwise composite likelihood was first suggested by Hudson (2001). The software package LDhat (McVean et al. 2004; Auton and McVean 2007) implemented the pairwise composite likelihood and embedded it within a Bayesian MCMC algorithm for inference. Chan et al. (2012) modified this algorithm in their program LDhelmet to efficiently utilize the aforementioned asymptotic formulas for the sampling probability, among other improvements. The program LDhot (Myers et al. 2005; Auton et al. 2014) uses the composite likelihood as a test statistic to detect recombination hotspots, in conjunction with coalescent simulation to determine appropriate null distributions.

Because of mathematical and computational challenges, LDhat, LDhelmet, and LDhot all assume a constant population size model to compute the two-locus sampling probabilities. This is an unrealistic assumption, and it would be desirable to account for known demographic events, such as bottlenecks or population growth. Previous studies (McVean et al. 2002; Smith and Fearnhead 2005; Chan et al. 2012) have shown that incorrectly assuming constant population size can lead these composite-likelihood methods to produce biased estimates. Furthermore, Johnston and Cutler (2012) observed that a sharp bottleneck followed by rapid growth can lead LDhat to infer spurious recombination hotspots if it assumes a constant population size.

Hudson (2001) proposed Monte Carlo computation of two-locus likelihoods by simulating genealogies. While this generalizes to arbitrarily complex demographies, it would be desirable to have a deterministic formula, as naive Monte Carlo computation sometimes has difficulty approximating small probabilities.

In this article, we show how to compute the two-locus sampling probability exactly under variable population size histories that are piecewise constant. Our approach relies on the Moran model (Moran 1958; Ethier and Kurtz 1993; Donnelly and Kurtz 1999), a stochastic process closely related to the coalescent. We have implemented our results in a freely available software package, LDpop, that efficiently produces lookup tables of two-locus likelihoods under variable population size. These lookup tables can then be used by other programs that use composite likelihoods to infer recombination maps.

Our main result is an exact formula, introduced in Theorem 1, that involves exponentiating sparse m × m matrices containing $O\left(m\right)$ nonzero entries, where $m=O\left(n^6\right)$ under a biallelic model, with n being the sample size. We derive this formula by constructing a Moran-like process in which sample paths can be coupled with the two-locus coalescent and by applying a reversibility argument.

Theorem 1 has a high computational cost, and our implementation in LDpop can practically handle low to moderate sample sizes ($n<50$) on a 24-core compute server. We have thus implemented an approximate formula that is much faster and scales to sample sizes in the hundreds. This formula is computed by exponentiating a sparse matrix with $O\left(n^3\right)$ nonzero entries and is based on a previous two-locus Moran process (Ethier and Kurtz 1993), which we have implemented and extended to the case of variable population size. While this formula does not give the exact likelihood, it provides a reasonable approximation and converges to the true value in an appropriate limit.

In addition to these exact and approximate formulas, LDpop also includes a highly efficient importance sampler for the posterior distribution of two-locus genealogies. This can be used to infer the genealogy at a pair of sites and also provides an alternative method for computing two-locus likelihoods. Our importance sampler is based on an optimal proposal distribution that we characterize in Theorem 2. It generalizes previous results for the constant-size case, which have been used to construct importance samplers for both the single-population, two-locus case (Fearnhead and Donnelly 2001; Dialdestoro et al. 2016) and other constant-demography coalescent scenarios (Stephens and Donnelly 2000; De Iorio and Griffiths 2004; Griffiths et al. 2008; Hobolth et al. 2008; Jenkins 2012; Koskela et al. 2015). The key ideas of Theorem 2 should similarly generalize to other contexts of importance sampling a time-inhomogeneous coalescent.

Using a simulation study, we show that using LDpop to account for demography substantially improves the composite-likelihood inference of recombination maps. We also use LDpop to gain a qualitative understanding of linkage disequilibrium by examining the $r^2$ statistic. Finally, we examine how LDpop scales in terms of sample size n and the number $\mathcal{D}$ of demographic epochs. The exact formula can handle n in the tens, while the approximate formula can handle n in the hundreds. Additionally, we find that the runtime of LDpop is not very sensitive to $\mathcal{D},$ so LDpop can handle size histories with a large number of pieces.

LDpop is freely available for download at https://github.com/popgenmethods/ldpop.

Background

Here we describe our notational convention and review some key concepts regarding the coalescent with recombination and the two-locus Moran model.

Notation

Let $\theta /2$ denote the mutation rate per locus per unit time, $P={\left(P_{ij}\right)}_{i,j\in \mathcal{A}}$ be the transition probabilities between alleles given a mutation, and $\mathcal{A}=\left\{0,1\right\}$ be the set of alleles (our formulas can be generalized to $\left|\mathcal{A}\right|>2,$ but this increases the computational complexity). Let $\rho /2$ denote the recombination rate per unit time. We consider a single panmictic population, with piecewise-constant effective population sizes. In particular, we assume D pieces, with endpoints $-\mathrm{\infty }=t_{-D}<t_{-D+1}<\cdots <t_{-1}<t_0=0,$ where 0 corresponds to the present and $t<0$ corresponds to a time in the past. The piece $\left(t_d,t_{d+1}\right]$ is assumed to have scaled population size ${\eta }_d.$ Going backward in time, two lineages coalesce (find a common ancestor) at rate $1/{\eta }_d$ within the interval $\left(t_d,t_{d+1}\right].$

We allow the haplotypes to have missing (unobserved) alleles at each locus and use * to denote such alleles. We denote each haplotype as having type a, b, or c, where a haplotypes are observed only at the left locus, b haplotypes are observed only at the right locus, and c haplotypes are observed at both loci. Overloading notation, we sometimes refer to the left locus as the a locus and the right locus as the b locus. We use $n={\left\{n_{i\ast },n_{\text{*}j},n_{k\ell }\right\}}_{i,j,k,\ell \in \mathcal{A}}$ to denote the configuration of an unordered collection of two-locus haplotypes, with $n_{i\ast }$ denoting the number of a types with allele i, $n_{\text{*}j}$ denoting the number of b types with allele j, and $n_{k\ell }$ denoting the number of c types with alleles k and $\ell .$

Suppose $n$ has $n^{\left(abc\right)}=\left(n^{\left(a\right)},n^{\left(b\right)},n^{\left(c\right)}\right)$ haplotypes of type $a,b,c,$ respectively. We define the sampling probability ${\mathrm{\mathbb{P}}}_t\left(n\right)$ to be the probability of sampling $n$ at time t, given that we observed $n^{\left(a\right)},n^{\left(b\right)},n^{\left(c\right)}$ haplotypes of type $a,b,c,$ under the coalescent with recombination (described below).

The ancestral recombination graph and the coalescent with recombination

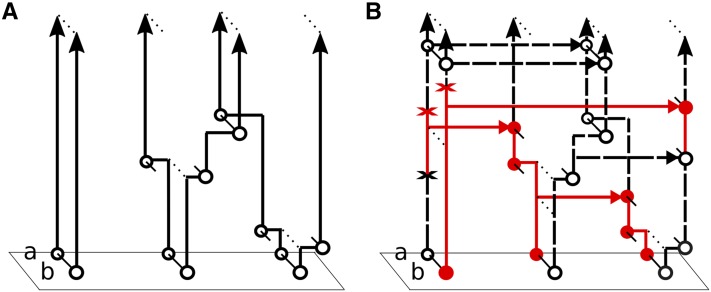
The ancestral recombination graph (ARG) is the multilocus genealogy relating a sample (Figure 1). The coalescent with recombination (Griffiths 1991) gives the limiting distribution of the ARG under a wide class of population models, including the Wright–Fisher model and the Moran model.

Figure 1.

An ancestral recombination graph (ARG) at two loci, labeled “a” and “b”, each with two alleles ($\mathrm{•}$ and $\circ$). The notations $n,n_{ij},n^{\left(abc\right)}$ are illustrated for the configuration between the first coalescence and second recombination event. The symbol $\mathrm{\ast }$ denotes a missing allele.

Let $n_t^{\left(c\right)}$ be the number of lineages at time t that are ancestral to the observed present-day sample at both loci. Similarly, let $n_t^{\left(a\right)}$ and $n_t^{\left(b\right)}$ be the number of lineages that are ancestral at only the a or b locus, respectively. Under the coalescent with recombination, $n_t^{\left(abc\right)}=\left(n_t^{\left(a\right)},n_t^{\left(b\right)},n_t^{\left(c\right)}\right)$ is a backward-in-time Markov chain, where each c-type lineage splits (recombines) into one a and one b lineage at rate $\rho /2,$ and each pair of lineages coalesces at rate $1/{\eta }_d$ within the time interval $\left(t_d,t_{d+1}\right].$ Table 1 gives the transition rates of $n_t^{\left(abc\right)}.$

Table 1. Backward-in-time transition rates of $n_t^{\left(abc\right)}=\left(n_t^{\left(a\right)},n_t^{\left(b\right)},n_t^{\left(c\right)}\right)$ within time interval $\left(t_d,t_{d+1}\right]$ under the coalescent with recombination.

End state	Rate
$n_t^{\left(a\right)}+1,n_t^{\left(b\right)}+1,n_t^{\left(c\right)}-1$	$\frac{\rho }{2}{n}_t^{\left(c\right)}$
$n_t^{\left(a\right)}-1,n_t^{\left(b\right)},n_t^{\left(c\right)}$	$\frac{1}{{\eta }_d}{n}_t^{\left(a\right)}\left(\frac{n_t^{\left(a\right)}-1}{2}+n_t^{\left(c\right)}\right)$
$n_t^{\left(a\right)},n_t^{\left(b\right)}-1,n_t^{\left(c\right)}$	$\frac{1}{{\eta }_d}{n}_t^{\left(b\right)}\left(\frac{n_t^{\left(b\right)}-1}{2}+n_t^{\left(c\right)}\right)$
$n_t^{\left(a\right)},n_t^{\left(b\right)},n_t^{\left(c\right)}-1$	$\frac{1}{{\eta }_d}\left(\begin{array}{c}{n}_t^{\left(c\right)}\\ 2\end{array}\right)$
$n_t^{\left(a\right)}-1,n_t^{\left(b\right)}-1,n_t^{\left(c\right)}+1$	$\frac{1}{{\eta }_d}{n}_t^{\left(a\right)}{n}_t^{\left(b\right)}$

After sampling the history of coalescence and recombination events ${\left\{n_t^{\left(abc\right)}\right\}}_{t\le 0},$ we drop mutations down at rate $\theta /2$ per locus, with alleles mutating according to $P,$ and the alleles of the common ancestor assumed to be at the stationary distribution. This gives us a sample path ${\left\{n_t\right\}}_{t\le 0},$ where $n_0$ is the observed sample at the present, and $n_t$ is the collection of ancestral haplotypes at time t. Under this notation, the sampling probability at time t is defined as

$${\mathrm{\mathbb{P}}}_t\left(n\right):=\mathrm{\mathbb{P}}\left(n_t=n|n_t^{\left(abc\right)}=n^{\left(abc\right)}\right).$$ (1)

Two-locus Moran model

The Moran model is a stochastic process closely related to the coalescent and plays a central role in our results. Here, we review a two-locus Moran model with recombination dynamics from Ethier and Kurtz (1993). We note that there are multiple versions of the two-locus Moran model, and in particular Donnelly and Kurtz (1999) describe a Moran model with different recombination dynamics.

The Moran model with N lineages is a finite population model evolving forward in time. In particular, let $M_t$ denote a collection of N two-locus haplotypes at time t (with no missing alleles). Then $M_t$ is a Markov chain going forward in time that changes due to mutation, recombination, and copying events.

Let ${\mathbf{\Lambda }}_{\left(N\right)}^d$ denote the transition matrix of $M_t$ within $\left(t_d,t_{d+1}\right].$ We describe the rates of ${\mathbf{\Lambda }}_{\left(N\right)}^d.$ For the mutation events, each allele mutates at rate $\theta /2$ according to transition matrix $P.$ For the copying events, each lineage of $M_t$ copies its haplotype onto each other lineage at rate $1/2{\eta }_d$ within the time interval $\left(t_d,t_{d+1}\right].$ Biologically, this corresponds to one lineage dying out and being replaced by the offspring of another lineage, which occurs more frequently when genetic drift is high (i.e., when the population size ${\eta }_d$ is small). Finally, every pair of lineages in $M_t$ swaps genetic material through a crossover recombination at rate $\rho /2\left(N-1\right).$ A crossover between haplotypes $\left(i_1,j_1\right)$ and $\left(i_2,j_2\right)$ results in new haplotypes $\left(i_1,j_2\right)$ and $\left(i_2,j_1\right),$ and the configuration resulting from the crossover is $M_t-e_{i_1,j_1}-e_{i_2,j_2}+e_{i_1,j_2}+e_{i_2,j_1}.$ See Figure 2 for illustration.

Figure 2.

A finite two-locus Moran model with $N=4$ particles. Each lineage copies itself onto every other lineage at rate $1/2\eta .$ Mutations arise at rate $\theta /2$ per allele per locus. Recombination follows dynamics from Ethier and Kurtz (1993): every pair of lineages experiences a crossover recombination at rate $\rho /2\left(N-1\right).$ Here, the second and third lineages swap their b alleles through a crossover. The sampling probability for this model agrees with the coalescent at each locus marginally, but not jointly at both loci (although the discrepancy disappears as $N\to \mathrm{\infty }$).

Let ${\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(n\right)$ be the probability of sampling $n$ at time t under this Moran model, for a configuration $n$ with sample size $n\le N.$ ${\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(n\right)$ is given by first sampling $M_{\min \left(t,t_{-D+1}\right)}$ from the stationary distribution ${\lambda }_{\left(N\right)}^{-D}$ of ${\Lambda }_{\left(N\right)}^{-D},$ then propagating ${\left\{M_s\right\}}_{s\le 0}$ forward in time to t, and then sampling $n$ without replacement from $M_t.$ So,

$$\begin{array}{c}{\left[{\mathrm{\mathbb{P}}}_{\left(N\right)}\left(M_t=M\right)\right]}_M={\lambda }_{\left(N\right)}^{-D}{\displaystyle \prod _{d=-D+1}^{-1}{e}^{{\Lambda }_{\left(N\right)}^d\left[\min \left(t,t_{d+1}\right)-\min \left(t,t_d\right)\right]}}\\ {\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(n\right)={\displaystyle \sum _M{\mathrm{\mathbb{P}}}_{\left(N\right)}\left(M_t=M\right)\mathrm{\mathbb{P}}\left(n|M\right)},\end{array}$$ (2)

where $\mathrm{\mathbb{P}}\left(n|M\right)$ denotes the probability of sampling $n$ without replacement from $M,$ and ${\left[{\mathrm{\mathbb{P}}}_{\left(N\right)}\left(M_t=M\right)\right]}_M$ and ${\lambda }_{\left(N\right)}^{-D}$ are row vectors here.

In general, ${\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(n\right)\ne {\mathrm{\mathbb{P}}}_t\left(n\right),$ so $M_t$ disagrees with the coalescent with recombination. However, the likelihood under $M_t$ converges to the correct value, ${\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(n\right)\to {\mathrm{\mathbb{P}}}_t\left(n\right)$ as $N\to \mathrm{\infty }.$ In fact, even for $N=n=20,$ we find that ${\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(n\right)$ provides a reasonable approximation for practical purposes (see Fine-scale recombination rate estimation and Accuracy of the approximate likelihood). We refer to (2), i.e., the likelihood under $M_t,$ as the “approximate-likelihood formula,” in contrast to the exact formula we present in Theorem 1 below. This approximate formula is included in LDpop as a faster, more scalable alternative to the exact formula of Theorem 1.

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article. Scripts to reproduce the simulated data analysis are available from the authors on request.

Theoretical Results

In this section, we describe our theoretical results. Proofs are deferred to the Appendix.

Exact formula for the sampling probability

Our main result is an explicit formula for the sampling probability $\mathrm{\mathbb{P}}\left(n\right),$ presented in Theorem 1. We present an outline here; the proof is shown in the Appendix.

The idea is to construct a forward-in-time Markov process ${\tilde{M}}_t$ and relate its distribution to the coalescent with recombination. ${\tilde{M}}_t$ is similar to the Moran model $M_t$ described above, except that ${\tilde{M}}_t$ allows partially specified a and b types, whereas all lineages in $M_t$ are fully specified c types. Specifically, the state space of ${\tilde{M}}_t$ is $\mathcal{N}=\left\{n:n^{\left(abc\right)}=\left(k,k,n-k\right),0\le k\le n\right\}$ the collection of sample configurations with n specified (nonmissing) alleles at each locus. The state of ${\tilde{M}}_t$ changes due to copying, mutation, recombination, and “recoalescence” events. Copying and mutation dynamics are similar to $M_t,$ but recombination is different: every c type splits into a and b types at rate $\rho /2,$ and every pair of a and b types “recoalesces” back into a c type at rate $1/{\eta }_d.$ An illustration is shown in Figure 3B; ${\tilde{M}}_t$ is described in more detail in the Appendix. Within interval $\left(t_d,t_{d+1}\right],$ we denote the transition rate matrix of ${\tilde{M}}_t$ as ${\tilde{\Lambda }}^d,$ a square matrix indexed by $\mathcal{N},$ with entries given in Table 2.

Figure 3.

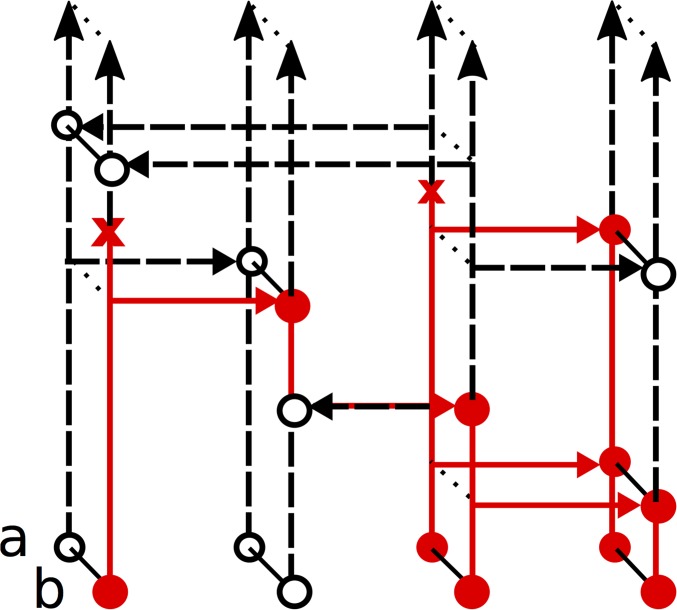
The process ${\left\{{\tilde{M}}_t\right\}}_{t\le 0}$ with rates ${\tilde{\Lambda }}^d$ (Table 2) used to prove Theorem 1. This process is similar to $\left\{M_t\right\}$ (Figure 2), in that n is fixed, and alleles change due to copying and mutation. However, ${\tilde{M}}_t$ allows partially specified a and b types, with c types recombining into a pair of a and b types, and pairs of a and b types recoalescing into c types. (A) The process ${\left\{C_t\right\}}_{t\le 0}$ of just recombination ($c\to a,b$) and recoalescence ($a,b\to c$) events. (B) The full process ${\left\{{\tilde{M}}_t\right\}}_{t\le 0}$ including copying, mutation, recombination, and recoalescence events.

Table 2. Nonzero entries of the rate matrix ${\tilde{\Lambda }}^d$ for the interval $\left(t_d,t_{d+1}\right]$.

$m$	${\tilde{\Lambda }}_{n,m}^d$
$n-e_{i\ast }+e_{j\ast }$	$\frac{1}{{\eta }_d}{n}_{i\ast }\left(\frac{1}{2}{n}_{j\ast }+{\displaystyle \sum _{k\in \mathcal{A}}{n}_{jk}}\right)+\frac{\theta }{2}{P}_{ij}{n}_{i\ast }$
$n-e_{\text{*}i}+e_{\text{*}j}$	$\frac{1}{{\eta }_d}{n}_{\text{*}i}\left(\frac{1}{2}{n}_{\text{*}j}+{\displaystyle \sum _{k\in \mathcal{A}}{n}_{kj}}\right)+\frac{\theta }{2}{P}_{ij}{n}_{\text{*}i}$
$n-e_{ij}+e_{kl}$	$\frac{1}{2{\eta }_d}{n}_{ij}{n}_{kl}+\frac{\theta }{2}\left({\delta }_{ik}{P}_{jl}+{\delta }_{jl}{P}_{ik}\right)n_{ij}$
$n-e_{ij}+e_{i\ast }+e_{\text{*}j}$	$\frac{\rho }{2}{n}_{ij}$
$n-e_{i\ast }-e_{\text{*}j}+e_{ij}$	$n_{i\ast }{n}_{\text{*}j}\frac{1}{{\eta }_d}$
$n$	$-\frac{1}{{\eta }_d}\left(\begin{array}{c}{n}^{\left(a\right)}+n^{\left(b\right)}+n^{\left(c\right)}\\ 2\end{array}\right)-\frac{\rho }{2}{n}^{\left(c\right)}-\frac{\theta }{2}{\displaystyle \sum _{i\in \mathcal{A}}{\displaystyle \sum _{j\in \mathcal{A\cup }\left\{\text{*}\right\}}\left(n_{ij}+n_{ji}\right)}}$

${\tilde{M}}_t$ does not itself yield the correct sampling probability. The basic issue is that ${\tilde{M}}_t$ has c types splitting into a and b types at rate $\rho /2$ going forward in time, but under the coalescent with recombination, this needs to happen at rate $\rho /2$ going backward in time. Similarly, pairs of a and b types merge into a single c type at rate $1/{\eta }_d$ going forward in time under ${\tilde{M}}_t,$ but going backward in time under the coalescent with recombination.

However, it is possible to “reverse” the direction of the recombinations ($c\to a,b$) and recoalescences ($a,b\to c$), to get a new process that does match the two-locus coalescent. In particular, let $C_t$ be the number of c types in ${\tilde{M}}_t,$ illustrated in Figure 3A. Then $C_t$ is a reversible Markov chain, whose rate matrix in $\left(t_d,t_{d+1}\right]$ is ${\Gamma }^d,$ a tridiagonal square matrix indexed by $\left\{0,1,\dots ,n\right\},$ with ${\mathrm{\Gamma }}_{m,m-1}^d=\left(\rho /2\right)m,$ ${\mathrm{\Gamma }}_{m,m+1}^d={\left(n-m\right)}^2\left(1/{\eta }_d\right),$ and ${\mathrm{\Gamma }}_{m,m}^d=-{\mathrm{\Gamma }}_{m,m-1}^d-{\mathrm{\Gamma }}_{m,m+1}^d.$ Exploiting the reversibility of $C_t$ allows us to relate the distribution of ${\tilde{M}}_t$ to the coalescent with recombination and obtain the following result:

Theorem 1. Let $\left({\gamma }_0^d,\dots ,{\gamma }_n^d\right)$ be the stationary distribution of ${\mathrm{\Gamma }}^d,$ and let the row vector ${\tilde{\gamma }}^d$ be indexed by $\mathcal{N},$ with ${\tilde{\gamma }}_n^d={\gamma }_m^d$ if $n$ has m lineages of type c. Denote the stationary distribution of ${\tilde{\mathrm{\Lambda }}}^d$ by the row vector ${\tilde{\mathrm{\Lambda }}}^d={\left({\lambda }_n^d\right)}_{n\in \mathcal{N}}.$ Let $\odot$ and $÷$ denote component-wise multiplication and division, and recursively define the row vector $p^d={\left(p_n^d\right)}_{n\in \mathcal{N}}$ by

$$\begin{array}{c}{p}^{-D+1}={\tilde{\lambda }}^{-D}÷{\tilde{\gamma }}^{-D}\\ p^{d+1}=\left[\left(p^d\odot {\tilde{\gamma }}^d\right)e^{{\tilde{\Lambda }}^d\left(t_{d+1}-t_d\right)}\right]\mathrm{÷}{\tilde{\gamma }}^d.\end{array}$$ (3)

Then, for $n\in \mathcal{N},$ we have ${\mathrm{\mathbb{P}}}_0\left(n\right)=p_n^0.$

Note that Theorem 1 gives ${\mathrm{\mathbb{P}}}_0\left(n\right)$ for $n\in \mathcal{N}.$ This includes all fully specified $n,$ i.e., with $n^{\left(abc\right)}=\left(0,0,n\right),$ and suffices for the application considered in Fine-scale recombination rate estimation. If necessary, ${\mathrm{\mathbb{P}}}_0\left(n\right)$ for partially specified $n$ can be computed by summing over the fully specified configurations consistent with $n.$

For $\left|\mathcal{A}\right|=2$ alleles per locus, ${\tilde{\Lambda }}^d$ is an $O\left(n^6\right)\times O\left(n^6\right)$ matrix, so naively computing the matrix multiplication in Theorem 1 would cost $O\left(n^{12}\right)$ time. However, ${\tilde{\Lambda }}^d$ is sparse, with $O\left(n^6\right)$ nonzero entries, allowing efficient algorithms to compute Theorem 1 (up to numerical precision) in $O\left(n^6\mathcal{T}\right)$ time, where $\mathcal{T}$ is some finite number of matrix–vector multiplications. See the Appendix for more details.

Importance sampling

In addition to the approximate (Equation 2) and exact (Equation 3) formulas for the sampling probability, LDpop includes an importance sampler for the two-locus ARG $n_{\le 0}={\left\{n_t\right\}}_{t\le 0}.$ This provides a method to sample from the posterior distribution of two-locus ARGs and also provides an alternative method for computing ${\mathrm{\mathbb{P}}}_0\left(n\right).$ This importance sampler is based on Theorem 2 below, which characterizes the optimal proposal distribution for the two-locus coalescent with recombination under variable population size.

Let the proposal distribution $Q\left(n_{\le 0}\right)$ be a probability distribution on $\left\{n_{\le 0}:n_0=n\right\}$ whose support contains that of $\mathrm{\mathbb{P}}\left(n_{\le 0}|n_0=n\right).$ Then we have

$${\mathrm{\mathbb{P}}}_0\left(n\right)={\displaystyle {\int }_{n_{\le 0}:n_0=n}\frac{d\mathrm{\mathbb{P}}\left(n_{\le 0}\right)}{dQ\left(n_{\le 0}\right)}dQ\left(n_{\le 0}\right)},$$

and so, if $n_{\le 0}^{\left(1\right)},\dots ,n_{\le 0}^{\left(K\right)}\sim Q$ i.i.d., the sum

$$\frac{1}{K}{\displaystyle \sum _{k=1}^K\frac{d\mathrm{\mathbb{P}}\left(n_{\le 0}^{\left(k\right)}\right)}{dQ\left(n_{\le 0}^{\left(k\right)}\right)}}$$ (4)

converges almost surely to ${\mathrm{\mathbb{P}}}_0\left(n\right)$ as $K\to \mathrm{\infty }$ by the law of large numbers. Hence, (4) provides a Monte Carlo approximation to ${\mathrm{\mathbb{P}}}_0\left(n\right).$ The optimal proposal is the posterior distribution $Q_{\mathrm{opt}}\left(n_{\le 0}\right)=\mathrm{\mathbb{P}}\left(n_{\le 0}|n_0\right),$ for then (4) is exactly

$$\frac{1}{K}{\displaystyle \sum _{k=1}^K\frac{d\mathrm{\mathbb{P}}\left(n_{\le 0}^{\left(k\right)}\right)}{d\mathrm{\mathbb{P}}\left(n_{\le 0}^{\left(k\right)}|n_0\right)}=\frac{1}{K}}{\displaystyle \sum _{k=1}^K\frac{d\mathrm{\mathbb{P}}\left(n_{\le 0}^{\left(k\right)}\right)}{d\mathrm{\mathbb{P}}\left(n_{\le 0}^{\left(k\right)}\right)/\mathrm{\mathbb{P}}\left(n_0\right)}}=\mathrm{\mathbb{P}}\left(n_0\right),$$

even for $K=1$.

The following theorem, which we prove in the Appendix, characterizes the optimal posterior distribution $Q_{\mathrm{opt}}\left(n_{\le 0}\right)=\mathrm{\mathbb{P}}\left(n_{\le 0}|n_0\right)$ for variable population size:

Theorem 2. The process ${\left\{n_t\right\}}_{t\le 0}$ is a backward-in-time Markov chain with inhomogeneous rates, whose rate matrix at time t is given by

$$q_{n,m}^{\left(t\right)}=\{\begin{array}{ll}{\phi }_{n,m}^{\left(t\right)}\frac{{\mathrm{\mathbb{P}}}_t\left(m\right)}{{\mathrm{\mathbb{P}}}_t\left(n\right)},\hfill & if m\ne n,\hfill \\ {\phi }_{n,n}^{\left(t\right)}-\frac{d}{dt}\log {\mathrm{\mathbb{P}}}_t\left(n\right),\hfill & if m=n,\hfill \end{array}$$

where ${\phi }^{\left(t\right)}=\left({\phi }_{n,m}^{\left(t\right)}\right)$ is a square matrix, indexed by configurations $n,$ with entries given by Table 3 and equal to

Table 3. Nonzero entries of the ${\mathbf{\phi }}^{\left(t\right)}$ matrix of Theorem 2, for $t\in \left(t_d,t_{d+1}\right]$.

$m$	${\mathbf{\phi }}_{n,m}^{\left(t\right)}$
$n-e_{i\ast }+e_{j\ast }$	$\frac{\theta }{2}{P}_{ji}\left(n_{j\ast }+1\right)$
$n-e_{\text{*}i}+e_{\text{*}j}$	$\frac{\theta }{2}{P}_{ji}\left(n_{\text{*}j}+1\right)$
$n-e_{ij}+e_{kl}$	$\frac{\theta }{2}\left({\delta }_{ik}{P}_{lj}+{\delta }_{jl}{P}_{ki}\right)\left(n_{kl}+1\right)$
$n-e_{ij}+e_{i\ast }+e_{\text{*}j}$	$\frac{\rho }{2}{n}^{\left(c\right)}\left(n_{i\ast }+1\right)\left(n_{\text{*}j}+1\right)$
$n-e_{ij}$	$\frac{1}{{\eta }_d}\left(\begin{array}{c}{n}^{\left(c\right)}\\ 2\end{array}\right)\left(n_{ij}-1\right)$
$n-e_{i\ast }$	$\frac{1}{{\eta }_d}\left[\left(\begin{array}{c}{n}^{\left(a\right)}\\ 2\end{array}\right)\left(n_{i\ast }-1\right)+n^{\left(a\right)}{n}^{\left(c\right)}{\displaystyle \sum _j{n}_{ij}}\right]$
$n-e_{\text{*}i}$	$\frac{1}{{\eta }_d}\left[\left(\begin{array}{c}{n}^{\left(b\right)}\\ 2\end{array}\right)\left(n_{\text{*}i}-1\right)+n^{\left(b\right)}{n}^{\left(c\right)}{\displaystyle \sum _j{n}_{ji}}\right]$
$n$	$-\frac{1}{{\eta }_d}\left(\begin{array}{c}n\\ 2\end{array}\right)-\frac{\rho }{2}{n}^{\left(c\right)}-\frac{\theta }{2}{\displaystyle \sum _i\left(1-P_{ii}\right)}\left[n_{i\ast }+n_{\text{*}i}+{\displaystyle \sum _j\left(n_{ij}+n_{ji}\right)}\right]$

$$\begin{array}{l}{\phi }_{n,m}^{\left(t\right)}=\frac{d}{ds}[\mathrm{\mathbb{P}}\left(n_{t-s}^{\left(abc\right)}=m^{\left(abc\right)}|n_t^{\left(abc\right)}=n^{\left(abc\right)}\right)\\ {\times \mathrm{\mathbb{P}}\left(n_t=n|n_{t-s}=m,n_t^{\left(abc\right)}=n^{\left(abc\right)}\right)]|}_{s=0}.\end{array}$$ (5)

Intuitively, the matrix ${\mathbf{\phi }}^{\left(t\right)}$ in Table 3 is a linear combination of two rate matrices, one for propagating $n_t^{\left(abc\right)}$ an infinitesimal distance backward in time and another for propagating $n_t$ an infinitesimal distance forward in time. This is because $n_t^{\left(abc\right)}$ is generated by sampling coalescent and recombination events backward in time, and then $n_t$ is generated by dropping mutations on the ARG and propagating the allele values forward in time.

Theorem 2 generalizes previous results for the optimal proposal distribution in the constant-size case (Stephens and Donnelly 2000; Fearnhead and Donnelly 2001). In that case, the conditional probability of the parent $m$ of $n$ is ${\phi }_{n,m}\left(\mathrm{\mathbb{P}}\left(m\right)/\mathrm{\mathbb{P}}\left(n\right)\right).$ Note the constant-size case is time homogeneous, so the dependence on t is dropped, and the waiting times between events in the ARG are not sampled (i.e., only the embedded jump chain of $n_{\le 0}$ is sampled).

We construct our proposal distribution $\widehat{Q}\left(n_{\le 0}\right)$ by approximating the optimal proposal distribution $Q_{\mathrm{opt}}\left(n_{\le 0}\right)=\mathrm{\mathbb{P}}\left(n_{\le 0}|n_0\right).$ This requires approximating the rate $q_{n,m}^{\left(t\right)}={\phi }_{n,m}^{\left(t\right)}\left({\mathrm{\mathbb{P}}}_t\left(m\right)/{\mathrm{\mathbb{P}}}_t\left(n\right)\right).$ We use the approximation ${\widehat{q}}_{n,m}^{\left(t\right)}={\phi }_{n,m}^{\left(t\right)}\left({\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(m\right)/{\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(n\right)\right),$ with ${\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(n\right)$ from the approximate-likelihood Equation 2. To save computation, we compute ${\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(n\right)$ only along a grid of time points and then linearly interpolate ${\widehat{q}}_{n,m}^{\left(t\right)}$ between the points. See the Appendix for more details on our proposal distribution $\widehat{Q}.$

As detailed in Runtime and accuracy of the importance sampler, $\widehat{Q}$ is a highly efficient proposal distribution, typically yielding effective sample sizes (ESS) between 80% and 100% per sample for the demography and ρ values we considered.

Application

Previous simulation studies (McVean et al. 2002; Smith and Fearnhead 2005; Chan et al. 2012) have shown that if the demographic model is misspecified, composite-likelihood methods (which so far have assumed a constant population size) can produce recombination rate estimates that are biased. Many populations, including those of humans and Drosophila melanogaster, have undergone bottlenecks and expansions in the recent past (Choudhary and Singh 1987; Gutenkunst et al. 2009), and it has been argued (Johnston and Cutler 2012) that such demographies can severely affect recombination rate estimation and can cause the appearance of spurious recombination hotspots.

In this section, we apply our software LDpop to show that accounting for demography improves fine-scale recombination rate estimation. We first examine how a population bottleneck followed by rapid growth affects the correlation between partially linked sites. We then study composite-likelihood estimation of recombination maps under a population bottleneck. We find that accounting for demography with either the exact (Theorem 1)- or approximate (Equation 2)-likelihood formula substantially improves accuracy. Furthermore, this improvement is robust to minor misspecification of the demography due to not knowing the true demography in practice.

Throughout this section, we use an example demography with $D=3$ epochs, consisting of a sharp population bottleneck followed by a rapid expansion. Specifically, the population size history $\eta \left(t\right),$ in coalescent-scaled units, is given by

$$\eta \left(t\right)=\{\begin{array}{ll}100,\hfill & -0.5<t\le 0,\hfill \\ 0.1,\hfill & -0.58<t\le -0.5,\hfill \\ 1,\hfill & t\le -\mathrm{0.58.}\hfill \end{array}$$ (6)

Under this model and $n=2,$ the expected time of the common ancestor is $\mathbb{E}\left[T_{\mathrm{MRCA}}\right]\approx 1.$ We thus compare this demography against a constant-size demography with coalescent-scaled size of $\eta \equiv 1,$ as this is the population size that would be estimated using the pairwise heterozygosity (Tajima 1983). We use a coalescent-scaled mutation rate of $\theta /2=0.004$ per base, which is roughly the mutation rate of D. melanogaster (Chan et al. 2012).

While the size history $\eta \left(t\right)$ of (6) is fairly simple, with only $\mathcal{D}=3$ epochs, we stress that LDpop can in fact handle much more complex size histories. For example, in Runtime and Accuracy of Likelihoods, we show that LDpop can easily handle a demography with $\mathcal{D}=64,$ with little additional cost in runtime.

Linkage disequilibrium and two-locus likelihoods

One statistic of linkage disequilibrium is

$${\widehat{r}}^2=\frac{{\left[{\widehat{x}}_{11}-{\widehat{x}}_1^{\left(a\right)}{\widehat{x}}_1^{\left(b\right)}\right]}^2}{{\widehat{x}}_0^{\left(a\right)}{\widehat{x}}_1^{\left(a\right)}{\widehat{x}}_0^{\left(b\right)}{\widehat{x}}_1^{\left(b\right)}},$$

where ${\widehat{x}}_{ij}=n_{ij}/n$ is the fraction of the sample with haplotype $ij,$ with ${\widehat{x}}_i^{\left(a\right)}={\displaystyle {\sum }_j{\widehat{x}}_{ij}}$ and ${\widehat{x}}_j^{\left(b\right)}={\displaystyle {\sum }_i{\widehat{x}}_{ij}}.$ In words, ${\widehat{r}}^2$ is the sample square correlation of a random allele at locus a with a random allele at locus b. We let $r^2={\lim }_{n\to \mathrm{\infty }}{\widehat{r}}^2$ denote the population square correlation. There has been considerable theoretical interest in understanding moments of $r^2,$ ${\widehat{r}}^2,$ and related statistics (Ohta and Kimura 1969; Maruyama 1982; Hudson 1985; McVean 2002; Song and Song 2007). Additionally, $n{\widehat{r}}^2$ approximately follows a ${\chi }_1^2$ distribution when $r^2=0,$ which provides a test for the statistical significance of linkage disequilibrium (Weir 1996, p. 113).

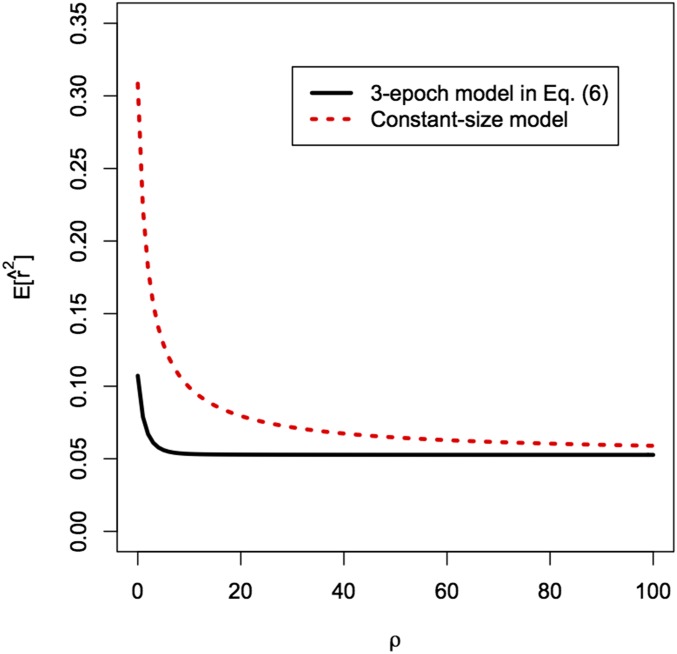
Using LDpop, we can compute the distribution of ${\widehat{r}}^2$ for piecewise constant models. In Figure 4, we show $\mathbb{E}\left[{\widehat{r}}^2\right]$ for a sample size $n=20$ under the three-epoch model (6) and the constant population size model. Under the three-epoch demography, $\mathbb{E}\left[{\widehat{r}}^2\right]$ is much lower for small ρ and decays more rapidly as $\rho \to \mathrm{\infty }.$ In other words, the constant model requires higher ρ to break down linkage disequilibrium (LD) to the same level, which suggests that incorrectly assuming a constant demography will lead to upward-biased estimates of the recombination rate (as pointed out by an anonymous reviewer). We confirm this below.

Figure 4.

Expected linkage disequilibrium $\mathbb{E}[{\widehat{r}}^2]$ for the three-epoch model in (6) and the constant-size model with $\eta \equiv 1,$ as a function of recombination rate ρ for a sample size of $n=20.$ Under the three-epoch model, even nearby sites are expected to be quite uncorrelated.

Fine-scale recombination rate estimation

For a sample of n haplotypes observed at L SNPs, let $n\left[a,b\right]$ be the two-locus sample observed at SNPs $a,b\in \left\{1,\dots ,L\right\},$ and let $\rho \left[a,b\right]$ be the recombination rate between SNPs a and b. The programs LDhat (McVean et al. 2002, 2004; Auton and McVean 2007), LDhot (Myers et al. 2005; Auton et al. 2014), and LDhelmet (Chan et al. 2012) infer hotspots and recombination maps $\rho ,$ using the composite likelihood due to Hudson (2001),

$${\displaystyle \prod _{a,b:0<b-a<W}\mathrm{\mathbb{P}}\left(n\left[a,b\right];\rho \left[a,b\right]\right)},$$ (7)

where W denotes some window size in which to consider pairs of sites [a finite window size W removes the computational burden and statistical noise from distant, uninformative sites (Fearnhead 2003; Smith and Fearnhead 2005)].

We used LDpop to generate four likelihood tables, which we then used with LDhat and LDhelmet to estimate recombination maps for simulated data. The four tables, denoted by ${\mathrm{ℒ}}_{\mathrm{const}},$ ${\mathrm{ℒ}}_{\text{exact}},$ ${\mathrm{ℒ}}_{\mathrm{approx}},$ and ${\mathrm{ℒ}}_{\mathrm{miss}},$ are defined as follows:

1. (“Constant”) ${\mathrm{ℒ}}_{\mathrm{const}}$ denotes a likelihood table that assumes a constant population size of $\eta \equiv 1.$

2. (“Exact”) ${\mathrm{ℒ}}_{\text{exact}}$ denotes a likelihood table that assumes the correct three-epoch population size history η defined in (6).

3. (“Approximate”) ${\mathrm{ℒ}}_{\mathrm{approx}}$ denotes a likelihood table with the correct size history η in (6), but using the (much faster) approximate-likelihood Equation 2 with $N=n$ Moran particles.

4. (“Misspecified”) ${\mathrm{ℒ}}_{\mathrm{miss}}$ denotes a likelihood table that assumes a misspecified demography $\widehat{\eta },$ defined by

   $$\widehat{\eta }\left(t\right)=\{\begin{array}{cc}90.5,& -0.534<t\le 0,\\ 0.167,& -0.66<t\le -0.534,\\ 1.0,& t\le -0.66,\end{array}$$ (8)

   • which was estimated from simulated data (Appendix)

Overall, we found that using the constant table ${\mathrm{ℒ}}_{\mathrm{const}}$ leads to very noisy and biased estimates of $\rho$ (as might be expected from Figure 4). The other tables ${\mathrm{ℒ}}_{\text{exact}},$ ${\mathrm{ℒ}}_{\mathrm{approx}},$ and ${\mathrm{ℒ}}_{\mathrm{miss}}$ all lead to much more accurate estimates. Using ${\mathrm{ℒ}}_{\text{exact}}$ (the exact-likelihood table with the true size history) produces slightly more accurate estimates of $\rho$ than using ${\mathrm{ℒ}}_{\mathrm{approx}}$ or ${\mathrm{ℒ}}_{\mathrm{miss}}.$ However, the three nonconstant tables ${\mathrm{ℒ}}_{\text{exact}},$ ${\mathrm{ℒ}}_{\mathrm{approx}},$ and ${\mathrm{ℒ}}_{\mathrm{miss}}$ all produce very similar results that are hard to distinguish from one another.

Figure 5 and Figure 6 show the accuracy of estimated recombination maps $\widehat{\rho }$ on simulated data. We simulated $n=20$ sequences under the three-epoch demography defined in (6), with the true maps $\rho$ taken from previous estimates for the X chromosome of D. melanogaster (Chan et al. 2012). In all, there were 110 independent data sets, with estimated maps $\widehat{\rho }$ of length 500 kb. See the Appendix for further details.

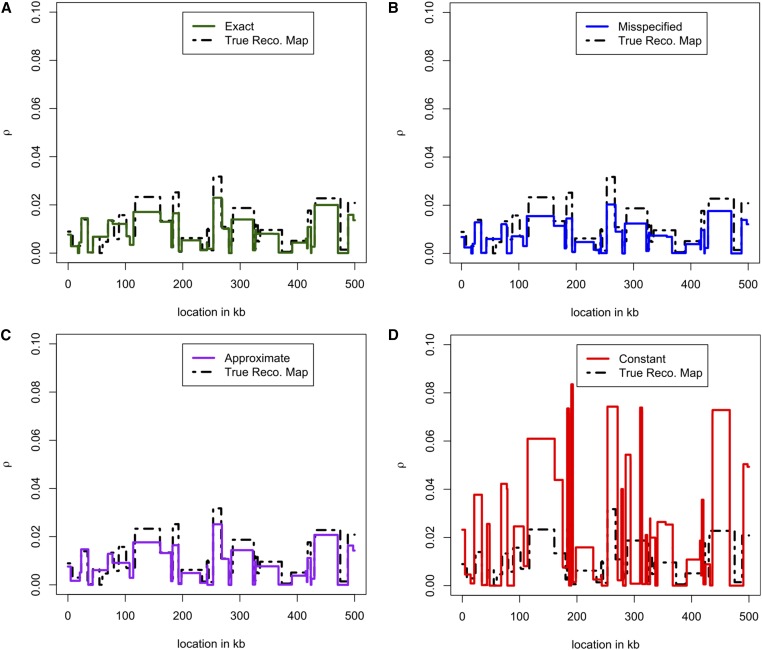
Figure 5.

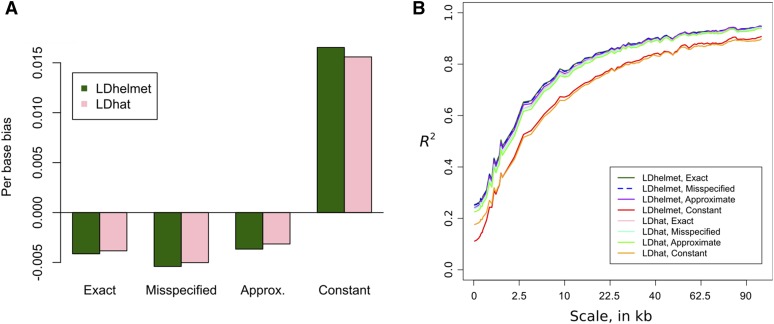
Comparison of recombination maps inferred using different lookup tables. We simulated $n=20$ haplotypes under the three-epoch model (6) and using the recombination map shown as a black dashed line. (A) Inferred map ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\text{exact}}}$ obtained using the exact likelihoods for the true demography. (B) Inferred map ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{miss}}}$ obtained using the empirically estimated demography in (8). (C) Inferred map ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{approx}}}$ obtained using an approximate lookup table for the true demography. (D) Inferred map ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{const}}}$ obtained assuming a constant population size of $\eta \equiv 1.$ Note that ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{const}}}$ is much noisier than the other estimates, while using an inferred demography or an approximate lookup table results in only a very mild reduction in accuracy compared to using the true sampling probabilities. These $\widehat{\rho }$ were produced with LDhelmet; using LDhat led to very similar results.

Figure 6.

Accuracy of the estimated maps ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\text{exact}}},{\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{miss}}},{\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{approx}}},{\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{const}}}$ over 110 simulations similar to Figure 5. The estimate ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{const}}}$ obtained assuming constant demography is substantially more biased and noisier than the other estimates. (A) The average per-base bias $\widehat{\rho }-\rho .$ (B) The square Pearson correlation coefficient $R^2$ over different scales. This $R^2$ is distinct from the $r^2$ statistic measuring linkage disequilibrium. To compute $R^2$ for scale s, the middle 500-kb region of each 1-Mb simulation was divided into nonoverlapping windows of size s and we compared the average of $\widehat{\rho }$ to the average of $\rho$ in each window. The x-axis is stretched by $x\mapsto \sqrt{x}.$

In Figure 5, we plot $\rho$ and $\widehat{\rho }$ for a particular 500-kb region. Qualitatively, the constant-size estimate ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{const}}}$ is less accurate and has wilder fluctuations. Figure 6 shows that over all 110 replicates, the constant-size estimate ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{const}}}$ has high bias and low correlation with the truth, compared to the estimates ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\text{exact}}},$ ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{miss}}},$ and ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{approx}}}$ that account for variable demography. Following Wegmann et al. (2011), we plot the correlation of $\widehat{\rho }$ with $\rho$ at multiple scales; at all scales, the constant-demography estimate ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{const}}}$ is considerably worse than the other estimates. In general, using an inferred demography or an approximate lookup table results in only a very mild reduction in accuracy compared to using the true sampling probabilities.

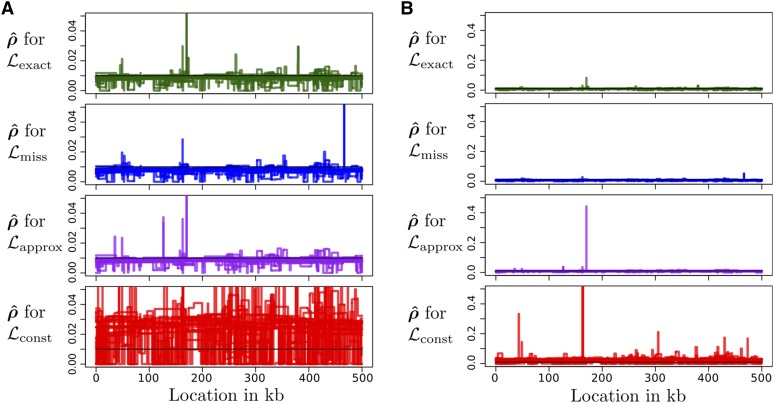
We also considered a constant (flat) map $\rho ;$ the estimated $\widehat{\rho }$ are shown in Figure 7. Consistent with Johnston and Cutler (2012), we find that the constant-demography estimate ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{const}}}$ can have extreme peaks and is generally very noisy. On the other hand, the estimates ${\widehat{\rho }}_{{\mathrm{ℒ}}_{\text{exact}}},{\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{miss}}},{\widehat{\rho }}_{{\mathrm{ℒ}}_{\mathrm{approx}}}$ that account for demography have less noise and fewer large deviations.

Figure 7.

Inferred recombination maps $\widehat{\rho }$ produced by LDhelmet using four different lookup tables (${\mathrm{ℒ}}_{\mathrm{const}},{\mathrm{ℒ}}_{\text{exact}},{\mathrm{ℒ}}_{\mathrm{approx}},{\mathrm{ℒ}}_{\mathrm{miss}}$), when the true recombination rate is constant at $\rho =0.01$/bp. Results for 20 simulated data sets are shown. Each simulation was done under the three-epoch demography defined in (6). Results for LDhat were very similar (not shown). (A) Inferred recombination maps $\widehat{\rho }.$ (B) The same plot but zoomed out. For the figure corresponding to ${\mathrm{ℒ}}_{\mathrm{const}},$ the highest peak reaches $\rho =2.5$ (not displayed), which is 250 times the true value.

Runtime and Accuracy of Likelihoods

Runtime of the exact and approximate-likelihood formulas

Both the approximate (Equation 2)- and exact-likelihood formulas (Theorem 1) require computing products $v{e}^A$ for some $k\times k$ matrix $A$ and $1\times k$ row vector $v.$ Naively, this kind of vector–matrix multiplication costs $O\left(k^2\right).$ However, in our case $A$ is sparse, with $O\left(k\right)$ nonzero entries, allowing us to compute $v{e}^A$ up to numerical precision in $O\left(k\mathcal{T}\right)$ time, where $\mathcal{T}$ is some finite number of sparse matrix–vector products depending on $A$ (Al-Mohy and Higham 2011). In particular, $k=O\left(n^3\right)$ for the approximate formula, whereas $k=O\left(n^6\right)$ for the exact formula. Thus, computing the likelihood table costs $O\left(n^3\mathcal{T}\right)$ and $O\left(n^6\mathcal{T}\right)$ for the approximate (Equation 2) and exact (Theorem 1) formulas, respectively. See the Appendix for a more detailed analysis of the computational complexity and a description of the algorithm for computing $v{e}^A.$ Note that $\mathcal{T}$ depends nontrivially on the sample size n, as well as the parameters ρ, θ, ${\eta }_d,$ and $t_d.$

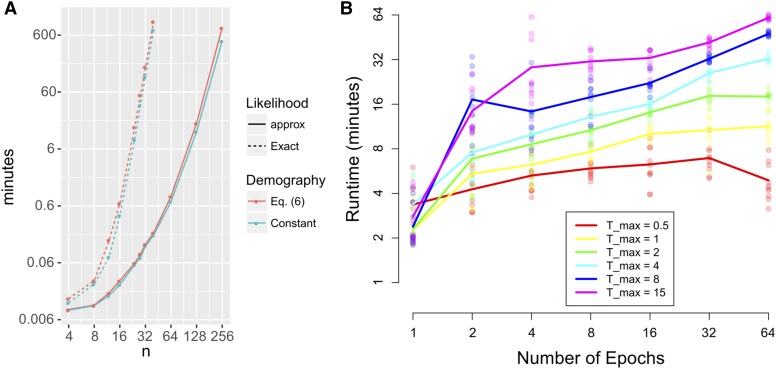
We present running times for LDpop in Figure 8. We used LDpop to generate likelihood tables with $\rho \in \left\{0,1,\dots ,100\right\},$ using 24 cores on a computer with 256 GB of RAM. On the three-epoch demography (Equation 6), we ran the exact formula up to $n=40$ (17 hr) and the approximate formula up to $n=256$ (13 hr). The constant demography takes nearly the same amount of time as the three-epoch demography, which agrees with our general experience that computing the initial stationary distribution ${\tilde{\lambda }}^{-D}$ is more expensive than multiplying the matrix exponentials $e^{{\tilde{\Lambda }}^{d}t}.$ Using faster algorithms to compute ${\tilde{\lambda }}^{-D}$ should lead to substantial improvements in runtime.

Figure 8.

Runtime of LDpop to compute a likelihood table with $\rho \in \left\{0,1,\dots ,100\right\}.$ Experiments were performed using 24 cores on a computer with 256 GB of RAM. (A) Runtime as a function of sample size, for both the approximate and exact formulas and for two demographies [a constant-size history and the three-epoch model (6)]. (B) Runtime as a function of the number of epochs $\mathcal{D}$ on $\left[-T_{\max },0\right],$ for the exact formula with $n=20,$ with 10 repetitions with random population sizes. Note that runtime depends more on $T_{\max }$ than $\mathcal{D}$ and grows sublinearly with $\mathcal{D}$ (a twofold increase of $\mathcal{D}$ yields less than a twofold increase in runtime).

Figure 8 also examines how LDpop scales with the number of epochs in the demography. We split $\left[-T_{\max },0\right]$ into $\mathcal{D}$ intervals of length $T_{\max }/\mathcal{D},$ each with a random population size $1/{\eta }_d\sim \log \text{Uniform}\left(0.1,10\right),$ with 10 repetitions per setting of $T_{\max }$ and $\mathcal{D}.$ Empirically, LDpop scales sublinearly with $\mathcal{D},$ and LDpop has no problem handling $\mathcal{D}=64$ epochs. We also note that $T_{\max }$ has a greater impact on runtime than $\mathcal{D};$ this is because the matrix exponentials are essentially computed by solving an ordinary differential equation (ODE) from $-T_{\max }$ to 0, as noted in the Appendix; see Computing the action of a sparse matrix exponential.

Accuracy of the approximate likelihood

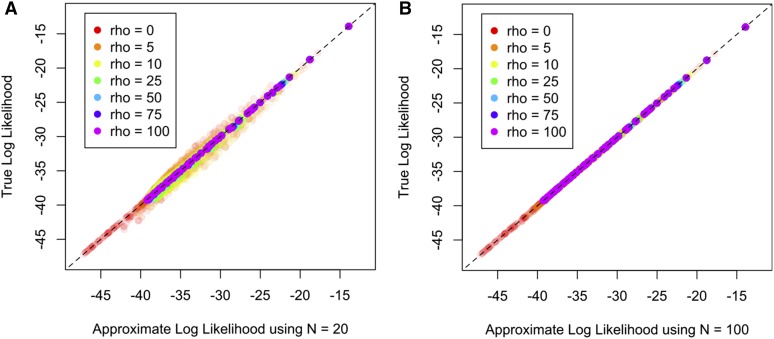
In the Fine-scale recombination rate estimation section, we found that using the approximate likelihood (Equation 2) has little impact on recombination rate estimation, suggesting that it is an accurate approximation to the exact formula in Theorem 1. We examine this in greater detail in Figure 9, for $n=20,$ the three-epoch demography (Equation 6), and a lookup table with $\rho \in \left\{0,1,\dots ,100\right\}.$ We compare the approximate against the exact values for $N=20$ and $N=100$ Moran particles in the approximate model. The approximate table with $N=20$ is reasonably accurate, with some mild deviations from the truth. The approximate table with $N=100$ is extremely accurate and visually indistinguishable from the true values.

Figure 9.

The approximate table $\left\{\log \widehat{\mathrm{\mathbb{P}}}\left(n\right)\right\}$ plotted against the exact table $\left\{\log \mathrm{\mathbb{P}}\left(n\right)\right\},$ for a lookup table with $n=20$ and $\rho \in \left\{0,1,\dots ,100\right\},$ under the three-epoch model in (6). (A) $N=20$ Moran particles. (B) $N=100$ Moran particles. Note that the approximate table with $N=100$ is extremely accurate and visually indistinguishable from the true values.

Runtime and accuracy of the importance sampler

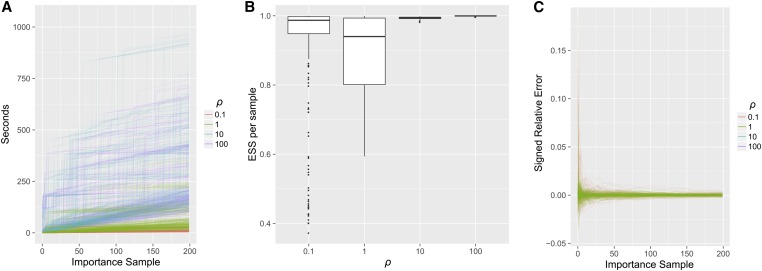
We plot the runtime of our importance sampler in Figure 10A. For the previous three-epoch demography (Equation 6), we drew $K=200$ importance samples for each of the 275 configurations $n$ with $n=n^{\left(c\right)}=20,$ with $\rho \in \left\{0.1,1,10,100\right\}.$ The runtime of the importance sampler generally increased with ρ; using 20 cores, sampling all 275 configurations took ∼4 min with $\rho =0.1,$ but about 1 hr with $\rho =100.$ We further analyze the computational complexity of the importance sampler in the Appendix.

Figure 10.

Accuracy and runtime of importance sampling, on the three-epoch demography (6) with $\theta =0.008$ and $\rho =1.0,$ drawing 200 genealogies for each of the 275 fully specified configurations $n$ with $n=20.$ (A) Runtime for each $n,$ as a function of the number of importance samples. Higher ρ generally took a longer time. Using 20 cores, the time to sample all 275 configurations took ∼4 min when $\rho =0.1,$ but 1 hr for $\rho =100.$ (B) The ESS per importance sample, for each configuration $n.$ (C) The signed relative error $\left(\mathrm{Est}-\text{Truth}\right)/\text{Truth}$ of $\log \widehat{\mathrm{\mathbb{P}}}\left(n\right),$ as a function of the number of importance samples. The true values were computed via Theorem 1.

The number K of importance samples required to reach a desired level of accuracy is typically measured with ESS,

$$\mathrm{ESS}=\frac{{\left({{{\displaystyle \sum }}^{\text{}}}_{k=1}^K{w}_k\right)}^2}{{{{\displaystyle \sum }}^{\text{}}}_{k=1}^K{w}_k^2},$$

where $w_k=d\mathrm{\mathbb{P}}\left(n_{\le 0}^{\left(k\right)}\right)/d\widehat{Q}\left(n_{\le 0}^{\left(k\right)}\right)$ denotes the importance weight of the kth sample (see Equation 4). Note that $\text{ESS}\le K$ always, with equality achieved only if the $w_k$ have 0 variance.

Compared to previous coalescent importance samplers, our proposal distribution is highly efficient. We plot the ESS per importance sample (i.e., $\text{ESS/}K$) in Figure 10B. Typically $\text{ESS/}K>0.8;$ for $\rho \in \left\{10,100\right\},$ the ESS is close to its optimal value, with $\text{ESS/}K\approx 1.$ In Figure 10C, we compare the log-likelihood estimated from importance sampling to the true value computed with Theorem 1; after $K=200$ importance samples, the signed relative error is well under $1\text{\%}$ for all $n.$

By contrast, the previous two-locus importance sampler of Fearnhead and Donnelly (2001), which assumes a constant population size, achieves ESS anywhere between $0.05K$ and $0.5K,$ depending on $n,\theta ,\rho$ (result not shown). This importance sampler is based on a similar result to that of Theorem 2, with optimal rates ${\phi }_{n,m}\left(\mathrm{\mathbb{P}}\left(m\right)/\mathrm{\mathbb{P}}\left(n\right)\right).$ However, to approximate $\mathrm{\mathbb{P}}\left(m\right)/\mathrm{\mathbb{P}}\left(n\right),$ previous approaches did not use a Moran model, but followed the approach of Stephens and Donnelly (2000), using an approximate “conditional sampling distribution” (CSD). We initially tried using the CSD of Fearnhead and Donnelly (2001) and later generalizations to variable demography (Sheehan et al. 2013; Steinrücken et al. 2015), but found that importance sampling failed under population bottleneck scenarios, with the ESS repeatedly crashing to lower and lower values. Previous attempts to perform importance sampling under variable demography (Ye et al. 2013) have also encountered low ESS, although in the context of an infinite-sites model (as opposed to a two-locus model). However, Dialdestoro et al. (2016) recently devised an efficient two-locus importance sampler using the CSD approach, in conjunction with advanced importance sampling techniques. Their importance sampler allows archaic samples and is thus time inhomogeneous, but it models only constant population size histories.

Discussion

In this article, we have developed a novel algorithm for computing the exact two-locus sampling probability under arbitrary piecewise-constant demographic histories. These two-locus likelihoods can be used to study the impact of demography on LD and also to improve fine-scale recombination rate estimation. Indeed, using two-locus sampling probabilities computed under the true or an inferred demography, we were able to obtain recombination rate estimates with substantially less noise and fewer spurious peaks that could potentially be mistaken for hotspots.

We have implemented our method in a freely available software package, LDpop. This program also includes an efficient approximation to the true sampling probability that easily scales to hundreds in sample size. In practice, highly accurate approximations to the true sampling probability for sample size n can be obtained quickly by first applying the approximate algorithm with N Moran particles >n and then downsampling to the desired sample size n.

In principle, one could also obtain an accurate approximation to the sampling probability using our importance sampler, which is also implemented in LDpop. We have not optimized this code, however, and we believe that its main utility will be in sampling two-locus ARGs from the posterior distribution. Finally, we note that, in addition to improving the inference of fine-scale recombination rate variation, our two-locus likelihoods can be utilized in other applications such as hotspot hypothesis testing and demographic inference.

Appendix

Proposal Distribution of Importance Sampler

For our importance sampler, we construct the proposal distribution $\widehat{Q}\left(n_{\le 0}\right)$ by approximating the optimal proposal distribution $Q_{\mathrm{opt}}\left(n_{\le 0}\right)=\mathrm{\mathbb{P}}\left(n{}_{\le 0}|n_0\right)$ given in Theorem 2. We start by choosing a grid of points $-\mathrm{\infty }<{\tau }_1<{\tau }_2<\cdots <{\tau }_J=0$ and then set $\widehat{Q}$ to be a backward-in-time Markov chain, whose rates at $t\in \left({\tau }_j,{\tau }_{j+1}\right)$ are the linear interpolation

$${\widehat{q}}_{n,m}^{\left(t\right)}=\frac{{\tau }_{j+1}-t}{{\tau }_{j+1}-{\tau }_j}{\widehat{q}}_{n,m}^{\left({\tau }_j\right)}+\frac{t-{\tau }_j}{{\tau }_{j+1}-{\tau }_j}{\widehat{q}}_{n,m}^{\left({\tau }_{j+1}\right)},$$ (A1)

with the rates at the grid points given by

$${\widehat{q}}_{n,m}^{\left({\tau }_j\right)}=\{\begin{array}{ll}{\phi }_{n,m}^{\left({\tau }_j\right)}\frac{{\widehat{\mathrm{\mathbb{P}}}}_{{\tau }_j}\left(m\right)}{{\widehat{\mathrm{\mathbb{P}}}}_{{\tau }_j}\left(n\right)},\hfill & \text{if }m\ne n,\hfill \\ -{\displaystyle \sum _{\mathit{\nu }\ne n}{\widehat{q}}_{n,\mathit{\nu }}^{\left({\tau }_j\right)}},\hfill & \text{if }m=n,\hfill \end{array}$$

with ${\widehat{\mathrm{\mathbb{P}}}}_{{\tau }_j}\left(n\right)$ an approximation to the likelihood ${\mathrm{\mathbb{P}}}_{{\tau }_j}\left(n\right).$ In particular, we set ${\widehat{\mathrm{\mathbb{P}}}}_{{\tau }_j}\left(n\right)={\mathrm{\mathbb{P}}}_{{\tau }_j}^{\left(N\right)}\left(n\right),$ using the approximate-likelihood formula (2). The approximate likelihoods $\left\{{\mathrm{\mathbb{P}}}_{{\tau }_j}^{\left(N\right)}\left(n\right)\right\}$ can be efficiently computed along a grid of points, using the method described below (see Computing the action of a sparse matrix exponential and Complexity of importance sampler).

To sample from $\widehat{Q},$ we note that for configuration $n$ at time t, the time $S<t$ of the next event has cumulative distribution function $\mathrm{\mathbb{P}}\left(S<s\right)=\exp \left({\displaystyle {\int }_S^t{\widehat{q}}_{n,n}^{\left(u\right)}du}\right)$ for $s<t.$ Thus, S can be sampled by first sampling $X\sim \text{Uniform}\left(0,1\right)$ and then solving for $\log \left(X\right)={\displaystyle {\int }_S^t{\widehat{q}}_{n,n}^{\left(u\right)}du}$ via the quadratic formula [since ${\widehat{q}}_{n,n}^{\left(u\right)}$ is piecewise linear; see (A1)]. Having sampled S, we can then sample the next configuration $m$ with probability $-{\widehat{q}}_{n,m}^{\left(S\right)}/{\widehat{q}}_{n,n}^{\left(S\right)}.$

Details of Simulation Study

Simulated data

We simulated independent 1-Mb segments with $n=20$ haplotypes under the three-epoch demography $\eta \left(t\right)$ in (6). To do so, we generated trees using the program MaCS (Chen et al. 2009) and then generated mutations according to a quadraallelic mutational model. For the variable recombination maps used in Figure 5 and Figure 6, we divided the recombination map of the X chromosome of D. melanogaster from Raleigh, North Carolina inferred by Chan et al. (2012) into 22 nonoverlapping 1-Mb windows and simulated five replicates, for a total of 110 Mb of simulated data. For the constant map used in Figure 7, we generated 20 data sets with $\rho =0.01$ per base.

Estimation of misspecified demography $\widehat{\eta }\left(t\right)$

To estimate the misspecified demography $\widehat{\eta }\left(t\right)$ of (8), we pooled all biallelic SNPs from the 110 simulated segments of the variable recombination map and then used the folded site frequency spectrum (SFS) of the simulated SNPs to estimate $\widehat{\eta }\left(t\right).$ Specifically, we fitted $\widehat{\eta }\left(t\right)$ by maximizing a composite likelihood, viewing each SNP as an independent draw from a multinomial distribution proportional to the expected SFS. We computed the expected SFS with the software package momi (Kamm et al. 2016) and fixed the most ancient population size to 1.0 due to scaling and identifiability issues.

Recombination map estimation

After removing all nonbiallelic SNPs, we ran both LDhat and LDhelmet on the resulting data, using a block penalty of 50 as recommended by Chan et al. (2012) for Drosophila-like data (the block penalty is a tuning parameter that is multiplied by the number of change points in the estimated map $\widehat{\rho }$ and added to the log composite likelihood; thus a high block penalty discourages overfitting). We took the posterior median inferred at each position to be the estimated map $\widehat{\rho }.$ We used only the centermost 500 kb of each estimate $\widehat{\rho }$ to avoid the issue of edge effects.

Computational Complexity

Computing the action of a sparse matrix exponential

Both Theorem 1 and the approximate formula (2) rely on “the action of the matrix exponential” (Al-Mohy and Higham 2011). Let $A$ be a $k\times k$ matrix and $v$ a $1\times k$ row vector. We need to compute expressions of the form $v{e}^A.$ Naively, this kind of vector–matrix multiplication costs $O\left(k^2\right).$ However, in our case $A$ will be sparse, with k nonzero entries, allowing us to more efficiently compute $v{e}^A.$

In particular, we use the algorithm of Al-Mohy and Higham (2011), as implemented in the Python package scipy. For $s\in {\mathrm{\mathbb{Z}}}_{+},$ define $T_m\left(s^{-1}A\right)={\displaystyle {\sum }_{i=0}^m{\left(s^{-1}A\right)}^i/i!},$ the truncated Taylor series approximation of $e^{s^{-1}A}.$ Then, we have

$$v{e}^A=v{\left(e^{s^{-1}A}\right)}^s\approx v{\left[T_m\left(s^{-1}A\right)\right]}^s.$$

Now let $b_j=v{\left[T_m\left(s^{-1}A\right)\right]}^j,$ so $B_j$ is a $1\times k$ row vector. Then

$$b_j=b_{j-1}{T}_m\left(s^{-1}A\right)={\displaystyle \sum _{i=0}^m{b}_{j-1}\frac{{\left(s^{-1}A\right)}^i}{i!}},$$

with $v{e}^A\approx b_s,$ and $b_s$ evaluated in $\mathcal{T}=ms$ vector–matrix multiplications, each costing $O\left(k\right)$ by the sparsity of $A.$ Approximating $v{e}^A$ thus costs $O\left(\mathcal{T}k\right)$ time. Both $m$ and s are chosen automatically to bound

$$\frac{{\Vert \mathrm{\Delta }A\Vert }_1}{{\Vert A\Vert }_1}\le \text{tolerance}\approx 1.1\times {10}^{-16},$$

with $\mathrm{\Delta }A$ defined by ${\left[T_m\left(s^{-1}A\right)\right]}^s=e^{A+\mathrm{\Delta }A}$ and the matrix norm given by $A_1={\sup }_{w\ne 0}\left({\Vert wA\Vert }_1/{\Vert w\Vert }_1\right).$ To avoid numerical instability, m is also bounded by $m\le m_{\max }=55.$ Al-Mohy and Higham (2011) provide some analysis for the size of $\mathcal{T}=ms,$ but this analysis is rather involved. Very roughly, $\mathcal{T}$ is proportional to $\Vert A\Vert$ (for arbitrary matrix norm $\Vert \cdot \Vert$), so computing $v{e}^{2A}$ takes twice as long as computing $v{e}^A,$ and computing $v{e}^{tA}$ is roughly proportional to t. This is because $v{e}^{tA}$ is essentially computed by numerically integrating the ODE $\nabla \mathit{f}\left(s\right)=\mathit{f}\left(s\right)A$ for $s\in \left[0,t\right].$

We note that $b_j\approx v{e}^{s^{-1}jA},$ and thus this algorithm approximates $v{e}^{tA}$ along a grid of points $t\in \left\{s^{-1},2s^{-1},\dots ,1\right\}.$ If $v{e}^{tA}$ is needed at additional points, then extra grid points can be added at those times.

Complexity of the exact-likelihood formula (Theorem 1)

We consider the computational complexity of computing ${\mathrm{\mathbb{P}}}_0\left(n\right)$ via Theorem 1. Note that the formula (3) simultaneously computes ${\mathrm{\mathbb{P}}}_0\left(n\right)$ for all configurations $n\in \mathcal{N}.$

As usual, we assume two alleles $\mathcal{A}=\left\{0,1\right\},$ as is assumed by LDhat and the applications considered in this article. We start by considering the dimensions of the sampling probability vectors $p^d$ and rate matrices ${\tilde{\Lambda }}^d$ for intervals $\left(t_d,t_{d+1}\right].$ The set of $a,b,c$ haplotypes is $H=\left\{00,01,10,11,0\text{*},1\text{*},\text{*}0,\text{*}1\right\},$ so $\left|H\right|=8.$ Thus, there are $O\left(n^6\right)$ possible configurations $n$ with $n^{\left(a\right)}=n^{\left(b\right)}=n-n^{\left(c\right)}.$ In particular, there are $O\left(n^6\right)$ ways to specify $n_{00},n_{01},n_{10},n_{11},n_{0\text{*}},n_{\text{*}0},$ and then $n_{1\text{*}}=n-{\displaystyle {\sum }_{i,j\in \left\{0,1\right\}}{n}_{ij}-n_{0\text{*}}}$ and $n_{\text{*}1}=n-{\displaystyle {\sum }_{i,j\in \left\{0,1\right\}}{n}_{ij}-n_{\text{*}0}}$ are determined. Thus, $p^d$ is a row vector of dimension $1\times O\left(n^6\right),$ and ${\tilde{\Lambda }}^d$ is a square matrix of dimension $O\left(n^6\right)\times O\left(n^6\right),$ but ${\tilde{\Lambda }}^d$ is sparse, with only $O\left(n^6\right)$ nonzero entries.

By using the aforementioned algorithm for computing the action of a sparse matrix exponential, we can compute $p^{d+1}=\left[\left(p^d\odot {\tilde{\gamma }}^d\right)e^{{\tilde{\Lambda }}^d\left(t_{d+1}-t_d\right)}\right]\mathrm{÷}{\tilde{\gamma }}^d$ from $p^d$ in $O\left({\mathcal{T}}_d{n}^6\right)$ time, where ${\mathcal{T}}_d$ is the number of vector–matrix multiplications to compute the action of $e^{{\tilde{\Lambda }}^d\left(t_{d+1}-t_d\right)}.$ We note that the stationary distribution $\left({\gamma }_0^d,\dots ,{\gamma }_n^d\right)$ can be computed in $n+1$ steps: ${\Gamma }^d$ is the rate matrix of a simple random walk with $n+1$ states, so ${\gamma }_{i+1}^d={\gamma }_i^d\left({\left[{\Gamma }^d\right]}_{i,i+1}/{\left[{\Gamma }^d\right]}_{i+1,i}\right)$ and ${\displaystyle {\sum }_i{\gamma }_i^d}=1.$

Similarly, the initial value $p^{-D+1}={\tilde{\lambda }}^{-D}\mathrm{÷}{\tilde{\gamma }}^{-D}$ can be computed via sparse vector–matrix multiplications, using the technique of power iteration. For $\mu =1/{\max }_{ij}{\left[{\tilde{\Lambda }}^{-D}\right]}_{ij}$ and arbitrary positive vector $v^{\left(0\right)}$ with ${\Vert v^{\left(0\right)}\Vert }_1=1,$ we have $v^{\left(i\right)}:=v^{\left(0\right)}{\left(\mu {\tilde{\Lambda }}^{-D}+I\right)}^i\to {\tilde{\lambda }}^{-D}$ as $i\to \mathrm{\infty }.$ In particular, we set the number of iterations, ${\mathcal{T}}_{-D},$ so that ${\Vert \log \left(v^{\left({\mathcal{T}}_{-D}\right)}\mathrm{÷}{v}^{\left({\mathcal{T}}_{-D}-1\right)}\right)\Vert }_1<1\times {10}^{-8},$ where $\log v$ is the element-wise $\log$ of $v.$ As noted in Runtime of the exact- and approximate-likelihood formulas, in practice we found ${\mathcal{T}}_{-D}\gg {\mathcal{T}}_d$ for $d>-D;$ i.e., computing the initial stationary distribution ${\tilde{\lambda }}^{-D}$ was more expensive than multiplying the matrix exponentials $e^{{\tilde{\Lambda }}^{d}t}.$

To summarize, computing ${\mathrm{\mathbb{P}}}_0\left(n\right)$ for all $O\left(n^6\right)$ configurations $n\in \mathcal{N}$ of size n costs $O\left(n^6\mathcal{T}\right),$ with $\mathcal{T}={\displaystyle {\sum }_{d=-D}^{-1}{\mathcal{T}}_d}.$ We caution that $\mathcal{T}$ depends on $n,\left\{t_d\right\},\left\{{\tilde{\Lambda }}^d\right\}.$

The memory cost of Theorem 1 is $O\left(n^6\right),$ since ${\tilde{\Lambda }}^d$ has $O\left(n^6\right)$ nonzero entries.

Comparison with Golding’s equations

Under constant population size, Golding (1984) proposed a method to compute ${\mathrm{\mathbb{P}}}_0\left(n\right)$ by solving a linear system of equations $gG=g,$ where $g={\left[{\mathrm{\mathbb{P}}}_0\left(n\right)\right]}_{n\in \mathcal{N}}{}^{\prime }$ is the vector of sampling probabilities indexed by the $O\left(n^8\right)$ configurations $\mathcal{N}\prime =\left\{n:\max \left(n^{\left(a\right)}+n^{\left(c\right)},n^{\left(b\right)}+n^{\left(c\right)}\right)\le n\right\}$ with at most n alleles at each locus. Hudson (2001) solves this linear system, costing $O\left(n^8\mathcal{T}\right)$ where (as above) $\mathcal{T}$ is some finite number of sparse matrix–vector multiplications.

For the case of constant population size, Theorem 1 reduces to solving a sparse system ${\tilde{\lambda }}^{-D}{\tilde{\Lambda }}^{-D}={\tilde{\lambda }}^{-D},$ which is similar in spirit to solving Golding’s equations $gG=g.$ The $O\left(n^6\mathcal{T}\right)$ runtime of Theorem 1 at first seems superior to the $O\left(n^8\mathcal{T}\right)$ runtime of Golding’s equations, but in fact the number of matrix multiplications $\mathcal{T}$ is not comparable between the two methods. Most importantly, Hudson (2001) exploits the structure of the $O\left(n^8\right)$ equations to decompose them into smaller subsystems of $O\left(n^4\right)$ equations, which may lead to smaller $\mathcal{T}.$ Algorithmic details also lead to important differences: we use power iteration, whereas Hudson (2001) uses a conjugate gradient method, with less stringent convergence criteria (stopping when the relative $l_2$ error for each subsystem of equations is $<{10}^{-4}$).

Preliminary tests suggest that the C code of Hudson (2001) and a similar implementation by Chan et al. (2012) are faster than our current method for solving ${\tilde{\lambda }}^{-D}{\tilde{\Lambda }}^{-D}={\tilde{\lambda }}^{-D}.$ We are planning future updates to LDpop that will speed up the initial stationary distribution ${\tilde{\lambda }}^{-D},$ either by changing the algorithmic details of our solver or by using Golding’s equations to compute ${\tilde{\lambda }}^{-D}$ instead.

Complexity of approximate-likelihood formula

The method of computing the approximate-likelihood formula (2) is similar to computing Theorem 1, in that we can compute an initial stationary distribution ${\lambda }_{\left(N\right)}^{-D}$ by power iteration and then propagate it forward in time by applying the action of the sparse matrix exponential $e^{{\Lambda }_{\left(N\right)}^d\left(t_{d+1}-t_d\right)}.$ However, instead of $O\left(n^6\right)$ states, there are $O\left(N^3\right)$ total states: there are four possible fully specified haplotypes $\left\{00,01,10,11\right\},$ and thus the requirement that the number of lineages sums to N yields $O\left(N^3\right)$ possible states for the Moran model $M_t.$ Thus, computing the approximate-likelihood formula (2) costs $O\left(N^3\mathcal{T}\right)$ time and $O\left(N^3\right)$ memory space.

Complexity of importance sampler

Here we examine the computational complexity of our importance sampler.

To construct the proposal distribution $\widehat{Q}$ described in Proposal Distribution of Importance Sampler, we must compute approximate likelihoods ${\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(n\right)$ defined by (2) along a grid of points $t\in \left\{{\tau }_1,{\tau }_2,\dots ,{\tau }_J\right\}.$ We start by computing the Moran likelihoods ${\left\{{\mathrm{\mathbb{P}}}_{\left(N\right)}\left(M_{{\tau }_j}\right)\right\}}_j,$ using the action of the sparse matrix exponential. As discussed above, the method of Al-Mohy and Higham (2011) yields ${\left\{{\mathrm{\mathbb{P}}}_{\left(N\right)}\left(M_{{\tau }_j}\right)\right\}}_j$ as a by-product of computing ${\mathrm{\mathbb{P}}}_{\left(N\right)}\left(M_0\right)$ at essentially no extra cost. Thus, computing the terms $\left\{{\mathrm{\mathbb{P}}}_{\left(N\right)}\left(M_t\right)\right\}$ costs $O\left(N^3\mathcal{T}\right)$ (absorbing the minor cost of an additional J extra grid points into $\mathcal{T}$).

We then compute ${\mathrm{\mathbb{P}}}_t^{\left(N\right)}\left(n\right)$ by subsampling from ${\mathrm{\mathbb{P}}}_{\left(N\right)}\left(M_t\right)$ as in (2) and thus set $N=2n,$ since $2n$ is the maximum number of individuals in $n$ (because each of the original n lineages can recombine into two lineages). However, it is inefficient to compute ${\widehat{\mathrm{\mathbb{P}}}}_t\left(n\right)$ by subsampling for every value of $n$ separately. Instead, it is better to use a dynamic program ${\widehat{\mathrm{\mathbb{P}}}}_t\left(n\right)={\displaystyle {\sum }_m{\widehat{\mathrm{\mathbb{P}}}}_t\left(m\right)\mathrm{\mathbb{P}}\left(n|m\right)},$ where the sum is over all configurations $m$ obtained by adding an additional sample to $n.$

This costs $O\left(n^{8}J\right)$ time and space, since there are J grid points and $O\left(n^8\right)$ possible configurations of $n.$ Then, assuming a reasonably efficient proposal, the expected cost to draw K importance samples is $O\left(nJK\right),$ since the expected number of coalescence, mutation, and recombination events before reaching the marginal common ancestor at each locus is $O\left(n\right)$ (Griffiths 1991). This approach thus takes $O\left(n^3\mathcal{T}+n^{8}J+n^{4}JK\right)$ expected time to compute ${\mathrm{\mathbb{P}}}_0\left(n\right)$ for all $O\left(n^3\right)$ possible $n.$ In practice, we precomputed ${\widehat{\mathrm{\mathbb{P}}}}_t\left(n\right)$ only for the $O\left(n^4\right)$ fully specified $n$ (without missing alleles), but computed and cached ${\widehat{\mathrm{\mathbb{P}}}}_t\left(n\right)$ as needed for partially specified $n$ (with missing alleles). The theoretical running time to compute the full lookup table is still $O\left(n^3\mathcal{T}D+n^{8}J+n^{4}JK\right),$ but in practice, many values of $n$ are highly unlikely and never encountered at each ${\tau }_j.$

Proofs

For a stochastic process ${\left\{X_t\right\}}_{t\le 0},$ we denote its partial sample paths with the following notation: $X_{s:t}=\left\{X_u:u\in \left(s,t\right]\right\}$ and $X_{\le s}=X_{-\mathrm{\infty }:s}.$

Proof of Theorem 1

We start by constructing a forward-in-time Markov jump process ${\tilde{M}}_{\le 0}$ with state space $\mathcal{N}=\left\{n:n^{\left(abc\right)}=\left(k,k,n-k\right),0\le k\le n\right\}.$ ${\tilde{M}}_t$ changes due to four types of events: mutation, copying, recoalescence, and “recombination”:

1. Individual alleles mutate at rate $\theta /2$ according to transition matrix $P.$

2. Lineages copy their alleles onto each other, with the rate depending on the lineage type. Each pair of a types experiences a copying event at rate $1/{\eta }_d,$ with the direction of copying chosen with probability $1/2.$ The rates are the same for every pair of b and every pair of c types. Pairs of $\left(a,c\right)$ and $\left(b,c\right)$ types also experience copying at rate $1/{\eta }_d;$ however, the direction of copying is always from the c type to the a or b type and happens only at one allele (left for a, right for b).

3. a types do not copy onto b types, and vice versa. Instead, they merge (recoalesce) into a single c type at rate $1/{\eta }_d$ per pair. Note this is similar to the coalescent, but here the recoalescence happens forward in time rather than backward in time.

4. Each c type splits into a and b types at rate $\rho /2.$ Again, this is similar to the coalescent; however, here the recombination happens forward in time, while in the coalescent with recombination it happens at rate $\rho /2$ going backward in time.

Then ${\tilde{M}}_t$ has forward-in-time rate matrix ${\Lambda }^d$ in $(t_d,t_{d+1}],$ with ${\Lambda }^d$ given in Table 2.

Now let $C_t$ denote the number of c types in ${\tilde{M}}_t$ (so the numbers of a and b types are each $n-C_t$). Note that $C_t$ is unaffected by mutation and copying events, and so $C_{t+h}$ is conditionally independent of ${\tilde{M}}_t$ given $C_t,$ for $h\ge 0.$ Thus $C_t$ is a Markov jump process with rate matrix ${\Gamma }^d$ in $(t_d,t_{d+1}],$ where ${\Gamma }^d$ is a tridiagonal square matrix indexed by $\left\{0,1,\dots ,n\right\},$ with ${\mathrm{\Gamma }}_{m,m-1}^d=\left(\rho /2\right)m,$ ${\mathrm{\Gamma }}_{m,m+1}^d={\left(n-m\right)}^2\left(1/{\eta }_d\right),$ and ${\mathrm{\Gamma }}_{m,m}^d=-{\mathrm{\Gamma }}_{m,m-1}^d-{\mathrm{\Gamma }}_{m,m+1}^d.$

We can therefore sample ${\tilde{M}}_{\le 0}$ in two steps, as illustrated in Figure 3:

1. First, sample the recoalescence and recombination events. In other words, sample $C_{\le 0}$ using its rate matrices $\left\{{\mathrm{\Gamma }}^d\right\}.$

2. Next, sample from $\mathrm{\mathbb{P}}\left({\tilde{M}}_{\le 0}|C_{\le 0}\right).$ For $h>0,$ ${\tilde{M}}_{t+h}$ can be obtained from ${\tilde{M}}_t$ and $C_{\le 0}$ by superimposing two Poisson point processes, conditionally independent given $C_{\le 0}:$

   1. a point process of directed edges between lineages (the copying events), with rate $1/2{\eta }_d$ for $a\to a,$ $b\to b,$ $c\to c$ edges and rate $1/{\eta }_d$ for $c\to a,$ $c\to b$ edges, and (b) a point process of mutations hitting the lineages, at rate $\theta /2$ per locus per lineage.

To see that this superpositioning of point processes yields the correct distribution $\mathrm{\mathbb{P}}\left({\tilde{M}}_{\le 0}\right),$ note that mutation and copying events do not affect the rates of recombination and recoalescence events and that the four types of jump events that make up the Markov jump process ${\tilde{M}}_{\le 0}$ occur at the desired rates given by $\left\{{\Lambda }^d\right\}.$

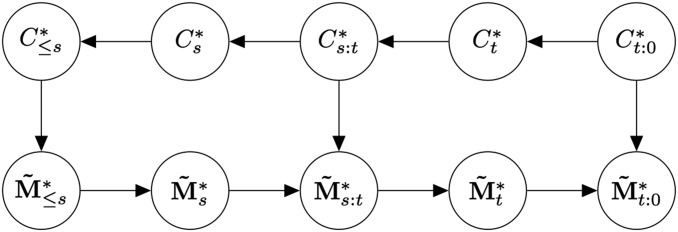
Now define $C_t^{\text{*}}$ to be the backward-in-time Markov chain with rates ${\Gamma }^d$ in $\left(t_d,t_{d+1}\right]$ (whereas $C_t$ has the same rates but going forward in time). Let ${\tilde{M}}_t^{\text{*}}$ be the stochastic process with conditional law $\mathrm{\mathbb{P}}\left({\tilde{M}}_{\le 0}^{\text{*}}|C_{\le 0}^{\text{*}}=\mathcal{C}\right)=\mathrm{\mathbb{P}}\left({\tilde{M}}_{\le 0}|C_{\le 0}=\mathcal{C}\right).$ Thus ${\tilde{M}}_{\le 0}^{\text{*}}$ can be sampled in the same two steps as ${\tilde{M}}_{\le 0},$ except the first step (coalescences and recombinations) is backward in time. We illustrate the conditional independence structure of ${\tilde{M}}_t^{\text{*}}$ and $C_t^{\text{*}}$ via a directed graphical model (Koller and Friedman 2009) in Figure A1. [A graphical model is a graph whose vertices represent random variables, with the property that if all paths between $V_1$ and $V_2$ pass through W, then there is conditional independence $\mathrm{\mathbb{P}}\left(V_1,V_2|W\right)=\mathrm{\mathbb{P}}\left(V_1|W\right)\mathrm{\mathbb{P}}\left(V_2|W\right)$].

We next show that for $n$ with $n^{\left(a\right)}=n^{\left(b\right)}=n-n^{\left(c\right)},$

$${\mathrm{\mathbb{P}}}_t\left(n\right)=\mathrm{\mathbb{P}}\left({\tilde{M}}_t^{\text{*}}=n|C_t^{\text{*}}=n^{\left(c\right)}\right).$$ (A2)

We use a similar argument as in Durrett (2008, theorem 1.30, p. 47), tracing the genealogy of $n$ backward in time (Figure 3B). Under $\mathrm{\mathbb{P}}\left(\tilde{M}\ast \right),$ recombination events occur backward in time at rate $\rho /2$ per c-type lineage, as in the coalescent. Likewise, coalescence between an a and a b type occurs at the usual rate $1/{\eta }_d.$ Next, note that copying events between ancestral lineages induce coalescences within the ARG; these are encountered as a Poisson point process at rate $1/{\eta }_d$ per ancestral pair not of type $\left(a,b\right).$ Thus, the embedded ARG is distributed as the coalescent with recombination. Finally, conditioning on the full history of recombination, copying, and coalescence events, we can drop down mutations as a Poisson point process with rate $\theta /2$ per locus per lineage, and so the ARG with mutations follows the coalescent with recombination and mutation. Note that the alleles at the common ancestors of each locus follow the stationary distribution: the common ancestors are fixed under the conditioning (of recombination, copying, and coalescence events), and if $v_s$ is the conditional distribution of an ancestral allele at time $s\le T_{\mathrm{MRCA}},$ then $v_s=v_{s\prime }{e}^{\left(P-I\right)\left(\theta /2\right)\left(s-s^{\prime }\right)}$ for $s^{\prime }<s;$ sending $s^{\prime }\to -\mathrm{\infty }$ yields the stationary distribution.

Having established (A2), we next observe

$$\begin{array}{c}{\mathrm{\mathbb{P}}}_{t_{d+1}}\left(n\right)=\mathrm{\mathbb{P}}\left({\tilde{M}}_{t_{d+1}}^{\text{*}}=n|C_{t_{d+1}}^{\text{*}}=n^{\left(c\right)}\right)\\ ={\displaystyle \sum _m\mathrm{\mathbb{P}}\left({\tilde{M}}_{t_d}^{\text{*}}=m|C_{t_d}^{\text{*}}=m^{\left(c\right)}\right)\mathrm{\mathbb{P}}\left(C_{t_d}^{\text{*}}=m^{\left(c\right)}|C_{t_{d+1}}^{\text{*}}=n^{\left(c\right)}\right)}\\ \times \mathrm{\mathbb{P}}\left({\tilde{M}}_{t_{d+1}}^{\text{*}}=n|C_{t_{d+1}}^{\text{*}}=n^{\left(c\right)},C_{t_d}^{\text{*}}=m^{\left(c\right)},{\tilde{M}}_{t_d}^{\text{*}}=m\right)\\ ={\displaystyle \sum _m{\mathrm{\mathbb{P}}}_{t_d}\left(m\right)\mathrm{\mathbb{P}}\left(C_{t_d}^{\text{*}}=m^{\left(c\right)}|C_{t_{d+1}}^{\text{*}}=n^{\left(c\right)}\right)}\\ \times \mathrm{\mathbb{P}}\left({\tilde{M}}_{t_{d+1}}=n|C_{t_{d+1}}=n^{\left(c\right)},C_{t_d}=m^{\left(c\right)},{\tilde{M}}_{t_d}=m\right).\end{array}$$ (A3)

Note that in the second equality, we use the conditional independence of ${\tilde{M}}_{t_d}^{\text{*}}$ and $C_{t_{d+1}}^{\text{*}}$ given $C_{t_d}^{\text{*}},$ which follows from the graphical model of Figure A1 by setting $s=t_d$ and $t=t_{d+1}.$

Next, note that ${\Gamma }^d$ is the transition matrix of a simple random walk with bounded state space and no absorbing states and thus is reversible. Thus, with ${\mathit{\gamma }}^d$ the stationary distribution of ${\Gamma }^d,$

$$\begin{array}{c}{\gamma }_{n^{\left(c\right)}}^d\mathrm{\mathbb{P}}\left(C_{t_d}^{\text{*}}=m^{\left(c\right)}|C_{t_{d+1}}^{\text{*}}=n^{\left(c\right)}\right)={\gamma }_{n^{\left(c\right)}}^d{\left[e^{{\mathrm{\Gamma }}^d\left(t_{d+1}-t_d\right)}\right]}_{n^{\left(c\right)},m^{\left(c\right)}}\\ ={\gamma }_{m^{\left(c\right)}}^d{\left[e^{{\mathrm{\Gamma }}^d\left(t_{d+1}-t_d\right)}\right]}_{m^{\left(c\right)},n^{\left(c\right)}}\\ ={\gamma }_{m^{\left(c\right)}}^d\mathrm{\mathbb{P}}\left(C_{t_{d+1}}=n^{\left(c\right)}|C_{t_d}=m^{\left(c\right)}\right).\end{array}$$ (A4)

Recall that we defined ${\tilde{\gamma }}_n^d={\gamma }_{n^{\left(c\right)}}^d.$ So plugging (A4) into (A3) yields

$$\begin{array}{c}{\mathrm{\mathbb{P}}}_{t_{d+1}}\left(n\right)={\displaystyle \sum _m{\mathrm{\mathbb{P}}}_{t_d}\left(m\right)\frac{{\tilde{\gamma }}_m^d}{{\tilde{\gamma }}_n^d}\mathrm{\mathbb{P}}\left(C_{t_{d+1}}=n^{\left(c\right)}|C_{t_d}=m^{\left(c\right)}\right)}\\ \hspace{1em}\times \mathrm{\mathbb{P}}\left({\tilde{M}}_{t_{d+1}}=n|C_{t_{d+1}}=n^{\left(c\right)},C_{t_d}=m^{\left(c\right)},{\tilde{M}}_{t_d}=m\right)\\ ={\displaystyle \sum _m{\mathrm{\mathbb{P}}}_{t_d}\left(m\right)\frac{{\tilde{\gamma }}_m^d}{{\tilde{\gamma }}_n^d}\mathrm{\mathbb{P}}\left(C_{t_{d+1}}=n^{\left(c\right)},{\tilde{M}}_{t_{d+1}}=n|C_{t_d}=m^{\left(c\right)},{\tilde{M}}_{t_d}=m\right)}\\ ={\displaystyle \sum _m{\mathrm{\mathbb{P}}}_{t_d}\left(m\right)\frac{{\tilde{\gamma }}_m^d}{{\tilde{\gamma }}_n^d}{\left[e^{{\tilde{\Lambda }}^d\left(t_{d+1}-t_d\right)}\right]}_{m,n}},\end{array}$$

which proves half of the desired result; i.e., $p^{d+1}=\left[\left(p^d\odot {\tilde{\gamma }}^d\right)e^{{\tilde{\Lambda }}^d\left(t_{d+1}-t_d\right)}\right]\mathrm{÷}{\tilde{\gamma }}^d,$ where $p^d={\left[{\mathrm{\mathbb{P}}}_{t_d}\left(n\right)\right]}^{\prime }{}_n.$ To show the other half, that $p^{-D+1}={\tilde{\lambda }}^{-D}\mathrm{÷}{\tilde{\lambda }}^{-D},$ where ${\tilde{\lambda }}^{-D}$ is the stationary distribution of ${\mathbf{\Lambda }}^{-D},$ we simply note that for all $t\le t_{-D+1},$

$$\begin{array}{c}{\mathrm{\mathbb{P}}}_t\left(n\right){\tilde{\gamma }}_n^{-D}=\mathrm{\mathbb{P}}\left({\tilde{M}}_t^{\text{*}}=n|C_t^{\text{*}}=n^{\left(c\right)}\right){\gamma }_{n^{\left(c\right)}}^{-D}\\ =\mathrm{\mathbb{P}}\left({\tilde{M}}_t=n|C_t=n^{\left(c\right)}\right){\gamma }_{n^{\left(c\right)}}^{-D}\\ =\mathrm{\mathbb{P}}\left({\tilde{M}}_t=n\right)\\ ={\tilde{\lambda }}_n^{-D},\end{array}$$

where the second equality follows by reversibility of ${\Gamma }^{-D},$ which implies $\mathrm{\mathbb{P}}\left(C_{\le t}|C_t\right)=\mathrm{\mathbb{P}}\left(C_{\le t}^{\text{*}}|C_t^{\text{*}}\right),$ and thus $\mathrm{\mathbb{P}}\left({\tilde{M}}_{\le t}|C_t\right)=\mathrm{\mathbb{P}}\left({\tilde{M}}_{\le t}^{\text{*}}|C_t^{\text{*}}\right).$

Proof of Theorem 2

We first check that $\mathrm{\mathbb{P}}\left(n_{s_1}|n_{s_2},n_{s_3}\right)=\mathrm{\mathbb{P}}\left(n_{s_1}|n_{s_2}\right),$ for $-\mathrm{\infty }<s_1<s_2<s_3\le 0,$ and so $n_t$ is a backward-in-time Markov chain.

Recall that we generate $n_t^{\left(abc\right)}$ as a backward-in-time Markov chain and then generate $n_t$ by dropping down mutations forward in time. The conditional independence structure of $n_{s_1},n_{s_2},n_{s_3}$ is thus described by the directed graphical model (Koller and Friedman 2009) in Figure A2.

Doing moralization and variable elimination (Koller and Friedman 2009) on Figure A2 results in the undirected graphical model in Figure A3. The graphical model of Figure A3 then implies

$$\begin{array}{c}\mathrm{\mathbb{P}}\left(n_{s_1}|n_{s_2},n_{s_3}\right)={\displaystyle \sum _{n_{s_2}^{\left(abc\right)}}\mathrm{\mathbb{P}}\left(n_{s_1}|n_{s_2},n_{s_2}^{\left(abc\right)}\right)\mathrm{\mathbb{P}}\left(n_{s_2}^{\left(abc\right)}|n_{s_2},n_{s_3}\right)}\\ =\mathrm{\mathbb{P}}\left(n_{s_1}|n_{s_2}\right),\end{array}$$

where the second equality follows because $n_{s_2}^{\left(abc\right)}$ is a deterministic function of $n_{s_2}.$ Thus, $n_t$ is a backward-in-time Markov chain.

We next compute the backward-in-time rates $q_{n,m}^{\left(t\right)}$ for the Markov chain $n_t$ at time t. Starting from the definition of $q_{n,m}^{\left(t\right)},$

$$\begin{array}{c}{q}_{n,m}^{\left(t\right)}=\frac{d}{ds}\mathrm{\mathbb{P}}{\left(n_{t-s}=m|n_t=n\right)|}_{s=0}\\ =\frac{d}{ds}{\frac{\mathrm{\mathbb{P}}\left(n_{t-s}=m,n_t=n|n_t^{\left(abc\right)}=n^{\left(abc\right)}\right)}{\mathrm{\mathbb{P}}\left(n_t=n|n_t^{\left(abc\right)}=n^{\left(abc\right)}\right)}|}_{s=0}\\ =\frac{1}{{\mathrm{\mathbb{P}}}_t\left(n\right)}\frac{d}{ds}{\left[\mathrm{\mathbb{P}}\left(n_{t-s}^{\left(abc\right)}=m^{\left(abc\right)}|n_t^{\left(abc\right)}=n^{\left(abc\right)}\right)\mathrm{\mathbb{P}}\left(n_t=n|n_t^{\left(abc\right)}=n^{\left(abc\right)},n_{t-s}=m\right){\mathrm{\mathbb{P}}}_{t-s}\left(m\right)\right]|}_{s=0}\\ =\frac{1}{{\mathrm{\mathbb{P}}}_t\left(n\right)}[\mathrm{\mathbb{P}}\left(n_t^{\left(abc\right)}=m^{\left(abc\right)}|n_t^{\left(abc\right)}=n^{\left(abc\right)}\right)\mathrm{\mathbb{P}}\left(n_t=n|n_t^{\left(abc\right)}=n^{\left(abc\right)},n_t=m\right)\frac{d}{ds}{\mathrm{\mathbb{P}}}_{t-s}{\left(m\right)|}_{s=0}\\ \hspace{1em}\hspace{1em}\hspace{1em}+{\phi }_{n,m}^{\left(t\right)}{\mathrm{\mathbb{P}}}_t\left(m\right)]\\ =\{\begin{array}{ll}{\phi }_{n,m}^{\left(t\right)}\frac{{\mathrm{\mathbb{P}}}_t\left(m\right)}{{\mathrm{\mathbb{P}}}_t\left(n\right)},\hfill & \text{if }m\ne n,\hfill \\ {\phi }_{n,n}^{\left(t\right)}-\frac{d}{dt}\log {\mathrm{\mathbb{P}}}_t\left(n\right),\hfill & \text{if }m=n,\hfill \end{array}\end{array}$$

where the penultimate equality follows from the product rule and the definition of ${\mathbf{\phi }}^{\left(t\right)}$ in (5).

The specific entries of ${\mathbf{\phi }}^{\left(t\right)}$ listed in Table 3 can be obtained by applying the product rule to (5) and noting that $\left(d/ds\right)\mathrm{\mathbb{P}}{\left(n_{t-s}^{\left(abc\right)}|n_t^{\left(abc\right)}\right)|}_{s=0}$ and $\left(d/ds\right)\mathrm{\mathbb{P}}{\left(n_t|n_t^{\left(abc\right)},n_{t-s}\right)|}_{s=0}$ are, respectively, the backward-in-time rates of $n_t^{\left(abc\right)}$ (as listed in Table 1) and the forward-in-time rates for dropping mutations on $n_t.$

Figure A1.

Probabilistic graphical model for the processes $C_t^{\text{*}}$ and ${\tilde{M}}_t^{\text{*}},$ with $-\mathrm{\infty }<s<t\le 0.$ Random variables are represented as vertices, and the edges encode conditional independence relationships. Specifically, if all paths between $V_1$ and $V_2$ pass through W, then there is conditional independence $\mathrm{\mathbb{P}}\left(V_1,V_2|W\right)=\mathrm{\mathbb{P}}\left(V_1|W\right)\mathrm{\mathbb{P}}\left(V_2|W\right).$

Figure A2.

Probabilistic graphical model for the coalescent with recombination and mutation, with $-\mathrm{\infty }<s_1<s_2<s_3\le 0.$

Figure A3.

Undirected graphical model, after moralization and variable elimination on Figure A2. We add edges to form cliques on the left and right sides of $n_{s_2}^{\left(abc\right)},n_{s_2}$ and then eliminate all the variables except the ones pictured here.