Selection and explosive growth alter genetic architecture and hamper the detection of causal rare variants

Abstract

The role of rare alleles in complex phenotypes has been hotly debated, but most rare variant association tests (RVATs) do not account for the evolutionary forces that affect genetic architecture. Here, we use simulation and numerical algorithms to show that explosive population growth, as experienced by human populations, can dramatically increase the impact of very rare alleles on trait variance. We then assess the ability of RVATs to detect causal loci using simulations and human RNA-seq data. Surprisingly, we find that statistical performance is worst for phenotypes in which genetic variance is due mainly to rare alleles, and explosive population growth decreases power. Although many studies have attempted to identify causal rare variants, few have reported novel associations. This has sometimes been interpreted to mean that rare variants make negligible contributions to complex trait heritability. Our work shows that RVATs are not robust to realistic human evolutionary forces, so general conclusions about the impact of rare variants on complex traits may be premature.

The role that rare variants play in shaping complex traits has been hotly debated (Pritchard 2001; Reich and Lander 2001; Pritchard and Cox 2002; Schork et al. 2009). Although studies of complex phenotypes have often suggested that most genetic variance is attributable to common variants of weak effect (Yang et al. 2010; Lohmueller et al. 2013; Gaugler et al. 2014; Igartua et al. 2015), recent work has implicated rare variants as a non-negligible source of variance for traits such as height (Yang et al. 2015) and prostate cancer (Mancuso et al. 2015). With many large-scale sequencing studies underway in an effort to discover the heritable basis of complex traits, it is imperative that geneticists be able to robustly identify association signals in this deluge of noisy data (Maher et al. 2012).

Unfortunately, statistical power to detect rare causal variants with single-marker tests of association is very low. Several rare variant association tests (RVATs) have therefore been developed that pool variants to boost performance (Morgenthaler and Thilly 2007; Li and Leal 2008; Madsen and Browning 2009; Hoffmann et al. 2010; Morris and Zeggini 2010; Neale et al. 2011; Wu et al. 2011; Lee et al. 2012a,b). However, few of these studies explicitly modeled the evolutionary forces that shape patterns of genetic variation when assessing statistical performance (King et al. 2010; Price et al. 2010; Thornton et al. 2013; Zuk et al. 2014; Uricchio et al. 2015). Natural selection is particularly relevant to rare variant associations, because rare variants can only explain a large portion of population variance if they have much larger effect sizes than common variants, which is most easily explained by the action of purifying selection (Eyre-Walker 2010).

Indeed, it is now well appreciated that natural selection (Eyre-Walker et al. 2006; Boyko et al. 2008; Lohmueller et al. 2011) and demographic forces (Auton et al. 2009; Gravel et al. 2011; Bhaskar et al. 2015) strongly impact patterns of human genetic variation genome-wide. It has also been shown that genetic architecture (Gazave et al. 2013; Simons et al. 2014), the performance of single-marker tests of association (Lohmueller 2014a,b), and selection scans (Teshima et al. 2006) are also sensitive to nonequilibrium evolutionary forces. However, these studies have focused on stepwise population growth (rather than state-of-the-art models of explosive growth) (Lohmueller 2014a,b), investigated simplified selection models (rather than models inferred from human polymorphism data) (Simons et al. 2014), or have only indirectly considered the impact on complex traits (Gazave et al. 2013). Some debate over the parameterization of complex trait models has resulted in a range of conclusions about the impact of evolutionary events on trait variance and the relative importance of rare alleles to complex traits (Lohmueller 2014b; Simons et al. 2014); and although recent work has argued that demographic events have had little effect on deleterious load in humans (Simons et al. 2014; Do et al. 2015), it is less clear how demography affects the genetic variance of traits under selection. Although deleterious load is of population-genetic interest, genetic architecture is more relevant to association studies, because power is dependent on the joint distribution of effect sizes and allele frequencies and not only the mean burden of deleterious alleles.

Here, we propose a novel model of complex traits that unifies previously studied models (Eyre-Walker 2010; Lohmueller 2014b; Simons et al. 2014) into a single framework. We use simulation and numerical algorithms to investigate a wide variety of human demographic and selection parameters for European and African populations and study the role of rare variants in complex phenotypes. We then use simulations and human RNA-seq data to ask whether the changes in genetic architecture driven by human selection and demography have implications for the statistical discovery of causal rare variants and consider the ramifications of our findings for studies of genetic architecture in human populations.

Results

An evolutionary model of complex phenotypes

We develop a phenotype model that explicitly captures the relationship between selection strength and effect size by unifying the models proposed in Eyre-Walker (2010) and Simons et al. (2014) (Methods). The parameters of our model capture both pleiotropy (through ρ) and the functional relationship between selection and effect size (through τ and δ). Variant alleles with fitness consequence s will have effect size z_s as follows:

$$z_s=\{\begin{array}{ll}\delta |s{|}^{\tau }& \text{with probability}\rho \\ \delta |s_r{|}^{\tau }& \text{otherwise}\end{array}$$ (1)

The δ and τ parameters were proposed by Eyre-Walker (2010) and allow the marginal distribution of effects to differ from the marginal distribution of selection coefficients. The ρ parameter is a generalization of the p parameter proposed by Simons et al. (2014) and allows for the introduction of pleiotropy without altering the overall marginal distribution of effects. With probability ρ, the effect size z_s of a site with selection coefficient s is chosen to be δ|s|^τ. Otherwise, z_s is determined by a random sample (s_r) from the marginal distribution of selection coefficients. δ is −1 or 1 with equal probability, allowing for trait-increasing and decreasing alleles.

From an evolutionary perspective, this model captures the idea that phenotypes under direct selection will have a tight correlation between selection strength and the absolute value of effect size (i.e., high ρ and high modularity of the causal genetic variation), but the marginal distribution of effects may grow faster or slower than the distribution of selection coefficients (i.e., τ can be a value greater than or less than 1). Due to pleiotropic effects, some sites may have large selection coefficients but small effects on the phenotype (i.e., decreasing ρ allows increased emphasis on pleiotropy). Both trait-increasing and trait-decreasing alleles are equally deleterious and equally probable, as might be expected for traits under stabilizing selection. A pictorial representation of the model is given in Supplemental Figure S1 (for further details, see Methods).

Selection and demography impact the genetic architecture of complex traits

Recent studies of deleterious alleles and complex demography have often focused primarily on genetic load rather than genetic architecture. In order to gain intuition about how the parameters of our model and evolutionary events impact time-dependent genetic architecture, we first studied our phenotype model under simplified conditions. We let τ = 1 and specify two categories of selected sites: one strong (s = −10⁻², 2Ns = −146) and one weak (s = −2 × 10⁻⁴, 2Ns = −2.92). Because this model has two selection coefficients, it will also have only two effect sizes, as mediated by the parameter ρ. It has been shown that deleterious allele load is not sensitive to demography under this model (Simons et al. 2014), but our interest is in understanding the implications for trait architecture.

We start by calculating the site frequency spectrum (SFS) as a function of time using a rescaling-based numerical solver (for a brief discussion of rescaling, see Hoggart et al. 2007) and stochastic simulations (Hernandez 2008). In a model of European demographic history (Methods; Gravel et al. 2011), our numerical calculations predict that the proportion of variable sites that are singletons (denoted ψ) is strongly impacted by demographic events (Fig. 1A, solid lines), and that the nonequilibrium predictions made under the model are in agreement with results from stochastic forward simulations (Fig. 1A, points). As expected, expansion events increase ψ, whereas contractions decrease ψ.

Figure 1.

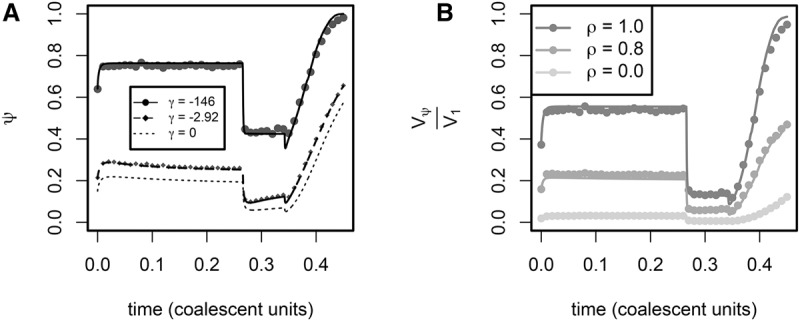
Time-dependence of singleton variants under a European growth model (Gravel et al. 2011). (A) The proportion of variable sites that are singletons (ψ). (B) The proportion of the genetic variance in a complex trait that is due to singletons. A sample of n = 500 chromosomes was used for each panel. The solid, dashed, and dotted lines show the results of our numerical algorithm, whereas the points are the results of stochastic forward simulations. Each point represents the mean across 100 simulations. The demographic model consists of an expansion event at time 0, successive bottlenecks at times 0.27 and 0.34, and sustained exponential growth after the last bottleneck (see Methods, “Calculating the impact of demographic events on genetic architecture” for complete model details).

In Figure 1B, we plot the proportion of the trait's genetic variance that is explained by singletons, V_ψ/V₁, which is a measure of the genetic architecture of the trait (V₁ is the variance explained by all alleles under frequency 1, and hence represents the total genetic variance in the trait). We find that V_ψ/V₁ is strongly impacted by demographic events and the relationship between selection and effect sizes. Expansions increase the role of rare variants in the trait, whereas contractions have the opposite effect. Sustained exponential growth results in a drastic increase in the role of rare alleles. Note that this time-dependent behavior for exponential expansion is qualitatively different from the stepwise ancestral expansion event at time 0, which results in an abrupt increase in the proportion of trait variance explained by rare alleles and a fast relaxation to a new equilibrium. Importantly, when ρ = 1 and causal loci are completely modular, sustained exponential growth increases the proportion of variance explained by rare alleles from ≈10% to nearly 100%, but this proportion rapidly drops off as ρ decreases.

We extended this analysis by simulating genotypes and phenotypes under a wide range of human-relevant parametric models (Methods). Briefly, we simulated a demographic model of Europeans and Africans (Gravel et al. 2011) while varying the rate of exponential growth and the distribution of selection coefficients. We focus on two categories of selection: one strong (E[2Ns] ≈ −450) based on estimates from coding regions in Boyko et al. (2008) (Fig. 2A,B); and one weak (E[2NS] ≈ −8) based on conserved noncoding regions in Torgerson et al. (2009) (Fig. 2C,D), which represent plausible extremes for the strength of selection acting on human genomic elements. Given the mean strength of selection, we then shift the variance of the distribution of selection coefficients (σ) across a broad range.

Figure 2.

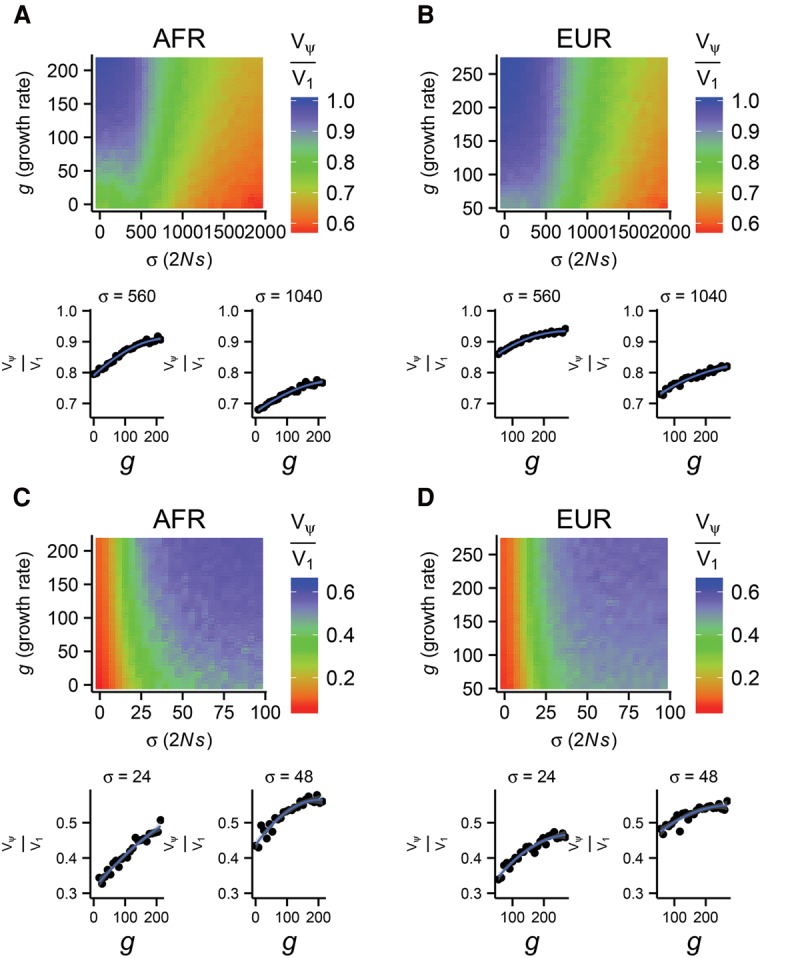
The fraction of the genetic variance that is contributed by singletons, V_ψ/V₁, in a sample of n = 10³ chromosomes as a function of growth rate (g) and standard deviation in selection strength (σ) in models of both African (A,C) and European (B,D) demographic history. The mean selection strength was fixed at 2Ns = −450 (A,B) and 2Ns = −8 (C,D), with ρ = 0.99 and τ = 1.0. The smaller panels plot two cross sections of each heat map to show changes in V_ψ/V₁.

In Figure 2, we show that for all models and populations considered, increasing the growth rate increases the proportion of the genetic variance that is driven by singletons, V_ψ/V₁. This suggests that a population's demographic history is a major determinant of the genetic architecture of complex traits.

Architecture of complex traits in human populations

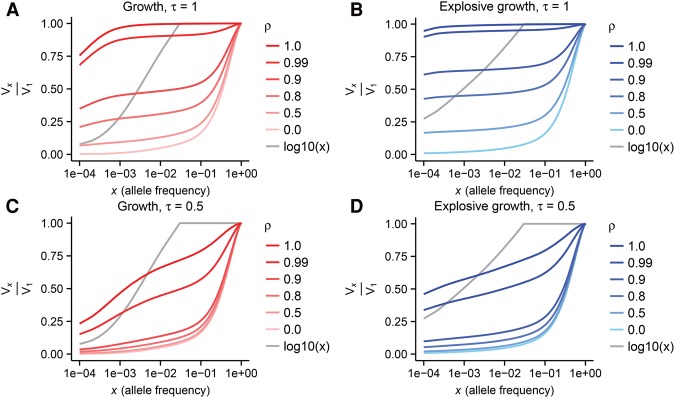
Because the rate of growth and the distribution of selection coefficients can have major impacts on the genetic architecture of complex traits, we focus in on parameters inferred from human data. In particular, the distribution of selection coefficients will follow the parameters estimated from nonsynonymous sites (Boyko et al. 2008) and two models of human history: the “growth” model of Gravel et al. (2011) and the “explosive growth” model of Tennessen et al. (2012). In Figure 3, we plot V_x/V₁, the cumulative proportion of the genetic variance due to variants under allele frequency x as a function of x for several values of ρ and τ in a sample of 5 × 10³ individuals. We find that a substantial proportion of the genetic variance is attributable to rare variants only when the selection strength is very tightly correlated with the absolute value of effect size (i.e., ρ ≈ 1). This generalizes the results of Simons et al. (2014) to a distribution of selection coefficients relevant to human coding variation. When ρ ≈ 1, rare alleles have much larger effect sizes than common alleles because the most deleterious alleles have very low frequencies. Explosive growth further increases the role of rare alleles for large ρ, because the increased population size results in an increased influx of new deleterious alleles. In addition, deleterious alleles that segregated at higher frequency before the growth event adjust their frequencies downward because of the effective increase in population scaled selection coefficient.

Figure 3.

The cumulative proportion of the genetic variance, V_x/V₁, explained by variants under allele frequency x for the European “growth” (A,C) and “explosive growth” (B,D) models of human history under two different values of τ for a sample of n = 10⁴ chromosomes.

Interestingly, among rare variants, the preponderance of variance is determined by singleton variants and not variants at more intermediate frequencies in the sample (Fig. 3; Supplemental Fig. S2). This result holds across all values of ρ when τ = 1 for both demographic models, but is more extreme in the explosive growth model. A different picture emerges when we plot V_x/V₁ using the log₁₀(x) effect size model of Wu et al. (2011) (originally used to evaluate the power of SKAT). Under this model, much more of the variance is attributable to variants at intermediate rare frequencies. We are not able to recapitulate the shape of V_x/V₁ we see with the Wu et al. model using our evolutionary approach, but we do see rare variants playing less of a role in genetic architecture when τ decreases to 0.5 (Fig. 3C,D). Nonetheless, for all values of τ investigated, as well as the log₁₀(x) model, explosive growth results in a larger fraction of variance being explained by singletons than under the growth model.

The power of conventional RVATs decreases when variance explained by rare variants increases

We investigated the power of rare variant association methods as a function of the proportion of variance explained by rare variants by altering the parameters ρ and τ in our simulations of complex phenotypes (Fig. 4; Supplemental Fig. S3). We examined multiple RVATs and found that power for each test is highly dependent on the phenotype model (Supplemental Fig. S4). We found that the SKAT framework was consistently among the most powerful, and hence focus our analysis on SKAT-O (Methods).

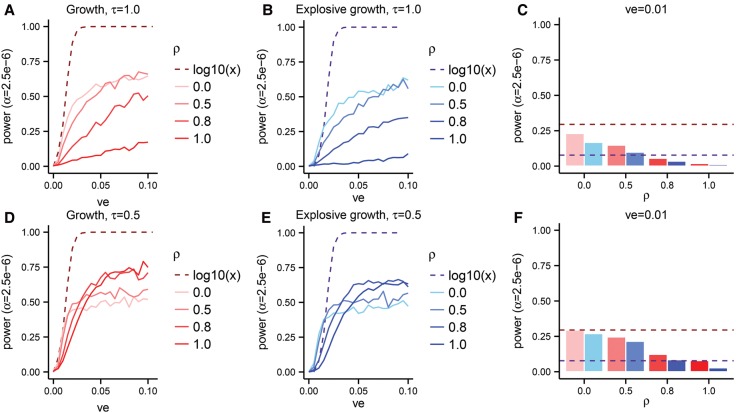
Figure 4.

The power of SKAT-O in Europeans as a function of the variance explained (ve) by a gene on a phenotype in a sample of size n = 10⁴ chromosomes under various effect size models. The explosive growth model (B,E) of Tennessen et al. (2012) is shown in shades of blue, and the growth model (A,D) of Gravel et al. (2011) is shown in shades of red. The dashed lines show the power when the effect sizes are taken to be proportional to log₁₀(x) for alleles at frequency x, whereas the solid lines (A,B,D,E) and bars (C,F) show results from our phenotype model. Panel C aggregates data from A and B for ve = 0.01, while panel F aggregates data from D and E for ve = 0.01.

We find that power is substantially lower when effects are drawn from our model as opposed to effects given by the Wu et al. (2011) model of log₁₀(x). This result holds for all model parameters and both demographic models that we considered. We also find that power is always substantially higher under the growth model than the explosive growth model. Under the explosive growth model, a larger proportion of the genetic variance is due to very rare variants (as opposed to more intermediate frequency rare variants).

Since RVATs are tuned to detect contributions from rare variants, we might expect power to increase as ρ increases, and rare variants drive a larger fraction of the variance in the trait. Surprisingly, we find the opposite. In Figure 4 and Supplemental Figures S3 and S4, we show that power decreases as ρ increases. This effect is most dramatic under the explosive growth model (blue lines/bars) and when τ = 1.0. When τ decreases to 0.5 (Fig. 4D–F), intermediate frequency rare variants play a larger role and the reduction in power is less pronounced.

We replicate the same general trends under an African demographic model (Supplemental Fig. S3), but power is higher than under the European demographic model (up to 50% under some conditions) (Supplemental Fig. S5). This may reflect both increased trait variance per gene and differences in genetic architecture due to demography, and suggests that the overemphasis on European populations in sequencing studies (Rosenberg et al. 2010; Bustamante et al. 2011) may slow the discovery of causal loci.

Shifting weight onto rare alleles boosts power but also false positive rates

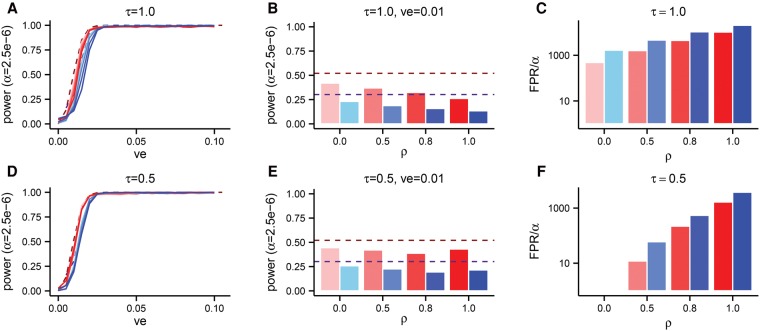
SKAT-O provides users with a flexible weight distribution over allele frequencies. The default distribution is a β-distribution with shape parameters 1 and 25, which gradually puts more weight on rarer alleles. Because populations that have undergone rapid population growth have increased trait variance contributed by very rare variants, the test may perform better when weight is further shifted toward rare alleles. We re-ran SKAT-O with the rare-shifted weight distribution recommended in Wu et al. (2011) when only very rare variants play a role in the phenotype (β[0.5, 0.5]). The rare-shifted weights resulted in substantial increases in power (Fig. 5; Supplemental Fig. S6), although power was often lower under our evolutionary model than under the log₁₀(x) model (Fig. 5A,D, dashed lines). We found that power was still sensitive to demography (Fig. 5B,E; Supplemental Fig. S6B,E), with the explosive growth model exhibiting lower power than the growth model.

Figure 5.

The power and false positive rate (FPR) of SKAT-O in Europeans with the weights of SKAT-O adjusted to β[0.5, 0.5], in a sample size of n = 10⁴ chromosomes. The explosive growth model of Tennessen et al. (2012) is shown in shades of blue, and the growth model of Gravel et al. (2011) is shown in shades of red. The dashed lines show the power when the effect sizes are taken to be proportional to log₁₀(x) for alleles at frequency x, whereas the solid lines (A,D) and bars (B,E) show results from our phenotype model. Each solid line in A and D corresponds to a different value of ρ, using the same color scheme as in the other panels. (B,E) Aggregate data from A and D, but specifically for variance explained (ve) equal to 0.01. In C and F, we plot the FPR divided by 2.5 × 10⁻⁶ (α), which represents the fold increase in FPR.

Unfortunately, this increase in power is costly. We permuted the phenotypes for the same simulations and ran SKAT-O on the permuted data set to obtain an empirical P-value distribution. We observe a much larger than expected fraction of P-values under 2.5 × 10⁻⁶ (Fig. 5C,F), and the rate is generally much higher under the explosive growth model and when the coupling between selection strength and effect size is highest (i.e., ρ is large). Assuming a trait has 20 causal genes and that the test is applied to all ∼2 × 10⁴ genes in the genome, even if power is at the optimistically high level of 50%, false discovery rates would exceed 90% for large values of ρ in populations with explosive recent growth.

Spurious positive results in human RNA-seq data

We found that shifting weights in SKAT-O toward rare variants increases the false-positive rate, thereby constraining our ability to perform genome-wide tests. However, hypothesis-driven studies that use fewer tests by focusing on a subset of putatively causal loci may benefit from the test's increased power while only modestly increasing the false discovery rate. We hypothesized that rare exonic variants of large effect in transcription factors under selection may impact the expression of downstream target genes. We tested this hypothesis for the transcription factor STAT1, which was inferred by Arbiza et al. (2013) to be among the transcription factors with the largest fraction of base pairs under selection in the human genome. We obtained a list of putative target genes for STAT1 (Bhinge et al. 2007) and cross-referenced it for genes that are expressed in the GEUVADIS project RNA-seq data set (Lappalainen et al. 2013), for a total of 211 target genes.

We ran a test of association between variation in STAT1 exons and expression level for each of these downstream genes using SKAT-O. Unadjusted P-values from SKAT-O suggest that expression patterns for at least one of these genes is partially driven by rare variants in STAT1, and shifting weight onto rare variants increases the number of significant positive tests from 1 to 2 (Fig. 6). Furthermore, eight genes had P-values under 10⁻², although only two are expected for this sample size under the null. However, when we permuted the phenotype residuals of the samples and re-ran the test, we discovered that these signals are all likely to be false positives and the test is anti-conservative for these phenotypes. Note, we do not mean to suggest that we can exclude a role for rare coding alleles in STAT1 on expression patterns for any of these 200 genes, as our sample size is quite small and we have already argued that our power should be modest in many scenarios. However, our results demonstrate that we have much less power to reject the null than the SKAT-O P-value distribution would suggest.

Figure 6.

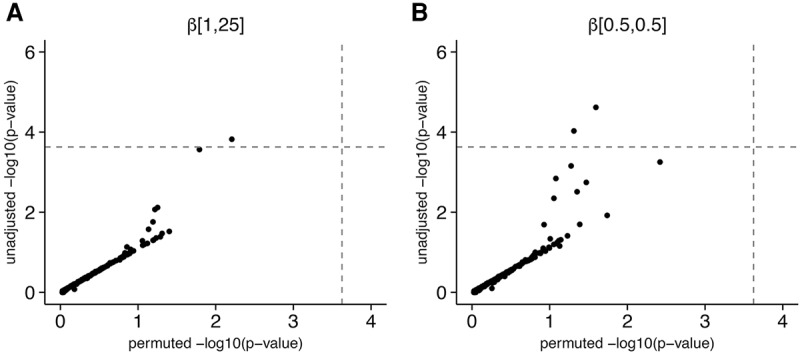
Scatter plots of unadjusted SKAT-O P-values against permutation-based P-values for tests of association between coding variation in STAT1 and RNA expression levels of STAT1 target genes. Each point represents a single target gene. (A) P-values for the default parameterization of SKAT-O. (B) P-values for the test with more weight shifted onto rare variants.

Discussion

A great deal of research interest has focused on the problem of “missing heritability,” which refers to the discrepancy between variance explained by genome-wide significant associated variants and estimates of the narrow-sense heritability of common, genetically complex phenotypes. Although there are many possible explanations for this discrepancy, one of the most popular is that rare variants may make up the difference. This hypothesis has been used as motivation for a number of sequencing studies of large cohorts. As sequencing technology has progressed to the point at which very rare (and potentially novel) variants are routinely detected in large samples, there has been a corresponding push to develop statistical tools to detect causal rare variants.

Large genotype and DNA sequence data sets have also provided insights into human demography (Schaffner et al. 2005; Gutenkunst et al. 2009; Gravel et al. 2011; Keinan and Clark 2012; Nelson et al. 2012; Tennessen et al. 2012; Bhaskar et al. 2015) and selection on human functional elements (Keightley and Eyre-Walker 2007; Boyko et al. 2008; Torgerson et al. 2009). These studies have generally agreed that patterns of human polymorphism provide strong evidence for the recent expansion of human populations and the action of selection on functional sites. Moreover, the joint distribution of effect sizes and allele frequencies for traits under selection is likely to be strongly impacted by these evolutionary forces (Lohmueller 2014b; Simons et al. 2014), and rare alleles can only contribute substantially to complex trait variance when selection acts on causal variation (Pritchard 2001), both of which suggest that human evolutionary models should guide efforts to design and test RVATs.

Although it is clear that RVATs can be very powerful for detecting associations under some phenotype models, it is not clear whether previously investigated phenotype models are biologically or evolutionarily plausible. Most studies of RVATs have applied phenotype models that map allele frequencies to effect sizes via simple functions, such as the log₁₀(x) (where x is allele frequency) function in Wu et al. (2011), without directly modeling the action of selection or taking advantage of recent estimates of the strength of selection on human functional elements. We developed a flexible, selection-based phenotype model that captures pleiotropy/modularity (through ρ) and fitness functions of varying shape (through τ). We then applied our phenotype model in concert with human evolutionary models to demonstrate that a wide range of possible joint distributions of effect size and allele frequency exist that are not consistent with the log₁₀(x) model. Importantly, when the genetic variation for the trait of interest is largely modular (i.e., ρ ≈ 1) and the effect on fitness is directly proportional to the effect size magnitude (τ = 1), we found that a very large proportion of the variance in the trait is contributed by very rare (e.g., singleton) alleles. When the causal genetic variation for the trait is somewhat pleiotropic (ρ < 0.9), the genetic variance explained by rare alleles drops off very quickly. This is in sharp contrast to the log₁₀(x) model, in which most phenotypic variance is contributed by intermediate-frequency rare alleles.

We also considered the impact of varying τ on genetic architecture. When τ = 0.5 and very deleterious alleles have smaller effect sizes relative to weakly deleterious alleles (as compared to τ = 1), we observe that less trait variance is driven by very rare alleles relative to intermediate frequency rare alleles. However, when τ = 0.5, we also observe a very sharp drop in variance explained by rare alleles as a function of increasing pleiotropy (i.e., variance explained by rare alleles is only appreciable when ρ ≈ 0.99 or higher, and the causal variation is almost entirely modular). Demography also has a profound impact on genetic architecture. We compared a “growth” model (Gravel et al. 2011) to an “explosive” growth model (Tennessen et al. 2012). Although explosive growth only slightly alters the total contribution of alleles under 1% in frequency to the trait, it greatly increases the proportion of trait variance that is explained by singleton alleles, potentially altering the performance of statistical tests that pool putatively causal rare variants.

Our results have surprising consequences for association tests. We found that RVAT power decreases as a function of increasing ρ values, meaning that statistical performance is worst when rare alleles make the largest contributions to trait variance. This is unexpected because RVATs are tuned to test for the contribution of rare alleles to trait variance, so one might expect (and hope) that RVATs will perform best when the rare allele signal (i.e., percent variance explained) is largest. Although surprising, our results can be understood by jointly considering the impact of evolutionary parameters on genetic architecture. When ρ is large and rare allele contributions are provided primarily by extremely rare alleles (e.g., singleton alleles), there is less information in the data about the relationship between phenotype and genotype than when intermediate-frequency rare alleles drive the signal. When populations grow rapidly, we found that the genetic variance explained by extremely rare alleles increases, and we observe a corresponding decrease in RVAT power.

We note that our results contrast those of Moutsianas et al. (2015), who used the Eyre-Walker (2010) model and found higher power for RVATs when rare alleles explain a large fraction of trait variance. However, we also note that their study predominantly focused on a model of binary traits that have unidirectional effects, whereas we have focused on a model of quantitative traits under stabilizing selection with bidirectional effects. In our view, it is not yet clear which of these models is most relevant for complex traits. One view is that risk-increasing alleles should be under stronger selection than protective alleles, and hence, effect sizes for disease-risk should be pointed in the same direction. An opposing view is that disease etiology is the result of processes playing out on the molecular scale, and hence, it is possible that both up or down dysregulation of molecular products could result in increased disease risk. In this scenario, two alleles might both raise disease risk on average but have opposing effects on the molecular product, and hence, their aggregate impact on disease risk would be masked in individuals carrying both alleles, even under additive trait models.

Although it is too early to assert that our model will be a good fit to human complex trait data, it is clear that any phenotype model that will be consistent with evolutionary theory and propose a non-negligible role for rare alleles must directly incorporate the impact of evolutionary forces such as demography and selection. Our model is very flexible and can accommodate any standard population genetic model of selection, demography, recombination, or mutation while using only two additional parameters to generate phenotypes and accommodates pleiotropy and fitness functions of variable shape. In general, generative evolutionary models such as ours should be preferred over arbitrary mapping functions in the assessment of association tests, because evolutionary models provide a mechanism for the increased role of rare variants in complex traits. Simple functions that map allele frequencies to effect sizes do not have this feature, and therefore may be inconsistent with evolutionary theory and mechanistic models of genetic architecture and make overly strong assumptions about the relationship between effect sizes and allele frequencies.

Still, it is important to consider the plausibility of our model in light of current knowledge of complex trait architecture. First, we note that many common alleles with detectable (albeit small) effects on trait variance have been discovered. However, except in a few cases, such variants explain a very small fraction of phenotypic variance. The extensive missing heritability that has not been explained by weak-effect common variants could potentially be explained by rare variants with ρ and τ near one. Further, a wide range of other parameterizations exist that are consistent with a non-negligible role for both rare and common alleles. If, for example, 0.9 < ρ < 1 and τ ≈ 0.5 for some phenotypes of interest, then common trait-associated alleles that have been discovered so far are likely to represent instances of highly pleiotropic sites, where the overall strength of selection is relaxed due to the compensatory effects of these sites on multiple phenotypes. Sites with increased phenotypic modularity are more likely to have large effects and be at low frequency, increasing the difficulty of detecting them. Moreover, recent work suggests some role for selection in shaping complex traits. Park et al. (2011) found a modest correlation between allele frequency and effect size for common, trait-associated variants, consistent with selection acting on trait-altering variation. Maher et al. (2012) found that trait-associated alleles are in regions of stronger selection than average sites in the genome, and in a model-based analysis of the role selection in shaping trait-altering variation for prostate cancer, Mancuso et al. (2015) estimated that τ = 0.42 under the model of Eyre-Walker (2010). More work is required to estimate the amount of pleiotropic selection on trait-altering variation before we can assert that rare alleles may play a substantial role in shaping trait variation for many important human phenotypes.

Genome-wide rare variant association studies (RVAS) have often been used in an attempt to bound the variance explained by rare alleles for complex traits (Lohmueller et al. 2013; Holmen et al. 2014; Igartua et al. 2015). In this study design, researchers scan the genome (or exome) for rare causal alleles with one or more RVATs and report that rare alleles are unlikely to be a driver of variance in the trait if no signal (or very few signals) are found. Although such study designs are sound if RVAT power is robust to the uncertainty in evolutionary parameters, we have shown that power is highly dependent on both evolutionary parameters and pleiotropy. Because we do not know these parameters with certainty for any phenotypes, it may be too early to exclude a role for rare variants in complex traits on the basis of genome-wide RVAS.

Given that natural selection and demography both alter genetic architecture, simple modifications to existing tests might boost their performance. In the case of SKAT-O, the obvious first step is to modify the β-distribution that serves as a prior over the effect sizes at each allele frequency. We demonstrated that shifting weight onto rarer alleles does increase power in our selection-based phenotype model, but also results in a highly elevated false-positive rate. In principle, the best weight distribution to use would correspond exactly to the joint distribution of effect sizes and allele frequencies that is generated by the evolutionary forces acting on the causal variation. However, because we do not know these evolutionary parameters exactly for any phenotypes, more work must be done to infer trait architecture as in Mancuso et al. (2015) before this approach can become a reality.

Model-based studies of the joint effects of selection and demography on genetic and phenotypic diversity have already provided some important insights into the impact of evolutionary forces on human variation (Gazave et al. 2013; Thornton et al. 2013; Lohmueller 2014b; Simons et al. 2014; Balick et al. 2015; Do et al. 2015; Zivković et al. 2015). Our results show that this literature must be taken into account when assessing association tests, because studies of selection and demography have strong implications for the joint distribution of allele frequencies and effect sizes of human traits under selection. Moreover, current association methods are underpowered to test for the contribution of rare variants to complex traits under a wide range of evolutionary model parameters. Fortunately, population-genetic models such as ours make strong predictions about observables, including the relationship between allele frequency and effect size and the distribution of phenotypes. In future studies, it will be advantageous to exploit these signals to compare various models of heritability and put firmer bounds on the proportion of the genetic variance that is determined by rare variants.

Methods

Model

Here, we will describe the models Eyre-Walker (2010) and Simons et al. (2014), motivate the modifications we have made, and discuss the ramifications of our model for RVATs.

The model of Eyre-Walker (2010) computes effect sizes as z = δ|s|^τ(1 + ε). δ is −1 or 1 with equal probability, thereby allowing for both trait-increasing and trait-decreasing mutations. τ is an exponent that transforms the distribution of selection coefficients to allow flexibility with respect to the distribution of phenotypic effects. The central idea is that effect sizes may not have the same marginal distribution as selection coefficients, but sites with larger effects on fitness will also have larger effects on the phenotype. As τ decreases, common alleles play a larger role in the phenotype because the effect sizes of weakly deleterious alleles increase relative to strongly deleterious alleles. ε is a random normal variable with mean zero and variance σ² that we do not include because it has no impact on genetic architecture (Eyre-Walker 2010).

In our study, we are concerned with how the joint distribution of effect sizes and allele frequencies impacts statistical power for discovering causal loci. It is plausible that power will depend on both the marginal distribution of effects and the relationship between effects and allele frequencies, so it is desirable to have a mechanism to hold the marginal distribution of effects constant in order to focus on the relationship between allele frequency and effects. In Simons et al. (2014), the authors proposed a model with two selection coefficients, one strong and one weak, that has this property. With probability ρ, a mutation has effect size proportional to its selection coefficient, and with probability 1 − ρ, it has an effect size randomly sampled from the marginal distribution of selection coefficients (and then scaled by a proportionality constant). Here, we extend this model by (1) including arbitrary distributions of selection coefficients, such as a Γ-distribution of selection coefficients that was inferred for human coding regions (Boyko et al. 2008); and (2) including both the τ and δ parameters from the model of Eyre-Walker (2010).

Thus, our model for effect sizes z_s for a site with selection coefficient s can be summarized with equation 1 (main text). When ρ = 1, we obtain exactly the model of Eyre-Walker (2010). When τ = 1, we obtain the model of Simons et al. (2014), but with arbitrary distributions of selection coefficients and the additional possibility for causal sites to be either trait increasing or decreasing.

As in the original Eyre-Walker (2010) model, we have assumed that trait-increasing and trait-decreasing alleles are equally likely to occur and are equally deleterious. Note that this assumption has no impact on the results pertaining to genetic architecture, because the architecture depends only on the mean squared effect sizes as a function of frequency. Moreover, this is a natural assumption in the case of a phenotype under stabilizing selection. Both trait-increasing and trait-decreasing alleles are more likely to decrease the fitness of an individual than increase fitness under mild assumptions about the shape of the trait distribution (namely, that it is roughly centered at its optimum value, and the phenotype values are roughly symmetric around the optimum).

Three-population forward simulations of human selection and demography

We used sfs_coder to perform forward simulations of human selection and demography (Uricchio et al. 2015). sfs_coder is a Python-based front-end to the forward simulation software SFS_CODE (Hernandez 2008) that includes several models of human demography and selection. The demographic models we simulated are those of Gravel et al. (2011) and Tennessen et al. (2012). Briefly, Gravel et al. (2011) includes three populations, namely the African, European, and Asian continental groups. The European and Asian populations are formed by a series of bottlenecks as the human population moved out of Africa, and the model also includes recent exponential growth in the European and Asian continental groups. Migration between all pairs of populations is also included in the model. The model of Tennessen et al. (2012) includes all of the above features, but also adds a second (more recent) phase of explosive exponential growth in the European continental group and includes recent exponential growth in the African continental group. Note that Tennessen et al. (2012) only inferred parameters of recent growth for Africans and Europeans, but we also simulate the Asian continental group as was inferred in Gravel et al. (2011) and as previously described in Uricchio et al. (2015). We refer to the model of Gravel et al. (2011) as the “growth” model, and the model of Tennessen et al. (2012) as “explosive growth.” We chose these two models because they both represent plausible demographic histories of human continental groups inferred from human sequence data and have identical parameters up until the very recent past, but propose dramatically different rates of recent expansion in Europeans and Africans, and hence, generate different patterns of variation in samples. In particular, the explosive growth of the model of Tennessen et al. (2012) results in a SFS that is skewed further toward rare variants in very large samples.

We used recently inferred selection models (Boyko et al. 2008; Torgerson et al. 2009), both of which are Γ-distributions of selection coefficients. For simulated coding regions, only nonsynonymous sites are under selection.

For the simulations that we used to calculate genetic architecture in Figure 2, we did not include migration, such that we could focus more directly on the role of exponential growth. To examine the effect of the growth rate, we increased the growth rate from the baseline inferred rate in Gravel et al. (2011) in both Europeans and Africans at time t_super = 0.39, which was the time of super exponential growth inferred in Tennessen et al. (2012). Hence, the parameters investigated include plausible extremes that are relevant to these continental level population groups.

For simulations that we used to make power calculations, we included 20 unlinked genes. Each gene was 1.65 × 10³ base pairs long, which is the mean length of a gene in RefSeq. Although each gene is unlinked, recombination was included within each gene. Assuming a per-base recombination rate of 4Nr = 10⁻³ and that the typical gene is composed of exons and introns spanning an average of 5.115 × 10⁴ bp, we set the per-base as follows:

$${\rho }_r=4Nr=\frac{5.115\times {10}^4\times {10}^{-3}}{1.65\times {10}^3}=\mathrm{0.031.}$$

Although this does not maintain the intron/exon structure of a gene, average linkage disequilibrium across the entire gene should be maintained.

For our power calculations, we performed 5 × 10³ simulations under each demographic model and sampled 5 × 10³ individuals from the African and European populations, as noted in the text (as described above, each simulation includes 20 simulated genes). The number of simulations was chosen in order to obtain sufficiently small standard error around our power estimates such that parameter sets investigated are distinguishable. At the end of each simulation, we use the simulated patterns of diversity and distributions of selection coefficients to simulate phenotypes, as described above.

Simulations of phenotypes

We simulated phenotypes under our selection-based model of complex traits, and also the allele frequency based model of Wu et al. (2011).

For simulations under our phenotype model, we do not have an analytical expectation for the distribution of sampled selection coefficients for the complicated three-population demographic models that we simulate here. For this reason, we use the sampled variants in any given simulation to provide a distribution on s. When τ = 1, ρ is also the Pearson correlation between the selection coefficient and the absolute value of effect size, but this is not the case when τ ≠ 1. However, the interpretation that a high value of ρ corresponds to a high correlation and a low value corresponds to a weak correlation holds across all values of τ. We only take nonsynonymous sites as causal; synonymous sites always have 0 effect in our simulations.

We also simulate phenotypes under the model of Wu et al. (2011). In this model, an allele with frequency x < 0.03 has effect size z(x) ∝ log₁₀(x) with probability 0.05, and otherwise has an effect size of zero. Here, we take all nonsynonymous sites under 3% frequency to be causal, such that the total number of causal sites are roughly comparable between simulations under our model and simulations using the effect size distribution of Wu et al. (2011). Note that our loci are shorter than the loci simulated by Wu et al. (2011) because we focus on genes, but by taking all the nonsynonymous low frequency variants as causal, we have close to the same expected number of causal variants within the locus as in their study, although we have far fewer nonassociated variants. In this sense, our simulations represent a “best-case” scenario, since a very high proportion of the sites within each test locus are causal for the trait, although some sites have very small effect sizes.

The statistical power of association tests is a function of the fraction of the variance in the phenotype that is explained by the test sequence. For this reason, we always fix the total contribution of the test loci at a prespecified amount (and hence any observed differences in power cannot be explained by systematic differences in the contribution of genetics to the phenotype). We simulated a polygenic model, in which genetic variation in the trait is driven by 20 genes, and fix the total contribution of genetics to the phenotype at 50% (i.e., h² = 0.5) in Europeans. We have conditioned on the heritability of Europeans because the majority of genetic studies to date have been performed in populations of European descent (Rosenberg et al. 2010; Bustamante et al. 2011), and the events in the African demographic model are a subset of those found in the European model. Hence, the heritability in Africans is not guaranteed to be exactly 0.5, but can be either smaller or larger in any given simulation, depending on the effect sizes and allele frequencies of the causal variants in the sampled African sequences.

Calculating the impact of demographic events on genetic architecture

We investigated the impact of selection and demography on the SFS, as well as the genetic architecture of complex traits, using numerical calculations under the Wright-Fisher model and stochastic forward simulations.

For our numerical calculations, we consider a model consisting of discrete and exponential population size changes. Although our software is generalizable to other demographic models of interest, here we focused on the marginal European demographic history (Gravel et al. 2011). This model includes population size changes of magnitudes ν = [1.9827, 0.1286, 0.5545] at times t = [0, 0.2658, 0.3425] (times are in coalescent units of 2N_A generations, where N_A is the ancestral population size). These events correspond to an expansion in the African ancestral population, an out-of-Africa bottleneck, and a second bottleneck with the founding of Europe. Immediately after the last bottleneck event, the population grows exponentially at rate 55.48 (scaled in coalescent units). For further details on the model parameters, see Gravel et al. (2011) or Uricchio et al. (2015).

To calculate the SFS as a function of time after demographic events, we propagated Wright-Fisher transition matrices forward in time. The transition probability for a site present in k copies in a population of size 2N to k* in the next generation with selection coefficient s is given as

$$\mathrm{Binomial}\left(k^{\ast };2N,\frac{(1+s)x}{1+sx}\right),$$ (2)

where x = k/2N, the allele frequency of the site. Discrete changes in population size change the state space on k, and hence, the rate at which drift happens in each subsequent generation, as well as the equilibrium proportion of variable sites present at any given frequency. However, to avoid the computational cost of changing the state space on k, we instead rescale both time and population size (Hoggart et al. 2007; Uricchio and Hernandez 2014). The code we developed is implemented in Python and is provided in the Supplemental Material.

We performed these calculations for two selection coefficients, s = −10⁻² and s = −2 × 10⁻⁴, each with identical underlying mutation rates, exactly as in the selection-based phenotype model of Simons et al. (2014). We assumed a human ancestral population size of 7.3 × 10³, as was inferred by Gravel et al. (2011), such that the γ = 2Ns = −146 for the large selection coefficient and γ = −2.92 for the small selection coefficient.

We used our code to calculate the proportion of variable sites that are present in a single copy (singletons) in a sample of 500 chromosomes for each of the selection coefficients in this model, which we denote as Ψ. We also calculated the genetic variance due to singleton sites as a function of ρ in our phenotype model, assuming that τ = 1.

We performed stochastic simulations under this model of selection and demography and sampled variants at time points from t = 0 to t = 0.45 (in coalescent units of 2N_A generations, where N_A is the ancestral population size). We performed 100 simulations per time point. Scripts for the simulations, which were performed using sfs_coder (Uricchio et al. 2015), are provided in the Supplemental Material.

Calculating the genetic variance

We follow several earlier studies in calculating the genetic variance due to alleles at frequency x, including Pritchard (2001) and Simons et al. (2014). Genetic variance V_x due to variants at or below allele frequency x is given by

$$V_x={\int }_{x=0}^x\frac{1}{2}E(z^2|x)f(x)(1-x)(x)dx,$$ (3)

where f(x) is the SFS, i.e., the proportion of sampled alleles at frequency x; and E(z²|x) is the mean-squared effect size of variants at frequency x. In order to obtain an accurate measure of the SFS and the effect sizes of variants at frequency x, we pool 250 simulations performed under each model, for a total of 5 × 10³ total simulated genes. We divide by V₁, the total variance explained by genetic factors, in order to obtain a value that represents the proportion of the genetic variance explained by variants under frequency x.

Power of rare variant tests

We obtained the SKAT-O R package from http://www.hsph.harvard.edu/skat/. We computed power as the proportion of simulations with P-values below 2.5 × 10⁻⁶. We used this threshold because our study focuses on selection in coding regions, and hence, our analysis is relevant to an exome sequencing study with ≈2 × 10⁴ genes. 2 × 10⁴ statistical tests correspond to a Bonferroni corrected P-value of 2.5 × 10⁻⁶. We used the default settings for SKAT-O unless otherwise stated.

We repeated this analysis for a subset of the parameter space for two other rare variant association tests in Europeans using the rvtests software (http://zhanxw.github.io/rvtests/), in particular CMC (Li and Leal 2008), the test of Morris and Zeggini (2010), and CMC-Wald, which first runs CMC and then the Wald test. We find that the overall trends are replicated for these tests, but that SKAT has better overall power (Supplemental Fig. S4).

If we were to relax our assumption that deleterious alleles are equally likely to be trait-increasing or decreasing, it is likely that the relative power of the statistical tests that we have investigated could change. However, we note that SKAT-O was specifically designed to retain power in both situations (equal and unequal proportions of trait-increasing/trait-decreasing variants) (Lee et al. 2012a,b), so we do not expect that the main results of the paper (i.e., that selection strength and growth rate alter architecture and power) are affected by this choice. Moreover, a recent study examined the Pearson correlation between P-values reported by a wide range of RVATs (Moutsianas et al. 2015), and found that SKAT-O is highly correlated to SKAT (0.93), C-ALPHA (Neale et al. 2011) (0.92), and KBAC (Liu and Leal 2010) (0.68). CMC is highly correlated to KBAC (0.66), the variable threshold test (Price et al. 2010) (0.63), and BURDEN (https://atgu.mgh.harvard.edu/plinkseq/) (0.77). Although these correlations are likely to depend somewhat on evolutionary parameters and genetic architecture, they constrain the ability of any of the tests to outperform the others.

False positive rates

We calculated false positive rates by permuting our simulated phenotypes and re-running SKAT-O. Under the null, we would expect 0.00025% of tests to result in P-values under 2.5 × 10⁻⁶.

Application to RNA-seq data

We obtained RNA-seq data from the GEUVADIS project for 360 individuals of European descent (Lappalainen et al. 2013). To remove potential confounders such as population structure and batch effects, we median normalized the samples and performed principal component analysis (PCA). The first 30 PCs in this analysis were taken as covariates in the ensuing analysis, and permutations were performed by permuting the residuals.

We cross-referenced genes in the GEUVADIS expression data set with transcription factors that were inferred to be under strong selection in Arbiza et al. (2013) and filtered for genes that are in the 95% tail of expression (i.e., are highly expressed). Among these, we selected STAT1, because its coding sequence is about twice as long (≈2200 bp) as the other candidates (which provides increased power for tests of association) and because a list of putative downstream targets of STAT1 was immediately available (Bhinge et al. 2007).

We obtained the coding sequence for STAT1 exons for each of the 360 individuals from the 1000 Genomes Project phase 3 data (The 1000 Genomes Project Consortium 2015). We then ran SKAT-O on the expression values and STAT1 genotypes for each of the STAT1 target genes that was expressed in the GEUVADIS data set. To obtain permutation-based P-values, we permuted the phenotype residuals for each gene 5000 times and used the empirical distribution of P-values from the permutations to obtain an estimate of the true P-value.