To Keep or Not to Keep? The Question of Crystallographic Waters for Enzyme Simulations in Organic Solvent

Abstract

The use of enzymes in non-aqueous solvents expands the use of biocatalysts to hydrophobic substrates, with the ability to tune selectivity of reactions through solvent selection. Non-aqueous enzymology also allows for fundamental studies on the role of water and other solvents in enzyme structure, dynamics, and function. Molecular dynamics simulations serve as a powerful tool in this area, providing detailed atomic information about the effect of solvents on enzyme properties. However, a common protocol for non-aqueous enzyme simulations does not exist. If you want to simulate enzymes in non-aqueous solutions, how many and which crystallographic waters do you keep? In the present work, this question is addressed by determining which crystallographic water molecules lead most quickly to an equilibrated protein structure. Five different methods of selecting and keeping crystallographic waters are used in order to discover which crystallographic waters lead the protein structure to reach an equilibrated structure more rapidly in organic solutions. It is found that buried waters contribute most to rapid equilibration in organic solvent, with slow-diffusing waters giving similar results.

1. Introduction

Non-aqueous enzymology is an important experimental [1–4] and theoretical [5–13] research focus that can answer questions about the role of water and non-aqueous solvents in enzyme structure, function and dynamics. Enzymes in non-aqueous solvents have practical importance, since many synthetically-useful enzymatic reactions, which do not occur favorably in water, are favored in organic solvents.[14] Modeling of solvent-compatible enzymes has given insight into solvent-dependent phenomena, including rationalizing the enantioselectivities of enzymatic reactions in organic media,[9,15] characterizing differences in active site hydrogen bonding for biodiesel production in multiple solvents,[6] and examining protein flexibility and solvent layer mobility with increasing water concentration.[16]

In protein simulations, the initial structure is typically obtained from the Protein Data Bank (PDB),[17] which contains structures gathered from X-ray crystallography experiments or, more rarely, NMR data. The PDB files include the positions of experimentally resolvable, tightly bound, stationary water molecules, which are generally called ‘crystallographic water molecules’. The number of crystallographic water molecules varies from protein to protein. Even lyophilized enzymes placed in anhydrous solvent have been found to contain residual water.[18] Since these waters can affect enzyme structure-function experimentally, it is important to simulate at least some residual waters, even in “non-aqueous” solvent environments. However, which residual waters should be kept—how many and where—has not been addressed until now.

In order to address the role of water in enzyme structure-function, scientists have looked at enzyme studies with different amounts of water.[19] It has been found that water activity has a profound effect on enzyme flexibility and function in organic solvents.[14] MD simulations have proven to be a powerful tool in this work, given their high spatial and temporal resolution. Wedberg et al. [16] carried out MD simulations of Candida antarctica lipase B (CALB) enzyme in different solvents at different water activities, showing that enzyme flexibility increases with water activity. Thus, the amount of water kept in simulations will affect enzyme structure and dynamics. Trodler and Pleiss [20] suggested that for CALB enzyme in the presence of hydrophobic solvents, more immobile water molecules, which would be present at the protein surface, place restrictions on protein flexibility. Researchers want to control the number of waters in simulations of enzymes in organic solvents, but it is not clear how to initialize the system with the desired amount of water. Table 1 summarizes the protocols for keeping/eliminating crystallographic waters that have been used previously in simulations of enzymes in organic solvents and water. It can be seen that among published work, different criteria have been used to keep crystallographic waters in MD simulations, even for the same system. The goal of the present work is to answer not just how many, but which, waters should be kept for “non-aqueous” and mixed aqueous organic solutions. As an approach to answering the question of which crystallographic water to keep, we have used a method to measure the time to reach equilibration under a number of protocols. At the very least, this approach of identifying the protocol with fastest equilibration enables the most efficient use of computational resources.

Table 1.

Different criteria used in past studies of MD simulations to keep crystallographic water

System	Solvent	Number of crystal water (criteria for keeping)
CALB [6]	tert-butanol, methanol	286 (all)
CALB [23]	Water	1 (buried)
CALB [5]	methanol, acetone, THF, chloroform, cyclopentane, hexane	92 (criteria for selection is not mentioned)
γ-chymotrypsin [7]	Acetonitrile	151 (all)
γ-chymotrypsin [8]	Hexane	50 (most tightly bound)
Subtilisin [11]	DMSO	(all)
Subtilisin [9]	DMF	50 (most strongly bound)

When equilibration stage is reached in MD simulations, the kinetic and potential energies reach an equilibrium value. However, as observed by Stella and Melchionna,[21] accurate equilibration of a system generally occurs at a later stage than potential energy relaxation. Therefore, potential energy relaxation cannot always be used as an indicator to determine that an equilibrium structure has been reached. The root mean square deviation (RMSD) method introduced by Daggett and Levitt [22] is the most common approach for determining equilibration in protein simulations.

The RMSD between two structures is defined as a function of reference time (t_ref) and simulation time (t) as follows:

$$\mathit{RMSD}(t_{\mathit{ref}},t)=\sqrt{\frac{1}{M}{\sum }_{i=0}^N{m}_i{\mid r_i(t_{\mathit{ref}})-r_i(t)\mid }^2}$$ (1)

where M represents the total mass of the system, N is the number of atoms in the system, m_i is the mass of atom i, and r_i is its position.

According to Stella and Melchionna,[21] if two mechanisms of attaining equilibrium, (1) relaxation towards a steady state and (2) the phase sampling, are not separated, the RMSD plateau value will be overestimated. In other words, true equilibration can be reached before the RMSD plateaus. Therefore, the authors proposed a way to analyze those two mechanisms separately. In the simple RMSD method, the reference structure is the original, initial structure (PDB). Note that the initial structure in MD simulations is typically the crystal structure (solid state), which would not be expected to be the exact equilibrium structure in solution. As an improvement, Stella and Melchionna [21] considered RMSD from several different intermediate reference structures at equal simulation time gaps in a modified RMSD method.

Walton and VanVliet [24] evaluated both the simple RMSD method and Stella method for the small BPT1 protein and the larger, more rigid streptavidin-biotin system. They found both methods to rely on the researchers’ judgment in applying the algorithm, and ambiguous for identifying equilibration of the two protein systems. Therefore, the authors suggested another objective and quantitative method to recognize the starting point of equilibrium phase space for protein simulations based on a physical model used in Normal Mode Analysis (NMA). In proteins, different processes are involved in relaxation,[25] and these different processes appear on different time scales.[24] By assuming the processes involved in calculating RMSD are represented by different decoupled vibrational and rotational modes, NMA analysis can be used for modeling, where the protein is treated as a combination of independent harmonic oscillators.[24] The RMSD of a selected protein can be represented using a mathematical expression as follows, according to this ‘multiple simple harmonic oscillator (MSHO) model [24]’

$$\mathit{RMSD}(t_{\mathit{ref}},t)={\sum }_{i=0}^N{A}_i(1-e^{-(t-t_{\mathit{ref}})/{\tau }_i}),$$ (2)

where N represents the number of independent harmonic oscillators, A_i is the pre-exponential constant and τ_i is the time constant for each harmonic oscillator i.

Walton and VanVliet [24] approximated Equation (2) using a stretched exponential function named the Kohlrausch-Williams-Watts (KWW) function. This is given in Equation (3). It has proven to be more convenient than the standard exponential function to model many relaxation processes.[26] Walton and VanVliet [24] proved the applicability of KWW model for the small BPTI protein, and for the larger, more rigid streptavidin-biotin system, too.

$$\mathit{RMSD}(t_{\mathit{ref}},t)\approx A_e(1-e^{-{[(t-t_{\mathit{ref}})/{\tau }_e]}^{\beta }})$$ (3)

In Equation 3, the RMSD is represented in terms of the KWW model; A_e and τ_e are the effective pre-exponential factor and effective time constant, respectively, while β represents the complexity of the system [27,28] with a scalar value ranging from 0 to 1. Using the method of Walton and VanVliet,[24] equilibration is identified as having been reached when A_e, τ_e, and β parameters no longer change with reference time (t_ref). In the present work, the time for two enzymes to reach equilibration in different solvents is determined by this method of Walton and VanVliet.

The impetus for using equilibration time as an evaluation of different methods for keeping crystallographic waters is two-fold. First, it is convenient to identify methods that lead to the most efficient use of computational time. Second, structures that rapidly equilibrate should better simulate the real system. According to Westhof and co-workers, “as the description of the system becomes more explicit and accurate, the structural and dynamical properties of the system are seen to remain close to those of the crystal structure or starting configuration. This implies that conservation of the structural interactions present in the initial system configuration, at least on short time scales, signals a true system equilibrium”.[29][underline ours] In the present study, if the protein starts out equilibrated, the waters are “where they belong” in the simulation. Our best guess is that these are the in vitro positions of water (perhaps where they stay when lyophilized). In the case of buried and slow-diffusing waters, this rationale makes sense in particular.

2. Methodology

Two different proteins: Candida antarctica lipase B (CALB) and horse heart cytochrome C (hh-CytC) were simulated in the present study. These two enzymes were selected for their reasonable sizes and retention of their catalytic activity in organic solvents.[30,31] CALB functions in strictly “non-aqueous” solvent, while hh-CytC functions in aqueous organic solutions. Thus, the two systems provide an opportunity to evaluate crystallographic waters in enzyme simulations for both pure organic solvent and aqueous-organic solutions. CALB enzyme is composed of 317 amino acid residues,[5] while hh-CytC protein consists of 104 amino acid residues in a single polypeptide chain, with a heme as the “105^th residue”.[32] Three trajectories were obtained for each system and method, using different randomly assigned initial velocities for statistical sampling. Each method involves a, different protocol for selecting and keeping crystallographic waters (detailed below).

CALB enzyme, which belongs to the α/β hydrolase fold family, was observed to retain its activity and to have interesting catalytic properties, such as higher thermostability and stereoselectivity,[30] in organic solvents. Therefore, four different solvent media were considered with CALB: n-butanol, tert-butanol, acetonitrile, and water. CALB has experimental uses in the presence of these solvents [33–37], which are water-miscible (but only at low water concentration for n-butanol). Meanwhile, horse heart cytochrome C (hh-CytC) is used as a model for the study of many biochemical phenomena in silico due to availability of its high-resolution three-dimensional structure, relatively small size, redox properties and distinct structural properties.[38,39] It has been observed to have catalytic activity in water-miscible organic solvents. Therefore, molecular dynamics trajectories were generated for hh-CytC in the presence of 20% aqueous methanol, 40% aqueous methanol and pure water (hh-CytC is stable in aqueous methanol concentrations under 50%).[40]

The starting coordinates of CALB enzyme were taken from the X-ray crystallographic structure (PDB ID: 1TCA, resolution: 1.55 Å). All the simulations were performed using GROMACS (version 4.6.3) [41] software package. GROMOS 53a6 [42] and OPLS force fields [43] were used for enzymes to check for force field dependence of results. Organic solvent force fields for alcohols are based on those developed by Jorgensen, [44,45] while the GROMOS force field was used for acetonitrile. The SPC/E water model [46] was used for water. The protein was centered in a cubic periodic box with a minimum distance of 0.8 nm between enzyme and any side of the box. Multiple protocols for retaining or eliminating crystallographic water were used, as explained below. Next, the enzyme was solvated in organic or mixed solvent, and one sodium counter ion was added to CALB by replacing one solvent molecule in order to obtain a neutral charge. Bond lengths were constrained using LINCS algorithm.[47] Electrostatic interactions were calculated using Particle Mesh Ewald summation.[48] For long-range interactions, a grid spacing of 0.12 nm combined with an interpolation order of 4 was used. Van der Waals interactions were calculated using a 1.4 nm cut-off. Energy minimization was done using steepest descent algorithm [49] to remove clashes between atoms that were too close. Position restraints were done on heavy atoms during annealing, when the system was gradually heated from 50 K to 300 K in 200 ps. The simulations were run at constant NPT (300 K, 1 bar) using V-rescale thermostat [50] and the Berendsen barostat [51] with a time step of 2 fs. V-rescale thermostat was used to control the temperature using a weak coupling to an external heat bath with a temperature-coupling constant of 0.1 ps. Berendsen barostat was used to keep the pressure of the system at 1 bar using a time constant of 1 ps.

As mentioned above, CALB was simulated in n-butanol, tert-butanol, acetonitrile, and water solvents, in order to evaluate a variety of solvent polarity, size/shape, and hydrogen bonding properties. With each solvent, five different protocols for keeping crystallographic waters were evaluated, in order to fulfill our goal: determining which crystallographic water molecules to keep (or eliminate) in molecular dynamics.

• Method 1) All the crystallographic water molecules (286 molecules) were kept.

• Method 2) Six buried crystallographic water molecules identified by Uppenberg et al. [52] were kept.

• Method 3) Slow-diffusing crystallographic water molecules were identified (as described below) and kept.

• Method 4) Crystallographic water molecules within 2.7 Å from CALB protein (based on crystal structure) were kept.

• Method 5) All of the crystallographic water molecules were removed.

For the method of keeping slow diffusing water molecules, first, a 10-ns simulation with all crystallographic water molecules was done. Then, individual diffusion coefficients for all crystallographic water molecules were calculated, and the average was found. Crystallographic water molecules with diffusion coefficients of less than 1/3^rd of the average were considered to be “slow-diffusing” water molecules; this initial cut-off was an arbitraty choice.

When slow-diffusing waters are identified from different trajectories, which are started with different randomly-assigned velocities, there is some variation in the set of slow waters that are identified (~60% are in common). So, we identified the set of crystallographic waters among different trajectories that have less than ~1/5^th average diffusion coefficient. Reassuringly, these slowest waters among slow-diffusing water molecules-- which almost certainly have a great effect on equilibration-- have the least variation in all sets. This revealed the importance of having multiple trajectories with different initial velocities to identify the slow-diffusing water molecules. In summary, analysis indicates that it is prudent to consider crystallographic water molecules to be “slow-diffusing” when they have diffusion coefficients of less than 1/5^th of the average value. In the present study, a value of 1/3^rd of the average was considered, in order to include a reasonable number of slow-diffusing crystallographic water in the presence of water for the CALB (7 slow-diffusing water molecules). Furthermore, a code was developed to identify slow-diffusing water molecules from a trajectory (provided in Supporting Information).

Results were obtained after 50 ns production runs for crystallographic water methods 1 (all waters) and 5 (none). Since equilibration (the criterion for evaluation) was reached within 10 nanoseconds for these two extremes, results were obtained after 10 ns trajectories for the other three methods.

The starting coordinates of the second system, hh-CytC were taken from the X-ray crystallographic structure (PDB ID: 1HRC, resolution: 1.90 Å). Molecular dynamics simulations were carried out using the same procedure as CALB, except for the following changes: seven chloride counter ions were added by replacing seven solvent molecule in order to obtain a neutral simulation box, Berendsen thermostat and barostat [51] were used to set temperature and pressure, respectively, with a 0.2 ps coupling time constant. All simulations were at constant NPT, with temperature of 298.15 K and 1 atm pressure. As mentioned above, 20% aqueous methanol, 40% aqueous methanol and pure water solvent media were used with hh-CytC. With each solvent, four different methods were used for keeping/eliminating crystallographic waters. Since all hh-CytC simulations contain water, we eliminated method 4 (keeping water molecules within 2.7 Å from protein) in mixed aqueous solvents.

• Method 1) All the crystallographic water molecules (124 molecules) were kept.

• Method 2) Two buried crystallographic water molecules identified by Brayer et al. [53] were kept. One of these (residue 112) was identified by NMR studies of Wand and co-workers [54] to be a structural water.

• Method 3) Slow-diffusing crystallographic water molecules were identified (using the same protocol as for CALB) and kept. The three waters clearly identified by NMR studies of Wand and co-workers [54] to be structural waters (which, by our analysis, seem to correspond to residues 112, 122, and 159) were slow diffusing in water and 20% methanol (but not in 40% methanol).

• Method 4) Not used.

• Method 5) All of the crystallographic water molecules were removed.

Results were obtained after 100 ns production run for methods 1 and 2. In the other two methods, results were obtained after 10 ns. Table 2 summarizes Methods 1 through 5: the protocols for keeping or removing crystallographic waters, for both CALB and hh-CytC simulations in pure organic and mixed aqueous-organic solutions.

Table 2.

Details of multiple protocols used for retaining or eliminating crystallographic water

Method number	Method name	Description	Number of crystallographic water molecules kept in CALB		Number of crystallographic water molecules kept in hh-CytC
1	All water	Keeping all crystallographic water molecules	286		124
2	Buried water	Keeping buried crystallographic water molecules	6		2
3	Slow-diffusing water	Keeping crystallographic water molecules, which were found to be slow-diffusing by having diffusion coefficients less than 1/3rd of the average, after 10 ns simulation with all crystal waters	Water solvent	7	Water solvent	43
			n-butanol solvent	105	20% aqueous methanol	30
			tert-butanol solvent	127	40% aqueous methanol	32
			Acetonitrile solvent	71
4	Water within 2.7 Å	Keeping crystallographic water molecules within 2.7 Å from protein	19		N/A
5	No water	Without keeping any crystallographic water	0		0

Equation 3 was used for evaluation of RMSD, and equilibration times were identified when the KWW model parameters: the pre-exponential factor (A_e); time constant (τ_e); and complexity of the system (β) no longer change as a function of time. Reference structures were generated at 0.5 ns intervals during simulation times from 0.5 to 2 ns, at 1 ns interval from 2 to 10 ns, and then at points around 12 ns, 15 ns and 20 ns. As suggested by VanVliet and co-workers,[24] the time intervals between reference structures were not kept constant, for better accuracy in determining equilibration times. Calculated RMSDs were fitted to the KWW model (Equation 3) with a non-linear curve fitting function, using Grace (version 5.1.16). For curve fitting, the method was revised slightly from the procedure of VanVliet and co-workers, giving an educated initial guess for the fitting parameters (pre-exponential factor (A_e), time constant (τ_e), and complexity of the system (β)). The estimates were done as follows: A 5 ns window, centered on t_ref was excluded, and a straight line for the remaining data (or average of the RMSD from 0.15 to 0.2 ns, in the case of t_ref > ~8 ns) was used for an initial value of pre-exponential factor (A_e). For the time constant (τ_e), a value of 5000 ps was the initial guess, based on the findings of Walton and VanVliet and general experience with protein simulations. Finally, the complexity (β) was estimated at 0.5, since a value of β=1 would correspond to a simple harmonic oscillator (not a good guess for proteins). Iterations were repeated until constant values were obtained for the fitting parameters A_e, τ_e, and β. Then, those fitting parameters were obtained for each value of t_ref, which is the simulation time at which a reference structure is obtained at given intervals. Equilibration is reached when parameters no longer change with time, as can be seen below in Figure 3. In the case where the parameters do not reach a steady-state value at the same point in time, the slowest-equilibrating parameter determines the overall equilibration time.

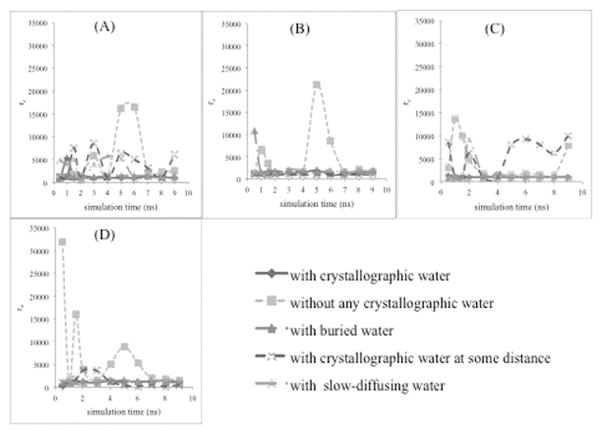
Figure 3.

Dependence of τ_e parameter on the simulation time. This parameter is for the nonlinear curve fitting of calculated RMSD of CALB in (A) water, (B) acetonitrile, (C) n-butanol, and (D) tert-butanol with the KWW model.

3. Results and Discussion

The goal of this work is to use equilibration time to determine which crystallographic water molecules to keep with proteins in MD simulations. The best method here is determined to be the one that leads to the most rapid equilibration of the protein structure in organic solvent, since this leads to the most efficient use of computational resources. The KWW model provides a quantitative measure of evaluating equilibration time.

To evaluate the validity of the KWW model for these systems, the model (Equation 3) must provide a good fit for the RMSD simulation data for CALB and hh-CytC in multiple solvents. The correlation coefficients for the entire non-linear curve fits were always greater than 0.80 for the both proteins used here, revealing the good agreement of calculated RMSD for the KWW model. Figure 2 shows an example of non-linear curve fitting of a calculated RMSD for the KWW model. Presented in Figure 2 is the RMSD of CALB in tert-butanol, using Method 5- no crystallographic waters. With the KWW model, the equilibration time is identified to be ~9 ns.

Figure 2.

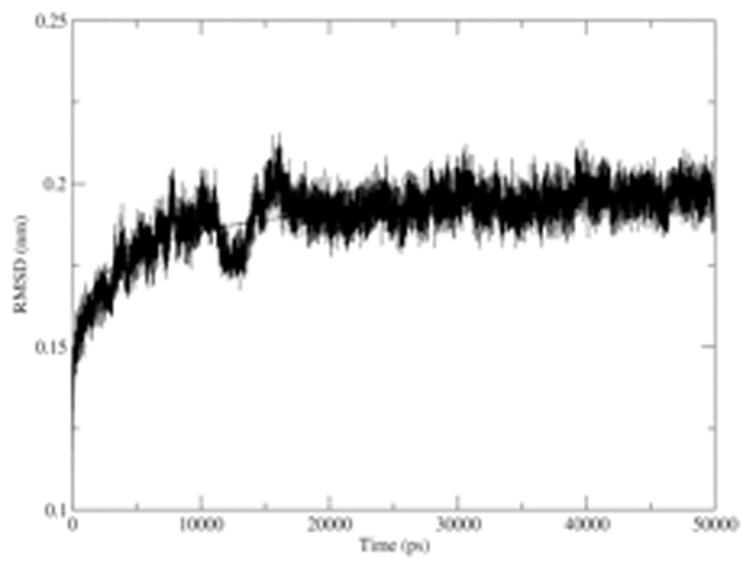
Non-linear curve fitting for the calculated RMSD of the CALB in tert-butanol with KWW model. The correlation coefficient for this fit is 0.85 (± 0.03).

Next, the force field dependence of results was examined. Comparison of equilibration time results between simulations of CALB and hh-CytC enzymes with GROMOS and OPLS-AA force fields are shown in supporting information Figures S2 and S3. Equilibration times with respect to both force fields are very similar (within 3 ns), revealing the minimal dependence of results on the force fields. Results presented below are for simulations with GROMOS force field.

3.1 Application to the CALB protein

Simulations of CALB were carried out in water, acetonitrile, n-butanol, and tert-butanol. Figure 3 shows how one of the fitting parameters in the KWW model, the time constant τ_e, varies with simulation time. As mentioned previously, protein equilibration is indicated when the fitting parameters no longer vary with time. Figures 3A–D show the variation of equilibration times for the 5 different water-keeping protocols in water, acetonitrile, n-butanol, and tert-butanol, respectively. Considering CALB in water, when all 286 crystallographic water molecules were present (method 1) and when only buried crystallographic water molecules were present (method 2), the trajectory reached equilibration stage virtually at the beginning of the simulation time, since fitting parameters came to a steady state well under 5 ns (~2 ns and ~3 ns respectively). The third position in ascending order of achieving fastest equilibrium (~6 ns) for CALB in water is owned by the method of keeping slow-diffusing water (method 3). Seven slow-diffusing water molecules (listed in supporting information Table S1) were identified for CALB in water solvent, and those water molecules were kept in this method (method 3). The other two methods: keeping crystallographic water within 2.7 Å from CALB protein (method 4) and eliminating all crystallographic waters (method 5) required 8–10 ns to reach an equilibrium stage.

When CALB protein is in acetonitrile solvent, analysis of calculated RMSD fitting parameters for the KWW model (Figure 3B) showed that all four methods of keeping different levels of crystallographic water led to an equilibrated structure at the beginning of the simulation time (≤ 2 ns), while method 5 of eliminating all crystallographic waters came to equilibrium at a later simulation time (8 ns).

For CALB in n-butanol, equilibration was reached near the beginning of the simulation (< 4 ns) for method 1 (all crystallographic waters), method 2 (buried waters), and method 3 (slow-diffusing waters). In contrast, method 5 (none) and method 4 (within 2.7 Å) required more than 8 ns to come to an equilibrium stage. This pattern is very similar to CALB in water solvent. The results in tert-butanol (Figure 3D) are qualitatively the same as in the presence of n-butanol solvent. The trajectory achieved equilibration stage at the beginning of the simulation time with methods 1, 2, and 3 (all, buried, slow-diffusing). Method 4 (within 2.7 Å) required more simulation time (~6 ns) to obtain equilibration than the other three methods of keeping crystallographic waters, while eliminating all crystallographic waters (method 5) led to a slower equilibration time (~9 ns).

Figure 4 and Table 3 summarize all the results of CALB in 4 solvents with respect to the five methods considered. The values are averaged over three trajectories per condition. The Figure 4 equilibration times were rounded to nearest nanoseconds, resulting in average values that sometimes have “zero-error”, but error bars are given where individual values deviated from the average. From Figure 3, it is clear that among all of the 286 crystallographic water molecules, the 6 buried crystallographic water molecules play a major role in reaching equilibrium, since in the presence of all studied solvents, both the methods of keeping all 286 crystallographic water molecules (method 1), and keeping only buried crystallographic water molecules (method 2) reached equilibration near the beginning of the simulation. For trajectories of CALB in organic solvent (acetonitrile, n-butanol, and tert-butanol), equilibration at the beginning of simulations also occurred when keeping only slow-diffusing water molecules (method 3). In the presence of water solvent, method 3 took somewhat longer (6 ns). Therefore, it is fair to say that slow-diffusing water molecules have an important role, too, in rapidly achieving equilibrium. Method 4, keeping crystallographic waters within 2.7 Å from CALB protein, had short equilibration times only when CALB is in the presence of acetonitrile solvent. In water and n-butanol solvents, this method did not show much difference from the method of keeping no crystallographic waters (method 5); that is to say, equilibration with method 4 took nearly 9 ns. In the presence of tert-butanol, keeping crystallographic water within 2.7 Å from CALB protein (method 4) required less simulation time (~6 ns) to attain equilibrium stage when compared with method 5 of keeping no waters (8–9 ns), offering a moderate improvement. In summary, method 4 (keeping water within 2.7 Å from CALB protein) requires more simulation time when compared to the other methods (1, 2, and 3) of keeping different levels of crystallographic water. Therefore, it is reasonable to say that the method of keeping crystallographic water within 2.7 Å from CALB protein is not very successful in accomplishing equilibrium stage.

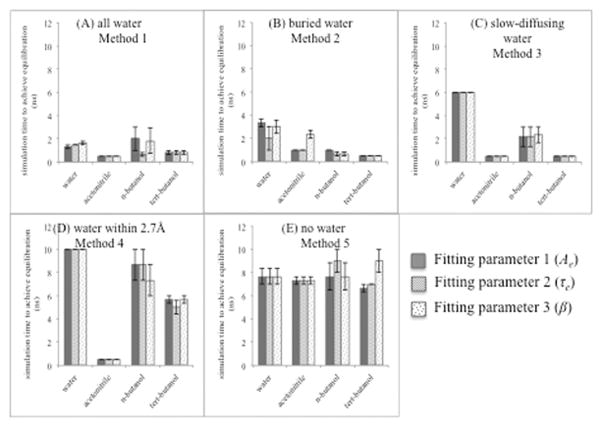
Figure 4.

Equilibration time for CALB in different solvents with respect to five methods: (A) all water (method 1) (B) buried water (method 2) (C) slow-diffusing water (method 3) (D) water within 2.7 Å (method 4) (E) no crystal water (method 5). This shows simulation time to achieve equilibration decided by each parameter: A_e (fitting parameter 1-blue), τ_e (fitting parameter 2-red), and β (fitting parameter 3-green). Error bars for the average over three trajectories are shown.

Table 3.

Summary of equilibration times for CALB

	Average simulation time to achieve equilibration for the each method in the presence of each solvent
	Method 1	Method 2	Method 3	Method 4	Method 5
Acetonitrile	0.5 ns	1.4 ns	0.5 ns	0.5 ns	7.7 ns
n-butanol	1.5 ns	0.8 ns	2.2 ns	8.2 ns	8.1 ns
tert-butanol	0.8 ns	0.5 ns	0.5 ns	5.4 ns	9.0 ns
Average for the organic solvent	0.9 ± 0.5 ns	0.9 ± 0.5 ns	1.1 ± 1.0 ns	4.7 ± 3.9 ns	8.3 ± 0.7 ns
Water (for comparison)	1.5 ns	2.8 ns	6.0 ns	10.0 ns	7.7 ns

Table 2 shows the wide variety of numbers of crystallographic waters kept among the 5 methods. Given the comparable results of methods 1, 2, and 3, we can say that the overall number of crystallographic water molecules does not affect equilibration time, since even in the presence of six buried water molecules, equilibration was quickly reached. Rather, it is the location of the waters that is critical.

For further analysis, common crystallographic water molecules in the studied methods were summarized in Table 4. It provides the answer to the natural question of why the method of keeping crystallographic water within 2.7 Å from CALB protein is not effective for rapid equilibrations, except in acetonitrile. As can be seen in the table, in the presence of acetonitrile solvent, two buried water molecules reside within 2.7 Å from CALB protein and those two water molecules are slow diffusing, too. These 2 common waters among methods 2, 3, and 4 appear to be the reason why method 4 is effective for rapid equilibration of CALB in acetonitrile. Detailed information on which waters are common to the different methods is provided in Table S1 in Supporting Information.

Table 4.

Number of common crystallographic water molecules for CALB enzyme in the studied methods

Methods	Number of common crystallographic water molecules for the mentioned methods
	Water	Acetonitrile	n-butanol	tert-butanol
Buried and Slow-diffusing	1	3	3	5
Water within 2.7 Å from CALB and Slow-diffusing	1	8	10	11
Buried and Water within 2.7 Å from CALB	2	2	2	2
Buried, Water within 2.7 Å from CALB and Slow-diffusing	1	2	1	1

Considering method 3 with slow-diffusing waters, it can be seen that in the presence of acetonitrile, n-butanol, and tert-butanol, the sets of slow-diffusing water molecules contain 3, 3 and 5 (of 6 total) buried crystallographic water molecules, respectively, for the organic solvents. This looks to be the reason for a fast equilibration in those situations. In the presence of water solvent, method 3 equilibration was slower than with organic solvents. The reason may be that, in the presence of water solvent, buried waters undergo rapid exchange with bulk solvent. This is evident in the fact that in aqueous solvent, the slow-diffusing water molecules include fewer buried water molecules (1 molecule), than in the presence of organic solvents. The one water that is both buried and slow-diffusing for aqueous CALB (residue number 406) is the one that Schopf and Warshel [23] identified as having a clear hydrogen bonding distance to Asp187, which is a catalytic triad residue. According to Uppenberg et al. [52], one of the other buried water molecules of CALB is hydrogen bonded to Thr103 and forms part of the turn around the active site serine. The four buried water molecules were found in the active site pocket by these authors.[52] The fact that only one of these was identified as slow-diffusing in water solvent indicates the lability of most active site buried waters, particularly in aqueous solvent.

Analysis of structural similarities among simulations with different protocols for crystallographic waters is provided by RMSD values after 10 ns simulations. These were obtained using as a reference structure CALB simulated in its respective solvent using method 1 (all water). These values are presented in Table 5. It can be seen that the largest RMSD values are for aqueous simulations. This likely reflects the higher flexibility of CALB in water. It has been documented experimentally [55] and by simulations [16,20,56,57] that enzymes are generally more rigid in organic solvents than in water.

Table 5.

RMSD with respect to method 1 for other four methods after 10 ns

	RMSD with each method after 10 ns with respect to method 1 after 10 ns (nm)
	Method 2	Method 3	Method 4	Method 5
Water	0.202 ± 0.013	0.222 ± 0.014	0.229 ± 0.006	0.206 ± 0.014
Acetonitrile	0.2076 ± 0.0001	0.2075 ± 0.0001	0.1927 ± 0.0003	0.2051 ± 0.0008
n-butanol	0.18583 ± 0.00006	0.17842 ± 0.00002	0.17815 ± 0.00002	0.190 ± 0.006
tert-butanol	0.190 ± 0.002	0.157 ± 0.003	0.191 ± 0.003	0.192 ± 0.007

Hydrophilic solvents usually have a greater tendency to strip tightly bound water [58] (crystallographic water), while the diffusion constant of water in less polar solvents is slow. This is reflected in the number of slow-diffusing waters identified among the different solvents. As shown in Table 2, there are only 7 slow-diffusing crystallographic waters in water solvent, while there are 71 in acetonitrile, 105 in n-butanol, and 127 in t-butanol. It has been shown here and elsewhere that equilibrated protein structures in hydrophobic organic solvents keep their native structures as a result of kinetic trapping in the absence of water.[59] This is due in part to stronger hydrogen bonding between the protein atoms, giving rise to a more rigid structure.[59] Verifying this, for CALB in the presence of organic solvents, lower values of RMSD in organic solvents were observed when compared to water after 10 ns (see Table 5). Therefore, less flexibility (a more rigid equilibrated structure) is found for CALB in the presence of organic solvents. The effects of crystallographic water methods and influence of hydrophobic/hydrophilic solvents is discussed below.

Do different methods of keeping crystallographic waters affect conformational dynamics?

CALB is known to undergo conformational changes related to lid opening for substrate binding and release. On the other hand, cytochrome c is a semirigid protein,[60] reflect in its relatively low RMSD value at the end of trajectories (~0.1 nm, cf. ~0.2 in CALB). Thus, in addressing the question of whether methods of keeping crystallographic waters influence conformational sampling, analysis is focused on CALB. In order to study protein conformational changes for CALB enzyme, the centre of mass distance between two lid-forming alpha helices (α5 and C-terminal half of α10) was measured as a function of time in each organic solvent and water for each trajectory (Supporting information Figure S4). For method 5 (no crystallographic waters), it can be seen that there are broad variations among the three trajectories in all the solvents, revealing the importance of keeping at least a minimum number of crystallographic waters when the simulation time is shorter. These differences in conformational sampling probably arise from the trajectory being at a higher point on the potential energy surface when all crystallographic waters are removed. That is to say, it is destabilizing to eliminate all waters. The work of Westhof and co-workers [29] on biomolecular equilibration in MD simulations supports this. They state, “inconstancy of structural and dynamical properties across a set of trajectories could possibly be indicative of the presence of artifactual behaviors due to unstable protocols and therefore have to be analyzed and interpreted with great care”.[29] Only method 5 shows inconstancy in structure-dynamics, while the other methods show convergence across multiple trajectories.

To assess conformational sampling of CALB, Blank and co-workers [61] partitioned the enzymes’ different conformations into three classes: closed (α5-α10 cleft distance < 1.52 nm), crystal-like (α5-α10 cleft distance = 1.52–1.90 nm), and open (α5-α10 cleft distance > 1.9 nm). Following the same classifications, it is clear that in the presence of n-butanol, CALB shows the same conformation (crystal-like) with all the methods when reaching 10 ns. With t-butanol solvent, CALB shows crystal-like and closed conformations for all methods except for method 3 (keeping slow-diffusing crystal waters), where it has an open conformation. This is reflected in the RMSD values of Table 5, where in the presence of t-butanol, CALB shows a structural difference with protocol 3. Of course, conformational changes in proteins are made possible by their flexibility. In the presence of water and acetonitrile, more flexibility is expected, driving conformational changes. The comparatively high dielectric constants of water and acetonitrile lead to weaker intra-protein electrostatic interactions, increasing protein flexibility.[62] Therefore, as expected, in the presence of acetonitrile, method 1 shows crystal-like conformation, method 2 shows crystal-like to open conformational changes, methods 3 and 4 show crystal-like to closed conformational changes, while method 5 trajectories diverge with two in the crystal-like conformation and one closed. In aqueous simulations, method 1 shows closed conformation, method 2 shows crystal-like to open conformational changes, methods 3 and 5 show crystal–like to closed conformations, and method 4 shows crystal-like to open and closed conformational changes.

To summarize, a surprising outcome of this assessment of the effect of crystallographic water method on conformational sampling is that the two methods that lead to most rapid equilibration (keeping buried and slow-diffusing) seem to favor divergent conformational dynamics. In all three trajectories in polar solvents, keeping buried waters favors open conformation, while keeping slow-diffusing waters leads to closed conformation. In contrast, in the butanol solvents, buried waters keep the enzyme in crystal-like conformation, while slow-diffusing waters lead to open conformation in t-butanol and maintain crystal-like conformation in n-butanol. This indicates that although both buried and slow-diffusing waters lead to rapid equilibration, they are likely on different places on the protein potential energy surface (in spite of the overlap of some crystallographic waters in each set). These differences in conformational sampling among methods could be used to leverage enhanced conformational sampling by varying the initial set-up of protein systems in organic solvents. That is to say, using multiple methods (buried and slow-diffusing waters) may lead to more complete sampling of the protein conformational landscape.

Figure 5 shows “freeze frames” of crystallographic water molecules at different time points in a simulation, illustrating water diffusion in the presence of n-butanol. Waters are color-coded by the method (slow-diffusing, buried, both, or other) that retains them under different protocols. Fast diffusing water molecules diffuse away from the protein with time, while slow diffusing water molecules stay near to the protein. It can be seen that at 30 ns simulation time, fast diffusing-buried water molecules have diffused away from the protein while slow diffusing-buried water molecules stay with the protein all the time.

Figure 5.

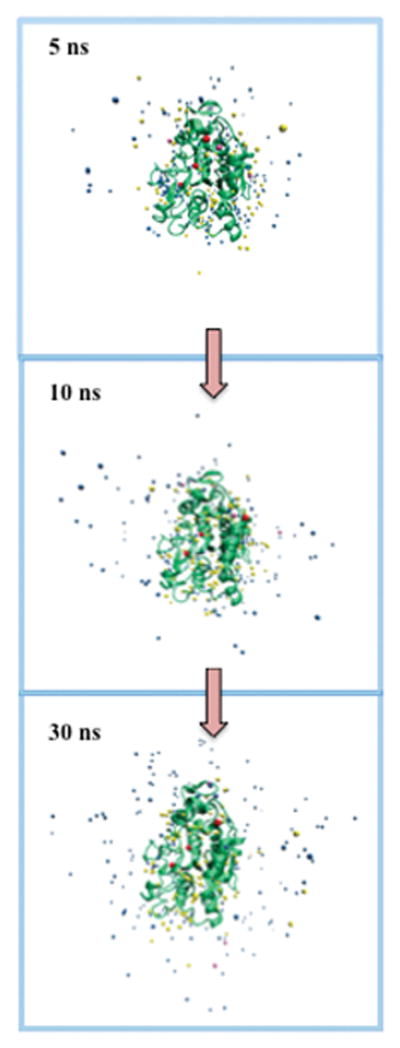
Snapshots of slow-diffusing (yellow), buried (pink), buried/slow-diffusing (red), and other crystallographic water molecules at different simulation times for the CALB enzyme in the presence of n-butanol.

3.2 Application to the hh-CytC protein

Simulations of horse heart cytochrome c (hh-CytC) were carried out in water, 20% aqueous methanol and 40% aqueous methanol. The results for τ_e are given in Figure 6. It can be seen that for hh-CytC in all solvents considered, when all 124 crystallographic water molecules were present (method 1), the trajectory was equilibrated from the beginning of the simulation time (< 2 ns), as fitting parameters are at a steady state from the beginning. Considering the results for hh-CytC in pure water, methods 2 and 3 (buried and slow-diffusing) took 4 and 6 ns, respectively, to reach equilibrium, which is no improvement over eliminating all crystallographic waters (5 ns for method 5).

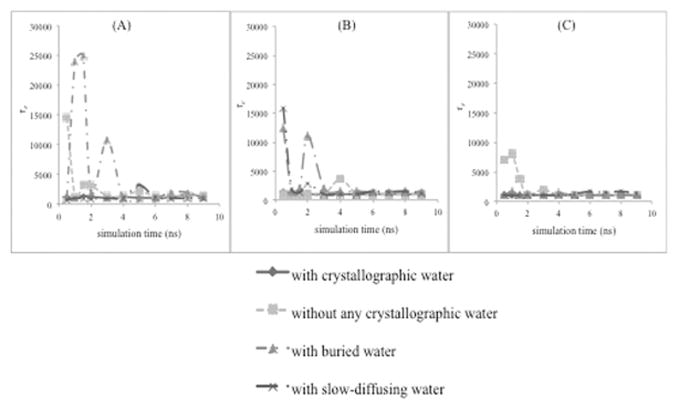
Figure 6.

Dependence of τ_e parameter on the simulation time. This parameter is for the nonlinear curve fitting of calculated RMSD of hh-CytC in (A) water, (B) 20% aqueous methanol, and (C) 40% aqueous methanol with the KWW model.

According to analysis of hh-CytC protein in 20% aqueous methanol (Figure 6B), methods 2 and 3 (buried and slow-diffusing crystallographic waters) required ~3 ns to reach equilibrium. On the other hand, when there were no crystallographic waters (method 5), more simulation time (~5 ns) was required to obtain equilibrium.

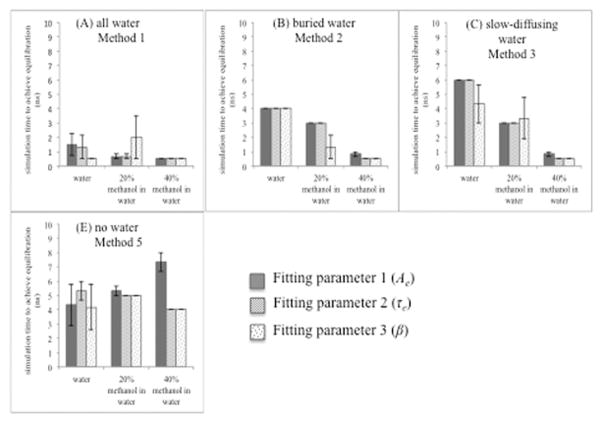
Considering hh-CytC protein in 40% aqueous methanol (Figure 6C), all three methods of keeping different levels of crystallographic water were at equilibrium stage from the beginning of the simulation, while method 5 (no crystallographic waters) came to equilibrium at a later simulation time (4 to 7 ns). Thus, the aqueous organic solvents showed a bigger difference (over aqueous simulations) between keeping (some) crystallographic waters and eliminating all of them. In fact, all methods of keeping waters (all, buried, slow-diffusing) gave comparable equilibration times in 20% and 40% aqueous methanol. These reached equilibrium much faster than method 5 (no crystallographic waters, at ~6 ns). However, for strictly aqueous simulations, only method 1 (keeping all) had a fast equilibration time (2 ns), while all other methods (buried, slow-diffusing, and none) gave similar performance (~5 ns equilibration time). Figure 7 and Table 6 summarize the results for hh-CytC in water, 20% aqueous methanol, and 40% aqueous methanol for four different protocols treating crystallographic waters.

Figure 7.

Equilibration time for the hh-CytC with different solvents with respect to four methods: (A) all water (method 1), (B) buried water (method 2), (C) slow diffusing water (method 3), and (D) no crystal water (method 5). This shows simulation time to achieve equilibration decided by each parameter: A_e (fitting parameter 1- blue), τ_e (fitting parameter 2- red), and β (fitting parameter 3- green). Error bars for the average over three trajectories are shown.

Table 6.

Summary of equilibration times for hh-CytC

	Average simulation time to achieve equilibration for the each method in the presence of each solvent (ns)
	Method 1	Method 2	Method 3	Method 5
Water	1.1 ns	4.0 ns	5.4 ns	4.6 ns
20% aqueous methanol	1.1 ns	2.4 ns	3.1 ns	5.1 ns
40% aqueous methanol	0.5 ns	0.6 ns	0.6 ns	5.1 ns
Average	0.9 ± 0.3 ns	2.3 ± 1.7 ns	3.0 ± 2.4 ns	4.9 ± 0.3 ns

For further analysis, the common water molecules among buried and slow-diffusing crystallographic water molecules were summarized in the Table 7. It can be seen that in the presence of 40% aqueous methanol in water solvent, the set of slow-diffusing water molecules (32 total) does not include either of the two buried crystallographic waters. Still, method 3 attained equilibrium stage at the beginning of simulation time (<2 ns). This reveals the importance of retaining slow-diffusing crystallographic water molecules, even in solvation environments that are predominantly composed of water.

Table 7.

Number of common crystallographic water molecules for hh-CytC enzyme in the studied methods

Methods	Number of common crystallographic water molecules for the mentioned methods
	Water	20% methanol in water	40% methanol in water
Buried and Slow-diffusing	1	1	0

3.3 Summary of the outcome

When summarizing the results for both proteins we used here, there is a clear difference in equilibration times between the methods of keeping (at least some) crystallographic waters and the method of eliminating all crystallographic water molecules. In most of the studied cases, the protocols of keeping buried crystallographic water molecules (method 2) and keeping slow-diffusing crystallographic waters (method 3) performed most similarly to the method of keeping all crystallographic water molecules (method 1). This is valuable information for researchers seeking to limit the number of waters when simulating enzymes in organic solvent, such as in studies that probe the effect of water activity on enzyme structure and dynamics.[16,56,63–67] Differences between methods 2 and 3 were more pronounced for CALB protein than for hh-CytC, and in water solvent (where method 2 was notably more effective than method 3 for both proteins).

Therefore, if simulation times are shorter (<15 ns), keeping crystallographic water molecules should be taken in to consideration, since otherwise the calculated trajectory time length will not be sufficient enough to gather all the required information after equilibration. In all cases, it is desirable to have the longest period of data collection possible for statistical analysis. For non-aqueous simulations, it is often desirable to restrict the number of waters. In this case, keeping buried crystallographic water molecules (method 2) will be the best alternative to keeping all the crystallographic water molecules. In the cases where buried crystallographic water molecules have not been identified, keeping slow-diffusing crystallographic water molecules (method 3) will be a good option, as reflected by the results. Method 2 requires previous knowledge of the system (we used published analysis), while method 3 (with slow-diffusing water) provides a protocol that can be used on new systems or those which lack published experimental data on buried waters. Analysis of waters in common to methods 2 and 3 (buried and slow-diffusing) indicates that many buried water are also identified as slow-diffusing. It is surprising, then, that these two methods led to divergent conformational sampling for CALB in short MD trajectories. These differences could be leveraged, however, to enhance conformational sampling in a set of trajectories initialized under the two methods.

This work indicates that a judicious choice of which crystallographic waters to keep can enhance simulation efficiency, even in aqueous systems. It also provides information for researchers seeking reliable methods in simulations of enzymes in organic solvents.

4. Conclusion

The purpose of this work is to identify a rational method for keeping and identifying “necessary” waters that should be retained in simulations of enzymes in “non-aqueous” or mixed organic solvents. Even lyophilized enzymes retain some waters,[18] and it would be ideal to know which. We postulate that buried and slow-diffusing waters will be the ones retained experimentally in the solvation layer. Thus, we recommend 2 methods: (1) keeping buried waters; (2) running a 5–10 ns trajectory, with all crystallographic waters retained, in the desired solvent to identify slow-diffusing waters. The slowest waters (< 1/5 average diffusion constant) are then retained for further simulation in organic solvent. Given water molecules’ faster diffusion in water, a criterion of 1/3 the average value is recommended as a cut-off to identify slow-diffusing waters in aqueous simulations. Assessment of conformational sampling among different methods revealed that keeping buried and slow-diffusing waters leads to divergent conformational sampling, in spite of the significant fraction of buried waters that are also identified as slow-diffusing. Therefore, a combination of the two methods (keeping buried and slow-diffusing crystallographic waters) when initializing simulations may be ideal for sampling a broader range of protein dynamics in any solvent (water or organic). By keeping buried or slow-diffusing crystallographic waters, simulations of protein structures more rapidly reach an equilibrium structure in organic solvent.

Figure 1.

Initial CALB crystallographic structure and initial orientations of slow diffusing (yellow), buried (pink), buried-slow diffusing (red), and other (blue) crystallographic water molecules in (A) water, (B) n-butanol, (C) tert-butanol, and (D) acetonitrile solvents. Back view is showing in Figure S1.