Regularized Structural Equation Modeling

Abstract

A new method is proposed that extends the use of regularization in both lasso and ridge regression to structural equation models. The method is termed regularized structural equation modeling (RegSEM). RegSEM penalizes specific parameters in structural equation models, with the goal of creating easier to understand and simpler models. Although regularization has gained wide adoption in regression, very little has transferred to models with latent variables. By adding penalties to specific parameters in a structural equation model, researchers have a high level of flexibility in reducing model complexity, overcoming poor fitting models, and the creation of models that are more likely to generalize to new samples. The proposed method was evaluated through a simulation study, two illustrative examples involving a measurement model, and one empirical example involving the structural part of the model to demonstrate RegSEM’s utility.

The desire for model simplicity in exploratory factor analysis (EFA) has led to the long-standing goal of achieving simple structure. By simple structure, we are broadly referring to a pattern of factor loadings where each indicator is influenced by a minimal number of latent factors, preferably one. Multiple researchers have set different criteria for achieving simple structure, with the most notable being Thurstone (1935, 1947). However, the desire for simplicity in model structure comes by many names, including the aforementioned simple structure (Thurstone, 1935), variable complexity (Browne, 2001), parsimony (Marsh & Hau, 1996; Raykov & Marcoulides, 1999), “sparse loadings” in the context of principal components analysis (PCA; Zou, Hastie, & Tibshirani, 2006), and finally, sparsistency, denoting that all parameters in a sparse model that are zero are correctly estimated as zero with probability tending to one (Lam & Fan, 2009). Across multiple fields and different terminology, the goal is roughly the same: to accurately and efficiently estimate a model that is parsimonious in allowing users to easily interpret the model’s representation of reality.

However, simpler is not always better. Overconstraining models in an attempt to make interpretation easier, can lead to unacceptable levels of misfit and biased parameter estimates (Hsu, Troncoso Skidmore, Li, & Thompson, 2014; Muthén & Asparouhov, 2012). In a confirmatory factor analysis (CFA), biased parameter estimates manifest as inflated covariances between latent factors caused by not allowing cross-loadings or residual covariances. It is not that the goal of simple structure is a poor choice, but that blind adherence to this strategy can lead to bias and misinterpretation in model evaluation and selection. Although more complex models typically fit better, improved fit comes at the loss of interpreting the meaning of each factor and relations between factors. In addition to the increased interpretability of simpler models, parameter estimates often have smaller standard errors, allowing for more precise substantive conclusions (Raykov & Marcoulides, 1999).

The question that remains is this: When we conduct a purely exploratory search or wish to improve on a poor fitting model, how can we conduct this search, and how do we do it well? Specification search (e.g., Kaplan, 1988; MacCallum, 1986) refers to the modification of a model to improve parsimony or fit. This exploratory phase of model modification in structural equation modeling (SEM) has traditionally been conducted using modification indices (for overview, see Chou & Huh, 2012). Conducting specification search with the use of modification indices is fraught with problems, including capitalizing on chance (MacCallum, Roznowski, & Necowitz, 1992), as well as a low probability of finding the best global solution (Chou & Bentler, 1990). Model modification with the use of modification indexes might work well if the number of misspecifications is small, but when there is a higher degree of uncertainty regarding the model structure, global search strategies are needed. This has led to the proposal of heuristic search algorithms such as ant colony optimization (Leite, Huang, & Marcoulides, 2008; Marcoulides & Drezner, 2003), genetic algorithm (Marcoulides & Drezner, 2001), and tabu search (Marcoulides, Drezner, & Schumacker, 1998; for overview, see Marcoulides & Ing, 2012).

Outside the field of psychometrics and SEM, there has been an increasing focus on developing methods for creating sparse models, particularly in regression and graphical modeling. Although it is beyond the scope of this article to provide a detailed account of this work (for overview, see Hastie, Tibshirani, & Wainwright, 2015; Rish & Grabarnik, 2014), there are specific developments with latent variable models that are noteworthy. These methods for sparsity have focused on the development of alternative cost functions that impose a penalty on the size of certain parameters. This method for penalizing the size of certain parameters is generally referred to as regularization, shrinkage, or penalization. The drawback of these alternative cost functions is that they induce model misfit and a reduction in explained variance. In the context of latent variable models, sparse estimation techniques were first applied to PCA through the use of penalization to create sparse loadings (Zou et al., 2006) along with alternative methods of rotation (Trendafilov & Adachi, 2014). Similar methods have also been applied to EFA through the use of penalized maximum likelihood estimation (Choi, Zou, & Oehlert, 2010; Hirose & Yamamoto, 2014a; Ning & Georgiou, 2011).

Although regularization has been introduced in the context of PCA and EFA, less research has been done in the context of CFA, or SEM in general, where the researcher has more influence in constraining the model parameters based on theory. An example is when a researcher is creating a psychometric scale that contains a mixture of items known to be good items of the construct of interest and items that have been recently developed. Factor loadings for the previously validated items could be left free and penalties could be added to the factor loadings of the newly created items. This allows the researcher to test the inclusion of the new items while leaving the loadings for the previously validated items unpenalized to stabilize the estimation of the factor(s) of interest. This is precisely the area between EFA and CFA, between purely unrestricted and restricted model specification, in which a void exists in options for model creation in the frequentist framework. Model creation is very rarely conducted in a purely exploratory or confirmatory manner. It is this middle ground that has led to problems, where researchers use CFA for exploratory purposes, when EFA would be best (Browne, 2001).

In an attempt to extend the use of regularization to SEM, a new method is proposed, termed regularized SEM (RegSEM). RegSEM adds penalties to specific model parameters set by the researcher, allowing greater flexibility in model specification and selection. Traditionally, model selection is a categorical choice; selection is between a small number of models that were either hypothesized or created as a result of poor fit. Adding a sequence of small penalties to specific parameters turns model selection into a continuous choice, where the resulting models lie somewhere on the continuum between the most unrestricted and restricted models. For instance, a researcher could start with a completely unconstrained factor model, selecting three latent factors, and allowing every item to load on every factor. Penalties for each factor loading parameter could be gradually increased until every loading equals zero. An external criterion such as performance in a holdout data set, or an information criterion that takes into account complexity, could then be used to choose one of the models. By building penalties directly into the estimation, the researcher has more flexibility in testing various models, while building in safeguards to prevent overfitting. Model selection of this nature is common in the data mining literature but in psychometrics it is rarely, if ever, used.

The objective in developing RegSEM is not necessarily to replace existing methods in psychometrics, but instead to tackle two different goals. One is to transfer the benefits of regularization to SEM. As demonstrated in the studies that follow, RegSEM can be applied in ways that no traditional method in psychometrics could be applied. The second goal is to show the general applicability of RegSEM for creating parsimonious SEMs.

The purpose of this article is to give a detailed overview of RegSEM, demonstrating its utility in a simulation study, two illustrative examples involving a measurement model, and one empirical example involving the structural part of the model. To set the stage for RegSEM we cover the matrix formulation of SEMs, as well as previous work on regularization in both regression and EFA. RegSEM is then discussed in detail, followed by a simulation study to test its ability to choose the correct model and evaluate various fit indexes in conjunction with RegSEM. More detail on choosing a final model and when RegSEM is and is not appropriate is then covered with two illustrative examples. Finally, an empirical example demonstrating the use of regularization at the structural level of an structural equation model is provided. We conclude with recommendations on the use of RegSEM across different contexts and directions for future applications and extensions.

BACKGROUND

Reticular Action Model

To provide the background on general SEM and make clear what matrices are available for regularization, we briefly detail Reticular Action Model (McArdle, 2005; RAM; McArdle & McDonald, 1984) notation as it provides a 1:1 correspondence between the graphical and matrix specifications (Boker, Neale, & Rausch, 2004), as well as only requiring three matrices to specify the full SEM. Additionally, the current implementation of RegSEM only uses the RAM matrices, making it necessary to understand the notation. One of the main benefits in using RAM notation is that only one matrix is needed to capture the direct effects. As direct effects might be the most natural parameters for regularization, this makes formulation simpler than having to add penalties to more than one matrix.

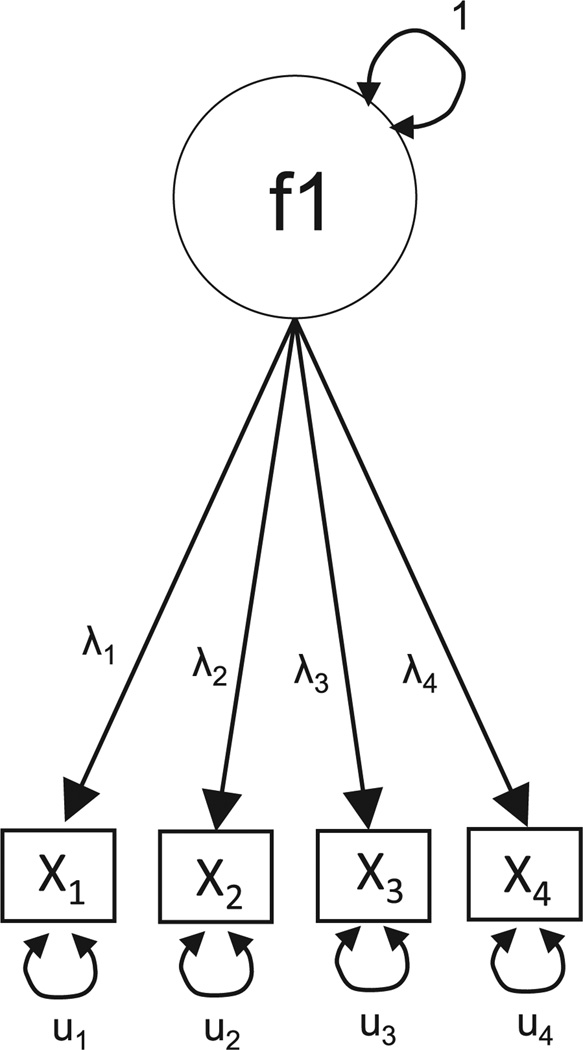
To illustrate the matrix specification with RAM notation, we use a one-factor CFA model. In this model, depicted in Figure 1, there is a single latent factor, f₁. For identification, we fixed the variance of f₁ to 1. This allows us to estimate factor loadings (λ₁ − λ₄) and unique variances (u₁−u₄) for each of the manifest variables (X₁−X₄).

FIGURE 1.

Example one factor confirmatory factor analysis model.

In RAM, the three matrices are the filter (F), the asymmetric (A), and the symmetric (S). The F matrix is a p × (p + l) matrix, where p is the number of manifest variables, and l is the number of latent variables. This matrix contains ones in the positions corresponding to each manifest variable, and zeros elsewhere. In this case, with four observed variables (X₁−X₄) and one latent variable (f₁), the F matrix has four rows and five columns, such that

$$\left[\begin{array}{ccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right]$$

Directional relationships, such as directed paths or regressions between variables (factor loadings), are contained in the A matrix. In Figure 1, the only directed paths are the four factor loadings, each originating from the factor f₁ and going to each of the observed variables. This results in an A matrix of

$$\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda }_1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda }_2\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda }_3\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\lambda }_4\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]$$

In A, there are no relationships between the observed variables (Columns 1–4), and the only entries are in Column 5 for the factor f₁. If we wished to incorporate the mean structure (necessary for longitudinal models), we would add an additional column to A to include the unit constant. Because none of the models tested in the remainder of this article include mean structures, details regarding their inclusion in matrices and the resultant expectations are omitted (see Grimm & McArdle, 2005; McArdle, 2005).

The S matrix is a square matrix that contains all two-headed arrows, which can be either variances or covariances. In Figure 1, there is a unique variance for each of the manifest variables and one variance for f₁. This results in

$$\left[\begin{array}{ccccc}\hfill {\mathrm{u}}_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{u}}_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{u}}_3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{u}}_4\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$

In this case, the factor variance has been constrained to 1. If, for instance, we wished to add a covariance between X₁ and X₂, we would add a free parameter to position [2,1] and [1,2] in S.

After having specified these three matrices, we can now calculate the expected covariance matrix (McArdle & McDonald, 1984),

$$\mathrm{\Sigma }=\mathrm{F}{(\mathrm{I}-\mathrm{A})}^{-1}\mathrm{S}{(\mathrm{I}-\mathrm{A})}^{-1\prime }\mathrm{F}\prime$$ (1)

where⁻¹ refers to the inverse of a matrix and ′ is the transpose operator. Once the expected covariance matrix is calculated, this can then be inserted into a loss function such as maximum likelihood (Jöreskog, 1969; ML; Lawley, 1940),

$${\mathrm{F}}_{\mathrm{M}\mathrm{L}}=\text{log}(|\mathrm{\Sigma }|)+\mathrm{t}\mathrm{r}(\mathrm{C}*{\mathrm{\Sigma }}^{-1})-\text{log}(|\mathrm{C}|)-\mathrm{p}$$ (2)

where C is the sample covariance matrix and | · | is the determinant. Given the brief overview of RAM and its reference to ML, we can now incorporate regularization. For further detail underlying matrix specification and algebra see McArdle (2005).

Regularized Regression

The two most common procedures for regularization in regression are the ridge (Hoerl & Kennard, 1970) and the least absolute shrinkage and selection operator (lasso; Tibshirani, 1996); however, there are various alternative forms that can be seen as subsets or generalizations of these two procedures. Both methods minimize a penalized residual sum of squares. Given an outcome vector y and predictor matrix X ε R^n×p, the ridge estimates are defined as

$${\hat{\mathrm{\beta }}}^{\text{ridge}}=\text{argmin}\{\sum _{\mathrm{i}=1}^{\mathrm{N}}{({\mathrm{y}}_{\mathrm{i}}-{\mathrm{\beta }}_0-\sum _{\mathrm{j}=1}^{\mathrm{p}}{\mathrm{x}}_{\mathrm{i}\mathrm{j}}{\mathrm{\beta }}_{\mathrm{j}})}^2+\mathrm{\lambda }\sum _{\mathrm{j}=1}^{\mathrm{p}}{\mathrm{\beta }}_{\mathrm{j}}^2\},$$ (3)

where β₀ is the intercept, β_j is the coefficient for x_j, and λ is the penalty that controls the amount of shrinkage. Note that when λ = 0, Equation 3 reduces to ordinary least squares regression. As λ is increased, the β_j parameters are shrunken towards zero. The lasso estimates are defined as

$${\hat{\mathrm{\beta }}}^{\text{lasso}}=\text{argmin}\{\sum _{\mathrm{i}=1}^{\mathrm{N}}{({\mathrm{y}}_{\mathrm{i}}-{\mathrm{\beta }}_0-\sum _{\mathrm{j}=1}^{\mathrm{p}}{\mathrm{x}}_{\mathrm{i}\mathrm{j}}{\mathrm{\beta }}_{\mathrm{j}})}^2+\mathrm{\lambda }\sum _{\mathrm{j}=1}^{\mathrm{p}}|{\mathrm{\beta }}_{\mathrm{j}}|\}.$$ (4)

In lasso regression, the l₁-norm is used, instead of l₂-norm as in ridge, which also shrinks the β parameters, but additionally drives the parameters all the way to zero, thus performing a form of subset selection (for more detail, see Hastie, Tibshirani, & Friedman, 2009; Tibshirani, 1996).

Although these methods for regularization are intuitively appealing, the question of how to best choose λ remains. Two different methods dominate: using a fit index that takes into account complexity, such as the Akaike information criteria (AIC; Akaike, 1973) or Bayesian information criteria (BIC; Schwarz, 1978), or using cross-validation (CV). The simplest form of CV, and the type that has been used widely in SEM applications (Browne, 2000), is splitting the sample into two: a training and test data set. A large number of prespecified λ values can be utilized (e.g., 40) with each of these models run on the training data set. Instead of examining the fit of the model at this point, the parameter estimates are then treated as fixed parameters and model fit is re-estimated on the test data set. This almost invariably results in worse model fit, but ultimately gives a more accurate estimate of the generalization of the model. After all of these models have generated fit on both the training and test data sets, it is common to pick the model that results in the best fit on the test data set, or choose the most penalized model (most sparse) within one standard error of the best fitting model (Hastie et al., 2009).

Regularized EFA and PCA

First proposed in the context of PCA (Jolliffe, Trendafilov, & Uddin, 2003; Zou et al., 2006), sparse estimation procedures for dimension reduction have flourished with a number of different methods proposed for both PCA and EFA (Choi et al., 2010; Hirose & Yamamoto, 2014b; Jung & Takane, 2008; Ning & Georgiou, 2011). Jung and Takane (2008) proposed penalizing the diagonal of the observed covariance or correlation matrix to overcome the propensity for EFA to yield improper solutions (negative unique variances). This is in contrast to other sparse EFA methods that explicitly use different forms of regularization as a method of achieving a sparse structure, similar to the original goal of achieving simple structure. A sparse structure denotes a factor loading matrix with a large number of zeroes, leading to simpler interpretations of each latent factor. This is in contrast to what is typically done in EFA (PCA), where an orthogonal factor (component) structure is estimated and a specific number of factors (components) are retained. This solution then undergoes rotation, either oblique or orthogonal, to achieve simple structure. An alternative method is that of target or procrustean rotation (Browne, 2001), where a mechanical rotation is replaced with researcher-specified target loadings of zero. This represents a more flexible approach, allowing for input from the researcher on producing a sparse structure. Typically, this rotation does not lead to loadings of exactly zero. Instead, loadings below some prespecified threshold are either omitted from display, or are replaced by truncated values. Needless to say, this is a nonoptimal solution to obtaining a sparse structure (Trendafilov & Adachi, 2014).

REGULARIZED STRUCTURAL EQUATION MODELING

As an attempt to generalize forms of regularization from the regression framework to that of SEMs a new general cost function is proposed for regularization. Although regularization could be added to any form of estimation, ML will be the only estimation method detailed. As previously detailed in Equation 2, the ML cost function can be written as

$${\mathrm{F}}_{\mathrm{M}\mathrm{L}}=\text{log}(|\mathrm{\Sigma }|)+\mathrm{t}\mathrm{r}(\mathrm{C}*{\mathrm{\Sigma }}^{-1})-\text{log}(|\mathrm{C}|)-\mathrm{p}.$$ (5)

Using the ML cost function as a base, the general form of RegSEM estimation is

$$F_{\mathit{\text{regsem}}}=F_{ML}+\lambda P(·)$$ (6)

where λ is the regularization parameter, and takes some value between zero and infinity. When λ is zero, ML estimation is performed. P(·) is a general function for summing the values of one or more matrices. The two most common forms of P(·) include both the lasso (‖·‖₁), which penalizes the sum of the absolute values of the parameters and ridge (‖·‖₂), which penalizes the sum of the squared values of the parameters. The norm in this case can take any form of either vector or matrix, and allows any combination of parameters or matrices. The general form of RegSEM is no different from other regularization equations. The distinction between RegSEM and other forms of regularization comes in the specification of which parameters to penalize. RegSEM allows the regularization of parameters from general SEM models. Regularized parameters can come from either the A or S matrices in RAM notation; however, it could easily be generalized to include matrices from other SEM matrix configurations (e.g., LISREL). Practically, because the value of λ is the same for every parameter, only parameters from either A or S, not both, should be penalized in a model. The penalization of parameters from one matrix in a sense pushes the parameter values into the other matrix (penalizing the A matrix (factor loadings) pushes the values into the corresponding entries of the S matrix (residual variances), and vice versa), therefore, estimation problems could occur if dependent parameters were both penalized. One important detail, with regard to implementation, is to standardize variables prior to estimation because of the summation of parameter estimates in the penalty term. By standardizing the variables, we ensure that each penalized parameter is given an equal weight in contributing to model fit.

The most obvious application of Equation 6 is to penalize the A matrix. As ML and ordinary least squares can be shown to be equivalent in regression under certain assumptions, the exact same estimates from lasso regression can be produced by adding lasso penalties to the direct effects in a regression model specified as a SEM. It is worth noting that to get an exact equivalence, the residual variance for the outcome variable needs to be fixed in structural equation model as this is not a freely estimated parameter in regression (instead a by-product of summing the squared residuals). As a result of this equivalence, RegSEM can be seen as a more general form of regularization, with lasso and ridge regression viewed as subsets.

As in regularized regression, an optimal value of λ is chosen by using a large number of values (typically 20–100) and running the model for each value of the penalty. In RegSEM, the initial penalty should be zero and the penalty should increase thereafter. This is done because of the propensity for estimation problems in SEMs with latent variables. Furthermore, instead of increasing the penalty until all penalized parameters reach zero, testing can be halted once estimation problems occur. This might be most relevant in penalizing factor loadings, where after a high enough penalty is reached, a latent factor no longer has strong enough indicators to reach a stable solution.

RegSEM is implemented as a package in R (R Core Team, 2015), termed regsem. The regsem package makes it easy for the researcher to fit a model with the lavaan package (Rosseel, 2012), and use this model as the basis for regularization with regsem. The regsem package uses the RAM matrices, and has built in capabilities for specifying a large number of penalties with and without cross-validation.

Degrees of Freedom

The degrees of freedom for a model using RAM matrices is

$$\mathrm{d}\mathrm{f}=\mathrm{r}(\mathrm{C})-\mathrm{r}(Ȧ,Ṡ)$$ (7)

where r(C) is the rank of the sample covariance matrix and r(Ȧ, Ṡ) is the rank of the matrix of first derivatives for A and S at the solution. When an element of A or S is shrunken to zero, the first derivative necessarily goes to zero, resulting in an increase in degrees of freedom. This concurs with work done on degrees of freedom for lasso regression, as Zou, Hastie, and Tibshirani (2007) proved that the number of nonzero coefficients is an unbiased estimate of the degrees of freedom for regression. Practically, the degrees of freedom changes only when the beta coefficient for a predictor is shrunken to zero. In the context of SEM, this translates to an increase in the degrees of freedom when a factor loading or covariance is shrunken to zero. It is worth noting that this only occurs for lasso penalties, as ridge parameters are not shrunken all the way to zero. Practically speaking, changing the degrees of freedom as parameters are shrunken to zero can have a large impact on assessing model fit. For instance, when assessing the fit on the training sample, introducing penalties without changing the degrees of freedom will only result in a decrement in fit (e.g., when using the root mean square error of approximation [RMSEA], Tucker–Lewis index [TLI], or comparative fit index [CFI]).

STUDY 1: SIMULATION

The purpose of Study 1 was to determine the ability of RegSEM with lasso penalties to perform a form of subset selection through choosing a final model with selected factor loadings specified as zero. To choose a final model, and it is unknown which fit index is best to use, across either the training or test data set. To examine this question, a number of different fit indices were used to choose a final model. Selection involved choosing the model that fit best according to each fit index. A CFA model was used, with the population parameters simulated at the values in Table 1. Dash marks refer to fixed values of zero in the population model. Performance was judged through measuring the percentage of false positives (number divided by 9), or choosing a final model that concluded factor loadings that were simulated as zero were in fact nonzero.

TABLE 1.

Simulated Factor Structure: Each Factor was Esimated With 6 Factor Loadings, 3 “True” Loadings and 3 “False” Loadings.

		Latent Factors
Items	F1	F2	F3
X1	1.0	-	0
X2	0.2	-	0
X3	1.0	-	0
X4	0	1	-
X5	0	0.2	-
X6	0	1	-
X7	-	0	1
X8	-	0	0.2
X9	-	0	1

Note. Loading entries with a dash were not included in the estimated structure.

Each model had nine factor loadings simulated with a true value of zero, but were in fact allowed to be freely estimated. The simulateData() function from the lavaan package (Rosseel, 2012) in R was used to simulate both training and test data sets that conformed to the factor structure and at the specified sample size. Four different sample sizes were used, 100, 400, 2,000, and 10,000. It was expected that performance would increase as sample size increased due to less random noise in the simulated factor loadings. The results of the simulation are displayed in Table 2.

TABLE 2.

Performance of Fit indexes in Choosing the Simulated Model

		Average False Positive Percentage
N	100	400	1,000	10,000
Ftrain	52.4	46.0	41.1	27.2
NCPtrain	43.3	40.9	37.0	26.9
RMSEAtrain	42.8	38.1	34.2	24.3
BICtrain	22.3	10.6	5.5	4.2
A1Ctrain	29.0	19.6	23.1	13.6
Ftest	28.1	30.0	31.9	24.7
NCPtest	23.2	22.6	22.6	17.7
RMSEAtest	22.2	12.6	12.4	10.6

Note. Each run was replicated 500 times. NCP=noncentrality parameter RMSEA=root mean square error of approximation; BIC=Bayesian information criterion; AIC=Akaike information criterion. Values in bold represent the lowest average false positive percentage for each sample size.

The fit indices used to judge performance included the ML cost function F_train and F_test, non-centrality parameter (NCP) NCP_train and NCP_test, and the root mean square error of approximation (RMSEA) RMSEA_train and RMSEA_test. In the test versions of each fit index, the covariance matrix from the test data set was used in Equation 7 instead of the train covariance matrix. Finally, both the AIC (AIC_train) and BIC (BIC_train) were only used with the training data set. This was due to the degree of penalty for extra parameters in Equation 9, which was thought to be enough to increase the generalizability to alternative data sets.

It is important to note that because both the NCP and RMSEA take into account degrees of freedom, their values could decrease (get better) even as the F_ML becomes worse. This is due to the degrees of freedom increasing as additional factor loadings are set to zero. Because of this, both the NCP and RMSEA might do well when using the train data despite F_ML monotonically increasing as λ is increased. The results of Study 1 are displayed in Table 2. False negatives (how often the final model over-penalized the true factor loading of 0.2 and concluded that it was zero) are not displayed because the percentage of errors was very low. Across the sample sizes, the BIC performed the best, especially for larger sample sizes. For N = 100, the RMSEA_test had the lowest percentage of error. This could be due to how sample size is factored into the BIC, whereas the RMSEA is not affected by sample size.

The results suggest that sample size played a large role in the use of regularization in SEM. Across all of the fit indices, model selection improved as sample size increased. Additionally, the results of all fit indices were better in the test sample versus the training. This is not surprising given the amount of research on regularization with cross-validation. It is interesting that even when combining a fit index that penalizes complexity, such as the NCP or RMSEA, none of the results suggest that RegSEM over-penalized models when examining the results from the test sample. The lack of false negatives, combined with none of the false positives reaching zero, provides evidence for this conclusion and might lend support to choosing the least complex model within one standard error of the best fit as in regression (Hastie et al., 2009). Additionally, with the RMSEA and NCP proving more accurate in model selection in comparison to F_ML, the importance of taking into account the change in degrees of freedom is highlighted.

Overall, the results are very promising. Even though error rates for some of the fit indexes were above 20%, this is not cause for concern. The resulting erroneous factor loadings were on the order of 0 to 0.1, and might be up for elimination simply on the grounds of their small magnitude. When the goal of regularization is to achieve simple structure or subset selection in the context of factor analysis, the BIC was best, with the RMSEA_test coming in a close second. More research is needed with other forms of structural equation models to determine if the same results hold. The purpose of this simulation was not to show that performing subset selection with RegSEM completely negates the need for human judgement, but instead that RegSEM can identify models that are closer to the truth and might indicate further model modification that could bring researchers closer to the right or best answer.

STUDY 2: FIT ILLUSTRATION

The question of when regularization can improve model fit, and when using non-penalized estimation might be best still remains. In some cases, the initial model might fit well, without too complex of a representation. Further, the addition of regularization might not improve the fit of the model on a holdout sample. The use of regularization does not guarantee improved model fit with respect to generalizability. In these scenarios, the starting structure of the model might be incorrect; either a different factor structure is needed or other model assumptions are violated. This can only be determined with a thorough examination, assessing multiple fit indices across a spectrum of penalties.

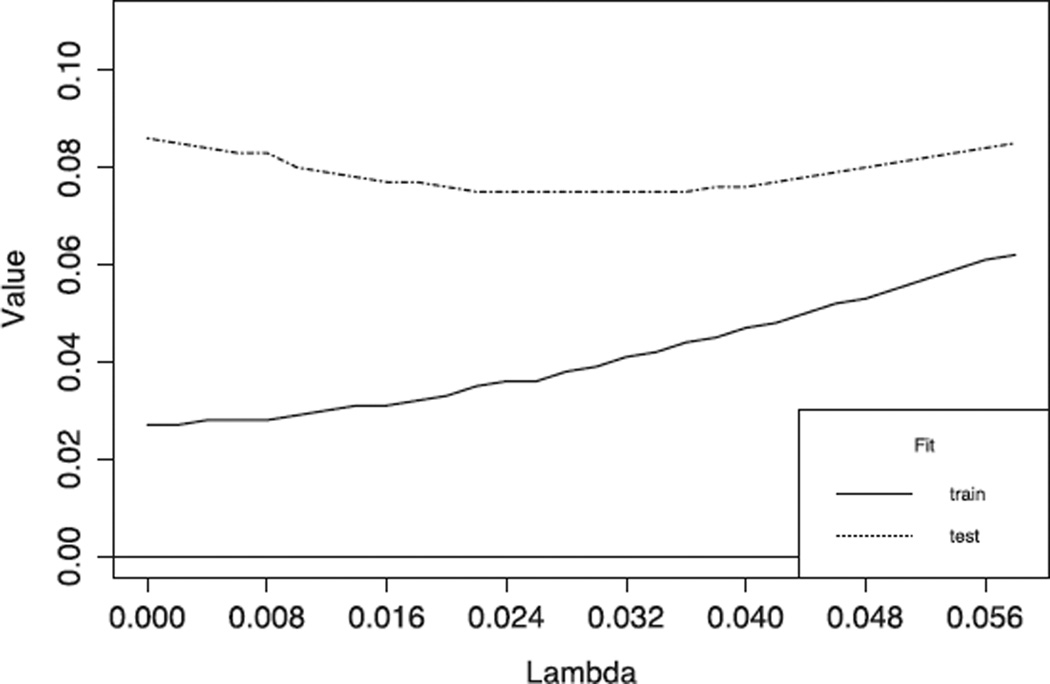
In the first illustrative example, data were simulated using the simulateData() function from the lavaan package. Using a sample size of 500, the population model was simulated to have three factors, with three manifest variables as indicators for each factor, with no cross-loadings. However, for demonstration purposes, RegSEM was used with a model that allowed three cross-loadings for each factor in addition to the three true loadings. To illustrate a situation where little was known regarding the structure of the factor loadings, other than that there were six plausible indicators for each factor, penalties were applied to all factor loadings (factor variances were constrained to be one). The values of F_ML for both the train and test data sets are displayed in Figure 2.

FIGURE 2.

Example analysis using 9 scales from a simulated data set demonstrating how fit of both the training and test data sets changes across increasing penalization.

The addition of shrinkage moved the cross-loading parameters closer to zero, resulting in a better fit on the test data set despite also penalizing the true factor loadings. This is evidenced by the slight convexity to the test fit line, with a minimum achieved at a value of λ greater than zero. Note that fit will always be worse on the training data set when using a fit index that does not account for model complexity. In this situation, a two-step strategy might be advisable. The first step penalizes all of the factor loadings to determine which loadings might be zero. Once the zero loadings are determined, re-fitting the model with only the non-zero factor loadings and no regularization.

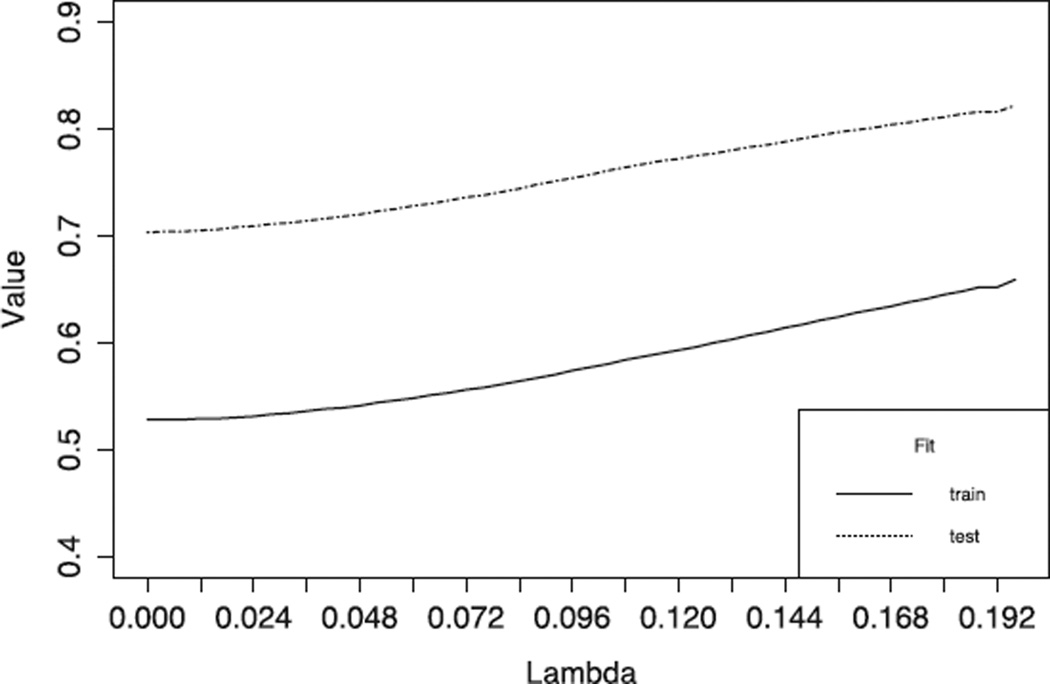
However, the use of penalties does not always improve test model fit, which is demonstrated in Figure 3. In Figure 3, the Holzinger-Swineford data set (Holzinger & Swineford, 1939) was used to test a one-factor model with a subset of nine cognitive scales. This initial fit was not good (χ² (27)= 348.7, p <.001), and the increase of penalties only made the train and test model fit become worse (monotonic increase in each fit line). In this case, it would be necessary to start with a different factor structure. The best fitting structure to these data is generally thought to be a bi-factor model with one general factor and three specific factors. In situations like this where the ML fit is poor and the use of regularization on the factor loadings only makes it worse, it might be advisable to conduct a search for the best model. To use RegSEM to search among different factor structures, not just for which indicators are necessary within a single factor structure, it is generally best to start with the most complex model and then add penalties to see which factors, loadings, and so on are unnecessary.

FIGURE 3.

Example analysis using 9 scales from the Holzinger – Swinefored data set demonstrating how fit of both the training and test data sets changes across increasing penalization.

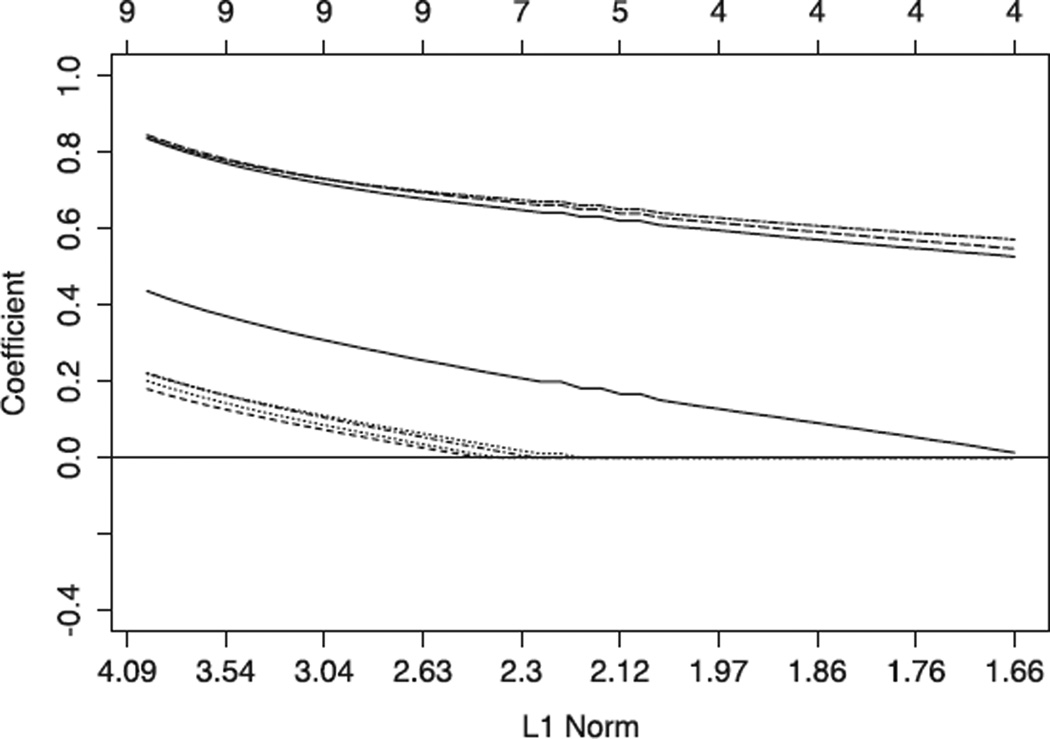
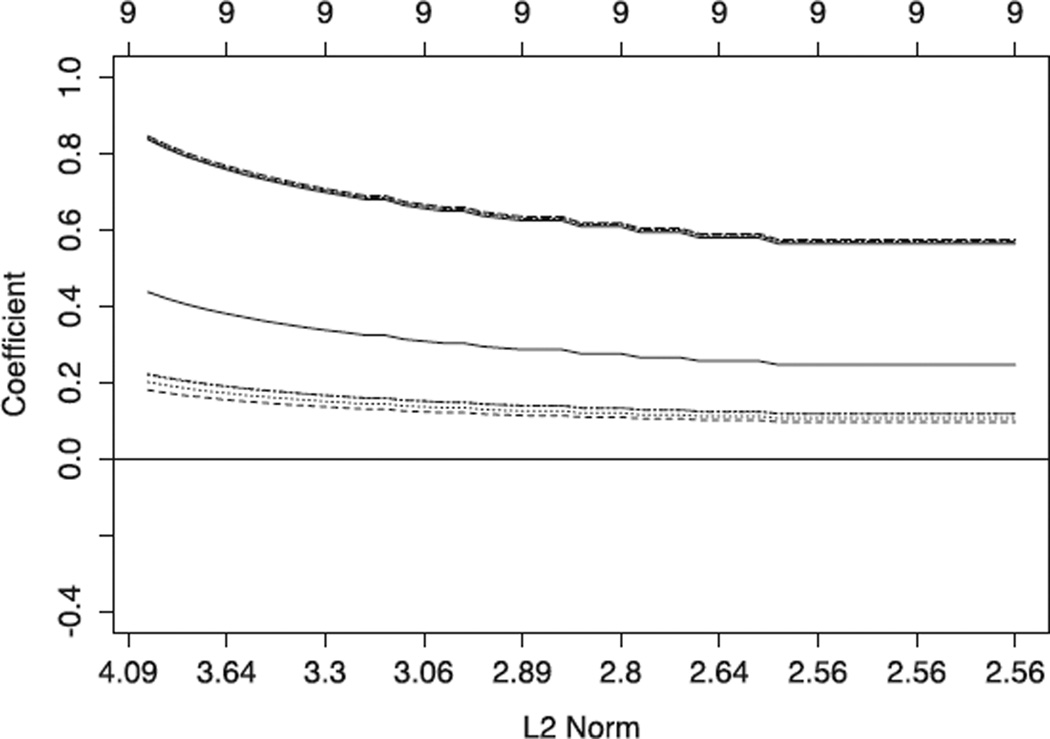
To get a feel for how regularization influences parameter estimates, the estimates for the nine factor loadings in the Holzinger-Swineford sample were plotted in Figure 4 for lasso penalties and in Figure 5 for ridge. In Figure 4, some factor loadings are quickly set to zero, whereas the estimates in Figure 5 all plateau at a point greater than zero. If the goal of regularization was to remove factor loadings (set to 0), then plotting the estimates across the range of λ values can be particularly helpful. This facilitates the inclusion of domain or theoretical knowledge into the decision-making process. For instance, in Figure 4, the factor loadings that were set to zero rather quickly could be the most natural candidates for removal, even without looking at the fit indices.

FIGURE 4.

Example analysis using 9 scales from the Holzinger–Swinefored data set. A one-factor model was used, penalizing the absolute the absolute value of each of the 9 factor loadings. The top axis denotes the number of nonzero loadings at every five iterations. The bottom axis details the sum of of the absolute values of the factor loadings at every 5 iterations.

FIGURE 5.

Example analysis using 9 scales from the Holzinger–Swinefored data set. A one-factor model was used, penalizing the 12 normal of each the 9 factor loadings. The top axis denotes the number of nonzero loadings at every five iterations. The bottom axis details the sum of the absolute values of the factor loadings at every 5 iterations.

STUDY 3: EMPIRICAL EXAMPLE

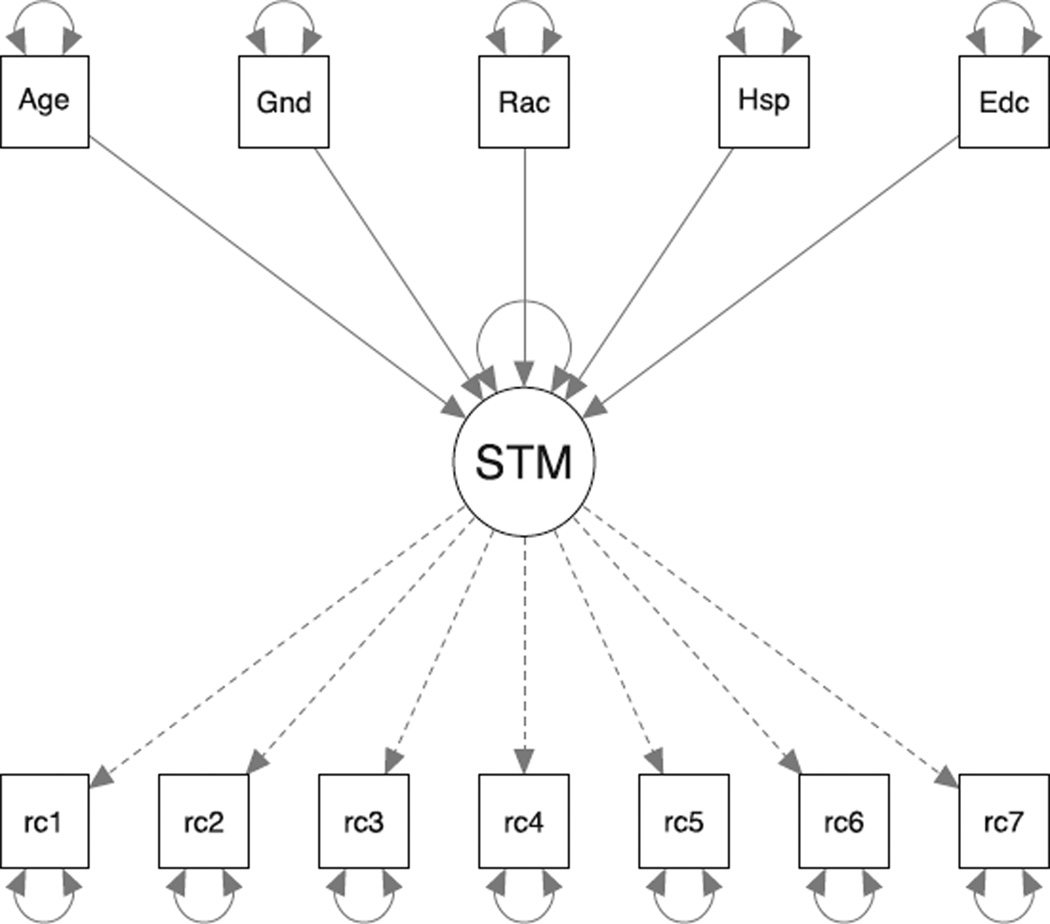
To demonstrate the utility of RegSEM at the structural part of a multiple indicators multiple causes (MIMIC) SEM, we analyzed data from the 2006 Health and Retirement Study (HRS; Juster & Suzman, 1995). The motivating model, depicted in Figure 6, was a one-factor CFA model using 7 items (rc1–rc7) from the Immediate Recall task. The latent variable, conceptualized as short-term memory (STM), was predicted by five covariates: age, gender, race, hispanic, and years of education (Ed). Fitting the non-regularized model (Model 1) resulted in the estimates for the regressions that are displayed in Table 3.

FIGURE 6.

Health and Retirement study structural equation model. Note. STM=short-tem memory.

TABLE 3.

Parameter Estimates From the Structural Part of the Heath and Retirement Study Structural Equation Model

		Structural Model
Covs	Model 1	Model 2	Model 3
age	−0.069	−0.038	−0.067
gender	0.078	0	0
race	−0.015	0	0
hispanic	0.012	0	0
education	0.013	0	0

All of the regression coefficients in Model 1 were significant at p <.001. The question we were trying to answer in this analysis was not what covariates have a significant relationship in predicting the latent variable, but instead, which regressions were likely to generalize beyond this sample. With a sample size of over 18,000, it was expected that every regression coefficient would be significant. One alternative is that we could have chosen which covariates to keep based on effect sizes, although this again does not get to the question of what is likely to generalize beyond the HRS sample. To get at generalizability, we turned to regularization.

Using RegSEM, we could apply either ridge or lasso penalties. We chose to use lasso penalties to stabilize the estimates and perform subset selection. Lasso penalties tend to over-penalize parameters that were not set to zero (Hastie et al., 2009). Away to overcome this is to use lasso penalties to first identify the nonzero paths, and then run an unconstrained model (i.e., linear regression with no penalties) using only these variables in the model. This is known as the relaxed lasso (Meinshausen, 2007). Therefore, in addition to using lasso penalties (Model 2), we kept the non-zero regressions from this model and re-estimated the model without penalties (Model 3). The factor loading estimates from Model 1 were used as fixed estimates for both Models 2 and 3. Imposing this form of invariance is necessary for both ensuring that the formulation of the latent construct stays the same across penalties, and also preventing the pushing of parameter estimates from the structural regression estimates to the factor loadings. Constraining the factor loadings ensures that the regularization only affects the regression parameters.

To choose the optimal value of penalty (λ), we used the RMSEA with cross-validation. The HRS sample was randomly split into two: a training and test data set. RegSEM was conducted on the train data set with twenty values of λ, and the RMSEA was tested on the test data set to get a better understanding of how the model will fit beyond the current sample.

The lowest value of RMSEA occurred at a λ of 0.7. Rerunning the RegSEM model at this penalty value produced the estimates in the column for Model 2 in Table 3. The only non-zero regression was for age. Removing the penalty and only keeping age as a predictor of STM for Model 3, we can see in Table 3 that the resulting parameter estimate is almost the same as in Model 1. As a result, using RegSEM with lasso penalties pared away all but one covariate, age, suggesting that going forward this might be the only important variable to use as a covariate for conditioning the model estimates.

DISCUSSION

The application of RegSEM in the above two studies reported here represents a small subset of the possible ways to use regularization with SEM models. These studies demonstrated that RegSEM makes model choice nearly continuous, and allows for a more flexible application of finding the model structure that increases both interpretability and generalizability. Study 1 showed RegSEM had a high propensity for choosing the correct model in a scenario where non-penalized estimation would result in choosing a model with a large number of non-zero factor loadings that are in reality zero. Study 2 provided a demonstration of scenarios where RegSEM can and cannot improve the fit of the initial model, and how plotting the fit across the range of λ values can assist in determining the best tool for the data. Finally, Study 3 demonstrated the application of RegSEM with lasso penalties on the structural part of a MIMIC model with the HRS data set. This example can be seen as a direct translation of lasso regression to the use of lasso penalties for the regression parameters in a structural equation model.

As it currently stands, we are unaware of any method to regularize specific parameters at the structural model of an SEM. Of course, one could test the measurement model, and then generate a factor score to be entered into one of the many pieces of software for conducting regularized regression. However, creating factor scores is fraught with problems (e.g., Grice, 2001), and this strategy does not generalize to more complicated models that might have more latent factors, for instance. Although Study 3 included only a small number of predictors in the structural model, this empirical example demonstrates an additional way that RegSEM can be used. With the advent of Big Data, it will become increasingly common to have extremely large models with possibly hundreds or thousands of covariates. To make sense out of this high level of complexity, using regularization with lasso penalties, for instance, will become increasingly useful to pare away unnecessary and uninformative parameters, allowing the researcher a clearer picture of what the model says about reality. RegSEM gives the researcher the flexibility to use theoretical input in shaping the model while exploring alternative specifications of both the measurement and structural parts of complex SEMs to enhance either interpretability or generalizability.

The purpose of introducing a new form of estimation for SEMs was not necessarily to show how it is better in certain scenarios, but instead to show that one general method can accomplish several tasks that would have required using separate methods. As previously mentioned, the contexts examined in Studies 1 through 3 represent a small subset of the possible applications of RegSEM. In addition to the aforementioned benefits, regularization can provide stable solutions in the case of multicollinearity among predictors and when the number of predictors is larger than the number of cases (p > n; for overview, see Hastie, et al. 2009; McNeish, 2015). Additionally, given the aforementioned advent of Big Data, regularization has provided more accurate solutions in the case of recovering high-dimensional signals in areas such as image reconstruction and genomic data, to name a few (for overview, see Hastie et al., 2015; Rish & Grabarnik, 2014). Given that this article has focused on using RegSEM mainly for model search and modification, future research should investigate other applications of RegSEM outside this context.

The question of whether ridge or lasso penalties (or other forms of penalty) should be used and in what circumstances remains. If subset selection is the aim, lasso penalties are clearly better. Lasso penalties shrink parameters all the way to zero, whereas ridge estimates never reach zero. RegSEM with ridge penalties can be seen as an extension of ridge SEM (Yuan & Chan, 2008; Yuan, Wu, & Bentler, 2011), where a ridge penalty is added to the diagonal of a covariance or correlation matrix. In contrast, RegSEM can be seen as a method for adding various types of penalties to any part of the SEM.

Although a limited number of applications of RegSEM are detailed, there are a wide array of possible applications not covered, particularly in more complex SEMs. One possibility is applying regularization to longitudinal models specifying multiple curves. This might be understood easiest with latent-growth curve models (McArdle & Epstein, 1987; Meredith & Tisak, 1990), where models can be tested with anywhere from a linear model with fixed factor loadings from the slope to the latent basis growth model, which can be seen as an exploratory approach to determining the optimal shape of development (Grimm, Steele, Ram, & Nesselroade, 2013). One could penalize the deviation in the slope from a linear curve, to produce a slope on the continuum between the most constrained, fixing all slope parameters as in the case of linear basis, to the least constrained, in the case of the latent basis growth model. Particularly through the use of cross-validation, the final model could be chosen on the potential for generalizability. RegSEM allows for more robust testing of models and their potential to generalize, overcoming the problems with only testing models that differed largely in their model specification. RegSEM turns model selection into a more continuous decision.

An area for future research is the comparison of frequentist and Bayesian methods for regularization in SEM. Although not marketed as a method for performing regularization or more broadly for achieving simple structure, Bayesian SEM (BSEM; Kaplan & Depaoli, 2012; Lee, 2007; Levy, 2011; Muthén & Asparouhov, 2011) allows the researcher a high level of flexibility in specifying model structure. Specifically, the Mplus implementation of BSEM (Muthén & Asparouhov, 2011) using small variance priors allows for parameter estimates to occupy the area between unconstrained and fully constrained, yielding a hybrid approach. Changing the prior variance on a parameter can either shrink or inflate the parameter estimates, resulting in a more continuous form of model selection. Setting the prior variance of some parameters to be small to restrict the likely range of estimates, allows the researcher to experiment with allowing more influence of some parameters and negating the influence of others. Although the equivalence or similarity between regularization in a frequentist and Bayesian framework has been established in the context of regression (Park & Casella, 2008; Tibshirani, 1996), this has not been the case in the context of SEM. Future research should compare the parameter estimates between RegSEM and BSEM with both Normal (ridge) and Laplace (lasso) distribution priors.

The applications discussed in this article have not addressed uncertainty regarding the number of factors in a model. This is a next step of examination, where the number of factors are allowed to vary in addition to the factor loading estimates. One could imagine starting with the largest number of factors possible (given identification constraints; e.g., Hayashi & Marcoulides, 2006), and through increasing the penalties to each factor loading, eliminate latent factors from the model when either the number of non-zero loadings or sum of loadings drops below a threshold. Although more complicated in its implementation, this form of testing of models is necessary to create a form of automatic model creation. The goal of testing both the number of factors and their respective loadings is more in line with the search algorithms described in the introduction (e.g., Marcoulides & Ing, 2012). It is worth testing whether these methods can produce similar results to RegSEM, and in what circumstances one might be preferred. One possibility is to incorporate one of the many genetic algorithm or tabu search R packages into regsem to provide a comparison, allowing the researcher greater flexibility in choosing the final model.

The accuracy of the final parameter estimates in Study 1 was not detailed. The reason for this is simple as in many cases a two-step strategy to deriving final model parameter estimates might be warranted. In lasso regression, it has been found that the lasso has a propensity to over shrink the coefficients, with these estimates biased toward zero (Hastie et al., 2009). Testing different forms of obtaining the final parameter estimates is an additional area for future study with regard to RegSEM, as it is unclear whether conducting a two-stage approach would be beneficial and in what circumstances.

Despite the lack of applications using regularization in the psychological and behavioral sciences, this will soon change. A recent overview of using the lasso for regression (McNeish, 2015), along with applications in differential item functioning (Magis, Tuerlinckx, & Boeck, 2014; Tutz & Schauberger, 2015), highlight this movement. It is fitting that regularization will start its proliferation at the same time that we face a crisis of replication (e.g., Pashler & Wagenmakers, 2012). This fact, in and of itself, is enough evidence that we need to find ways to measure the propensity to replicate or generalize. RegSEM, seen as a family of tools for regularization with psychological and behavioral data, offers a flexible approach to model generation and modification, with an emphasis on generalizability. This article represents a first step in the application and evaluation of RegSEM.