A Maximum-Likelihood Method to Estimate a Single ADC Value of Lesions Using Diffusion MRI

Abstract

Purpose

Design a statistically rigorous procedure to estimate a single apparent diffusion coefficient (ADC) of lesion from the mean lesion signal intensity in diffusion MRI.

Theory and Methods

A rigorous maximum-likelihood (ML) technique that incorporated the statistics of the mean lesion intensity and accounted for lesion heterogeneity was derived to estimate the ADC value. Performance evaluation included comparison with the conventionally used linear-regression (LR) and a statistically rigorous ADC-map technique using realistic and clinically relevant simulation studies conducted with assistance of patient data for homogeneous and heterogeneous lesion models.

Results

The proposed technique outperformed the LR and ADC-map approaches over a large spectrum of SNR, ADC, lesion size, image-misalignment parameters, including at no image misalignment, and different amounts of lesion heterogeneity. The method was also superior at different sets of b values and in studies from specific patient-image-derived data. The technique takes less than a second to execute.

Conclusions

A rigorous, computationally fast, easy-to-implement, and convenient-to-use ML technique was proposed to estimate a single ADC value of the lesion. Results provide strong evidence in support of the method.

Introduction

Diffusion is described as the thermally induced behavior of molecules moving in a microscopic random pattern in a fluid. Diffusion-weighted magnetic resonance imaging (DWMRI) is sensitive to this microscopic motion, which can be quantified by means of an apparent diffusion coefficient (ADC) [1], [2]. Since cellular structures generally restrict water mobility, a change in the lesion anatomy in response to therapy typically results in a change in the ADC value of the lesion. There is considerable evidence in preclinical models that the ADC in tumors increases early in response to successful therapies [3]. Clinical trials have begun to examine the effectiveness of the ADC as an early surrogate marker for therapy response [4]–[7]. However, for DWMRI to function as a reliable imaging biomarker, accurate ADC estimation is critical.

There is considerable research on ADC estimation in diffusion-weighted (DW) images. Several statistically rigorous methods that account for the Rician distributed noise in DW images have been proposed to compute the ADC of the lesion on a pixel-by-pixel basis [8]–[12], yielding an ADC map of the lesion. However, these techniques require that the images acquired at the different b values be perfectly registered with each other. Similarly, statistically rigorous techniques to model the Rician noise distribution have also been proposed in the context of estimating relaxation parameters from magnitude MR images [13]–[15]. However, these techniques again estimate the relaxation parameter in each pixel of the region of interest (ROI) on a pixel-by-pixel basis. Thus, their application to the problem of ADC estimation requires perfectly registered images at the different b values.

In lesions in organs such as the liver, kidney, or spleen, possible movement of the organ across the different b-value scans could result in misalignment of the images at the different b values [6], [7]. Consequently, computing the ADC map on a pixel-by-pixel basis is error-prone [6]. To reduce the misalignment-related inaccuracies, the lesion is instead individually segmented at the different b values, and the mean signal intensity of the lesion pixels at the different b values is computed. This parameter is less variant to lesion movement and is used to compute a single ADC value for the lesion [6], [7], [16]–[18]. To compute this single ADC value, a linear-regression (LR) technique is currently used [6], [16]. However, as we show later, this LR method is based on an incorrect noise model and does not explicitly account for lesion heterogeneity, thus leading to biased ADC estimates in several clinically relevant scenarios. Statistically rigorous methods similar to those proposed for computing ADC or relaxation-parameter maps are not available for computing this single ADC value from the mean signal intensity values. Thus, in this paper, our objective was to design a statistically rigorous estimator for this single ADC value that incorporates an accurate statistical model of the noise in the measured mean signal intensity and accounts for lesion heterogeneity.

Another motivation for devising a estimator for the single ADC value of a lesion was that in several DWMRI studies, including those where the images at different b values are assumed perfectly aligned, often only a single ADC value of the lesion is used for further analysis, comparison, and reporting [19]–[23]. An often-used method to estimate this single ADC value is by estimating the ADC of all the image pixels, i.e. an ADC map, using a ADC-map technique, and then computing the mean ADC over all the lesion pixels. Statistically rigorous ADC-map techniques are often computationally intensive due to the large number of lesion pixels for which the ADC must be evaluated [9]. Further, ADC-map techniques use the individual pixel intensities as inputs, which is potentially a more noisy measurement than the measured mean signal intensity of the entire lesion. Additionally, the ADC-map techniques have not been designed to estimate a single ADC value for the lesion, and thus might not be the optimal method for estimating a single ADC value. For example, the ADC-map techniques are based on the noise statistics of the individual pixel intensities, and not the mean measured signal intensity over the lesion. In fact, we have previously shown that using the measured mean lesion intensity in conjunction with a simple ADC estimation approach yields a more accurate estimate for the single ADC value for homogeneous lesions in comparison to ADC-map approaches that use regression techniques [17], [24]. These observations led to further interest in designing an estimator for the single ADC value of the lesion from the mean lesion intensity measurements, and comparing it with statistically rigorous ADC-map techniques [9].

Theory

Problem Formulation

Let N be the number of b values at which the lesion is imaged. Let b_i denote the b value for the i^th scan, for i = 1,…, N. For the j^th lesion pixel at the i^th b value, let s_ij and m_ij denote the true signal magnitude and the measured (noisy) signal magnitude, respectively. Also, let us denote the true and measured mean intensity value of the lesion at b value b_i by s̄_i and m̄_i, respectively. Using this mean signal intensity at the different b values, a single ADC value, denoted by a, must be estimated for the lesion, which is required to satisfy the mono-exponential diffusion model [6]

$${\overline{s}}_i=S_0\text{ exp}(-a{b}_i),$$ (1)

where S₀ is another unknown parameter. The measured mean signal intensity at b value b_i is computed as

$${\overline{m}}_i=\frac{1}{J}\sum _{j=1}^J{m}_{ij},$$ (2)

where J is the total number of lesion pixels in the image. Let M̄ = {m̄_i, i = 1,…, N} denote the vector of measured mean signal intensities at the different b values. Our objective is to estimate the ADC value a and the parameter S₀ given the mean measured signal intensities M̄.

Linear-Regression Approach

The LR approach is conventionally used to estimate the single ADC value a [6], [16], [25]. Denoting the noise in the measured mean signal intensity at b value b_i by n_i, we can write

$${\overline{m}}_i={\overline{s}}_i+n_i=S_0\text{exp}(-a{b}_i)+n_i,$$ (3)

using Eq. (1). Taking the logarithm on both sides of the above equation yields

$$\text{log }{\overline{m}}_i=\text{log }{S}_0-a{b}_i+\text{log}{n}_i.$$ (4)

We thus obtain a linear equation relating a and log(m̄_i). In the LR approach, a least-squares minimization technique is used to estimate a and S₀. However, least-squares techniques are optimal when the dependent random variable, in this case log(m̄_i), is normally distributed [26]. However, as we discuss later, this is not the case. Another issue with the LR method is that in DWMRI, at different b values, the variance of the measured mean signal intensities is different [9], [10] due to reasons such as dependence of noise on true signal magnitude, lesion heterogeneity, non-linearity of the scanner in different acquisitions, dynamic behavior of the organ under consideration, and flow effects around the organ. The LR method does not model these factors. Thus, as shown in the Results section, it often yields biased results in several clinically relevant scenarios.

Proposed Maximum-Likelihood Approach

To overcome the issues with the LR approach, we must accurately account for the statistics of the measured mean signal intensity m̄_i while deriving the estimation technique. It would also be preferable to have an estimation technique that is optimal in some sense. In this regard, the maximum-likelihood (ML) estimator has several useful properties. If an efficient estimator exists, i.e. an estimator that is unbiased and attains the lower bound on the variance of any unbiased estimator, then the ML estimator is efficient. We thus derive a ML estimator of the ADC value. The objective in the ML approach is to obtain values of {a, S₀} that maximize the probability of occurrence of the measured mean signal intensities at all the b values. Therefore, the ML approach requires an accurate and rigorous formulation of the probability model of the measured mean signal intensity.

We consider the general case of a heterogeneous lesion. It is well known that MR images are corrupted by Rician noise [27]. Let us denote the variance of this noise by σ_r. Thus, at b value b_i, for the j^th lesion pixel, the probability model for the measured signal intensity m_ij is given by

$$\text{pr}(m_{ij}|s_{ij},{\sigma }_{\mathrm{r}})=\frac{m_{ij}}{{\sigma }_{\mathrm{r}}^2}\text{exp}[\frac{-(m_{ij}^2+s_{ij}^2)}{2{\sigma }_{\mathrm{r}}^2}\left]I_0\right(\frac{m_{ij}{s}_{ij}}{{\sigma }_{\mathrm{r}}^2}),$$ (5)

where pr(m_ij|s_ij, σ_r) denotes the conditional probability distribution function (pdf) of m_ij given s_ij and σ_r and I₀(x) denotes the zeroth-order modified Bessel function of the first kind. From Eq. (2), m̄_i is the sum of J Rician-distributed random variables, {m_ij, j = 1,…, J}. We assume that the noise is independent and identically distributed (i.i.d) across all the pixels. Therefore, the J Rician-distributed random variables m_ij will also be independent of each other. However, they might not be identically distributed since in a heterogeneous lesion each pixel could have a different true intensity s_ij.

Our objective is to determine the pdf of m̄_i, or alternatively, the pdf of the sum of N independent, but not identically distributed Rician random variables {m_ij, j = 1, 2,‥, N}. The presence of the modified-Bessel function and the Heaviside function in the Rice distribution complicates this task. Even simple cases like the true magnitude being equal to zero are addressed in terms of approximate schemes such as saddle-point integration or infinite summation [12]. It has been shown using simulations that the sum of Rician random variables with the same mean value tends to a normal distribution [12]. In our problem, due to lesion heterogeneity, the Rician random variables {m_ij, j = 1, 2,…, J} do not have the same mean. Although we can show using the central limit theorem that the sum of Rician random variables approaches a normal distribution, determining the mean of this normal distribution is still complex, since the mean of a Rice distribution is a complicated expression with Bessel functions. We instead use the fact that if the signal-to-noise ratio (SNR) of each lesion pixel, i.e. s_ij/σ_r, is greater than 2.64, then the Rice distribution of m_ij will approach a normal distribution with mean $\sqrt{s_{ij}^2+{\sigma }_{\mathrm{r}}^2}$ and variance ${\sigma }_{\mathrm{r}}^2$ [9], [27]. On our dataset of lesion images, we empirically verified that the assumption of SNR > 2.64 is true with most lesion pixels. With this assumption, {m_ij, j = 1,…, J} are normal and independently distributed random variables.

Next, it can be shown, either using characteristic functions [26] or the convolution method [28], that the sum of J independent normal random variables will also be a normal random variable, with a mean and variance equal to the sum of the means and sum of variances of the J random variables, respectively. Since we have established that {m_ij, j = 1, 2,…, J} are normal and independently distributed, using Eq. (2) we can infer that m̄_i is normally distributed with mean

$${\mu }_i=\frac{1}{J}\sum _{j=1}^J\sqrt{s_{ij}^2+{\sigma }_{\mathrm{r}}^2}$$ (6)

and variance σ_r²/J. Therefore, the expression for the PDF of m̄_i can be written as

$$\text{pr}({\overline{m}}_i|{\mu }_i,{\sigma }_{\mathrm{r}})=\sqrt{\frac{J}{2\pi {\sigma }_{\mathrm{r}}^2}}\text{exp}[-\frac{{({\overline{m}}_i-{\mu }_i)}^2}{2{\sigma }_{\mathrm{r}}^2/J}].$$ (7)

However, this probability model is still not useful since computing μ_i requires a knowledge of the unknown true signal intensity of each lesion pixel s_ij. In the ML scheme, we would like to express the unknown value in terms of S₀ and a, but we cannot express s_ij in terms of S₀ or a. To circumvent this issue, we rewrite each s_ij as the sum of s̄_i and the deviation of s_ij from the mean, which we denote by δ_ij, i.e.

$$s_{ij}={\overline{s}}_i+{\delta }_{ij}.$$ (8)

Substituting Eq. (8) in Eq. (6), we can rewrite the mean of m̄_i as

$${\mu }_i=\frac{1}{J}\sum _{j=1}^J\sqrt{{({\overline{s}}_i+{\delta }_{ij})}^2+{\sigma }_{\mathrm{r}}^2}=\frac{{\overline{s}}_i}{J}\sum _{j=1}^J\sqrt{1+\frac{2{\overline{s}}_i{\delta }_{ij}+{\delta }_{ij}^2+{\sigma }_{\mathrm{r}}^2}{{\overline{s}}_i^2}}.$$ (9)

We use the Taylor series to expand the term in the square root. Assuming that the heterogeneity of the lesion is not high, the second and higher-order terms in the expansion can be neglected. Consequently, the expression for μ_i can be simplified to yield

$${\mu }_i={\overline{s}}_i+\frac{1}{J}\sum _{j=1}^J{\delta }_{ij}+\frac{1}{2{\overline{s}}_{i}J}\sum _{j=1}^J({\delta }_{ij}^2+{\sigma }_{\mathrm{r}}^2).$$ (10)

We recognize that since δ_ij represents the deviation of s_ij from the mean signal intensity s̄_i, ${\sum }_{j=1}^J{\delta }_{ij}$ is equal to 0. Also, $\frac{1}{J}{\sum }_{j=1}^J{\delta }_{ij}^2$ is the sample variance of s_ij over the whole lesion, while ${\sigma }_{\mathrm{r}}^2$ is the variance of MR noise. Since the noise and true signal intensity are independent of each other, $\frac{1}{J}{\sum }_{j=1}^J({\delta }_{ij}^2+{\sigma }_{\mathrm{r}}^2)$ is the sample variance of m_i over all the lesion pixels for the i^th b value. We denote this term for the i^th b value by ${\sigma }_i^2$, and it can be estimated from the measured lesion pixel intensities as

$${\hat{\sigma }}_i^2=\frac{1}{J-1}\sum _{j=1}^J{(m_{ij}-{\overline{m}}_i)}^2,$$ (11)

where σ̂_i denotes the estimated value of σ_i. Using Eqs. (10) and (11), μ_i can be further rewritten as

$${\mu }_i={\overline{s}}_i+\frac{1}{2{\overline{s}}_i}{\hat{\sigma }}_i^2.$$ (12)

Substituting this expression in Eq. (7), we can rewrite the expression for the PDF of m̄_i as

$$\text{pr}({\overline{m}}_i|{\overline{s}}_i,{\sigma }_{\mathrm{r}})=\sqrt{\frac{J}{2\pi {\sigma }_{\mathrm{r}}^2}}\text{exp}[-\frac{{({\overline{m}}_i-{\overline{s}}_i-\frac{{\hat{\sigma }}_i^2}{2{\overline{s}}_i})}^2}{2{\sigma }_{\mathrm{r}}^2/J}].$$ (13)

For the measurements at the different b values, the noise terms are independent of each other. We can write the complete probability model for the vector of measured mean signal intensities M̄ = {m̄_i, i = 1,…, N} as

$$\text{pr}(\overline{\mathbf{M}}|\overline{\mathbf{S}},{\sigma }_{\mathrm{r}})=\prod _{i=1}^N\text{pr}({\overline{m}}_i|{\overline{s}}_i,{\sigma }_{\mathrm{r}}),$$ (14)

where S̄ = {s̄_i, i = 1,…, N} is the vector of true mean signal intensities. We note from Eq. (1) that each of these s̄_i is related to the ADC value a and the parameter S₀. Our objective is to compute the values of {a, S₀} that maximize the probability of the measured mean signal intensities M̄. Thus, from Eq. (14), we obtain the likelihood function that we have to maximize:

$$L(a,S_0;\overline{\mathbf{M}},{\sigma }_{\mathrm{r}})=\text{pr}(\overline{\mathbf{M}}|a,S_0,{\sigma }_{\mathrm{r}})=\prod _{i=1}^N\text{pr}({\overline{m}}_i|S_0,a,{\sigma }_{\mathrm{r}}).$$ (15)

For computational efficiency, we maximize the logarithm of the likelihood function given by

$$\lambda (a,S_0;\overline{\mathbf{M}},{\sigma }_{\mathrm{r}})=\sum _{i=1}^N\text{log pr}({\overline{m}}_i|S_0,a,{\sigma }_{\mathrm{r}}).$$ (16)

Substituting the expression for pr(M̄|a, S₀, σ_r), or equivalently, pr(m̄_i|s̄_i, σ_r) from Eq. (13) into the above expression and ignoring terms that do not depend on {a, S₀}, we derive that the ML estimates of {a, S₀} should minimize the function

$$\lambda (a,S_0;\overline{\mathbf{M}})=\sum _{i=1}^N{[{\overline{m}}_i-S_0\text{exp}(-a{b}_i)-\frac{{\hat{\sigma }}_i^2}{2S_0\text{exp}(-a{b}_i)}]}^2$$ (17)

Therefore, the ML estimate of the ADC value of the lesion can be determined. We note that the function λ(a, S₀, M̄) does not require us to explicitly compute σ_r, although there is dependence with respect to σ_r that is hidden in the term σ̂_i. Generally σ_r is computed from the signal intensities in the background regions of the image by maximizing the log-likelihood for the Rayleigh-distributed data in that region [9]. However, such an estimate is error-prone since signal artifacts could conceivably enter such regions [9]. Samuel-Walker et al. [9] suggest that a more robust approach is to instead directly estimate the noise variance from the measured intensity of the lesion pixels. Our method implicitly takes the same approach since it estimates the variance σ_i from the lesion pixels instead of explicitly estimating σ_r.

Methods

In-Vivo Imaging

Our research group used DWMRI to monitor the therapeutic response in breast cancer patients with metastases to the liver [7]. Conventional T1 and T2-weighted imaging was performed at 1.5 T, along with DW single-shot echo-planar imaging (DW-SSEPI) using b values of 0, 150, 300 and 450 s/mm². To maintain good signal sensitivity in the images, larger b-values were not used in this study. Image parameters for the DW-SSEPI images were as follows: TE = 103 ms, 128 × 90 image matrix, FOV = 36 × 27 cm, TR = 6 s, 100 kHz receiver. DWMRI image pairs (b=0 and 150, b=0 and 300, and b=0 and 450 s/mm², respectively) were collected, where each pair was collected within a single breath hold. Each patient was imaged at day 0 (baseline), 4, 11 and 39 following the commencement of cytotoxic therapy. All patients had provided informed written consent, had a minimum of one liver metastasis measurable over 1.2 cm in at least two dimensions, were not pregnant, of at least 18 years of age, and scheduled to initiate a new chemotherapy regimen for their metastatic disease. The imaging protocol was approved by the University‘s institutional review board and conducted in accordance with the Health Insurance Portability and Accountability Act. From this in-vivo study, considering only the baseline images for each patient, we obtained image data at all b values from 14 lesions in 7 patients.

Implementation of the Algorithm

To estimate the ADC of the lesion, the only inputs required by the proposed algorithm are M̄ and {σ̂_i}, which can be easily obtained by drawing a ROI or segmenting the lesion and using the lesion pixel intensity values. We developed an automated image-segmentation software [29] to segment the lesions in the images at the different b values. The values of a and S₀ were estimated by maximizing the likelihood function given by Eq. (17) using an optimization routine in Matlab software (Mathworks, Natick, Mass). We also derived expressions for the derivative of the likelihood function with respect to a and S₀, and passed these to the optimization routine. The method was implemented on a Pentium 4 computer (Gateway, CA) and was constrained to search only between reasonable values of the parameters. We fixed the search space for the ADC value between 0.1 × 10⁻³mm²/s to 5.0 × 10⁻³mm²/s, to cover the range of values typically measured in-vivo [9]. The initial ADC value was kept as 2.0 × 10⁻³mm²/s. Further, since S₀ should be close to the signal strength value at b value 0 s/mm², we fixed the initial value for S₀ to this measured value, and upper and lower bounded the search space by adding and subtracting, respectively, twice the standard deviation computed at b value 0 s/mm² from the signal strength observed at b value 0 s/mm². The whole optimization task took less than a second to execute. An easy-to-use and computationally fast ADC estimator based on the proposed ML algorithm was thus developed.

Evaluation of the Algorithm

The true ADC value of the lesion in the in-vivo studies was not known since the histological analysis of the tumors was not performed. Thus evaluating the method using in-vivo data was not possible. In fact, even if the histological analysis were to be performed, the evaluation of the method with in-vivo data would hold only if the lesions were perfectly homogeneous. Thus, to evaluate the proposed method, we instead performed realistic simulation studies where the true ADC value of the lesion was known. The performance of the algorithm was compared with the conventional LR approach and an ADC-map approach on the task of estimating a single ADC value of the lesion. These realistic studies were guided by available patient data. To compute the ADC map, we used a statistically rigorous and well-known ML-based technique [9] that accounts for the Rician distribution of the MR noise. The mean ADC of all the lesion pixels in the ADC map is often reported as the single ADC value for the lesion [21], [23], [30]. We thus computed the mean ADC value of the lesion pixels from the ADC map, and compared this estimated value with the ADC estimate using the proposed technique.

We now describe the methods for the simulation study, starting with the considered lesion models.

Lesion Models

The distribution of ADC values in liver lesions is a subject under investigation [31], and both homogeneous [31] and heterogeneous [4], [31], [32] lesions have been observed. To perform a comprehensive analysis, we conducted experiments with both lesion types. In the homogeneous lesions, as the name suggests, the ADC values were constant throughout the lesion. Homogeneous lesions are observed in cases such as colorectal hepatic metastases [31]. In the experiments on the homogeneous lesion models, the parameters of ADC, lesion SNR and lesion size were varied.

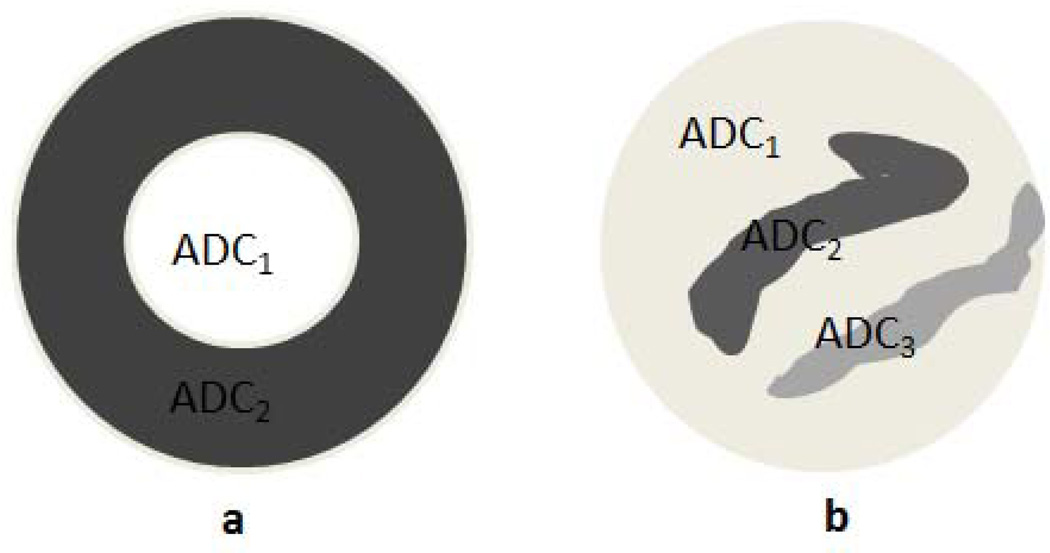
The distribution of ADC values in heterogeneous lesions varies significantly within a ROI, due to factors such as necrosis. Therefore, it is not uncommon to observe bimodal or even tri-modal distributions in liver lesions following a treatment. We studied three liver-lesion models based on discussions with radiologists, prior research in this field, and our dataset of patient images. The first model had a uniform distribution of ADC values in the lesion, similar to the model proposed in Walker-Samuel et al. [32]. The other two lesion models were simplistic representations of tumor distributions, inspired by the study in Scurr et al. [31] and using data in Koh et al. [33]. The rim model was a bimodal distribution of a metastatic lesion, with the rim having a lower ADC value than the center [31]–[33]. This represented a lesion where significant necrosis has occurred at the center of the metastasis. Since necrotic tissues show less impeded water diffusion than cellular tumor tissues, the central necrotic area of a metastasis shows lower MR-signal attenuation than the more cellular tumor periphery, yielding the rim appearance in DW images. This structure is typically seen for large lesions (size > 1 cm) [31]. The third model was a variegated lesion model consisting of low-ADC regions interspersed by sub-regions with heterogeneous low and high ADC values [31]. The rim and variegated lesion models are graphically shown in Fig. 1. The true ADC value of simulated heterogeneous lesions was computed from Eq. (1) using the true mean lesion intensities at b values of 0 s/mm² and 150 s/mm².

Fig. 1.

Graphical representations of the (a) rim and (b) variegated lesion models. The graphical representations are enlarged for visual clarity.

Lesion simulation

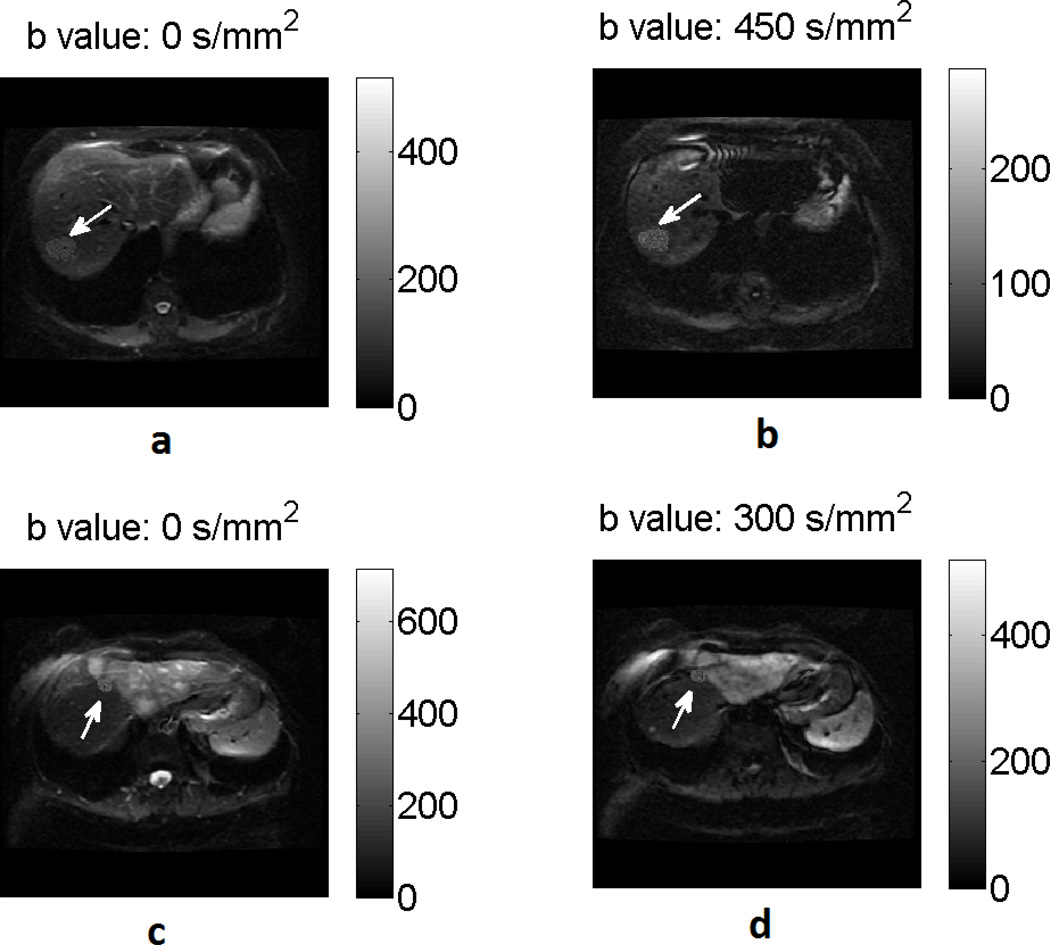
We used the available dataset of patient images to obtain the template for the lesion and the rest of the image. To explain the procedure, we first define an image dataset for a particular lesion in a given patient as all the DW images of that patient that contain the considered lesion. For a given patient image dataset, the considered lesion was segmented in the images at all the four b values, i.e. 0, 150, 300 and 450 s/mm². The union of the segmented lesion regions at all the b values yielded a template for the shape of the lesion. Next, for a given set of imaging and lesion parameters, the lesion pixel intensities were obtained by sampling the corresponding Rice distribution (Eq. (5)). The value of S₀ was kept as a constant over the entire lesion. In our experiments, the lesions were simulated for different parameters, which included the lesion ADC value, lesion size, SNR at b value s/mm² (denoted by SNR_b0 and defined as S₀/σ_r), image misalignment values, different lesion models, and different amounts of heterogeneity. For a given set of parameters, 100 noise realizations of the simulated lesions were generated. The simulated lesion was inserted into the patient image from where the lesion was segmented, where a simulated lesion at a given b value was inserted into the patient image at the same b value. Thus, at the end of this process, realistically simulated lesions with known ADC inserted in real patient images were obtained, as illustrated by two examples in Fig. 2.

Fig. 2.

A homogeneous lesion (i.e. one with a constant ADC value for all lesion pixels) simulated at b values of (a) 0 s/mm² and 450 s/mm² inserted in the corresponding real patient images. Another homogeneous lesion of smaller size simulated at b value of (c) 0s/mm² and (d) 300s/mm² inserted in the corresponding real patient image.

For each noise realization, the values of the mean and variance of signal intensities of the lesion pixels over the true lesion ROI were determined from the simulated images. Using these values, the ADC of the lesion was estimated using the proposed and the LR techniques. Also, the ADC map was evaluated over the true lesion ROI, and the mean ADC value over the lesion ROI in the ADC map was computed.

Simulating Image Misalignment Across b values

We mentioned previously that an important advantage of the proposed method, in comparison to methods that compute the single ADC value from an ADC map, is the reduced sensitivity of the proposed approach to misalignment of the images across the different b values. To demonstrate this advantage, we conducted experiments that simulated simple motion misalignment of the lesion across the different b values. The amount of misalignment in a given experiment was obtained by sampling three integer values from a uniform distribution between 0 and m_max pixels. The simulated images at b values of 150, 300 and 450 s/mm² were synthetically misaligned in the horizontal and the vertical direction by these three integer values. The ADC was estimated for different values of m_max using the proposed, LR, and the ADC-map [9] approaches. For the proposed and LR approaches, the lesion ROI was individually determined at all the b values using the true ROI template, while for the ADC-map approach, the ROI at b value 0 mm²/s was considered as the ROI template for all the b values.

Evaluation with Patient-Dataset Parameters

In the above-mentioned experiments, the proposed technique was evaluated over a range of different parameters, including the ADC values, SNR, size, and misalignment between images at different b values. We also studied the performance of the technique for specific values of these parameters obtained directly from the patient images. For this purpose, we used the available in-vivo dataset of 14 lesions. The lesions were manually segmented in the images at the different b values. For the segmented lesions, an estimate of ADC and S₀ was obtained using the proposed ML technique. Further, an estimate of the Rician noise variance σ_r for each lesion image dataset was estimated from regions of background noise using the technique proposed in Sijbers et al. [8]. Using these estimates, 100 noisy realizations of homogeneous lesions were simulated at the b values of 0, 150, 300 and 450 s/mm². These lesions were then inserted into the corresponding patient images at the corresponding b values. At the end of this process, we had image datasets to study the performance of the proposed method in clinically relevant scenarios.

Evaluation at Higher b values

In several DWMRI studies, especially those where the organ of interest is other than the liver, higher b values, commonly around 1000 s/mm² are used [5]. At the higher b values, the SNR reduces, which affects the performance of ADC estimation procedures. To evaluate the utility of the proposed technique for higher b values, in a subset of the experiments, we also simulated homogeneous lesions at b values of 0, 500, and 1000 s/mm².

Results

Homogeneous Lesions

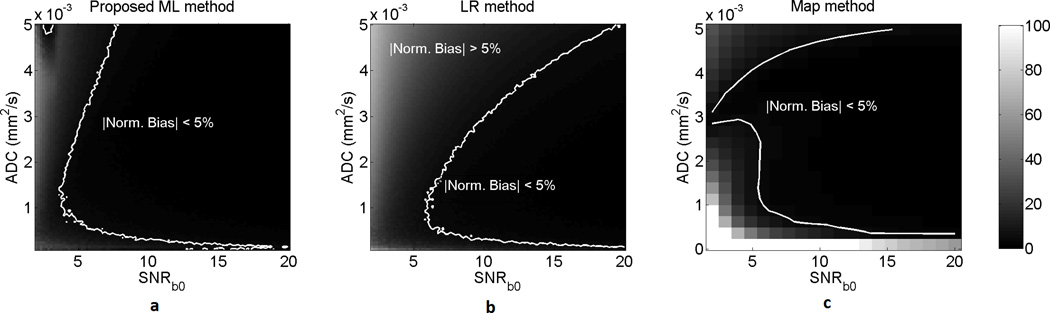
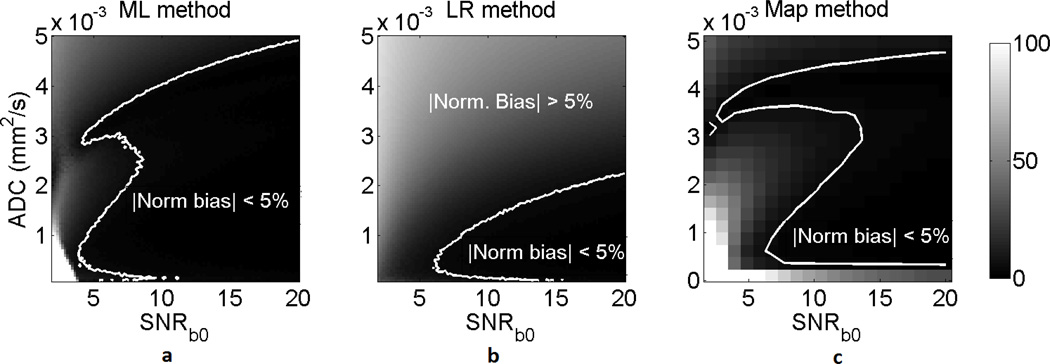
A homogeneous lesion with the same template as in Fig. 2(a)–(b) (size of 292 pixels) was considered. The ADC and SNR_b0 of the lesion were varied from 0.1 × 10⁻³ mm²/s to 5 × 10⁻³ mm²/s and from 2 to 20, respectively. The results presented in Fig. 3 show that the ML approach had a lower normalized bias than the LR and ADC-map approach over a large spectrum of ADC and SNR values of the lesion, and especially at low SNR values.

Fig. 3.

The normalized bias of the (a) ML, (b) LR, and (c) ADC-map approach on estimating the ADC of homogeneous lesions for various values of ADC and SNR_b0. The normalized bias is expressed in percentage units. The ADC-map technique was computationally very intensive [9], and thus was executed over a smaller set of ADC and SNR values. The proposed ML approach outperforms the LR and ADC-map approaches, especially at low SNR values.

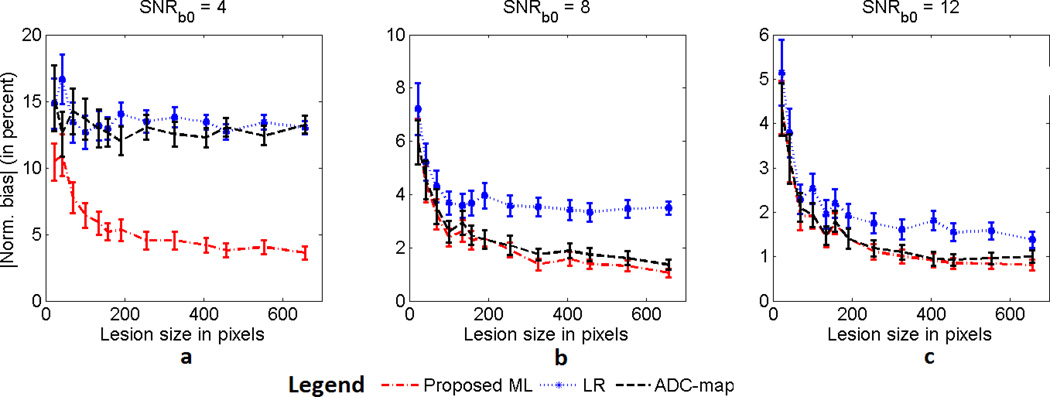
To study the performance of the proposed method for different lesion sizes, a lesion with template as in Fig. 2(c) was considered. The size of the lesion was varied through morphological operations of image erosion and dilation. The ADC of the lesion was fixed at 1.5 × 10⁻³ mm²/s and three SNR_b0 values of 4, 8, and 12 were considered. The results of this experiment presented in Fig. 4 show that the proposed ML approach had a lower normalized bias than the LR and ADC-map approaches over a large set of lesion sizes for the considered SNR values. The proposed method was again especially more effective when the SNR was low.

Fig. 4.

The absolute value of the normalized bias of the ML, LR, and ADC-map approaches in estimating the ADC of homogeneous lesions as the size of the lesion is varied. The experiment was conducted for SNR_b0 values of (a) 4, (b) 8 and (c) 12. The error bars denote 95% confidence intervals.

The absolute value of the normalized bias averaged over the varied parameter and over all 100 noise realizations, as presented in the first row of Table I, was about a factor of two larger for the LR and ADC-map techniques in comparison to the proposed ML method.

TABLE I.

Absolute value of the average normalized bias (averaged over the parameter that is varied and the noise realizations) of the ADC values estimated using the LR, ADC-map, and proposed ML estimation methods. The bias is expressed in percentage units.

Type of lesion	Parameter varied	ML	LR	ADC-map
Homogeneous	ADC and SNR	4.63	10.55	16.00
	Size	3.33	6.66	5.82
Heterogeneous
-uniformly distributed	SNR	2.98	6.22	5.36
	Size	3.33	7.27	4.81
Heterogeneous
-rim model	SNR	3.00	6.29	4.83
	Size	3.19	7.23	4.78
Heterogeneous
-variegated lesion model	SNR	6.53	12.31	9.31
	Size	5.06	7.69	9.63

Heterogeneous Lesions

The ADC values of the lesion pixels for the uniformly distributed lesion were sampled from a uniform distribution between 1 × 10⁻³ mm²/s to 2 × 10⁻³ mm²/s. For the rim model, the ADC of the center and rim of the lesion were fixed to 2 × 10⁻³ mm²/s and 1.5 × 10⁻³ mm²/s, respectively. Finally, for the variegated lesion model, the lesion consisted of three regions: The main region had an ADC value of 1 × 10⁻³ mm²/s, and the sub-regions had ADC values of 2 × 10⁻³ mm²/s and 2.5 × 10⁻³ mm²/s, respectively. For each of these lesion models, we conducted two experiments. In the first experiment, the lesion template was chosen as in Fig. 2(a)–(b) and the value of SNR_b0 was varied from 2 to 20. In the second experiment, the lesion template was chosen as in Fig. 2(c)–(d), the value of SNR_b0 was fixed at 6, and the size of lesion was varied.

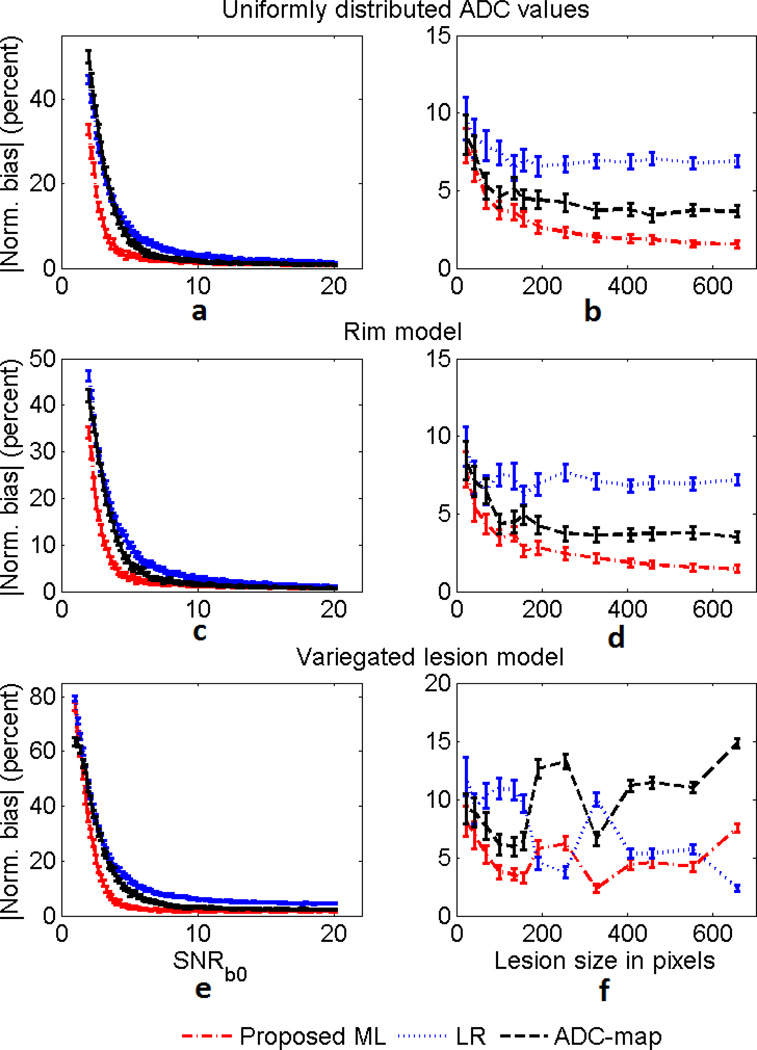
The results from the experiment, presented in Fig. 5, show that the ML approach had a lower bias than the LR and ADC-map approaches for all the heterogeneous lesion models and a large spectrum of the considered values of SNR_b0 and lesion size. These results are summarized in Table I, where we observe that the average of the absolute value of the normalized bias is lower with the proposed method in comparison to the LR and ADC-map method.

Fig. 5.

The absolute value of the normalized bias of the proposed ML, LR and ADC-map estimation techniques in estimating ADC values of heterogeneous lesions. Models investigated include (a)–(b) lesion with uniform distribution of ADC values (c)–(d) rim lesion model (e)–(f) variegated lesion model. The left and right side plots study the variation with lesion SNR_b0 and lesion size, respectively. The error bars denote 95% confidence intervals.

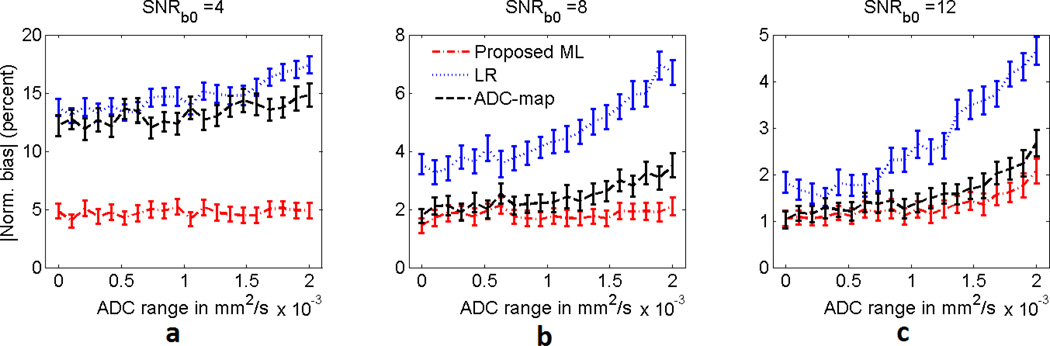
We next studied the effect of increasing the lesion heterogeneity on the performance of the proposed technique. The heterogeneous lesion with uniformly distributed ADC values and template as in Fig. 2(a)–(b) was considered. The mean value of this uniform distribution of ADC values was fixed to 1.5 × 10⁻³mm²/s. To simulate different amounts of heterogeneity, the range of the uniform distribution was varied from 0 mm²/s to 2 × 10⁻³mm²/s. The experiment was conducted for lesion SNR_b0 values equal to 4, 8, and 12. The results from this experiment, as presented in Fig. 6, show that as the heterogeneity of the lesion increased, the performance of the LR method deteriorated significantly. However, the performance of the proposed technique was only mildly affected by the increase in heterogeneity for all values of SNR_b0. This was expected since in deriving the ML technique, we had accounted for some amount of heterogeneity of the lesion. Further, the proposed technique consistently outperformed the LR and ADC-map techniques.

Fig. 6.

The absolute value of the normalized bias of the ML, LR, and ADC-map estimation techniques for various amounts of heterogeneity in a heterogeneous lesion with uniform distribution of ADC values. The variation in heterogeneity is quantified by the range of the ADC values in this lesion. The experiment was performed for SNR_b0 values equal to (a) 4, (b) 8, and (c) 12. The error bars denote 95% confidence intervals.

Effect of Misalignment

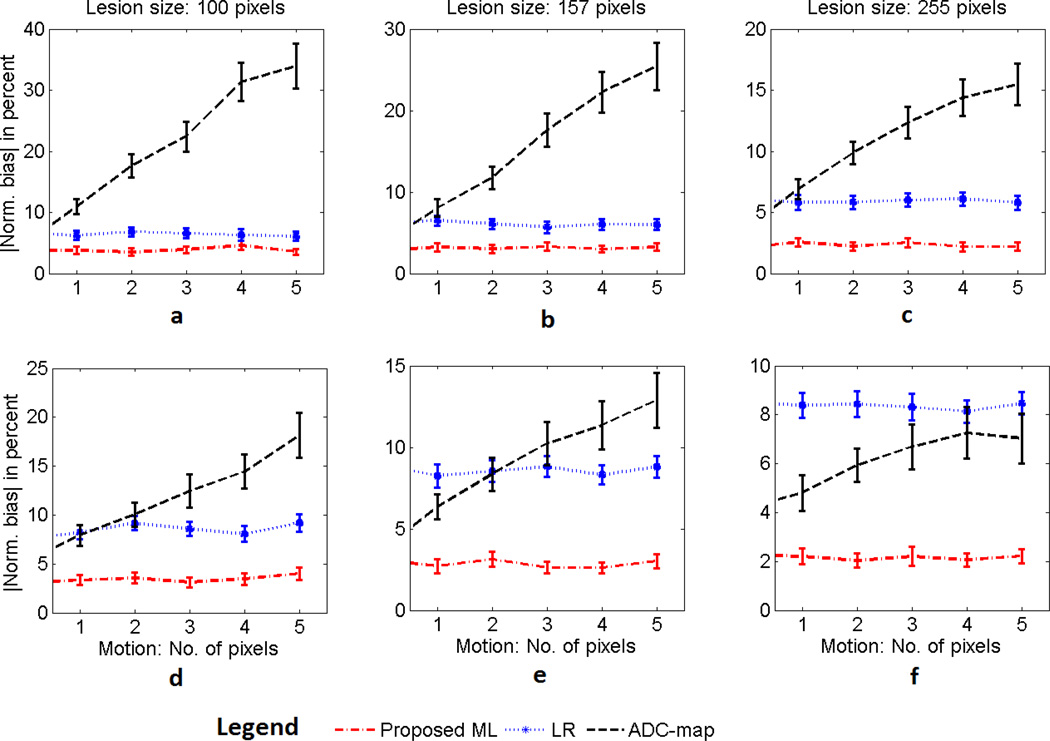
The simulated image in Fig. 2(c)–(d) was considered. The value of SNR_b0 for the simulated lesions was fixed to 6, based on the estimated value of SNR_b0 for the corresponding actual lesion in the patient image. The magnitude of misalignment in the images at the four different b values, as quantified by the value of m_max, was varied from 0 to 5 pixels. The effect of motion misalignment was studied with lesions of different sizes, where the size of the lesion was varied using image dilation. As shown in the results in Fig. 7, the performance of the ADC-map method deteriorated heavily, yielding a bias of up to 12–35% for different lesion sizes. As expected, the proposed ML technique was not effected by this misalignment.

Fig. 7.

Comparing the performance of the ML, LR, and ADC-map approaches in estimating the ADC value as the misalignment between the images at the different b values increases. The experiment is performed for different sizes of both (a)–(c) homogeneous lesions with an ADC value of 1.5 × 10⁻³mm²/s and (d)–(f) heterogeneous lesions with uniform distribution of ADC values between 1 × 10⁻³ mm²/s to 3 × 10⁻³ mm²/s. For both these lesion models and for different sizes of the lesion, the performance of ADC-map approach deteriorates as the amount of misalignment between the images increases. The error bars denote 95% confidence intervals.

Using Specific Patient-Image Derived Data

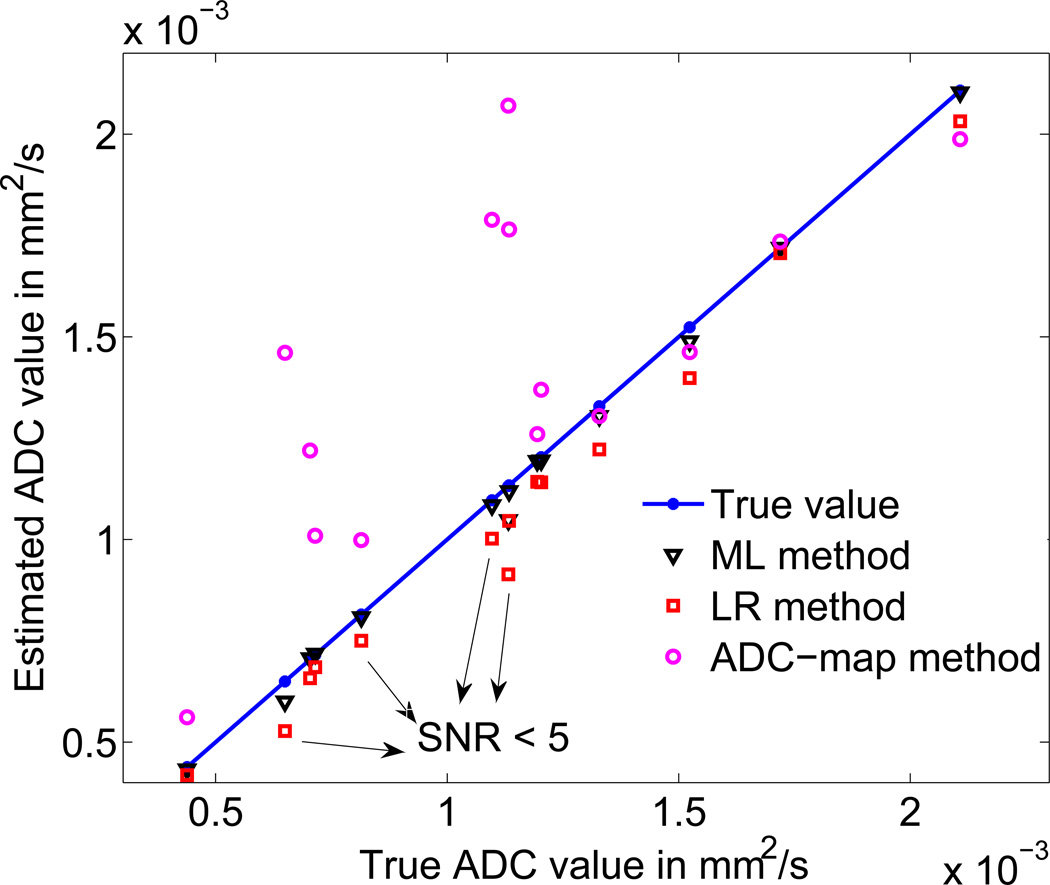
A scatter plot of the ADC values estimated using the different procedures for the 14-lesion patient dataset is shown in Fig. 8. Note that in this experiment, the lesion, imaging, and misalignment parameters were directly obtained from the available patient dataset. As marked in the figure, often the value of SNR_b0 was less than 5 in these image datasets, in which case, the LR method yielded an average normalized bias of up to 12.5%. The ADC-map method yielded inaccurate results in several cases, reflecting the error that motion misalignment can cause in clinically realistic scenarios. The ML method yielded a less biased estimate than the LR technique in 11 of 14 cases. The reduction in bias was statistically significant, as shown by the Student’s t test on the bias of the estimators (p value < 0.04 for all 11 cases). In the other 3 cases, the performance of the two methods was statistically equivalent. Similarly, the ML method was less biased than the ADC-map technique in 13/14 cases, where again, the Student’s t test showed that the reduction in bias was statistically significant (p value < 0.005). For the remaining case, the performance of the ML and ADC-map techniques was statistically equivalent. The improved performance of the proposed technique in these very realistic clinical scenarios demonstrates the clinical relevance and value of the technique.

Fig. 8.

Comparing the performance of the ML, LR, and ADC-map techniques in estimating the ADC values for specific lesion and motion misalignment parameters derived directly from patient images. The average of the estimated ADC value using the different methods over the 100 noise realizations is plotted. The LR-based technique is not accurate for several lesions, for which, the SNR_b0 values were smaller than 5. The ADC-map approach had high values of bias due to the misalignment between the images at the different b values. In all the cases in this realistic patient dataset, the proposed ML-based technique outperformed the LR and ADC-map approaches.

Performance at Higher b Values

Diffusion images corresponding to homogeneous lesions imaged at b values of 0, 500 and 1000 s/mm² were simulated. The ADC and SNR_b0 for the lesions were varied. The ADC of the simulated lesions was estimated using the proposed, LR, and ADC-map techniques. The results, as shown in Fig. 9, show that even for these higher set of b values, the proposed method outperformed the LR and ADC-map methods. In fact, even when the SNR_b0 values were not as low (~ 10) and the ADC values were between 1 × 10⁻³ and 3 × 10⁻³ mm²/s, the LR and ADC-map technique had more than 5% bias, mainly due to the low SNR at high b values. The proposed ML-approach yielded more accurate estimates for these SNR and ADC values.

Fig. 9.

The absolute value of the normalized bias of the (a) ML, (b) LR, and (c) ADC-map approach on estimating the ADC of homogeneous lesions for various values of ADC and SNR_b0 for b values of 0, 500 and 1000 s/mm². The normalized bias is expressed in percentage units. The ADC-map technique was executed over a smaller set of ADC and SNR values for computational reasons. The proposed ML approach again outperforms the LR and ADC-map approaches, especially at low SNR values.

Discussions

The results showed that the LR technique was heavily biased for both homogeneous and heterogeneous lesions, with average bias values close to 10%. The bias was especially visible in images with low SNR values (SNR_b0 < 5), which were often observed in our patient dataset. The proposed ML technique yielded a less biased estimate for the single ADC value of the lesion for both homogeneous and heterogeneous lesion models for a large spectrum of ADC values, size, and SNR, including at low SNR values. Further, in the presence of misalignment between images at different b values, as often observed in our patient dataset, the ML method clearly outperformed the ADC-map method. Thus, in those clinical scenarios where the images are misaligned at the different b values and only a single ADC value of the lesion is desired, the results present strong evidence in favor of the proposed ML technique.

Further, even in the absence of motion, the proposed ML technique was more accurate than a statistically rigorous map-based ADC estimation technique for both homogeneous and heterogeneous lesions. This is best demonstrated with the results for homogeneous lesions, where the proposed method, especially for low SNR values, had a reduced bias in comparison to the ADC-map technique (Fig. 3). The bias with the ADC-map technique has been observed previously [9] and is attributed to the likelihood function flattening out at low SNR values. The proposed technique yielded accurate performance in this case. This advantage of the proposed technique was even more evident when a higher set of b values were considered (Fig. 9). Higher b values are often used in organs other than the liver [5], and thus the results provide evidence for the general utility of the method. The ADC-map method is essential to study the heterogeneity of the lesion. Further, often the statistical distribution of ADC values is of clinical interest, and currently the proposed method is not able to provide this information. While this is a limitation of the proposed method, often in DWMRI studies, only a single ADC value of the lesion is used for reporting or evaluation purposes [3], [20], [21], [23], [30]. The experimental results present strong support for the use of the proposed method to compute this single ADC value instead of the ADC-map methods. Based on these results, it seems that in the absence of motion misalignment, a good strategy could be to use the ADC-map method to study and evaluate heterogeneity and distribution of ADC values, and use the proposed method to compute the single ADC value of the lesion.

The proposed ML method was on average, upto two orders of magnitude faster than the ADC-map technique. For example, for a lesion of size 279 pixels, executing the proposed ML, LR and ADC-map techniques for 10 trials required 0.36 s, 0.02 s and 99.5 s, respectively. The method is easy to implement and convenient to use, since segmenting the lesion using a segmentation algorithm, such as a clustering-based technique we designed for diffusion MR images [18], was sufficient to obtain all the required input data for the proposed ML approach. The method does not require the user to mark a background region to obtain the Rician noise variance, as is required by some other methods [9], [10].

In the experiments related to simulating misalignment of the images, it was observed that the performance of the ADC-map technique deteriorated significantly with increasing misalignment. To overcome this misalignment-related issue, the images at the different b values could be registered. This could improve the performance of the ADC-map technique, but would require an extra registration step. If the registration is erroneous, then the performance of the ADC-map technique will suffer. Comparing the performance of the proposed technique with an ADC-map technique that uses a prior image-registration step would be an important area of future study. Also, if the misalignment is due to motion, it could affect the signal intensity at the different b values, and therefore, further bias the ADC estimate. In our simulations, we did not model this effect, which is another limitation of this study. However, note that this effect would also bias the LR and ADC-map methods apart from the proposed technique. Modeling for this effect in the ADC estimation procedure is another important area for future investigation.

One method to reduce the noise-related inaccuracies in ADC estimation is to take multiple images of the patient at the same b value. However, as we have shown [24], even in this case a simple ML-based method that uses a less rigorous probability model for the measured mean signal intensity is more accurate than a ADC-map method. The accuracy of this simple ML-based method can be improved further using the framework proposed in this paper.

The proposed ML method can be extended to scenarios where the measured signal is statistically the mean of Rician distributed random variables. For example, the method can be adapted to estimate a single value of the spin-spin T2 relaxation parameter from the mean magnitude MR data over a ROI. The evaluation of the accuracy and clinical relevance of a method similar to the proposed method but for estimating the single T2 relaxation parameter is another important area for future investigation.

We mentioned earlier that it is complicated to evaluate the proposed method with real patient data since the gold standard of the ADC value is not known. In this regard, we have developed a no-gold-standard (NGS) technique to evaluate segmentation algorithms for diffusion images [34], [35]. The NGS technique could be extended to evaluate the proposed technique with patient data. However, currently the NGS method requires several patient studies that were not available. We are currently investigating methods to reduce this requirement [36].

Conclusions

A statistically rigorous, computationally fast, easy-to-implement, and convenient-to-use ML method has been proposed to estimate the ADC of the lesion from the mean signal intensity measurements at the different b values. The method accounts for lesion heterogeneity and is based on an accurate noise model for the mean signal intensity in a DW MR image. A comprehensive realistic simulation study shows that the proposed method is more accurate than the conventionally used LR and an ADC-map approach over a wide spectrum of possible ADC, SNR, and lesion sizes for both homogeneous and heterogeneous lesions. The proposed method is also more accurate than the LR and ADC-map techniques for different amounts of heterogeneity in a heterogeneous lesion model. These results were observed in both the presence and absence of misalignment between the images at the different b values. Further, the performance of the proposed algorithm is superior for different sets of b values and in studies with specific patient-image-derived data. Thus, overall, the results provide strong evidence supporting the use of this method when the end task is estimating a single ADC value of the lesion.