Muscle shortening velocity depends on tissue inertia and level of activation during submaximal contractions

Abstract

In order to perform external work, muscles must do additional internal work to deform their tissue, and in particular, to overcome the inertia due to their internal mass. However, the contribution of the internal mass within a muscle to the mechanical output of that muscle has only rarely been studied. Here, we use a dynamic, multi-element Hill-type muscle model to examine the effects of the inertial mass within muscle on its contractile performance. We find that the maximum strain-rate of muscle is slower for lower activations and larger muscle sizes. As muscle size increases, the ability of the muscle to overcome its inertial load will decrease, as muscle tension is proportional to cross-sectional area and inertial load is proportional to mass. Thus, muscles that are larger in size will have a higher inertial cost to contraction. Similarly, when muscle size and inertial load are held constant, decreasing muscle activation will increase inertial cost to contraction by reducing muscle tension. These results show that inertial loads within muscle contribute to a slowing of muscle contractile velocities (strain-rates), particularly at the submaximal activations that are typical during animal locomotion.

1. Introduction

Muscle contractions rarely reach maximum levels during our daily activities. However, much of what we know about the tension that whole muscles produce, and thus their function, is derived from experiments on maximally activated isolated muscle fibres [1–5]. Mammalian muscle contains many muscle fibres that are activated in groups called motor units. However, muscles are typically considered to act as if they were individual fibres that had been scaled up to the size of whole muscle [6–9].

A.V. Hill published a thought experiment in 1970 about a muscle that contained a mixed population of different fibre-types: he suggested that the fastest contraction velocity of such a muscle would equal the velocity of the fastest fibre within it [10]. Josephson & Edman [11] confirmed this with experimental measures of isolated fibres, but they suggested that inactive fibres within a submaximally activated muscle may provide resistance to slow the muscle down. Recently, Holt and co-workers measured the force–velocity properties of submaximally activated whole muscle (rat plantaris), and found that submaximally activated muscle contracted slower than fully activated muscle, even if the activated portion of the muscle comprised the faster fibre-types. They proposed that physical properties of muscle may modify and potentially obscure any effect of activating different motor unit types [12].

Experimental studies have thus attributed unexplained forces within muscle to the resistance or inertia of the tissue, and this would include inactive fibres. However, virtually all Hill-type muscle models, which are ubiquitously used in biomechanics to understand and predict muscle behaviour, ignore the inertial effect of tissue mass. The importance of inertial effects within muscle was recently demonstrated in a second-order dynamic model that distributed the tissue mass in a series of discrete points through the muscle [13]. This mass model showed time-delays in force development that were due to the internal inertial mass, with the effect being more pronounced for larger muscle where the ratio of mass to contractile force was greater. This model makes it possible to consider the inertial effects of fibres within whole muscle, even if they are inactive during submaximal contractions; however, this was not studied at the time [13]. Inertial effects may be considerable for muscles that have a large mass, particularly when activations are low and there is little contractile force to move the inertial load.

In this study, we use a Hill-type muscle model that incorporates inertial properties to test how the size and activity of a muscle affect its shortening speed. As the model contains no additional damping and the passive fibre properties are insignificant at the muscle lengths at which the speeds are evaluated, the differences in model performance are governed by the balance between the activity-dependent force and the size-dependent inertial properties.

2. Material and methods

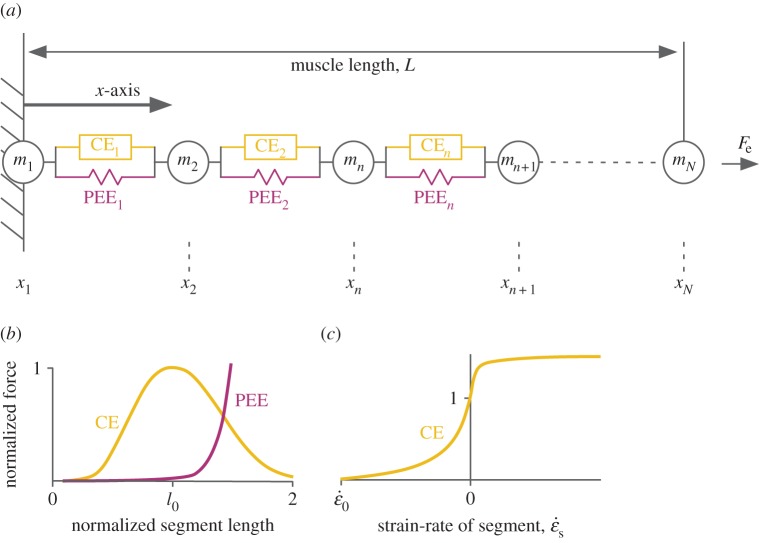
A Hill-type model was developed, with its mass evenly distributed along its length in a manner put forth by Günther and co-workers [13]. Model details are shown in figure 1 and described with their assumptions in the electronic supplementary material. In brief, the muscle mass M was divided into N equally spaced points of mass m = M/N. The segments between the point masses contained a contractile element (CE) and a parallel elastic element (PEE). The force of the CE, which represented a portion of contractile muscle tissue, depended on its activation state, length and velocity. The PEE represented connective tissue in parallel with the CE and developed force as a function of only its length. The whole muscle length was equal to the sum of the individual segment lengths and shortened as the muscle contracted against a load that was an isotonic external force F_e.

Figure 1.

Second-order dynamic Hill-type muscle model (a). The mass of the model is evenly distributed along its length at rest such that each point mass m has the same mass and each segment has the same initial length. The force of each segment is the sum of the force from the parallel elastic element PEE (b), and the contractile element CE, which in turn is the product of its activation state, force–length (b) and force–velocity characteristics (c). The displacement of each mass depends on the balance of forces from the adjacent segments or from the external force F_e for the end mass.

The size, activation state, fibre-type characteristics and initial length of the muscle were varied. The base model had dimensions to represent a rat plantaris muscle (optimal muscle length L₀ 34 mm, cross-sectional area 29 mm² and mass 1.05 g; [14]). The geometry of the base model was uniformly scaled up to 16.33 kg, which reasonably approximates the mass of an elephant leg muscle [15]. Activation state was held constant across all segments and differed between 20 and 100%. The muscles behaved as either slow or fast, with input maximum unloaded strain-rates of the CEs 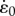set at −5 or −10 s⁻¹, respectively. The initial set of simulations (I) started contractions with the muscle at L₀ and a second set of simulations (II) started with longer initial lengths so that the maximum shortening strain-rate 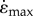was achieved when the muscle had shortened to L₀.

A single set of simulations were run for each possible combination of input parameters with the load ranging from 0.01 to 0.9 of the maximum isometric force F₀. The output maximum shortening velocity of the whole muscle was determined for each load and expressed as a 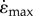relative to L₀. Initial simulations confirmed previous findings [13] that increasing the number of point masses beyond 16 did not substantially alter the model output. Therefore, further analyses concentrated on simulations for N = 16 point masses.

3. Results and discussion

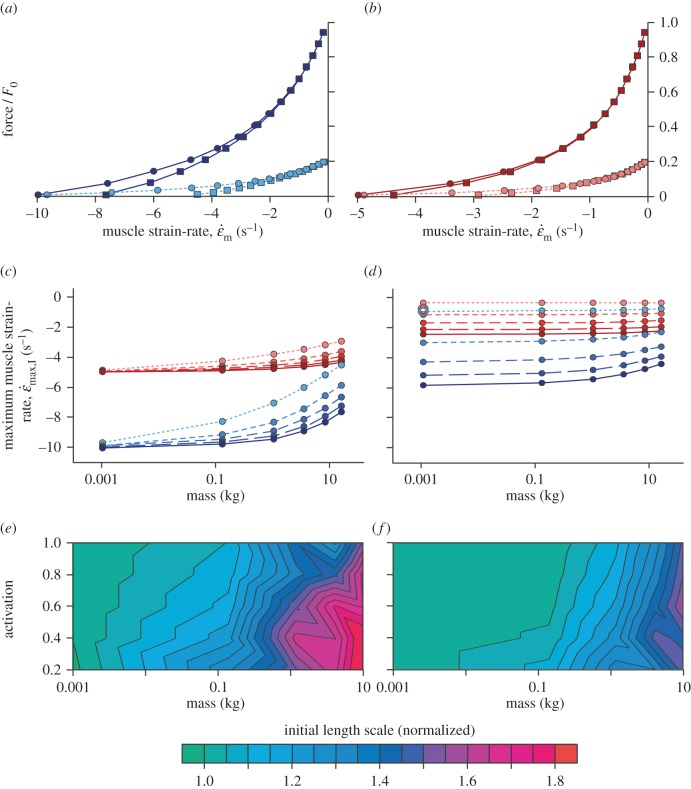
The initial simulations (I) started at optimal muscle lengths to mimic previous experimental protocols [4,12,16]. The muscle inertia caused a delay in the time to reach maximum velocity [13] and this delay was greatest for large muscle and submaximal activations. Maximum velocities were achieved at progressively shorter muscle lengths (relative to L₀) for larger muscles and lower activations, resulting in lower 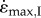for these conditions, matching previous experimental findings [12]. The whole muscle contracted with a hyperbolic force–velocity relationship (figure 2a,b) similar to that for the underlying CEs (figure 1). Muscles with fast-fibre properties showed a more pronounced decrease in 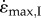at the larger sizes than did those with slow-fibre properties (figure 2c). Similar to increases in size, decreases in activation would reduce the contractile force available to accelerate the inertial load. Indeed, lower activations resulted in slower 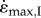, with this effect being more pronounced for the faster muscles (figure 2c).

Figure 2.

Force–velocity relations for fast (a) and slow (b) muscle, calculated from simulation-I. Simulations are shown for maximal (solid lines), and 20% activation (dashed lines), and for muscle mass of 1.05 g (circles) and 16.33 kg (squares). 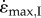achieved at 0.01F₀ with no external load (c) and the strain-rate achieved at 0.15F₀ with an added external load of 0.6M (d) are shown for a range from maximal (solid lines) through to 20% activation (shortest dashes). Note the similar strain-rates for fast and slow muscles at 20 and 30% activation (open circles), respectively, representing data from Holt et al. [12]. Fast muscle is shown in blue and slow muscle in red for (a–d). The initial lengths required to achieve 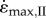at L₀ are shown as a function of muscle mass and activation for the fast (e) and slow (f) muscle for simulation-II.

The phenomenon of submaximally active muscle showing similar 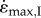if either the faster or the slower fibres were activated, with these contractile velocities being less than if the muscle were fully active [12], was most closely achieved for the larger muscle sizes than for the rat-sized muscle, for which the experimental observations were originally made (figure 2c). However, it should be noted that additional mass from connective tissue within the muscle, from partial or intact limb segments, and from elements of the measuring system, will all place a load on the muscle and so whole muscles are rarely fully unloaded in in vitro, in situ and even in vivo situations. When such an additional mass of 0.6 M was added to the load of 0.15F₀, the behaviour of the 20% activated fast muscle was similar to that of the 30% activated slow muscle even for the rat-sized muscle in a way that mimics recent experiments [12] (figure 2d). These results show that inertial loads within the muscle contribute to a slowing of the muscle contraction velocities, particularly for submaximally activated muscles. Such effects can mask the contractile differences between the fast- and slow-fibres [12].

To overcome the length-dependence of the point where the maximum velocity was achieved, the second set of simulations (II) optimized the initial length so that the muscle would be at L₀ at the time 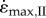was achieved. For this set of simulations, there was no effect of either activation or muscle size on 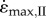. However, these simulations had to be started at ever-greater initial lengths as the muscle size increased and activation decreased (figure 2). In order to compute these simulations it was necessary to decrease the stiffness of the PEE; otherwise the passive forces would result in excessive velocities at the longest muscle lengths. Even with this modification, the initial length was too long to compute for the 16.3 kg muscle with slow-fibres and for the 8.4 kg muscle with fast-fibres. These extreme long lengths and reduced passive tension may be un-physiological, and so it is suggested that the first set of simulations (I), where 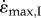decreased at lower activations and larger sizes, more closely reflect the behaviour of muscles in vivo.

The ability of a muscle to contract and shorten depends on the tension it can produce to overcome opposing external forces, as well as forces that arise from the structural and material properties of the muscle itself. Based on the results of this study, it appears that inertial resistance due to a muscle's mass is one such factor that can modulate its mechanical output during contraction. Inertial resistance dominates more at submaximal activations, as the actively contracting muscle fibres must work to accelerate not only their own mass, but also the mass of the remaining inactive fibres. Similarly, larger muscles have reduced cross-sectional area to volume ratio, which amplifies the relative resistance due to mass. Owing to these findings, it may not be reasonable to neglect mass within Hill-type models of whole muscle, particularly under natural conditions in which the muscle is not fully active or the muscle is large.

Data accessibility

Simulation data are available from Dryad (http://dx.doi.org/10.5061/dryad.qh376).

Authors' contributions

J.M.W. conceived the study. S.A.R. and J.M.W. participated in the design of the model and simulation of the results. S.A.R. was the primary author of the manuscript and J.M.W. revised it. Both authors read and approved the final manuscript and agree to be held accountable for its contents.

Competing interests

We have no competing interests.

Funding

The study was funded by a Natural Sciences and Engineering Research Council of Canada Discovery Grant to J.M.W.