Electrocaloric and elastocaloric effects in soft materials

Abstract

Materials with large caloric effect have the promise of realizing solid-state refrigeration which has potential to be more efficient and environmentally friendly compared with current cooling technologies. Recently, the focus of caloric effects investigations has shifted towards soft materials. An overview of recent direct measurements of the large electrocaloric effect (ECE) in a composite mixture of a liquid crystal and nanoparticles (NPs) and large elastocaloric (eC) effect in main-chain liquid crystal elastomers is given. In mixtures of 12CB liquid crystal with functionalized CdSSe NPs, an ECE exceeding 5 K was found in the vicinity of the isotropic to smectic A phase transition. It is shown that the NPs smear the isotropic to smectic coexistence range in which a large ECE is observed due to latent heat enhancement. NPs acting as traps for ions reduce the moving-ion density and consequently the Joule heating. Direct eC measurements indicate that the significant eC response can be found in main-chain liquid crystalline elastomers, but at a fraction of the stress field in contrast to other eC materials. Both soft materials could play a significant role as active cooling elements or parts of thermal diodes in development of new cooling devices.

This article is part of the themed issue ‘Taking the temperature of phase transitions in cool materials’.

1. Introduction

Caloric effects, such as electrocaloric (EC) and elastocaloric (eC) effects, have recently become very attractive phenomena with potential use in various applications, such as in heat pumps and cooling devices of the new generation, which have great potential to be more environmentally friendly and with better energy efficiency than existing cooling techniques. The electrocaloric effect (ECE) is found in dielectric materials, i.e. in materials with inducible dipoles [1]. It requires a coupling of the electric field to dipolar entities which by changing the electric field will result in changes of the dielectric subsystem entropy [2]. The ECE is manifested in the heating or cooling of an EC material due to the application or removal of the electric field under adiabatic conditions, respectively. On the macroscopic scale, the phenomenological description of ECE revolves around the entropy exchange between the two entropy reservoirs, i.e. dielectric or dipolar and vibrational subsystems [3]. In particular, the application of the electric field causes changes of the dielectric state in a dielectric material, from the less ordered into a more ordered one, and vice versa, when an electric field is removed [4–7]. If such changes are fast enough so that the heat flow from the material to the surrounding bath can be neglected, they can be considered as adiabatic. In an analogy to the magnetocaloric effect [8] and other caloric effects, the total entropy of a dielectric material must be preserved and the drop in a dielectric subsystem entropy is compensated by an increase of the vibrational subsystem entropy, resulting in an increase of temperature of the system, and vice versa if the field is removed.

A typical example of such an EC system is a ferroelectric material in which polarization as an order parameter is linearly coupled to the electric field. It was shown recently that a giant ECE can be observed in inorganic perovskite ferroelectric thin films [1–4,6,9,10] as well as in organic, P(VDF-TrFE)-based ferroelectric copolymers [1,11,12]. First proof of concept cooling devices were produced from these solid-state materials, but with rather low power density due to the relatively large EC inactive regenerator mass [13,14]. The natural idea is to replace for instance the EC inactive fluid regenerator with the EC active dielectric fluid, which may improve the power density of EC cooling devices. Examples of such EC active dielectric fluids are nematic liquid crystals (LCs) in which the nematic order parameter is coupled to the electric field via dielectric anisotropy. It was shown recently that in nematic liquid crystal 5CB a significant entropy change of 23 J kg K⁻¹ can be observed at 900 kV cm⁻¹ of electric field change, which corresponds to a temperature change of 2.1 K [15,16]. In both cases, the best EC response was observed at the phase transition from the disordered to ordered phase, i.e. from paraelectric to ferroelectric phase or isotropic to nematic phase in case of ferroelectrics or nematic liquid crystals, respectively.

By contrast, in eC systems a stress field is coupled with the strain field. Examples of such systems are Ni_50.2Ti_49.8 shape memory alloy wires in which the eC temperature change of 40 K was observed at the applied stress of 0.8 GPa [10,17]. The large stress fields required in these materials typically require rather heavy experimental set-ups, thus making miniaturization of cooling devices difficult, as is the case with magnetocaloric materials. Therefore, it is imperative to find suitable eC candidates among soft materials in which order of magnitude smaller stress field would still produce sizable entropy changes. One of possible candidates are the so-called liquid crystal elastomers (LCEs) with a giant thermomechanical response [18]. Two types of LCEs are mainly used, side-chain and main-chain LCEs. Side-chain LCEs are composed of an elastomer polymer network cross-linked by cross-linking molecules (cross-linkers) and mesogens that are side-attached to polymer chains and which constitute most of the total mass of LCEs [18,19]. In main-chain LCEs, the mesogens as components of polymer chains are parts of the polymer network. Owing to the special preparation via a two-step cross-linking process, the LCEs are stretched by the external stress field so that mesogens form the nematic structure and the corresponding stress field is internally imprinted in the polymer network memory during the second cross-linking step [19]. Such imprinted-stress memory results in a large thermomechanical effect in which by changing the temperature strain up to 100% or more can be observed. Since in LCEs the external stress field is directly coupled to the nematic order parameter it is plausible to expect that the application of the external stress field would result in an eC response.

In this work, we will address the two caloric effects in soft materials by direct experimental methods. In the first section, direct EC measurements of the EC response in a mixture of smectic liquid crystal 12CB and semiconductive CdSSe NPs will be presented. In the next section, the direct eC measurements of the eC effect in main-chain LCE will be discussed. In the final section, the discussion of the importance and a summary of the above results will be given.

2. Electrocaloric effect in mixture of smectic liquid crystal 12CB and CdSSe nanoparticles: experiments and discussion

Let us consider a thermotropic liquid crystal with positive dielectric anisotropy Δε exhibiting isotropic (I), nematic (N) and smectic A (A) LC phases; the presence of the last two phases depends on the coupling strength between the orientational and the translational degree of ordering. In a framework of the Landau–de Gennes phenomenological description, the free energy density can be expressed as

2.1

Here, the orientational and translational mesoscopic scale ordering are described with the uniaxial tensor order parameter 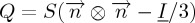and the complex order parameter ψ=η e^iϕ, respectively. The uniaxial orientational order parameter 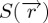and the translational order parameter field 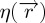reveal the degree of orientational and translational ordering, respectively. a₀, b, c, α₀, β are phenomenological constants, independent of temperature and D measures the coupling strength between the orientational and the translational order parameter.

The electric field which is coupled with the nematic order parameter S drives both order parameters, thus potentially enhancing the ECE in contrast to purely nematic LCs. It is therefore better to look for LC systems that are close to the isotropic–nematic–smectic A (I-N-A) triple point. Such a suitable material is 12CB, one of the higher homologues of the n-alcyl cyanobiphenyl family of liquid crystals (nCBs, n=5−14) which have extensively studied by different techniques in the last 30 years due to their stability and excellent electro-optical properties close to room temperature [20–22]. 12CB is according to the nCB composition phase diagram [22] close to the I-N-A triple point, which in the composition axis is approximately half way between 9CB and 10CB. In addition, latent heat (L) released at the direct isotropic to smectic A (I-A) transition is much larger in 12CB (L=12.2 J g⁻¹) than that for the isotropic to nematic transition in the case of the 5CB compound (L=1.56 J g⁻¹) [23]. It is therefore plausible to expect that 12CB would have enhanced ECE due to the coupling between the nematic and the smectic orders as well as to the additional enhancement of the larger released or absorbed latent heat at the I-A phase transition. Similar to what was found in nematic LCs [15,16], the maximum EC response in 12CB is expected at the melting I-A transition. The maximum enhancement due to the latent heat released within the coexistence range of isotropic and smectic phases (denoted by c.r. in figure 1) is expected if the field (ΔE) is applied just at the upper edge of the c.r., so that the phase transition is induced to the smectic A phase (see vertical arrow denoting the induced crossover from isotropic to smectic A phase in figure 1). In this case, the smectic phase front is expanding until all the sample is transformed into the smectic A phase (see the optical-microscopy snapshot in the inset to figure 1). The latent heat released during crossing the coexistence range is expected to additionally enhance the ECE.

Figure 1.

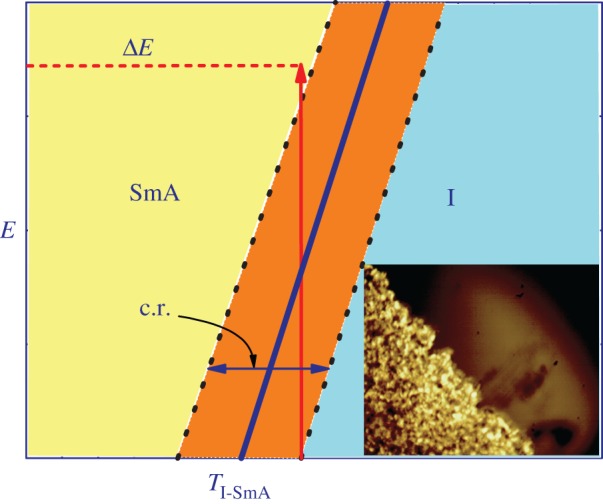
Schematic electric field-temperature phase diagram for smectic A to isotropic phase transition.

The shortcomings of using pure 12CB are related to the narrow coexistence range (less than 0.2 K) and rather significant Joule heating due to ionic impurities and corresponding low resistivity. Such Joule heating was found to be of the order of 30% of the observed EC response. The remedy for both problems is found to be the addition of nanoparticles (NPs) in small weight concentrations to the bulk LC. For instance, it was shown by calorimetric experiments that the melting coexistence range can be for more than an order of magnitude expanded by the addition of micellar NPs to the host liquid crystal [24]. Moreover, it was shown that addition of different types of NPs ranging from insulating to ferroelectric NPs can significantly reduce the density of moving charge carriers via the ion-trapping effect [25]. For instance, it was demonstrated that addition of insulating NPs can reduce conductivity due to the ion-trapping effect for more than an order of magnitude [26]. In order to test the ECE in such NP-modified liquid crystals a 5 wt% mixture was prepared composed of 12CB with semiconductive CdSSe NPs, which were used already in our other studies of impact of NPs on liquid crystal ordering [27]. The experimental details and results are given below.

The high-purity chiral liquid crystal 12CB was synthesized at Likchem, Warsaw, Poland (with mentioned purity higher than 99.92%). The CdS_xSe_1−x NPs were synthesized at the National Centre for Scientific Research ‘Demokritos’ for x=0.5. Atomic force microscopy measurements, performed at Jozef Stefan Institute, yielded a diameter value of 3.4±0.3 nm [27]. The surface of NPs is functionalized with flexible chains of oleyl amine and tri-octyl phosphine. Such a coating has been shown very effective for homogeneous dispersion of various types of spherical NPs in liquid crystals (see more details in [27]).

A mixture with CdSSe concentration of x=0.05 has been prepared, where x is defined as the mass of NPs over the total mass of the sample, i.e. x=m_NP/(m_LC+m_NP). For the mixture preparation, a well-established protocol has been followed [27]. Within this protocol, an ultrasonic bath was applied to break any aggregates in the NPs solution. Next, the solution of solvent, liquid crystal and NPs was mixed by magnetic stirring at elevated temperatures in order to slowly evaporate the solvent, and, finally, drying under vacuum was performed in order to remove any solvent remains. Afterwards, a mixture quantity of about 6 mg was loaded into a high-purity glass cell composed of two 140 μm thick glass plates, which were coated by ITO electrodes and separated by a 120 μm thick Mylar spacer. The temperature variation of the cell was measured by a small bead thermistor attached to the glass plate (figure 2). The protocol of the EC measurement is described in detail in [28]. Here, the step-like pulses were applied always starting from zero. The duration of the pulses was long enough to allow the sample to reach thermal equilibrium with the surrounding bath, typically much longer than the external thermal time scale of ≈100 s. The relaxation of the temperature of the whole system was monitored, 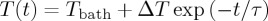. The heat change of the liquid crystal mixture was determined by taking into account the geometry of the sample cell and the heat capacities of its constituents 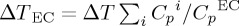. Here, C_pⁱ represents the heat capacity of each constituent, i.e. the heat capacities of the sample, glass plates, thermistor, attaching wires, etc. C_p^EC stands for the heat capacity of the active material. The typical internal time scale that the whole system takes to reach internal thermal equilibrium was about 20 s.

Figure 2.

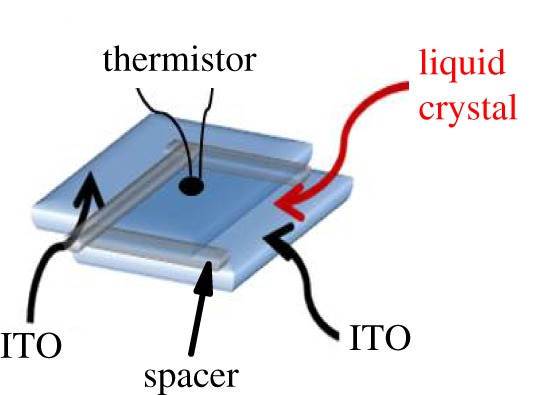
Schematic of a sample cell arrangement.

In order to check the impact of NPs on the broadening of the coexistence range and the I-A phase transition temperature, the dielectric constant of the mixture was measured at 10 kHz in the vicinity of the I-A phase transition for both pure 12CB and a mixture of 12CB and CdSSe NPs. As shown in figure 3, the phase transition temperature is shifted to lower temperatures for about 0.5 K while the coexistence range is broadened from about 0.2 K in pure 12CB to more than 2 K in the mixture of 12CB with NPs.

Figure 3.

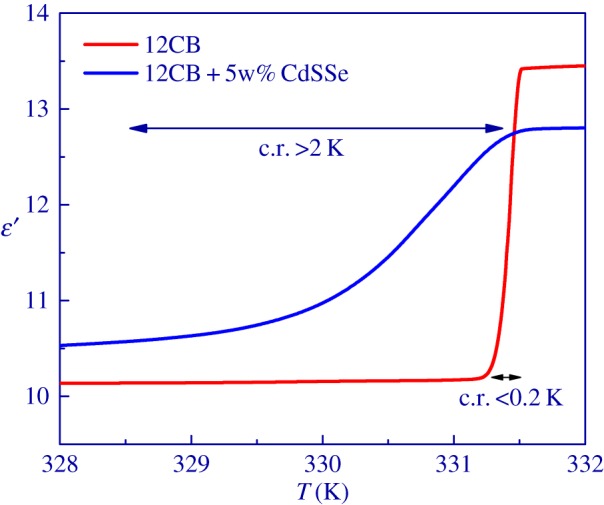
The dielectric constant of pure 12CB and the mixture of 12CB and CdSSe NPs in the vicinity of the I-A phase transition. The coexistence range (c.r.) is smeared over much broader temperature range in the mixture than in pure 12CB.

ΔT_EC was measured as a function of temperature at constant amplitude of the electric field pulses and in the vicinity of the isotropic to smectic A phase transition. Comparison of the EC response when the field was switched on in pure 12CB and in the mixture with NPs (figure 4) shows that the Joule heating, observed as an elevated plateau at longer times when the field is still on, is greatly reduced in the mixture, thus demonstrating the ability of CdSSe NPs to act as effective traps for charge carriers. Owing to very small hysteresis, a nearly symmetric EC cooling response was observed upon field removal. Consequently, we focus only on the magnitude of the ECE as observed upon removal of the electric field. The actual change of temperature is in this case negative; however, we choose to represent the magnitude of the EC as a positive quantity in order not to interfere with the data presentation of the so-called negative ECE typically observed in antiferroelectrics. In this case, the inverted EC response is usually presented with negative data values. Figure 5 shows the EC response ΔT_EC as a function of temperature in the vicinity of the I-A phase transition for the mixture of 12CB and CdSSe NPs. Significant enhancement of the ECE is observed within the coexistence range of the I-A transition due to the released latent heat in which the EC response reaches 5.18 K. Similar magnitude was observed in pure 12CB, but in a much narrower temperature range and with significantly larger Joule heating. As expected due to the stiffening deeper in the smectic A phase, the ECE decreases rapidly below the transition.

Figure 4.

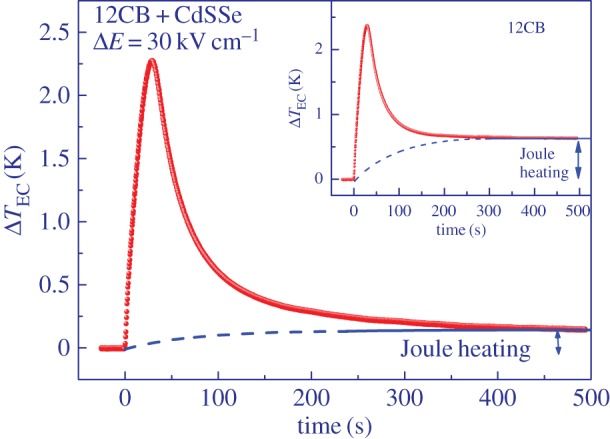
EC change of temperature ΔT_EC as a function of time immediately after the field is switched on at t=0. Lower plateau at longer times in the mixture indicates a significantly lower Joule heating as in pure 12CB (inset). (Online version in colour.)

Figure 5.

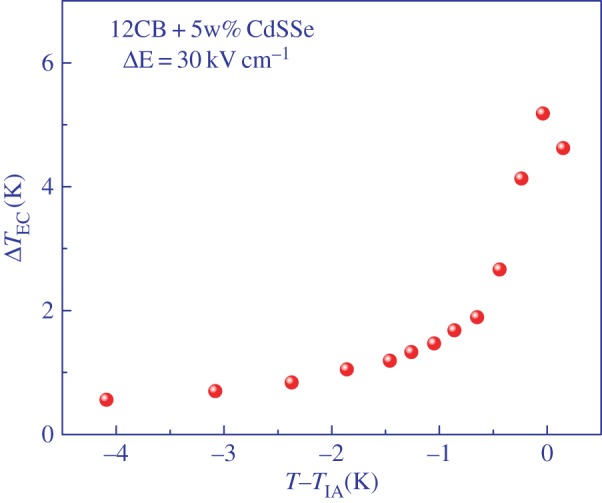
EC response ΔT_EC as a function of temperature in the vicinity of the I-A phase transition for the mixture of 12CB and CdSSe NPs. (Online version in colour.)

Although the exact time scale of the EC response on switching the electric field on or off is not exactly known, due to convolution of the thermal signal by the internal thermal time scale of the sample cell, it is possible to estimate that most of the EC response is fast while part of it is sluggish due to the slow kinetics of smectic domain growth, which could at lower electric fields take up to a few tens of seconds to complete. Nevertheless, the above EC experiments demonstrate the existence of a large EC response in 12CB liquid crystal modified by the addition of CdSSe NPs that significantly reduced the Joule heating and expanded the temperature range in which the latent heat helps to enhance the EC response.

3. Elastocaloric effect in main-chain liquid crystal elastomer: experiments and discussion

Let us consider a main-chain single liquid crystal elastomer that can exhibit transformation of mesogens ordering upon cooling from the isotropic (or paranematic) to the nematic phase. Such transformation can be described by using Landau–de Gennes free energy [29,30],

3.1

Here, the stress field G coupled to the nematic order parameter S is composed of distributed internal random stress fields and the external stress field applied to the sample. Owing to internal inhomogeneity and size-distributed domains, both parameters T_* and G can be viewed as distributed. The above equation shows the possibility to change the entropy of the system by an external stress field coupled to the nematic order parameter, hence the possibility to induce the eC effect. In this section, experimental details and results of studies of the eC effect in main-chain LCE are presented.

Main-chain LCE materials consisting of a backbone with siloxane-based chain extenders, rod-like mesogenic molecules and isotropic cross-linkers with five cross-linking point were synthesized as described in [19,31]. Accordingly, the second cross-linking step was carried out in the nematic state. The internal stress locked in during the second cross-linking step allowed temperature-driven thermoelastic stretching of the main-chain elastomer of about 75%. The concentration of cross-linkers was 0.08. More details about the sample preparation can be found in [19,31]. A sample of 5.75×4.75×0.4 mm³ geometry was mounted in a measurement set-up composed of precise translator capable of measuring accurately strains, temperature-stabilized copper sample chamber and stress/force sensor. The sample temperature variations during the eC measurements were measured by a small bead thermistor attached directly to the sample. Note that within 5%, the same magnitude of the eC response was observed upon application or removal of the stress field. Therefore, we show only the magnitude of the eC effect as observed upon removal of the stress field. Although the actual change of temperature in such a case is negative, following the same approach as in the case of ECE, we present the magnitude of the eC temperature change as a positive quantity.

Figure 6 shows the eC response ΔT_eC at selected strains as a function of temperature in the vicinity of the isotropic to nematic phase transition for the main-chain LCE. As expected, the maximum eC response is achieved near the phase transition taking place at about 340 K and which is slightly shifted to higher temperatures with increasing applied stress field.

Figure 6.

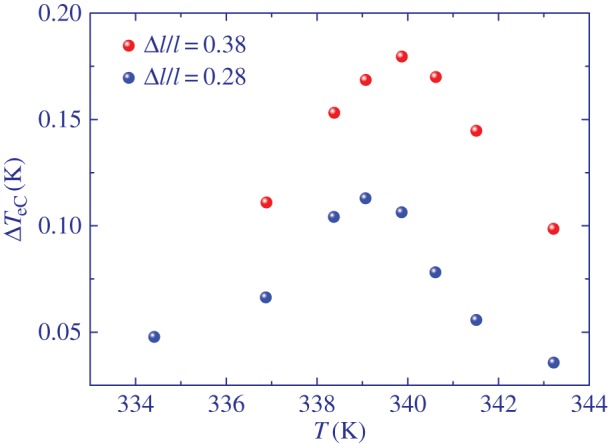
Elastocaloric response ΔT_eC as a function of temperature for two selected strains of main-chain LCE in the vicinity of the isotropic to nematic transition.

Next we focus on the stress-field dependence of the eC response, i.e. dependence on the magnitude of the stretching at the isotropic to nematic phase transition at which the maximum eC response is observed. Figures 7 and 8 show the eC temperature change ΔT_eC as a function of stress change Δσ and strain Δl/l, respectively.

Figure 7.

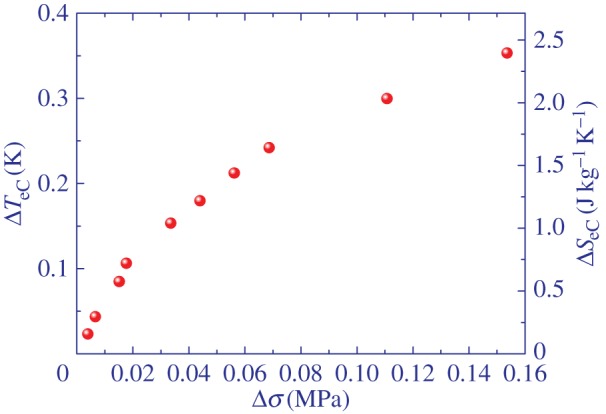
Elastocaloric temperature change ΔT_eC as a function of stress change Δσ of main-chain LCE at the isotropic to nematic transition. (Online version in colour.)

Figure 8.

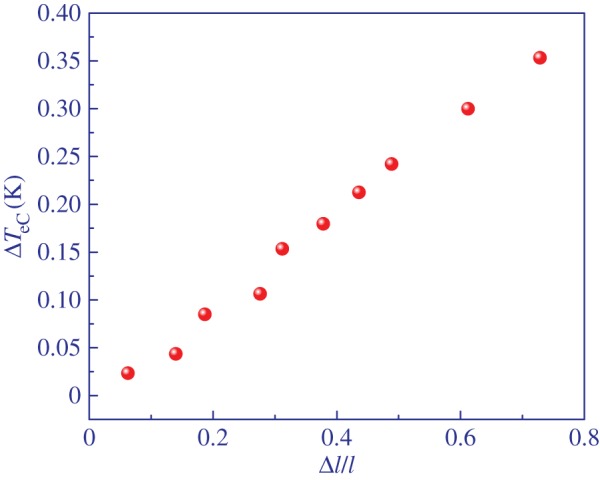
Elastocaloric temperature change ΔT_eC as a function of strain Δl/l of main-chain LCE at the isotropic to nematic transition. (Online version in colour.)

Figure 7 shows slight nonlinear dependence of the eC response on the change in the stress field. By contrast, the eC response is nearly linearly dependent on the strain as shown in figure 8. For relatively small strains of 75% a sizable eC effect of 0.35 K was observed. This is indeed nearly two orders of magnitude smaller eC response than that observed in the best eC materials. However, in the case of LCE, a stress field four orders of magnitude smaller was applied. Taking into account that in side- and main-chain LCEs strains of 400–600% can easily be achieved [32], it is plausible to expect an eC response of several degrees in these materials. This is supported by the relatively weak dependence of the eC responsivity ΔT_eC/Δσ on the strain as shown in figure 9.

Figure 9.

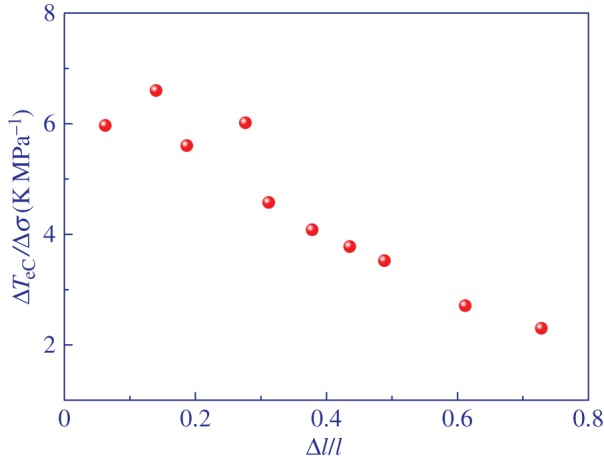
Elastocaloric responsivity ΔT_eC/Δσ as a function of the strain Δl/l in main-chain LCE at the isotropic to nematic transition. (Online version in colour.)

It is interesting to note that the magnitude of the eC responsivity in LCE of ≈4 K MPa⁻¹ is two orders of magnitude larger than the average eC responsivity of ≈0.04 K MPa⁻¹ found in the best shape memory alloys [10].

4. Conclusion

We investigated by direct experiments EC and eC effects in a mixture of liquid crystal 12CB and CdSSe NPs and in a main-chain liquid crystal elastomer, respectively. We have shown the existence of large ECE in the LC mixture with a maximum value of 5.18 K, which was achieved by the latent heat enhancement within the coexistence range of the isotropic to smectic A transition. We demonstrated how a soft LC EC material can be additionally enhanced by the addition of NPs. Slight modification of 12CB by addition of 5 wt% of CdSSe NPs has two positive effects: (i) the coexistence range in which the latent heat enhancing the ECE is released or absorbed was expanded for more than an order of magnitude, (ii) the Joule heating was suppressed by an order of magnitude via the NP ion-trapping mechanism in which the density of moving charge carriers is greatly reduced. Such modification of LCs by NPs is significantly enhances their usefulness as EC cooling materials.

In addition, we have demonstrated the existence of a sizable eC effect in a main-chain liquid crystal elastomer. It is shown that even for small stress fields below 0.10 MPa the eC temperature change of 0.35 K has been achieved. Nearly linear dependence of the eC response on the strain, two orders of magnitude larger eC responsivity (≈6 K MPa⁻¹) than that found in shape memory alloys and large specific heat of ≈2200 J kg⁻¹ K⁻¹ establish LCEs with large strains as most serious candidates for the large power eC cooling or heating applications driven by relatively small stress fields.

Authors' contributions

M.T. and M.L. carried out experiments and data analysis on the LC mixture and LCE, respectively. V.T. and G.N. provided CdSSe NPs, G.C. and B.Z. provided 12CB and LCE. B.Z. provided kindly the facilities for eC experimental set-up. Z.K. conceived of and designed the study, and drafted the manuscript with the help of B.R. All authors read and approved the manuscript.

Competing interests

The authors declare that they have no competing interests.

Funding

This work was supported by the by the Slovenian Research Agency under program P1-0125 and projects J2-6779 and L2-6768. V.T. and G. N. have been supported in part by the ARISTEIA I grant no. 1125, administered by the Genetral Secretariat of Research and Technology of Greece, co-financed by the European Social Fund and the State of Greece.