Abstract
We develop a general thermodynamic framework to investigate multicaloric effects in multiferroic materials. This is applied to the study of both magnetostructural and magnetoelectric multiferroics. Landau models with appropriate interplay between the corresponding ferroic properties (order parameters) are proposed for metamagnetic shape-memory and ferrotoroidic materials, which, respectively, belong to the two classes of multiferroics. For each ferroic property, caloric effects are quantified by the isothermal entropy change induced by the application of the corresponding thermodynamically conjugated field. The multicaloric effect is obtained as a function of the two relevant applied fields in each class of multiferroics. It is further shown that multicaloric effects comprise the corresponding contributions from caloric effects associated with each ferroic property and the cross-contribution arising from the interplay between these ferroic properties.
This article is part of the themed issue ‘Taking the temperature of phase transitions in cool materials’.
Keywords: caloric effects, multiferroics, magnetoelectric, magnetostructural
1. Introduction
Any material thermally responds to changes in its properties induced by application or removal of an external field. The reversible component of this response provides the basis for the caloric properties. In general, caloric effects are quantified by the response corresponding to isothermal and adiabatic variations of the field. In the first case, the response is given by the heat exchanged with the surroundings that results in a change of the entropy of the material, whereas, in the second, it is measured by the corresponding change of temperature [1]. Among the different caloric properties, the magnetocaloric effect is a well-known phenomenon that has been widely used for low-temperature cryogenic applications. The discovery of a giant magnetocaloric response close to room temperature in Gd5(SixGe1−x)4 [2] has opened the route to propose the magnetocaloric effect as an actual alternative to vapour-compression technology for room-temperature refrigeration. More recently, materials that display large mechano- and electrocaloric effects have also been developed [3]. In general, solid-state refrigeration technologies based on caloric effects are expected to contribute to reducing global energy consumption and minimizing the use of ozone-depleting and greenhouse chemicals that are unavoidable in present refrigeration technologies.
Ferroic materials, such as ferroelastic, ferroelectric and ferromagnetic, are expected to show a large caloric response near the phase transition at which the ferroic property spontaneously emerges. Depending on symmetry-dictated conditions and possible coupling of the ferroic property to secondary parameters, this transition is either continuous or first order. The last case is especially interesting, because, then, the transition can be field induced and a giant caloric response is expected when the transition latent heat is large [4]. In this paper, we are mainly interested in the case of multiferroics with two or more coupled ferroic properties, which enables cross-response to multiple fields [5]. Therefore, this class of systems offers us new possibilities as multifunctional materials. In particular, they have been envisaged as materials susceptible to display multicaloric effects, which means that caloric effects associated with each kind of ferroicity are expected to occur in an interdependent manner. The cross-effect is enhanced in those multiferroics where the two (or more) ferroic orders emerge simultaneously, which requires a strong interplay (i.e. coupling) between different ferroicities.
Among the class of multiferroic materials, here we will consider the magnetostructural and magnetoelectric families. The former may display simultaneous ferroelastic and ferromagnetic orders, whereas the latter (usually simply known as multiferroics) display ferroelectric and ferromagnetic orders. We will pay special attention to metamagnetic shape-memory alloys [6], which constitute an interesting class of magnetostructual multiferroics, and to ferrotoroidic systems, in which the ordering of toroidal moments leads to an intrinsic antisymmetric magnetoelectric interplay [7].
The paper is organized as follows. In §2, we discuss recent experimental results that show the relevance of the interplay between different properties in multiferroic materials for the caloric response. In §3, we summarize the main thermodynamic results describing multicaloric effects. In §4, we study multicaloric effects within the framework of the Landau approach. This method is applied to the study of multicaloric effects in metamagnetic shape-memory and ferrotoroidic materials described by appropriate Landau free energies taken as examples of magnetostructural and magnetoelectric multiferroics. Finally, in §5, we summarize the main results and conclude.
2. Review of experimental results
In order to avoid ambiguities, we will start with a reminder of the accepted definition of a multicaloric material as proposed by Moya et al. [4]. According to these authors, a multicaloric material is one that can support more than one type of caloric effect. Therefore, we assume that multicaloric effects occur if more than one type of caloric effect can be driven either simultaneously or sequentially in a given system. In this paper, we are essentially interested in the case where the diverse caloric effects do not occur independently of each other but rather where the cross-response effects arising from the interplay between the different properties influence the caloric response associated with a given property. These effects are indeed expected to occur in both magnetostructural and magnetoelectric multiferroic materials.
Many materials have proven to support more than one caloric effect. Actually, most of the prototypical magnetocaloric materials such as Gd–Si–Ge [8], La–Fe–Si [9], Fe–Rh [10] and NiMn-based Heusler alloys [11,12] have been recently reported to display interesting mechanocaloric (either baro- or both baro- and elastocaloric) effects. Electrocaloric materials are also known to display elasto- [13] or barocaloric effects [14]. In some cases, the elastocaloric response in these materials has even been shown to display a larger strength than the primary electrocaloric effect [15].
Besides the previously mentioned and similar reported results, to date relatively few research efforts have been devoted to the study of multicaloric cross-response in multiferroic materials. Some important results are the following. The influence of an applied hydrostatic pressure on the magnetocaloric effect in MnAs [16], Gd5Si2Ge2 [17] and hydrogenated LaFeSi has been shown to occur as a result of volume changes arising from magnetostructural interplay. The influence of pressure produces quite diverse effects in magnetocaloric materials. While in MnAs the magnetocaloric effect increases with pressure, in Gd5Si2Ge2 it decreases, because application of pressure makes the magnetostructural transition from the monoclinic to orthorhombic phase to approach the Curie temperature of the monoclinic phase. At a given pressure of 6 kbar, both transitions merge into a single one, which becomes of second order. Above this pressure, the magnetocaloric effect remains pressure independent, showing the features of the magnetocaloric effect associated with a second-order transition. In the case of La(FeSi)13Hx compounds, it has been reported [18] that, while the magnetocaloric effect decreases under an applied pressure in LaFe11.57Si1.43 (LaFeSi), it is instead enhanced in the LaFe11.57Si1.43H1.64 hydride. In both LaFeSi and LaFeSi-hydride, the magnetostructural transition is shifted to lower temperatures by increasing the applied pressure. The different effect of pressure on the magnetocaloric response seems to be a consequence of the fact that, while the magnetization change at the transition strongly decreases by application of pressure in LaFeSi, it is almost pressure independent in the hydrides.
Pressure experiments reported by Caron et al. [19] in hexagonal Ni2In-type Mn1xCrxCoGe compounds reveal that pressure is able to tune the temperature at which the magnetostructural phase transition occurs. However, the magnitude of the magnetocaloric effect is almost insensitive to the applied pressure. Samanta et al. [20] have studied similar MnNiSi-based compounds. They took advantage of the fact that the magnetovolume interplay can be strongly enhanced by isostructurally alloying 46% of MnNiSi with 54% MnFeGe. In the resulting system, application of a moderate pressure of about 2.5 kbar enables doubling of the isothermal magnetic field-induced entropy change, owing to a huge volume change of 7% taking place at the magnetostructural transition undergone by the compound close to room temperature.
This effect of pressure on the magnetocaloric properties of the Heusler NiCoMnSb alloy has been reported in [21]. In this system, the magnetocaloric effect is inverse and application of a magnetic field shifts the martensitic transition to lower temperatures. However, pressure has an opposite effect and, thus, application of pressure decreases the magnitude of the magnetic field-induced entropy change. The effect is however very sensitive to the composition. For instance, under application of a magnetic field of 5 T, the induced entropy change decreases from 33 to 16 J kg−1 K−1 by application of 8.5 kbar in Ni46Co4Mn38Sb12, whereas it changes from 41.4 to 33 J kg K−1 in Ni45Co5Mn38Sb12 for the same pressure variation. The authors claim that, by adjusting the Co concentration and applying suitable pressure, a large magnetocaloric effect can be tuned over a large temperature range around room temperature, which improves the potential refrigerant capacity of the system.
In figure 1, we show, for the above-discussed materials, the dependence of the maximum of the entropy change (absolute value, 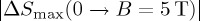 ) on the applied pressure obtained under isothermal application of a magnetic field of 5 T. Taking into account that the obtained behaviour is linear to a reasonably good approximation, in relation to the magnetocaloric response, the strength of the magnetovolume interplay can be measured by the rate of change of the induced entropy change at a given applied field with pressure,
) on the applied pressure obtained under isothermal application of a magnetic field of 5 T. Taking into account that the obtained behaviour is linear to a reasonably good approximation, in relation to the magnetocaloric response, the strength of the magnetovolume interplay can be measured by the rate of change of the induced entropy change at a given applied field with pressure, 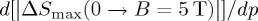 . We have obtained a very large value of approximately 18 J (K kg kbar)−1 for the MnNiSi-based compound, approximately 2 J (K kg kbar)−1 for LaFeSi-hydride and negative low values, approximately −1.8 J (K kg kbar)−1, for the remaining compounds.
. We have obtained a very large value of approximately 18 J (K kg kbar)−1 for the MnNiSi-based compound, approximately 2 J (K kg kbar)−1 for LaFeSi-hydride and negative low values, approximately −1.8 J (K kg kbar)−1, for the remaining compounds.
Figure 1.
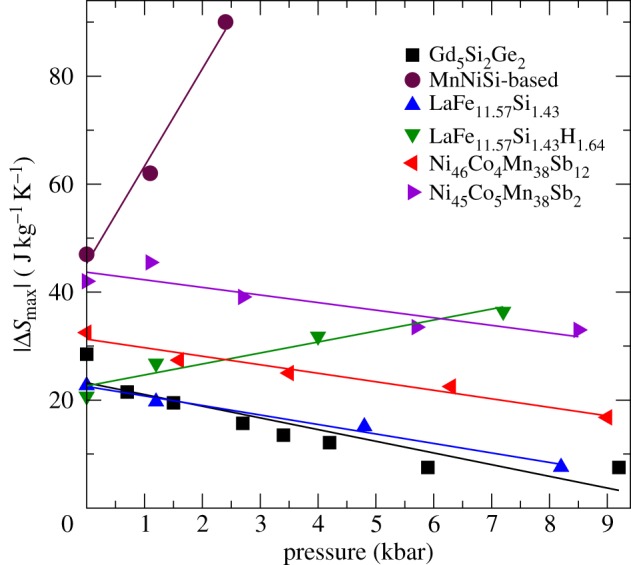
Maximum value of the entropy change, 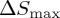 , obtained by isothermal application of a magnetic field of 5 T as a function of the hydrostatic pressure.
, obtained by isothermal application of a magnetic field of 5 T as a function of the hydrostatic pressure.
In the case of Heusler alloys, the influence of a magnetic field on the elastocaloric effect induced by the application of uniaxial compressive stress has been reported in [22]. In spite of the fact that only relatively low stresses (about 10 MPa) were applied owing to poor mechanical properties characteristic of this class of materials, results provide evidence for a significant elastocaloric effect associated with the large entropy change at the magnetostructural phase transition undergone by the material. Interestingly, application of a magnetic field below 1 T was found to increase the elastocaloric relative cooling power by about 20%. Similarly, the effect of an applied electric field on the elastocaloric response of ferroelectric Pb(Mn1/3Nb2/3)O3–32PbTiO3 single crystals induced by uniaxial compressive stress has been reported in [23]. The effect has been found to be quite small. More interesting seems to be the enhancement of the electrocaloric effect associated with an applied uniaxial compressive stress.
The possibility of electric control of the magnetocaloric effect (or, conversely, magnetic control of the electrocaloric effect) in strain-mediated extrinsic multiferroic systems has been foreseen by Moya et al. [24]. With this aim, they studied the extrinsic magnetocaloric effect in ferromagnetic La0.7Ca0.3MnO3 manganite grown on ferroelectric–ferroelastic BaTiO3 substrates owing to strain-mediated feedback associated with its first-order structural phase transition. On the other hand, inspired by the large magnetoelectric coupling arising from transferred stress in FeRh/BaTiO3 heterostructures that enables the magnetic first-order transition in FeRh to be modified [25], Gong et al. [26] prepared ribbons of Ni44Co5.2Mn36.7In14.1 (NiCoMnIn) combined with La0.7Sr0.3MnO3/Pb(Mg1/3Nb2/3)O3–PbTiO3 (PMN–PT) substrate to investigate the effect of electric field on the magnetocaloric effect in NiCoMnIn. This material is a well-known Heusler shape-memory alloy undergoing a magnetostructural transition that displays an inverse magnetocaloric effect and the heterostructural films of PMN–PT enable the necessary strain to be induced that can tune the magnetocaloric effect by application of an electric field. The obtained results, while not spectacular, clearly demonstrate that the magnetocaloric effect can be controlled by the applied electric field.
More recently, good multicaloric properties have been predicted in laminated multiferroic composites designed with layers of Gd and Hf0.2Zr0.8O2, which are, respectively, good magnetocaloric and electrocaloric materials with almost the same Curie transition temperatures as the corresponding ferromagnetic and ferroelectric phases [27].
To the best of our knowledge, no similar studies have been performed so far in intrinsic magnetoelectric multiferroics, probably because few exist in Nature or have been synthesized in the laboratory.
Finally, it is worth pointing out that multicaloric effects have also been studied from first-principle calculations. It has been shown that this is a method to find efficient mechanisms leading to an enhancement of interplay between ferroic properties that could provide new routes for designing new multiferroic materials with optimal multicaloric effects [28,29].
In general, results demonstrating the influence of interplay (i.e. coupling) between ferroic properties are interesting not only because they enable information to be gained on the mechanisms at the origin of interplay, but also because the possibility of inducing large thermal effects by combining diverse external fields may open up a new strategy for improving the efficiency of solid-state cooling devices. In §3, we establish the thermodynamic basis that enables a quantitative study of cross-response caloric effects.
3. Thermodynamics
For the sake of generality, let us consider a multiferroic material characterized by n (not independent) ferroic properties (or generalized displacements) {xi} with corresponding thermodynamically conjugated fields (or generalized forces) {Y
i}. Pairs of these variables can be magnetization and magnetic field, polarization and electric field, or strain and stress. Variables in each pair have the same tensorial order, so that the tensorial product Y
i⋅xi is a scalar (with units of energy density). The two relevant caloric responses are the isothermal and adiabatic responses to an applied field Y
j measured, respectively, by 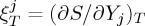 and
and 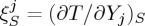 , where S and T are entropy and temperature, respectively, and the derivatives are computed keeping the fields {Y
k≠j} constant. Using Maxwell relations,1 these response functions can be written as
, where S and T are entropy and temperature, respectively, and the derivatives are computed keeping the fields {Y
k≠j} constant. Using Maxwell relations,1 these response functions can be written as 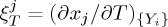 and
and  . It is then straightforward to see that
. It is then straightforward to see that 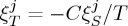 , where C=T(∂S/∂T){Yi} is a heat capacity. In the case of the magnetocaloric effect, the relevant response function is
, where C=T(∂S/∂T){Yi} is a heat capacity. In the case of the magnetocaloric effect, the relevant response function is 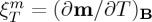 , where m and B are the magnetization and magnetic field, respectively. For the electrocaloric effect, the corresponding relevant quantities are polarization, p, and electric field, E, whereas strain,
, where m and B are the magnetization and magnetic field, respectively. For the electrocaloric effect, the corresponding relevant quantities are polarization, p, and electric field, E, whereas strain,  , and stress,
, and stress,  , are the relevant variables in the case of the mechanocaloric effect. Note that for magneto- and electrocaloric effects these variables are vectors, whereas they are second-rank tensors in the case of the mechanocaloric effect.
, are the relevant variables in the case of the mechanocaloric effect. Note that for magneto- and electrocaloric effects these variables are vectors, whereas they are second-rank tensors in the case of the mechanocaloric effect.
Changes of entropy and temperature associated with a finite variation of the field are obtained by integration of 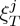 or
or 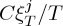 , respectively. Usually, the field is assumed to change only in magnitude. Nevertheless, it is worth pointing out that the study of magnetocaloric effect associated with field rotation in highly anisotropic magnetic materials has recently attracted some interest [30,31]. However, we will not consider here such situations and, in what follows, we will discuss only caloric and multicaloric effects associated with changes of magnitude of the fields.
, respectively. Usually, the field is assumed to change only in magnitude. Nevertheless, it is worth pointing out that the study of magnetocaloric effect associated with field rotation in highly anisotropic magnetic materials has recently attracted some interest [30,31]. However, we will not consider here such situations and, in what follows, we will discuss only caloric and multicaloric effects associated with changes of magnitude of the fields.
Although not imposed by thermodynamics, the response functions 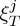 are in general negative, because ferroic properties are expected to reach a maximum value in the ground state. Therefore, in general, the entropy decreases when a field is applied isothermally while temperature increases when it is applied adiabatically. This corresponds to conventional caloric effects. Nevertheless, in some regions of the space of thermodynamic parameters,
are in general negative, because ferroic properties are expected to reach a maximum value in the ground state. Therefore, in general, the entropy decreases when a field is applied isothermally while temperature increases when it is applied adiabatically. This corresponds to conventional caloric effects. Nevertheless, in some regions of the space of thermodynamic parameters, 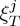 can be positive and, then, the caloric effect is denoted inverse, which means that entropy increases when the field is applied isothermally, whereas temperature decreases when it is applied adiabatically. This behaviour can occur near a phase transition owing, for instance, to specific features of the interplay between ferroic properties, or associated with frustration effects, or a combination of both [6,32].
can be positive and, then, the caloric effect is denoted inverse, which means that entropy increases when the field is applied isothermally, whereas temperature decreases when it is applied adiabatically. This behaviour can occur near a phase transition owing, for instance, to specific features of the interplay between ferroic properties, or associated with frustration effects, or a combination of both [6,32].
Let us now discuss multicaloric effects induced by application of more than one field. We summarize here the thermodynamic development published in [33]. For the sake of practical applications, we consider systems with two ferroic properties x1 and x2 with thermodynamically conjugated fields Y1 and Y2, respectively. Assuming that the system responds isotropically to the applied fields, the change of entropy induced by isothermal changes of the magnitude of both fields can be expressed as
| 3.1 |
where, if, for instance, x and Y are vectors, x will be the projection of x in the direction of the applied field, while if they are tensors, then x corresponds to the same combination of tensor elements as in Y .
In the expression (3.1), the first term on the right-hand side is simply the entropy change that quantifies the caloric effect associated with the ferroic property x1. The second term can be written as the sum of terms that measure the caloric effect associated with the induced change of the property x2 and a caloric cross-response contribution. That is,
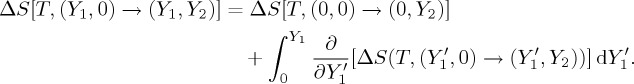 |
3.2 |
After some straightforward calculation, the cross-response contribution can be expressed as
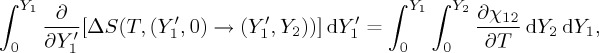 |
3.3 |
where χ12 (=χ21) is the cross-susceptibility that quantifies the response of x1 (x2) to the non-conjugated field Y 2 (Y 1). Therefore, in the presence of interplay between both ferroic properties, the multicaloric effect is not the simple sum of the caloric effects associated with each one independently. The lack of additivity is controlled by the temperature dependence of the cross-susceptibility.2
It is worth pointing out that in some cases it is useful to decompose the pure caloric terms 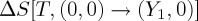 and
and 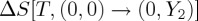 , as the sum of contributions, respectively, associated with the properties x1 and x2. The following result is obtained after some calculation:
, as the sum of contributions, respectively, associated with the properties x1 and x2. The following result is obtained after some calculation:
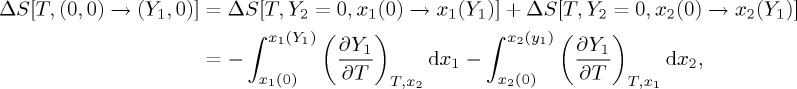 |
3.4 |
and a similar equation for the entropy change induced by the application of field Y 2. Note that the second term on the right-hand side of equation (3.4) only vanishes when there is no interplay between the properties x1 and x2.
4. Landau approach
In this section, we aim to apply the thermodynamic formalism summarized in §3 to the study of multicaloric effects near phase transitions of a system described by two ferroic properties within the framework of the Landau approach. Ferroic properties are convenient order parameters, which will be assumed to be one-component (scalar)-order parameters. This is consistent with the isotropy assumption made in §3. The free energy function will contain pure contributions associated with each ferroic property and a term accounting for their interplay. That is,
| 4.1 |
Within the Landau theory, near a phase transition, these contributions are expressed as series expansions of the order parameters. To ensure that the free energy function is invariant under the symmetry operations of the system, only terms allowed by symmetry must be included in the expansion. Expansion coefficients are material dependent and explicitly bring in the dependence on temperature. The approach is phenomenological and its natural combination with the thermodynamic formalism provides a powerful method to study the behaviour of thermodynamic quantities near phase transitions. The presence of external fields thermodynamically conjugated to the order parameters (ferroic properties) can be taken into account by introducing Gibbs-like free energies through the Legendre transforms, G1=F1−Y
1x1 and G2=F2−Y
2x2. Then, the equilibrium values of the ferroic properties at a given temperature in the presence of applied fields are obtained from minimization of G=G1+G2+F12. Usually, temperature dependence is assumed only in the lowest-order quadratic terms of F1 and F2, imposing that the high-temperature susceptibilities associated with properties x1 and x2 satisfy Curie–Weiss dependence. That is, it is assumed that 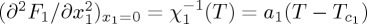 and
and 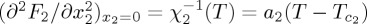 , where Tc1 and Tc2 are limits of stability of pure high-temperature phases 1 and 2, respectively. Taking into account that entropy is given by S=−∂G/∂T, the entropy change induced by isothermal consecutive application of fields Y
1 and Y
2 can be expressed as
, where Tc1 and Tc2 are limits of stability of pure high-temperature phases 1 and 2, respectively. Taking into account that entropy is given by S=−∂G/∂T, the entropy change induced by isothermal consecutive application of fields Y
1 and Y
2 can be expressed as
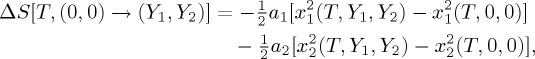 |
4.2 |
where the values of the ferroic properties on the right-hand side of (4.2) are the equilibrium values and thus solutions of ∂G/∂x1=∂G/∂x2=0 for the indicated values of the fields Y 1 and Y 2. Of course, the same entropy change is obtained, regardless of the order of application of the fields. It is straightforward to see that expression (4.2) is equivalent to the previous general thermodynamic expression (3.2) and thus provides an alternative procedure to compute field-induced entropy changes. After some algebra equation (4.2) can be written in the form
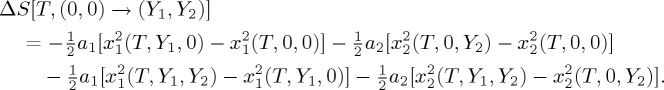 |
4.3 |
Note that this expression explicitly takes into account the decomposition considered in equation (3.4). Actually, the first two terms on the right-hand side correspond to the pure contributions associated with both ferroic properties and the last two terms quantify the cross-response. Each one of these two last terms represents the entropy change associated with a given property keeping the non-conjugated field at a non-zero constant value. Indeed, these terms vanish in the absence of interplay between ferroic properties.
It is worth pointing out that, when explicit temperature dependence of higher-order coefficients in the Landau expansion is assumed, equation (4.2) must be replaced by an expression in the form of an expansion with coefficients given by temperature derivatives of the successive terms that carry an explicit temperature dependence in the Landau free energy function.
(a). Application to metamagnetic shape-memory alloys
A metamagnetic shape-memory alloy is a material undergoing a martensitic transition with associated shape-memory properties that exhibits different magnetic orders in the high- (parent) and low-temperature (martensitic) phases. Usually, the parent phase is ferromagnetic, and there is a re-entrance towards a paramagnetic phase3 at the transition which is a consequence of strong magnetostructural interplay [34]. At a microscopic level, this interplay can be understood as being the result of the strong sensitivity of the oscillatory exchange coupling of localized magnetic moments (RKKY-type exchange mediated by the conduction electrons) to small changes in the distances of the atoms carrying the moments induced by the structural transition, which leads to a competition between ferro- and antiferromagnetism [35]. Therefore, these materials must be classified within the family of the magnetostructural multiferroics. The structural transition is essentially described by a shear mechanism, but also involves a significant volume change. Lattice Hamiltonians with parameters obtained from ab initio calculations have been proposed to account for the magnetocaloric properties of this class of materials [36]. In addition, mean field models have been reported.4 Nevertheless, such models do not take into account the effect of pressure. In the present model, we assume that the shear, ε, and the magnetization, m, are primary-order parameters describing the symmetry breaking taking place at the transitions, while the relative volume change, ω, is a secondary-order parameter coupled to the shear.5 We propose the following Landau free energy function to study this class of materials:
| 4.4 |
where Fε and Fm are the following expansions that include only even powers of the corresponding order parameters adequate for a first-order structural transition and for a continuous ferromagnetic transition, respectively:
| 4.5 |
and
| 4.6 |
In the previous expansions, all the coefficients are assumed to be positive. The minus sign of the ε4 coefficient ensures that Fε describes a first-order transition. The term ω2/2D is the elastic energy associated with volume change and thus D is a compressibility coefficient. The last two terms in equation (4.4) are isotropic coupling terms between shear and magnetization and between shear and volume, respectively. It is worth pointing out that, in spite of being permitted by symmetry, a direct coupling, ωm2, between volume and magnetization is assumed to be negligibly small and thus not included in the model. This is suggested by the very weak effect of an applied hydrostatic pressure on the Curie temperature in metamagnetic shape-memory alloys [39]. Note that in the free energy expansion only the coefficients of the harmonic terms in Fε and Fm depend explicitly on temperature.6 T0 and Tc are the lower stability limits of the pure paraelastic parent phase and paramagnetic phase, respectively. Because we will assume that the magnetic transition occurs first during cooling from high temperature, Tc will correspond to the Curie temperature of the para- to ferromagnetic continuous transition.
In the presence of external fields coupled to ε, m and ω, a Gibbs-like free energy function, G, is defined as
| 4.7 |
where σ is the shear stress, B is the magnetic field and p is the hydrostatic pressure.
After minimization of G with respect to ω and m, the following equations of state are obtained:
| 4.8 |
and
| 4.9 |
When the first of these equations is substituted in G (equation (4.7)), an effective Gibbs-like free energy expansion Gε−m with biquadratic coupling between the order parameters ε and m is obtained. The thermodynamics of this class of Landau model has been studied in detail in [33]. In the absence of an applied field (B=σ=p=0), the resulting effective free energy function can be written as
| 4.10 |
where the re-scaled tilde-parameters are now explicit functions of the parameters κ1 and κ2 given by 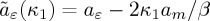 ,
, 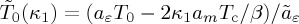 ,
, 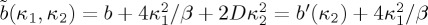 . The temperature of the structural transition is given by
. The temperature of the structural transition is given by
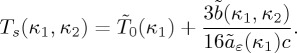 |
4.11 |
In this case (absence of applied field), taking into account equation (4.9), it is expected that, in the temperature region Ts<T<Tc, m2=am(Tc−T)/β. For T≤Ts, m2=−[2κ1ε2−am(Tc−T)]/β. It is worth noting that for 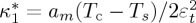 , where εt is the strain discontinuity, m vanishes at the magnetostructural transition. This condition is satisfied along the curve
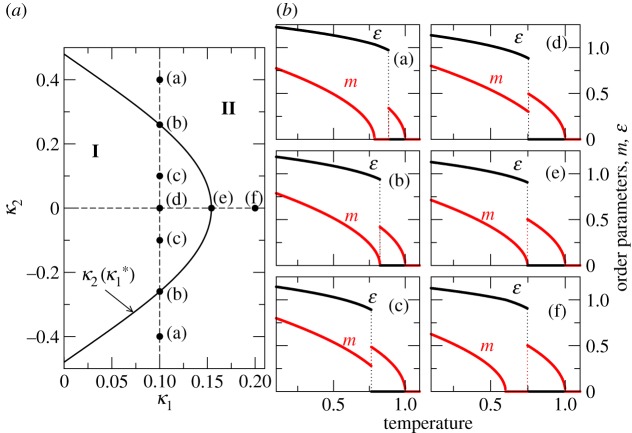
, where εt is the strain discontinuity, m vanishes at the magnetostructural transition. This condition is satisfied along the curve 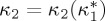 (figure 2). For values of |κ2| inside the curve (region I), the magnetization decreases but does not vanish at the structural transition. For values outside the curve (region II), the magnetization remains zero in a certain temperature range below the structural transition. Therefore, in this last case, a second magnetic transition (from a high-temperature paramagnetic martensite to a low-temperature ferromagnetic martensite) occurs at a temperature TcM<Ts. Actually, both situations have been experimentally observed in metamagnetic shape-memory materials.7 Thus, the model is able to nicely reproduce the behaviour of magnetization observed in this class of metamagnetic materials that should occur for specific values of the magnetostructural coupling. In particular, it reproduces the re-entrance to the paramagnetic state observed in this class of materials. In figure 2, we show the behaviour of m and ε versus T for particular values of κ1 and κ2 within regions I and II.8
(figure 2). For values of |κ2| inside the curve (region I), the magnetization decreases but does not vanish at the structural transition. For values outside the curve (region II), the magnetization remains zero in a certain temperature range below the structural transition. Therefore, in this last case, a second magnetic transition (from a high-temperature paramagnetic martensite to a low-temperature ferromagnetic martensite) occurs at a temperature TcM<Ts. Actually, both situations have been experimentally observed in metamagnetic shape-memory materials.7 Thus, the model is able to nicely reproduce the behaviour of magnetization observed in this class of metamagnetic materials that should occur for specific values of the magnetostructural coupling. In particular, it reproduces the re-entrance to the paramagnetic state observed in this class of materials. In figure 2, we show the behaviour of m and ε versus T for particular values of κ1 and κ2 within regions I and II.8
Figure 2.
(a) Space of interplay parameters κ1–κ2. (b) Examples of magnetization, m, and strain, ε, as a function of temperature (in reduced units) for particular values of κ1 and κ2 indicated along the two dashed lines plotted in (a).
The entropy change at the magnetostructural transition can be obtained as 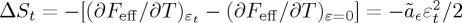 , where
, where 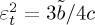 . For
. For 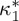 values of the magneto- structural coupling for which m vanishes at the magnetostructural transition, we obtain that ΔSt depends on the difference between the Curie temperature and the magnetostructural transition as
values of the magneto- structural coupling for which m vanishes at the magnetostructural transition, we obtain that ΔSt depends on the difference between the Curie temperature and the magnetostructural transition as
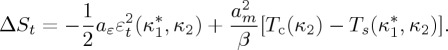 |
4.12 |
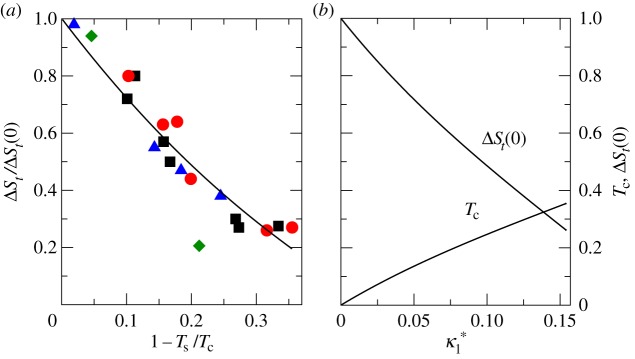
Therefore, the absolute value of the transition entropy change is expected to decrease as the temperature difference between the magnetostructural and the magnetic transition increases. This is a consequence of the competition between the structural and the magnetic contributions to the whole entropy change, which are of opposite signs. ΔSt as a function of Tc−Ts can be computed by solving self-consistently equation (4.12) and the equations defining 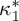 and εt. In figure 3a, ΔSt/ΔSt(0) versus 1−Ts/Tc (ΔSt(0)=ΔSt at Ts=Tc) obtained from the present Landau model (the example corresponds to κ2 on the parabolic line separating regions I and II) is compared with experimental data reported in [41,42] for Ni50MnxIn1−x, Ni45Co5MnxIn1−x and Ni42.5Co7.5MnxIn1−x metamagnetic shape-memory alloys. Very good agreement is obtained after re-scaling linearly the vertical and horizontal axes. This re-scaling is assumed in order to take into account a possible dependence of Tc and ΔSt(0) on
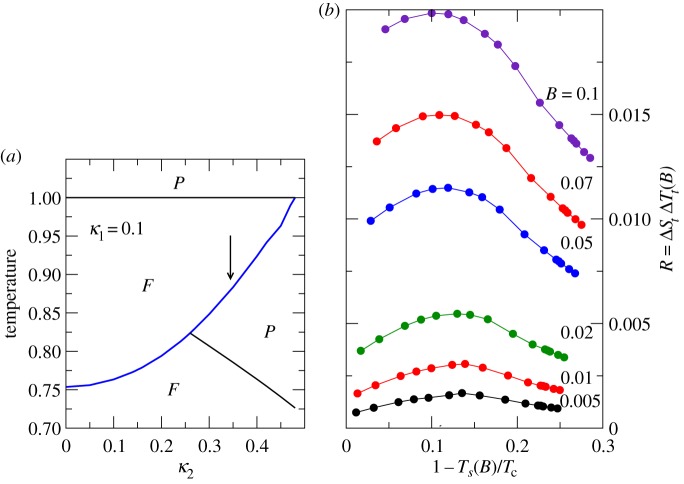
and εt. In figure 3a, ΔSt/ΔSt(0) versus 1−Ts/Tc (ΔSt(0)=ΔSt at Ts=Tc) obtained from the present Landau model (the example corresponds to κ2 on the parabolic line separating regions I and II) is compared with experimental data reported in [41,42] for Ni50MnxIn1−x, Ni45Co5MnxIn1−x and Ni42.5Co7.5MnxIn1−x metamagnetic shape-memory alloys. Very good agreement is obtained after re-scaling linearly the vertical and horizontal axes. This re-scaling is assumed in order to take into account a possible dependence of Tc and ΔSt(0) on 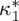 , which may reflect the expected variation of the Curie temperature and entropy change on alloy composition (see [41]) or their change with atomic order induced by means of heat treatment (see [42]). The assumed dependence is shown in figure 3b. Taking into account that Tc−Ts depends on specific interplay conditions, results prove that the decrease of ΔSt with the difference Tc−Ts is a result of the competition between the structural and magnetic contributions to the change of entropy. This is in agreement with the analysis of entropy contributions to the whole transition entropy change recently reported for the metamagnetic NiMnCoIn shape-memory alloy in [43]. These results have tremendous consequences for the multicaloric properties of this class of materials, because ΔSt represents to a large extent the available entropy content in both the mechano- and magnetocaloric effects. As a criterion, for a given applied magnetic field B, we may assume that the material (defined in the model by the parameters κ1 and κ2) with optimal caloric properties is the one that maximizes the product (see [44]) R=ΔStΔT(B), where ΔT(B) is the shift of the structural transition induced by the applied magnetic field (obtained by means of the Clausius–Clapeyron equation). Note that this shift provides a good estimate of the temperature change induced under adiabatic application of the field and thus R is a good measure of the refrigerant capacity. The product R as a function of the reduced temperature distance between Curie and structural transitions, 1−Ts(B)/Tc, along the line κ1=0.1, for selected values of the applied magnetic field is depicted in figure 4. Results show that, in spite of the decrease of ΔSt, the refrigerant capacity shows a maximum at a given value of the difference between Tc and Ts.
, which may reflect the expected variation of the Curie temperature and entropy change on alloy composition (see [41]) or their change with atomic order induced by means of heat treatment (see [42]). The assumed dependence is shown in figure 3b. Taking into account that Tc−Ts depends on specific interplay conditions, results prove that the decrease of ΔSt with the difference Tc−Ts is a result of the competition between the structural and magnetic contributions to the change of entropy. This is in agreement with the analysis of entropy contributions to the whole transition entropy change recently reported for the metamagnetic NiMnCoIn shape-memory alloy in [43]. These results have tremendous consequences for the multicaloric properties of this class of materials, because ΔSt represents to a large extent the available entropy content in both the mechano- and magnetocaloric effects. As a criterion, for a given applied magnetic field B, we may assume that the material (defined in the model by the parameters κ1 and κ2) with optimal caloric properties is the one that maximizes the product (see [44]) R=ΔStΔT(B), where ΔT(B) is the shift of the structural transition induced by the applied magnetic field (obtained by means of the Clausius–Clapeyron equation). Note that this shift provides a good estimate of the temperature change induced under adiabatic application of the field and thus R is a good measure of the refrigerant capacity. The product R as a function of the reduced temperature distance between Curie and structural transitions, 1−Ts(B)/Tc, along the line κ1=0.1, for selected values of the applied magnetic field is depicted in figure 4. Results show that, in spite of the decrease of ΔSt, the refrigerant capacity shows a maximum at a given value of the difference between Tc and Ts.
Figure 3.
(a) ΔSt/ΔSt(0) versus 1−Ts/Tc (continuousline—parabolic to a very good approximation). Symbols correspond to experimental data for Ni50MnxIn1−x (diamonds), Ni45Co5MnxIn1−x (squares) and Ni42.5Co7.5MnxIn1−x (triangles) metamagnetic shape-memory alloys. Circles correspond to a Ni45Co5Mn36.7In13.3 alloy subjected to heat treatment that enables the atomic order to be selected [ΔSt(0)=40 J K kg−1]. For Ni50MnxIn1−x, ΔSt(0)= 32 J K kg−1; for Ni45Co5MnxIn1−x, ΔSt(0)=60 J K kg−1; and for Ni42.5Co7.5MnxIn1−x, ΔSt(0)=50 J K kg−1. (b) ΔSt(0) and Tc (in reduced units) versus 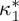 used for scaling the data in panel (a).
used for scaling the data in panel (a).
Figure 4.
(a) Details of the phasediagram in the relevant region. Paramagnetic (P) and ferromagnetic (F) regions are indicated. The blue line is the structural transition line. (b) Refrigerant capacity R=ΔStΔT(B) as a function of the reduced temperature difference between Curie and structural transitions along the line κ1=0.1 for selected values of the applied magnetic field. The arrow in (a) locates the region where the maximum of the refrigerant capacity occurs (corresponding to a value κ2≃0.35). Temperature and entropy are given in reduced units.
Now, we are prepared to study multicaloric effects in metamagnetic shape-memory materials. In the vicinity of the magnetostructural transition, the studied metamagnetic systems are expected to display elastocaloric, barocaloric and magnetocaloric effects, which should occur interdependently. As an illustration, we will analyse here the effect of pressure on the magnetocaloric effect. Therefore, we assume that the external applied stress is zero and compute the change of entropy induced by isothermal application of a magnetic field at given applied pressures for a given difference Tc−Ts, which corresponds to specific values of coupling parameters κ1 and κ2. We obtain
| 4.13 |
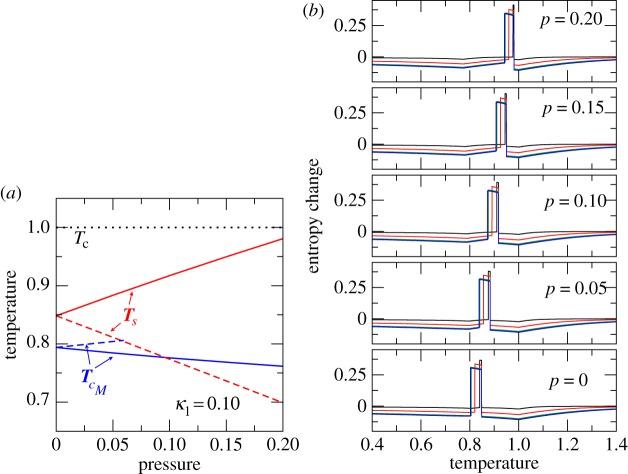
where ε and m are equilibrium values of the strain and magnetization, respectively, with given values of the applied magnetic field B and pressure p. It is worth remembering that the effect of pressure is only relevant when κ2≠0 (otherwise, there is no interplay between primary-order parameters and volume). There are thus two situations to be considered, κ2>0 and κ2<0. The corresponding phase diagram for a given value of κ1 is shown in figure 5a. In the first case (κ2>0) volume decreases at the transition and Ts increases with the applied pressure, whereas in the second case (κ2<0) volume increases and transition temperature decreases. This indicates that the barocaloric effect should be conventional in the first case, but inverse in the second. Because, in the region of the magnetostructural transition, the magnetocaloric effect is expected to be inverse, we will analyse the case κ2>0, as the caloric responses to pressure and magnetic field are expected to compete.
Figure 5.
(a) Transition temperatures Tc, Ts and TcM as a function of pressure for κ2=0.3 (continuous lines) and κ2=−0.3 (discontinuous lines), κ1=0.1. The dashed line corresponds to Tc. (b) Changesof entropy induced by isothermal application of selected magnetic fields at given values of the applied hydrostatic pressure as a function of temperature for κ1=0.1 and κ2=0.3. Temperature, pressure and entropy are given in reduced units.
Changes of entropy induced by isothermal application of selected magnetic fields at given applied hydrostatic pressures are shown as a function of temperature in figure 5b. A significant magnetocaloric peak occurs in the region of the magnetostructural transition. Note that in this region the entropy increases when the magnetic field is applied, which confirms the inverse character of the magnetocaloric effect. Outside the magnetostructural transition region, the magnetocaloric effect is weak and conventional.
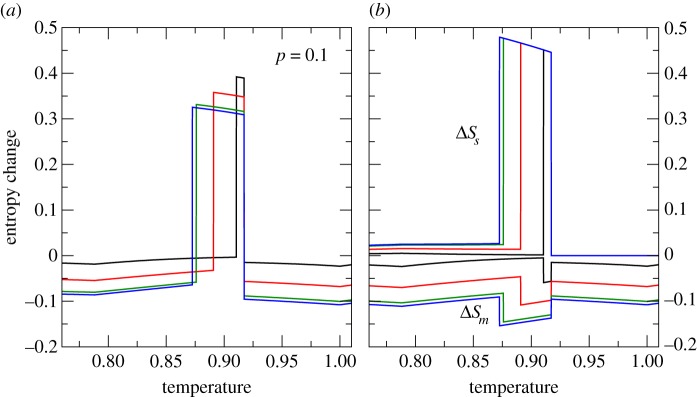
In figure 6a, we show the magnetocaloric peak for a given value of the hydrostatic pressure in more detail. It is interesting to note that the maximum value of the entropy change decreases as the applied magnetic field is increased. Because the application of the magnetic field shifts the magnetostructural transition to lower temperatures, the observed behaviour is consistent with the previously discussed decrease in the transition entropy with the difference between the Curie and structural transitions. In figure 6, we show the corresponding structural and magnetic contributions to the whole magnetocaloric peak. In agreement with reported experimental studies [43], the present results also indicate that the magnetocaloric effect in the vicinity of the magnetostructural transition is dominated by the structural contribution to the entropy. In any case, note that, despite the fact that the magnetostructural transition can be induced by application of pressure, there is no volume contribution to the entropy change.
Figure 6.
(a) Detail of a magnetocaloric peak for selected values of the applied magnetic field and an applied pressure, p=0.1. The magnetic field B takes values 0.01, 0.05, 0.09, and 0.1 for curves from top to bottom. (b) Corresponding magnetic and structural contributions to the entropy change. Temperature, pressure and entropy are given in reduced units.
(b). Application to ferrotoroidics
Ferrotoroidics are materials where toroidal moments show cooperative order [7,45]. This order is expected to spontaneously emerge at a phase transition at which both time and spatial inversion symmetries are simultaneously broken. Therefore, the transition combines the symmetry changes characterizing the occurrence of both ferromagnetism and ferroelectricity, respectively [46]. Consequently, these materials intrinsically belong to the class of magnetoelectric multiferroics [47]. Here we will consider systems with magnetic-vortex-like structures characterized by a dipolar toroidal moment.9 These complex structures have been observed in LiCo(PO4)3 using second harmonic generation [49].
Given a distribution m(r) in a volume v, the magnetic dipolar toroidal moment can be defined as
| 4.14 |
In the continuum limit, the toroidization τ is then given by the volume density of toroidal moments. While the natural conjugated field of toroidization is ∇×B, where B is a magnetic field, because we are considering only homogeneous macroscopic bodies in thermodynamic equilibrium, from symmetry considerations, we make the usual assumption that G=E×B, where E is an electric field, is the appropriate conjugated field [50]. This assumption is in agreement with recent experiments [51] showing that this field enables external control of the toroidization. The energy associated with the coupling with the external field will be −G⋅τ, which leads to a polarization, pt=B×τ, and a magnetization, mt=τ×E, induced under the application of magnetic and electric fields, respectively. These expressions show the intrinsic (asymmetric) magnetoelectric nature of this class of materials. The fundamental thermodynamic equation for these materials reads
| 4.15 |
where U is the internal energy and p=pt+pi and m=mt+mi include intrinsic contributions in addition to terms arising from toroidization.
The entropy change associated with the toroidal contributions of polarization and magnetization induced by isothermal application of electric and magnetic fields leading to a toroidal field G=E×B is given by
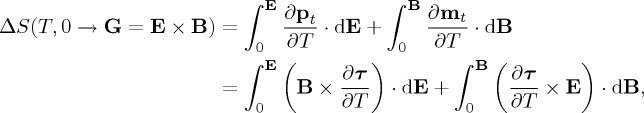 |
4.16 |
which can be simply written as
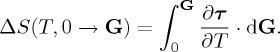 |
4.17 |
In order to develop a Landau model for a ferrotoroidal transition, toroidization must be chosen as the primary-order parameter but magnetization and polarization must also be included in the free energy expansion. We follow here the point of view proposed in [52] and take into account that the symmetries which allow for a macroscopic toroidal moment are the same as those that give rise to an antisymmetric component of the linear magnetoelectric tensor. Then, the simplest possible Landau free energy expansion that describes a phase transition between paratoroidic and ferrotoroidic phases that include the energies associated with the effect of electric and magnetic fields on polarization and magnetization, and their coupling to toroidization, should have the following form:
| 4.18 |
where χp and χm are the electric and magnetic susceptibilities respectively, aτ is the toroidic stiffness and C>0 is the nonlinear toroidic coefficient. Here η measures the strength of the magnetoelectric coupling. The last term in the above free energy represents the lowest possible order coupling term between the three order parameters consistent with the required space and time reversal symmetries. Minimization of this free energy with respect to polarization and magnetization provides their equilibrium values, which are given by
| 4.19 |
and
| 4.20 |
Assuming isotropy, with E applied along the x-axis and B along the y-axis, p≃χpE−αB=pi+pt and m≃χmB−αE=mi+mt, where nonlinear magnetoelectric terms have been neglected. For the sake of consistency with the magnetoelectric equations, the parameter α must coincide with τ, and thus ηχpχm=1. Substitution of these equations for p and m in equation (4.18) gives the following effective free energy function:
| 4.21 |
where 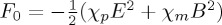 ,
, 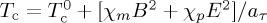 and β=3G=3EB. The effective free energy obtained corresponds to the free energy of a toroidal system subjected to an applied toroidal field G. Interestingly, the third-order term coefficient is proportional to the applied field G. Therefore, when G=0, the free energy (4.21) describes a paratoroidal-to-ferrotoroidal second-order phase transition. Under the application of a toroidal field G≠0, the transition becomes first order for G2<1/C2. It is worth pointing out that the addition of magnetoelectric nonlinear terms would lead to higher-order terms in the expansion (4.21) that go beyond the minimal model. However, within the spirit of the Landau approach, it is expected that such terms are not essential.
and β=3G=3EB. The effective free energy obtained corresponds to the free energy of a toroidal system subjected to an applied toroidal field G. Interestingly, the third-order term coefficient is proportional to the applied field G. Therefore, when G=0, the free energy (4.21) describes a paratoroidal-to-ferrotoroidal second-order phase transition. Under the application of a toroidal field G≠0, the transition becomes first order for G2<1/C2. It is worth pointing out that the addition of magnetoelectric nonlinear terms would lead to higher-order terms in the expansion (4.21) that go beyond the minimal model. However, within the spirit of the Landau approach, it is expected that such terms are not essential.
Assuming that the susceptibilities χp and χm are not temperature dependent, the entropy of the system can be obtained as 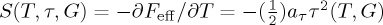 , where τ(T,G) is the equilibrium value of the toroidization, which is a solution of ∂Feff/∂τ=0. Then, the change of entropy isothermally induced by application of a toroidal field is obtained as
, where τ(T,G) is the equilibrium value of the toroidization, which is a solution of ∂Feff/∂τ=0. Then, the change of entropy isothermally induced by application of a toroidal field is obtained as
| 4.22 |
Taking into account the equations giving pt=τB and mt=τE, it is straightforward to show that, in addition to a pure toroidal contribution, this change of entropy comprises polar and magnetic contributions given by
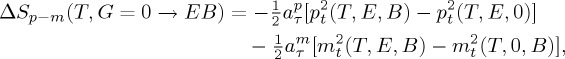 |
4.23 |
where 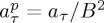 and
and 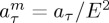 . The toroidocaloric entropy change is shown in figure 7. The sum of polar and magnetic contributions is also shown. The difference between the total entropy changes and this sum determines the pure toroidal contribution, which is only significant in the temperature region of the continuous toroidal transition.
. The toroidocaloric entropy change is shown in figure 7. The sum of polar and magnetic contributions is also shown. The difference between the total entropy changes and this sum determines the pure toroidal contribution, which is only significant in the temperature region of the continuous toroidal transition.
Figure 7.
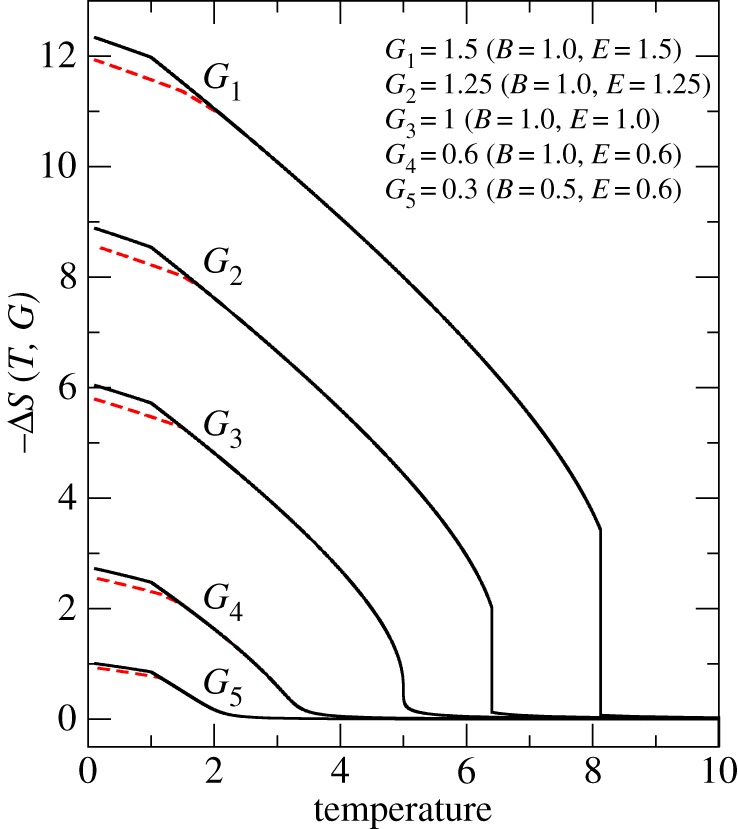
Toroidocaloric entropy change as a function of temperature for applied toroidal fields above and below thefield G3=1 at which a first-order transition starts to occur. The continuous line gives the total contribution, whereas the discontinuous line gives the sum of the polar and magnetic contributions induced by the external field. The pure toroidal contribution is given by the difference. All quantities are given in reduced units.
5. Summary and conclusion
Caloric effects are becoming potentially important for refrigeration and related technologies. A caloric effect is expected to occur that is associated with each primary ferroic property. Magnetocaloric, electrocaloric and mechanocaloric effects have been the subject of intense experimental and theoretical research. In contrast, the toroidocaloric effect has been predicted but not experimentally confirmed [53]. Multiferroics involve at least two coupled ferroic properties and are thus likely to exhibit multicaloric effects. We have developed a general thermodynamic framework for systems displaying interplay between multiple ferroic properties. Within this framework, we have analysed multicaloric effects in magnetostructural metamagnetic shape-memory and magnetoelectric ferrotoroidic materials. These systems have been described within a Landau model with suitable coupling between order parameters. We expect that our phenomenological Landau results combined with first-principle calculations will provide in the near future a route for designing materials with improved multicaloric effects.
Acknowledgements
Stimulating discussions with our colleagues L. Mañosa, E. Stern-Taulats, P. Lloveras, J. Gebbia, E. Vives and X. Moya are gratefully acknowledged.
Footnotes
Maxwell relations are a consequence of the fact that the generalized vector for {yi} is conservative.
Note that in §2 we have quantified the effect of the magnetovolume interplay on the magnetocaloric effect through the derivative of the magnetic field-induced entropy change with respect to pressure. This is the derivative that appears in the second term on the right-hand side of equation (3.2), which gives the contribution to the caloric effect from the interplay between the two ferroic properties.
This phase is weakly magnetic, and, despite some authors claiming that it is paramagnetic, its actual magnetic order is still the subject of debate.
The coupling between volume and shear is allowed, because shear is a scalar in the present model.
The remaining terms are not expected to vary rapidly with temperature in the vicinity of the transitions and, hence, are assumed to be temperature independent.
It has been shown that, depending on heat treatments, m goes to zero or remains finite at the structural transition. See, for instance, [40]. These results can be understood by taking into account that the heat treatment can modify the lattice distribution of magnetic atoms and thus the magnetostructural interplay.
Present results have been obtained with aε=1, am=1, Tc=1, T0=0.6, b=1, c=1 and β=1.
A long-standing question has been whether the toroidal moment is merely a side effect of antiferromagnetism with vortex-like alignment of the magnetic moments or whether it is the primary-order parameter in a ferroic phase transition. Recently, it has been justified that ferrotoroidics belong to the class of primary ferroics. See [48].
Authors' contributions
All authors contributed equally to the manuscript.
Competing interests
The authors declare that they have no competing interests.
Funding
Financial support is acknowledged to CICyT, project no. MAT2013-40590-P, and the U.S. Department of Energy.
References
- 1.Tishin AM, Spichkin YI. 2003. The magnetocaloric effect and its applications. Bristol, UK: Institute of Physics. [Google Scholar]
- 2.Pecharsky VK, Gschneidner KA. 1997. Giant magnetocaloric effect in Gd5(Si2Ge2). Phys. Rev. Lett. 78, 4494–4497. ( 10.1103/PhysRevLett.78.4494) [DOI] [PubMed] [Google Scholar]
- 3.Mañosa L, Planes A, Acet M. 2013. Advanced materials for solid-state refrigeration. J. Mater. Chem. A 1, 4925–4936. ( 10.1039/c3ta01289a) [DOI] [Google Scholar]
- 4.Moya X, Kar-Narayan S, Mathur ND. 2014. Caloric materials near ferroic phase transitions. Nat. Mater. 13, 439–450. ( 10.1038/nmat3951) [DOI] [PubMed] [Google Scholar]
- 5.Wang KF, Liu J-M, Ren ZF. 2009. Multiferroicity: the coupling between magnetic and polar orders. Adv. Phys. 58, 321–448. ( 10.1080/00018730902920554) [DOI] [Google Scholar]
- 6.Planes A, Mañosa L, Acet M. 2009. Magnetocaloric effect and its relation to shape-memory properties in ferromagnetic Heusler alloys. J. Phys. Condens. Matter 21, 233201 ( 10.1088/0953-8984/21/23/233201) [DOI] [PubMed] [Google Scholar]
- 7.Spaldin NA, Fiebig M, Mostovoy M. 2008. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys. Condens. Matter 20, 434203 ( 10.1088/0953-8984/20/43/434203) [DOI] [Google Scholar]
- 8.Yuce S. et al. 2012. Barocaloric effect in the magnetocaloric prototype Gd5Si2Ge2. Appl. Phys. Lett. 101, 071906 ( 10.1063/1.4745920) [DOI] [Google Scholar]
- 9.Mañosa L, González-Alonso D, Planes A, Barrio M, Tamarit JL, Titov IS, Acet M, Bhattacharyya A, Majumdar S. 2011. Inverse barocaloric effect in the giant magnetocaloric La–Fe–Si–Co compound. Nat. Commun. 2, 595 ( 10.1038/ncomms1606) [DOI] [PubMed] [Google Scholar]
- 10.Stern-Taulats E, Lloveras P, Barrio M, Tamarit JL, Pramanick S, Majumdar S, Mañosa L. 2014. Barocaloric and magnetocaloric effects in Fe49Rh51. Phys. Rev. B 89, 214105 ( 10.1103/PhysRevB.89.214105) [DOI] [Google Scholar]
- 11.Mañosa L, Gozález-Alonso D, Planes A, Bonnot E, Barrio M, Tamarit JL, Aksoy S, Acet M. 2010. Giant solid-state barocaloric effect in the Ni–Mn–In magnetic shape-memory alloy. Nat. Mater. 9, 478–481. ( 10.1038/nmat2731) [DOI] [PubMed] [Google Scholar]
- 12.Millán-Solsona R, Stern-Taulats E, Vives E, Planes A, Sharma J, Nayak AK, Suresh KG, Mañosa L. 2014. Large entropy change associated with elastocaloric effect in polycrystalline Ni–Mn–Sb–Co magnetic shape memory alloy. Appl. Phys. Lett. 105, 241901 ( 10.1063/1.4904419) [DOI] [Google Scholar]
- 13.Chauhan A, Patel S, Vaish R. 2015. Multicaloric effect in Pb(Mn1/3Nb2/3)O3-32PbTiO3 single crystals: modes of measurement. Acta Mater. 97, 17–28. ( 10.1016/j.actamat.2015.06.027) [DOI] [Google Scholar]
- 14.Lloveras P. et al. 2015. Giant barocaloric effects at low pressure in ferrielectric ammonium sulphate. Nat. Commun. 6, 8801 ( 10.1038/ncomms9801) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chauhan A, Patel S, Vaish R. 2015. Elastocaloric effect in ferroelectric ceramic. Appl. Phys. Lett. 106, 172901 ( 10.1063/1.4919453) [DOI] [Google Scholar]
- 16.Gama S, de Campos A, Magnus A, Carvalho G, Coelho AA, Gandra FCG, von Ranke PJ, de Oliveira NA. 2004. Pressure-induced colossal magnetocaloric effect in MnAs. Phys. Rev. Lett. 93, 237202 ( 10.1103/PhysRevLett.93.237202) [DOI] [PubMed] [Google Scholar]
- 17.Magnus A, Carvalho G, Alves CS, de Campos A, Coelho AA, Gama S, Gandra FCG, von Ranke PJ, Oliveira NA. 2005. The magnetic and magnetocaloric properties of Gd5Ge2Si2 compound under hydrostatic pressure. J. Appl. Phys. 97, 10M320 ( 10.1063/1.1860932) [DOI] [Google Scholar]
- 18.Lyubina J, Nenkov K, Schultz L, Gutfleisch O. 2008. Multiple metamagnetic transitions in the magnetic refrigerant La(FeSi)13Hx. Phys. Rev. Lett. 101, 177203 ( 10.1103/PhysRevLett.101.177203) [DOI] [PubMed] [Google Scholar]
- 19.Caron L, Trung NT, Brück E. 2011. Pressure-tuned magnetocaloric effect in Mn0.93Cr0.07CoGe. Phys. Rev. B 84, 020414 ( 10.1103/PhysRevB.84.020414) [DOI] [Google Scholar]
- 20.Samanta T. et al 2015. Hydrostatic pressure-induced modifications of structural transition that lead to large enhancements of magnetocaloric effects in MnNiSi-based systems. Phys. Rev. B 91, 020401 ( 10.1103/PhysRevB.91.020401) [DOI] [Google Scholar]
- 21.Nayak AK, Suresh KG, Nigam AK, Coelho AA, Gama S. 2009. Pressure induced magnetic and magnetocaloric properties in NiCoMnSb Heusler alloy. J. Appl. Phys. 106, 053901 ( 10.1063/1.3208064) [DOI] [Google Scholar]
- 22.Castillo-Villa PO, Soto-Parra DE, Matutes-Aquino JA, Ochoa-Gamboa RA, Planes A, Mañosa L, González-Alonso D, Stipcich M, Romero R. 2011. Caloric effects induced by magnetic and mechanical fields in a Ni50Mn25−xGa25Cox magnetic shape memory alloy. Phys. Rev. B 83, 174109 ( 10.1103/PhysRevB.83.174109) [DOI] [Google Scholar]
- 23.Chauhan A, Patel S, Vaish R. 2015. Multicaloric effect in Pb(Mn1/3Nb2/3)O3-32PbTiO3 single crystals. Acta Mater. 89, 384–395. ( 10.1016/j.actamat.2015.01.070) [DOI] [Google Scholar]
- 24.Moya X. et al. 2012. Giant and reversible extrinsic magnetocaloric effects in La0.7Ca0.3MnO3 films due to strain. Nat. Mater. 12, 52–58. ( 10.1038/nmat3463) [DOI] [PubMed] [Google Scholar]
- 25.Cherifi RO. et al. 2014. Electric-field control of magnetic order above room temperature. Nat. Mater. 13, 345–351. ( 10.1038/nmat3870) [DOI] [PubMed] [Google Scholar]
- 26.Gong Y-Y, Wang D-H, Cao Q-Q, Liu E-K, Liu J, Du Y-W. 2015. Electric field control of the magnetocaloric effect. Adv. Mater. 27, 801–805. ( 10.1002/adma.201404725) [DOI] [PubMed] [Google Scholar]
- 27.Vopson MM, Zhou D, Caruntu G. 2015. Multicaloric effect in bi-layer multiferroic composites. Appl. Phys. Lett. 107, 182905 ( 10.1063/1.4935216) [DOI] [Google Scholar]
- 28.Lisenkov S, Ponomareva I. 2013. Giant elastocaloric effect in ferroelectric Ba0.5Sr0.5TiO3 alloys from first-principles. Phys. Rev. B 86, 104103 ( 10.1103/PhysRevB.86.104103) [DOI] [Google Scholar]
- 29.Chang CM, Mani BK, Lisenkov S, Ponomareva I. 2015. Thermally mediated mechanism to enhance magnetoelectric coupling in multiferroics. Phys. Rev. Lett. 114, 177205 ( 10.1103/PhysRevLett.114.177205) [DOI] [PubMed] [Google Scholar]
- 30.Nikitin SA, Skokov KP, Koshkidko YuS, Pastushenkov YuG, Ivanova TI. 2010. Giant rotating magnetocaloric effect in the region of spin-reorientation transition in the NdCo5 single crystal. Phys. Rev. Lett. 105, 137205 ( 10.1103/PhysRevLett.105.137205) [DOI] [PubMed] [Google Scholar]
- 31.Balli M, Jandl S, Fournier P, Gospodinov MM. 2014. Anisotropy-enhanced giant reversible rotating magnetocaloric effect in HoMn2O5 single crystals. Appl. Phys. Lett. 104, 232402 ( 10.1063/1.4880818) [DOI] [Google Scholar]
- 32.Matsunami D, Fujita A, Takenaka K, Kano M. 2014. Giant barocaloric effect enhanced by the frustration of the antiferromagnetic phase in Mn3GaN. Nat. Mater. 14, 73–78. ( 10.1038/nmat4117) [DOI] [PubMed] [Google Scholar]
- 33.Planes A, Castán T, Saxena A. 2014. Thermodynamics of multicaloric effects in multiferroics. Philos. Mag. 94, 1893–1908. ( 10.1080/14786435.2014.899438) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Planes A, Mañosa L, Acet M. 2013. Recent progress and future perspectives in magnetic and metamagnetic shape-memory Heusler alloys. Mater. Sci. Forum 738–739, 391–399. ( 10.4028/www.scientific.net/MSF.738-739.391) [DOI] [Google Scholar]
- 35.Buchelnikov VD, Entel P, Taskaev SV, Sokolovskiy VV, Hucht A, Ogura M, Akai H, Gruner ME, Nayak SK. 2008. Monte Carlo study of the influence of antiferromagnetic exchange interactions on the phase transitions of ferromagnetic Ni–Mn–X alloys (X=In,Sn,Sb). Phys. Rev. B 78, 184427 ( 10.1103/PhysRevB.78.184427) [DOI] [Google Scholar]
- 36.Buchelnikov VD. et al. 2011. Monte Carlo simulation of the magnetocaloric effect in magnetic Ni–Mn–X (X = Ga, In) Heusler alloys. J. Phys. D, Appl. Phys. 44, 064012 ( 10.1088/0022-3727/44/6/064012) [DOI] [Google Scholar]
- 37.Recarte V, Pérez-Landazabal JI, Sánchez-Alarcos V, Zablotskii VV, Cesari E, Kustov S. 2012. Entropy change linked to the martensitic transformation in metamagnetic shape memory alloys. Acta Mater. 60, 3168–3175. ( 10.1016/j.actamat.2012.02.022) [DOI] [Google Scholar]
- 38.L’vov VA, Kosogor A, Barandiaran J, Chernenko VA. 2016. Theoretical description of magnetocaloric effect in the shape memory alloy exhibiting metamagnetic behavior. J. Appl. Phys. 119, 013902 ( 10.1063/1.4939556) [DOI] [Google Scholar]
- 39.Mañosa L. 2008. Effects of hydrostatic pressure on the magnetism and martensitic transition of Ni–Mn–In magnetic superelastic alloys. Appl. Phys. Lett. 92, 012515 ( 10.1063/1.2830999) [DOI] [Google Scholar]
- 40.Bruno NM, Cengiz Y, Karaman I, Chen J-H, Ross JH, Liu J, Li J. 2014. The effect of heat treatments on Ni43Mn42Co4Sn11 meta-magnetic shape memory alloys for magnetic refrigeration. Acta Mater. 74, 66–84. ( 10.1016/j.actamat.2014.03.020) [DOI] [Google Scholar]
- 41.Ito W, Imano Y, Kainuma R, Sutou Y, Oikawa K, Ishida K. 2007. Martensitic and magnetic transformation behaviors in Heusler-type NiMnIn and NiCoMnIn metamagnetic shape memory alloys. Metall. Trans. A 38A, 759–766. ( 10.1007/s11661-007-9094-9) [DOI] [Google Scholar]
- 42.Kustov S, Corró ML, Pons J, Cesari E. 2009. Entropy change and effect of magnetic field on martensitic transformation in a metamagnetic Ni–Co–Mn–In shape memory alloy. Appl. Phys. Lett. 94, 191901 ( 10.1063/1.3130229) [DOI] [Google Scholar]
- 43.Kihara T, Xu X, Ito W, Kainuma R, Tokunaga M. 2014. Direct measurements of inverse magnetocaloric effects in metamagnetic shape-memory alloy NiCoMnIn. Phys. Rev. B 90, 214409 ( 10.1103/PhysRevB.90.214409) [DOI] [Google Scholar]
- 44.Wood ME, Potter WH. 1985. General analysis of magnetic refrigeration and its optimization using a new concept: maximization of refrigerant capacity. Cryogenics 25, 667–683. ( 10.1016/0011-2275(85)90187-0) [DOI] [Google Scholar]
- 45.Dubovik VM, Tugushev VV. 1990. Toroid moments in electrodynamics and solid-state physics. Phys. Rep. 187, 145–202. ( 10.1016/0370-1573(90)90042-Z) [DOI] [Google Scholar]
- 46.Saxena A, Lookman T. 2011. Magnetic symmetry of low dimensional multiferroics and ferroelastics. Phase Trans. 84, 421–437. ( 10.1080/01411594.2011.553171) [DOI] [Google Scholar]
- 47.Khomskii D. 2009. Classifying multiferroics: mechanisms and effects. Physics 2, 20 ( 10.1103/Physics.2.20) [DOI] [Google Scholar]
- 48.Tolédano P, Ackermann M, Bohatý L, Becker P, Lorenz T, Leo N, Fiebig M. 2015. Primary ferrotoroidicity in antiferromagnets. Phys. Rev. B 92, 094431 ( 10.1103/PhysRevB.92.094431) [DOI] [Google Scholar]
- 49.Van Aken BB, Rivera JP, Schmid H, Fiebig M. 2007. Observation of ferrotoroidic domains. Nature 449, 702–705. ( 10.1038/nature06139) [DOI] [PubMed] [Google Scholar]
- 50.Planes A, Castán T, Saxena A. 2014. Recent progress in the thermodynamics of ferrotoroidic materials. Multiferr. Mater. 1, 9–22. ( 10.2478/muma-2014-0002) [DOI] [Google Scholar]
- 51.Baum M, Schmalzl K, Steffens P, Hiess A, Regnault LP, Meven M, Becker P. 2013. Controlling toroidal moments by crossed electric and magnetic fields. Phys. Rev. B 88, 024414 ( 10.1103/PhysRevB.88.024414) [DOI] [Google Scholar]
- 52.Ederer C, Spaldin N. 2007. Towards a microscopic theory of toroidal moments in bulk periodic crystals. Phys. Rev. B 76, 214404 ( 10.1103/PhysRevB.76.214404) [DOI] [Google Scholar]
- 53.Castán T, Planes A, Saxena A. 2012. Thermodynamics of ferrotoroidic materials: toroidocaloric effect. Phys. Rev. B 85, 144429 ( 10.1103/PhysRevB.85.144429) [DOI] [Google Scholar]