Mastering hysteresis in magnetocaloric materials

Abstract

Hysteresis is more than just an interesting oddity that occurs in materials with a first-order transition. It is a real obstacle on the path from existing laboratory-scale prototypes of magnetic refrigerators towards commercialization of this potentially disruptive cooling technology. Indeed, the reversibility of the magnetocaloric effect, being essential for magnetic heat pumps, strongly depends on the width of the thermal hysteresis and, therefore, it is necessary to understand the mechanisms causing hysteresis and to find solutions to minimize losses associated with thermal hysteresis in order to maximize the efficiency of magnetic cooling devices. In this work, we discuss the fundamental aspects that can contribute to thermal hysteresis and the strategies that we are developing to at least partially overcome the hysteresis problem in some selected classes of magnetocaloric materials with large application potential. In doing so, we refer to the most relevant classes of magnetic refrigerants La–Fe–Si-, Heusler- and Fe₂P-type compounds.

This article is part of the themed issue ‘Taking the temperature of phase transitions in cool materials’.

1. Introduction

Magnetic refrigeration technology is a rapidly developing technology that is assumed to be capable of competing with and hopefully surpassing traditional vapour-compression refrigeration in terms of efficiency, device volume and ecological impact in the near future [1]. From this point of view, magnetic compounds exhibiting large magnetocaloric effects (MCEs) in the temperature range of 270–320 K (under magnetic field changes of Δ(μ₀H)=1–2 T) are attracting much attention due to their potential application in magnetic refrigeration at room temperature [2–6]. The search for new magnetocaloric materials as well as the optimization of known materials is a growing field of interest, and the new magnetic materials showing a large MCE with narrow hysteresis, particularly around room temperature, are the subject of intensive research activity. A variety of new materials have been synthesized since the discovery of the first giant magnetocaloric material Gd₅(Si,Ge)₄ in 1997 [7,8], and some of them have proved to be very promising for applications. The main issue related to giant MCE materials is the hysteresis of the first-order transition, which is one of the main factors delaying the development of this novel and disruptive cooling technology. This paper aims to (i) summarize the fundamental phenomena that can contribute to thermal and magnetic hysteresis and (ii) develop strategies for at least partially overcoming or bypassing the hysteresis problem in some selected classes of magnetocaloric materials with large application potential.

The MCE itself can be defined as the reversible change of the thermodynamic variables of a sample—temperature T and entropy S—as a result of a variation in the applied external magnetic field. If the magnetization or demagnetization of the sample is performed under adiabatic conditions, it results in heating or cooling of the material. In this case, the total entropy S remains constant and the MCE manifests itself in an adiabatic temperature change, ΔT_ad. Alternatively, by keeping the temperature T constant during magnetization or demagnetization (isothermal conditions), the MCE leads to a transfer of thermal energy between the sample and the environment. The amount of heat Q transferred in this process can be quantified as Q=TΔS_m, where ΔS_m is the isothermal magnetic entropy change.

An overwhelming majority of researchers investigate MCEs by measuring the isothermal M(H)_T or isofield M(T)_H magnetization with subsequent recalculation (the indirect method) of ΔS_m(T) by using the Maxwell relation. As a result, most of the published MCE data are temperature dependences of magnetic entropy changes ΔS_m(T) obtained in this way. The ΔS_m is an important parameter, but, at the same time, a high value of ΔS_m is not sufficient for a material to be a good magnetic refrigerant [9,10]. Furthermore, the integration of the ΔS_m(T) curve (sometimes referred to as the relative cooling power, RCP=ΔS_m∂T_FWHM [6]) is usually misleading [11]. To assess the magnetocaloric properties adequately, the adiabatic temperature change ΔT_ad also needs to be taken into account. However, experimental data on ΔT_ad are rather scarce in the literature.

Thus, by using both ΔT_ad and ΔS_m, it is possible to comprehensively characterize magnetocaloric materials in terms of their potential for magnetic refrigerators. Both ΔT_ad and ΔS_m can be described within the framework of the S(T) diagram, which can be plotted by using temperature dependences of heat capacity c_p measured in different magnetic fields. The conventional S(T) diagram describes the thermal equilibrium situation and it does not take into account metastability and hysteresis of materials with first-order transition. Moreover, this thermal equilibrium would be achieved only after a very long time. As in a magnetic refrigerator the magnetocaloric material should be magnetized and demagnetized very rapidly, but standard calorimetry followed by subsequent analysis of the equilibrium S(T) diagram cannot mirror these operating conditions. Furthermore, we found that the S(T) diagram obtained under continuous heating and cooling fails to describe the reversible magnetocaloric properties of minor loops under cycling [12]. At the same time, cyclic measurements of the adiabatic temperature change together with calorimetric data allow us to determine the reversible magnetic field-induced entropy change ΔS_m in rapid operation that is comparable with real device conditions; this can, in principle, be applied to every magnetocaloric material with a first-order transition.

Along with ΔS_m and ΔT_ad, the third primary parameter which characterizes the suitability of a magnetocaloric material is the thermal conductivity λ=αρc_p, where α is the thermal diffusivity and ρ is the density of the material. The thermal conductivity determines the ability of the material to transfer thermal energy to the heat exchange fluid. The thermal conductivity is one factor limiting the maximum operation frequency of the magnetocaloric material and, therefore, has to be considered together with ΔS_m and ΔT_ad when discussing the applicability and efficiency of a material as a magnetic refrigerant [13–18].

In order to use a magnetocaloric material in a magnetic refrigerator, it should on the one hand be machined into a heat exchanger with a fine porous structure, designed to provide the largest possible contact surface area to the heat transfer liquid. On the other hand, the effective volume of the MCE heat exchanger needs to be maximized for an efficient utilization of the (Nd–Fe–B) permanent magnet field source. The magnetic system is the most costly part of the device, and it has the highest negative environmental footprint, as shown in a life-cycle analysis of a magnetic refrigerator [19,20], and, therefore, should be used as economically as possible. Another significant issue during the machining process of the magnetocaloric material into plates or porous structures is the possible reduction of its magnetocaloric properties [21]. As a result, a material with a high MCE in bulk form can show only a modest MCE after it has been shaped into a heat exchanger with sub-millimetre channels [22,23].

2. First- and second-order transitions, conventional and inverse magnetocaloric effect

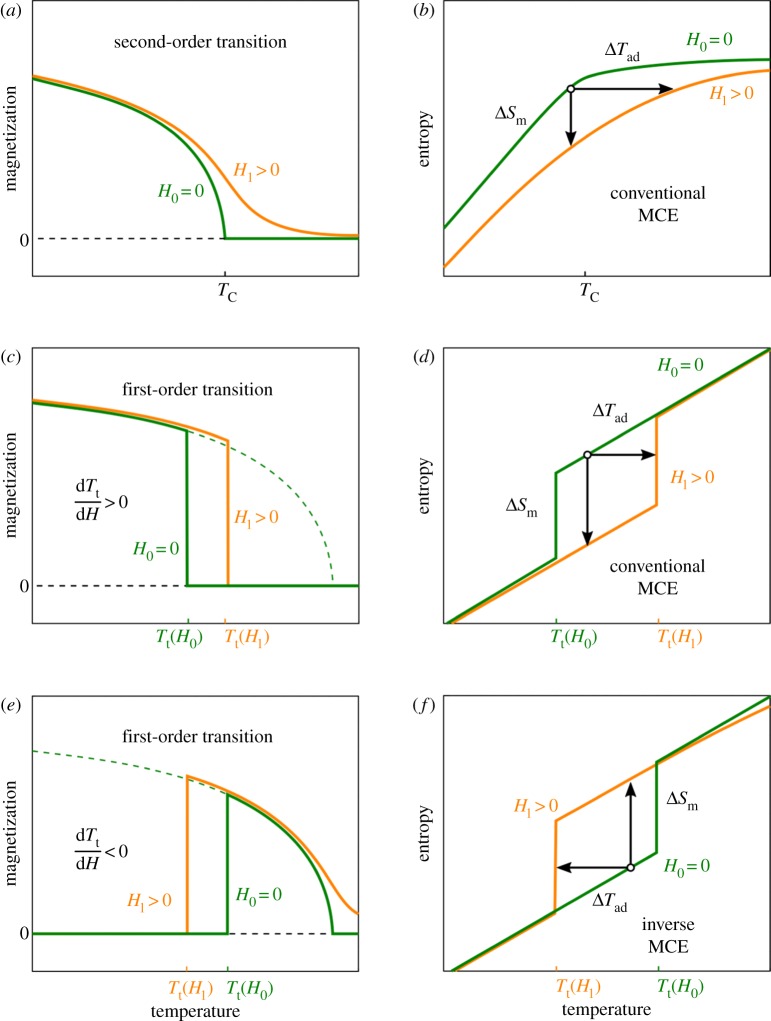
In figure 1a, a schematic of the magnetic behaviour near the Curie temperature T_C of a ferromagnetic material is illustrated. The green curve represents M(T) in zero field. At T_C, the magnetization vanishes and the ferromagnet turns into a paramagnet. This purely magnetic transition is a thermodynamic transformation of second order. The element Gd is one of the most prominent materials undergoing such a transformation near room temperature [25]. It is worth noting that the zero-field magnetization curve cannot be measured directly due to the formation of magnetic domains, but it can be calculated, for instance, by Kuz’min’s approach [26]. In magnetic fields, a certain magnetization is also observed in the paramagnetic phase due to the partial alignment of the spins. The magnetic susceptibility of a paramagnet χ, being the ratio of the magnetization M and the magnetic field H, decreases with temperature, which can be described by the Curie–Weiss law [27]:

where C is the Curie constant. Figure 1b shows the entropy of the material as a function of temperature in the vicinity of the second-order transition. The total entropy is a combination of three terms, namely the contribution of the lattice S_lat, the magnetic moments S_mag and the electronic contribution S_el, resulting in [2]

The temperature dependence of the total entropy without a magnetic field is schematically shown as a green curve in figure 1b. By applying a magnetic field, the magnetic moments align to some extent. Therefore, the order of the magnetic system increases, which relates to a decrease in the magnetic entropy. For this reason, the external magnetic field lowers the entropy, which is illustrated by the orange curve in figure 1b. This decrease in entropy is observed under isothermal conditions. The respective entropy change ΔS_m is plotted as a vertical arrow. Under adiabatic conditions, the total entropy remains constant. In order to compensate for the decrease in the magnetic contribution, the lattice entropy increases. For this reason, the application of a magnetic field results in a heating of the material by ΔT_ad, which is illustrated as a horizontal arrow.

Figure 1.

Schematic of the temperature dependence of magnetization and the total entropy with and without a magnetic field of a conventional second-order transition in (a,b), of a conventional first-order transformation in (c,d) and of an inverse first-order transition in (e,f) [24].

In contrast with this, a conventional first-order transition is schematically shown in figure 1c,d. Such a transformation is, for instance, observed in the material La–Fe–Si [28]. A discontinuity in magnetization is observed in both the magnetic and total entropy curves, due to the transformation between two different phases. In the idealized picture in figure 1c, the ferromagnetic phase is stable at low temperatures. At T_t, the material transforms into the high-temperature phase with low magnetization. In principle, the low-temperature phase would still be ferromagnetic up to its Curie temperature, which is illustrated by the extrapolated magnetization curve (green dashed line). However, this is prevented by the magnetostructural or magnetoelastic transition.

The application of a magnetic field results in the shift of the transition temperature T_t. This is happening because the magnetic field stabilizes the phase with higher magnetization, this being the low-temperature phase [29]. The shift of the transition temperature in magnetic fields dT_t/dH, which is positive for a conventional first-order transition, can be understood as the driving force of the MCE in such a material. For instance, if a material remains in the paramagnetic phase at a temperature between T_t(H₀) and T_t(H₁), the application of the magnetic field H₁ would result in the conversion of that material into the low-temperature phase. In terms of the MCE, it now depends on whether isothermal or adiabatic conditions are present.

The corresponding total entropy diagram is shown in figure 1d. Also in the entropy curve, a discontinuity is visible in the ideal case. However, due to the shift of the transition temperature in magnetic fields, the S(T) diagram has the shape of a parallelogram (green and orange curves in figure 1d [9]). When keeping the temperature constant, the entropy decreases under field application. Therefore, ΔS_m is also negative (vertical arrow in figure 1d), as was the case for the second-order transition above. When a magnetic field is applied adiabatically, the S(T) diagram is crossed horizontally, which results in an increase in the temperature of the material. It is worth noting that, in the schematic, the entropy curves do not overlap in the low-temperature region of figure 1c,d. This is because the magnetic field affects the ferromagnetic phase by slightly increasing the ordering of the magnetic moments, counteracting the disorder due to thermal fluctuations. Therefore, the magnetization is slightly increased, as shown by the difference between the green and the orange curves in figure 1c. Consequently, the total entropy is slightly reduced in the ferromagnetic phase under magnetic field application (also the case for the paramagnetic phase but less pronounced). A similar effect is also observed in figure 1a,b, which is related to the purely second-order transition. This implies that, in figure 1, both the first- and the second-order transitions overlap.

As a third example, the inverse first-order transformation is schematically illustrated in figure 1e,f. Such a transition is observed for instance in Ni–Mn–X–Heusler alloys with X = Sn, Sb and In [30] or in Fe–Rh [31]. In the inverse case, a structural phase conversion is also taking place. In contrast with figure 1c,d, the low-temperature phase has a low and the high-temperature phase has a high magnetization (figure 1e). For this reason, a magnetic field shifts the transition to lower temperatures and dT_t/dH is negative. The corresponding total entropy diagram is shown in figure 1f. In the ideal case, the S(T) diagram has the shape of a parallelogram too, but in comparison with figure 1d the green and the orange curves are swapped. As a result, the adiabatic temperature change ΔT_ad is negative and the isothermal entropy change ΔS_m is positive. Again, the first- and the second-order transitions are overlapping, which can be seen by the increased magnetization in magnetic fields in figure 1e and by the crossing of the green and the orange S(T) curves in figure 1f. It is worth noting that both the curves come together again for temperature well above the Curie point.

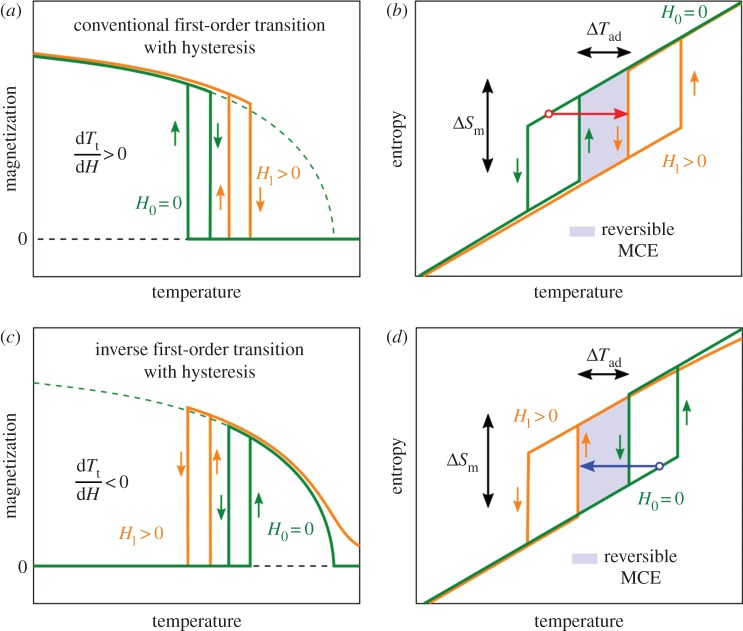
The situation changes with magnetocaloric materials of first order, which show a thermal hysteresis. This means that the back and forth transformation does not take place at the same temperature. In fact, the heating and the cooling branch of the magnetization curve are separated by the thermal hysteresis, which is illustrated for a conventional first-order transition in figure 2a. The corresponding S(T) diagram is shown in figure 2b. Such a behaviour is, for instance, observed in certain Fe₂P-type materials or in La–Fe–Si [32]. Owing to the existence of the thermal hysteresis, the entropy curves under heating and cooling also do not coincide. This has far-reaching consequences for the MCE under magnetic-field cycling. If there is no thermal hysteresis related to the transition, then the ΔT_ad and ΔS_m as shown in figure 1a–f would be the same in the cyclic operation. But, due to the hysteresis, a reversible effect can only be obtained in the highlighted area.

Figure 2.

Schematic illustration of the temperature dependence of magnetization and entropy of a conventional (a,b) and an inverse (c,d) first-order transition considering thermal hysteresis [24].

The horizontal arrow in figure 2b illustrates how the material in the purely high-temperature phase (after cooling from temperatures well above the transition) would heat when the magnetic field is applied for the first time. About half of the material would transform in this example. However, when the magnetic field is removed again, the initial state would not be reached. In fact, the adiabatic temperature change under cycling would be smaller, as indicated by the horizontal double-sided arrow. This description of the thermal hysteresis can be transferred straightforwardly to the first-order transition of inverse magnetocaloric materials, which is shown in figure 2c,d.

3. Magnetic refrigeration and magnetocaloric materials

The development of a magnetocaloric cooling system based on the magnetocaloric principle at ambient temperature has not yet been realized as an economic and industrial product. Since the first demonstrator developed by Brown in 1976 [33], only a few research groups around the world have worked on demonstrators operating close to ambient temperature [26,34–39]. There are a number of problems to be solved, most importantly to find suitable materials with large MCEs in small fields using non-critical materials and efficient heat exchangers operating at high frequencies. Recently, new but yet to be validated design concepts have been proposed; for example, the combination of the electrocaloric effect and the MCE [40] or the utilization of the thermal-diode mechanism [41]. Until now, a coordinated research effort involving engineers tackling design issues of the machine, on the one hand, and material scientists (theory and experiment) performing fundamental research, on the other hand, has not been realized.

There are four main issues that need to be solved before the technology of magnetic refrigeration can move forward from prototypes to mass production.

• (1) The availability of low-cost, low-hysteresis magnetic refrigerants that can provide a substantial cooling power in magnetizing fields which are small enough to be provided by permanent magnets (e.g. Nd–Fe–B), rather than by superconducting or electro-magnets.

• (2) The price of the magnetic system, made from permanent magnets that create a magnetic field change of ideally 0.5–1.2 T, needs to be reduced significantly [35].

• (3) The switching of the heat exchange fluid needs to be drastically accelerated and the valves need to be able to commutate the hot and cold heat exchange fluid at frequencies of 10 Hz or higher [42].

• (4) The time of heat transfer from the magnetocaloric material to the liquid needs to be reduced down to 20–50 ms and in this time scale the heat exchange should have 80–90% of the theoretical efficiency [43].

This last issue requires magnetocaloric materials with outstanding MCEs, excellent mechanical integrity, chemical stability and high thermal conductivity, shaped into a porous structure with fine and straight channels.

Currently, the materials used as magnetic refrigerants in existing prototypes of magnetic refrigerators can be divided into the following three classes based on their hysteresis width [36]. In order to improve the comparability of the magnetocaloric properties of the different materials, we linearly interpolate the given literature values of the adiabatic temperature change and the isothermal entropy change to a magnetic field change of Δ(μ₀H)=1 T. It is worth noting that a certain error is associated with this approach because the scaling of the MCE is not necessarily linear [44,45].

The first class (non-hysteretic materials with second-order transition, as in figure 1a,b) includes elemental Gd and Gd-based rare-earth alloys, such as Gd–Y, Gd–Tb, etc. Pure Gd metal is the benchmark magnetocaloric material, exhibiting an isothermal entropy change of ΔS_m≈3 J kg⁻¹ K⁻¹ and an adiabatic temperature change of ΔT_ad≈2.5 K under Δ(μ₀H)=1 T [25]. This metal is rather ductile and can be easily machined into heat exchangers [33,46]. However, this rare-earth metal is critical in terms of its resource efficiency and environmental footprint and would soon be too expensive when used in large amounts, assuming that market entry and mass production of magnetic refrigerators will be achieved [20,47].

La_0.67Ca_0.33-xSr_xMnO₃ (LCSM) manganites with a second-order transition (figure 1a,b) have a low cost and good corrosion resistance, but their MCE is rather modest. Under magnetic field change of Δ(μ₀H)=1 T, they exhibit ΔT_ad≈1.5 K and ΔS_m≈5 J kg⁻¹ K⁻¹ [48].

The second class (first-order materials with narrow thermal hysteresis, figure 1c,d) includes La(Fe,Si)₁₃-based alloys and Fe₂P-type compounds such as Mn–Fe–P–Si. Being much more abundant and thus much cheaper than Gd metal, these materials are very attractive for commercial usage. With respect to the substitution metal used to bring the alloy’s transition temperature to room temperature, it can be divided into two subclasses: La(Fe,Co,Si)₁₃ and La(Fe,Mn,Si)₁₃H_x. Under a magnetic field change of Δ(μ₀H)=1 T, despite the low value of ΔT_ad≈1.5 K, La(Fe,Co,Si)₁₃ materials demonstrate rather high ΔS_m≈5 J kg⁻¹ K⁻¹ [49–51]. Nevertheless, these materials are brittle and it is necessary to use a special processing route in order to bring this material into the required form [22,52–54].

La(Fe,Mn,Si)₁₃H_x-based alloys show attractive magnetocaloric properties under Δμ₀H=1 T: ΔS_m≈10 J kg⁻¹ K⁻¹ and ΔT_ad≈3.5 K [13,28,55]. However, after hydrogenation these alloys exist only in powder form due to the inevitable decrepitation of the initial bulk alloy. This powder can be embedded in a polymer–binder matrix and can, for example, be shaped into a heat exchanger with certain geometry. Conversely, the epoxy dilutes the MCE material and the properties of the composite can be significantly different from the pure La(Fe,Mn,Si)₁₃H_x powder, as reported in the literature [23,55,56].

The Mn–Fe–P–Si compounds are also regarded as promising for application of magnetic refrigeration at room temperature, but they are still not widely used in prototypes. Their thermal conductivity is rather low, which in turn limits the maximal operating frequency of the Fe₂P-type materials as magnetic refrigerants [13,17]. In these compounds, ΔT_ad≈2.8 K and ΔS_m≈11 J kg⁻¹ K⁻¹ can be achieved in a magnetic field change of Δ(μ₀H)=1 T [57,58].

The third class includes materials with large thermal hysteresis, as in figure 2. One important example is the family of Heusler alloys, which have an inverse magnetostructural transition (figure 2c,d) (ΔT_ad≈3–4 K, ΔS_m≈10–20 J kg⁻¹ K⁻¹ in Δ(μ₀H)=1 T) [12,59,60]. Owing to the large thermal hysteresis in Heusler alloys, high magnetic fields need to be applied in order to drive the transition to be fully reversible. When only small alternating magnetic fields of Δ(μ₀H)=1–2 T are available, their efficiency is drastically reduced. The same applies for Gd₅(Si,Ge)₄ with ΔT_ad≈3.5 K and ΔS_m≈4–10 J kg⁻¹ K⁻¹ in Δ(μ₀H)=1 T [61].

Among the magnetocaloric materials with first-order magnetic phase transitions, FeRh alloys hold a special place. It has been reported that the ΔT_ad in FeRh is 12.9 K in Δ(μ₀H)=1.95 T [31] or 7.9 K in Δ(μ₀H)=1.93 T [62], obtained in direct measurements, and these are the highest values ever recorded for any material under a magnetic field change up to 2 T. Although the raw material costs impede implementing FeRh in bulk form in a real magnetic refrigerator, this alloy is still interesting from a fundamental point of view as a model system for solid-state refrigeration near room temperature. Our recent experiments show that, under a magnetic field change of Δ(μ₀H)=1 T, the alloy Fe₄₉Rh₅₁ exhibits ΔT_ad≈3.6 K and ΔS_m≈11 J kg⁻¹ K⁻¹ [63].

4. Magnetocaloric effects and thermal hysteresis

One of the most important issues related to the magnetocaloric properties of materials such as La(Fe,Co,Si)₁₃, La(Fe,Mn,Si)₁₃H_x, Gd₅(Si,Ge)₄, Heusler alloys and Mn–Fe–P–Si is the hysteresis of the first-order magnetostructural transition. The discontinuous nature of the transition is the feature that provides the large ΔS_m. Only very recently, more research efforts have been directed to resolve issues related to transitional hysteresis [64,65]. New ideas have been emerging about how the hysteresis problem can be circumvented so that it is possible to ‘live with’ or bypass hysteresis to some extent and how the hysteresis can be made narrower by manipulating the microstructure or by tuning the composition [66,67].

The temperature width of the transitional hysteresis is the main factor affecting the reversibility of ΔT_ad and ΔS_m when applying and removing a magnetic field. It is, therefore, necessary to understand the mechanisms causing hysteresis.

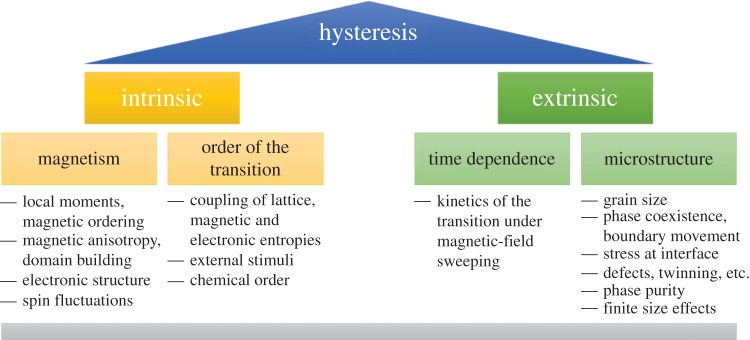
The origins of hysteresis can be separated into intrinsic contributions (linked to the electronic properties on the atomic scale) and into extrinsic influences (related to microstructure) as illustrated in figure 3. The reversibility of the MCE, being essential for magnetic heat pumps, strongly depends on the width of the thermal hysteresis. Hysteresis can be tolerable in some cases, and in other cases its width can be adjusted.

Figure 3.

Hysteresis is related to the intrinsic and extrinsic origins listed and grouped in the figure. Detailed investigations are needed to understand how to overcome the hysteresis problem or how to obtain a substantial reversible MCE despite hysteresis. (Online version in colour.)

We distinguish two main categories for intrinsic origins: magnetism and the order character of the transition, as shown in figure 3. Our recent studies have shown that the magnetism is one of the key parameters which not only governs the magnetostructural transition, but also influences the width of the hysteresis [68]. A detailed understanding of the properties of the local moments, the magnetic ordering, magnetic anisotropy and domain formation within the framework of the complex electronic structure is required.

The order of the transition also plays a crucial role. While a first-order transition shows a hysteresis in general, a second-order transition is hysteresis free. The big advantage of first-order materials is a relatively small magnetic field, which is needed for the switching of the sample between the PM and FM states. This allows magnetocaloric cooling devices to be designed with a magnetic system made from permanent magnets with relatively small magnetic field changes of 1–2 T, in which it is possible to use the large entropy change associated with the magnetostructural transformation. On the other hand, the hysteresis drastically reduces the MCE when the magnetic field is applied under cycling conditions [63,69,70] and efforts are directed at overcoming the transitional hysteresis. The most important task here is to reach the tricritical point [71,72], where a first-order transition becomes second order. In this case, one can use the entropic benefits of the first-order transition without any reduction of the MCE under cycling. In particular, if the volume difference between the parent and the product phase can be eliminated, the hysteresis of a first-order transition narrows or even vanishes. If, in addition, the crystallographic structures of the parent and product phases remain the same, the transition might become second order and the hysteresis will be eliminated. In order to achieve this goal, good selection criteria for identification of the tricritical point are indispensable.

The order of the transition and the crossover from first to second order needs to be understood by theoretical and experimental methods. For example, the order of the transition and hysteresis width can be adjusted under the external stimuli, such as pressure [60], magnetic field, temperature and the local deviations in the chemical ordering and bonding [55].

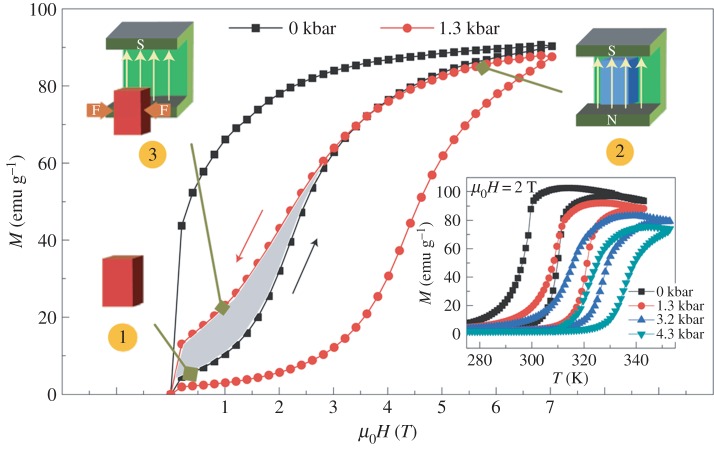
The thermal hysteresis behaviour can be manipulated by applying multiple stimuli other than a magnetic field or by moving in minor loops of the transition instead of completely transforming the material from one phase to another. As demonstrated in Gd₅Si₂Ge₂ [73] and La(Fe,Si)₁₃H_x [74], these conventional MCE first-order type materials show an inverse barocaloric effect. Referring to the Clausius–Clapeyron equation for the application of hydrostatic pressure, the magnitude of the barocaloric effect is related to the volume change during the transformation and the shift in the transition temperature by pressure. In Ni_49.26Mn_36.08In_14.66, an external pressure shifts the equilibrium martensitic transformation temperature T_t by 2 K kbar⁻¹ [75], while for the Ni_45.2Mn_36.7In₁₃Co_5.1 alloy this increase of T_t is 4.4 K kbar⁻¹, which is much more pronounced (figure 4). So it is also important to state that inverse MCE materials such as Ni–Mn–Co–In demonstrate a conventional barocaloric effect. As shown in figure 4, the magnetic hysteresis can be significantly reduced if the sample is magnetized without bias stress but demagnetized under an external pressure. Furthermore, theoretical calculations predict that the efficiency of a magnetocaloric material can be improved when implemented in a device with precisely adjustable applied magnetic field and pressure, compared with a device where only the magnetic field can be varied [76].

Figure 4.

The large thermal irreversibility can be overcome by the combination of applied magnetic and mechanical forces. M–T curves under 0 and 1.3 kbar hydrostatic pressure at 308 K are shown for Ni_45.2Mn_36.7In₁₃Co_5.1. The bottom right corner inset shows the shift of martensitic transition temperatures by the application of a hydrostatic pressure up to 4.3 kbar. The forward and reverse transitions can be induced in a relatively low field (with little hysteresis—shaded region in the main figure) when the sample is magnetized in zero pressure but demagnetized under an external pressure. This process is also demonstrated schematically (originally published in [60]).

The extrinsic origins of hysteresis can also be divided into two categories: microstructural and time dependent, as shown in figure 3. The microstructure involves grain size, phase coexistence and phase-boundary movement, interfacial stress, defects and phase purity. Besides this, the size of the sample can also affect the thermal hysteresis, which acts mainly on the mesoscopic scale. The time dependence of these transformation mechanisms is an issue on its own and involves the response to external stimuli. Our recent experiments show that the hysteresis increases when a magnetic field is applied with very high change rates [77,78]. As first-order transitions are driven by nucleation and growth, these processes need a certain time to take place. When the magnetic-field rate is too high, the material simply cannot follow and, consequently, a broadening of the hysteresis is observed. These limitations in the transformation speed need to be considered especially for magnetocaloric applications operating at high frequencies.

An additional problem of materials undergoing a sharp first-order transition is the volume change leading to mechanical stress causing, in turn, the occurrence of dislocations, micro-cracks, and even major cracks, resulting in pulverization when the material undergoes several temperature or field cycles [79]. The smaller fragments require less elastic energy to complete the transformation and, consequently, a reduced hysteresis is observed [80,81].

Investigations of the first-order transition kinetics in the giant magnetocaloric material LaFe_11.8Si_1.2 were performed by an in situ X-ray diffraction experiment and by magnetometry. Owing to the difference in the lattice parameters of the ferromagnetic and the paramagnetic phase, they mechanically interact with each other in the temperature range of coexistence. As a result, huge strains appear at the phase boundary, which leads to the formation of cracks during the first cooling sequence. The corresponding X-ray tomography image of the sample is shown in figure 5. One can see that the interlocked particles are separated from each other by significant gaps of widths in the range d=2–6 μm, but the whole particle ensemble nonetheless holds together despite the existence of cracks. Magnetic measurements were carried out on (i) the sample with cracks as a whole and (ii) all separate fragments together, obtained after the sample was disassembled into individual grains (figure 5).

Figure 5.

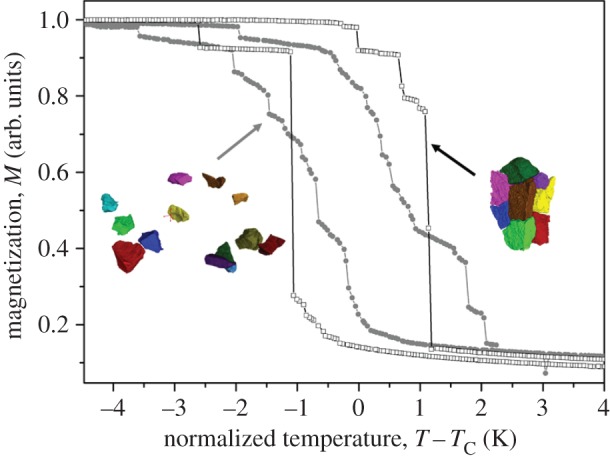
The magnetic transition of an interlocked particle ensemble (open squares) is very sharp even though most particles are separated by cracks. For a well-separated particle ensemble (solid circles), the transition broadens significantly, indicating that proximity of particles—and not necessarily a mechanical connection—is required to maintain a sharp, first-order-like transition. The sample images show the measured particle ensembles imaged with computed tomography [82]. (Copyright granted, licence no. 3847701318380.)

Isofield magnetization curves of this interlocked structure in an external magnetic field of μ₀H=10 mT demonstrate a very sharp transition (squares in figure 5), indicating that the interlocked particle ensemble still transforms together as one piece. As the tomography reveals, all particles of the interlocked ensemble are connected to the surface and thus can change their volume without the severe constraints that a particle would experience when surrounded by other particles. The magnetic transition of clearly separated particles (figure 5, solid circles) is much broader than the interlocked particle ensemble. The transformation proceeds in many small steps, presumably representing the T_t distribution of the individual particles. This raises the question of which coupling mechanism is causing the sharp transition in the interlocked state, where particles are only loosely connected. Following Lovell et al. [83], we propose that magnetostatic interactions, which do not require direct contact between particles, facilitate the nucleation in neighbouring particles and lead to an avalanche-like sharp transition.

In addition to this effect, depending on the choice of the measurement protocol, different values of the MCE might be observed in materials with a first-order transformation associated with thermal hysteresis. Most of the ΔS_m data reported for materials with first-order transitions are obtained under a ‘discontinuous’ measurement protocol [84,85], which allows the ΔS_m value to be maximized but at the same time is far from real operating conditions. A magnetic refrigerator operates in a cyclic manner, which is usually not replicated in laboratory tests. Whereas single sweep laboratory characterization provides important information on the material properties, these measurements are not necessarily adequate for an assessment of the suitability of a material for its application for room temperature magnetic refrigeration [70].

In our recent works [63,86], a rigorous method is proposed for extracting the cyclic magnetic entropy change of a magnetocaloric material even if the characterization is performed under quasi-static non-cyclic conditions. Results show that the cyclic response coincides with the intersection of the heating and cooling curves measured using protocols which prevent the appearance of spurious spikes upon the application of the Maxwell relation. This method provides a basis for a comparison of the suitability of different hysteretic magnetocaloric materials for their application in a magnetic refrigerator.

5. La(Fe,Co,Si)₁₃

In the La–Fe–Si material family, the thermal hysteresis can be tuned down by the specific substitution of elements [87,88]. The greater challenge is to increase the transformation temperature of the itinerant electronic transition to room temperature without diminishing the magnetocaloric properties.

To show the whole picture of magnetocaloric properties of the La(Fe,Co,Si)₁₃ alloys, we collect our ΔS_m(T) and ΔT_ad(T) dependences together in a single plot in figure 6a. The substitution of Co results in a shift of the Curie temperature up to room temperature, but it is simultaneously accompanied by a decrease in ΔS_m and ΔT_ad. Increasing the Co content changes the type of the transition from first to second order. Consequently, the magnetovolume change shows the same trend as ΔT_ad. This demonstrates that the magnetoelastic contribution plays a key role in order to obtain a large MCE but, at the same time, the thermal hysteresis grows.

Figure 6.

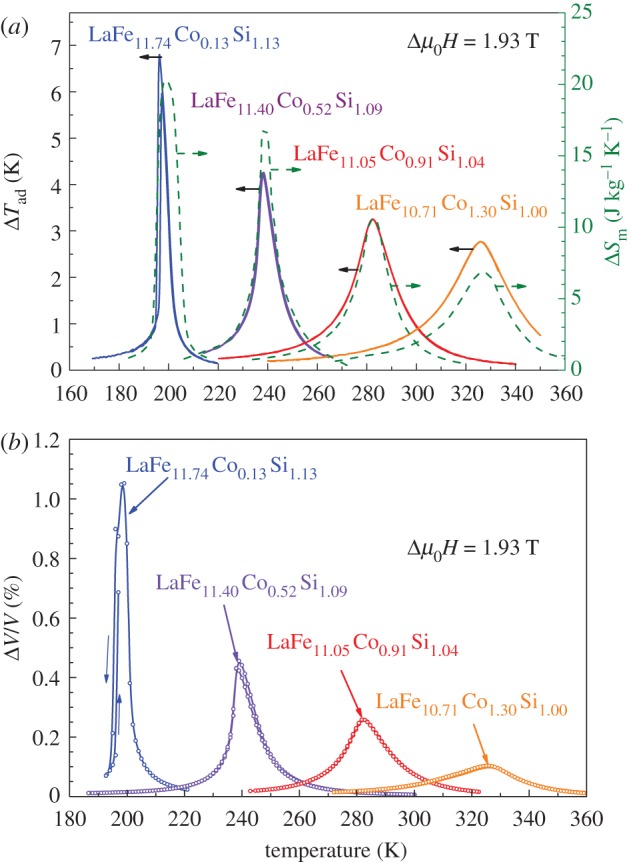
(a) Isothermal magnetic entropy change ΔS_m and adiabatic temperature change ΔT_ad for four selected La(FeCoSi)₁₃ compounds measured under magnetic field change Δμ₀H=1.93 T and (b) isothermal magnetovolume effect.

In our previous work [22], we demonstrated how more sophisticated geometries can be made by using selective laser melting, a rapid prototyping technique to form three-dimensional shapes. Using the excellent magnetocaloric material La(Fe,Co,Si)₁₃ as starting powder, we made two geometries: a wavy-channel block with a high surface-to-volume ratio and an array of fine-shaped rods, which eliminate unwanted heat conduction along the magnetic part. After annealing treatment, the geometries were intact and survived more than 10⁶ cycles of applying a magnetic field while still maintaining good magnetocaloric properties. This fabrication approach is promising for making near-net shaped magnetic refrigerants with superior heat transfer properties and performance.

6. La(Fe,Mn,Si)₁₃H_X

By modulating the magnetic environment of the Fe atoms, the ferromagnetic state can be stabilized either by elemental substitution of Fe (by Co, Mn, Si, etc.) or by interstitial insertion of small atoms such as C, N, B and H; hence, T_t can be changed from 190 K up to room temperature and above (340 K). The hydrogenation of La(Fe,Si)₁₃ is the most efficient method of bringing T_t near room temperature as the large MCE is retained. On the other hand, in order to precisely adjust T_t to the desired working temperature, partial hydrogen absorption or desorption is required. Process parameters such as pressure, temperature and dwell need to be adjusted carefully. Moreover, the long-term stability of such partial hydrogenated compounds is not guaranteed, as has been reported recently [89]. Therefore, a quaternary compound with Mn has been suggested to adjust T_t of the fully hydrogenated material. Comparable with Si and Co, with increasing Mn content, the type of the magnetic transition is shifted gradually from first to second order and the MCE decreases.

We and others demonstrated that the hydrogenation of La(Fe,Si,Mn)₁₃ is a simple and efficient way to use this compound as a first-order-type material at room temperature [90,91]. The T_t of the non-hydrogenated sample is determined by the Mn content of the parent sample, as well as its MCE. This is attributed to the gradual change of the phase transition from first to second order and the reduction of the thermal hysteresis of the non-hydrogenated sample, as can be seen in figure 7a. In figure 7b, the magnetocaloric properties of fully hydrogenated non-compacted powder with working temperatures around room temperature are shown. These materials were commercially produced by Vacuumschmelze GmbH. As in the case of the non-hydrogenated compound, Mn decreases the transition temperature and the MCE. At the same time, the transition is of first-order type and the thermal hysteresis is negligible.

Figure 7.

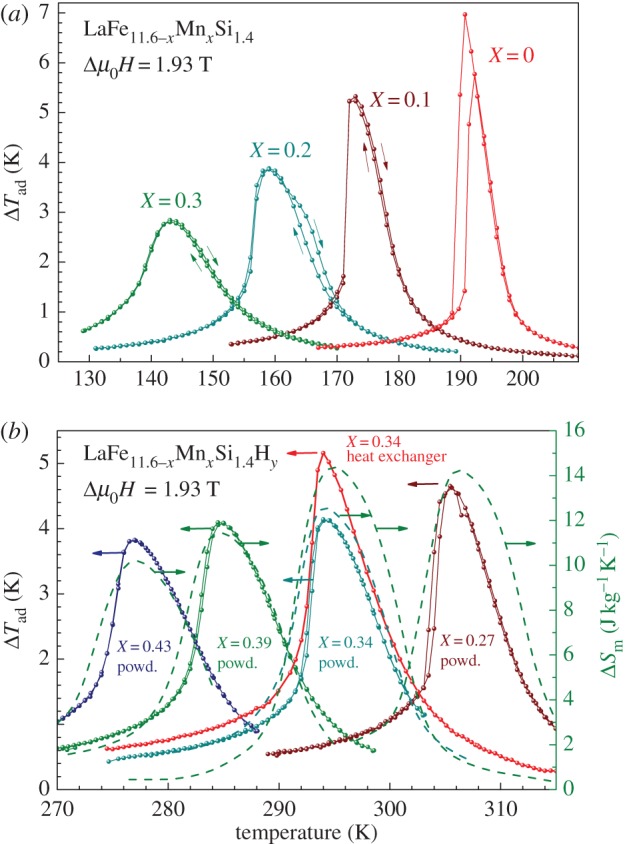
Adiabatic temperature change ΔT_ad as a function of temperature for parent compounds LaFe_11.6-xMn_xSi_1.4 (a) and their hydrogenated samples (b). The Mn content increases from right to left, i.e. with decreasing T_Peak.

Owing to the hydrogenation process, the decrepitation of the material into powder is inevitable. Therefore, it is not possible to manufacture heat exchangers as plates in bulk form. A simple solution is the compaction of powder into thin plates. Adhesive-bonding techniques can provide mechanical stability and corrosion protection and enable the production of net-shaped modules in a single-step manufacturing process. In order to obtain an excellent magnetocaloric heat exchanger from a precursor material such as hydrogenated La(Fe,Si,Mn)₁₃, a systematic study on making an epoxy composite with this material was performed [55] and the influence of the powder particle size, adhesive type, adhesive concentration and compaction pressure on the magnetocaloric properties of the polymer-bonded La(Fe,Mn,Si)₁₃H_x material was investigated in detail.

After the optimization of all compaction parameters, the adiabatic temperature change (heat exchanger curve in figure 7b) of the fully dense La(Fe,Mn,Si)₁₃H_x composite in a magnetic field change of Δ(μ₀H)=1.93 T (4.9 K) is comparable with the ΔT_ad of Gd metal (ΔT_ad=5.1 K) and significantly exceeds the ΔT_ad of La(Fe, Co, Si)₁₃ (ΔT_ad=3.1 K). The value of the volumetric magnetic entropy change of the composite La(Fe, Mn, Si)₁₃H_x (63 mJ cm⁻³ K⁻¹) is comparable to that of bulk La(Fe,Co,Si)₁₃ (70 mJ cm⁻³ K⁻¹) and 50% higher than that of Gd metal (40 mJ cm⁻³ K⁻¹). The thermal conductivity of the polymer-bonded La(Fe, Mn, Si)₁₃H_x is about 5 W K⁻¹ m⁻¹ near room temperature [55]. This is 2.5 times less than that of bulk La(Fe,Co,Si)₁₃ and Gd metal, but still five times higher than that of MnAs and Fe₂P-type materials. This means that a device using a composite material will have 1.5 times lower maximum operating frequency than a device using bulk material.

7. Fe₂P-type compounds

Another class of very promising rare-earth-free materials are the Fe₂P-type compounds. The family is derived from the prototypical Fe₂P-based compound, showing a sharp first-order phase transition at T_t=217 K [92,93]. In 2002, the compound MnFeP_0.4As_0.55 was reported by Tegus et al. [94] to exhibit a giant MCE near room temperature at which the structural and magnetic transformations coincide. Besides the large thermal hysteresis, the other drawback of this type of alloy is the content of toxic arsenic, which limits its use in a domestic refrigeration appliance. Since the discovery of this alloy, large efforts have been focused on tuning the transition and especially on the substitution of critical elements in this system. The As could be completely replaced by Si, thus conserving the magnetocaloric properties. Furthermore, the transition temperature is highly tuneable by adjusting the Mn and Si content [95]. In this material class, the first-order transition also manifests itself in a large volume change of the hexagonal structure. Conventionally, the desired phase is prepared by ball milling of precursor powders, compaction and a subsequent heat treatment procedure for sintering [95] or by melt spinning [96].

Studies in the class of Mn–Fe–P–Si-type alloys have shown that the hysteresis could be minimized by fine adjustment of the Mn/Fe and P/Si ratio. The drawback of this adjustment is the decrease in overall magnetization and, therefore, a decrease in ΔM at the transition. In order to increase both values, one has to work at the optimum composition of MnFeP_0.66Si_0.33 [97,98]. This composition has a low value of ΔT_ad (≈2 K in 1 T), but, at the same time, shows a rather high value of ΔS_m=−8 J kg⁻¹ K⁻¹ [99]. A major drawback of these compounds is mechanical instability. The instability is considered to be from the volume change of +0.2% [97] when crossing the transition temperature, leading to embrittlement of the bulk samples.

Recently, the above-mentioned issues were tackled by applying internal pressure to the compound by adding boron to the system [100]. For the compound MnFe_0.95P_0.595B_0.075Si_0.33, a cyclic adiabatic temperature change of ΔT_ad=2.55 K with a cyclic ΔS_m≈10 J kg⁻¹ K⁻¹ in a field change of 1 T with a thermal hysteresis of 1.6 K was observed. This enhancement of properties is ascribed to the larger field dependence of T_C and lower latent heat of this material compared with Mn–Fe–P–Si. Furthermore, the mechanical integrity of this compound was reported to be optimized to a point where no breaking or cracking of the samples could be observed, even after 10 000 cycles of magnetization and demagnetization [101]. This improvement in the structural integrity was ascribed to the fact that there is no discontinuous volume change present when passing through the transition but a comparable change in the a/c lattice parameters of the base Mn–Fe–P–Si compound is preserved.

It was also shown that the B-containing compounds Mn_xFe_(1.95−x)P_(1−y−z)Si_zB_y are highly tuneable while preserving the giant MCE with a limited thermal hysteresis in a broad temperature range [58]. Very recent works show that boron can also be substituted by nitrogen, possibly increasing the industrial applicability of this compound [102].

In summary, the compounds of Mn–Fe–P–Si–B/N are, as for the La(Fe,Mn,Si)₁₃H_x-type alloys, a highly promising class of materials for magnetic refrigeration due to their precisely tuneable transition temperatures with low hysteresis and high reversible values of ΔS_m and ΔT_ad at low fields applicable in a refrigeration device. Furthermore, they also consist of cheap, non-toxic and readily available elements.

8. Heusler alloys

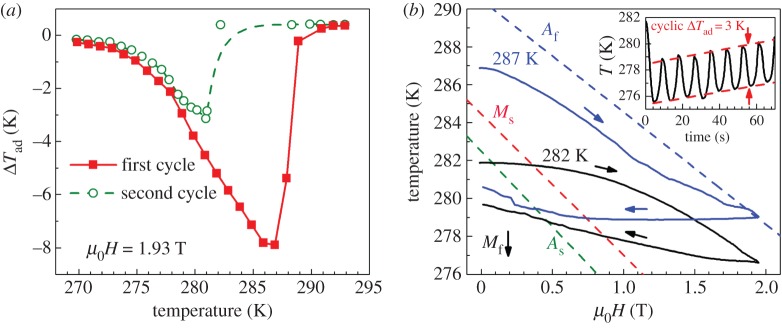
The large MCE in Heusler compounds is due to the first-order magnetostructural transition between the low-temperature martensite and the high-temperature austenite phase [60,103]. Significant entropy and temperature changes can be achieved with these materials [104]. On the other hand, the thermal hysteresis is large, which impedes the cyclability of the effect. Direct measurements on the Heusler alloy Ni_45.7Mn_36.6In_13.5Co_4.2 revealed a very large adiabatic temperature change ΔT_ad of −8 K in a magnetic field change of only 1.93 T, as shown in figure 8a. Because of the large thermal hysteresis, which is in the range of 10 K, this large effect cannot be achieved in the second field application cycle.

Figure 8.

(a) ΔT_ad upon the first and second application of 1.93 T. (b) Temperature progression of the Heusler compound Ni_45.7Mn_36.6In_13.5Co_4.2 starting from different temperatures. The inset shows the cyclic response of the material [59]. (Copyright granted, licence no. 3850160649979.)

The negative effect of thermal hysteresis can be reduced in Heusler alloys when following a minor loop of hysteresis instead of completely transforming the material between martensite and austenite [59]. Such a minor loop is in principle only possible if the transition is continuous and not jump-like, as shown schematically in figure 2d. However, real magnetocaloric Heusler alloys always have a finite transition width. This was explained by partly preventing the nucleation of martensite in the mixed-phase region of minor loops, which would require more energy than the simple phase-boundary movement. We related this effect to the strong sensitivity of the transition temperature T_t to internal stress, which is created by the large volume change of the transition.

The reversible MCE accounts for −3 K when moving in minor loops of hysteresis, as shown in figure 8b. The origin of this was investigated by temperature-dependent optical microscopy and it turned out that the energy-intense nucleation of the low-temperature phase can be partly avoided in the minor loop. In this case, the sample transforms mainly by phase-boundary movement, which is less costly in energy, and, therefore, the reversibility of the first-order transition is increased [59]. This important finding brings Heusler alloys closer to application, as the reversible ΔT_ad is now comparable to that of other magnetocaloric materials such as La(Fe,Si,Co)₁₃.

9. Conclusion

In this paper, we have summarized the main causes of hysteresis in different magnetocaloric material classes and discussed the possibilities to reduce it or to use a material despite a large hysteresis. We separated the origins for hysteresis into intrinsic contributions (linked to the electronic properties on the atomic scale) and extrinsic factors (related to microstructure). The reversibility of the MCE, which is essential for magnetic refrigeration, strongly depends on the width of the thermal hysteresis. It is, therefore, absolutely required to measure the adiabatic temperature change as well as the isothermal entropy change under cyclic conditions in order to assess the suitability of a material in a meaningful way. The width of the hysteresis reduces when approaching the tricritical point, at which the mismatch between the high- and the low-temperature phase vanishes. This can be reached for instance by chemical substitution or by the application of external stimuli. Even though the reversibility enhances by this approach, a reduction in the magnetocaloric properties can occur when the order of the transformation changes. By contrast, a material with a first-order transition and a certain hysteresis should have a sharp transformation in order to obtain large MCEs. Such a transition is driven by nucleation and growth; therefore, the size of the material as well as the kinetics may also influence the hysteresis.

We reviewed recent achievements for the most promising magnetocaloric materials with great potential for room temperature applications. Non-hysteretic materials such as prototypical Gd act as a reference to determine whether hysteretic materials can be tuned to outperform them.

By adding Co to the material La(Fe,Si)₁₃, it is possible to shift T_t to room temperature. Furthermore, the character of the phase transition of the material changes from first to second order, and thus the thermal hysteresis is reduced. However, this effect is accompanied by a reduction of the MCE.

Another possibility to tune La(Fe,Si)₁₃ is the hydrogenation of the base material. By this approach, the phase transition is still of first-order type and the MCE remains large. At the same time, the hysteresis remains small enough to make the material very promising. The main drawback is the high brittleness and poor machinability, which can be overcome by binding the material in a matrix. This, however, dilutes the MCE.

Fe₂P-type compounds have been successfully tuned to exhibit a transformation near room temperature. Reports show that the addition of B and N can largely eliminate the volume change in the material and, in this way, the hysteresis could be reduced down to 1 K. Furthermore, the addition of B prevents cracking and the material could prove to be useful for application.

Heusler alloys can also be useful despite a large hysteresis. By operating in minor loops of the thermal hysteresis, it is still possible to have a significant magnetocaloric performance under cyclic conditions. The reason for this is the large number of martensitic nucleation sites that remain in the material if it is not transformed completely.

In materials with a large volume change during the transformation, the application of pressure influences the transition temperature and the width of the thermal hysteresis. When close to the tricritical point, the thermal hysteresis can be reduced significantly. If this condition is not fulfilled, the combination of both an external magnetic field and pressure can help to enhance the cyclability.

In the last decade, significant progress in the optimization of known materials and in the identification of new potential materials has emerged. However, these achievements could not yet drive this interesting field of magnetic refrigeration to market entry on a large scale. It is obvious that a magnetocaloric material with a drastically enhanced reversible entropy and temperature change would draw a lot attention in fundamental material science and physics, but this alone is not sufficient to design a solid-state refrigerator that is competitive with conventional technology in terms of price, weight and efficiency. In order to achieve this goal, considerable joint efforts of fundamental science on the one hand and mechanical engineering on the other need to be made. This is the indispensable prerequisite to pave the way for a bright future of magnetic refrigeration.

Authors' contributions

OG coordinated and authored the manuscript. KS was the deputy coordinator, drafted several paragraphs and collected literature values of the magnetocaloric effect. TG provided the schematics. MF, DB, TG, IR and KS performed measurements and contributed to several paragraphs. HW, MG, MA, PE and MF assisted in manuscript preparation and contributed to the general discussion of the mastery of hysteresis.

Competing interests

We have no competing interests.

Funding

This work has been, in part, funded by the European Community’s 7th Framework Programme under grant agreement no. 310748 ‘DRREAM’ and also the DFG SPP 1599 priority programme. We also want to thank the DFG for financial support in the framework of the Excellence Initiative, Darmstadt Graduate School of Excellence Energy Science and Engineering (GSC 1070).