Association between Changes in Mammographic Image Features and Risk for Near-term Breast Cancer Development

Abstract

The purpose of this study is to develop and test a new computerized model for predicting near-term breast cancer risk based on quantitative assessment of bilateral mammographic image feature variations in a series of negative full-field digital mammography (FFDM) images. The retrospective dataset included series of four sequential FFDM examinations of 335 women. The last examination in each series (“current”) and the three most recent “prior” examinations were obtained. All “prior” examinations were interpreted as negative during the original clinical image reading, while in the “current” examinations 159 cancers were detected and pathologically verified and 176 cases remained cancer-free. From each image, we initially computed 158 mammographic density, structural similarity, and texture based image features. The absolute subtraction value between the left and right breasts was selected to represent each feature. We then built three support vector machine (SVM) based risk models, which were trained and tested using a leave-one-case-out based cross-validation method. The actual features used in each SVM model were selected using a nested stepwise regression analysis method. The computed areas under receiver operating characteristic curves monotonically increased from 0.666±0.029 to 0.730±0.027 as the time-lag between the “prior” (3 to 1) and “current” examinations decreases. The maximum adjusted odds ratios were 5.63, 7.43, and 11.1 for the three “prior” (3 to 1) sets of examinations, respectively. This study demonstrated a positive association between the risk scores generated by a bilateral mammographic feature difference based risk model and an increasing trend of the near-term risk for having mammography-detected breast cancer.

I. Introduction

Mammography is an only population-based breast cancer screening imaging modality accepted in current clinical practice. However, its efficacy is controversial [1, 2]. Hence, developing new personalized breast cancer screening paradigms has attracted research interest [3, 4]. A number of recent studies has tried to identify small groups of women with substantially higher-than-average risk for developing breast cancer based on the epidemiology study identified risk factors, genomic information and breast density [3, 5–8]. However, these risk prediction models do not yield a clinically acceptable discriminatory power when applied at the individual level [9]. Hence, in order to develop a new personalized cancer screening paradigm, it is important to identify the effective near-term risk factors which increase the prediction values as the time lag between the negative and positive screening decreases. As a result, the physicians can make individualized recommendation of cancer screening and only a small fraction of women who have higher risk of developing imaging detectable cancer in the near term (e.g., 1 to 3 years) need to be closely monitored and frequently screened (e.g., annually), while the majority of women with low near-term cancer risk could be screened less frequently (e.g., every 2 or 3 years) until and if their near-term risk levels increase significantly during future assessments.

Since breast cancer usually develops in one breast in a progressive manner, we hypothesized that bilateral asymmetry of mammographic density image features between the left and right breasts could provide useful time dependent information or constitute a clinical marker to predict near-term risk of cancer development. To test this hypothesis, we recently performed several studies that investigated the feasibility of predicting risk of women having mammography detectable cancer in the next sequential annual screening after a negative screening of interest using the new risk prediction models built from the quantitative analysis of bilateral mammographic image feature differences [10–13]. The purpose of this study is to identify more effective image features in an attempt to further improve the performance of the new near-term breast cancer risk models. The most important, we investigated a possible association or a trend between the model-generated risk scores and the time lag between the negative and positive screenings using a unique image dataset with 4 sequential mammography examinations obtained from each woman.

II. Image Dataset

Under an institutional review board approved data collection protocol, we retrospectively collected series of 4 sequential, fully anonymized images of 335 women who underwent at least 4 routine full-field digital mammography (FFDM) screening examinations at the University of Pittsburgh Medical Center. We divided the dataset based on the verified diagnostic outcome of these women in the latest (termed the “current”) examination. During the “current” screening, cancers were detected and verified in 159. The rest of 176 women were cancer-free. Eighty one were screening negative (not-recalled) and 95 were recalled for the suspicious finding but later proven as benign during the imaging diagnostic workup and/or biopsy. All “cancer-free” women remained negative/benign at least 2 screenings ascertained subsequent to “current” examination.

For each case, we collected the three most recent FFDM examinations prior to the “current” examination. All “prior” FFDM images had been read and interpreted by radiologists as “negative” (screening BIRADS 1) or “definitely benign” (screening BIRADS 2). Hence, all “prior” examinations were not recalled and cases that were recalled were only present in the “current” sets of examinations. The average elapsed time between the “current” and each of “prior” #1, #2 and #3 studies was 1.16±0.41, 2.30±0.55 and 3.44±0.72 years, respectively.

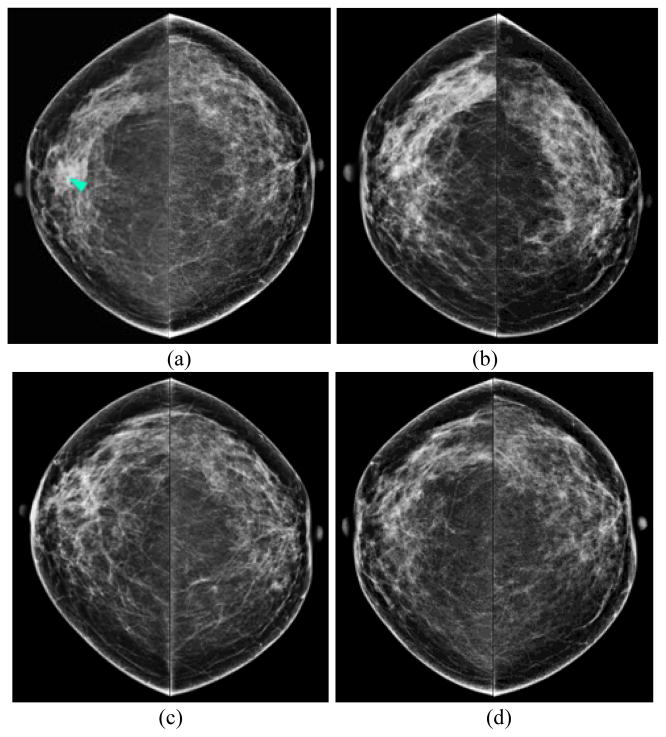
Fig. 1 displays an example of 4 sets of bilateral CC view FFDM images of the left and right breasts, which were acquired from the “current” (Fig. 1(a)) and 3 previous FFDM screenings in order (“prior” #1 to #3) of acquisition (Fig. 1(b)–(d)). All “prior” images were screening negative and a right breast mass was detected as suspicious in the “current” image and later pathologically confirmed as an invasive ductal carcinoma (IDC). The series shows a consistent trend of gradual increase of the bilateral mammographic tissue density asymmetry.

Fig. 1.

An example of a positive case showing 4 sets of bilateral CC views acquired during the “current” (a) and the 3 most recent “prior” FFDM screenings (b)–(d). A mass (arrow) was detected on the “current” image and later confirmed by pathology as IDC, whereas all three “prior” examinations were previously clinically interpreted as “negative”.

III. Methodology

A. Mammographic Feature Extraction

We applied a computer-aided detection (CAD) scheme to segment the whole breast region depicted on each image [14]. From the segmented breast region, we initially computed 158 image features to assess mammographic tissue patterns and/or image characteristics. These features are divided into 4 subgroups, namely: (1) 8 structural similarity features, (2) 40 Weber local descriptor (WLD) and Gabor directional similarity (GDS) features, (3) 80 run length statistics (RLS) and gray level co-occurrence matrix (GLCM) based features, and (4) 30 other texture and gray level magnitude based features.

1) Structural Similarity Features

Wang et al. [15] proposed a new SSIM index and a computational method that uses structural similarity to assess image quality measures. The SSIM compares the local patterns of pixel intensities that have been normalized for luminance and contrast. Thus, it provides a reasonable approximation of the human visual system, which is adapted for extracting structural information from a particular scene. Given that x = {x_i | i = 1,..., M} and y = {y_i | i = 1,..., M} are two nonnegative image signals that have been aligned with each other, such as two spatial patches extracted from each image, a specific form of the SSIM index is provided in [17] as:

$$\text{SSIM}(\mathbf{x},\mathbf{y})=\frac{\left(2{\mu }_x{\mu }_y+C_1\right)\left(2{\sigma }_{xy}+C_2\right)}{\left({{\mu }_x}^2+{{\mu }_y}^2+C_1\right)\left({{\sigma }_x}^2+{{\sigma }_y}^2+C_2\right)}$$ (1)

where ${\sigma }_{xy}=1/M{\displaystyle \sum _{i=1}^M}\left(x_i-{\mu }_x\right)\left(y_i-{\mu }_y\right),{\mu }_x=1/M{\displaystyle \sum _{i=1}^M}{x}_i,{\sigma }_x^2=1/M{\displaystyle \sum _{i=1}^M}{\left(x_i-{\mu }_x\right)}^2$, and C₁ and C₂ are two small positive constants. The maximum value of the SSIM index is 1 and is achieved if and only if x and y are identical.

Recently, Casti et al. presented a Correlation-Based SSIM or CB-SSIM index that enables direct estimation of structural similarity between different-sized regions [16] and showed that SSIM and CB-SSIM indices had potential to effectively detect bilateral asymmetry through quantification of structural similarity between paired mammographic regions. Given a pair of right and left rectangular regions, x_R and y_L of size A × B and P × Q pixels, respectively, the CB-SSIM index is defined as:

$$\text{CB}-\text{SSIM}({\mathbf{x}}_R,{\mathbf{y}}_L)=\frac{\left(2{\mu }_R{\mu }_L+K_1\right)\left\{2max[\mathit{corr}\left({\mathbf{x}}_R,{\mathbf{y}}_L\right)\right\}}{\left({{\mu }_R}^2+{{\mu }_L}^2+K_1\right)\left\{max[\mathit{corr}\left({\mathbf{x}}_R,{\mathbf{x}}_R\right)]+max[\mathit{corr}\left({\mathbf{y}}_L,{\mathbf{y}}_L\right)]\right\}}$$ (2)

where μ_R and μ_L are the mean values of pixels within the right and left breast regions, respectively, and a 2D (two-dimensional) cross-correlation between the 2 regions, corr(x_R, y_L) is defined as:

$$\mathit{corr}\left({\mathbf{x}}_R,{\mathbf{y}}_L\right)=\sum _{a=0}^{A-1}\sum _{b=0}^{B-1}\left\{\left[{\mathbf{x}}_R(a,b)-{\mu }_R\right]\left[{\mathbf{y}}_L\left(a-p,b-q\right)-{\mu }_L\right]\right\}$$ (3)

where −P + 1 ≤ p ≤ A − 1 and −Q + 1 ≤ q ≤ B − 1; corr(x_R, x_R) and corr(y_L, y_L) are two auto-correlation functions of x_R and y_L, respectively. K₁ is a small positive constant aimed at improving the robustness of the index and was set to 0.01 [16], [16]. The CB-SSIM index is equal to the standard SSIM index if P = A and Q = B. CB-SSIM = 1, if x_R and y_L are identical.

A limitation of SSIM index is its high sensitivity to geometric and scale distortions. Thus, Sampat et al. [17] proposed a novel Complex Wavelet SSIM index (CW-SSIM) as a general image similarity measurement index, which has 3 advantages. First, CW-SSIM does not require an explicit correspondence between the pixels being compared. Second, CW-SSIM is largely insensitive to small geometric distortions, such as small rotations, differences in scale, and/or translations. Third, CW-SSIM also compares the structural and textural properties of localized regions of an image pair. CW-SSIM index was defined in [17] as:

$$\text{CW}-\text{SSIM}({\mathbf{c}}_x,{\mathbf{c}}_y)=\frac{2\left|{\displaystyle \sum _{i=1}^N}{c}_{x,i}{c}_{y,i}^{\ast }\right|+K}{{\displaystyle \sum _{i=1}^N}{\left|c_{x,i}\right|}^2+{\displaystyle \sum _{i=1}^N}{\left|c_{y,i}\right|}^2+K}$$ (4)

where c_x = {c_x,i | i = 1,..., N} and c_y = {c_y,i | i = 1,..., N} are two sets of coefficients extracted at the same spatial location in the same wavelet subbands of the two images being compared in the complex wavelet transform domain, c^* denotes the complex conjugate of c, and K is a small positive constant.

Casti et al. [16] also postulated that advantages of CW-SSIM and in particular the use of steerable pyramid decomposition [18] in its computation, which is more effective in comparisons of the bilateral mammographic image feature asymmetry, whereby distortions caused by breast compression and relative translations during the imaging procedure of the two breasts can generate FP results. Thus, similar to what was performed in the spatial domain, the authors defined a new correlation-based complex wavelet SIMilarity (CB-CW-SSIM) index, as follows:

$$\text{CB}-\text{CW}-\text{SSIM}({\mathbf{c}}_R,{\mathbf{c}}_L)=\frac{2{max}_{p,q}\left\{\left|{\displaystyle \sum _{i,j}}\left[{\mathbf{c}}_R(i,j){\mathbf{c}}_L^{\ast }(i-p,j-q)\right]\right|\right\}}{{\displaystyle \sum _{i,j}}{|{\mathbf{c}}_R(i,j)|}^2+{\displaystyle \sum _{s,t}}{|{\mathbf{c}}_L(s,t)|}^2}$$ (5)

where c_R and c_L are the complex wavelet coefficients obtained by decomposing regions x_R and y_L, respectively, with a 3-scale, 16-orientation steerable pyramid decomposition procedure [17, 18].

In this study, we replicated all parameters recommended in [15–17] to compute SSIM, CB-SSIM, CW-SSIM, and CB-CW-SSIM based structural similarity features to assess bilateral mammographic feature differences between the left and right breasts. We computed 4 features on 2 rectangular central regions extracted from the whole breast regions similarly to the manner performed in [16].

In order to generate and align the paired 2 regions extracted from two bilateral mammograms, we first set up a bounding box to cover the entire segmented breast area in one image. We then extracted a rectangular region of the breast in the center of the bounding box with a size of 80% of the box to omit some portions of the non-breast (air) pixels. However, since the sizes of 2 regions extracted from two bilateral images are typically not equal, we aligned 2 regions by registering their centers. We used a smaller region as a reference to generate 2 rectangular regions of the same size by eliminating the pixels outside the overlapped regions. In this way, all similarity features were computed from 2 bilateral regions with the equal size.

We also computed the same set of similarity features based only on the dense breast pixels inside the 2 paired regions. Using the previously defined method in [13], the dense breast pixels were detected if their pixel values are greater than the median value of the whole breast region. All other pixels with smaller values are ignored in feature computation. Namely, we hypothesize that different information extracted from the dense and whole breast regions may be beneficial in bilateral directional similarity analysis. Thus, altogether 8 structural similarity features were computed for each case.

2) Weber Local Descriptor (WLD) and Gabor Directional Similarity Features

In addition to analyses of similarities in spatial distribution of gray scale values between 2 breasts, we computed WLD features to investigate bilateral differences in the directional components (or structural orientation) of the breast tissue parenchyma. Inspired by Weber’s Law, WLD features are simple, yet powerful and robust local descriptors with 2 differential excitation and orientation components [19]. The differential excitation component of WLD is computed as a ratio between two terms: (1) the relative intensity differences of a pixel of interest from its neighbors (e.g., a 3 × 3 square region); and, (2) the actual intensity of the pixel. By computing the differential excitation component, local salient patterns in an image are extracted. The gradient orientation component of WLD is computed for each pixel. Studies have shown that WLD outperformed other widely used descriptors including Gabor [20], scale-invariant feature transform (SIFT) [21], and conventional multiscale local binary pattern (LBP) features in image pattern detection and recognition [19].

In this study, we computed similarity features described in the previous subsection (Sec. III.A.1) on the WLD differential excitation and gradient orientation filtered images of each case in our dataset. A detailed derivation and computation approach is given in [20]. In brief, the differential excitation ξ(x_c) of a current pixel x_c is computed as:

$$\xi (x_c)=arctan\left[\sum _{i=0}^{p-1}\left(\frac{x_i-x_c}{x_c}\right)\right]$$ (6)

where x_i (i = 0, 1, …, p − 1) denotes the ith neighbors of x_c and p is the number of neighbors. In this study, we computed multiscale WLD features for p = 8, 16 and 24 using the method described in [21]. The orientation component of WLD is the gradient orientation [22], and was computed as:

$$\theta \left(x_c\right)=arctan\left(\frac{x_7-x_3}{x_5-x_1}\right)$$ (7)

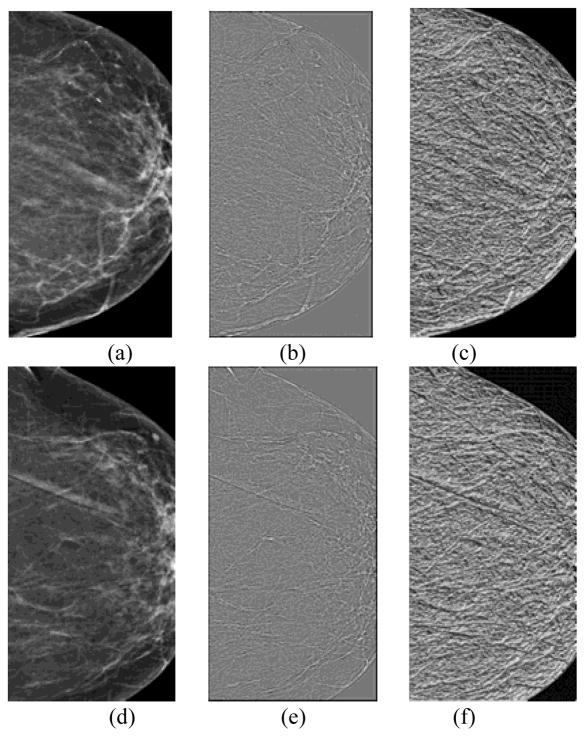
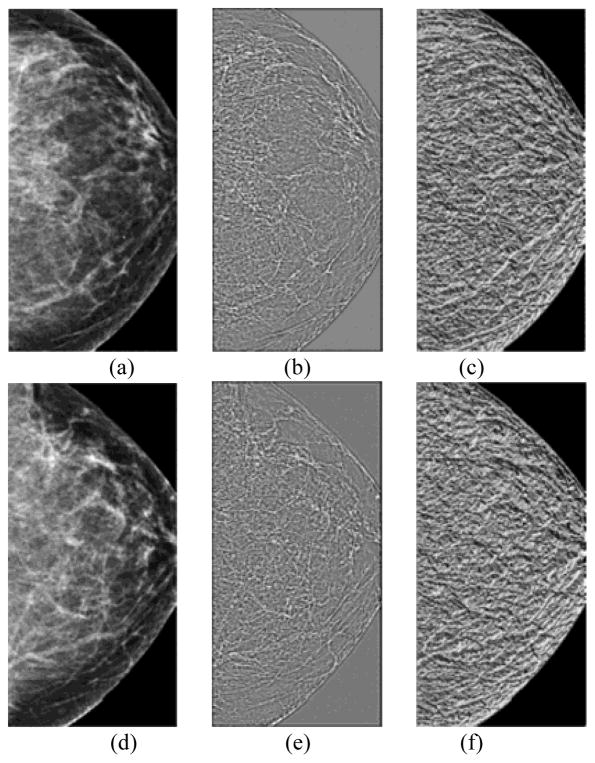
As we used 3 scales (p = 8, 16 and 24) in the multiscale framework of WLD feature computation, hence, altogether 24 differential excitation and gradient orientation based features were computed per case. Figs. 2 and 3 show examples of the WLD differential excitation and gradient orientation responses of the central regions segmented from “prior” #1 images computed with the first scale (p = 8). One of the related “current” images was positive (cancer detected) and the other remained negative (cancer-free). The values of 7 out of 8 structural similarity features computed on the differential excitation and gradient orientation images, the features computed on the positive case (Fig. 2) were lower than on the negative case (Fig. 3), suggesting that “higher risk” images have lower values of computed structural similarity.

Fig. 2.

An example of a positive case in which cancer was detected on the “current” mammogram of left breast. It includes central regions extracted from the “prior #1” mammograms of the left (a) and right breast (d); WLD differential excitation images of the left (b) and right breast (e); and WLD gradient orientation images of the left (c) and right breast (f).

Fig. 3.

An example of a negative case. It includes central regions extracted from the “prior #1” mammograms of the left (a) and right breast (d); WLD differential excitation images of the left (b) and right breast (e); and WLD gradient orientation images of the left (c) and right breast (f).

Furthermore, by replicating most of the parameters specified in [16], we compared performance of WLD similarity features with the similarity features computed on the magnitude and phase responses for a set of 18 equally spaced Gabor filters. In the spatial domain, the kernel oriented at −π/2 is defined as:

$$g\left(x,y\right)=\frac{1}{2\pi {\sigma }_x{\sigma }_y}exp\left[-\frac{1}{2}\left(\frac{x^2}{{\sigma }_x^2}+\frac{y^2}{{\sigma }_y^2}\right)\right]cos\left(2\pi \frac{x}{\tau }\right)$$ (8)

where σ_x and σ_y are the standard deviations of the Gaussian envelop along the x and y directions, respectively. In addition, thickness of the filter is defined as $\tau =2{\sigma }_x\sqrt{2log(2)}$, which is the spatial periodicity of the cosine modulation. The filter elongation is defined as l = σ_y/σ_x. We used τ = 6 pixels and l = 8. The filters oriented at 18 different angles were obtained by rotating the kernel over the angular range of [−π/2, π/2].

The magnitude response is obtained by assigning to each pixel the maximum response over all N filters for the given pixel. The phase response is obtained by assigning to the pixel the corresponding orientation [16]. We computed SSIM, CB-SSIM, CW-SSIM, and CB-CW-SSIM structural similarity features on the Gabor magnitude and phase responses of the image central regions to analyze the bilateral differences computed from these directional similarity based features. We also computed 4 similarity features for the central dense breast regions. Thus, we computed total 16 Gabor features per case.

3) RLS and GLCM Based Features

In a previous study [10], we showed that gray level RLS based features had the highest discriminatory power amongst 8 image based feature groups in predicting near-term breast cancer risk using “prior” #1 images. In this study, we extended this type of feature analysis to “prior” #2 and #3 images. We computed 11 RLS features on both the whole and dense breast regions, separately. These features are short and long run emphasis; run length non-uniformity; low and high gray level run emphasis; short run low and high gray level emphasis; long run low and high gray level emphasis; gray level non-uniformity; and run percentage. To compute each feature, we reduced image gray level range from 4096 to 256 gray levels (8 bit) and computed 4 RL matrices along 4 directions: 0°, 45°, 90°, and 135°. Two final feature values were computed as the average and maximum values of each RLS feature along the 4 directions.

Since GLCM features have been applied to assess mammographic tissue characterization [22–25], we also computed 9 GLCM based features, which relate to contrast, energy, homogeneity defined by Soh and Tsatsoulis [26], homogeneity as defined in Matlab®, inverse difference normalized and inverse difference moment normalized [27], the maximum probability, correlation as defined in Matlab®, and correlation as defined in [28]. We computed these features in 4 directions of 0°, 45°, 90°, and 135° using the reduced gray level range images (8 bit) at distance d = 1. We then computed the average and maximum values of the features along the 4 directions on the whole and dense breast regions. As a result, a total of 22 RLS features and 18 GLCM features were computed from whole breast regions, and the same number of RLS and GLCM features was computed on the dense breast regions.

4) Other Texture and Gray Level Magnitude Based Features

We computed 30 additional texture and gray level magnitude based features [22, 23] from the whole breast region. First, we computed 5 moments based features namely, mean, standard deviation, skewness, kurtosis, and entropy of gray level values. Second, we computed percentage density (PD) measures that are computed as the ratios of the area within the segmented breast with intensity values exceeding the mean intensity value for the segmented breast to the whole segmented breast region, which is similar to that computed using Cumulus software [29]. Specifically, we computed 3 PD measures using 3 thresholds of: (1) ≥ the maximum; (2) ≤ the minimum; and (3) > mean intensity values of the segmented breast regions, respectively. Third, we computed 6 features defined in [22] namely: 1) MinCDF; 2) MaxCDF; 3) 70%CDF; 4) 30%CDF; 5) Balance; and, 6) Balance2. Fourth, we computed the mean, maximum, minimum, and standard deviation of the directional gradients computed along the x and y axes using a Sobel gradient operator. Fifth, we computed the mean, maximum, minimum, and standard deviation of the gradient magnitude and the mean, maximum, and standard deviation of the gradient direction using a Sobel operator. We also computed the difference in area (number of pixels) between two breasts.

B. Feature Selection and Classification Methodology

After each image feature was computed separately from the left and right breasts of both CC and MLO view mammograms, we computed an absolute subtraction value to represent each asymmetrical feature of two bilateral mammograms. Next, we applied a support vector machine (SVM) based machine learning method to build a new near-term risk model to predict the risk of a woman having mammography detectable cancers during the “current” examination. The SVM was built using a linear kernel to compute the Gram matrix and a sequential minimal optimization (SMO) optimization routine [30]. We applied a leave-one-case-out (LOCO) based validation method to train and test the risk prediction model. In each training and testing cycle, we first applied a standard stepwise regression based feature selection method [22, 23], to automatically select “effective” and “relevant” features from the initial feature pool of 158 features reported in section III.A. This step eliminated redundant image features and reduced the curse of dimensionality or the risk of “overfitting” the classifier during the training procedure. This feature selection process was embedded within each LOCO based cross-validation cycle to avoid case selection bias during the SVM optimization task [31]. The SVM training and testing procedure using the selected features was iteratively executed until all 335 cases in our dataset were tested. Thus, each case has a SVM-generated risk score. A higher score indicates a higher risk (or probability) of having a mammography detectable breast cancer during the “current” examination. We repeated this LOCO cross-validation method 3 times using 3 sets of “prior” examinations (i.e. “prior” #1, #2, and, #3), respectively.

We used an area under a receiver operating characteristic (ROC) curve (AUC) and an adjusted odds ratio (OR) as 2 summary performance measures of the new SVM-based risk prediction models. First, using all SVM model-generated risk scores from one set of “prior” FFDM images, we computed AUC and 95% confidence interval (CI) using a maximum likelihood data analysis based ROC curve fitting program (ROCKIT http://www.-radiology.uchicago.edu/krl/). Second, we sorted the SVM-generated risk scores in ascending order, and selected 5 threshold values to segment all cases into 5 subgroups with an equal number of cases within each subgroup (i.e., 335/5 = 67 cases). We then calculated the adjusted ORs based on a multivariate statistical model using a statistical software package (R version 2.1.1, http://www.r-project.org). A possible OR increasing trend with increasing risk prediction scores was computed and analyzed. The performance results from these assessments were then tabulated and compared.

In order to evaluate “an absolute” prediction accuracy for future clinical applications, we applied an operation threshold at the midpoint of the SVM-generated risk prediction scores. Using this operational threshold, we computed the overall prediction accuracy, as well as positive and negative predictive values of applying our new risk model to the testing dataset.

We also performed a number of additional studies. First, in addition to analyze the trend of the risk scores generated by the new risk models cross 3 “prior” screening cycles, we analyzed the trend of the change of each selected individual image feature values between the positive and negative case groups cross the 3 “prior” screening cycles. For this purpose, we computed mean and standard deviation of the feature values between the 2 groups of positive and negative cases using the images acquired from “prior” #1 to #3, respectively. We then computed the difference of the feature value distributions between two case groups using the student-t test. Finally, we compared 3 computed p-values of each feature using “prior” #1, #2 and #3 images and detected the trend or pattern of the features cross 3 “prior” screening cycles.

Second, given the fact that the positive populations in our dataset were on average approximately 9 years older than the negative populations (Table I), we performed two data analysis tasks using two age-matched criteria of ±1 and ±3 years. We generated two new age-matched image datasets. Using ±3 year and ±1 year matching criterion, we selected 120 and 107 pairs of age-matched positive and negative cases, or 240 and 214 cases, respectively. We then repeated SVM classifier training and testing by applying the same feature selection and LOCO validation method to two new image datasets, respectively.

TABLE I.

Baseline Characteristics of positive (Cancer) and negative (Cancer-Free) Cases in Our Dataset of 335 Cases.

Risk factor	Category	Positive	Negative	P-value from t-test
Age, years	Mean ± SD	60.2±10.6	51.2± 7.4	< 0.01
Density BIRADS, unadjusted				0.01 a
	Almost all fatty tissue	7 (4.4%)	6 (3.4%)
	Scattered fibro-glandular densities	64 (40.3%)	50 (28.4%)
	Heterogeneously dense	83 (52.2%)	107 (60.8%)
	Extremely dense	5 (3.1%)	13 (7.4%)
Family history				0.20
	No family history known	83 (52.2%)	84 (47.7%)
	Cancers in the 1st degree relatives	39 (24.5%)	43 (24.4%)
	Cancers in the 2nd degree relatives	34 (21.4%)	39 (22.2%)
	Cancers in the 3rd degree relatives	3 (1.9%)	10 (5.7%)
Age at menarche, years				0.89
	< 12	26 (16.4%)	27 (15.6%)
	12 to 13	104 (65.4%)	106 (61.3%)
	≥ 14	29 (18.2%)	40 (23.1%)
	Missing b	0	3
Parous		128 (80.5%)	128 (72.7%)	0.09
Age at first birth, years				0.41
	< 30	91 (57.2%)	80 (45.5%)
	≥ 30 or nulliparous	68 (42.8%)	96 (54.5 %)
Menopausal status				< 0.01
	Premenopausal	35 (22.0%)	99 (56.3%)
	Postmenopausal, natural	118 (74.2%)	71 (40.3%)
	Postmenopausal, surgical	3 (1.9%)	4 (2.3%)
	Postmenopausal, unknown	3 (1.9%)	2 (1.1%)

^aAge-adjustment attenuated the difference in density BIRADS ratings between the cancer and “cancer-free” groups (age-adjusted P-value: ±1 year = 0.75; ±3 years = 0.31).

^bMissing values were omitted from the percentage calculations.

Third, in order to analyze the clinical utility of the 3 SVM-based risk models and investigate the risk trend or progression across the 3 “prior” years, we iteratively trained the risk models using the features selected from only one “prior” year (e.g., “Prior” #1), and used these features and LOCO method to train and test the risk models using images of the other two “prior” years (e.g., “Prior” #2 and #3). By repeating this process 3 times (selecting features based on “Prior” #1, #2 and #3, respectively), we analyzed whether there is a progression trend in the risk prediction results from “prior” years 1 to 3 no matter which “prior” image dataset was used as the primary feature selection dataset. We also repeated the experiments using the two new image datasets generated using two age matching criteria within ±1and ±3 years

IV. Results

Table I summaries the baseline characteristics of our image dataset. Except age and menopausal status, there is no significantly difference among other characteristics between positive and negative case groups (p > 0.05). Fig. 4 shows 3 ROC curves computed using SVM-generated risk scores for the 3 sets of “prior” FFDM screening images. The corresponding AUC values, 95% CIs, and the image features selected in more than 50% of 335 LOCO cross-validation runs are listed in Table II. The AUCs show an increasing trend from 0.666 to 0.730 as the time lag between the negative and positive screenings decreases from “prior #3” to “prior #1” screening cycle. The AUC value difference between “prior #1” and “prior #3” cycles is greatest as comparing to the differences between “prior #1” and “prior #2” and between “prior #2” and “prior #3” screening cycles. The combination of features from both views also yielded the highest AUC values for all 3 “prior” years. Namely, for “prior #1,” AUCs obtained using features from CC or MLO view only were 0.656±0.030 and 0.567±0.031, respectively, while using features combined from both views, AUC increased to 0.730±0.027. For “prior #2,” the corresponding AUC values were 0.658±0.029, 0.462±0.031 and 0.710±0.028, respectively. For “prior #3,” the AUC values were 0.529±0.032, 0.649±0.030 and 0.666±0.029, respectively.

Fig. 4.

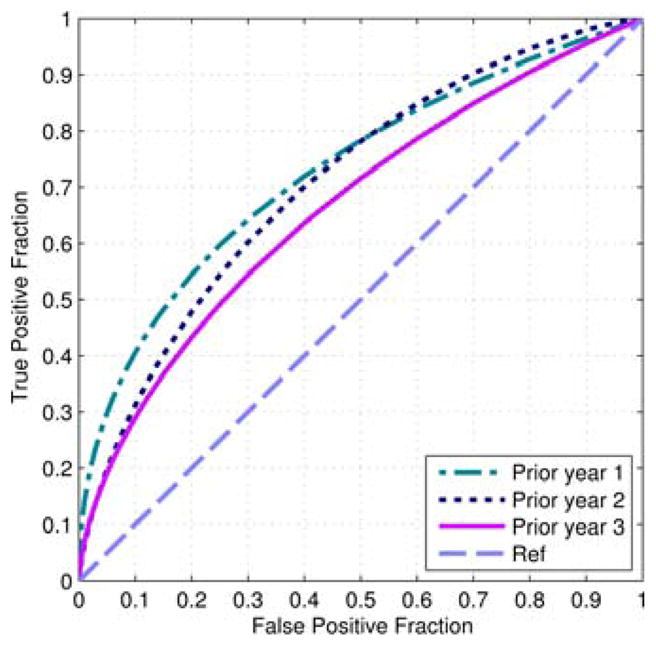
Three ROC curves of applying SVM models to 3 “prior” image sets.

TABLE II.

Computed AUC Values (Estimated Standard Error, SE) and Corresponding 95% Confidence Intervals (CI) When applying the SVM-based Risk Models to “Prior #1, #2 and #3” Image sets Using a Leave-One-case-Out Cross-Validation Method. Features Selected in More Than 50% of the Cross-Validation Runs From the Craniocaudal (CC) and Mediolateral Oblique (MLO) Views are Also Listed

“Prior” screening	AUC (SE)	95% CI	Selected CC and MLO based features in more than 50% of cross-validation runs
1	0.730 (0.027)	[0.674 – 0.781]	CC: CB-SSIM of WLD gradient orientation image (p = 24), CW-SSIM of WLD gradient orientation image (p = 16), max. contrast (whole breast region), mean short run low gray-level emphasis (whole breast region), entropy, std. dev. of gradient direction MLO: CB-CW-SSIM of WLD gradient orientation image (p = 24), mean contrast (whole breast region), PD computed with min. intensity value of segmented breast, min. directional gradient computed along y axis, mean gradient magnitude, mean gradient direction
2	0.710 (0.028)	[0.653 – 0.762]	CC: CB-SSIM of WLD gradient orientation image (p = 24), CW-SSIM of WLD gradient orientation image (p = 8), mean short run high gray-level emphasis (whole breast region), skewness, entropy, balance, min. directional gradient computed along x axis, std. dev. of directional gradient computed along x axis MLO: Balance, min. gradient magnitude
3	0.666 (0.029)	[0.607 – 0.721]	CC: CW-SSIM (dense breast region), mean contrast (dense breast region), max correlation defined in Haralick (dense breast region), max short run low gray-level emphasis (whole breast region), max low gray-level run emphasis (dense breast region), mean short run high gray-level emphasis (dense breast region), PD computed with max intensity value of segmented breast, max. directional gradient computed along x axis, min. directional gradient computed along y axis, std. dev. of directional gradient computed along y axis MLO: CW-SSIM of Gabor phase image (whole breast region), CW-SSIM of WLD gradient orientation image (p = 24), CB-CW-SSIM of WLD gradient orientation image (p = 8), CB-CW-SSIM of WLD gradient orientation image (p = 24), max inverse difference normalized feature (dense breast region), max. low gray-level run emphasis (whole breast region), mean directional gradient computed along y axis

As shown in Table II, a total of 22 and 14 image features were selected with more than 50% frequency in 335 LOCO iterations for the bilateral CC and MLO view images, respectively. By comparing the differences of the computed mean values and p-values for each individual feature between the positive and negative case groups, we observed different trends of the selected features cross 3 “prior” screening cycles. Table III lists 5 example features computed in bilateral CC view images, which represent different trends or patterns including (1) having significant discriminatory power (p < 0.05) in all 3 “prior” screening cycles or (2) only in one or two “prior” screening cycles, as well as (3) without significant discriminatory power in any “prior” screening cycle. Among 36 selected features (listed in Table II), 4 have p < 0.05 in all 3 “prior” cycles, 9 have p < 0.05 in 2 “prior” cycles, 6 have p < 0.05 in “prior” #1, 3 have p < 0.05 in “prior” #2, 4 have p < 0.05 in “prior” #3, and 10 have p > 0.05 in all 3 “prior” cycles. The results indicated that (1) identifying and selecting effective and relevant features is important in developing quantitative image feature analysis based risk models, and (2) although some individual features have poorer discriminatory power (e.g., p > 0.05), a multi-feature based machine learning classifier (e.g., a SVM) enables to use and integrate the selected features to produce substantially higher risk prediction accuracy than using individual image features.

TABLE III.

Characteristics of the Selected Features in Table II and Analysis of Their Changes Over Three “Prior” Screening Cycles

Selected feature	Prior #1 Mean (SD)		Prior #2 Mean (SD)		Prior #3 Mean (SD)		P-value a	P-value b	P-value c
	Positive	Negative	Positive	Negative	Positive	Negative
CW-SSIM (dense breast region)	0.410 (0.037)	0.425 (0.025)	0.408 (0.041)	0.423 (0.044)	0.407 (0.042)	0.427 (0.036)	<0.01	<0.01	<0.01
Maximum short run low GL emphasis (whole breast)	3.06e−4 (4.17e−4)	1.86e−4 (1.71e−4)	2.77e−4 (3.63e−4)	1.99e−4 (2.50e−4)	2.87e−4 (3.98e−4)	3.09e−4 (5.31e−4)	0.001	0.02	0.67
CB-SSIM of WLD gradient orientation image (p = 24)	0.280 (0.073)	0.263 (0.066)	0.275 (0.072)	0.269 (0.080)	0.274 (0.072)	0.274 (0.070)	0.03	0.49	0.95
PD computed with max. intensity of segmented breast	1.25e−4 (2.91e−4)	8.46e−5 (2.86e−4)	1.17e−4 (2.35e−4)	8.34e−5 (1.83e−4)	2.29e−4 (7.72e−4)	5.62e−5 (1.51e−4)	0.20	0.14	<0.01
Standard deviation of directional gradient computed along x axis	222.5 (143.3)	201.4 (128.1)	230.6 (139.4)	194.4 (121.3)	217.6 (147.3)	191.7 (132.2)	0.16	0.01	0.09
Mean contrast (whole breast region)	26.4 (24.1)	22.8 (17.9)	24.1 (20.2)	27.9 (23.6)	29.0 (33.4)	27.1 (25.7)	0.12	0.12	0.55

^aP-value from t-test for positive versus negative cases in “prior” #1 images,

^b”prior” #2 images, and

^c”prior” #3 images.

Table IV summarizes adjusted ORs and the corresponding 95% CIs for 5 subgroups of cases using the risk prediction scores generated by the SVM-based risk models that were trained using “prior” #1, #2 and #3 sets of FFDM images, respectively. The results demonstrate 3 increasing trends in OR values as a function of risk score increases. The results show that ORs increased from 1.00 in subgroup 1 to 5.63 in subgroup 5 (with 95% CI of 2.67–11.87), 1 to 7.43 (with 95% CI of 3.46–15.97), and 1 to 11.1 (with a 95% CI of 4.97–24.93) when applying the SVM-based risk models to “prior” #3, #2 and #1 image sets, respectively, which shows a monotonically increasing trend of the maximum adjusted ORs as time lag between negative and positive FFDM screening gets shorter.

TABLE IV.

Adjusted Odds Ratios (ORs) and 95% Confidence Intervals (CIs) for 5 Subgroups with Increasing Levels of SVM-Generated Risk Scores Trained on the different sets of “Prior” images

“Prior” screening	Sub-group	P and N cases a	Adjusted OR	95% CI	P-value b
1	1	17 – 50	1.00	Baseline	0.009
	2	18 – 49	1.08	[0.50, 2.34]
	3	34 – 33	3.03	[1.46, 6.29]
	4	37 – 30	3.63	[1.75, 7.54]
	5	53 – 14	11.1	[4.97, 24.9]
2	1	17 – 50	1.00	Baseline	0.018
	2	19 – 48	1.16	[0.54, 2.50]
	3	39 – 28	4.10	[1.97, 8.53]
	4	36 – 31	3.42	[1.65, 7.09]
	5	48 – 19	7.43	[3.46, 16.0]
3	1	23 – 47	1.00	Baseline	0.037
	2	19 – 48	0.76	[0.36, 1.58]
	3	33 – 38	1.86	[0.93, 3.72]
	4	34 – 33	1.97	[0.98, 3.95]
	5	50 – 17	5.63	[2.67, 11.9]

^aNumber of P (cancer) and N (cancer free) cases in the corresponding subgroup of cases.

^bP-value to analyze whether the slope of the regression trend line between the risk scores and the adjusted ORs is significantly different from zero.

The results in Table IV show that all the regression slopes (trend lines) between the risk prediction scores and the adjusted ORs are significantly different from zero (p < 0.05), which also indicates an increasing trend between the risk prediction score generated by the SVM-based risk models and actual risk of women having mammography-detectable breast cancer during the “following” 1 to 3 screening cycles.

At an operational threshold at the midpoint of the SVM-generated risk prediction scores, the overall prediction accuracy of the SVM-based risk models was 65.7% namely, 220 of the 335 cases were correctly classified, while 34.3% (115/335) cases were misclassified, which corresponds to a 46.5% (74/159) prediction “sensitivity” at an 83.0% (146/176) prediction “specificity.” The positive predictive value (PPV) of the SVM-based risk model was 71.2% (74/104) and the negative predictive value (NPV) was 63.2% (146/231).

When applying two age-matching datasets (with ±1 and ±3 year matching criteria) to train and test SVM-based risk models, no significant difference was observed in risk prediction performance. For example, when using the image feature computed using “prior #1” images, the AUC values are 0.673±0.036, 0.673±0.034 and 0.730±0.027 with ±1 and ±3 year matching criteria and without age matching, respectively. Although using the image dataset generated without age matching yielded the highest AUC value, the differences are not statistically significant (p > 0.05). The similar results were observed using “prior” #2 and #3 images. As a result, although there is age bias in our image dataset (as shown in Table I), the risk prediction performance levels (e.g., AUC values) using the SVMs trained and tested using the image datasets with and without age-matching are not significantly different.

Table V summarizes the AUC values computed using the third additional study as described in section III-B. The first 3 rows in the Table show AUC values computed using the entire original image dataset with age matching. The AUC values listed in these 3 rows showed that the highest AUC values in three columns of “prior” 1 to “prior” 3 was always obtained by testing on the same “prior” year as the one used for selecting features (as shown by the underline marked AUC values). Furthermore, a decreasing trend in the results was also observed with an increasing number of “prior” years (or time lag between the negative and positive screening). For example, when the features were selected from the training subsets using the “prior” 2 cases, testing on the “prior” 2 cases yielded the highest AUC = 0.710. Testing on the “prior” 1 cases yielded a slightly lower AUC result of 0.684 and a substantially lower result of 0.616 on the “prior” 3 cases. Similar results were observed in the other experiments, which show that there is a positive association between the risk scores generated by our quantitative mammographic image feature difference based risk models with an increasing trend of the near-term risk for having mammography-detectable breast cancer from “prior” #3 to “prior” #1 (the decrease of time lag between the negative and positive screening). A similar trend was also observed using 2 age-matched image datasets (shown in rows 4 to 9 of Table V).

TABLE V.

Computed AUC Values Obtained for Features Selected From One “Prior” Screening Cycle and Tested on All Three “Prior” Screening Cycles Using a Leave-One-case-Out Cross-Validation Method with and Without Age Matching

Age matching criterion	Testing “prior” cycle	Features selected from “prior” screening cycle
		“Prior” 1	“Prior” 2	“Prior” 3
Without age matching	1	0.730	0.684	0.651
	2	0.701	0.710	0.632
	3	0.617	0.616	0.666
±3 years	1	0.677	0.665	0.594
	2	0.586	0.675	0.553
	3	0.472	0.471	0.719
±1 year	1	0.681	0.653	0.556
	2	0.642	0.694	0.556
	3	0.578	0.539	0.650

V. Discussion

This paper reported a new study with a number of unique characteristics. First, unlike our previous studies [10–13] that analyzed solely the feasibility to predict the likelihood of a woman having a cancer detected during the next screening cycle (namely, “prior” #1), this study expanded our analysis to multiple “prior” screening cycles using an image database with 4 sequential FFDM images of 335 women. This is our first study to investigate possible association between the bilateral mammographic image feature changes over time and an increasing risk trend for early cancer detected in the individual women following one or a series of negative screenings. The study results demonstrated an increasing trend in the computed AUCs and adjusted OR values as the time lag between a negative and a positive screening decreases (Tables II and IV). The finding shows an important difference between our near-term risk model, which generates time-dependent risk scores based on the unpredictable variation of mammographic image features of individual women over time, and the existing epidemiology based risk models [36] in which cancer risk factors are either fixed (e.g., BRCA1/2 gene mutation and family history of breast cancer) or predictable (e.g., women’s age increase and breast density decrease as age increase). As a result, the time dependent progressing differences in bilateral mammographic image feature asymmetry have potential to be used in the effective near-term breast cancer risk models, which constitute a fundamental prerequisite to eventually establish a new personalized breast cancer screening paradigm with adaptively adjustable individualized recommendations for screening interval and/or type of imaging modalities to be used.

Second, since breast or mammographic density is widely considered as a strong breast cancer risk factor [32], many mammographic image features have been investigated in previous studies. However, how to identify a small set of optimal image features remains a challenge. In this study, we performed a comprehensive analysis of many promising mammographic density, texture, and structural similarity based features reported in the literature and introduced several new features. Specifically, we expanded our initial feature pool that included conventional and correlation-based structural similarity features (SSIM, CW-SSIM, CB-SSIM, and CB-CW-SSIM) computed on both dense and whole breast regions, respectively, along with many other image features including the multiscale WLD descriptors computed on dense and whole breast regions, and other mammographic density based features (e.g., gray level magnitude and texture). The feature selection results (Tables II and III) indicated that the WLD directional similarity features, RLS, texture and gray level magnitude based features were most effective. In comparison, the structural similarity, GLCM, and Gabor directional similarity features yielded lower performance.

Third, to minimize the potential training and testing bias, we used a LOCO cross-validation method in which a feature selection method was embedded [31] to replace a 10-fold cross-validation method used in our previous studies [10, 13]. The features selected in all 355 LOCO runs were quite consistent (Table II). Although the number of features used in each SVM model is much smaller than 316 features computed in both bilateral CC and MLO view images in the initial feature pool (typically ≤ 15), the SVM used feature set covers features selected from all 4 feature categories as discussed in section III-A, which shows that this feature selection method can take advantages of different categories of features while controlling the actual number of features used to train SVM models. In this study, we also found that SVMs built using the image features computed from the CC view only achieved higher performance than using only the MLO view image features, while combining both CC and MLO view image features has potential to yield further improved risk prediction performance.

Fourth, we observed that the performance of applying our SVM based risk prediction models to “prior” #1 FFDM cases (AUC = 0.730±0.027 and maximum adjusted OR of 11.1) was higher than applying to the FFDM cases acquired in “prior” #2 and #3 screenings with AUC = 0.718±0.028; OR = 7.43 and AUC = 0.666±0.029; OR = 5.63, respectively. Also, although a decreasing trend was observed from “prior” #1 to #3 screenings, the performance difference between “prior” #1 and #2 was higher than between “prior” #2 and #3 screenings. This observation may indicate that the variation of mammographic tissue patterns from the negative to positive screening does not have a linear relationship. The mammographic tissue and density based differences could have a more aggressive development rate as the time lag between negative and positive screening reduces (e.g., the “prior” #1 FFDM images).

Fifth, we optimized 3 sets of SVM based risk models using 3 sets of image features separately selected from 3 sets of “prior” images and compared performance levels of the risk models (Table II and IV). We also selected image features from one set of “prior” images and train/test 3 SVMs using 3 sets of “prior” images (Table V). Since in future clinical application, only one risk model is needed (because we do not have pre-knowledge that a new testing case belongs to which “prior” year model), we should use the retrospectively collected “prior” #1 images as training dataset. As shown in Table V, by using “prior” #1 images as samples to select image features, AUC values from LOCO validation results are 0.730, 0.701 and 0.617 applying to “prior” #1 to #3 images, respectively, which shows greater performance difference (or risk trend) as comparing to the 3 AUC values of 0.730, 0.701 and 0.666 displayed in Table II.

Sixth, although our previous studies [11, 12] showed that the average bilateral mammographic image feature asymmetry level of a recalled benign case group was greater than screening negative (not recalled) case group, we combined the screening negative and recalled benign cases into one cancer-free (negative) group. In this way, one near-term risk model trained using the screening negative (e.g., “prior” #1) images can be directly applied to all “current” screening cases acquired in the clinical practice. We can also assess the potential of applying this new risk model to reduce benign recalls, which is an important issue to improve breast cancer screening efficacy [2].

Last, since all cases were randomly selected by the research staff not involved in any aspect of model development, the average age of women in positive case group is significantly higher than that in negative case group (Table I), which is consistent with screening practice because the age is the strongest breast cancer risk factor [32]. In order to avoid bias in this retrospective study, woman’s age and other clinical information (i.e., breast density rated by BIRADS) were not used in the risk model development. We also performed two age-matched experiments and demonstrated the similar risk increase trend or association as the time lag decreases between the negative and positive screenings (Table V), which indicates that the near-term cancer risk factor based on bilateral mammographic image feature asymmetry is not age-dependent.

In this study, we observed an overall prediction accuracy of 65.7% and a PPV of 71.2% when applying our new model to our testing dataset of 335 cases. From the study result, we may preliminarily explain its potential clinical relevance of applying this new risk model in the future screening environment. We project the result of 46.5% (74/159) prediction “sensitivity” at an 83.0% (146/176) “specificity” level yielded in this study to the population-based screening environment in which we assume a cancer detection yield of 0.5% (5 per 1000 screenings) in the next (non-baseline) annual FFDM screening. In this scenario, our risk model may enable to identify approximately 17.0% (170/1000) “high-risk” women, while the rest of 83.0% (830/1000) are “low-risk” women. Among the 170 “high-risk” women, 3 cancers are expected to be detected during the next annual screening, which constitutes a significantly higher cancer detection yield of 1.8% (3/170) or 3.5 times higher than current 0.5% cancer detection yield.

We recognized that this is a laboratory-based retrospective study with a limited image dataset. Whether results yielded in this study are generalizable to the general screening population has to be validated in future prospective studies. This study also has a number of limitations that need to be better addressed in future studies. First, since this is a new image feature based risk model, similar to all other CAD schemes, the computed image features and reproducibility of model prediction results may be affected by variation of image acquisition and noise. Although our risk model focuses on analysis of bilateral mammographic image feature asymmetry of the same woman and variation of one imaging technologist who performs one examination on one woman is likely to be smaller, how to optimally minimize the negative impact of the potential difference in image acquisition needs to be further investigated in future studies.

Second, the new risk models only included global image features computed on whole breast and/or dense breast regions. Local region based bilateral image features have not been used in this risk model, which could result in further improvements in discriminatory power as suggested by other researchers [16].

Third, we investigated a quantitative image feature analysis based risk prediction model that does not include other known breast cancer risk factors. Fusion of image and non-image features has the potential to further improve risk prediction performance as showed in our previous study [11].

Fourth, although our mammographic image feature based risk models could achieve higher near-term breast cancer risk prediction accuracy than using the existing epidemiology study based breast cancer risk factors or models (e.g., [12]), the positive predictive values at the individual level still remains relatively low and may not be acceptable for use in clinical practice [9]. Further studies to combine image and other genomic or demographic risk factors are needed.

Fifth, from Table I, the number of premenopausal women who have cancer is much fewer than the number of premenopausal women who are cancer-free; thus, it is difficult to perform an age-matched study to analyze the differences in results between pre- and postmenopausal women.

Last, in this preliminary study we only analyzed the features at each individual time point (each “prior” year) and did not examine how the features varied between the different “prior” years (e.g., to compute the absolute subtraction feature between “prior” year 1 and “prior” year 2). Thus, in the future studies, we need to analyze the aspect of change, namely to incorporate the feature changes between different “prior” years.

In summary, in this study we developed a unique near-term breast cancer risk prediction model based on quantitative analysis of bilateral mammographic image feature asymmetry. We also demonstrated the association between changes in mammographic image features and risk for near-term breast cancer development using 3 sets of “prior” FFDM screening examinations. If successful, applying this new risk model will have higher clinical impact. For example, new American Cancer Society guideline has recommended that women 55 years and older should transition to biennial screening or have the opportunity to continue screening annually [33]. Thus, identifying women with significantly higher risk of developing breast cancer in the near-term is important to determine who should be screened annually or biennially in the near-term.