A marginal rank-based inverse normal transformation approach to comparing multiple clinical trial endpoints

Abstract

The increase in incidence of obesity and chronic diseases and their health care costs have raised the importance of quality diet on the health policy agendas. The healthy eating index is an important measure for diet quality which consists of 12 components derived from ratios of dependent variables with distributions hard to specify, measurement errors and excessive zero observations difficult to model parametrically. Hypothesis testing involving data of such nature poses challenges because the widely used multiple comparison procedures such as Hotelling’s T² test and Bonferroni correction may suffer from substantial loss of efficiency. We propose a marginal rank-based inverse normal transformation approach to normalizing the marginal distribution of the data before employing a multivariate test procedure. Extensive simulation was conducted to demonstrate the ability of the proposed approach to adequately control the type I error rate as well as increase the power of the test, with data particularly from non-symmetric or heavy-tailed distributions. The methods are exemplified with data from a dietary intervention study for type I diabetic children.

1. Introduction

The increase in incidence of obesity and chronic diseases and their health care costs have raised the importance of quality diet and healthy eating behavior on the health policy agendas. Healthy diet plays a critical role in promoting long-term health, such as managing diabetes and reducing risk of cardiovascular disease, since many chronic diseases are modifiable with the help of balanced diets and other behavioral changes. The healthy eating index (HEI) [1] is an important measure for diet quality that assesses conformance to federal dietary guidance. The index consists of 12 components, each of which corresponds to a specific food category, and is quantified with a truncated score by rescaling the ratio of the amount of food in a specific category to the amount of energy intake. The HEI data often involve unavoidable measurement errors from inaccurate food recalls, excessive zero observations due to episodic consumption of certain foods, and unjustifiable distribution assumptions on the ratios, all of which make the statistical analysis challenging.

Motivated by a dietary intervention study for children with type 1 diabetes, investigators are interested in testing whether diet quality can be improved through active dietary intervention, as compared to the usual standard care. The commonly used Hotelling’s T² test or Bonferroni’s correction are usually efficient when multivariate normality assumption holds. Violation of the assumptions may result in substantial loss in the power of the tests, especially for data with non-symmetric or heavy-tailed distributions, which is the case in our intervention study.

In the present paper, we propose a marginal rank-based inverse normal transformation approach to comparing multidimensional outcomes such as dietary quality data. The method, as described in Section 2, first normalizes data via an inverse normal transformation of ranks, and then applies an existing test procedure such as the Hotelling’s T² to the transformed data. Extensive simulations were conducted in Section 3 to demonstrate that the proposed rank-based inverse normal transformation method effectively remedies the conservatism of a test in controlling type I error rate caused by skewness and heavy tail density of the distribution, and increases the power of the test for a variety of non-normally distributed data. In Section 4, the proposed rank-based inverse normal transformation method is exemplified with data from the dietary intervention study for type 1 diabetic children. The paper ends with some discussions in Section 5.

2. The rank-based inverse normal transformation approach

Suppose that a clinical trial enrolls n₁ independent subjects randomized to treatment 1 (intervention group) and n₂ independent subjects randomized to treatment 2 (control group). There are K correlated outcome variables of interest (endpoints) to be examined. Let X_ijk represent the measurement on the k^th endpoint for the j^th subject in the i^th group (k=1, … ,K, j=1,…, n_i, i=1,2). The vectors of observations, Xij = (X_ij1, … , X_ijk), are assumed to be independently distributed with expected value E(X_ijk)=μ_ik (i=1,2) and (for simplicity) common variance-covariance matrix defined by, Cov(X_ijk, X_ijk′) = σ_kk′ (k, k′=1,2, … K).

Since higher HEI scores reflect better diet quality, we expect higher HEI scores in the intervention group for all components. To evaluate how diet quality of the children in the intervention group is improved over that in the control group, we test the following hypothesis:

$$H_0:{\mu }_{1k}={\mu }_{2k}\text{for}\text{all}k\text{vs}{H}_a:{\mu }_{1k}>{\mu }_{2k}\text{for}\text{some}k.$$

The proposed marginal rank-based inverse normal transformation method is a way to transform the modified marginal rank of a multivariate sample to its corresponding normal quantile. The main idea is to get the normal scores by converting each observation to its rank among all observations for each variable, then use the information of sample quantile with a fractional offset to adjust the minimum and maximum observations to avoid infinite value after transformation. To be more specific, let r_jk represent the rank of the j^th observation among the N=n₁ + n₂ combined observations, X_11k, … , X_1n1k; X_21k, … , X_2n2k, of the k^th variable from the two treatment groups. Denote by c the value of the fractional offset. The transformed value Yjk for the j^th observation of the k^th variable is then given by eq. (1) below:

$$Y_{jk}={\mathrm{\Phi }}^{-1}(\frac{r_{jk}-c}{N-2c+1})$$ (1)

In the present paper, we will focus on the most commonly used fractional offset value c=3/8 as recommended by Blom [2] in our simulation and data examples. Other fractional offset values are also recommended, such as those in [3] (c = 1/3) and [4] (c = 1/2). Choices in [4] and [5] will not make much difference to the expected normal scores, because the transformed values are virtually linear transformations of Blom’s [2, 3]; see also [6].

The marginal rank-based inverse normal transformation approach then applies a multivariate test procedure to the post-transformation data {Y_ijk} instead of the original data {X_ijk}.

In recent years it has been witnessed more frequent use of inverse normal transformation in genetic association studies [7–15]. A thorough review and further evaluation of its performance is provided in [6] in the context of genetic association studies which presents situations where the transformation gains or loses efficiency in term of type I error and power. It is worth noting that up to date, application of the method has mainly focused on univariate outcome. Its performance remains to be evaluated when used to compare multidimensional outcomes simultaneously between independent groups, such as in a clinical trial setting with multiple primary endpoints.

3. Simulations

We conducted extensive simulations to compare the operating characteristics (type I error and power) of the proposed method to that of two widely used, and typical, test procedures, the Hotelling’s T² and the Bonferroni’s correction, the former being known for its dependence on multivariate normality and the latter for its conservatism in controlling type I error rates.

The Hotelling's T² test statistic for two-sample comparison of their mean vectors is defined as in eq. (2)–(4) below:

$$T^2={({\overline{Y}}_1-{\overline{Y}}_2)}^{\prime }{\{S^2(\frac{1}{n_1}+\frac{1}{n_2})\}}^{-1}({\overline{Y}}_1-{\overline{Y}}_2)$$ (2)

$${\overline{Y}}_i=\frac{1}{n_i}{\sum }_{j=1}^{n_i}{Y}_{ij}$$ (3)

$$S^2=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2}$$ (4)

where Y_ij are vectors with dimension K, $S_1^2$ and $S_2^2$ are the sample variance-covariance matrices calculated from each group. With multivariate normality or large samples, under the null hypothesis of common mean vectors, the two-sample Hotelling's T² statistic has or approximately so a chi-square distribution with K degrees of freedom. For small samples, we can simply transform the two-sample Hotelling's T² statistic into an F-statistic:

$$F=\frac{n_1+n_2-K-1}{k(n_1+n_2-2)}{T}^2~F_{K,n_1+n_2-K-1}$$ (5)

Compared to other procedures, the Bonferroni’s correction procedure is simple to perform but can be very conservative in controlling the type I error rates. It simply applies the two-sample t-test (or other appropriate tests) to each variable separately with a common significant level α/K. The global null hypothesis is rejected if the result of the t-test of any variable comes out significant.

The performance of the proposed marginal rank-based inverse normal transformation method was evaluated with Hotelling’s T² test and Bonferroni’s correction applied to both original data and post-transformation data. Our aim is to demonstrate that a test procedure (Hotelling’s T² test or Bonferroni’s correction) when applied to the transformed data outperforms the same procedure when applied to the original data.

Our simulation studies considered two samples with various dimensions and sizes. For each case, type I error and test power were simulated before and after the data were transformed with inverse normal transformation method. In the simulation, the first sample was assumed to come from the intervention group, and the second from the control group. We considered one-sided t-test for Bonferroni’s correction and assumed that an outcome variable tends to be larger on average in the first sample. A common correlation structure among multiple outcome variables was assumed for the two samples. Data from seven typical multivariate distributions were generated to examine the performance of the methods with various sample sizes and dimensions.

To explore how our method works on symmetric and light-tailed distributions, the first three distributions were selected from the multivariate exponential power distribution family with location parameter Σ, scale parameter _ and shape parameter β. The distributions in this family are all symmetric and their tails become lighter when the shape parameter grows larger. This family of distributions include the multivariate Laplace (MVL) distribution (when β=1), the multivariate normal (MVN) distribution (when β=2) and the multivariate uniform (MVU) distribution (when β → ∞). For the simulation, all three distributions have finite first and second moments, and for the control group, were assumed to be

$$\mu ={(0,0\dots \dots 0)}_k^T\mathrm{\sum }=\left[\begin{array}{ccc}1& \cdots & \rho \\ ⋮& \ddots & ⋮\\ \rho & \cdots & 1\end{array}\right]$$ (6)

Secondly, multivariate gamma (MVG) distributions and multivariate log-normal (MVLN) distributions were considered to explore the robustness of the inverse normal transformation method on distributions with different levels of skewness. The MVG distribution we used is induced by Xijk = U_ijk + U_ij0, k=1,2,…,K, where U_ij0, U_ij1, Uij2,…,Uijk are independent univariate gamma (α,β) variables. The rate parameter β was set to 2 to ensure that the marginal distribution of X is Gamma; the shape parameter α was set to be from 0.1 to 4 to reflect different skewness of the marginal distribution. The MVLN distribution we used is simply an exponential transformation from MVN distribution with location parameter equal to μ, scale parameter to σ *Σ, with σ ranging from 1 to 2 to get different skewness of the marginal distribution.

To evaluate the performance of the inverse normal transformation method on heavy-tailed distributions, we further considered multivariate t (MVT) distributions with 2 degrees of freedom (df=2) and multivariate Cauchy (MVC) distributions that have heavier tail density than MVT distributions.

3.1. Type I error rate

Simulated type I error rates based on 10000 replicates are presented in Table 1.1–1.3 to evaluate whether the proposed marginal inverse normal transformation method improves controllability over type I error rate as compared to Hotelling’s T² test and Bonferroni’s correction, for various scenarios of distributions and sample sizes. The nominal level of significance was set to be 0.05.

Table 1.

Simulated type I error rates

Table 1.1. Symmetric and light-tailed distributions
	ρ=0.1						ρ=0.5				ρ=0.9
Distribution	k	n	Bon	Bon(INT)	T-sq	T-sq(INT)	Bon	Bon(INT)	T-sq	T-sq(INT)	Bon	Bon(INT)	T-sq	T-sq(INT)
Normal	5	30	0.0463	0.0472	0.0496	0.0486	0.0371	0.0378	0.0479	0.0482	0.022	0.0222	0.0514	0.0485
		50	0.0472	0.0489	0.0476	0.0471	0.0411	0.0411	0.0471	0.0481	0.0215	0.022	0.0523	0.0546
		100	0.0488	0.0479	0.0569	0.0568	0.0406	0.0402	0.0491	0.0504	0.0232	0.023	0.0506	0.0499
		200	0.0485	0.048	0.0508	0.0496	0.0414	0.0404	0.0511	0.0519	0.0214	0.0216	0.0509	0.0505
	10	30	0.0489	0.0496	0.0514	0.0489	0.036	0.036	0.0535	0.0549	0.0145	0.0157	0.0516	0.0542
		50	0.0456	0.0453	0.0505	0.0503	0.0388	0.039	0.0498	0.0519	0.0156	0.0151	0.0506	0.0499
		100	0.0505	0.0506	0.0512	0.0527	0.0359	0.036	0.052	0.0514	0.0157	0.0157	0.049	0.0482
		200	0.051	0.051	0.0549	0.0557	0.0417	0.0421	0.0496	0.0485	0.0157	0.0163	0.0474	0.0467
	20	30	0.0463	0.0459	0.0507	0.0494	0.0354	0.0352	0.0518	0.0526	0.0123	0.0128	0.0512	0.0506
		50	0.0428	0.043	0.051	0.0522	0.0338	0.0341	0.0464	0.046	0.0111	0.0117	0.0513	0.0485
		100	0.0486	0.0479	0.0564	0.0557	0.0324	0.0322	0.0501	0.051	0.0115	0.0111	0.0499	0.0519
		200	0.0451	0.0463	0.0502	0.0488	0.0358	0.0352	0.052	0.0525	0.0092	0.0092	0.0486	0.0485
Laplace	5	30	0.0425	0.0494	0.0454	0.0521	0.0368	0.0396	0.0447	0.0488	0.0211	0.0236	0.0415	0.044
		50	0.0477	0.0485	0.046	0.0474	0.0379	0.0398	0.0406	0.0419	0.0216	0.0246	0.0452	0.046
		100	0.047	0.0503	0.0475	0.0488	0.0382	0.0409	0.0459	0.0483	0.0227	0.0253	0.048	0.0481
		200	0.0469	0.049	0.0488	0.0487	0.0403	0.0421	0.0509	0.0493	0.022	0.023	0.0486	0.0498
	10	30	0.0439	0.0485	0.0386	0.0469	0.0349	0.0387	0.0392	0.0422	0.0145	0.0158	0.0383	0.0407
		50	0.0423	0.0443	0.0436	0.0496	0.0356	0.0383	0.0396	0.0444	0.0154	0.016	0.0405	0.0448
		100	0.0492	0.0498	0.0446	0.0465	0.0342	0.0346	0.0476	0.0481	0.0163	0.0166	0.0463	0.0486
		200	0.0493	0.0489	0.0476	0.049	0.0358	0.0367	0.0454	0.0491	0.0143	0.0154	0.0451	0.0469
	20	30	0.0386	0.0479	0.0348	0.0426	0.0307	0.0338	0.0363	0.0408	0.0097	0.0122	0.032	0.035
		50	0.0433	0.0469	0.0371	0.0409	0.0315	0.0351	0.0371	0.0447	0.0095	0.0125	0.0388	0.041
		100	0.0461	0.0488	0.0406	0.0431	0.0319	0.0319	0.0397	0.0422	0.0084	0.01	0.0428	0.0452
		200	0.0475	0.047	0.0445	0.0457	0.0343	0.0361	0.0451	0.0462	0.0081	0.0091	0.0449	0.0452
Uniform	5	30	0.0485	0.0472	0.0516	0.05	0.0471	0.0452	0.0538	0.052	0.0207	0.0212	0.0463	0.0489
		50	0.052	0.0516	0.0522	0.0528	0.0436	0.0421	0.0526	0.053	0.0252	0.0243	0.0526	0.0532
		100	0.0512	0.0505	0.0476	0.0485	0.0408	0.0391	0.05	0.047	0.0227	0.0233	0.0509	0.0525
		200	0.0414	0.0443	0.0504	0.0503	0.0413	0.0407	0.0512	0.052	0.0235	0.0227	0.052	0.0499
	10	30	0.0496	0.0467	0.049	0.0465	0.0386	0.0389	0.0518	0.051	0.0158	0.0154	0.0466	0.0482
		50	0.0516	0.0484	0.0497	0.0477	0.0358	0.0324	0.0499	0.0493	0.0166	0.015	0.0518	0.0498
		100	0.0466	0.0454	0.0477	0.0468	0.039	0.0376	0.0496	0.048	0.0161	0.0155	0.0511	0.0513
		200	0.0519	0.0529	0.0529	0.0529	0.0379	0.0371	0.0532	0.0524	0.0165	0.0169	0.0508	0.0493
	20	30	0.0492	0.0451	0.0473	0.0487	0.0344	0.0319	0.0518	0.0482	0.0139	0.0123	0.0447	0.0506
		50	0.0539	0.0537	0.0524	0.0544	0.033	0.0322	0.0483	0.0498	0.0088	0.0093	0.0451	0.0467
		100	0.0476	0.0469	0.0506	0.0502	0.0356	0.0352	0.0505	0.0505	0.0091	0.0094	0.0495	0.0525
		200	0.0522	0.0508	0.0512	0.0512	0.0324	0.0339	0.0463	0.0481	0.0132	0.0135	0.0496	0.05

Table 1.2. Skewed distributions
Distribution	k	n	Bon	Bon(INT)	T-sq	T-sq(INT)	Distribution	k	n	Bon	Bon(INT)	T-sq	T-sq(INT)
Gamma(α=4)	5	30	0.0421	0.0459	0.0521	0.0506	Lognormal(σ=1)	5	30	0.027	0.0463	0.0319	0.0487
		50	0.0399	0.0419	0.05	0.0483			50	0.0307	0.0458	0.0367	0.0476
		100	0.0356	0.0373	0.0461	0.0452			100	0.036	0.0422	0.0418	0.0492
		200	0.0368	0.0356	0.0471	0.0494			200	0.0427	0.0467	0.0423	0.0531
	10	30	0.0362	0.0386	0.0462	0.045		10	30	0.0193	0.0404	0.0283	0.05
		50	0.0361	0.0385	0.0511	0.0509			50	0.0274	0.0419	0.0345	0.0511
		100	0.0341	0.0382	0.0488	0.0503			100	0.0324	0.0429	0.0375	0.0473
		200	0.0374	0.0379	0.0499	0.0508			200	0.0351	0.0416	0.0393	0.0492
	20	30	0.0305	0.0344	0.0479	0.0478		20	30	0.0158	0.0406	0.0288	0.049
		50	0.0316	0.0334	0.0497	0.051			50	0.0215	0.0459	0.0339	0.0491
		100	0.0325	0.034	0.054	0.0517			100	0.0276	0.0425	0.0365	0.0486
		200	0.0337	0.0342	0.0516	0.0526			200	0.0329	0.0419	0.0422	0.0497
Gamma(α=0.1)	5	30	0.0092	0.0403	0.0143	0.0425	Lognormal(σ=2)	5	30	0.0102	0.0465	0.0132	0.0536
		50	0.018	0.0422	0.0204	0.049			50	0.0115	0.0466	0.0176	0.0507
		100	0.0304	0.0412	0.0311	0.05			100	0.0166	0.046	0.0181	0.0484
		200	0.0348	0.0463	0.0382	0.053			200	0.0211	0.0438	0.0239	0.0505
	10	30	0.006	0.0415	0.0146	0.0428		10	30	0.0054	0.0436	0.0145	0.0499
		50	0.0117	0.0417	0.0209	0.0451			50	0.0084	0.0425	0.0156	0.0512
		100	0.0223	0.0402	0.0299	0.0444			100	0.0126	0.0401	0.0167	0.0481
		200	0.0292	0.0439	0.0381	0.0499			200	0.0154	0.0431	0.022	0.0479
	20	30	0.0017	0.0403	0.0149	0.0367		20	30	0.0025	0.0412	0.0107	0.0538
		50	0.0059	0.0334	0.0184	0.0379			50	0.0045	0.0451	0.0116	0.0514
		100	0.0139	0.0362	0.027	0.0461			100	0.0057	0.0431	0.0167	0.053
		200	0.0201	0.0348	0.0339	0.048			200	0.0093	0.0406	0.0212	0.0492

Table 1.3. Heavy-tailed distributions
Distribution	k	n	Bon	Bon(INT)	T-sq	T-sq(INT)	Distribution	k	n	Bon	Bon(INT)	T-sq	T-sq(INT)
T(df=2)	5	30	0.0309	0.0446	0.033	0.0461	T(df=1)/Cauchy	5	30	0.0103	0.0464	0.0136	0.0448
		50	0.0325	0.047	0.0374	0.051			50	0.0105	0.0448	0.0155	0.0475
		100	0.0311	0.043	0.0387	0.0498			100	0.0109	0.0483	0.0145	0.0478
		200	0.0395	0.048	0.0393	0.049			200	0.011	0.0438	0.0136	0.0459
	10	30	0.0266	0.045	0.031	0.0444		10	30	0.0059	0.0432	0.0179	0.0433
		50	0.0283	0.0453	0.0326	0.0467			50	0.0069	0.0422	0.0146	0.0416
		100	0.0283	0.0438	0.0356	0.0475			100	0.0073	0.0493	0.014	0.0483
		200	0.0296	0.0459	0.0368	0.0504			200	0.0074	0.0506	0.0162	0.0477
	20	30	0.0181	0.0419	0.0311	0.0414		20	30	0.0036	0.0443	0.0187	0.0363
		50	0.0208	0.041	0.0303	0.0455			50	0.004	0.0438	0.0135	0.0389
		100	0.0234	0.0407	0.0329	0.0425			100	0.0052	0.0428	0.0116	0.04
		200	0.0273	0.042	0.0318	0.0487			200	0.0045	0.0414	0.013	0.043

Results in Table 1.1–1.3 clearly demonstrate that for highly skewed or heavy-tailed distributions, the proposed marginal rank-based inverse normal transformation approach effectively remedies the conservatism in controlling type I error rate in that when the original test has a type I error rate away from the nominal level, the transformation approach brings the type I error rate back to be closer to the nominal level. Moreover, the proposed method increases the power of the test for a variety of non-normally distributed data. Table 1.1 also examines the impact of correlation on type I error with data from normal-like distributions (eliminate the potential influence of skewness and tail density). As expected, the Bonferroni’s correction becomes more conservative as the correlation gets larger, which cannot be corrected by the marginal rank-based inverse normal transformation approach. Hotelling’s T² test appears to maintain a type I error around the nominal level as correlation increases when applied to either the original data or the post-transformation test. A closer examination of the results also reveals the following observations concerning type I error rates.

3.1.1 Symmetric and light-tailed distributions with various correlations

Table 1.1 presents simulated type I error rates for MVN, MVL and MVU distributions, all are members of the multivariate exponential power distribution family, and are symmetric or relatively light-tailed. Overall, the improvement in type I error rates for these distributions are minimal from the marginal rank-based inverse normal transformation method.

For multivariate distribution with relatively low correlation among variables (ρ=0.1), all results already yielded a type I error rates very close to nominal level. For this situation, there is no effect of marginal rank-based inverse normal transformation method on either test.

For multivariate distribution with increasing correlation among variables (ρ= 0.5 or 0.9), data from multivariate exponential power distribution family ensure the influence on type I error is solely caused by the high correlation among variables (excluding the potential effect of skewness or heavy tail density). The simulation results show that increasing of correlation among variables will cause greater conservatism on type I error of Bonferroni’s correction, which cannot be fixed by the inverse normal transformation method; On the other hand, increasing correlation among variables doesn’t have obvious impact on type I error of Hotelling’s T² test, neither does the inverse normal transformation method.

3.1.2 Skewed distributions

Simulated type I error rates are presented in Table 1.2 for MVG and MVLN (ρ = 0.3) distributions, both skewed. When applied to the original data both Hotelling’s T² test and Bonferroni’s correction become more conservative as the skewness of the distribution grows. In contrast the proposed marginal rank-based inverse normal transformation method provides a much better control over type I error rates. Furthermore, the improvement of the inverse normal transformation method on controlling type I error becomes more substantial when the skewness of the distributions increases. For MVG distribution with shape parameter α=0.1 (skewness of the marginal distribution is 6.32), the improvement is pretty obvious, especially for small sizes. Before transformation, the type I error rates can be so conservative that they are even below 0.01. After transformation, the type I error rates of Bonferroni’s correction are all greater than 0.03, thus considerably correcting the conservatism with the original data. The type I error rate of Hotelling’s T² test with post-transformation data is satisfactorily close to 0.05. Similar trends were found for MVLN distribution in controlling type I error rates and correcting for conservatism. Note that setting σ=2 for the MVLN yields a skewness of 414.36 for the marginal distribution, extremely high as compared to others. Both Hotelling’s T² and the Bonferroni correction, when applied to the transformed data, produced type I error rates much closer to the nominal level of 0.5. (As demonstrated in 3.1.1, that the type I error of Bonferroni’s correction applied to the transformed data is still lower than the nominal level 0.05 is caused by the non-zero correlation between variables, which cannot be fixed by our proposed method. More results on the influence of correlation on type I error rates are presented in supplemental materials.) The improvement is more obvious for data from more skewed distributions.

3.1.3 Heavy-tailed distributions

For heavy-tailed MVT (ρ = 0.3) distribution with df=2 and MVC (ρ = 0.3) distribution, the simulated type I error rates are tabulated in Table 1.3. Once again, conservatism occurs, especially for Bonferroni’s correction under MVC, and more serious so as the tail density grows larger. When applied the test procedures to the data transformed by the inverse normal transformation, the conservatism was adequately corrected, resulting in type I error rates much closer to the desired nominal level. (Again, extra conservatism of Bonferroni’s correction is caused by the non-zero correlation between variables.) The improvement is seen to be considerable for data from distributions with heavier tail density.

3.2. Power of the Test

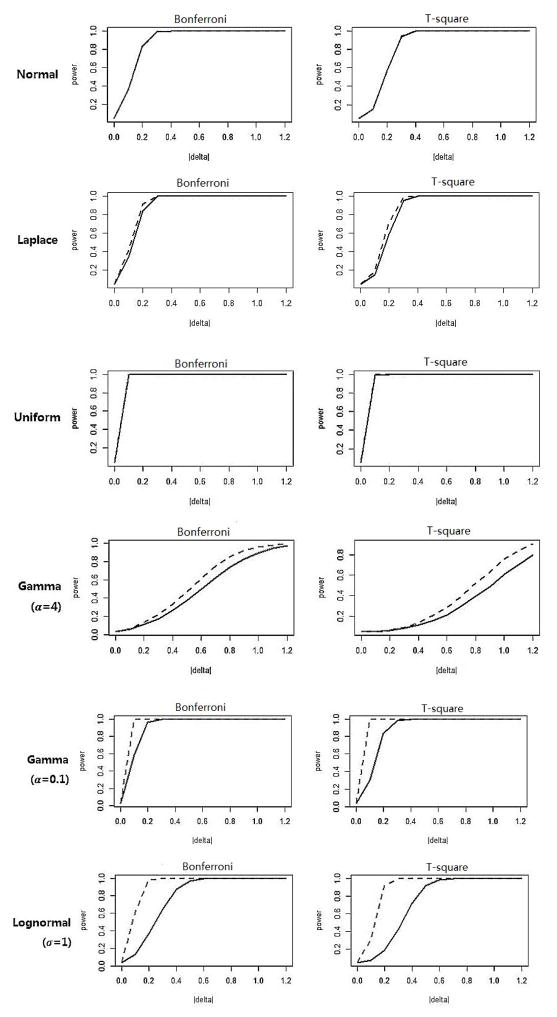
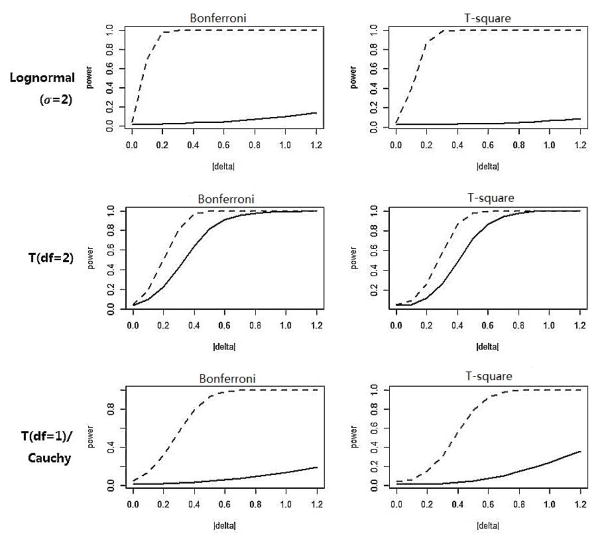
Simulations were conducted to evaluate whether the marginal inverse normal transformation method also maintains satisfactory power as compared to its counterpart (the same test procedure applied to the untransformed data), as well as to other tests. To this end, the alternative distribution was obtained by adding a positive constant value Δ to the corresponding null distribution F₀(x), so that the mean values were elevated but the variances remain unchanged. Again, 10000 Monte Carlo simulations on the grid of Δ∈ [0, 1.2] were conducted. For demonstration, the simulated power under various alternatives is plotted against Δ in Figure 1 for K=10 and sample sizes n₁=n₂=200. For the first three symmetric and light-tailed distributions (normal, Laplace, uniform), the powers of the tests are almost identical.

Figure 1.

Simulated power for tests on data with K=10 and n₁=n₂=200. The solid line indicates the power curve of the test applied on the original data, the dashed line indicates the power curve of the the test applied on the post-transformation data.

For skewed distributions (gamma, lognormal), the power of both tests increases faster to 1 when the test procedures are applied to the transformed data, especially for the ones with larger marginal distribution skewness (gamma with α = 0.01 and lognormal with α = 2). Similar phenomenon was observed for distributions with heavy-tailed density (multivariate T and Cauchy distribution). For example, for the multivariate Cauchy distribution, when the two samples’ mean difference equal to 0.8, both Bonferroni’s correction and Hotelling’s T² produce powers about five times larger than the powers of their corresponding counterparts.

In summary, for all seven representational distributions, the marginal inverse normal transformation method improves or at least maintains the tests’ controllability of type I error and power. Substantial improvement is observed for highly-skewed or heavy-tailed distributions.

4. An example: Comparison of dietary quality data

The CHEF (Cultivating Healthy Environments in Families with Type 1 Diabetes) study [15] is a randomized behavioral intervention trial among children with type 1 diabetes to promote increased consumption of carbohydrates from low glycemic index, nutrient-dense whole foods, and decreased consumption of highly processed carbohydrate-containing foods. The intervention consisted of a number of family-based and group-based sessions, including behavioral techniques and educational content. Dietary data were collected at 6 time points during the 18-month study duration based on 3-day diet records. One primary objective is to compare between the intervention and usual care groups the total scores of the Healthy Eating Index-2005 (HEI2005; an index measuring conformance to the 2005 United States Dietary Guidelines for Americans). At the end of accrual, a total of 136 participants were enrolled into the study with n₁= 66 in the intervention group, and n₂ = 70 in the usual care group.

As aforementioned, the total HEI score is the summation of the scores of the 12 individual components, and simultaneous comparison of part or all of these individual components is also of primary interest. (Indeed, one may argue that comparison of total HEI score is one way to address the issue.) To best demonstrate our methods, we consider comparing between the intervention and usual care the changes of dietary quality from baseline to the last follow-up (18 months) of various subgroups of the HEI components. For a specific food category an HEI component corresponds to, we use the difference in actual ratio rather than its truncation for comparison. Thus for the k^th food category of the j^th subject in the i^th treatment group, we have, in term of the notations in Section 2,

$$X_{\mathit{ijk}}=\frac{\text{dietary}\text{intake}\text{at}18\text{months}}{\text{energy}\text{intake}\text{at}18\text{months}}-\frac{\text{dietary}\text{intake}\text{at}\text{baseline}}{\text{energy}\text{intake}\text{at}\text{baseline}}.$$

Table 2 presents the test results from Hotellin’s T² test and Bonferroni correction applied to the original data and the data after the inverse normal transformation. For the selected combination of food categories, the inverse normal transformation method shows that the intervention significantly (at 5% level of significance) improves the dietary quality over the usual care; in contrast, the usual Hotellin’s T² test and Bonferroni correction both failed to show such significance.

Table 2.

Analysis of Dietary Quality Data

Variable Combination	Bon	Bon (INT)	T-sq	T-sq (INT)
Whole Fruit, Meat and Beans, SOFAAS	0.05375	0.04587	0.07790	0.04835
Vegetables, Meat and Beans, Saturated Fat	0.05375	0.04587	0.10155	0.04999
Sodium, Vegetables, Meat and Beans	0.05375	0.04587	0.09438	0.03482
Whole Fruit, Vegetables, Meat and Beans	0.05375	0.04587	0.07046	0.03057
Vegetables, Meat and Bean, SOFAAS	0.05375	0.04587	0.09511	0.04321

6. Discussion

In clinical trials with the same treatment effect direction on all endpoints, our marginal rank-based inverse normal transformation method provides adequate control over type I error and maintains power as well as or better than its counterpart, especially for distributions with heavy tail or skewness. The method is essentially a nonparametric procedure which is robust against distribution assumptions. Our simulation studies and the dietary quality data example demonstrate that the proposed method was able to detect meaningful significant differences while its counterpart failed to do so.

In this paper, we mainly consider three possible features of a distribution that might cause loss of efficiency of a test: high skewness and heavy tail density of the marginal distributions, and high correlations among variables. Distributions with even only one feature may result in considerable conservatism for some tests on type I error, as well as loss in power. Our simulation focused on investigating whether the proposed inverse normal transformation method can remedy the conservatism of the tests caused by these features from non-normal data, while in the meantime maintain satisfactory power. For distributions with high skewness and/or heavy tail density, we found that the transformation approach effectively remedies the conservatism of a test by bringing the type I error rate substantially closer to the nominal level. When the tests already have type I error close to that of a normal-like distribution, the inverse normal transformation method does not help much in term of either type I error or power. It is worth pointing out that, if the conservatism of the Bonferroni’s correction is caused by high correlation among variables, then the improvement from the transformation approach is minimal.

Our investigation focuses on the popular Hotelling’s T² test and the Bonferroni correction. Other multivariate test procedures developed in the literature can also be applied to the transformed data by the inverse normal transformation. While it remains to be seen on its efficiency, we believe the proposed approach provides a good alternative to the existing procedures. Besides, most distributions we studied in this paper have dependence structure among variables (i.e. copula) similar to the multivariate normal/elliptical distribution. The results of some extra study of marginal rank-based inverse normal transformation method on data from distributions with other dependence structures (such as the Archimedean copula) in some rare extreme cases are not very promising on controlling type I error and maintaining power; results on INT method on Clayton Copula with several marginal distributions can be found in supplemental materials). For distributions other that those we studied, a normal/elliptical distribution test might be necessary before using INT approach.