Reinforcement learning with Marr

Abstract

To many, the poster child for David Marr’s famous three levels of scientific inquiry is reinforcement learning—a computational theory of reward optimization, which readily prescribes algorithmic solutions that evidence striking resemblance to signals found in the brain, suggesting a straightforward neural implementation. Here we review questions that remain open at each level of analysis, concluding that the path forward to their resolution calls for inspiration across levels, rather than a focus on mutual constraints.

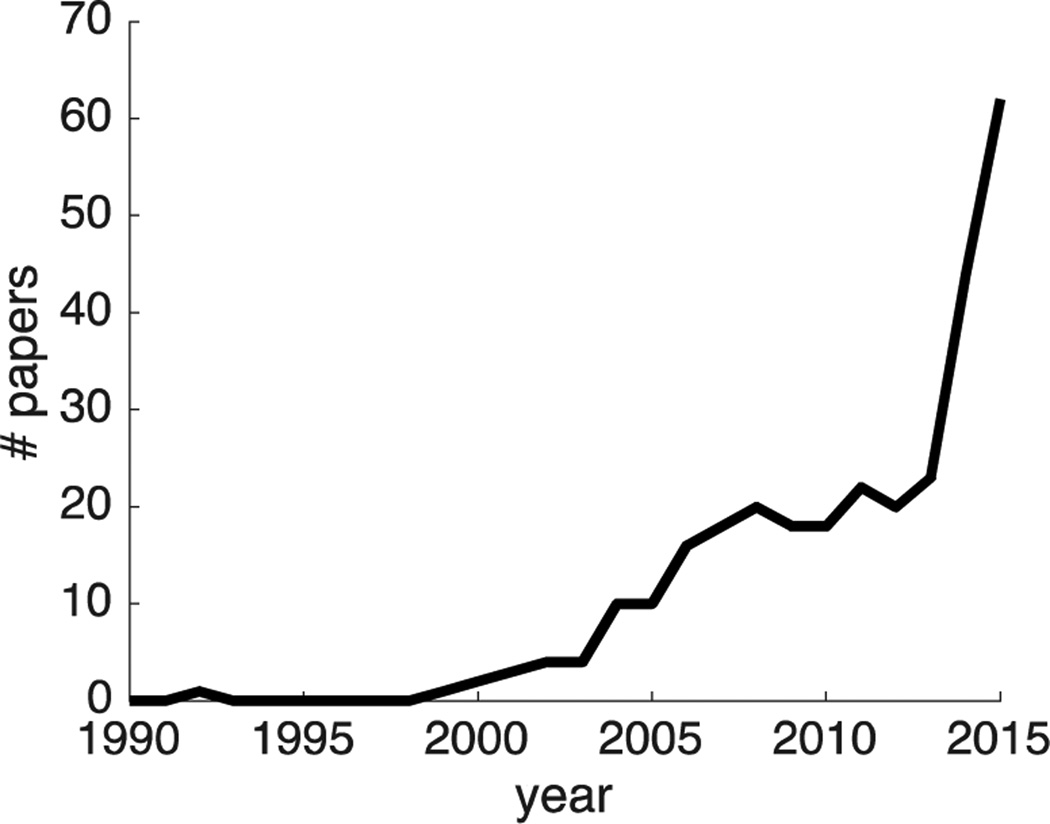
Over the past 25 years, reinforcement learning (RL) has risen from relative obscurity to scientific stardom (Figure 1), now encompassing hundreds of researchers in disciplines as varied as economics, computer science, robotics, psychology, ethology and neuroscience. Arguably this success can be attributed the fact that, as a field, RL straddles all three levels of Marr’s famous framework of scientific inquiry in computational neuroscience [1]. At the computational level, RL defines a small set of normative targets (accurately predicting the sum of future rewards, choosing actions that maximize reward attained, etc.). The algorithmic level—a host of solutions that achieve these normative goals—elegantly derives directly from the definition of the computational targets [2]. In particular, describing decision making problems in terms of Markov (memoryless) decision processes allows for recursive computation of both reward predictions and action values, using local prediction errors [3,4]. Finally, at the implementational level, these algorithms have been closely tied to neural substrates of learning and prediction in the basal ganglia [5–8], and in particular, prediction errors have been linked to dopaminergic signaling in the brain [9–11]. At the risk of drawing boundaries that are sometimes artificial, here we summarize at each of these levels recent findings and current open questions in the field of RL as it is studied in the fields of psychology and neuroscience. Marr’s levels, as an organizing principle, serve to highlight conceptual differences between questions asked at each level, and how findings at one level can inspire progress in another.

Figure 1.

Number of papers containing the term "reinforcement learning” published by Nature Publishing Group between 1990 and 2015

The computational level: The goals of a decision-making system

At the computational level, the basic goal of an agent or a decision-making system is to maximize reward and minimize punishment. Although one might argue whether this is the true goal of agents from an evolutionary perspective, different definitions of reward and punishment allow considerable flexibility. Indeed, work in recent years has elaborated on what constitutes a reward—in addition to the obvious food and shelter (and their associated conditioned reinforcers) there seem to be other forms of reward that are perhaps similarly primary in nature [12]. For instance, ‘curiosity’ can be seen as motivated by the goal of seeking information [13,14], and work on intrinsic motivation [15] has suggested that agents may maximize not only the sum of future rewards, but also the reduction of uncertainty about rewards in the environment [16–18]. Moreover, behavioral results, and corresponding neural recordings in monkeys, have convincingly shown that advance information is valuable in of itself, that is, even if this information cannot be acted upon [19–23].

A related line of work has asked what fictitious, internal rewards an animal (or experimenter) could design, that would assist in ultimately achieving highest fitness in the environment. In this framework of ‘shaping rewards’ the computational-level question is: what is the optimal (pseudo-)reward function with which learning with a specific (possibly limited) set of algorithms would end up maximizing real reward or evolutionary fitness? Recent findings have highlighted that separating the evaluative role of reward functions from their policy-shaping role is beneficial for agents that are bounded (e.g., in terms of the accuracy of their representation of the environment, their capacity for planning, or the learning algorithms they are restricted to use). That is, for different statistics of environments and structure of agents, there exist internal reward functions that lead to faster learning and higher asymptotic behavior, and these are different from the objective reward function [24,25]. By reinforcing behaviors such as exploration or information seeking that are only indirectly related to objective fitness these internal reward functions mitigate the boundedness of the agent [26], although one might argue that this is due to the reward function providing the agent with information (e.g., from past history) that was otherwise unavailable to it. In general, these questions about what constitutes a reward link back to work in the 1940s by Hull [27], with the advent of algorithms and neuroscientific tools that allow precise quantification of the reward value of different events resurrecting hitherto unanswerable questions [28,29]. Moreover, this question now has practical import, for instance in mobile-health applications and other adaptive interventions where an optimal pseudo-reward function can promote adherence to health recommendations (e.g., exercise regimens) towards the long-term goal of improved health [30,31].

One relatively neglected computational-level goal for animals is to define (and, algorithmically, learn) an optimal representation for a task. Different representations of the same task can render it easy (in the case of a small number of Markov states, or with states that allow a smooth value function), hard (when unnecessary detail is represented in the states), verging on intractable (for non-Markov partially-observable representations) or even impossible to solve (if information that is critical to task performance is not included in the representation). Different state representations also give rise to values or policies that generalize differently to new tasks [32]. Therefore, alongside the normative goal of maximizing reward, one might define a (subsidiary) goal of optimizing task representation. Although RL applications often use a predesigned representation, in the animal (and human) kingdom most task representations are not ‘given’ but rather must be learned through experience, raising the algorithmic question of how this computational goal can be achieved [33]. The advent of principled, statistical methods for studying trial-by-trial learning dynamics [34] has allowed critical examination of the early phases of learning, when animals learn the ‘rules of the game’ (or the state representation). Behavioral findings point to a process akin to Bayesian inference in which animals attempt to use observed information to infer the unobservable (latent) causal structure of the task, which is then used to craft task states that accurately describe the task dynamics [35–38]. This ‘representation learning’ process has been linked to memory processes [39,40] as well as neural selective attention mechanisms [41]. As is the case here, computational level questions in RL link intimately with the algorithmic level, to which we now turn.

The algorithmic level: multiple solutions to the decision-making problem

Given the computational goal of maximizing reward, how does a decision-making agent learn which states of the world predict reward, and what actions enable their attainment? RL provides multiple algorithmic solutions to the problem of credit assignment (i.e. correctly assigning credit or laying blame for an outcome on preceding actions or states). Many of these algorithms proceed through the incremental update of state- and action-specific ‘values’ defined as the (discounted) sum of future expected rewards. This update hinges on the calculation of reward prediction errors that compare the predicted value to the current outcome plus expected future value [4].

A major focus in recent years has been uncovering the neural substrates of computations of the economic value of goods [42]. Here, a major algorithmic question is whether reward is indeed evaluated in terms of common currency that allows maximization over bundles of outcomes. This idea, central to economics and especially to the field of neuroeconomics, has found some support [43–45]. However, it is not yet clear that common-currency values are at all necessary in order to achieve optimality. Alternative methods for RL that hail from engineering and computer science search instead in the space of behavioral policies and can find the best policy without computing the reward value of different actions [46–48]. Indeed, recent evidence suggests that prediction error signals in the brain correspond to value differences between actions, which can supply the appropriate gradient for such “policy search” algorithms [49].

In addition to learning values, a ubiquitous aspect of real-world tasks is time: learning when a reward will occur is sometimes as important as learning that it will occur. Indeed, at the heart of RL algorithms is the temporal-difference method that compares predictions across consecutive time points in a task. However, one might argue that time has been mistreated in RL, typically simplified and discretized in order to conform to the Markov assumption [50]. For example, in “tapped delay line” or “serial compound” representations, the passage of time is modeled using discrete sequential states that each accrue a separate value. This redundancy of values requires additional mechanisms to accelerate learning (e.g., eligibility traces [2]), and results in erroneous predictions when outcomes arrive earlier than expected [51]. Moreover, discretizing time raises the question of an appropriate resolution, and is hard-pressed to account for well-established phenomena such as scalar timing noise. Recent work attempting to address these issues proposed distributed temporal representations that span multiple durations, thereby allowing multi-timescale learning in an elegant way [52,53]. Another promising alternative is to model learning using a semi-Markov framework where (continuous) duration is an explicit property of each state, along with value [51,54]. Here learning when things will happen proceeds in parallel to learning what will happen, allowing the temporal representation to adapt to the properties of the task [55], in line with recent work suggesting that neurons in the striatum indeed represent time in a task-relevant, adaptive way [56–58].

More generally, the efficiency and correctness of different RL algorithms depends critically on how states and actions are represented, highlighting again the centrality of (environment-)appropriate representations in trial-and-error learning. For instance, an active area of research seeks to extend RL to address scenarios that have hierarchical structure (e.g., navigating a building or cooking a meal), in which tasks can be subdivided into a series of simpler subtasks (with their associated subgoals) to aid learning and simplify action selection [59,60]. Many real-world tasks have such structure, and moreover, different tasks often share subcomponents. Thus encapsulation of the policy that achieves a particular subgoal (e.g., finding the elevator) allows easy transfer to other tasks that involve this same subgoal, making the learning of novel tasks more efficient. As a result, algorithmic issues involved in parsing a task to useful subcomponents interact with a computational-level goal of not only solving the current task, but also acquiring a useful ‘toolkit’ of policies that can be composed to solve many other tasks. This brings to the fore questions about how a task should be optimally hierarchically decomposed [61], and how to quantify the future benefits of a certain decomposition so they may be weighed against the resulting costs to performance and learning of the current task.

This attempt to divine structure in the learning problem relates more broadly to the necessity of dealing effectively with partially-observable environments where current observations (i.e., perceptual cues) are only probabilistically related to the underlying state that generated them. Optimal RL in partially-observable environments is theoretically possible, although practically intractable [62]. The problem is that the non- Markovian observations are inappropriate as inputs to RL algorithms. Instead, one must compute a Bayesian “belief state” over the underlying states, which does have the Markov property, but is high dimensional and continuous. In practice, approximate solutions have been suggested. For instance, recent work marrying the principles of ‘deep’ representations with RL has exceeded human performance in simple Atari games [63]. This work established the robustness and flexibility of relatively naïve RL methods when learning in the space of abstract, generalized representations.

Finally, nodding to the implementational level is the question of which RL algorithm is implemented in the brain, and the inevitable conclusion that several algorithms may be at play at once. Considering the multiplicity of algorithmic solutions that RL offers, each enjoying different strengths and suffering from its own shortcomings, it may indeed be optimal for learning to proceed via parallel, likely interacting, learning and decision making systems [64,65]. Much recent work has studied the interplay between so-called model-based and model-free modes of RL, capturing and explaining the behavioral consequences of calculating reward predictions using prospection in an internal model of the environment (model-based decision making, also called goal-directed behavior), versus using previously cached values that were learned incrementally through experience (model-free decision making, or habitual behavior) [66–68]. This dualsystems approach is increasingly applied to understanding abnormal behavior as an imbalance in computationally distinct learning systems [39,69,70]. Similarly inspired by the multiplicity of pathways through the basal ganglia, more mechanistic models of action learning have suggested that action values are a product of parallel, balanced, ‘go’ (excitatory) and ‘no-go’ (inhibitory) action selection systems, with recent instantiations of this framework directly implementing model-free RL [71,72]. Such a composite approach to understanding learning processes underlying rich behavior has been attractive in bridging the algorithmic level of RL with its neural implementation, suggesting a mapping from component algorithms to identifiable and distinct neural structures and circuits, as will be discussed below.

The implementational level: Dopamine-dependent learning in the basal ganglia

At the final level of the hierarchy, neuroscientists have had considerable success in mapping functions implied by RL algorithms to neurobiological substrates. Whereas some of the computational and algorithmic questions highlighted above revolved around scaling RL to environments with real-world action and state complexity, the problems at the implementational level arise from the sheer complexity of the neural system, as well as the limitations of different experimental methods.

Much of this work has focused on the basal ganglia, a collection of forebrain nuclei that have long been associated with learning, action selection and decision making. The idea that the basal ganglia implement formal RL algorithms stems from the close correspondence between the responses of midbrain dopamine neurons and the reward prediction-error signal at the heart of RL algorithms [10,73]. The striatum, the input structure of the basal ganglia and a primary target of the widely broadcast dopaminergic neuromodulation, is a prime candidate for learning values and biasing action selection so as to implement RL policies. Indeed, plasticity in cortico-striatal synapses is modulated by dopamine signaling [74], in perfect accord with the effect of reward prediction errors on learning in RL algorithms [75].

Despite the seemingly direct correspondence between RL and the function of the basal ganglia, many aspects of this mapping remain open. Primary among these is how are reward prediction errors computed by dopaminergic neurons. The circuit mechanism that compares predictions associated with past and present states as is necessary for computing temporal-difference prediction errors is the subject of a number of mechanistic models (e.g., [6,76–78]). Many models posit that this computation derives from the difference in sign of direct and indirect inputs from the striatum to dopamine neurons, however, it remains unclear whether these implementations have the necessary fidelity to the known anatomy [79]. Curiously, few models place the burden of the difference computation on local circuitry in dopaminergic areas [80,81].

Alongside this question, the perennial doubt of whether dopamine signals correspond to prediction error signals lingers. Here, the question has evolved from initial skepticism [82,83] that has mostly been put to rest [84], to understanding the heterogeneity of dopaminergic responses to both appetitive and aversive stimuli [85–88]. Recent findings illustrating the complexity of what was once thought to be a scalar signal broadcast widely—a last haven of apparent simplicity in brain signaling—suggest a relatively broad mapping between the algorithmic and implementation levels, preserving the spirit, if not the letter, of RL algorithms. However, some implementations of RL actually require multiple parallel prediction errors (e.g., hierarchical RL [89] and successor representation frameworks [90,91]), suggesting that diversity is perhaps a feature of the system rather than a bug. Still, the relationship between dopamine signals and areas that represent positive prediction errors for aversive stimuli (such as the lateral habenula [92,93]) is unclear. In addition, dopamine release has long been associated with action initiation [94,95] and energization [82], suggesting a functional role for dopamine beyond reward prediction-error signaling. Dopamine aside, much work has focused on the interplay between dual excitatory (so-called ‘go’) and inhibitory (‘no-go’) pathways through the basal ganglia, and whether this architecture can be mapped onto RL action-selection mechanisms [71,96,97]. New optogenetic and imaging techniques in mice now allow the basic tenets of these dual-pathway action-selection models to be directly tested, with sometimes surprising results [98–100].

Finally, the almost-exclusive focus of research in the last two decades on implementations of model-free incremental RL in the basal ganglia and in dopaminergic signaling has recently been challenged by demonstrations of model-based signals in the same neural substrates [66]. While these findings may be taken to suggest that the basal ganglia do not implement RL-based learning and action selection, an alternative interpretation is that model-based and model-free RL methods are not as separated in the brain as lesion studies first suggested [101]. Perhaps the strong appeal of a simple dichotomic implementation of two different algorithmic solutions has led researchers to overly-simplified interpretations of data. Ultimately, the intricate nature of a neural implementation of RL is likely due to the variety of interrelated goals that this system must fulfill in complex environments (optimizing reward, transferring learning to new situations, scaling to the current context, etc.), as well as to the fact that different brain areas function together and not in isolation.

One cautionary tale is that a simple model, while extremely powerful at understanding the functions of different neural substrates, is at the same time limited and should not be expected to explain all aspects of the signaling in these areas. The bidirectional interaction between models and neural findings suggests iterative refinement of the models to widen their scope to more phenomena. Progressively more complex experimental designs that are specifically tailored to asking algorithmic (or even computational level) questions are invaluable in this effort – simple designs can elucidate basic principles, but the reach of the conclusions that one can draw from these experiments should not be overextended. Indeed, optogenetics and other targeted neural manipulations now allow powerful tests of models of RL at the level of neural implementation [102,103]. However, the ability to transiently perturb neural activity with cell-type selectivity and temporal precision during ongoing behavior demands that precise hypotheses be articulated at the mechanistic level, and behavioral paradigms be sensibly exploited.

Conclusion – inspiration across levels

Reinforcement learning is perhaps the poster child of Marr’s levels of analysis – a computational problem that, expressed formally, leads to a host of algorithmic solutions that seem to be implemented in human and animal brains. However, as with many classification schemes, too much emphasis on delineation of levels can distract from the holistic nature of scientific inquiry. As we have shown, the boundaries between the levels are not clear cut, and cross-disciplinary interaction among researchers from different fields and focusing on different levels has only served to advance the field. By some accounts, the different levels should be used to constrain each other – implementational limitations determining which algorithms are feasible, algorithmic (in)efficiencies affecting which computational problems are solvable, etc. However, we feel that this approach is optimistic at best, and misleading at worst – given the degrees of freedom at each level, hard constraints are difficult to derive, and may lead to unnecessary restrictions on creativity at other levels. Instead, to paraphrase Rich Sutton (personal communication, Barbados 2008), Marr’s levels serve scientific inquiry much better when used to inspire one another.

Highlights.

• Reinforcement learning as a field spans all three of Marr’s levels of analysis

• Despite much progress, open questions remain at every level

• These call for multidisciplinary research that crosses boundaries between levels