DISJUNCTIVE NORMAL SHAPE MODELS

Abstract

A novel implicit parametric shape model is proposed for segmentation and analysis of medical images. Functions representing the shape of an object can be approximated as a union of N polytopes. Each polytope is obtained by the intersection of M half-spaces. The shape function can be approximated as a disjunction of conjunctions, using the disjunctive normal form. The shape model is initialized using seed points defined by the user. We define a cost function based on the Chan-Vese energy functional. The model is differentiable, hence, gradient based optimization algorithms are used to find the model parameters.

1. INTRODUCTION

Shape models play an important role in many problems in biomedical imaging such as segmentation and analysis of variability in populations. Shape models can be categorized into several broad categories. First, shape models are either explicit where points on the curve/surface being modeled are directly represented or they are implicit where points on the curve/surface are embedded as a level set of a function. Second, shape models can also be categorized as parametric or non-parametric. A list of points on a 3D surface would be considered a non-parametric explicit model whereas snakes [1] and B-splines [2] are parametric explicit models. The most common implicit shape representation is the level set method [3, 4, 5], which is non-parametric. Parametric, implicit models are rarer and include algebraic curves and surfaces [6, 7]. In this paper, we propose a novel parametric, implicit shape model which we call the Disjunctive Normal Shape Model (DNSM). We approximate the characteristic function of a shape as a union of convex polytopes which themselves are represented as intersections of half-spaces in 2D or 3D. This type of representation of a Boolean function is known as the disjunctive normal form [8]. Next, we convert the disjunctive normal form into a differentiable model by: 1) using DeMorgan’s laws [8] to replace unions with intersections and complements, 2) representing intersections of half spaces as a product of perceptron equations and 3) relaxing the perceptrons used in representing the half-spaces to logistic sigmoid functions. We also take a variational approach and propose a simple cost function based on the Chan-Vese energy that can be used to drive the proposed model for segmenting objects in biomedical images. In this paper, we demonstrate the experimental results of segmentation for different modalities, retinal cells from confocal microscopy images in zebrafish, cardiac CT image, knee MR image, tumors in multimodal MRI brain images. While we focus on the mathematical foundation of the proposed model and its application to data-driven, region-based image segmentation in this paper, it is possible to extend its use to other segmentation scenarios. For instance, given a set of training shapes, prior distributions for the model parameters can be learned and used in segmenting new images. Along with such prior distributions, one can also use DNSMs in conjunction with atlas-based initializations. Finally, the statistics of the model parameters can also be useful in analyzing shape variability.

2. RELATED WORK

The pioneering work of Mumford and Shah [9] exemplifies variational approaches to image segmentation without any explicit ties to a shape model. Methods such as snakes [1] also employ energy minimization in conjunction with a specific shape model. Among such methods, variational image segmentation with level-sets has been a popular choice due to properties such as adaptive topology of level sets which can naturally change during evolution [10, 11]. However, due to their non-parametric nature level-set propagation always has to include a regularization term such as a penalty on curve length/surface area or curvature [12]. On the other hand, regularization is inherent in our model due to the limited amount of representation power afforded by its parametric nature. The proposed DNSM model is implicit and parametric. It has the advantage of being parametric which will can allow us to easily learn statistics and place regularizing priors on the shape model and it has the advantage of being an implicit representation which allows the model to naturally change topology during its evolution if needed. Graph-cut methods have become a popular alternative to level-set based segmentation [13, 14]. The use of interactive segmentation methods have been favored in scenarios when we need to segment a variety of regions. The GrabCut algorithm [15] uses iterative graph-cuts in an interactive fashion. Another popular interactive segmentation method is the random walks [16]. Our work is motivated by the recently proposed logistic disjunctive normal classifier [17].

3. METHODS

Shapes can be represented with their characteristic function f : Rⁿ → B where B = {0, 1}. Let Ω_f = {x ∈ Rⁿ : f(x) = 1} represent the foreground region. The foreground region Ω_f can be approximated as the union of N convex polytopes ${\tilde{\Omega }}_f={\bigcup }_{i=1}^N{P}_i$ where the i^th polytope is the intersection $P_i={\bigcap }_{j=1}^M{H}_{ij}$ of M half-spaces H_ij = {x ∈ Rⁿ : h_ij(x)}. The half-space H_ij, in arbitrary dimensions is defined using the perceptron equation

$$h_{ij}\left(\mathrm{x}\right)=\{\begin{array}{cc}1,\hfill & \sum _{k=0}^n{w}_{ijk}{x}_k\ge 0\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (1)

where w_ijk are the weights. Using Boolean logic any function b : Bⁿ → B can be represented as a disjunction of conjunctions, known as the disjunctive normal form [8]. Hence, we can formulate the characteristic function for ${\tilde{\Omega }}_f$ as

$$\tilde{f}\left(\mathrm{x}\right)=\underset{i=1}{\overset{N}{\bigvee }}\underset{d_i\left(\mathrm{x}\right)}{\underbrace{\left(\underset{j=1}{\overset{M}{\bigwedge }}{h}_{ij}\left(\mathrm{x}\right)\right)}}$$ (2)

such that ${\tilde{\Omega }}_f=\{\mathrm{x}\in {\mathbf{R}}^n:\tilde{f}(\mathrm{x})=1\}$. We would like to convert the disjunctive normal form of the function to a differentiable model. First, the conjunction of binary variables ${\bigwedge }_{j=1}^M{h}_{ij}\left(\mathrm{x}\right)$ is equivalent to the product ${\prod }_{j=1}^M{h}_{ij}\left(\mathrm{x}\right)$. Next, using De Morgan’s laws, we can express the disjunction ${\bigvee }_{i=1}^N{d}_i\left(\mathrm{x}\right)$ as negation of conjunctions, $\neg {\bigwedge }_{i=1}^N\neg d_i\left(\mathrm{x}\right)$, which in turn can be replaced by $1-{\prod }_{i=1}^N(1-d_i(\mathrm{x}\left)\right)$. Finally, we relax the binary perceptrons h_ij(x) to logistic sigmoid functions,

$${\sigma }_{ij}\left(\mathrm{x}\right)=\frac{1}{1+e^{\sum _{k=0}^n{w}_{ijk}{x}_k}}$$ (3)

The resulting approximation to the shape characteristic functions is then given as

$$\widehat{f}\left(\mathrm{x}\right)=1-\prod _{i=1}^N(1-\underset{g_i\left(\mathrm{x}\right)}{\underbrace{\prod _{j=1}^M{\sigma }_{ij}\left(\mathrm{x}\right))}}$$ (4)

3.1. Parameter initialization

The parameters are initialized interactively using inputs from the user. The user defines a set of N seed points, C_i, i = 1 to N, for the foreground object such that they are well distributed in the region of interest. Using these seed points, we initialize the shape model with N polytopes and M = 32 logistic sigmoids per polytope. The polytopes are approximated as spheres with a fixed radius. This approximation is obtained by choosing the parameters as

$$w_{ijk}=\{\begin{array}{cc}\cos {\theta }_p\sin {\varphi }_q,\hfill & k=0\hfill \\ \sin {\theta }_p\sin {\varphi }_q,\hfill & k=1\hfill \\ \cos {\varphi }_q,\hfill & k=2\hfill \\ -(r+C_{i_x}\cos {\theta }_p\sin {\varphi }_q+C_{i_y}\sin {\theta }_p\sin {\varphi }_q+C_{i_z}\cos {\varphi }_q),\hfill & k=3\hfill \end{array}\phantom{\}}$$

for varying values of θ_p, ϕ_q. We choose ${\theta }_p=\frac{\pi }{4}p$ and ${\varphi }_q=\frac{\pi }{4}q$ for p = [1 ⋯ 8] and q = [1 ⋯ 4]. By using different combinations of θ_p and ϕ_q, we get parameters representing different planes.

3.2. Energy Minimization

The cost function based on the Chan-Vese energy segments the image into foreground and background regions.

$$\begin{array}{cc}\hfill E\left(W\right)& ={\int }_{{\Omega }_f}{\left(I\right(\mathrm{x})-c_f)}^{2}d\mathrm{x}+{\int }_{{\Omega }_0}{\left(I\right(\mathrm{x})-c_0)}^{2}d\mathrm{x}\hfill \\ \hfill & ={\int }_{\Omega }{\left(I\right(\mathrm{x})-c_f)}^{2}f\left(\mathrm{x}\right)+{\left(I\right(\mathrm{x})-c_0)}^2(1-f(\mathrm{x}\left)\right)d\mathrm{x}\hfill \end{array}$$ (5)

where c_f and c₀ are the average intensities in the foreground and background region and Ω₀ represents the background region. We fit the model to the data by minimizing this energy with respect to the weights W, using gradient descent. The gradient of the energy function with respect to the weights w_ijk is evaluated as follows:

$$\begin{array}{cc}\hfill \frac{\partial E}{\partial w_{ijk}}& =[{\left(I\right(\mathrm{x})-c_f)}^2-{\left(I\right(\mathrm{x})-c_0)}^2]f{\left(\mathrm{x}\right)}^{\prime }\hfill \\ \hfill f{\left(\mathrm{x}\right)}^{\prime }& =\frac{\partial }{\partial w_{ijk}}\left(1-\prod _{r=1}^N(1-g_r(\mathrm{x}\left)\right)\right)\hfill \\ \hfill & =\left(\prod _{r\ne i}(1-g_r(\mathrm{x}\left)\right)\right)\frac{\partial g_i\left(\mathrm{x}\right)}{\partial w_{ijk}}\hfill \\ \hfill & =\left(\prod _{r\ne i}(1-g_r(\mathrm{x}\left)\right)\right)\left(\prod _{l\ne j}^M{\sigma }_{il}\left(\mathrm{x}\right)\right)\frac{\partial {\sigma }_{ij}\left(\mathrm{x}\right)}{\partial w_{ijk}}\hfill \\ \hfill & =-\left(\prod _{r\ne i}(1-g_r(\mathrm{x}\left)\right)\right)g_i\left(\mathrm{x}\right)(1-{\sigma }_{ij}(\mathrm{x}\left)\right)x_k\hfill \end{array}$$

The update equation is given as $w_{ijk}\leftarrow w_{ijk}-\eta \frac{\partial E}{\partial w_{ijk}}$, where η is the step-size which needs to be tuned for every dataset.

4. RESULTS

We present three experimental setups. We first experimented with confocal images to learn representations of retinal cells in zebrafish embryos. The underlying cell shapes are obtained by smoothing and thresholding the actual image. Segmentation of a cell with increasingly complex models is shown in Figure 1. We first start the segmentation with a single polytope, N = 1 and then refine the segmentation by increasing the number of polytopes. By comparing the segmentations for N = {1 ⋯ 5} polytopes, we see that the DNSM can capture complex boundaries. In this case, N = 3 captures most of the shape information while N = 5 provides almost a perfect representation.

Fig. 1.

Segmentation of retinal cell in zebrafish embryo for N = 1 ⋯ 5.

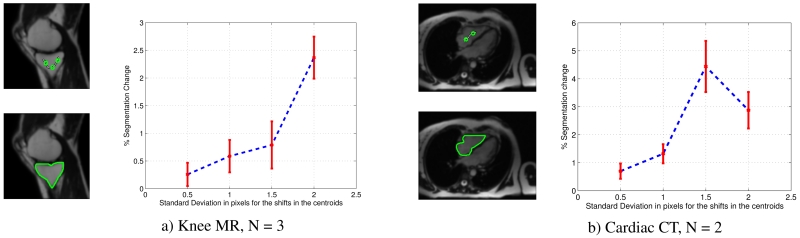
Next, to demonstrate the general applicability of our segmentation, we segment images of different organs from different modalities. The objects of interest in these images are varying in size, shape, and contrast. We need to determine the number of polytopes needed to segment a region. We do this by varying the value of N and calculating the optimized energy of the DNSM, as seen in Figure 2. We see that the energy defined in Equation (5) decreases initially and stabilizes at N = 3, giving us the minimum number of polytopes needed to represent this object. We see in Figure 3(a), that the chosen N fits the knee nicely in terms of complexity. Since our algorithm is interactive, we also studied how sensitive the results are to the selection of seed points. The sensitivity of the placement of seed points is studied for a knee MR image and a CT cardiac image. The user defines a set of N seed points. These seed points are randomly shifted, the displacements are drawn from a normal distribution N(0, σ²). The segmentation is recomputed for the shifted seed points. The change in segmentation is calculated as the ratio of pixels that switched labels to the number of pixels originally labeled as foreground. The original images, segmentations and experimental results are shown in Figure 3. The experimental results are averaged over 20 trials. From the results, we observe that the algorithm is stable and produces a small change in segmentation for small displacements of the seed points.

Fig. 2.

Optimized energy of the shape model for varying N (knee MR image).

Fig. 3.

Sensitivity analysis of segmentation over 20 trials. Left: Seed initialization in green on original 2D image, the segmented region boundary in green, Right: Experimental results. The x-axis represents the standard deviation in pixels for the shift in the centroid positions. The y-axis represents the change in segmentation. The plotted line represents the mean, with error bar indicating the standard deviation.

While the previous results focused on demonstrating how the techniques works and sensitivity analysis, the last experiment is designed to obtain a quantitative assessment of the segmentation accuracy provided by our method. We applied our method to segment tumors in multimodal brain images in the BRATS-2012 dataset. We used the training set images which consists of 20 high grade images and 10 low grade images. The manual segmentations given had three intensity levels: 1 for edema, 2 for active tumor, and 0 for everything else. We only segmented the active tumor regions in this paper and used N = 5, M = 32. The visual segmentation results for the high grade and low grade real images are shown in Figure 4. Quantitative results for comparing the segmentation with automatic [18, 19] and semiautomatic [20] methods in [21] is given in Table 1. We use the DICE coefficients to compute the similarity between the segmented shape and the manual segmentations. We see that the performance of our algorithm is comparable to the methods in the challenge for high grade images, while it outperforms them for low grade images.

Fig. 4.

Segmentation results for the BRATS 2012 dataset. Left: input weighted image (α T2 + β T1), manual segmentation (gray - edema, white - tumor), segmentation overlay on input image, Right: segmentation overlay on manual segmentation. The Top row shows an example of a high grade (HG) image and the bottom row shows an example of a low grade (LG) image.

Table 1.

Quantitative comparison of DICE coefficients for segmentation of the BRATS-2012 dataset (HG - high grade images, LG - low grade images).

Method	HG	LG
Zikic et al. [18]	0.71	0.62
Bauer et al. [19] (with std. dev.)	0.62±0.27	0.49±0.26
Hamamci et al.[20]	0.73	0.71
Our method	0.73	0.74

5. CONCLUSION

We proposed a novel implicit parametric shape model and an associated energy to segment objects of interest in medical images. The proposed method provides good segmentations even on low grade tumor images. We examined the sensitivity of the algorithm to the placement of seeds needed to represent a region. We also illustrated how we can capture complex boundaries by increasing the number of polytopes in the model for segmentation. A local Chan-Vese model can be used to further improve our segmentation results. One direction for future work is fully automated segmentation using the proposed model and atlas based initializations for tasks such as prostate or hippocampus segmentation. While we have used conjunctions of half-spaces in our current work, more application specific shape primitives will be considered in future work. Finally, given a set of training shapes, prior distributions for the model parameters can be learned and used as a regularization term in segmenting new images.