Abstract
The patch-clamp technique is a powerful and versatile method to investigate the cystic fibrosis transmem-brane conductance regulator (CFTR) Cl− channel, its malfunction in disease and modulation by small molecules. Here, we discuss how the molecular behaviour of CFTR is investigated using high-resolution single-channel recording and kinetic analyses of channel gating. We review methods used to quantify how cystic fibrosis (CF) mutants perturb the biophysical properties and regulation of CFTR. By explaining the relationship between macroscopic and single-channel currents, we demonstrate how single-channel data provide molecular explanations for changes in CFTR-mediated transepithelial ion transport elicited by CF mutants.
Keywords: ATP-binding cassette transporter, CFTR, chloride ion channel, patch-clamp technique, single-channel recording, channel gating
1. Introduction
The patch-clamp technique (1, 2) is the method of choice to investigate the molecular and cellular behaviour of the cystic fibrosis transmembrane conductance regulator (CFTR) Cl− channel. In combination with site-directed mutagenesis, this technique has provided invaluable insight into the relationship between CFTR structure and function, the malfunction of CFTR in disease and the use of small molecules to restore channel activity to cystic fibrosis (CF) mutants.
Because the CFTR Cl− channel is regulated by cAMP-dependent phosphorylation and cycles of ATP binding and hydrolysis (3–5), CFTR is best studied using the excised inside-out configuration of the patch-clamp technique, which provides ready access to the intracellular side of the cell membrane. Here, we discuss how excised inside-out membrane patches are used to investigate the single-channel activity of wild-type CFTR and CF mutants. For information about the theory and operation of the patch-clamp technique, we refer the reader to Single Channel Recording (6), the reference book for this electrophysiological technique. Because the scope of this chapter is limited, we refer the reader to (7) and (8) for further information about how other configurations of the patch-clamp technique are used to investigate the CFTR Cl− channel. For excellent reviews of the application of single-channel recording to the study of CFTR, see (9–12). For a review of strategies to investigate small molecules that modulate CFTR function, see (13).
2. Use of Excised Membrane Patches to Study the CFTR Cl− Channel
Critical to the success of patch-clamp studies of CFTR are appropriate cells, solutions and reagents. These are required to optimize seal formation and ensure the detection of CFTR and not other ion channels.
2.1. Cells and CFTR Expression
For studies of CFTR structure and function, we prefer to heterologously express CFTR variants in mammalian cells that do not routinely express CFTR and possess no cAMP-stimulated Cl− channels. Our cell lines of choice for single-channel recording are C127 (a mouse mammary epithelial cell line), CHO and NIH 3T3 cells (14–16). However, a wide variety of mammalian and non-mammalian cells have been used to heterologously express CFTR. Because of the difficulty of forming seals on epithelial cells, we do not routinely use native epithelial cells for structure–function studies. However, we recognize fully that it is important to use polarized epithelia to understand the physiological role of CFTR and its regulation.
The choice of cell lines is particularly pertinent for studies of CF mutants. Many CF mutants, including the most common F508del-CFTR, disrupt the processing of CFTR protein and its delivery to the cell surface (17). Because the trafficking defect of F508del-CFTR is attenuated in Xenopus oocytes (18), it is preferable to test the effects of CF mutants on CFTR function using mammalian cells (see below, Section 6).
In general, higher rates of seal formation can be achieved using stable cell lines rather than cells transiently expressing CFTR. Stable cell lines may provide more uniform levels of CFTR expression than transiently transfected cells. However, it is not practical to use stable cell lines to study CFTR variants especially when one has to study many mutants. When transient expression is necessary, we co-transfect CHO cells with plasmids encoding CFTR and green fluorescent protein (GFP) and then use a microscope equipped with epi-fluorescence to select fluorescent cells for study. In this way, data acquisition is efficient. For an example of this approach, see (19).
2.2. Experimental Solutions
To magnify the small single-channel current amplitude of CFTR, we routinely impose a large Cl− concentration gradient across membrane patches by replacing most Cl− in the pipette (extra-cellular) solution with the impermeant anion aspartate. However, it is important to ensure that there is a high concentration of electrolytes (~150 mM salt) in the bath (intracellular) solution to optimize channel gating (20). To prevent the activation of contaminating currents, we manipulate the composition of bath and pipette solutions. For example, we routinely use the large impermeant cation N-methyl-D-glucamine (NMDG) to preclude contaminating Na+ and K+ currents. To stop the activation of Ca2+-activated Cl− currents, we use CsEGTA to buffer [Ca2+]free to ≤ 10 nM in the bath solution.
We routinely use the biological buffer TES or HEPES to buffer the pH of solutions. However, when present in the bath solution, many large anions such as biological buffers (e.g. MOPS and TES) cause a flickery block of CFTR that is most pronounced at strong negative voltages. Indeed, because tricine failed to block CFTR when present in the bath solution, Ishihara and Welsh (21) recommend the use of tricine-buffered bath solutions to study the conductance of CFTR (for discussion, see (21)).
Because CFTR Cl− channels are regulated by cAMP-dependent phosphorylation and cycles of ATP binding and hydrolysis (3, 4), the bath solution must contain Mg2+. To facilitate seal formation, the pipette solution contains millimolar Ca2+. A sample of the composition of our bath and pipette solutions is listed below (mM):
Bath solution: 140 NMDG, 3 MgCl2, 1 CsEGTA, 10 TES, pH 7.3 with 1 M HCl ([Cl−]Int, 147 mM; [Ca2+]free, ≤ 10 nM; osmolarity, 281 ± 0.5 mOsm (n = 4)).
Pipette solution: 140 NMDG, 5 CaCl2, 2 MgSO4, 140 aspartic acid, 10 TES, pH 7.3 with 1 M Tris ([Cl−]Ext, 10 mM; osmolarity, 279 ± 0.5 mOsm (n = 7)).
These bath and pipette solutions are not suitable for studies of the CFTR Cl− channel using other configurations of the patch-clamp technique. For advice on the preparation of solutions for whole-cell and cell-attached recording, see (7) and (8).
We prepare bath and pipette solutions frequently (≤2 weeks) and store them at +4°C when not in use. To verify that solutions have been prepared correctly, we check their osmolarity.
2.3. Reagents
Phosphorylation of the R domain by protein kinase A (PKA) is critical for activation of the CFTR Cl− channel (3, 22). In experiments using the excised inside-out configuration of the patch-clamp technique, the most effective way to phosphorylate CFTR at PKA consensus sites is to add the catalytic subunit of PKA (75–200 nM) to the intracellular solution in the presence of millimolar concentrations of ATP. Because of wide variation of the specific activity of commercial PKA and likely association of protein phophatases in the membrane patch, channel activation upon addition of PKA and ATP can vary greatly. Therefore, it is important to ensure the full activation of CFTR by continuously monitoring channel activity in real time. Even when CFTR is fully activated, phosphorylated CFTR is particularly susceptible to channel rundown. Rundown of CFTR is both phosphorylation-dependent and phosphorylation-independent. To prevent phosphorylation-dependent rundown, we add the catalytic subunit of PKA to all bath solutions. However, this does not guarantee the stability of channel activity. In our experience, PKA purified from bovine heart is more efficacious than recombinant PKA at stimulating CFTR and preventing rundown. However, batch-to-batch variation in the efficacy of PKA is not unknown. If rundown of CFTR becomes a problem, we recommend that the supply of PKA is checked first.
Once wild-type CFTR is phosphorylated, opening and closing (gating) are controlled by ATP. We store aliquots of ATP disodium salt desiccated at −20°C. For experiments, we prepare a stock of ATP (100–275 mM) dissolved in bath solution. Alternatively, the stock can be stored at −80°C for months. Other nucleotides are similarly stored and prepared. It is important to note that ATP acidifies the bath solution. We therefore add the required amount of NaOH to all bath solutions to readjust pH to 7.3. (Because CFTR channel gating is modulated by intracellular pH (23), we routinely test all agents added to the bath solution for their effects on pH).
CFTR modulators are prepared in their specified solvents, aliquoted into appropriate amounts and stored at −20°C in the dark. We test the effects of all solvents on the activity of CFTR in the absence of any modulator. Our preferred solvent is DMSO, which is without effect on the single-channel activity of CFTR (14). We draw the readers’ attention to the fact that tetrahydrofuran, a widely used solvent in chemistry, weakly potentiates CFTR channel gating (24).
Clean solutions are a prerequisite for successful seal formation. Therefore, we filter all bath and pipette solutions using 0.45 μm disposable filters prior to use.
3. Distinguishing CFTR Cl− Channels and Currents
Using cells expressing recombinant CFTR and the recording conditions described above, CFTR will likely be the dominant channel observed. However, it is feasible that contaminating channels (e.g. large conductance anion channels or outwardly rectifying Cl− channels) will be observed. For this reason, the experimenter must be able to identify with confidence the CFTR Cl− channel.
CFTR Cl− channels have a number of defining characteristics:
They have a small single-channel conductance (6–10 pS).
The current–voltage (I–V) relationship is linear (but see (25)).
They are selective for anions over cations.
The anion permeability sequence is Br− ≥ Cl− > I−.
They show time- and voltage-independent gating behaviour.
Channel activity is strictly dependent on cAMP-dependent phosphorylation and intracellular ATP (for discussion, see (3–5)).
CFTR channels open in bursts that typically last for hundreds of millisecond. Within each burst, one can easily discern short flickery closures with a lifetime <10 ms. These flickery closings show voltage dependence with fewer flickers observed at positive membrane voltages (25, 26).
The dependence of CFTR Cl− currents on intracellular ATP is the simplest way to discriminate CFTR from other ion channels. Withdrawal of ATP from the bath solution rapidly decreases the activity of CFTR Cl− channels (27). Although it was reported that this deactivation of CFTR can be irreversible (28), in most studies, one can readily reopen the closed channels. It is also important to note that a finite open probability is observed even in the absence of ATP (29).
4. Quantification of Single-Channel Conductance
Single-channel conductance is a measure of the ease with which ions flow through an ion channel. To determine single-channel conductance, the relationship between single-channel current amplitude (i) and voltage (V) is plotted over a range of voltages (e.g. −100 to +100 mV). If this relationship (termed a current–voltage (I–V) relationship) obeys Ohm’s law, then the data can be fit with a first-order regression function and the slope of the line is a measure of single-channel conductance.
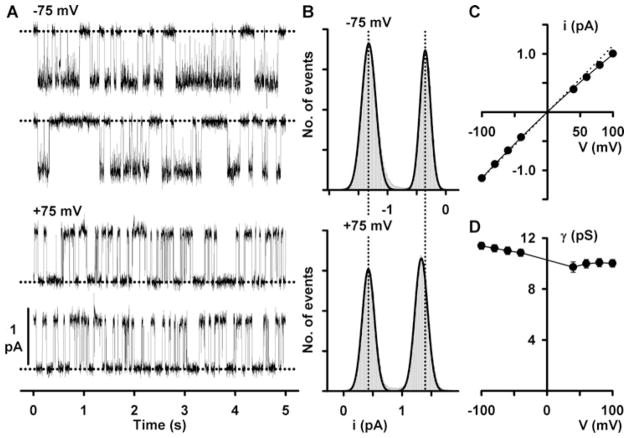
To measure single-channel current amplitude, a current amplitude histogram is created from a single-channel record (Fig. 27.1) and fitted with a two-component Gaussian function (assuming that the membrane patch contains just one active channel) to determine the mean closed and open levels. The difference between the closed and open levels in the current amplitude histogram provides a measure of single-channel current amplitude (Fig. 27.1). To avoid errors when measuring single-channel current amplitude, it is important to avoid baseline drift, current “glitches” and distorted channel openings.
Fig. 27.1. Effect of voltage on the single-channel activity of CFTR.
(a) Representative recordings of a single CFTR Cl− channel at −75 mV (top) and +75 mV (bottom) in an excised inside-out membrane patch. The membrane patch was bathed in symmetrical 147 mM NMDGCl solutions, and ATP (1 mM) and PKA (75 nM) were continuously present in the intracellular solution. Dotted lines indicate the closed channel state. Downward and upward deflections correspond to channel openings at −75 and +75 mV, respectively. Each trace is 10 s long. (b) Single-channel current amplitude histograms of a single CFTR Cl− channel at the indicated voltages. At −75 mV (top), the closed channel amplitude is shown on the right, whereas at +75 mV (bottom), the closed channel amplitude is shown on the left. The continuous lines represent the fit of Gaussian distributions to the data. The vertical dotted lines indicate the positions of the open and closed levels at −75 mV. (c) Single-channel I–V relationship of CFTR. Data are means ± SEM (n = 10); error bars are smaller than symbol size. The dotted line shows the I–V relationship of an ion channel with ohmic behaviour. (d) Relationship between chord conductance and voltage for the data shown in (c). For further information, see Cai et al. (25). Modified from The Journal of General Physiology 2003, 122:605–620. Copyright 2003 The Rockefeller University Press.
Figure 27.1c demonstrates that the single-channel I–V relationship of wild-type CFTR weakly inwardly rectifies at positive voltages. To quantify this rectification, we measured chord conductance. Chord conductance is determined by dividing unitary current by the difference between the applied voltage and the reversal potential. Figure 27.1d demonstrates that the chord conductance of wild-type CFTR decreases from 11.4 ± 0.3 pS at −100 mV to 10.0 ± 0.3 pS at +100 mV (n = 10; P < 0.01).
As discussed further below in Section 6, measurement of single-channel conductance is used to identify CF mutations that disrupt Cl− ion flow through the CFTR pore. An alternative method to generate an I–V relationship is to use a voltage ramp. This method for generating an I–V relationship can be used in an excised inside-out membrane patch containing large numbers of active channels (25, 30) or one single channel locked in an open state (31). Summation of single-channel currents generated by a voltage ramp protocol can also be used to demonstrate the relationship between single-channel and macroscopic currents (25).
Discussion of studies of CFTR permeation is beyond the scope of this chapter. We therefore refer the reader to (9) and (11) for excellent overviews of how to measure anion permeation through the CFTR pore.
5. Quantification of CFTR Channel Gating
The methods used to analyse CFTR channel gating are standard electrophysiological procedures. They involve a number of steps: (i) single-channel current amplitude is determined using a current amplitude histogram, as described above in Section 4; (ii) single-channel currents are idealized (e.g. Fig. 27.2); (iii) channel opening and closing events are detected and an events list is generated; (iv) open and closed times are plotted as either survivor functions or dwell-time histograms; and (v) exponential functions or probability density functions (pdfs) are fitted to estimate mean dwell times (e.g. Fig. 27.2). These procedures can be performed using standard data analysis software (e.g. IGOR Pro, WaveMetrics Inc., Lake Oswego, OR, USA), electrophysiological data analysis software (e.g. pCLAMP, Molecular Devices, Sunnyvale, CA, USA) or data analysis software custom designed to analyse CFTR channel gating (32). The theory and operation of the different steps involved in the analysis of single-channel data are thoroughly explained in the book Single Channel Recording (6). Here, we provide specific guidance on the analysis of CFTR channel gating.
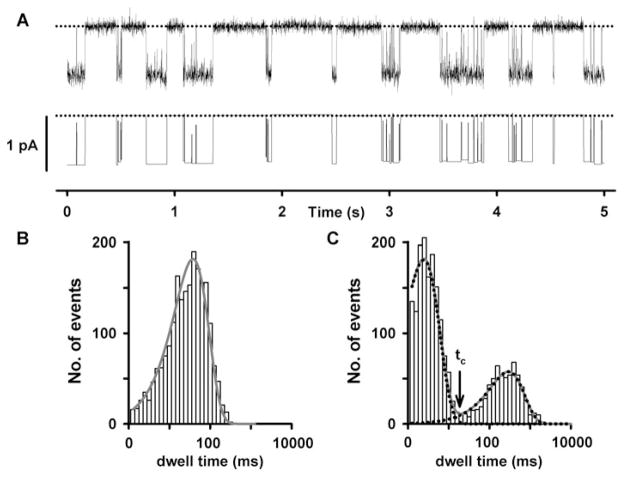
Fig. 27.2. Dwell-time analysis of a single CFTR Cl− channel.
(a) Representative recording of a single wild-type human CFTR Cl− channel (top) and its corresponding idealized record (bottom). Dotted lines indicate where the channel is closed and downward deflections correspond to channel openings. For further information, see Cai et al. (37). (b, c) Representative open and closed dwell-time histograms, respectively. For the open-time histogram (b), the continuous line is the fit of a one-component exponential function. For the closed dwell-time histogram, the continuous line is the fit of a two-component exponential function. Dotted lines show the individual components of the exponential functions. The vertical arrow indicates the delimiter time (tc) that separates interburst closures from intraburst closures.
For accurate analysis of CFTR channel gating, it is important to acquire data that are kinetically stable over time. It is therefore critical to prevent the rundown of CFTR Cl− channels in excised inside-out membrane patches (see above Section 2.3). Experimentalists therefore need to be vigilant when acquiring single-channel data to ensure that data are kinetically stable and suitable for gating analysis.
5.1. Determination of Number of Active Channels and Open Probability
The number (N) of active CFTR Cl− channels in a membrane patch is determined from the maximum number of channels simultaneously observed using experimental conditions that maximally stimulate CFTR. For wild-type CFTR, we use enough PKA (i.e. 75 nM) to strongly phosphorylate CFTR and saturating concentrations of ATP (i.e. > 1 mM). However, for CF mutants, these conditions are not sufficient to maximally stimulate channel activity. We therefore use PKA (75 nM), ATP (1 mM) and a CFTR potentiator (e.g. phloxine B (5 μM)) (33) to maximally stimulate channel activity. Sometimes non-hydrolysable ATP analogues (e.g. AMP-PNP) (34) or the inorganic phosphate analogue (pyrophosphate) (35) are used to “lock open” channels to more easily detect the maximum number of active channels. For three reasons, these agents should be used with great care: (i) the effects of these agents are not completely reversible; (ii) AMP-PNP may not be effective at physiological temperatures; and (iii) pyrophosphate itself opens CFTR (36).
Open probability (Po) is a measure of the average fraction of time that a channel is open. The open probability of CFTR can be calculated using the area under each peak in the current amplitude histogram and the number of active channels (N) as follows:
| [1] |
The area under each peak is calculated using either the relevant macro in data analysis software or the parameters are obtained from the Gaussian function fitted to each peak.
Alternatively, Po is calculated from open- and closed-times as follows:
| [2] |
where N is the number of active channels, Ttot is the total time analysed, T1 is the time that one or more channels are open, T2 is the time two or more channels are open and so on. In practice, we prefer not to use membrane patches that contain more than five active channels to determine Po. In the case of uncertainty about the number of active channels, apparent open probability (NPo) is calculated as follows:
| [3] |
A major problem with using the maximum number of channel openings to determine the number of active channels in the membrane patch is that this method inevitably grossly overestimates Po when Po values are very low. Based on probability theorem, when a channel has a Po of 0.01 in a membrane patch with two active channels, the probability that both channels are simultaneously open is 0.0001. Thus, for every 1,000 s recorded from this membrane patch, the two channels will be simultaneously open for only 1 s. If instead the membrane patch contained 100 channels each with a Po of 0.01, it would be impossible to observe the simultaneous openings of all 100 channels. This technical issue is especially relevant when dealing with CF mutants that profoundly disrupt CFTR channel gating (e.g. G551D-CFTR (37, 38)).
To minimize errors when counting the number of active channels, we record channel activity for prolonged periods (i.e. >30 min including multiple interventions) and verify that recordings are of sufficient length to ascertain the correct number of active channels. To verify that recordings are of sufficient length, we use the method of Venglarik et al. (39). The time required to observe at least one single all-open event is (3τ o/N)/(Po)N where τo is the open-time constant; N the number of active channels; and Po the open probability.
5.2. Dwell-Time Analysis
Once CFTR is phosphorylated by PKA, channel gating is controlled by ATP (5). Thus, the main goal of kinetic analysis is to quantify ATP-dependent transitions to understand how ATP gates the channel, how CF mutants perturb gating and how small molecules rescue gating. However, not all gating transitions observed in single-channel records of CFTR are ATP dependent. It is therefore important to identify, with confidence, the ATP-dependent gating transitions of CFTR.
CFTR channel gating is characterized by bursts of channel openings that are separated by long closures in the range of hundreds of milliseconds to seconds (Figs. 27.1a and 27.2a). As discussed above (Section 4), each individual open burst is interrupted by brief closures in the range of several to tens of milliseconds (Figs. 27.1a and 27.2a). Because the ATP-independent brief flickery closures occur on a time scale much shorter than that of the ATP-dependent transitions, these fast events can be removed by filtering heavily the single-channel records prior to their analysis. For example, Zeltwanger et al. (40) demonstrated that filtering data at 25 Hz prior to digitization had little effect on ATP-dependent channel gating, but nearly completely eliminated brief, flickery closures. However, it should be recognized that heavy filtering causes a loss of information about the kinetics of channel gating. Researchers need to consider carefully the optimal settings for filtering and digitizing their data to address their particular research question. In general, we find that filtering and digitizing single-channel records of wild-type CFTR at 500 Hz and 5 kHz, respectively, provides good resolution of brief, flickery closures interrupting channel openings while still permitting clear separation of intraburst closures from interburst closures. Researchers also need to consider carefully the potential effects of their recording conditions on the single-channel activity of CFTR. Besides phosphorylation and ATP, the duration of CFTR channel openings and closings is influenced by temperature (41), voltage (25) and intracellular pH (23).
Temporal information about CFTR channel gating can be extracted from single-channel records by analysing the lifetimes (dwell times) of channel openings and closings. Because open and closed times are distributed exponentially, the time constant (τ ) of the distribution can be derived from the exponential probability density function. We routinely plot dwell-time histograms using a logarithmic abscissa for dwell time and a linear ordinate for number of observations. With a logarithmic dwell-time scale, the exponential decay is transformed into a bell-shaped curve. As a result, the number of component exponential functions required to fit the data is readily determined from visual inspection of the dwell-time histogram. For example, in Fig. 27.2b the open-time histogram of wild-type CFTR is best described by a one-component exponential function, the open-time constant (τo). By contrast, the closed-time histogram is best described by a two-component exponential function (Fig. 27.2c). In Fig. 27.2c, the tall bell-shaped peak on the left, which represents the brief flickery closures interrupting bursts of channel openings, is described by a fast closed-time constant (τcf). The short bell-shaped peak on the right, which represents the long closures separating bursts, is described by a slow closed-time constant (τcs) (Fig. 27.2c).
An alternative approach to analyse the open- and closed-times of CFTR is to construct a “survivor plot” (42). The events list is sorted according to time interval from shortest to longest. Then, the events list is plotted against the upper cumulative probability that a particular opening or closing event will last at least time t. Note that the probability of an event being the shortest in the events list is 1. The resulting curve is fitted with one-or more-component exponential functions to determine the time constants that describe the open- and closed-times of CFTR.
The principal difficulty with dwell-time analysis of CFTR channel gating is the requirement of a large amount of data to generate histograms that convincingly describe open- and closed-times under specific experimental conditions. Because CFTR gates slowly, this is sometimes an almost insurmountable challenge particularly when studying CFTR inhibition by small molecules or CF mutants that perturb channel gating. Of note, using a dephosphorylation-resistant CFTR mutant, Bompadre et al. (29, 43) were able to acquire sufficient gating transitions to demonstrate the presence of multiple open- and closed-time components.
5.3. Burst Analysis
Burst analysis of CFTR channel gating depends critically on the choice of the burst delimiter (tc, the time that separates inter-burst closures from intraburst closures). Theoretically, closures with a duration longer than tc are classified as interburst closures, whereas closures shorter than tc are classified as intraburst closures (Fig. 27.2c). We determine tc by inspecting closed-time histograms to select the time value at the nadir separating the two closed-time populations, representing the brief, flickery closures interrupting bursts of channel openings and the prolonged closures separating bursts of channel openings, respectively (Fig. 27.2c). The large difference between the fast and slow time constants argues that errors caused by the misclassification of bursts should be rare. An alternative approach to inspecting experimental fits to closed-time distributions of CFTR constructs studied under the experimental conditions in question is to empirically choose tc using the method of Sigurdson et al. (44). Using either method, the calculated mean open and closed times (or burst duration and interburst interval) for wild-type human CFTR are in the range of hundreds of milliseconds in the presence of saturating [ATP]. Based on the idea that the hydrolysis cycle of CFTR is coupled to the gating cycle of the channel, the data predict that the ATP hydrolysis rate of CFTR is ~1/s as indeed reported by Li et al. (45).
Because CFTR Cl− channels seldom open in the absence of ATP, it is also possible to calculate burst duration by relaxation analysis of macroscopic currents. In excised inside-out membrane patches containing hundreds of CFTR Cl− channels, the sudden withdrawal of ATP causes an exponential decay of the macroscopic current. The relaxation time constant determined by fit-ting the time course of current decay with a single exponential function is a measure of CFTR’s burst duration (46). Relaxation analysis of macroscopic current can also be used to identify two populations of channel openings, when the exponential decay of macroscopic current is better fit by a double exponential function, resulting in two different relaxation time constants (e.g. (36); Fig. 27.3b). Furthermore, relaxation analysis of macroscopic currents is the method of choice to analyse the burst duration of CFTR constructs that open for tens of hundreds of seconds (e.g. E1371Q, (47)), because it can be very difficult to collect sufficient gating transitions for microscopic kinetic analysis of channel gating for these CFTR constructs.
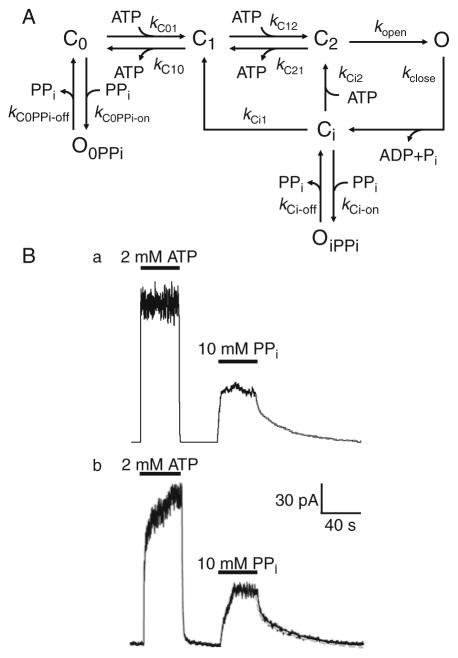
Fig. 27.3. Monte Carlo simulation of the effects of pyrophosphate on macroscopic CFTR Cl− currents.
(a) A kinetic model to simulate the reopening of macroscopic CFTR Cl− currents induced by pyrophosphate (PPi). In this model, C0, C1 and C2 are closed states with zero, one and two ATP molecule bound, respectively, while Ci is an intermediate closed state sensitive to PPi. O, OiPPi and O0PPi are open states, with the latter two open states induced by PPi binding from the Ci and C0 states, respectively. The rate constants describing transitions between the different states are shown. (b) Comparison of (a) simulated and (b) experimental macroscopic current data for the PPi-induced reopening of CFTR channels after removal of ATP. Double exponential fits to current relaxations after removal of PPi are denoted by continuous and dashed lines in the simulated (a) and experimental (b) data, respectively. Time constants: (a) τ fast: 1.7 s, τ slow: 32.1 s; (b) τ fast: 1.9 s, τ slow: 32.4 s. For further information, see (36). Modified from The Journal of General Physiology 2009, 133:405–419. Copyright 2009 The Rockefeller University Press.
5.4. Analysing Recordings from Multiple Channels to Obtain Kinetic Information
In Sections 5.2 and 5.3, we describe the analytical methods applicable to excised inside-out membrane patches containing a single active CFTR Cl− channel. Unfortunately, such recordings are the exception, not the norm.
To circumvent this obstacle, Csanády (32) developed a suite of software programs to extract kinetic constants from membrane patches containing multiple active channels. Although this custom-designed software is powerful and rapid, it uses simple kinetic models to analyse CFTR channel gating and cannot accommodate cyclic gating schemes. Nevertheless, this methodology has been used successfully in several studies of CFTR channel gating (e.g. 38, 47–49).
5.5. Data Interpretation and Mathematical Modelling
Dwell-time analysis of the ATP dependence of CFTR channel gating provides invaluable insight into the molecular mechanisms that control Cl− flow through the CFTR pore. For example, Zeltwanger et al. (40) demonstrated that the closed-time histogram of CFTR contains a negative exponential component, suggesting that CFTR channel gating is not in equilibrium. Based on this result, the authors proposed a gating scheme with an irreversible step to describe CFTR channel gating (40). This gating scheme argues that ATP hydrolysis is strictly coupled to channel gating in the CFTR Cl− channel.
Many studies have explored the relationship between ATP concentration and the kinetics of CFTR channel gating (e.g. 33, 40, 48). The data reveal that mean open time varies little with ATP concentration. By contrast, the relationship between mean closed time and ATP concentration is described by a simple Michaelis–Menten function. This result suggests that the rate-limiting step of channel opening occurs after ATP binding. Taken together, the data argue that CFTR channel gating is described by a cyclic scheme, which includes the irreversible step of ATP hydrolysis (47, 48, 50).
With these fundamental concepts of CFTR channel gating, it is possible to use Monte Carlo simulation to investigate whether kinetic models describe accurately CFTR channel gating. For this purpose, simulated single-channel currents based on a given kinetic model are analysed in an identical manner to real data. Then, the simulated and real data are compared to explore the underlying kinetic model. Importantly, Monte Carlo simulation can be used to model channel behaviour at steady state and during responses to channel modulators (Fig. 27.3). For examples of this type of approach, see (32, 38, 50).
In a given model, the mean lifetime of state i, MLT(i) is calculated using the equation:
| [4] |
The actual lifetime of state i at each individual transition, LT(i) is calculated as follows:
| [5] |
where MLT(i) is the mean lifetime of state i and Rnd is a random number between 0 and 1.
The probability that the channel moves from state i to one of the adjacent states (state j) is calculated using the equation:
| [6] |
where kij is the rate constant from state i to state j (51).
To determine which state the channel moves to next after leaving state i, a computer-generated random number between 0 and 1 is used to calculate the cumulative distribution of the probabilities of leaving the state by the different possible pathways. To calculate the duration of individual open (or closed) events, the calculated lifetimes (durations) (LT(i)) of sequential states in the open (or closed) configurations are summed (52).
Next, the simulated current recordings are analysed in an identical way to the experimental data. Importantly, Monte Carlo simulation of CFTR channel gating provides values for the identical parameters used to analyse real data (e.g. relaxation time constants; Fig. 27.3). the results of this analysis of simulated data are then compared with the analysis of the real experimental data to statistically test the validity of a kinetic model of CFTR channel gating. Successful reproduction of multiple different experimental data by a single kinetic model would validate a particular model of CFTR channel gating.
6. Characterization of CF Mutants
To date, more than 1,600 mutations have been identified in the CFTR gene (www.genet.sickkids.on.ca/). Mutations associated with CF and CFTR-related disorders (e.g. congenital bilateral absence of the vas deferens and chronic pancreatitis) cause a loss of CFTR function by a number of different mechanisms: defective protein production (class I), defective protein processing (class II), defective regulation (class III), defective conductance (class IV) and reduced protein synthesis (class V) (53, 54). Electrophysiological techniques, including single-channel recording, play an important role in elucidating how CF mutants cause a loss of CFTR function and evaluating their severity.
The first step when characterizing a novel CF mutant is to learn whether the mutant generates functional CFTR Cl− channels and quantify the magnitude of residual cAMP-stimulated Cl− current relative to that of wild-type CFTR. For this purpose, either the Ussing chamber technique can be used to measure cAMP-stimulated apical membrane Cl− currents (see below, Section 7) or the whole-cell configuration of the patch-clamp technique is used to measure macroscopic currents in mammalian cells heterologously expressing wild-type or mutant CFTR. Once the whole-cell configuration is achieved, the cAMP agonist forskolin (10 μM) and the membrane-permeant cAMP analogue 8-(4-chlorophenylthio)adenosine 3′:5′-cyclic monophosphate (CPT-cAMP; 100 μM) are used to stimulate CFTR Cl− currents (55, 56). The mean current density is calculated using the mean current (maximal current minus leak current) and the membrane capacitance (obtained from the amplifier after compensation of the capacitance current). By averaging mean current density in many cells, it is possible to determine the average mean current density for the CF mutant.
Mean macroscopic CFTR Cl− current (I) is the product of the number of CFTR Cl− channels present in the cell membrane (N), the current flowing through an individual CFTR Cl− channel (i) and the open probability of CFTR (Po):
| [7] |
Thus, a decrease in macroscopic CFTR Cl− current might be caused by a decrease in N (classes I, II and V), i (class IV), Po (class III) or a combination of several classes.
For CF mutants that only affect the number of functional channels in the plasma membrane (classes I, II and V), the comparison of whole-cell cAMP-stimulated current density between wild-type and mutant CFTR provides a quantitative assessment of the severity of the mutation. However, these mutations might be associated with other functional defects. For example, the most common CF mutation, F508del, not only disrupts the biosynthesis of CFTR protein (17), but also perturbs the gating behaviour of any mutant channels that reach the cell membrane (57). To identify and quantify these defects, single-channel recording using excised inside-out membrane patches is the method of choice.
The effect of a CF mutation on the cell surface expression of CFTR can be estimated from the magnitude of macroscopic whole-cell current. The ratio of the whole-cell CFTR Cl− current of a CF mutant relative to that of wild-type CFTR (Imutant/IWT) is proportional to the ratio of the number of channels at the cells surface (Nmutant/NWT). If single-channel conductance and Po are unaltered by the CF mutant, then we can obtain the decrease in number of channels at the cell surface from the ratio of whole-cell CFTR Cl− current (Imutant/IWT).
In Section 5, we emphasized the importance of kinetically stable recordings for kinetic analyses of CFTR channel gating and the need to guard against phosphorylation-dependent and -independent channel rundown. We find that phosphorylation-independent rundown is especially a problem when studying some CF mutants. For example, the F508del-CFTR Cl− channel is structurally unstable, especially at elevated temperatures (58). At room temperature, F508del-CFTR is stable in excised inside-out membrane patches and amendable to study. By contrast, at 37°C, F508del-CFTR is thermally sensitive, leading to the rundown of many F508del-CFTR Cl− channels within 10 min of patch excision. This rundown of F508del-CFTR at elevated temperatures constrains the design of experimental protocols to investigate the mechanism of dysfunction of F508del-CFTR and its rescue by small molecules.
The third most common CF mutation G551D is a classic example of a class III mutation because it completely abrogates the ATP-dependence of CFTR channel gating (38). Because of the extremely low Po of G551D-CFTR, the methods used to study the single-channel behaviour of wild-type CFTR require some refinement before they can be applied to G551D-CFTR. As discussed above in Section 5.1 it is very difficult to determine accurately the Po of these channels. The issue resides in the difficulty of properly assessing the number of channels (N) present in the membrane patch given the very low Po of G551D-CFTR. Although it is tempting to assume that N is equivalent to the number of simultaneous channel openings observed, in the case of G551D-CFTR, this can lead to a gross underestimation of N. Because G551D-CFTR Cl− channels remain closed most of the time, different channel openings will likely originate from different channels present in the same membrane patch (for a discussion of this problem, see (51)). To have any possibility of estimating N for G551D-CFTR, the experimental conditions should be adjusted to maximize Po. One manoeuvre that has been successfully employed with wild-type CFTR is to use either AMP-PNP or pyrophosphate, which locks open channels for many seconds. Unfortunately, these reagents do not always work with CF mutants. For example, AMP-PNP and pyrophosphate fail to lock-open the G551D-CFTR Cl− channel (37, 38).
A compromise method used by Bompadre et al. (38) offers a rough estimation of the Po of G551D-CFTR. When CHO cells are transfected with the same amount of cDNA encoding wild-type or G551D-CFTR, Western blot analysis demonstrates that the cells produce similar amounts of band C (mature protein) for the two constructs (38). This indicates that similar numbers of wild-type and G551D-CFTR Cl− channels are present at the cell surface. In excised inside-out membrane patches, the mean current amplitude is measured after the channels are activated by PKA and ATP. Because neither the number of active channels nor the single-channel current amplitude is altered by the G551D mutation, the mean current amplitude directly reflects Po. To obtain accurate results with this type of experiment, it is necessary to perform many experiments to overcome the variation observed between individual membrane patches.
One potential solution to the technical difficulty of measuring the Po of CF mutants like G551D is to use CFTR potentiators or ATP analogues to augment robustly channel gating and hence Po. However, so far in the literature, the most efficacious small molecules only increase the Po of G551D-CFTR by ~ 5-fold, far lower than the ~100-fold decrease of Po caused by this mutation. More efficacious CFTR potentiators are urgently required to address properly this issue.
Class IV mutations (defective conductance) attenuate the flow of Cl− ions through the channel pore. As a result, these CF mutants (e.g. R334W and R347P; 59, 60) diminish single-channel current amplitude (i). To determine single-channel conductance, we measure single-channel current amplitude using current amplitude histograms, construct an I–V relationship and measure the slope of the line. In the case of some CF mutants, individual channel openings might not be easily resolvable. In this case, a large Cl− concentration gradient and strong membrane hyperpolarization might be employed to magnify CFTR Cl− currents. (Note that very tight seals are essential to successfully perform this type of experiment.) If individual channel openings remain unresolvable, non-stationary noise analysis might be applied to macroscopic CFTR Cl− currents to calculate single-channel current amplitude. For this purpose, a low concentration of PKA (e.g. 20 nM) is used to slow the rate of channel activation (61).
It is important to note that if a CF mutation alters the single-channel conductance of CFTR, this does not necessarily mean that the affected amino acid residue lines the channel pore. A CF mutation might alter the packing of transmembrane segments and hence, the overall structure of the pore, causing a diminution of single-channel conductance. Consideration should also be given to the possibility that a CF mutation might reduce current flow through the CFTR pore by altering anion selectivity. For example, the CF mutant, P99L, in the first transmembrane segment attenuated the single-channel conductance (wild-type, 7.72 ± 0.22 pS (means ± SEM; n = 4); P99L, 4.97 ± 0.24 pS (n = 5, p < 0.0001)) and altered the anion selectivity sequence (wild-type, Br− = Cl− > I−; P99L, Br− ≥ Cl− ≥I−) (62). However, Akabas et al. (63) concluded that P99 does not line the CFTR pore because the site-directed mutant P99C did not react with methanethiosulfonate reagents. This example illustrates the types of studies required to elucidate how an individual CF mutant disrupts CFTR function. As indicated earlier in this section, a single mutation might perturb CFTR function by multiple mechanisms. Experimentalists should be alert to this possibility.
7. Relationship Between Single-Channel and Macroscopic Behaviour
Studies of the biosynthesis and single-channel behaviour of CF mutants provide a molecular explanation for the greatly diminished cAMP-activated CFTR Cl− current generated by CF mutants in the apical membrane of epithelia. Apical CFTR Cl−current (ICFTR(apical)) is determined by the product of the number of CFTR Cl− channels in the apical membrane (N), the current amplitude (i) of an individual CFTR Cl− channel and probability (Po) that a single CFTR Cl− channel is open: ICFTR(apical) = N × i × Po (Eq. 7). Using biochemical (N) and functional (i and Po) data, the apical CFTR Cl− current generated by F508del-CFTR and other CF-associated mutants can be predicted. For this purpose, N, i and Po are set to 100% for wild-type CFTR. Table 27.1 compares the predicted values of N × i × Po with the observed values of ICFTR(apical) measured in FRT epithelia for F508del-CFTR and the CF mutants, R117H, G551D and P574H, which disrupt CFTR function by different mechanisms (33, 37, 59, 64, 65). Despite possible errors resulting from (i) the assumption that N is equivalent to the amount of fully glycosylated protein (band C) and (ii) the supposition that the Po of CFTR Cl− channels in the apical membrane of FRT epithelia is equivalent to values measured in excised membrane patches from non-polarized cells, the predicted values agree well with the measured data. The predicted values for F508del-CFTR also concur with values calculated by other investigators (e.g. Haws et al. (66), 2% and Wang et al. (67), 0.4%). Thus, the data demonstrate that biochemical and functional studies may be used to provide a molecular explanation for the quantitative decrease in cAMP-activated CFTR Cl− current generated by CF-associated mutants.
Table 27.1.
Comparison of predicted apical membrane Cl− current and measured cAMP-activated apical membrane Cl− current for wild-type and mutant CFTRs
| CFTR | N (%) | i (%) | Po (%) | N × i × Po (%) | ICFTR (apical) (%) |
|---|---|---|---|---|---|
| Wild-type | 100 | 100 | 100 | 100 | 100 |
| F508del | 4 | 100 | 30 | 1.2 | 0 |
| G551D | 100 | 100 | 2.5 | 2.5 | 1.5 |
| R117H | 100 | 86 | 28 | 24 | 15 |
| P574H | 15 | 100 | 139 | 21.1 | 17 |
N, the number of Cl− channels in the apical membrane; i, single-channel current amplitude; Po, open probability; N × i × Po, the predicted apical membrane Cl− current; ICFTR (apical), measured cAMP-activated apical membrane Cl− current. Based on Cai & Sheppard (33), the Po of F508del was set to 30% that of wild-type CFTR. Other details as in Sheppard and Ostedgaard (68). For G551D data, N and ICFTR values are from Bompadre et al. (38) and Zegarra-Moran et al. (64), while i and Po data are from Cai et al. (37). Modified, with permission, from Sheppard and Ostedgaard (68).
8. Conclusions
The excised inside-out configuration of the patch-clamp technique is the premier method to investigate the CFTR Cl− channel. The technique offers researchers the unique opportunity to observe in real-time conformational changes in a single membrane protein driven by cycles of ATP binding and hydrolysis. The sheer excitement of such experiments more than compensates for the technical challenges of high-resolution recording of single CFTR Cl− channels.
Acknowledgments
We thank our laboratory colleagues for valuable discussions. During the preparation of this chapter, DN Sheppard was supported by the Cystic Fibrosis Trust and EuroCareCF (LSHM-CT-2005-018932), Y Sohma by a Grant-in-Aid for Scientific Research (C) from the Japan Society for the Promotion of Science (JSPS) (19590215 and 22590212) and T-C Hwang by the National Institutes of Health (R01DK55835 and R01HL53445) and Cystic Fibrosis Foundation.
References
- 1.Neher E, Sakmann B. Single-channel currents recorded from membrane of denervated frog muscle fibres. Nature. 1976;260:799–802. doi: 10.1038/260799a0. [DOI] [PubMed] [Google Scholar]
- 2.Hamill OP, Marty A, Neher E, Sakmann B, Sigworth FJ. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 1981;391:85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
- 3.Ostedgaard LS, Baldursson O, Welsh MJ. Regulation of the cystic fibrosis transmembrane conductance regulator Cl− channel by its R domain. J Biol Chem. 2001;276:7689–7692. doi: 10.1074/jbc.R100001200. [DOI] [PubMed] [Google Scholar]
- 4.Gadsby DC, Vergani P, Csanády L. The ABC protein turned chloride channel whose failure causes cystic fibrosis. Nature. 2006;440:477–483. doi: 10.1038/nature04712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hwang TC, Sheppard DN. Gating of the CFTR Cl− channel by ATP-driven nucleotide-binding domain dimerisation. J Physiol. 2009;587:2151–2161. doi: 10.1113/jphysiol.2009.171595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sakmann B, Neher E. Single-channel recording. 2. Plenum; New York, NY: 1995. [Google Scholar]
- 7.Hug MJ. The whole-cell patch-clamp technique – a powerful tool to approach CFTR function. [Accessed 11 March 2010];Virtual Repository of Methods and Reagents for CFTR Expression and Functional Studies. 2002 http://central.igc.gulbenkian.pt/cftr/vr/physiology.html.
- 8.Gray MA. Investigating the properties of the CFTR channel using the cell-attached configuration of the patch clamp – monitoring single channel activity in a living cell. [Accessed 11 March 2010];Virtual Repository of Methods and Reagents for CFTR Expression and Functional Studies. 2002 http://central.igc.gulbenkian.pt/cftr/vr/physiology.html.
- 9.Hanrahan JW, Kone Z, Mathews CJ, Luo J, Jia Y, Linsdell P. Patch-clamp studies of cystic fibrosis transmem-brane conductance regulator chloride channel. Methods Enzymol. 1998;293:169–194. doi: 10.1016/s0076-6879(98)93014-2. [DOI] [PubMed] [Google Scholar]
- 10.Scott-Ward TS, Chen JH, Li H, Cai Z, Sheppard DN. Measurement of Cl− flow through CFTR channels using the excised inside-out patch-clamp Virtual Repository of Methods and Reagents for CFTR Expression and Functional Studies. [Accessed 11 March 2010];2002 http://central.igc.gulbenkian.pt/cftr/vr/physiology.html.
- 11.Gong X, Gupta J, Linsdell P. Measurement of the permeation and conduction properties of the CFTR chloride channel using excised inside-out membrane. [Accessed 11 March 2010];Virtual Repository of Methods and Reagents for CFTR Expression and Functional Studies. 2002 http://central.igc.gulbenkian.pt/cftr/vr/physiology.html.
- 12.Sohma Y, Hwang TC. Kinetic analysis of CFTR single-channel data. [Accessed 11 March 2010];Virtual Repository of Methods and Reagents for CFTR Expression and Functional Studies. 2002 http://central.igc.gulbenkian.pt/cftr/vr/physiology.html.
- 13.Cai Z, Scott-Ward TS, Li H, Schmidt A, Sheppard DN. Strategies to investigate the mechanism of action of CFTR modulators Virtual Repository of Methods and Reagents for CFTR Expression and Functional Studies. [Accessed 11 March 2010];2002 http://central.igc.gulbenkian.pt/cftr/vr/physiology.html.
- 14.Sheppard DN, Robinson KA. Mechanism of glibenclamide inhibition of cystic fibrosis transmembrane conductance regulator Cl− channels expressed in a murine cell line. J Physiol. 1997;503:333–346. doi: 10.1111/j.1469-7793.1997.333bh.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lansdell KA, Delaney SJ, Lunn DP, Thomson SA, Sheppard DN, Wainwright BJ. Comparison of the gating behaviour of human and murine cystic fibrosis transmembrane conductance regulator Cl− channels expressed in mammalian cells. J Physiol. 1998;508:379–392. doi: 10.1111/j.1469-7793.1998.379bq.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Anderson MP, Gregory RJ, Thompson S, Souza DW, Paul S, Mulligan RC, et al. Demonstration that CFTR is a chloride channel by alteration of its anion selectivity. Science. 1991;253:202–205. doi: 10.1126/science.1712984. [DOI] [PubMed] [Google Scholar]
- 17.Cheng SH, Gregory RJ, Marshall J, Paul S, Souza DW, White GA, et al. Defective intracellular transport and processing of CFTR is the molecular basis of most cystic fibrosis. Cell. 1990;63:827–834. doi: 10.1016/0092-8674(90)90148-8. [DOI] [PubMed] [Google Scholar]
- 18.Drumm ML, Wilkinson DJ, Smit LS, Worrell RT, Strong TV, Frizzell RA, et al. Chloride conductance expressed by ΔF508 and other mutant CFTRs in Xenopus oocytes. Science. 1991;254:1797–1799. doi: 10.1126/science.1722350. [DOI] [PubMed] [Google Scholar]
- 19.Scott-Ward TS, Cai Z, Dawson ES, Doherty A, Da Paula AC, Davidson H, et al. Chimeric constructs endow the human CFTR Cl− channel with the gating behavior of murine CFTR. Proc Natl Acad Sci USA. 2007;104:16365–16370. doi: 10.1073/pnas.0701562104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wu JV, Joo NS, Krouse ME, Wine JJ. Cystic fibrosis transmem-brane conductance regulator gating requires cytosolic electrolytes. J Biol Chem. 2001;276:6473–6478. doi: 10.1074/jbc.M009305200. [DOI] [PubMed] [Google Scholar]
- 21.Ishihara H, Welsh MJ. Block by MOPS reveals a conformation change in the CFTR pore produced by ATP hydrolysis. Am J Physiol. 1997;273:C1278–C1289. doi: 10.1152/ajpcell.1997.273.4.C1278. [DOI] [PubMed] [Google Scholar]
- 22.Tabcharani JA, Chang XB, Riordan JR, Hanrahan JW. Phosphorylation-regulated Cl− channel in CHO cells stably expressing the cystic fibrosis gene. Nature. 1991;352:628–631. doi: 10.1038/352628a0. [DOI] [PubMed] [Google Scholar]
- 23.Chen JH, Cai Z, Sheppard DN. Direct sensing of intracellular pH by the cystic fibrosis transmembrane conductance regulator (CFTR) Cl− channel. J Biol Chem. 2009;284:35495–35506. doi: 10.1074/jbc.M109.072678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hughes LK, Ju M, Sheppard DN. Potentiation of cystic fibrosis trans-membrane conductance regulator (CFTR) Cl− currents by the chemical solvent tetrahydrofuran. Mol Membr Biol. 2008;25:528–538. doi: 10.1080/09687680802487967. [DOI] [PubMed] [Google Scholar]
- 25.Cai Z, Scott-Ward TS, Sheppard DN. Voltage-dependent gating of the cystic fibrosis transmembrane conductance regulator Cl− channel. J Gen Physiol. 2003;122:605–620. doi: 10.1085/jgp.200308921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhou Z, Hu S, Hwang TC. Voltage-dependent flickery block of an open cystic fibrosis transmembrane conductance regulator (CFTR) channel pore. J Physiol. 2001;532:435–448. doi: 10.1111/j.1469-7793.2001.0435f.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Anderson MP, Berger HA, Rich DP, Gregory RJ, Smith AE, Welsh MJ. Nucleoside triphosphates are required to open the CFTR chloride channel. Cell. 1991;67:775–784. doi: 10.1016/0092-8674(91)90072-7. [DOI] [PubMed] [Google Scholar]
- 28.Schultz BD, Frizzell RA, Bridges RJ. Rescue of dysfunctional ΔF508-CFTR chloride channel activity by IBMX. J Membr Biol. 1999;170:51–66. doi: 10.1007/s002329900537. [DOI] [PubMed] [Google Scholar]
- 29.Bompadre SG, Cho JH, Wang X, Zou X, Sohma Y, Li M, et al. CFTR gating II: effects of nucleotide binding on the stability of open states. J Gen Physiol. 2005;125:377–394. doi: 10.1085/jgp.200409228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Linsdell P, Hanrahan JW. Disulphonic stilbene block of cystic fibrosis transmembrane conductance regulator Cl− channels expressed in a mammalian cell line and its regulation by a critical pore residue. J Physiol. 1996;496:687–693. doi: 10.1113/jphysiol.1996.sp021719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhou Z, Hu S, Hwang TC. Probing an open CFTR pore with organic anion blockers. J Gen Physiol. 2002;120:647–662. doi: 10.1085/jgp.20028685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Csanády L, Chan KW, Seto-Young D, Kopsco DC, Nairn AC, Gadsby DC. Severed channels probe regulation of gating of cystic fibrosis transmem-brane conductance regulator by its cytoplasmic domains. J Gen Physiol. 2000;116:477–500. doi: 10.1085/jgp.116.3.477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cai Z, Sheppard DN. Phloxine B interacts with the cystic fibrosis trans-membrane conductance regulator at multiple sites to modulate channel activity. J Biol Chem. 2002;277:19546–19553. doi: 10.1074/jbc.M108023200. [DOI] [PubMed] [Google Scholar]
- 34.Hwang TC, Nagel G, Nairn AC, Gadsby DC. Regulation of the gating of cystic fibrosis transmem-brane conductance regulator C1 channels by phosphorylation and ATP hydrolysis. Proc Natl Acad Sci USA. 1994;91:4698–4702. doi: 10.1073/pnas.91.11.4698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Carson MR, Winter MC, Travis SM, Welsh MJ. Pyrophosphate stimulates wild-type and mutant cystic fibrosis transmembrane conductance regulator Cl− channels. J Biol Chem. 1995;270:20466–20472. doi: 10.1074/jbc.270.35.20466. [DOI] [PubMed] [Google Scholar]
- 36.Tsai MF, Shimizu H, Sohma Y, Li M, Hwang TC. State-dependent modulation of CFTR gating by pyrophosphate. J Gen Physiol. 2009;133:405–419. doi: 10.1085/jgp.200810186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cai Z, Taddei A, Sheppard DN. Differential sensitivity of the cystic fibrosis (CF)-associated mutants G551D and G1349D to potentiators of the cystic fibrosis transmembrane conductance regulator (CFTR) Cl− channel. J Biol Chem. 2006;281:1970–1977. doi: 10.1074/jbc.M510576200. [DOI] [PubMed] [Google Scholar]
- 38.Bompadre SG, Sohma Y, Li M, Hwang TC. G551D and G1349D, two CF-associated mutations in the signature sequences of CFTR, exhibit distinct gating defects. J Gen Physiol. 2007;129:285–298. doi: 10.1085/jgp.200609667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Venglarik CJ, Schultz BD, Frizzell RA, Bridges RJ. ATP alters current fluctuations of cystic fibrosis transmem-brane conductance regulator: evidence for a three-state activation mechanism. J Gen Physiol. 1994;104:123–146. doi: 10.1085/jgp.104.1.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zeltwanger S, Wang F, Wang GT, Gillis KD, Hwang TC. Gating of cystic fibrosis transmembrane conductance regulator chloride channels by adenosine triphosphate hydrolysis. Quantitative analysis of a cyclic gating scheme. J Gen Physiol. 1999;113:541–554. doi: 10.1085/jgp.113.4.541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Aleksandrov AA, Riordan JR. Regulation of CFTR ion channel gating by MgATP. FEBS Lett. 1998;431:97–101. doi: 10.1016/s0014-5793(98)00713-3. [DOI] [PubMed] [Google Scholar]
- 42.Baukrowitz T, Hwang TC, Nairn AC, Gadsby DC. Coupling of CFTR Cl− channel gating to an ATP hydrolysis cycle. Neuron. 1994;12:473–482. doi: 10.1016/0896-6273(94)90206-2. [DOI] [PubMed] [Google Scholar]
- 43.Bompadre SG, Ai T, Cho JH, Wang X, Sohma Y, Li M, et al. CFTR gating I: characterization of the ATP-dependent gating of a phosphorylation-independent CFTR channel (ΔR-CFTR) J Gen Physiol. 2005;125:361–375. doi: 10.1085/jgp.200409227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sigurdson WJ, Morris CE, Brezden BL, Gardner DR. Stretch activation of a K+ channel in molluscan heart cells. J Exp Biol. 1987;127:191–209. [Google Scholar]
- 45.Li C, Ramjeesingh M, Wang W, Garami E, Hewryk M, Lee D, et al. ATPase activity of the cystic fibrosis trans-membrane conductance regulator. J Biol Chem. 1996;271:28463–28468. doi: 10.1074/jbc.271.45.28463. [DOI] [PubMed] [Google Scholar]
- 46.Weinreich F, Riordan JR, Nagel G. Dual effects of ADP and adenylylimidodiphosphate on CFTR channel kinetics show binding to two different nucleotide binding sites. J Gen Physiol. 1999;114:55–70. doi: 10.1085/jgp.114.1.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Vergani P, Lockless SW, Nairn AC, Gadsby DC. CFTR channel opening by ATP-driven tight dimerization of its nucleotide-binding domains. Nature. 2005;433:876–880. doi: 10.1038/nature03313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Vergani P, Nairn AC, Gadsby DC. On the mechanism of MgATP-dependent gating of CFTR Cl− channels. J Gen Physiol. 2003;121:17–36. doi: 10.1085/jgp.20028673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Zhou Z, Wang X, Liu HY, Zou X, Li M, Hwang TC. The two ATP binding sites of cystic fibrosis transmembrane conductance regulator (CFTR) play distinct roles in gating kinetics and energetics. J Gen Physiol. 2006;128:413–422. doi: 10.1085/jgp.200609622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Csanády L, Vergani P, Gadsby DC. Strict coupling between CFTR’s catalytic cycle and gating of its Cl− ion pore revealed by distributions of open channel burst durations. Proc Natl Acad Sci USA. 2010;107:1241–1246. doi: 10.1073/pnas.0911061107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Colquhoun D, Hawkes AG. The principles of stochastic interpretation of ion-channel mechanisms. In: Sakmann B, Neher E, editors. Single-channel recording. 2. Plenum; New York, NY: 1995. [Google Scholar]
- 52.Blatz AL, Magleby KL. Quantitative description of three modes of activity of fast chloride channels from rat skeletal muscle. J Physiol. 1986;378:141–174. doi: 10.1113/jphysiol.1986.sp016212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Welsh MJ, Smith AE. Molecular mechanisms of CFTR chloride channel dysfunction in cystic fibrosis. Cell. 1993;73:1251–1254. doi: 10.1016/0092-8674(93)90353-r. [DOI] [PubMed] [Google Scholar]
- 54.Zielenski J, Tsui LC. Cystic fibrosis: genotypic and phenotypic variations. Annu Rev Genet. 1995;29:777–807. doi: 10.1146/annurev.ge.29.120195.004021. [DOI] [PubMed] [Google Scholar]
- 55.Hwang TC, Wang F, Yang IC, Reenstra WW. Genistein potentiates wild-type and F508-CFTR channel activity. Am J Physiol. 1997;273:C988–C998. doi: 10.1152/ajpcell.1997.273.3.C988. [DOI] [PubMed] [Google Scholar]
- 56.Al-Nakkash L, Hwang TC. Activation of wild-type and ΔF508-CFTR by phosphodiesterase inhibitors through cAMP-dependent and -independent mechanisms. Pflugers Arch. 1999;437:553–561. doi: 10.1007/s004240050817. [DOI] [PubMed] [Google Scholar]
- 57.Dalemans W, Barbry P, Champigny G, Jallat S, Dott K, Dreyer D, et al. Altered chloride ion channel kinetics associated with the ΔF508 cystic fibrosis mutation. Nature. 1991;354:526–528. doi: 10.1038/354526a0. [DOI] [PubMed] [Google Scholar]
- 58.Hegedus T, Aleksandrov A, Cui L, Gentzsch M, Chang XB, Riordan JR. F508del CFTR with two altered RXR motifs escapes from ER quality control but its channel activity is thermally sensitive. Biochim Biophys Acta. 2006;1758:565–572. doi: 10.1016/j.bbamem.2006.03.006. [DOI] [PubMed] [Google Scholar]
- 59.Sheppard DN, Rich DP, Ostedgaard LS, Gregory RJ, Smith AE, Welsh MJ. Mutations in CFTR associated with mild-disease-form Cl− channels with altered pore properties. Nature. 1993;362:160–164. doi: 10.1038/362160a0. [DOI] [PubMed] [Google Scholar]
- 60.Gong X, Linsdell P. Maximization of the rate of chloride conduction in the CFTR channel pore by ion-ion interactions. Arch Biochem Biophys. 2004;426:78–82. doi: 10.1016/j.abb.2004.03.033. [DOI] [PubMed] [Google Scholar]
- 61.Linsdell P. Relationship between anion binding and anion permeability revealed by mutagenesis within the cystic fibrosis transmembrane conductance regulator chloride channel pore. J Physiol. 2001;531:51–66. doi: 10.1111/j.1469-7793.2001.0051j.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Sheppard DN, Travis SM, Ishihara H, Welsh MJ. Contribution of proline residues in the membrane-spanning domains of cystic fibrosis trans-membrane conductance regulator to chloride channel function. J Biol Chem. 1996;271:14995–15001. doi: 10.1074/jbc.271.25.14995. [DOI] [PubMed] [Google Scholar]
- 63.Akabas MH, Kaufmann C, Cook TA, Archdeacon P. Amino acid residues lining the chloride channel of the cystic fibrosis transmembrane conductance regulator. J Biol Chem. 1994;269:14865–14868. [PubMed] [Google Scholar]
- 64.Zegarra-Moran O, Romio L, Folli C, Caci E, Becq F, Vierfond JM, et al. Correction of G551D-CFTR transport defect in epithelial monolayers by genistein but not by CPX or MPB-07. Br J Pharmacol. 2002;137:504–512. doi: 10.1038/sj.bjp.0704882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Sheppard DN, Ostedgaard LS, Winter MC, Welsh MJ. Mechanism of dysfunction of two nucleotide binding domain mutations in cystic fibrosis trans-membrane conductance regulator that are associated with pancreatic sufficiency. EMBO J. 1995;14:876–883. doi: 10.1002/j.1460-2075.1995.tb07069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Haws CM, Nepomuceno IB, Krouse ME, Wakelee H, Law T, Xia Y, et al. ΔF508-CFTR channels: kinetics, activation by forskolin, and potentiation by xanthines. Am J Physiol. 1996;270:C1544–C1555. doi: 10.1152/ajpcell.1996.270.5.C1544. [DOI] [PubMed] [Google Scholar]
- 67.Wang F, Zeltwanger S, Hu S, Hwang TC. Deletion of phenylalanine 508 causes attenuated phosphorylation-dependent activation of CFTR chloride channels. J Physiol. 2000;524:637–648. doi: 10.1111/j.1469-7793.2000.00637.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Sheppard DN, Ostedgaard LS. Understanding how cystic fibrosis mutations cause a loss of Cl− channel function. Mol Med Today. 1996;2:290–297. doi: 10.1016/1357-4310(96)10028-9. [DOI] [PubMed] [Google Scholar]