Multi-ion free energy landscapes underscore the microscopic mechanism of ion selectivity in the KcsA channel

Abstract

Potassium (K⁺) channels are transmembrane proteins that passively and selectively allow K⁺ ions to flow through them, after opening in response to an external stimulus. One of the most critical functional aspects of their function is their ability to remain very selective for K⁺ over Na⁺ while allowing high-throughput ion conduction at a rate close to the diffusion limit. Classically, it is assumed that the free energy difference between K⁺ and Na⁺ in the pore relative to the bulk solution is the critical quantity at the origin of selectivity. This is the thermodynamic view of ion selectivity. An alternative view assumes that kinetic factor play the dominant role. Recent results from a number of studies have also highlighted the great importance of the multi-ion single file on the selectivity of K⁺ channels. The data indicate that having multiple K⁺ ions bound simultaneously is required for selective K⁺ conduction, and that a reduction in the number of bound K⁺ ions destroys the multi-ion selectivity mechanism utilized by K⁺ channels. In the present study, multi-ion potential of mean force molecular dynamics computations are carried out to clarify the mechanism of ion selectivity in the KcsA channel. The computations show that the multi-ion character of the permeation process is a critical element for establishing the selective ion conductivity through K⁺-channels.

INTRODUCTION

Potassium (K⁺) channels are a ubiquitous class of transmembrane proteins that passively and selectively allow K⁺ ions to flow through them, after opening in response to an external stimulus (1). These channels are perhaps best known for being a key component of the action potential in excitable cells – but are found in a variety of different cell types and organisms, in all domains of life, and can be activated by a variety of different stimuli. Their functionality gives them a key role, in the cell, in regulating the cytoplasmic K⁺ concentration and the electrochemical potential across the cell membrane. Potassium channels have been implicated in human cardiac disorders, such as long-QT syndrome, and in cancers. They are a common target of natural peptide toxins, and are an important target for therapeutic pharmacology.

One of the most critical functional aspects of K⁺ channel is their ability to remain very selective for K⁺ over Na⁺ while allowing high-throughput ion conduction at a rate close to the diffusion limit (2–4). In practice, however, the concept of selectivity for an ion channel can means different things depending on whether the system is probed experimentally via equilibrium binding assays or non-equilibrium ionic current measurements. Classically, ion channel selectivity has been characterized by determining the permeability ratio from the reversal potential (zero net current) under bionic conditions. However, measurements of reversal potentials become difficult for highly selective channels such as the K⁺ channels. In this case, alternate methods such as Ba²⁺ blockade relief (5, 6) or Na⁺ punchthrough (7), provide more effective methods to characterize selectivity with quantitative accuracy. Each method reports on different aspect of the system, e.g., Ba²⁺ block is more sensitive to the depth of the free energy minima of the binding sites (i.e., equilibrium binding), while Na⁺ punchthrough is more sensitive to the height of free energy barriers (i.e., non-equilibrium rates).

The classic explanation of selectivity posits that the free energy difference between K⁺ and Na⁺ in the pore relative to the bulk solution is the critical quantity at the origin of selectivity (3, 4). This “thermodynamic” view is strongly supported by the Ba²⁺ blockade experiments of Miller and co-workers (5, 6, 8), and by the ITC microcalorimetry measurements of Lockless et al (9), which offer experimental evidence of equilibrium binding site selectivity in the KcsA channel. Because the blocks by Ba²⁺ last for a very long time, the experiment allows an estimate of the quasi-equilibrium dissociation constant of Na⁺ or K⁺ for a binding site called the “external lock-in site”. While the basic concepts of the thermodynamic view are well established, additional studies demonstrated that additional factors can play an important role. For instance, Nimigean and Allen have clarified kinetic aspects of selectivity based on studies of Na⁺ blocks in the bacterial KcsA channel (10–12).

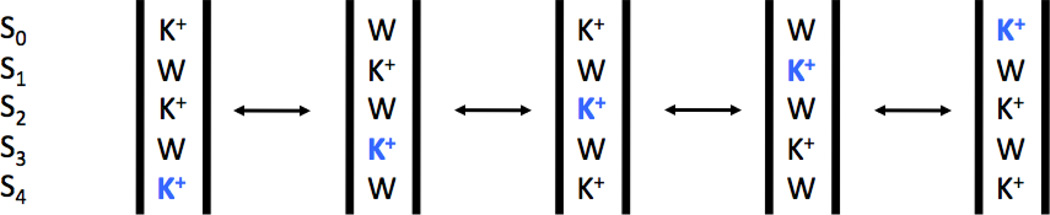
More recently, results from a number of studies have highlighted the remarkable importance of the multi-ion single file on the selectivity of K⁺ channels. By examining the properties of MthK(13) and NaK (14, 15) mutants, Jiang and co-workers showed that the channel becomes selective only if four consecutive binding sites exist along the narrow selectivity filter. This has culminated more recently with studies of two engineered mutants of the NaK channel, referred to as “NaK2K” and “NaK2CNG” (16, 17). According to reversal potential measurements from single-channel electrophysiology, the NaK2K construct is K⁺-selective and the NaK2CNG construct is non-selective. Remarkably, despite being non-selective in ion permeation, the NaK2CNG filter display equilibrium binding preference for K⁺ over Na⁺, as indicated by measurements with isothermal titration calorimetry (ITC) and concentration-dependent ion replacement within the filter observed through crystallographic titration experiments. The K⁺-selective channels bind two or more K⁺ ions in the narrow filter, whereas the non-selective channels bind fewer ions. Based on the crystallographic titration experiments, the NaK2K construct has two high-affinity K⁺ sites while the NaK2CNG construct has only one K⁺-selective site. These experiments show that both K⁺-selective and non-selective channels select K⁺ over Na⁺ ions at equilibrium, implying that equilibrium selectivity is insufficient to determine the selectivity of ion permeation (16, 17). The data indicate that having multiple K⁺ ions bound simultaneously is required for selective K⁺ conduction, and that a reduction in the number of bound K⁺ ions destroys the multi-ion selectivity mechanism utilized by K⁺ channels. To explain K⁺ channel selectivity, a simple kinetic model with two K⁺ high-affinity sites and a double-barrier was proposed (17). However, while these experimental results are intriguing, the underlying microscopic mechanism remains unclear. Fundamental questions remain about the mechanism of selective ion conduction and whether it is supported by some multi-site/multi-ion kinetic processes, or by near-equilibrium binding site thermodynamic processes is unclear. Obviously, selectivity reported by ion permeation reflects the non-equilibrium dynamic process of multi-ion translocation across the filter and this needs to be taken into account in the discussion.

While the thermodynamic/kinetic debate can be resolved in terms of classic arguments (the mechanism is controlled by free energy differences at the bottom of the binding wells versus the top of the activation barriers), the critical multi-ion character of the selectivity revealed by the recent studies forces us to reformulate these classic arguments in a broader context. The implication is that the multi-ion character of the permeation process must, somehow, be a critical element for establishing the selective ion conductive through K⁺-channels. How this mechanism is encoded into the three-dimensional molecular structure of the protein is an unresolved question.

Our goal is to use molecular dynamics (MD) computations to quantitatively outline the step-by-step multi-ion processes through the K⁺ channel selectivity filter that underlies selective permeation. We choose to base our computations on the well-characterized prokaryotic potassium channel KcsA from Streptomyces lividans (18). This was the first selective biological ion channel for which a crystal structure was determined to atomic resolution (19), and it has ever since proven to be a tremendously useful model system for computational studies of the different functional aspects of K⁺ channels, including permeation (20–23), selectivity (10, 11, 24), and C-type inactivation(25–29). Most of the previous MD simulation studies of ion permeation through the selectivity filter of the KcsA channel have relied on the high-resolution crystallographic structure in complex with a Fab antibody (PDB id 1K4C) (30), which has its intracellular activation gate in the closed state. Recently, Luis Cuello and collaborators have obtained a high-resolution structure of the KcsA channel with an open intracellular activation gate and a selectivity filter in the conductive conformation (private communication). The main advantage of using a structure with an open intracellular gate is that we include configurations with an ion in the cavity and one ion in the site S4, which are energetically unfavorable (21).

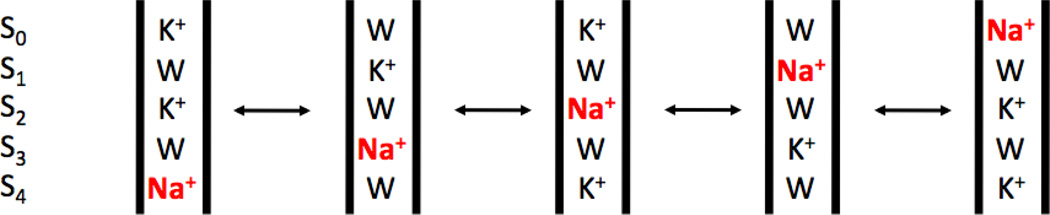
Conceptually, the permeation process of K⁺ ions through the KcsA channel is believed to proceed predominantly as a “knock-on” mechanism in which the single-file translocation of 2–3 K⁺ ions interspersed by water molecules through the narrow selectivity filter (21, 31), Logically, under conditions corresponding to high K⁺ concentration, the permeation of one isolated Na⁺ “defect” is likely to be chaperoned by the predominant K⁺ ions fore and aft, and proceed according to the following steps, The new X-ray structure (Luis Cuello, private communication) provides a unique opportunity to examine the problem of ion permeation through a channel in its functional “open-conductive” state.

To characterize the process of selective permeation through the KcsA channel in the open-conductive state according to the Schemes 1 and 2 above, we compute the multi-ion potential of mean force (PMF) that underlies the multi-ion permeation process using umbrella sampling MD simulations. To ascertain the selectivity of the channel, therefore, we compare the multi-ion PMF of K⁺ ions moving as a K⁺/K⁺/K⁺ single-file through the filter (Scheme 1) with that of a K⁺/Na⁺/K⁺ single-file (Scheme 2). The umbrella sampling computations allow us to map the free energy landscape for the complete multi-ion translocation event of the single file of multiple ions across the entire filter. We then use the string method (32–34) to analyze and visualize the multi-ion transition in terms of an optimal pathway along the free energy landscape.

Scheme 1.

Scheme 2.

METHODS AND COMPUTATIONAL DETAILS

The high-resolution X-ray crystallographic structure of open-conductive KcsA was inserted into a previously equilibrated solvated bilayer simulation system based on the moderate resolution (3.2 Å) X-ray structure (PDB id 3F5W) (27). The simulation system comprises a bilayer of 112 DPPC molecules, surrounded by a 150mM KCl aqueous salt solution to ensure electrical neutrality, for a total of ~43k atoms (28). The glutamic acid at position 71 was protonated (Bernèche and Roux, 2002) and the termini were patched with standard N- and C-terminal capping groups. Engineered disulfide bonds between positions 28 and 118, necessary to lock the channel into the open-state in the high-resolution X-ray structure, were maintained. The protein was modeled after the CHARMM force-field; CHARMM22 with CMAP corrections for protein (35) and CHARMM36 for lipids (36). The water model is TIP3P (37), the K⁺ ion is from ref (38), and the Na⁺ is from ref (24). Following Noskov et al. (24), adjusted non-bonded parameters were used for interactions between protein carbonyl oxygens and cations. An additional artificial dihedral restraint was added to keep the carbonyls of Val76 in their crystallographic orientation and prevent them from ‘flipping’, as used elsewhere (39). Another system was simulated where three of the four subunits’ Val76 were prevented from flipping while the fourth was artificially restrained into a flipped position. Using the same methodology, one additional simulation system was prepared where Gly77 was substituted by a D-Alanine, as experimentally studied by Valiyaveetil et al. (40). The D-alanine force field was taken from Ingolfsson et al. (41). In all cases, the initial system was briefly minimized and equilibrated with restraints to keep the protein in its crystallographic position, and then run for 4ns of unrestrained dynamics. All simulations were carried with the NAMD program (42). A Langevin thermostat held the system at 315K. The timesteps was 2 fs. Electrostatic interactions were treated with particle-mesh Ewald (43) with a 12 Å real-space cutoff.

To characterize the selectivity of the channel, we choose a multi-ion biased sampling PMF approach rather than monitoring spontaneous permeation events through long unbiased MD simulations in the presence of a membrane potential (44). This offers the most effective strategy to draw meaningful conclusions about ion selectivity of K⁺ channels for the following reason: a multi-ion PMF provides a satisfying conceptual framework to discuss the permeation process compared to counting ion passage events in unbiased nonequilibrium simulations. The PMF, which is a thermodynamic equilibrium quantity, can also be calculated from the average spatial density of ions from long unbiased MD simulation (45). But, as permeation rates are very sensitive to free energy barriers, a PMF-based framework can help overcome inaccuracies in the force field more readily by delivering free energy barriers directly rather than trying to evaluate those from unbiased MD simulations.

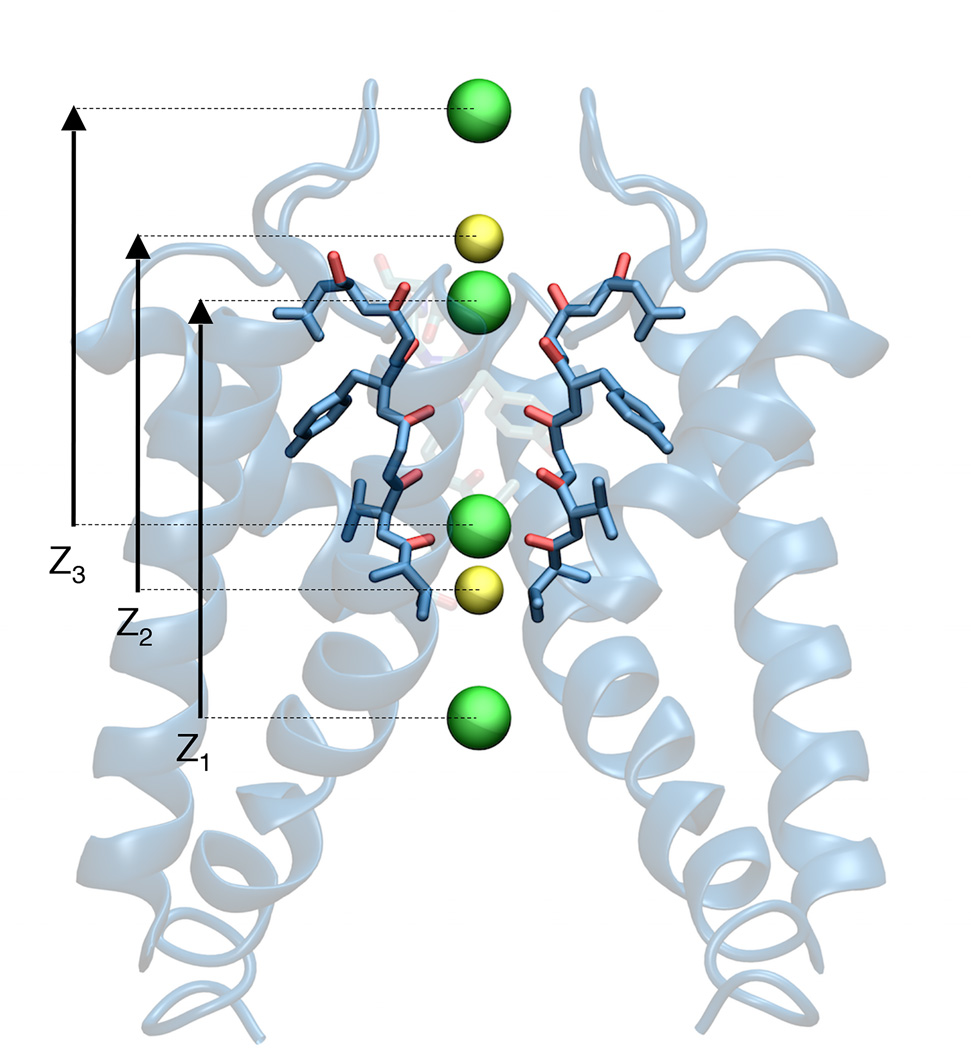
Umbrella sampling windows were constructed and equilibrated for each model. In each window, three ions were placed in single file, aligned vertically in the membrane-normal Z direction along the central ion pore axis. Ion positions were placed in a 0.75 Å grid, with neighboring ions placed at distances between 3 Å and 9 Å, and the top and bottom ions not more than 15 Å apart. The central ion was placed at positions ranging from 5.75 Å below, to 10.75 Å above, the center-of-mass (CoM) of the backbone atoms of residues 75 through 78 (this CoM position is used as the reference zero position for Z throughout this paper). The spatial range covered by the umbrella sampling windows is depicted in Fig. 1. It is important to note that the ion configurations associated with the umbrella sampling windows are constructed such that a single continuous PMF covers essentially the entire transit of the central ion through the filter. This is in contrast with earlier work (10, 11, 20–24), where only a partial ion translocation across the selectivity filter could be monitored. The top and bottom of the three ions were always K⁺, the middle one prepared both as a K⁺ and as a Na⁺. The sampling for the central ion goes from −5.75 Å to 10.75 Å relative to the center of mass of the selectivity filter (the backbone of residues 75 to 78). This corresponds to the central ion moving from the site S4 to the site S0. Previous studies have shown that a mechanism consisting of single file of K⁺ ions each separated by a single water molecule is either the dominant (21), or at least a major (22), conduction mode. Furthermore, this mechanism is consistent with streaming potential measurements indicating that about 1 water molecule is transported on average for each permeating K⁺ ion (46). An alternative conduction mechanism recently proposed that K⁺ simultaneously occupy adjacent sites with no intervening water on the basis of long nonequilibrium simulations (47), however this mechanism is not consistent with streaming potential measurements. Therefore, in each window, a water molecule was initially placed at the midpoint between each pair of adjacent ions (though afterwards left unrestrained). For each of the six PMFs, 1763 unique windows were created.

Figure 1.

Schematic illustration of the configuration of the 3 ions along the axis of the selectivity filter of the KcsA channel that are included in the Potential of Mean Force (PMF) calculation. The figure shows the topmost and bottommost umbrella sampling window configurations. The central permeating ion, either Na⁺ or K⁺ (in yellow), is bracketed by two K⁺ ions (green). The sampling for the central ion covers a 16.5 Å range, going from −5.75 Å to 10.75 Å relative to the center of mass of the selectivity filter (the backbone of residues 75 to 78). This corresponds to the movement from the site S4 to the site S0. Intermediate windows were places on a 0.75 Å grid, with neighboring ions spaced between 3 Å and 9 Å apart, and the top and bottom ions not more than 15 Å apart.

The atomic configurations for each umbrella sampling window was briefly optimized by energy minimization, and then simulated for 515 ps with MD in the NVT ensemble. To restrain the ions near their initial positions, harmonic restraints with a force constant of 10 kcal/molŲ in the Z direction relative to the center-of-mass of backbone atoms of the selectivity filter were applied throughout the MD simulation. Of each 515ps trajectory, the first 55ps were discarded, and the remaining 460ps were used with the weighted histogram analysis method (WHAM) (48, 49), with a bin-width of 0.25 Å, to compute the three-dimensional PMF. The total aggregate simulation time for each PMF is ~0.8 µs.

The present umbrella sampling methodology follows largely from previous work (23). There are considerable similarities with the PMF calculations of Furini and Domene (22), with some importance differences. As in the present US calculations, harmonic potentials only along the Z-axis were applied to the ions relative to the CoM of the selectivity filter. Furini and Domene calculated the PMF for 4 ions from 100 ps simulations with 3 biasing potentials, applied to the innermost and outermost ions, and to the CoM of the 2 central ions, and the dependence on the position of the two central ions may suffer from insufficient sampling in view of the short US simulations. Furthermore, no explicit attempt was made to resolve the complete 4-ion PMF, and large free energy barriers present in the 4d-PMF may not be observed in projection to lower dimension (even if the 4d PMF is itself well sampled). Here, the 3d-PMF was explicitly determined from 460 ps simulations, with separate biased potentials applied to each of the 3 ions in the filter.

The minimum-energy path through the computed PMF was represented as a chain of 40 “images” of the system in the subspace of the three variables (Z₁, Z₂, Z₃). To determine the optimal path, an initial straight line of 40 points was constructed with the first and last point (corresponding to the two chosen minima) held fixed at all times. An iterative Monte Carlo procedure perturbs each of the remaining points by a random distance drawn from a Gaussian distribution with standard deviation set to one-quarter the initial distance between each point. After each perturbation, the new points are redistributed equidistantly along a spline curve fit through them – corresponding to ‘reparametrization’ in the String Method (32, 33). The sum of the PMF along the string (taken from interpolated values of the WHAM output) is then computed, and the move accepted or rejected based on a metropolis criterion, with an arbitrary temperature set to a high value for the first 500 attempts (to generate a diversity of configurations), and then gradually reduced in a simulated annealing procedure for 500 more steps. To keep the string relatively straight and prevent it from coiling up upon itself in low-energy regions, an additional arbitrary punishment term is added to the string energy when the ith image is too near the i+5th or i+10th image. Since this algorithm represents only a local search of the PMF, it is run 1000 times, and only the lowest energy final strings are used – it can be considered converged when the lowest energy strings are tightly clustered in space.

RESULTS AND DISCUSSION

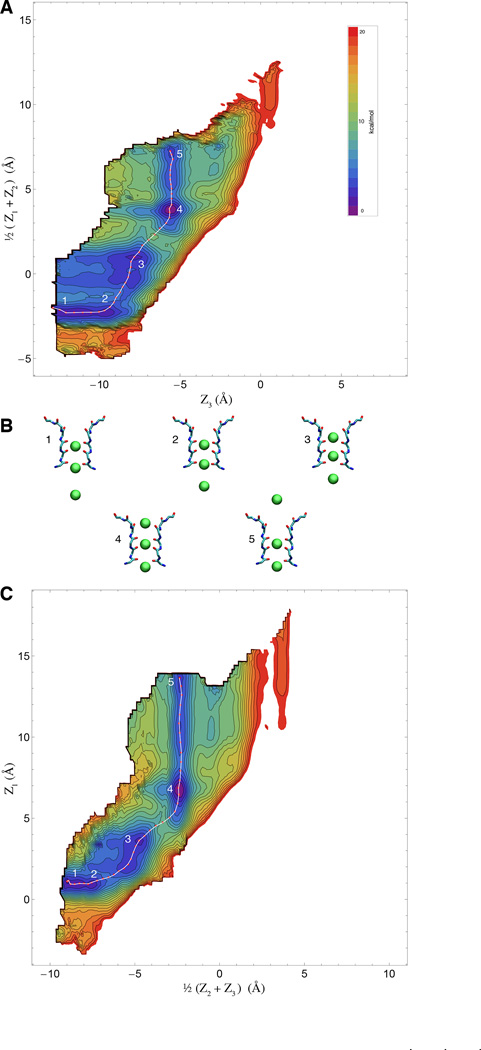
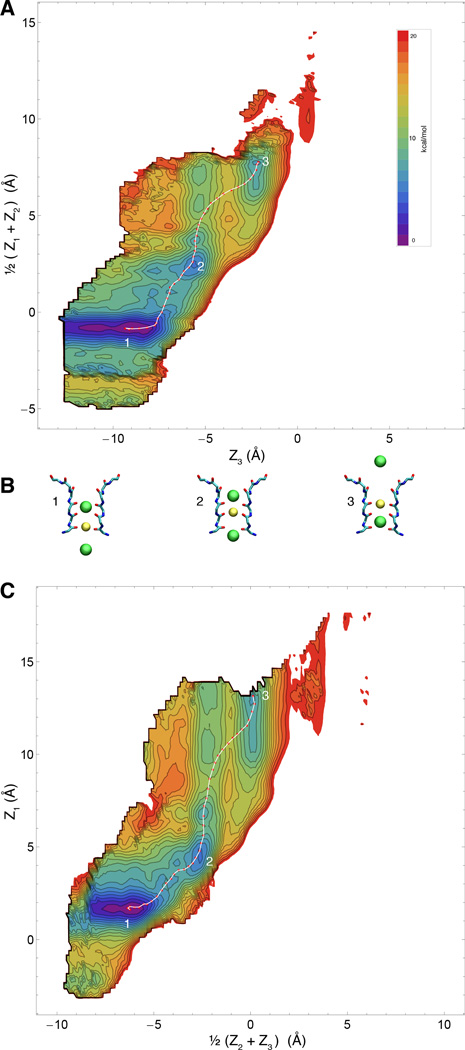
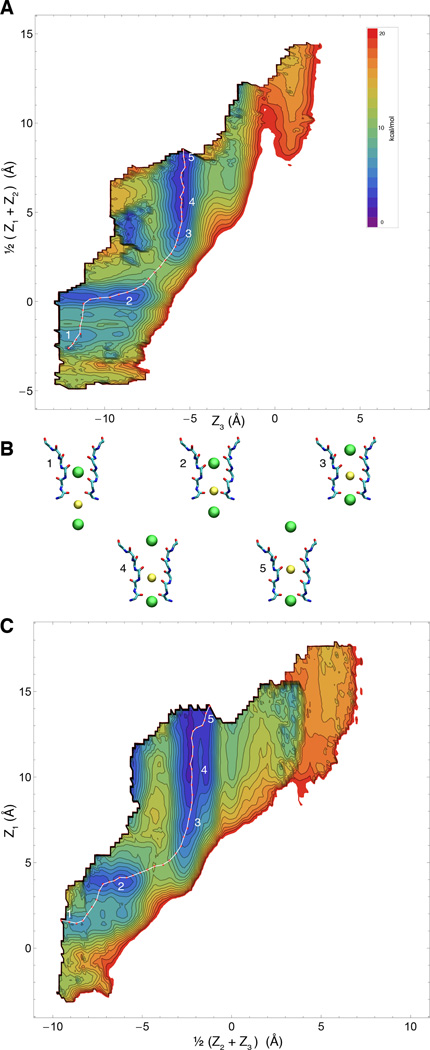
Because of its highly concerted nature, ion conduction through the narrow selectivity filter of K⁺ channels is a multi-ion process that involves the evolution of several dynamical variables that are tightly coupled. Since the ions in the filter move in single file through a narrow pore, it is natural to consider that the most relevant degrees of freedom to account for the conduction process correspond to the displacement of the ions along the channel axis. In comparison, the protein undergoes fast Å-scale fluctuations, and a reasonable assumption is that those degrees of freedom are not strongly coupled with the conduction process and can be integrated out. While this is certainly a simplification, the implication is that at least 3 relevant variables are required to describe the ion conduction process, Z₁, Z₂, and Z₃. Based on these arguments, our expectation is that the 3-ion PMF W(Z₁, Z₂, Z₃), will contain all the critical information to explain selective ion conduction in KcsA. It is worth noting that the present 3-ion PMF calculations are representative of a permeation mechanism involving a single file of K⁺ ions each separated by a single water molecule. This mechanism is consistent with streaming potential measurements indicating that about 1 water molecules is transported on average for every ion conducted through the filter (46). An alternative conduction mechanism observed in some computational studies (22, 47), in which K⁺ simultaneously occupy adjacent sites with no intervening water molecules, is not considered in the present PMF calculations. The 3d-PMFs are shown as 2d projections in Figs. 2 and 3, for K⁺ and Na⁺, respectively. The free energy landscape appears to be markedly more favorable for the conduction of K⁺/K⁺/K⁺ compared to K⁺/Na⁺/K⁺. This can be observed from the 2d maps, where a low-energy pathway is readily apparent for pure K⁺. Furthermore, ion selectivity can be observed directly by comparing the free energy landscape for the single-file movements with K⁺/K⁺/K⁺ and K⁺/Na⁺/K⁺ in the 2d projection of the 3d-PMFs W(Z₁, Z₂, Z₃).

Figure 2.

Free energy landscape of the permeation process for K⁺/K⁺/K⁺ (WT filter) A & C) Two 2-dimensional representations of the computed 3d PMF for pure potassium conduction overlaid with computed minimum-energy pathway. B) Representative snapshots of five numbered points along the pathway, corresponding to local minima and maxima along the pathway.

Figure 3.

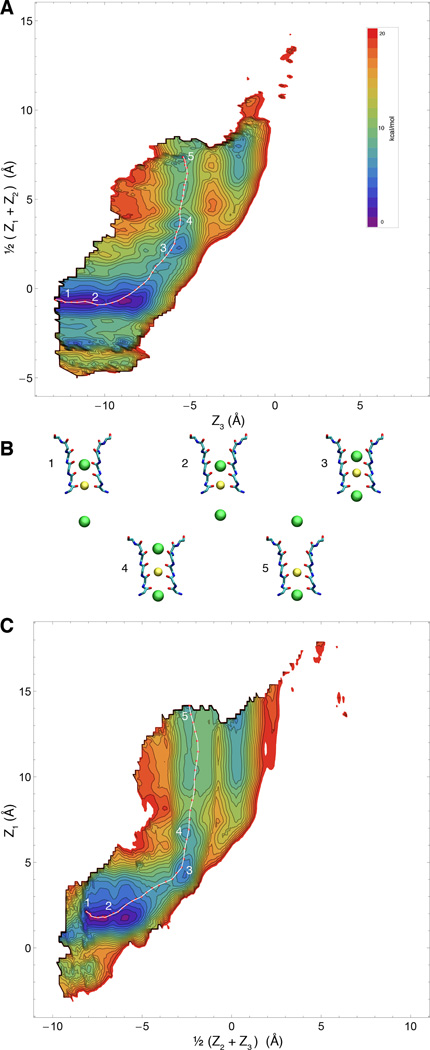
Free energy landscape of the permeation process for K⁺/Na⁺/K⁺ (WT filter) A & C) Two 2-dimensional views of the computed PMF for conduction of an Na⁺ ion chaperoned by two K⁺, overlaid with computed minimum-energy pathway. B) Representative snapshots of three numbered points along the pathway, corresponding to local minima along the pathway.

The debate about the thermodynamic or kinetic views for ion selectivity can be framed in terms of classic arguments—the former assumes that the mechanism is controlled by free energy differences at the bottom of the binding wells, while the latter assumes that the mechanism is controlled by free energy differences at the top of the activation barriers. Furthermore, if selectivity is a thermodynamically-controlled multi-ion process, then free energy differences between K⁺ and Na⁺ ought to be apparent at the bottom of the binding wells. Alternatively, if selectivity is a kinetically-controlled multi-ion process, then free energy differences between K⁺ and Na⁺ ought to be apparent at the top of the rate-limiting activation barriers.

As previously reported from other computational studies (10, 11), it is clear that the Na⁺ displays a different set of preferred low-energy configuration in the selectivity filter compared with K⁺. Specifically, K⁺ prefers to bind at the center of the crystallographically determined sites S₀-S₄, between two layers of selectivity-filter comprising four backbone carbonyls for a total of eight nearest neighbors, whereas the Na⁺ displays a marked preference to bind in-plane of the carbonyls. For instance, the global minimum of the WT with one Na⁺ ion in the filter corresponds to an “in-plane” location with respect to the carbonyls of residue Thr75. The lack of exact correspondence between the binding sites occupied by different species is one reason why simply studying the free energy difference of substituting a Na⁺ into known pure-K⁺ configurations can be misleading.

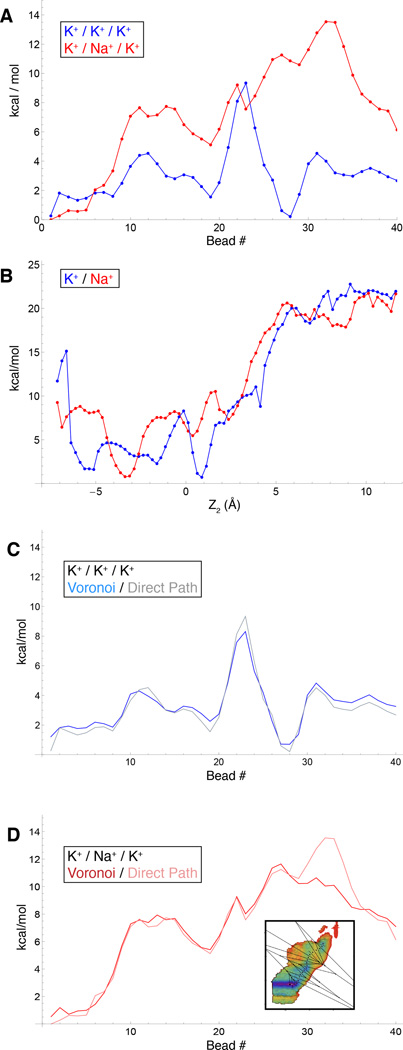
To further visualize the free energy landscape experienced by the system during the multi-ion translocation process, we determined the optimal maximum-likelihood path between two stable end-states using the string method (32, 33). Rather than using the mean drift from swarms-of-trajectories to optimize the string (34), an iterative Monte Carlo procedure was designed to determine the pathway directly on the 3d-PMFs obtained by umbrella sampling (see Methods). The lowest free energy pathway for the K⁺/K⁺/K⁺ system can be gleamed from the 2-D maps, but can be made even clearer by considering the variation of the free energy along an effective reaction coordinate corresponding to the multi-ion translocation process. This is displayed in Fig. 4A. Comparing the optimum pathways for K⁺/Na⁺/K⁺ and K⁺/K⁺/K⁺, it is clear that the former is consistently less favorable energetically throughout the whole translocation process, and approximately ~4kcal/mol less favorable when comparing peak-to-peak. The optimal pathway determined from the string method onto the PMFs are themselves, somewhat complex. As shown in Fig. 5, translocation proceeds with a clear coordinated ordering of ion motions, and even small retrograde motions by some ions. Along the minimum free energy path (obtained by the string method on the 3d-PMF), the selectivity for K⁺ over Na⁺ is the largest when the central ion crosses the site S₂. This analysis that ion selectivity for K⁺ over Na⁺ effectively results from a difference in a free energy barrier along the pathway rather than from a difference in the depth of a free energy well. The important implication of this result is that, with respect to the ion conduction process, selectivity arises from kinetic rather than thermodynamic factors.

Figure 4.

Comparison of different free energy profiles along the multi-ion permeation process in the case of K⁺/K⁺/K⁺ (left) and K⁺/Na⁺/K⁺ (right). A. Comparison of PMF along computed minimum-energy paths for pure K⁺ (red) and K⁺/Na⁺/K⁺ WT PMFs, showing clear thermodynamic selectivity of K⁺ over Na⁺. B) Effective 1d-PMFs over the coordinate of the middle ion obtained by Boltzmann integration of the 3d-PMFs. C and D show the free energy profile computed by Boltzmann integration of the 3d-PMFs within Voronoi cells (cartoon shown in inset) along the string pathway.

Figure 5.

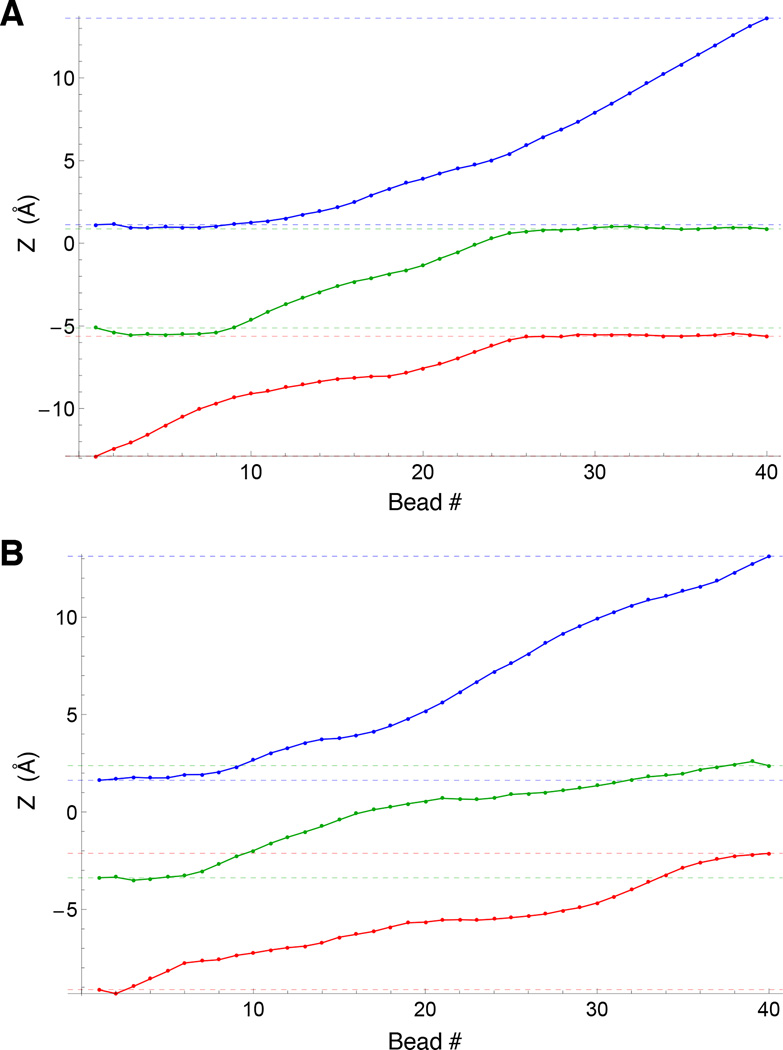
Coordinated movements of all 3 ions along the Z axis during the permeation process extracted from the optimal pathway from the string method. A) Optimal path for K⁺/K⁺/K⁺, B) optimal path for K⁺/Na⁺/K⁺. The transition is separated into the individual motions of the three ions along the path in each case. Blue, green, and red represent the top, middle, and bottom ions respectively, while dashed horizontal lines in each color represent the initial and final positions.

Because a PMF depending on many variables is difficult to visualize, previous studies of ion permeation in the KcsA channel have considered PMFs reduced to depend on either 1 or 2 variables (10, 11, 21–23). However, while Boltzmann integration of variables leads to thermodynamically correct results with respect to equilibrium properties, a projection onto a space of lower dimensionality can lump together low-energy regions that are actually separated by high barriers. Because of such configurational degeneracies, Boltzmann integration can yield apparent low-energy pathways that provide a distorted view of the rate-limiting free energy barriers for ion conduction. This is perhaps most important when considering classic treatments to describe ion permeation in terms of an effective 1d “free energy profile” associated with the movement of a single tagged ion. For example, in trying to ascertain selectivity in the KcsA channel, it would seems reasonable to tag the central ion the central ion in K⁺/K⁺/K⁺ versus K⁺/Na⁺/K⁺, and integrate-out the two other ions in the pore. This procedure defines the 1d free energy profile,

$$w_{1\mathrm{d}}(Z_2)=-k_{\mathrm{B}}T\text{ln}[\int d{Z}_{1}d{Z}_3{e}^{-W(Z_1,Z_2,Z_3)/k_{\mathrm{B}}T}]$$ Eq. (1)

which follows the progress of the central ion under the influence of a Boltzmann-averaged environment of the other ions inside the selectivity filter. The results are shown in shown in Fig. 4B. If the channel were indeed intrinsically selective on a 1-ion basis, one would expect to observe a quantitative difference in the free energy barrier along the effective 1d free energy profile for the tagged (central) ion. Remarkably, when the 3d-PMFs are integrated to yield an effective 1-ion fee energy profile for the central ion only, the selectivity that is apparent in the optimal minimum free energy reaction pathway obtained with the string disappears. The resulting 1d-PMFs for a central K⁺ or Na⁺ look very similar to one another, without any clear differences in the overall free energy barriers. What this means is that the effective 1d free energy profile does not contain the ingredients to support selective K⁺ conduction. This is in clear contrast to the free energy along the optimal multi-ion translocation path. The elements of selectivity are also visible in the 2d-PMFs, which in show clear and strong selectivity for K⁺ over Na⁺.

To show that the loss of selectivity in the 1d free energy profile following the evolution of the central ion is not a simple artifact that is trivially caused by dimensionality reduction, we split up the full 3d-PMFs into Voronoi cells surrounding the minimum-energy paths, and integrate those regions together again following the same equation. In this case, the results look quite similar to simply reading off the energies along the pathway, and retain the key feature of significant thermodynamic selectivity (Fig. 4C, D). This computational experiment demonstrates that, somehow, there is no intrinsic selectivity when considering only an effective translocation process that follows only the progress of the central ion. If selectivity were an intrinsic property felt individually by each ion in the pore, whatever their position, any reduction of the multi-ion PMF to an effective 1d free energy profile would display selectivity. Yet, it does not. Fundamentally the issue is about identifying the true relevant “slow variable”, i.e., the reaction coordinate that controls the multi-ion conduction process.

Traditionally, it is assumed that motion of a tagged ion along the pore axis is a reasonably good reaction coordinate. But for K⁺ channels, the concerted movement of all the ions along the channel axis matters. Comparing Figs. 4A and 4B makes it clear that one needs the two other ions to bracket and restrain the central ion (K⁺ or Na⁺) to display selective ion conduction. If one allows these two other ions to relax completely, or sample a Boltzmann-weighted average of their available positions according to Eq (1), then the system does not display any selectivity with respect to the translocation of the central ion (K⁺ or Na⁺). This is truly an unexpected result, demonstrating that selectivity arises as the result of a multi-ion process in this system. The selectivity for K⁺ over Na⁺ in the KcsA channel is a feature that emerges only as the result of the multi-ion process.

Consideration of the computed optimal pathway in the 3d subspace reveals that conduction through the selectivity filter of the KcsA channel is a complex and concerted multi-ion process—not simply a single-file of three ions moving simultaneously along the pore. In the case of pure K⁺ conduction, starting from an S₂/S₄/cavity configuration and viewing the pathway in the extracellular direction, the bottom ion clearly moves first (Fig. 5A), followed by a concerted movement of the top two ions into the canonical S₁/S₃ positions. In the next step, which in the 3d-PMF is clearly the highest barrier, the central ion nestles into S₂ while the outermost one remains essentially in S₁. This is then eventually resolved, with another favorable configuration where the outermost ion finally hops into S₀, the central ion occupies S₂, and the lower ion is in S₄. This 3-ion S₀/S₂/S₄ configuration was first reported in (21, 50). From here, the outermost ion is now free to leave to the external solution, while the two other ions remain in the filter. Thus, the occupancy of the filter has cycled from and back to the S₂/S₄ configuration, while conducting one net ion toward the extracellular side. Similar complex retrograde movements of the ions during K⁺ conduction can also be gleamed from the minimum free energy path of Furini and Domene (22). In contrast, the permeation process with Na⁺ in the pore displays fewer significant free energy minima. In accordance with the findings of others (10, 11), the free energy minima have the Na⁺ ion occupy the plane of the filter carbonyls rather than in the standard K⁺ binding sites, which at the center of a box formed by 8 carbonyl oxygens.

In the case of pure K⁺ conduction (K⁺/K⁺/K⁺), where we would expect the PMF to be favorable for rapid permeation throughout, there is one small region of the PMF which is quite unfavorable – with an energy of ~8 kcal/mol. This point on the PMF corresponds to a short-lived configuration where the central and outermost ions (in S2) approach one another closely. Such a large barrier is surprising given that conduction is known to be rapid according to experiments (51). One explanation is that additional kinetic factors slower than the time-scales accessible by our sampling facilitate permeation at this point. Given that permeation is a microsecond-scale process (52), such a step could be much slower than the umbrella sampling simulations can capture, while still being easily fast enough to cycle during each permeation event. Alternately, it is likely that inaccuracies in the force field could be leading to a spurious or exaggerated barrieRrecent multi-microsecond simulations of a K⁺ channel conducting under voltage reported conductance rates consistently below those expected from experiment (44). Nonetheless, though the selectivity filter may briefly adjust itself during the permeation process, given the crystallographic and computational evidence for the canonical ‘conductive’ filter state, we are confident that the relevant configurations are sampled in the 3d-PMF calculations.

Several groups have observed a tendency for the backbone carbonyl of the conserved valine in the selectivity filter signature sequence TTVGYGD (Val76 in KcsA) to ‘flip’ from the canonical crystallographic conformation, pointing away from the permeation axis (53–55). In some simulations, the flipped state was short lived (ns), while in others it could persist for very long times (39). As mentioned above, the umbrella sampling MD simulations for the WT structure include an additional term to explicitly prevent this. From this point of view, the 3d-PMF computations represent the free energy landscape under the condition that the flipped state of Val76 is excluded. Previous simulations have also applied energy restraints to the backbone of the selectivity filter to restrict its configuration to the ion conductive state (39, 44, 56). To ascertain the impact of the flipped state, we repeated the PMF calculations with three of the four Val76 prevented from flipping, and the fourth held in a flipped state (Figs. 6 and 7). Several features are apparent from these PMFs corresponding to a partially flipped state of the filter. These calculations indicate that the flipped state is less amenable to permeation of K⁺, as previously reported (54), with a new second large energy barrier added between an S2/S4/cavity state and one where S3 is occupied and two ions are in the cavity. Furthermore, the 3d-PMF of the K⁺/Na⁺/K⁺ system with Val76 flipped appears much less forbidding to conduction compared to the corresponding 3d-PMF where the flipped states were excluded. This observation is consistent with earlier free energy perturbation (FEP) results, which showed reduced selectivity for K⁺ over Na⁺ (54). While in neither case would we expect the flipped state to be responsible for very strong conduction, it is possible that experimental measurements of K⁺-channel selectivity are not directly probing the thermodynamic selectivity of the conductive filter conformation, but also the relative tendency of a channel to transiently visit less selective ‘flipped’ states. Ultimately, it seems unlikely that ions translocation through the filter is strongly coupled to the flip of Val76, in the sense that the two processes would have to take place in a concerted fashion to sustain steady state conduction. Nevertheless, because the flip of Val76 is sensitive to the backbone dihedral potential—one of the most difficult aspects of a biomolecular force field to evaluate—there remains considerable uncertainty about this issue.

Figure 6.

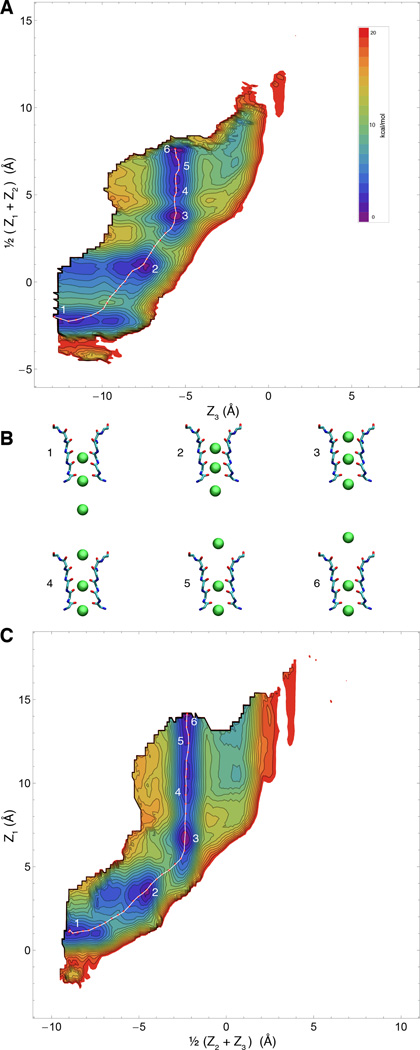
Free energy landscape of the permeation process for K⁺/K⁺/K⁺ (Val76-flip filter) A & C) Different 2-d representations of the computed 3d PMF for pure potassium conduction displayed according to the projection coordinates used previously (21) and overlaid with the computed minimum-energy pathway. B) Representative snapshots of five numbered points along the pathway, corresponding to local minima and maxima along the pathway.

Figure 7.

Free energy landscape of the permeation process for K⁺/Na⁺/K⁺ (Val76-flip filter) A & C) Two 2-dimensional views of the computed PMF for conduction of an Na⁺ ion chaperoned by two K⁺, in the style of Berneche and Roux (21), overlaid with computed minimum-energy pathway. B) Representative snapshots of five numbered points along the pathway, corresponding to local minima along the pathway.

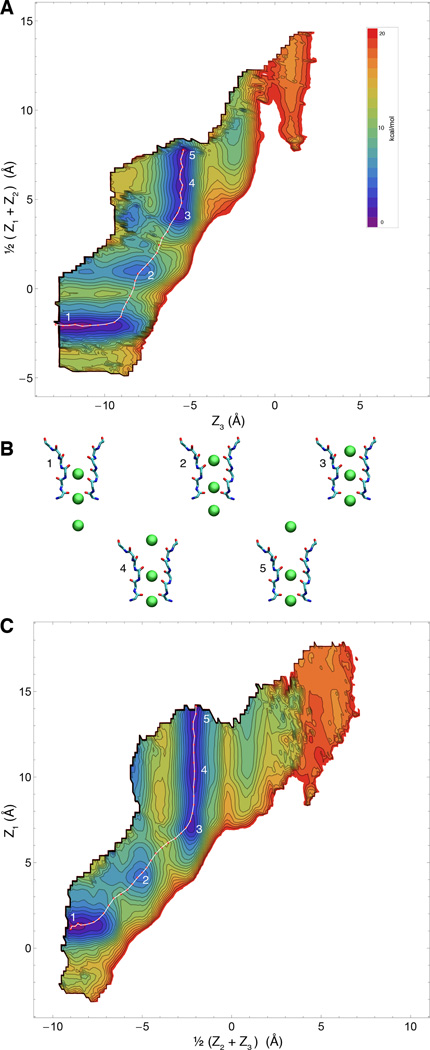
The molecular determinants of selectivity are entangled with many of the complex factors responsible for the overall conformational plasticity and relative stability of the conductive and non-conductive form of the filter (57–64). For instance, the filter of some K⁺ channels is unable to remain in its conductive conformation when exposed to an ionic solution with few or no K⁺ ions. Under such conditions, the filter of KcsA rapidly converts to a non-conductive state because K⁺ ions are needed to maintain the conductive state of the channel, giving rise to some kind of conformationally-driven super-selectivity, a complex phenomenon that must be distinguished from the more traditional notion of conductive-state selectivity (65, 66). In this regard, studies of a K⁺ channel “locked” in its conductive conformation, constructed using a semisynthetic form of the KcsA channel in which the highly conserved glycine at position 77 was substituted by the d-enantiomer of alanine (KcsA^D-ala77) are extremely interesting (40). It was observed that this channel retained some selectivity in the presence of K⁺, but was able to conduct Na⁺ in the absence of K⁺, demonstrating that a fundamental aspect of ion selectivity is the ability of K⁺ and Na⁺ ions to compete for the conductive pore. Experimentally, KcsA^D-ala77 channel appears to be permissive to Na⁺ conduction at low K⁺ concentration, in contrast to the wild-type channel that remains strongly selective against Na⁺ regardless of K⁺ concentration (40). To examine the properties of the KcsA^D-ala77 channel at the atomic level, PMF calculations were carried out. The computational results for the KcsA^D-ala77 channel are shown in Figs. 8 and 9. Most strikingly, selectivity appears to be dramatically reduced. The free energy barrier opposing the ion translocation of the K⁺/Na⁺/K⁺ system is considerably smaller in the semisynthetic KcsA^D-ala77 than that in the WT channel. On the other hand, the semisynthetic KcsA^D-ala77 channel is predicted to have a smaller K⁺ conductance than WT, with a second large barrier appearing in addition to the recurrent one seen in the WT. The additional free energy barrier lies between the S2/S4/cavity and S3/cavity/cavity configurations (with some similarities to the PMF of the flipped state).

Figure 8.

Free energy landscape of the permeation process for K⁺/K⁺/K⁺ (D-Ala77 filter) A & C) Two 2-dimensional views of the computed PMF for conduction of an Na⁺ ion chaperoned by two K⁺, in the style of Berneche and Roux (21), overlaid with computed minimum-energy pathway. B) Representative snapshots of six numbered points along the pathway, corresponding to local minima along the pathway.

Figure 9.

Free energy landscape of the permeation process for K⁺/Na⁺/K⁺ (D-Ala77 filter) A & C) Two 2-dimensional views of the computed PMF for conduction of an Na⁺ ion chaperoned by two K⁺, overlaid with computed minimum-energy pathway. B) Representative snapshots of six numbered points along the pathway, corresponding to local minima along the pathway.

CONCLUDING DISCUSSION

The classic “thermodynamic” view of selectivity posits that the free energy difference between K⁺ and Na⁺ in the pore relative to the bulk solution is the critical quantity at the origin of selectivity. Such a thermodynamic view is strongly supported by the Ba²⁺ blockade experiments of Miller and co-workers, and by the microcalorimetry measurements of Lockless et al (9), which offer experimental evidence of equilibrium binding site selectivity in the KcsA channel. Ba²⁺ block experiments provide the most quantitatively informative measurements of binding site selectivity (5, 6, 8). Because the blocks by Ba²⁺ last for a very long time, the experiment allows an estimate of the quasi-equilibrium dissociation constant of Na⁺ or K⁺ for a binding site called the “external lock-in site”. However, while Ba²⁺ block experiments demonstrate without ambiguity that KcsA is extremely selective for K⁺ over Na⁺ (8), an interpretation that is consistent with available X-ray structural data is not straightforward (9, 67). The last few years have seen an emergence of new ideas challenging the classic views. Nimigean and Allen have emphasized the kinetic aspects of selectivity based on studies of Na+ blocks in the bacterial KcsA channel (10–12). At the same time, Jiang et al have emphasized the multi-ion aspects of selectivity in K⁺ channels. By examining the properties of MthK (13) and NaK (14, 15) mutants, they showed that the channel becomes selective only if there are four consecutive binding sites along the filter. While the thermodynamic/kinetic debate can be resolved in terms of classic arguments (the mechanism is controlled by free energy differences at the bottom of the binding wells versus the top of the activation barriers), the recent multi-ion data forces us to reformulate this classic argument to account for the multi-site/multi-ion aspect of selectivity.

The PMF strategy used here offers a powerful computational framework that can help resolve the multi-ion aspects of selectivity. The use of the string method allowed maximum-likelihood pathways to be found through PMFs of high dimensionality. The computations demonstrate that an effective 1d free energy profile tagging the central ion does not contain the ingredients to support selective conduction. Structurally, other ions are needed to bracket and restrain the central ion (K⁺ or Na⁺) to display selective ion conduction. The pore does not display selective ion conduction when all but one ion are allowed to adopt equilibrium Boltzmann-weighted distributions. Thus, the selectivity for K⁺ over Na⁺ in the KcsA channel is a feature that emerges only as the result of the multi-ion process. Future work shall focus on testing this hypothesis using the high-resolution structures for MthK(13) and NaK channels,(14, 15). The role of Val76 is also of potential future interest. Several simulation efforts on potassium channels have previously suggested that this highly conserved residue is quite prone to ‘flipping’ away from its standard conductive state with backbone carbonyl pointing towards the conduction pathway, even on extremely fast nanosecond timescales. Our results show that, with even one subunit’s Val76 in its flipped conformation, conduction of potassium would be significantly reduced, but selectivity against sodium would also be abolished. Potentially, regulating this flipping behavior might be a way for a channel to control both its potassium conductance and its selectivity.