Chemically Accurate Simulation of a Polyatomic Molecule-Metal Surface Reaction

Abstract

Although important to heterogeneous catalysis, the ability to accurately model reactions of polyatomic molecules with metal surfaces has not kept pace with developments in gas phase dynamics. Partnering the specific reaction parameter (SRP) approach to density functional theory with ab initio molecular dynamics (AIMD) extends our ability to model reactions with metals with quantitative accuracy from only the lightest reactant, H₂, to essentially all molecules. This is demonstrated with AIMD calculations on CHD₃ + Ni(111) in which the SRP functional is fitted to supersonic beam experiments, and validated by showing that AIMD with the resulting functional reproduces initial-state selected sticking measurements with chemical accuracy (4.2 kJ/mol ≈ 1 kcal/mol). The need for only semilocal exchange makes our scheme computationally tractable for dissociation on transition metals.

The ability to model bond cleavage and formation is central to chemistry. The high accuracy of ab initio methods has enabled quantitatively accurate descriptions of bimolecular gas phase reactions involving polyatomic molecules.^1,2 However, for reactions of molecules on metal surfaces the need for a simultaneously accurate description of the molecule and the metal poses notorious challenges to both density functional theory (DFT)³ and ab initio^4,5 electronic structure methods. As a result, dynamics calculations on dissociative chemisorption reactions of polyatomic molecules⁶⁻¹³ generally achieve only semiquantitative agreement with experiments. The sketched state of affairs is unfortunate, as accurate theoretical data for surface reactions representing rate limiting steps could help with modeling heterogeneously catalyzed reactions more accurately¹⁴ than now possible.¹⁵

Present hurdles to theoretical progress with reactions of polyatomic molecules with metals are both computational and experimental. The only computationally tractable electronic structure theory applicable within a dynamics framework is DFT at the gradient and meta-gradient approximation levels.¹⁶ Benchmark studies of gas phase reactions suggest that the corresponding functionals are not capable of predicting reaction barriers with chemical accuracy^16,17 (1 kcal/mol ≈ 4.2 kJ/mol). In dynamics, the accurate description of surface reactions involving molecules heavier than H₂ necessitates modeling effects of surface atom vibrations, which may modulate the reaction barrier height⁷ or mediate energy transfer between molecular and surface motion.¹⁸ Experiments useful¹⁶ for quantitative comparison with theory were often performed under conditions that require quantum dynamics for an accurate description.^6,19−22 To be feasible, such simulations still require drastic approximations including the neglect^6,8 or approximate^10,11 modeling of degrees of freedom important to the reaction.

As an example of a polyatomic molecule-metal surface reaction, dissociative chemisorption of methane is interesting for practical and fundamental reasons. Its dissociation on catalytic Ni surfaces is a rate-determining step in the current commercial process for hydrogen production (steam reforming²³). Methane + metal surface systems represent important models for identifying reactivity patterns unique to polyatomic reagents.^19−22,24 For instance, the reaction in methane + Ni and the very similar¹¹ methane + Pt systems is nonstatistical: the reaction probability depends sensitively on the identity of methane’s vibrational state and not just on the total available energy.^19,20,24 The reactivity of partially deuterated methane, CHD₃, is bond selective: pre-exciting one quantum of the ν₁ C–H stretch vibration can lead to a 100-fold increase in the ratio of C–H to C–D bond cleavage reaction products on Ni(111).²²

To demonstrate a novel, joint theoretical-experimental approach to accurately model reactions of polyatomic molecules on metals, we select the CHD₃ + Ni(111) system, and proceed as follows. First, experiments are done to measure an observable that is sensitive to the reaction barrier height in our specific system. We select conditions that ensure that the quasi-classical trajectory (QCT) method, which we use in the Ab Initio Molecular Dynamics (AIMD), enables an accurate comparison.⁹ Specifically, we perform supersonic molecular beam measurements²⁵ of the probability that CHD₃ reacts with Ni(111) for conditions (incidence energy E_i, vibrational energy) such that reaction occurs in the “over the barrier” energy regime. The experiments use beams seeded with H₂, allowing high E_i (up to 160 kJ/mol) to be achieved with the lowest possible nozzle temperature T_n (≤900 K), so that the experiments probe the reactivity of CHD₃ in its vibrational ground state as much as possible. The experiments are done for a surface temperature (T_s, 550 K) that exceeds the surface Debye temperature of Ni(111) (370 ± 5K²⁶), so that energy exchange with the surface phonons is in the classical regime. The measured “laser-off” reaction probabilities (S₀^off) are plotted in Figure 1.

Figure 1.

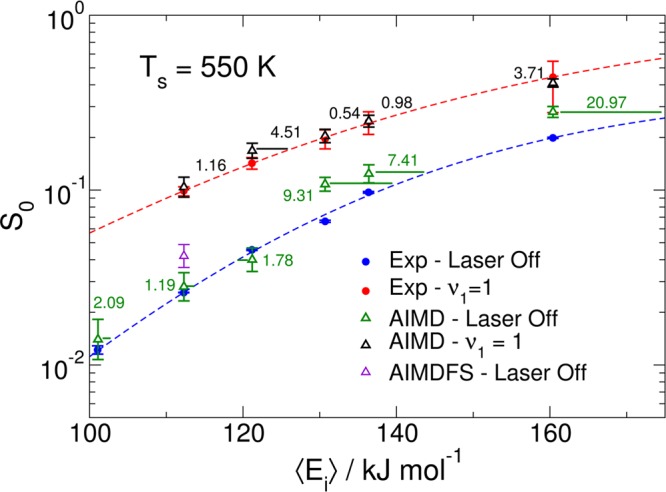
Comparison of calculated and experimental reaction probabilities. The blue and red dashed lines are fits to the corresponding experimental values (solid circles) for S₀^off and S₀. AIMD results appear as open symbols. Numbers indicate the horizontal offsets (in kJ/mol) between the computed reaction probabilities and the fitted experimental S₀ curves. Error bars represent 68% confidence intervals. One AIMD result for a frozen surface (AIMDFS) is added for laser-off reaction at 112 kJ/mol (open purple triangle).

Next, we perform calculations using AIMD,^9,27 with the forces directly obtained from DFT using a specific reaction parameter (SRP) functional,²⁸ employing the ab initio total-energy and molecular-dynamics program VASP.^29,30 Crucially, AIMD allows the modeling of surface atom motion that may facilitate dissociative chemisorption or hinder it,^7,18 in addition to the motion in all molecular degrees of freedom. In the spirit of SRP–DFT,^28,31 an adjustable exchange-correlation functional is used

1

Here, E_C^vdW–DF is a nonlocal, nonempirical correlation functional that also describes the dispersion van der Waals forces.³² The exchange functional E_X is interpolated between the exchange parts of two functionals on which the same physical constraints have been imposed, that is, the general purpose PBE³³ functional, and the RPBE functional that is more adept at describing chemisorption on metals.³⁴ Previous experience with other systems suggests that this interpolation allows an accurate description of the height of the barrier for dissociative chemisorption on late transition metals, with the added bonus of an improved description of the van der Waals forces.

We fit the SRP functional (x in eq 1) to the “laser-off” experiments, requiring that the computed S₀^off reproduce the measured values at E_i just above the classical threshold. With the T_n used (550–650 K), at these E_i (between 101 and 121 kJ/mol) the molecules are predominantly in the ground vibrational state (population ≥ 60%), which should make a quasiclassical description accurate. A trial and error procedure results in good agreement with experiment (see Figure 1) for the stated E_i with x = 0.32, which we use in all subsequent calculations. The lesser agreement with the data for higher E_i does not invalidate the functional: We argue that classical mechanics might not properly account for surface induced quasi-resonant energy transfer among the C–D bonds in the vibrationally excited molecules, which make up more than 40% of the beam’s population at these E_i.

To validate the fitted functional, we measure and compute initial state-selected reaction probabilities, for the CH-stretch vibration laser excited with one quantum (ν₁ = 1, “laser-on” experiments). Quantitative agreement is obtained (Figure 1), as seen using two different methods to assess accuracy. In method 1, which can be motivated on the basis of a classical hole model,³¹ we measure the displacements along the energy axis between the computed S₀ and S-shaped S₀ curves fitted to the experiments. Because the displacements are less than 4.2 kJ/mol for four out of five data points (Figure 1), we say that the calculations reproduce the measurements for ν₁ = 1 with chemical accuracy. We attribute the observation of a slightly larger displacement for one data point (4.5 kJ/mol for E_i = 121 kJ/mol) to statistical error; shifting down this computed point by one σ reduces the difference to much less than 4.2 kJ/mol, and such a fluctuation may be expected for one out of five data points. In method 2, which takes such statistical fluctuations into account, we test the null hypothesis that the computed S₀ are, within statistical uncertainties, equal to the measured ones, using a Stouffer’s Z-score test.³⁵ Application of this test to the ν₁ = 1 data shows that this hypothesis can be accepted with a p-value of 0.47; one would normally only reject this hypothesis if the p value would be less than 0.05.

We attribute the success of the SRP functional to accurately describe experiments probing the barrier geometry, the barrier height, and its dependence on the molecule’s impact site and orientation to two facts. First, we interpolate between exchange functionals to ensure an accurate description of experiments sensitive to the minimum reaction barrier height. Second, taking the weighted average of these functionals ensures that the resulting functional is soundly based on the same physical principles used to construct the individual functionals.³²⁻³⁴ As a result, the SRP functional also correctly predicts the extent to which vibrational pre-excitation of the CH-stretch vibration promotes reaction, and reproduces the state-selected experiments over a wide range of incidence energies. Application of Polanyi’s rules³⁶ and of the hole model³¹ then suggests that the SRP functional correctly describes the CH bond distance at the barrier and the dependence of the molecule surface interaction on the molecule’s point of impact on, and/or its orientation relative to the surface.

We also use the hole model to argue³¹ that the minimum barrier height E_b extractable with the SRP functional exhibits chemical accuracy if the computed and measured reaction probability curves agree to within 4.2 kJ/mol. Using the climbing image nudged elastic band (CINEB) method to identify the transition state we find that E_b = 97.9 kJ/mol for methane interacting with a cold, undistorted Ni(111) surface (Figure 2).

Figure 2.

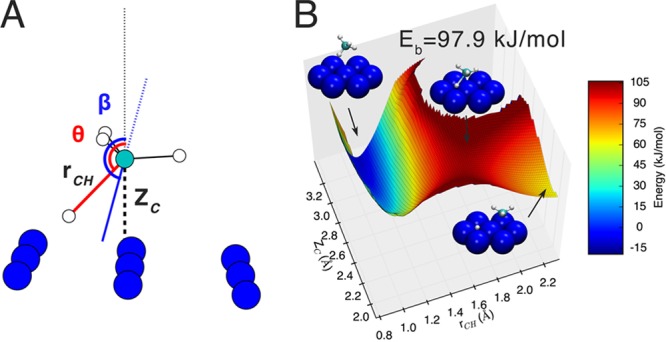
Coordinates, transition state geometry, and potential energy surface for CHD₃ dissociation on Ni(111). (A) In the transition state, Z_C is the distance from the C atom to the surface (2.18 Å) and r_CH the C–H distance of the dissociating bond (1.61 Å). The dissociating CH bond is oriented at angle θ = 136°, and the principal axis of the methyl fragment at angle β = 165° with respect to the surface normal. (B) Two dimensional cut of the potential energy surface as a function of Z_C and r_CH following minimization with respect to all other molecular degrees of freedom. Insets illustrate the reactant state, the transition state, and the separated products.

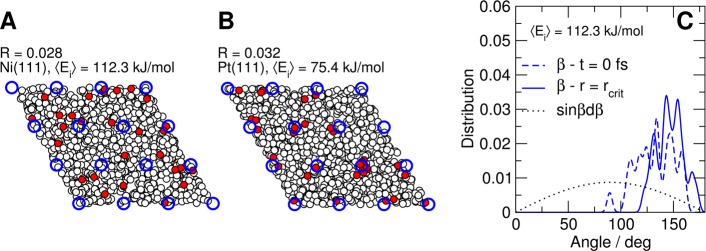
With AIMD one can explore features of the reaction dynamics without pre-existing biases of reduced dimensionality calculations. For similar S₀ (S₀ ≈ 0.03), reaction on Ni(111) occurs at a wide range of impact sites (Figure 3A), whereas CHD₃ reacts only near on-top sites⁹ in the very similar¹¹ methane + Pt(111) system (Figure 3B). These findings have implications for the dynamical treatment of the azimuthal ϕ-rotation of the molecule around the surface normal (Figure 2). At the on-top site, the interaction potential shows little dependence on ϕ.³⁷Figure 3B then suggests that approximations neglecting this dependence⁸ should work well for Pt(111) at low E_i. A more accurate treatment (sudden, i.e., with simple averaging over ϕ,^12,38 or fully coupled dynamics³⁸) should be used for Ni(111), for which reaction also occurs at other sites (Figure 3A), where the molecule–surface interaction varies greatly with ϕ.¹² Very recent work on CH₄ + Ni(111) indeed shows that fully azimuthally coupled results differ considerably from results of calculations performed for a single value of ϕ, even if the results are averaged over impact sites.³⁸

Figure 3.

Impact sites and molecular orientation in collisions of CHD₃ with Ni(111) and Pt(111). (A,B) Initial distribution of impact sites for reacting (red circles) and scattering (white circles) molecules above Ni(111) at E_i = 112.3 kJ/mol (A) and Pt(111) at E_i = 75.4 kJ/mol⁹ (B). Blue circles indicate first layer atoms in ideal positions. (C) Molecular orientation of reactive trajectories for CHD₃ + Ni(111) at E_i = 112.3 kJ/mol, showing the angle β defined in Figure 2 (blue traces). Dashed (solid) traces represent the orientation at time zero (at the time of reaction). The dotted line illustrates random uniform sampling.

In a similar vein, the AIMD calculations show that the β angle between the umbrella axis of reacting CHD₃ and the surface normal (Figure 2) changes considerably on approaching the surface for E_i = 112.3 kJ/mol (Figure 3C), as in reaction on Pt(111).³⁹ Sudden approximations to the associated tumbling rotation should then be inaccurate. Our results for Ni(111) confirm findings for Pt(111)⁹ that the rotations can not be treated with the rotationally adiabatic approximation,¹¹ which would only hold if the initial β distribution of reacting methane would roughly equal the uniform sampling sin β distribution in Figure 3C.

Finally, our AIMD calculations impart thermal motion to all surface atoms and allow them to respond to the incoming molecule. We gain unique insight into the role of surface atom motion by comparing our results with AIMD calculations in which the surface is kept frozen at its ideal 0K configuration (AIMDFS, see Figure 1). Comparison of the AIMD and AIMDFS results at E_i = 112 kJ/mol suggests that when reaction occurs in the classical, over the barrier regime, surface motion hinders rather than promotes reaction. This is consistent with earlier results of Nave and Jackson for CH₄ on Ni(111)⁴⁰ and can be attributed to reaction being hindered by surface recoil at high E_i.

Although we used state-resolved reactivity measurements to validate the SRP functional, other experiments can also be used for validation. In principle the SRP–DFT–AIMD approach should be applicable to any molecule reacting with a metal surface, as long as experiments can be devised on the system that are amenable to an accurate quasiclassical dynamical treatment. The present work and previous experience suggest that accurate results are attainable for molecules dissociating on transition metals with SRP functionals containing semilocal exchange (eq 1), making our scheme widely applicable. This is not self-evident: DFT studies show that GGA functionals like PBE and RPBE systematically underestimate barrier heights of a wide variety of gas phase reactions.⁴¹ This failure has been attributed to gradient corrected functionals predicting too low energies for transition states in which electrons delocalize over the nuclei involved in the reaction.⁴² Assuming the essential ideas underlying this explanation to be correct, the good performance of these functionals for dissociation on transition metals can be explained as follows: although the GGA description of the delocalization of the electrons in the breaking molecular bond should overstabilize the transition state, the localization of two electrons coming from the metal in the emerging metal-molecular fragment bonds apparently cancels this effect. Additional research is needed to provide this explanation with a firm theoretical basis.

The dynamical insights and SRP functional extracted for specific polyatomic molecule-metal surface systems can help to test and guide the design of quantum dynamical methods for these systems.⁶⁻¹² Provided that enough degrees of freedom are modeled and that any dynamical approximations are sufficiently accurate, quantum dynamics calculations using a PES based on converged DFT calculations with our SRP functional should reproduce measured sticking probabilities for methane + Ni(111). The reaction barriers extractable for such systems with our approach can be used to benchmark¹⁶ electronic structure methods holding promise for achieving chemical accuracy for the systems of interest in future.^4,5 Finally, extension to reactions affected by nonadiabatic effects,⁴³ like electron–hole pair excitation, should be possible by combining the SRP approach with AIMD with electronic friction (AIMDEF).⁴⁴

Here, we have taken the step of advancing from a semiquantitatively to a quantitatively accurate computational description of the activated reaction of a polyatomic molecule with a metal surface. Pairing the SRP approach to DFT²⁸ with AIMD^9,27 extends our ability to model reactions with metal surfaces with quantitative accuracy from only the lightest reactant, H₂,³¹ to essentially all reactant molecules. We have demonstrated this with AIMD calculations on CHD₃ + Ni(111) in which the SRP functional has been fitted to supersonic molecular beam experiments and validated by showing that AIMD with the resulting functional reproduces measured initial-state selected reaction probabilities with chemical accuracy over a large range of E_i. The present work and previous experience suggest that the SRP–DFT–AIMD scheme can be applied to molecules dissociating on transition metals in a computationally efficient manner, using semilocal exchange only, and an explanation has been offered for this surprising finding.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.6b01022.

• Supporting text describing the experimental and theoretical methods, the Stouffer’s Z-score statistical test, the determination of the SRP density functional, consequences of different ways of extracting initial state-selected reaction probabilities from experiments for the comparison with theory, extracted minimum barrier heights and PES information, additional AIMD results, and the accuracy of approaches using only semilocal exchange for computing dissociation barriers for molecules on transition metals. Molecular beam parameters (Table S1), effect of intrapolyad cooling (Table S2), parameters used to predict excited state population (Table S3), DFT convergence tests (Table S4), parameters of fitted reaction probability curves (Table S5), transition state energies (Table S6). Calculated vibrational state populations (Figure S1), molecular beam reflectivity measurement (Figure S2), predicted excited state population vs bolometer signal (Figure S3), previous and present experimental sticking probabilities (Figure S4), computed van der Waals interaction (Figure S5), trial and error procedure for determining SRP functional (Figure S6), computed fraction of CHD₃ molecules reacting by C–H bond cleavage (Figure S7), comparisons computed and experimentally determined state-selected reaction probabilities (Figures S8 and S9), illustration of fit functions (Figure S10), reactive impact parameter distributions (Figure S11), initial distributions of reactive and nonreactive impact sites (Figure S12), distance traveled along surface for reactive and nonreactive encounters (Figure S13), molecular orientation in reactive collisions (Figure S14). (PDF)

The authors declare no competing financial interest.