A New Method for Determining Structure Ensemble: Application to a RNA Binding Di-Domain Protein

Abstract

Structure ensemble determination is the basis of understanding the structure-function relationship of a multidomain protein with weak domain-domain interactions. Paramagnetic relaxation enhancement has been proven a powerful tool in the study of structure ensembles, but there exist a number of challenges such as spin-label flexibility, domain dynamics, and overfitting. Here we propose a new (to our knowledge) method to describe structure ensembles using a minimal number of conformers. In this method, individual domains are considered rigid; the position of each spin-label conformer and the structure of each protein conformer are defined by three and six orthogonal parameters, respectively. First, the spin-label ensemble is determined by optimizing the positions and populations of spin-label conformers against intradomain paramagnetic relaxation enhancements with a genetic algorithm. Subsequently, the protein structure ensemble is optimized using a more efficient genetic algorithm-based approach and an overfitting indicator, both of which were established in this work. The method was validated using a reference ensemble with a set of conformers whose populations and structures are known. This method was also applied to study the structure ensemble of the tandem di-domain of a poly (U) binding protein. The determined ensemble was supported by small-angle x-ray scattering and nuclear magnetic resonance relaxation data. The ensemble obtained suggests an induced fit mechanism for recognition of target RNA by the protein.

Introduction

Many multiple domain proteins possess domain motions. Such motions result in coexistence of multiple conformers with different populations or a structure ensemble in solution. The motions often play key roles in protein functions (1, 2, 3, 4) such as catalysis, regulatory activity, and cellular locomotion. Recently, intensive efforts have been made to investigate the less populated conformers and structure ensembles using various experimental methods (5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17). Paramagnetic relaxation enhancement (PRE) (18) technique has been proven to be a powerful method in conformational ensemble study (19, 20, 21). In PRE experiments, the detectable distance (r) between a paramagnetic center located at a spin-label and an observed proton can reach up to ∼35 Å, providing long-distance information for structure determination. Besides, the proportional property of PRE to $\langle r^{-6}\rangle$ allows lowly populated (<10%) conformations to contribute significantly to experiment observables (22), provided that proper spin-labeling sites are chosen. In terms of structure, however, interpretation of PRE data, which are the weighted averages of physical quantities over all conformers truly existing in a dynamic system, is challenging due to inherent protein dynamics and extra flexibility of spin-labels.

Currently, a number of methods have been proposed to calculate a structure ensemble from experimental data such as PREs. The strategies utilized in these methods can be classified into direct and indirect strategies (23, 24). The direct strategy is to calculate a structure ensemble from PREs and other possible restraints by simulated annealing (provided by Xplor-NIH) (20, 21, 25). The indirect strategy is to create a pool of structures and then search for an ensemble of candidates from the pool (26, 27, 28, 29, 30, 31). Both strategies optimize the agreement between experimental PREs and backcalculated PREs from the derived ensemble. In general, the agreement improves gradually with the increase of ensemble size (number of structures) and often reaches a plateau at relatively large ensemble sizes. In fact, the exact ensemble size is uncertain and the use of a large number of conformers to represent the ensemble is often inevitable, which may lead to ambiguous interpretations of the structure-function relationship of a multidomain protein. Furthermore, overfitting often occurs when too many variables (or protein structures) are used to interpret a limited number of observables. The overfitting may result in some false structures, which can mislead our understanding of the structure-function relationship.

Here, we present a new (to our knowledge) method, denoted as orthogonal-parameters-based ensemble optimization (OPEO), aiming for using a minimal ensemble size to interpret PREs of a di-domain protein. In this method, individual domain structures were assumed to be known and rigid; spin-label and protein conformations were defined by three and six orthogonal parameters, respectively. First, the ensemble representation of each spin-label was solved by fitting conformer populations and orthogonal parameters against intradomain PREs. Subsequently, the protein structure ensemble was determined from interdomain PREs. To prevent overfitting caused by excessive protein ensemble members, a new (to our knowledge) criterion was established. As demonstrated on a reference ensemble (24) with predefined protein conformer number, conformations, and populations, the method and criterion proposed here can produce correct ensembles that agree very well with the input reference ensemble. We also applied the method to determine the structure ensemble of the di-domain of a poly (U) binding protein (Pub1p) in Saccharomyces cerevisiae.

Pub1p is known as an important regulator of cellular mRNA decay (32, 33). It modulates mRNA stability and turnover by blocking different degradation pathways and responds to various stresses such as glucose starvation, heat shock, arsenite, sodium azide, and high ethanol levels (34, 35, 36, 37). Pub1p is a multidomain protein containing two tandem RNA recognition motif (RRM) domains in the N-terminal region, one RRM domain in the C-terminal region, and a conserved methionine- and asparagine-rich domain between RRMs 2 and 3. Previous studies indicate that individual RRM domains bind to poly(U) with similar affinity, but the two tandem RRM domains connected by a 10-residue linker, here denoted as PubRRM12, have significantly higher affinity than the individual domains. The crystal structure of PubRRM12 has been reported in Li et al. (38), indicating that the two RRM domains do not interact. To understand the molecular mechanism of RRM-mediated RNA/DNA recognition, we solved the individual domain structures of PubRRM12 by nuclear magnetic resonance (NMR) and then used the method developed here to determine the structure ensemble. We showed that the tandem di-domain exists in four conformers in solution, and that none of them is in a fully open conformation that can readily interact with single-stranded RNA.

Materials and Methods

Protein expression and purification

Recombinant PubRRM12 (residues E71–K240), RRM1 (residues E71–S154), and RRM2 (residues Q155–K240) were cloned into a pETM vector and transformed into BL21(DE3) strain. ¹⁵N spin-labeled (¹⁵N, ¹³C spin-labeled) proteins were expressed overnight in M9 minimal medium containing 1 g/L ¹⁵N NH₄Cl (1 g/L ¹⁵N NH₄Cl and 2 g/L ¹³C spin-labeled glucose) at 20°C. The proteins were purified using Ni-NTA beads followed by cleavage of the His-tag with thrombin and further purification with a gel filtration column Superdex 75 (GE Healthcare Life Sciences, Marlborough, MA). The final buffer used contained 20 mM NaCl and 20 mM sodium phosphate at pH 6.5.

Spin-labeling

The wild-type PubRRM12 contains no cysteine residues. Single-cysteine mutants were prepared by site-directed mutagenesis at residues M107, H123, N148, S190, and N218. ¹⁵N-labeled mutants were expressed and purified using the same protocol as for the wild-type PubRRM12. Just before spin-labeling, the purified proteins were treated for 4 h with 5 mM DTT (dithiothreitol) at room temperature. DTT was then removed from the sample using a gel filtration column Superdex 75 (GE Healthcare Life Sciences). The eluted protein was immediately incubated with a 10-fold molar excess of MTSL overnight at 4°C. The free MTSL was removed using a gel filtration column again. The eluted protein was concentrated to ∼0.2 mM in a buffer of 20 mM NaCl and 20 mM sodium phosphate at pH 6.5, and then used for NMR experiments.

NMR spectroscopy and structure determination of individual domains

All NMR experiments were performed on an Avance 800 spectrometer (Bruker, Billerica, MA) equipped with a cryo-probe at 25°C. To determine the structure, two-dimensional (2D) HSQC, three-dimensional HNCA, HNCOCA, MQ-(H)CCH-TOCSY (39), and four-dimensional (4D) NOESY (40, 41) were recorded on a ¹³C,¹⁵N spin-labeled PubRRM12 sample at a protein concentration of 1.0 mM in a buffer with 90% H₂O, 10% D₂O, 20 mM NaCl, and 20 mM sodium phosphate (pH 6.5). ¹⁵N relaxation rates R₁ and R₂ and heteronuclear ¹⁵N nuclear Overhauser effects (NOEs) were measured on ¹⁵N-labeled samples with ∼0.2 mM protein. Generalized order parameter (S²) and localized correlation time (τ_loc) were extracted on a per-residue basis from R₁, R₂, and NOE data using a simple method based on the Lipari-Szabo model, as described previously in Yang et al. (42). This method can be used to obtain dynamics parameters for nonspherical proteins. To examine if the two domains interact with each other, 2D ¹H-¹⁵N HSQC spectra of RRM1, RRM2, and PubRRM12 were acquired on ¹⁵N spin-labeled samples (∼2 mg/mL) in the same buffer. PRE data were obtained from measurements of ¹H_N transverse relaxation rates (R₂) of spin-labeled and unlabeled proteins using a two time-point method with a relaxation delay of 4 ms between the two time points (43).

NMR spectra were processed using NMRPipe (44) and analyzed using SPARKY. Backbone and side-chain resonance assignments were achieved using the 4D NOESY-based strategy described previously in Xu et al. (40). Unambiguous NOEs were obtained from three subspectra: ¹³C,¹⁵N-edited; ¹³C,¹³C-edited; and ¹⁵N,¹⁵N-edited 4D NOESY. Ambiguous NOEs were further assigned during iterated structure calculation and refinement. Distance constraints were obtained from the NOEs assigned, while dihedral angle restraints of φ and ψ were calculated with TALOS+ (45) using the assigned chemical shifts of C_α, C_β, N, H_α, and HN. One-hundred conformers were calculated with Xplor-NIH (46, 47) using the standard simulated annealing method. Twenty conformers with the lowest target function values were selected for analysis.

Chemical shift perturbation

The combined chemical shift difference of an amide in two samples was calculated by (48):

$$\Delta \delta ={\left[\left(\Delta {\delta }_{NH}^2+\Delta {\delta }_N^2/25\right)/2\right]}^{0.5},$$

where Δδ_NH (Δδ_N) is the ¹H_N (¹⁵N) chemical shift difference between PubRRM12 and RRM1 or between PubRRM12 and RRM2.

Synthetic PREs

To test performance of the method proposed here, we synthesized intradomain and interdomain PREs based on a reference ensemble method (24) then employed the synthetic PREs to calculate a structural ensemble, and finally compared the calculated and reference ensembles. The reference ensemble of PubRRM12 was generated in two steps by assuming that each domain adopts the lowest energy NMR conformation and is rigid, while the linker is fully flexible. First, a pool of protein structures was created by randomly rotating φ- and ψ-angles of the linker residues without steric clashes between any residues. Second, three structures with significant differences were arbitrarily selected as the structure ensemble members, and the populations of the three conformers were assigned as 0.6, 0.2, and 0.2, respectively. Due to its flexibility, MTSL can adopt multiple conformations. An ensemble of MTSL conformers was generated by random dynamic simulation using Xplor-NIH (46, 47) while fixing the protein backbone. The MTSL ensemble used here consisted of 3, 20, or 100 conformers with equal populations. Five sets of PRE data were synthesized from five MTSL-labeled variants by assuming the labeling sites at respective residues M107, H123, N148, S190, and N218. For each set of the data, the PRE of each amide proton was calculated using Eqs. 2 and 3 based on the generated spin-label conformers and protein structure ensemble. Coordinates of the free electron in MTSL were assumed the same as those of the nitroxide oxygen. The apparent correlation time (τ_c^app) used in Eq. 2 was set to 6 ns for all the electron-proton vectors in all the spin-labeled variants.

To account for the uncertainty in distances derived from PREs that is caused by PRE measurement errors and unknown protein and spin-label dynamics, random Gaussian noise was added to each synthetic PRE value. The random noise included a constant error of 3 s⁻¹ that accounted for the measurement errors for both spin-labeled and unlabeled samples and a proportional error of 30% of the PRE value. Introduction of the proportional error is based on the fact that the larger the PRE value, the larger its measurement error (in absolute value) and the larger the PRE uncertainty caused by the unknown dynamics. Eighty-percent PREs were randomly selected for ensemble calculations, and the remaining 20% were used for cross validation.

Small angle x-ray scattering data collection and analysis

Small angle x-ray scattering (SAXS) data were measured with a NanoStar SAXS instrument (Bruker) equipped with a Metal-Jet x-ray source (Excillum, Karlsruhe, Germany) and VÅNTEC 2000-detector system (Bruker) as described previously in Tay et al. (49). SAXS experiments were carried out at 15°C in a series of protein concentrations ranging from 0.5 to 2.0 mg/mL, for a sample volume of 40 μL. The data were collected with six frames at 5 min intervals, and no radiation damage was detected by comparing these frames. The scattering of the buffer was subtracted from the scattering of the sample, and all the scattering data were normalized by the concentration as well as the incoming intensity.

All the data were processed using the program package PRIMUS (50). Quantitative assessment of the protein flexibility was done using the ensemble optimization method (EOM) 2.0 (51). In EOM 2.0, a pool of 10,000 independent models is created first by randomly varying the domain linker conformations. Afterwards, a genetic algorithm (GA) is used to select ensembles with varying numbers of conformers by calculating the average theoretical profile and fitting it to the experimental SAXS data. For each PubRRM12, the GA was repeated 100 independent times and the ensemble with the lowest discrepancy value (χ²) was reported as the best solution out of 100 final ensembles.

Computational strategy

To simplify the complexity caused by spin-label flexibility and protein domain dynamics, a two-step calculation method (25) with a rigid body model is implemented. In all calculations, individual protein domains are assumed to be rigid; the dynamics of a spin-label is represented by a limited number of conformers (m); and the spin-label in each conformer is considered as a single point whose three orthogonal parameters or coordinates (x_k, y_k, z_k) represent the location of the free electron in the label. In the first step, for the ith spin-label with a given ensemble size m, the values x_k, y_k, and z_k, and population (p_k) (k = 1, 2, … m, ∑p_k = 1) are determined from its intradomain PREs by minimizing the Q factor using the conventional GA (52). The optimal ensemble size is determined from the dependence of the Q factor on m. The Q factor for the ith spin-labeled variant is given by:

$$Q_i=\sqrt{\frac{\sum _j{\left\{{\Gamma }_2^{\text{obs}}\left(j\right)-{\Gamma }_2^{\text{cal}}\left(j\right)\right\}}^2}{\sum _j\left\{{\Gamma }_2^{\text{obs}}{\left(j\right)}^2\right\}}},$$ (1)

where Γ₂^obs(j) (Γ₂^cal(j)) is the experimental/synthetic (calculated) intradomain PRE of nuclear spin j; the sum extends over the spins located in the same domain as the spin-label anchoring residue; and Γ₂^cal is given by:

$${\Gamma }_2^{\text{cal}}\left(j\right)=K\langle r_j^{-6}\rangle \left[4{\tau }_c^{\text{app}}+\frac{3{\tau }_c^{\text{app}}}{1+{\left({\omega }_H{\tau }_{\text{c}}^{\text{app}}\right)}^2}\right],$$ (2)

where K = 1.23 × 10⁻⁴⁴ m⁶/s² and ω_H is the proton Larmor frequency. The value $\langle r_j^{-6}\rangle$ is an ensemble-average and given by:

$$\langle r_j^{-6}\rangle =\sum _{k=1}^m{p}_k{r}_{jk}^{-6},$$ (3)

where $r_{jk}={\left[{\left(x_j-x_k\right)}^2+{\left(y_j-y_k\right)}^2+{\left(z_j-z_k\right)}^2\right]}^{0.5}$, which is the distance between spin j and the free electron in the kth conformer; and x_j, y_j, and z_j are the coordinates of spin j. In Eq. 2, τ_c^app is the apparent correlation time and given by τ_c^∗S², where τ_c and S² are the correlation time and generalized order parameter of an electron-proton vector, respectively. For MTSL whose electron relaxation time is much longer than the protein overall rotational time, (τ_r) (21), τ_c = τ_r. The value τ_c^app is assumed identical for all the electron-proton vectors.

For the spins with Γ₂^obs values >80 s⁻¹ or with undetectable HSQC peaks after spin-labeling, their Γ₂^ob values are considered as 80 s⁻¹ in the Q-factor calculation. Similarly, when Γ₂^cal > 80 s⁻¹, Γ₂^cal is treated as 80 s⁻¹.

For each spin-labeled variant, the τ_c^app together with spin-label positions is estimated initially by minimizing the Q factor defined by Eq. 1 (53). Normally, the τ_c^app values for different variants do not vary significantly. So a uniform τ_c^app is assumed for all the variants and its value is set as the average of the estimated τ_c^app values for all the variants. Subsequently, the ensemble of each spin-label is determined using the uniform τ_c^app.

After obtaining the spin-label ensembles, we determine the number of protein conformers (n), relative separation and orientation of two domains, and population (P) of each conformer in the second step. The separation of the two domains is defined by three spherical coordinates (rd, θ, and φ) where rd is the distance between the two domain centers, and θ and φ are the polar and azimuthal angles, respectively, while the relative orientation is expressed by three Euler angles (α, β, and γ). Interdomain PREs of spins located in a domain different from the spin-label anchoring domain are used to calculate n, rd_j, θ_j, φ_j, α_j, β_j, γ_j, and P_j, where j = 1, 2, …, n. Several sets of PRE data obtained from different spin-labeled variants are often used for protein structure ensemble determination. So, an overall Q factor (Q_all) is used for minimization:

$$Q_{\text{all}}=\sqrt{\frac{\sum k_i{Q}_i^2}{\sum k_i}},$$ (4)

where Q_i is the Q factor for the ith spin-labeled variant, and k_i is the number of PREs used in the calculation of Q_i. Spins with Γ₂^obs values <10 s⁻¹ are not counted in the calculation of k_i but included in the calculation of Q_i because they are more error-prone.

Besides the agreement between experimental/synthetic and calculated Γ₂ values, the spatial domain-domain conflict (P_clash) and restraint imposed by the linker between two domains (P_linker) needs to be considered in structure calculations. The final Q factor used for a candidate ensemble is given by:

$$Q=Q_{\text{all}}+P_{\text{clash}}+P_{\text{linker}}.$$ (5)

The dummy residue method is used to evaluate the domain-domain conflict (54). The value P_clash = 100 if the distance between any two C_α atoms in two different domains is smaller than a preset distance limit (6 Å in this study), otherwise P_clash = 0. The value P_linker = 100 if the distance between the C_α atoms in the C-terminus of domain 1 and N-terminus of domain 2 is larger than a limit (23 Å in this study), otherwise P_linker = 0. To cross validate the calculated protein structure ensemble, a small portion of interdomain PREs (10–20%), which is randomly chosen, is not used directly in the optimization. The Q factor calculated from this portion of PREs is denoted as Q_free.

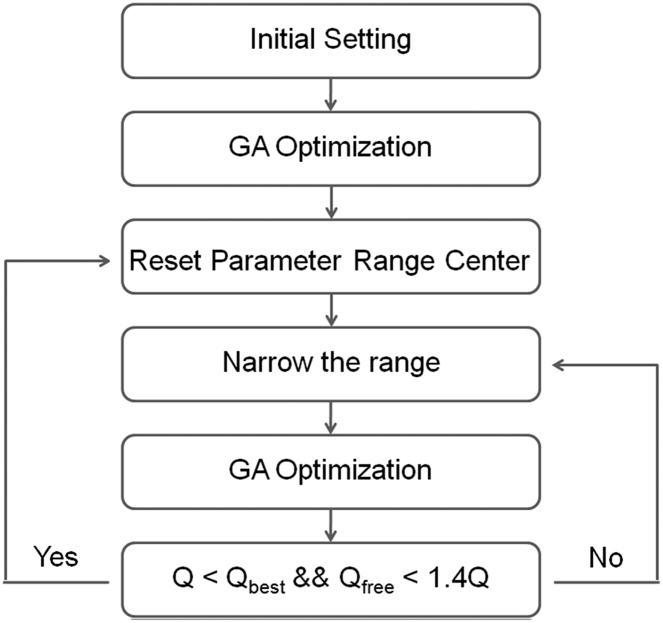
For a given protein ensemble size n, the values rd_j, θ_j, φ_j, α_j, β_j, γ_j, and P_j (j = 1, 2, …, n, ∑P_j = 1) can be optimized by the GA. However, the traditional GA becomes very time-consuming when n is large. To reduce computation time, we developed a progressive narrowing GA protocol (PNGA) (Fig. 1). In the first round of optimization, all the variables are allowed to vary in the entire possible ranges. The Q factor obtained from the optimized ensemble is recorded as the best Q factor (Q_best), and all parameters corresponding to this ensemble are recorded as the best variable values. In the next round of optimization, the range of each variable is reduced by a small fraction (F_red, which is an adjustable parameter and in a range of 1–5%) and the center of the variable range is at the best value obtained in the previous round. If the Q factor obtained from this round of optimization is smaller than Q_best and passes cross validation (Q_free< 1.4Q), the new result will become Q_best; the best variable values will be changed accordingly, the centers of all variable ranges will be reset, and all variable ranges will be reduced further by F_red for the next round of optimization. Otherwise, all parameters will remain unchanged, but the ranges will be reduced by another F_red for the next round of optimization. This optimization process is repeated until the Q-factor value converges. The entire calculation process can be repeated several times to avoid local minimum traps. Because the structures are calculated through orthogonal-parameter-based ensemble optimization, our computational strategy is denoted as OPEO.

Figure 1.

Flowchart describing the PNGA protocol.

Results

Validation of method OPEO with error-free synthetic data

The PREs used in this section were synthesized using a reference ensemble that contained three protein conformers (Fig. S1 in the Supporting Material) in which each spin-label adopted three conformations with equal populations. The synthetic PREs were assumed to have no errors. Using the synthetic intradomain PREs for a variant spin-labeled at M107, we optimized the positions of the three spin-label conformers by fixing τ_c^app at 6 ns. This procedure was repeated for the other four variants spin-labeled at respective sites H123, N148, S190, and N218. The derived positions were very similar to the input ones with differences in a range of 0.3–1.0 Å (Table S1) when the population of each spin-label conformer was fixed at the input value (1/3) during the optimization. The differences in spin-label positions became larger (1.0–2.4 Å) when the population was not fixed but used as a fitting parameter. We found that the Q factor became smaller than 0.01 and was relatively insensitive to the change of spin-label positions once the positions were very close to the true positions. So, the true spin-label positions were difficult to identify. To overcome this drawback, development of other minimization target functions will be necessary in further studies.

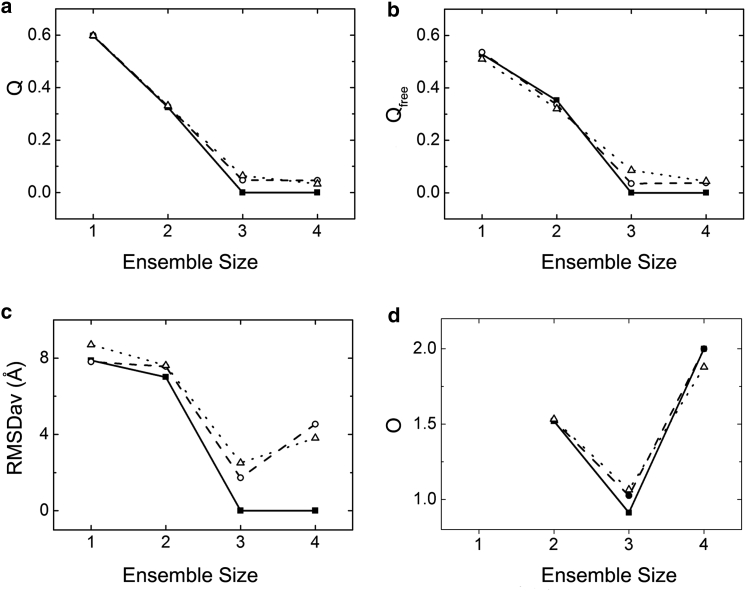
After the spin-label positions in the five variants were determined, protein structure ensembles were calculated with OPEO from interdomain PREs of all the variants by gradually increasing the ensemble size (n) (from 1 to 4). The Q and Q_free factors reached nearly a plateau when the protein ensemble size was three (Fig. 2, a and b). The optimized protein ensembles resembled very closely the reference one with root mean-square deviation (RMSD) values of 1.7 and 2.4 Å for fixed and unfixed spin-label conformer populations, respectively (Fig. 2 c). Although the Q-factor value decreased further with the increase of the ensemble size, the RMSD values between the calculated and reference ensembles became larger when n > 3 (Fig. 2, a–c), indicating occurrence of overfitting. The structure difference between the input and calculated ensembles with three structure members should be caused by deviations of the calculated spin-label positions from the input reference ones. When the spin-label positions were assumed the same as the input ones, the RMSD was nearly zero (Fig. 2 c). Therefore, a correct structure ensemble can be determined from PRE data using the method proposed here.

Figure 2.

Dependences of Q (a), Q_free (b), RMSD_av (c), and O (d) factors on protein ensemble size, which were derived from synthetic PREs. RMSD_av is the average RMSD between the calculated and reference ensembles ($RMS{D}_{av}={\sum }_i{P}_i\times RMS{D}_i$, where P_i is the population of the calculated ith protein conformer, RMSD_i is the RMSD value between the calculated ith conformer and its closest reference/input conformer). Equation 6 defines the O factor that is an overfitting indicator. The results for the cases with fixed and unfixed spin-label populations are indicated by ○ and ▵, respectively. The results for the case where the spin-label conformations used in the protein ensemble calculation are identical to the reference ones are shown by ▪. In this particular case, the calculated third- and fourth-ensemble members have nearly identical structures.

Number of pseudo spin-label conformers

Due to spin-label flexibility, the exact spin-label conformer number and conformations are unknown. Even if such information is available, it is very difficult, if not impossible, to handle computationally a large number of spin-label conformations when a GA is used to calculate a structure ensemble from a limited number of PREs. Is it good enough to use a few pseudo conformers to represent a group of spin-label conformers? To address this question, we assessed the influence of the pseudo spin-label conformer number on the calculated protein structure ensemble using a reference ensemble. The reference ensemble used here was similar to the one used above, but each spin-label in one protein conformer was assumed to have 100 conformers with equal populations (Fig. S1). First, for each spin-label variant we determined the spin-label positions and populations from intradomain PREs through Q-factor minimization by assuming that the spin-label was represented by 1, 3, 5, 7, and 9 pseudo conformers, respectively. The Q factors decreased sharply when the number of the pseudo conformers increased from 1 to 3. Further reduction was insignificant with the increase of the number from 3 to 9. A previous work showed that a five-conformer ensemble represents the dynamic MTSL better than a single conformer (55), which is consistent with our result. Subsequently, protein structure ensembles were calculated with OPEO by fixing the protein ensemble size at three (n = 3).

When the pseudo spin-label conformer numbers were 1–9, the RMSD values between the reference and calculated protein ensembles were 4.5–6 Å and did not display an obvious trend in the absence of PRE errors (Fig. S2 a). In addition, the total population differences were in a range of 0.15–0.3 (Fig. S2 b), although the synthetic PREs matched the backcalculated PREs extremely well (Fig. S3) with a Q factor of ∼0.09. To evaluate the effects of PRE errors on the structure and population differences, three groups of PRE data with different random errors were used to calculate structure ensembles. The ensembles obtained varied, and were also slightly different from those calculated from the data without errors (Fig. S2, a–c), although the back-calculated PREs matched the synthetic PREs quite well (Figs. S4–S6) with Q-factor values ranging from 0.19 to 0.26 (Fig. S2 c). The result indicates that the calculated ensemble is influenced not only by the magnitude of the errors but also by the distribution of the errors among different residues. It is noteworthy that the magnitudes of the three sets of errors were identical and were larger than the upper limit of potential errors in most cases. Surprisingly, the errors did not necessarily cause deterioration in the overall structural quality (Fig. S2, a and b).

To examine if the structure difference is influenced by the number of spin-label conformers existing in a reference ensemble, we prepared another reference ensemble in which each spin-label in a protein conformer had 20 random conformations and the protein ensemble was the same as the one used above. Similarly, the RMSD values between the reference and calculated protein ensembles fluctuated with the pseudo-conformer numbers (1–9) in a range of 3.5–5.5 Å, slightly smaller than those shown in Fig. S2 a. Our results suggest that the deviations in structures and populations should be caused mainly by using a small number of pseudo conformers to represent a large number of spin-label conformers and by the mutual compensation of conformer structures and populations in terms of PREs as further discussed below.

Taking into account computation time that increases with the number of pseudo spin-label conformers as well as differences in structure and population, we proposed to use three pseudo conformers to represent the effective positions of a dynamic MTSL. The previous study on protein/DNA complexes incorporated with dT-EDTA-Mn²⁺ in the DNA has also suggested that a three-conformer model is generally sufficient to represent the spin-label in accurate backcalculation of PRE data (56). According to the results obtained here, the RMSD between the calculated and reference protein ensembles is <6.5 Å but >2 Å, which is insensitive to PRE errors, when three pseudo MTSL conformers are assumed. With this kind of structure accuracy, one shall not look at detailed structures at residue level, but instead focus on the overall structural states of a multidomain protein such as the open and closed states.

Efficiency of progressive narrowing genetic algorithm

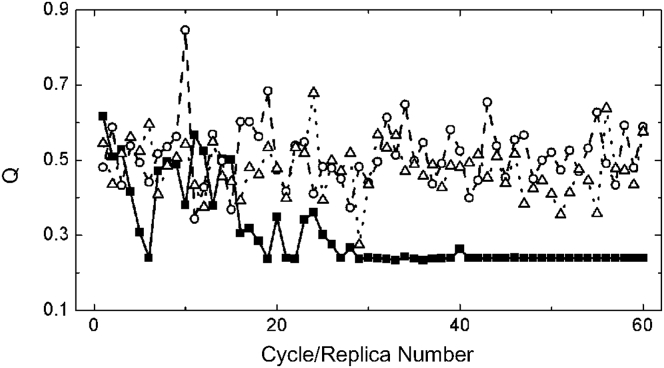
We proposed a PNGA for structure ensemble calculation to reduce computation time. Fig. 3 shows the improvement in comparison with the conventional GA. When the conventional GA was employed to calculate ensembles with four members using a population size of 1200 for 60 replicas, the Q factor always oscillated at a high level. Using a population size of 12,000, the Q factor oscillated at a lower level. When the PNGA was used with a population size of 1200 and a F_red value of 5%, the Q factor reached its lowest value before 20 cycles and completely converged after 40 cycles. The converged Q value was even slightly lower than the minimal value obtained by the conventional GA with a 10-times larger population size. Therefore, PNGA is significantly more efficient (∼20 times faster) than the conventional GA.

Figure 3.

Comparison of results obtained using PNGA with a population size of 1200, progressive narrowing factor (F_red) of 5% (▪), conventional GA with population sizes of 1200 (○) and 12,000 (▵).

Overfitting

We examined overfitting phenomena using reference ensembles, and observed two types of overfittings. When the ensemble size was set at the correct value, the calculated structure ensemble might fit very well to the PRE data used in the calculation, but did not fit well to the unused PRE data, i.e., the Q factor was small but Q_free was large. This type of overfitting can be easily ruled out by checking both Q and Q_free values. Another type of overfitting occurred when excessive ensemble members were used or the ensemble size was larger than the true size. This type of overfitting is often difficult to identify using Q and Q_free because they decrease with the increase of the ensemble size without very obvious minima (Figs. 2 and S7). The overfitting might be evidenced by the increase of RMSD between the calculated and reference ensembles. In practice, the RMSD is not available because the true structure ensemble is unknown for a real system. To avoid this type of overfitting, we have to establish a new criterion.

One feature of the second type overfitting is that unnecessary ensemble members do not improve the Q value as much as the necessary ones do. Thus, we would expect a turning point in the plot of Q factor against the ensemble size when overfitting occurred. In practice, however, the turning point may not be obvious (Figs. 2 and S7). Accordingly, it is more reasonable to consider both the decreasing speed of Q factor against the ensemble size and the Q values than to consider only the Q values in identifying overfitting. Thus an O factor is defined as:

$$O=\frac{2\left(Q_{n-2}-Q_{n-1}\right)}{Q_{n-2}-Q_n}+Q_n,$$ (6)

where Q_n-2, Q_n-1, and Q_n are the Q values for ensemble sizes of n-2, n-1, and n; n ≥ 2; and Q₀ = 1. The first term is the ratio of the Q-factor reduction rate from size n-2 to n-1 to that from size n-2 to n. Normally, it ranges from 1 when the nth ensemble member improves the Q factor as much as the (n-1)th member (i.e., Q_n-2 – Q_n-1 = Q_n-1 – Q_n) to 2 when the nth member has no improvement to the Q factor (i.e., Q_n = Q_n-1). A sharp increase in the ratio is expected when an unnecessary ensemble member is introduced or overfitting occurs. Before occurrence of the overfitting, the ratio may fluctuate with the increase of the ensemble size. It is possible to observe a turning point in a plot of the ratio against the ensemble size even when the Q factor is still relatively large. To eliminate these turning points before overfitting, the second term in Eq. 6 is introduced because the Q factor decreases with the increase of the ensemble size. According to our results obtained from the reference ensembles, the turning points in the O factor plots were much more obvious than those in the Q-factor plots (Figs. 2 d and S7 d). Therefore, the correct ensemble size can be identified from the turning point in an O-factor plot.

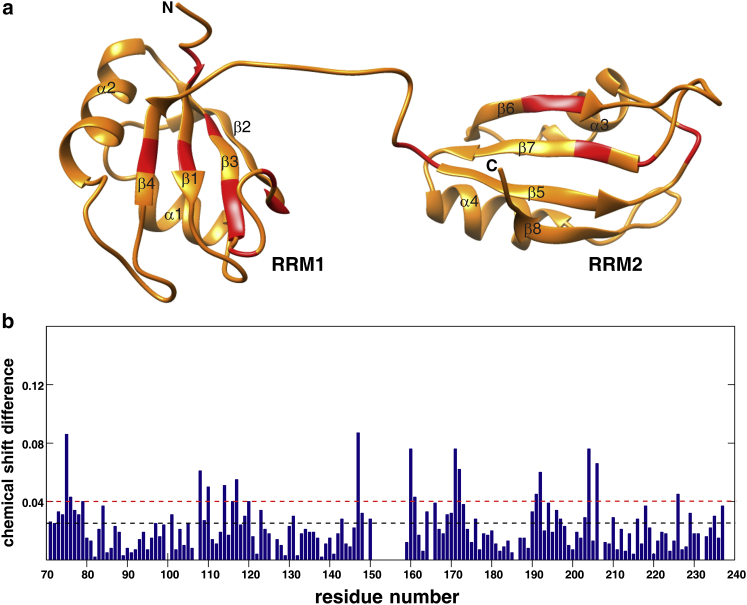
Individual domain structures in solution

Using triple resonance NMR experimental data (Table S2), three-dimensional structures of individual PubRRM12 domains were solved (Fig. 4 a). However, domain-domain orientation could not be determined due to the absence of NOEs between the two domains. Each domain exhibits a canonical βαββαβ fold (57). The structure of each domain obtained here is very similar to the crystal structure solved previously in Li et al. (38) with pairwise backbone RMSD values <1 Å.

Figure 4.

PubRRM12 structure and chemical shift perturbations (Δδ) caused by domain-domain interaction. (a) Ribbon representation with highlighted residues (red) that displayed significant chemical shift perturbations (i.e., Δδ > Δδ_av + SD). (b) Combined chemical shift differences between PubRRM12 and RRM1 and between PubRRM12 and RRM2. The blue-dashed line represents the average Δδ value over all available residues (Δδ_av), while the red-dashed line denotes the value of Δδ_av + SD, where SD is the standard deviation of Δδ values for all available residues. To see this figure in color, go online.

Domain-domain Interaction

To determine whether there are weak interactions between the two domains, isolated RRM1 and RRM2 were compared with the intact PubRRM12 in amide chemical shifts at low protein concentrations (∼2 mg/mL). Interestingly, some residues located far away in sequence from the linker displayed significant chemical shift differences between the intact di-domain and isolated individual domains (Fig. 4 b). As shown below, PubRRM12 existed in monomer at a protein concentration of ∼2 mg/mL. Therefore, the observed chemical shift differences are caused by weak domain-domain interactions rather than weak oligomerization or aggregation.

Structure ensemble of PubRRM12

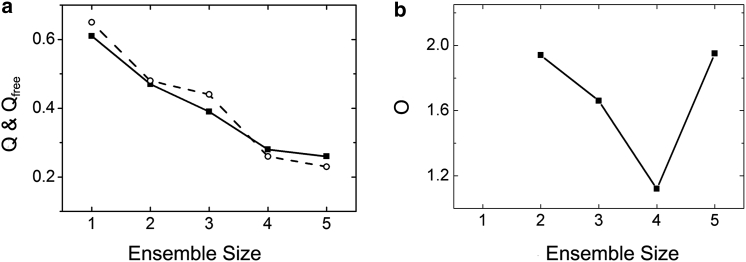
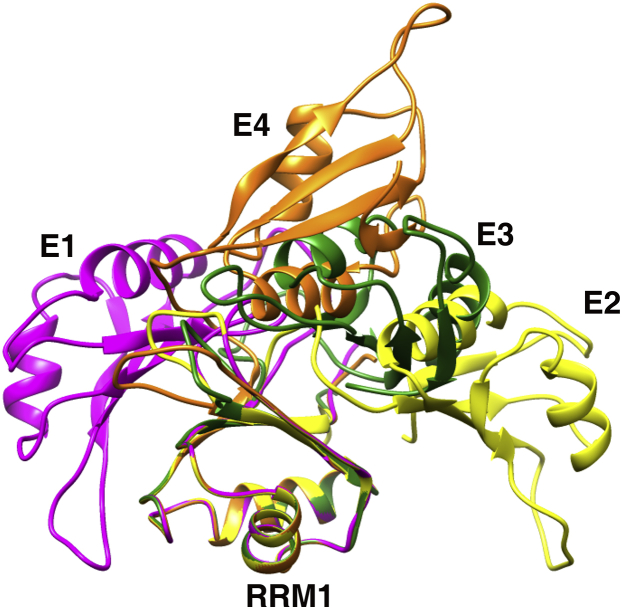
Five PubRRM12 mutants each with one MTSL at respective residues M107, H123, N148, S190, and N218 were used in PRE data collection. In total, 548 PRE restraints collected from the five spin-labeled mutants were used in structure ensemble calculation (Fig. S8), excluding the domain-domain linker region, a loop in RRM2 (195–202), and termini, which are relatively flexible. Ten-percent of PREs for each mutant were randomly chosen for cross validation, and the rest were used in structure calculation. For each spin-label site, an ensemble of three MTSL conformers was used to represent MTSL’s dynamics. The τ_c^app values optimized from the intradomain PREs were in 5.3–6.6 ns for the five variants. A uniform τ_c^app of 6 ns, the average value over all the variants, was used to calculate MTSL positions and protein structures. The Q, Q_free, and O factors against the ensemble size are shown in Fig. 5. Overfitting occurred when the ensemble size reached 5 as indicated by a sharp turning point at an ensemble size of 4 (Fig. 5 b). Thus, the structure ensemble of PubRRM12 could be represented by four members (Fig. 6) with populations of 43.6% (E1), 6.9% (E2), 43.2% (E3), and 6.3% (E4). The calculated structure ensemble fits very well to the experimental PREs (Fig. S8), indicating that E1–E4 reflect the domain dynamics of PubRRM12 in solution.

Figure 5.

Dependences of Q (▪) and Q_free (○) (a) and O (b) factors on the ensemble size of PubRRM12, which were derived from experimental PREs.

Figure 6.

Ribbon diagrams of four ensemble members (E1, E2, E3, and E4) of PubRRM12. E1, E2, E3, and E4 are shown in magenta, yellow, green, and orange. RRM1 domain structures are superimposed.

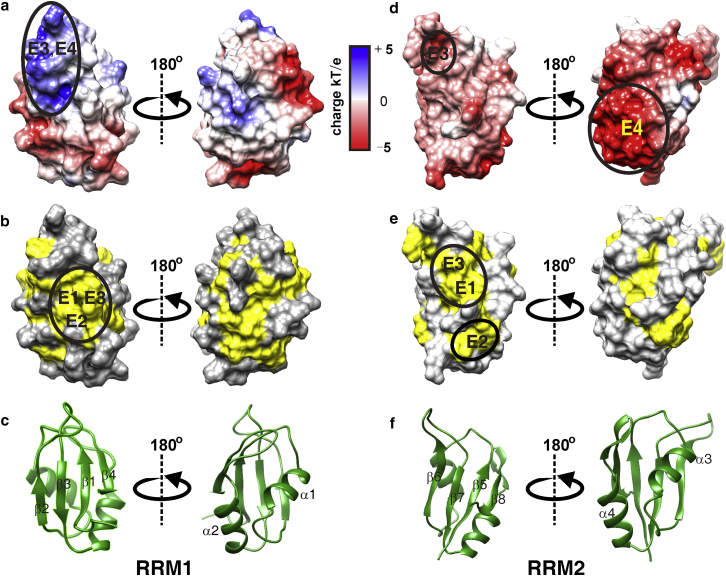
According to the structures, both E1 and E3 are stabilized mainly by hydrophobic interactions involving two large and protrusive hydrophobic patches: one on sheet β1–β4 in RRM1 and the other on β5–β8 in RRM2 (Fig. 7). In addition, electrostatic interaction may contribute to the stability of E3 because the positive patch in RRM1 can interact with the negative patch in RRM2. The hydrophobic patch on β1–β4 is also important for the stability of E2 because it interacts with the protrusive hydrophobic patch formed by β5 and α4. Different from E1–E3, E4 is driven mainly by electrostatic interactions through the negative patch in RRM2 and the positive patch in RRM1. The domain-domain interaction interfaces in E1–E4 are consistent with the chemical shift perturbation regions, which are mainly located in the two β-sheets (Fig. 4). Although four distinct conformers coexist in solution, only one set of NMR signals was observed, indicating that the conformers are in fast exchange on the chemical shift timescale.

Figure 7.

Domain-domain interaction sites highlighted by solid circles. The interaction regions found in structure ensembles E1, E2, E3, and E4 are indicated by labels E1, E2, E3, and E4, respectively. (a and d) Electrostatic potential surfaces of RRM1 and RRM2 calculated by using DELPHI. Electrostatic potential is colored from blue (positive charge) to red (negative charge). (b and e) Hydrophobic surfaces of RRM1 and RRM2. Hydrophobic residues (Phe, Trp, Tyr, Leu, Ile, Val, Met, Ala, Pro, and Gly) are colored in yellow, while hydrophilic residues (Thr, Ser, Lys, His, Glu, Gln, Asn, Asp, and Arg) are in gray. (c and f) Ribbon diagrams of RRM1 and RRM2 domains showing the orientation of each domain in the surface representations.

Validation of the calculated ensemble

To investigate whether the two domains rotate independently or cooperatively in solution, we conducted ¹⁵N relaxation experiments. The localized correlation times and order parameters derived from the relaxation data are shown in Fig. S9. Except for a few residues located in the linker, C-terminus, N-terminus, and long loop, the observed correlation times are mainly in a range of 8–10 ns, which is close to the rotational correlation times of globular ∼19 kDa proteins (∼11.5 ns) (58). If the two domains (each comprising ∼80 residues) rotate independently in solution, the correlation times should be similar to the overall tumbling times of the individual domains (∼5.6 ns). Therefore, the two domains in the di-domain protein do not rotate either independently or fully coherently, indicating existence of domain dynamics or relative domain motions due to weak domain-domain interactions.

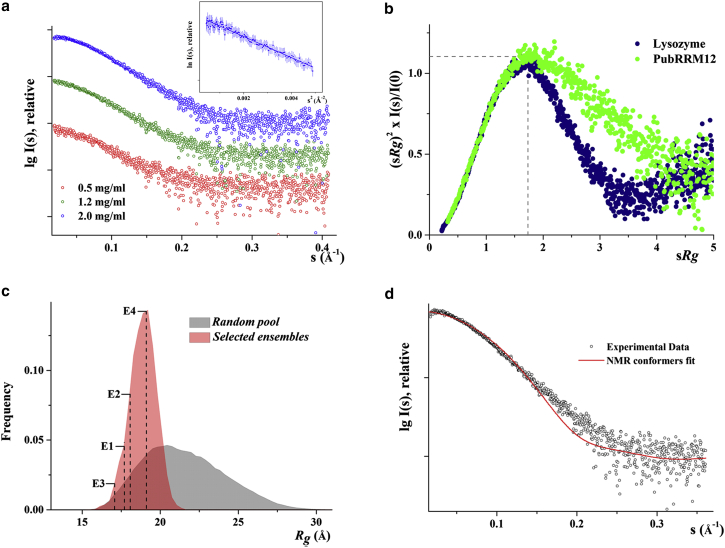
As a complementary tool to the NMR-studies described above, solution x-ray scattering experiments were performed on PubRRM12 at protein concentrations of 0.5, 1.2, and 2.0 mg/mL, respectively. Extrapolation to theoretical infinite dilution was used for analysis (Fig. 8 a; Table S3). The Guinier plot at low angles for different concentrations appeared linear and confirmed good data quality and monodispersity of PubRRM12 with no indication of protein aggregation (Fig. 8 a, inset). The molecular mass estimated from the 0.5 and 2.0 mg/mL scattering data was 16 ± 3 kDa (Table S3), indicating that the protein is monomeric at the concentrations studied. From the Guinier approximation a radius of gyration (R_g) of 18.66 ± 0.53 Å was derived. According to the structures of E1–E4, N148 is close to the domain-domain interface. To assess if the MTSL attached at N148 interferes with domain-domain arrangements, we collected SAXS data of the spin-labeled variant. The SAXS profiles for the spin-labeled sample and wild-type PubRRM12 were nearly identical (Fig. S10), indicating that the MTSL at N148 does not change the structure ensemble.

Figure 8.

Solution x-ray scattering studies of PubRRM12. (a) Small angle x-ray scattering patterns (○). (Inset) Guinier plot shows linearity for PubRRM12 at the highest concentration of 2.0 mg/mL. (b) Normalized Kratky plot of PubRRM12 (solid green circles) compared to the compact globular lysozyme with a peak (—; solid blue circles). (c) Comparison of the R_g distributions (random pool, gray; selected ensemble, red). The R_g value of E1–E4 derived from NMR are indicated by dashed lines. (d) Comparison of experimental scattering data (o) and computed curve (solid line) by combining theoretical scattering intensities from NMR-derived structures E1–E4. To see this figure in color, go online.

The scattering pattern of PubRRM12 exhibits a broad bell-shaped profile shifted toward the right with respect to standard globular lysozyme (Fig. 8 b), indicating existence of multiple conformers that are in dynamic equilibrium (59). To characterize dynamic behavior of PubRRM12, the ensemble optimization method (51) was performed. As a result, the ensemble solution selected by EOM 2.0 provided a discrepancy of χ² = 0.225 by selecting an ensemble of four structures. The R_g distribution for the ensembles that each fit well to the SAXS data is much narrower than that for a random pool of structures (Fig. 8 c). The R_g values of structures E1–E4 are all located inside the red area (Fig. 8 c), indicating the structures derived from the experimental PREs agree with the SAXS data. Despite the overall agreement, the apparent (or weighted average) R_g value for the NMR-derived ensemble is ∼2 Å smaller than the R_g measured by SAXS (18.66 Å), suggesting the NMR model is slightly more compact. This may be caused by the difference in protein concentration (∼4 mg/mL for PRE experiments versus ≤2 mg/mL for SAXS). A concentration-dependent alteration from a more extended to a more compact conformer at higher concentrations is a common phenomenon of two domain proteins. In addition, it is possible that there exist a small fraction of extended conformers, which give rise to negligible interdomain PREs and cannot be detected by PRE-based methods, but contribute significantly to the R_g measured by SAXS. The SAXS profile computed by combining theoretical scattering intensities from structures E1–E4 is very consistent with the experimental data (Fig. 8 d), further supporting that the structure ensemble of E1–E4 is a good representation of the true ensemble in solution.

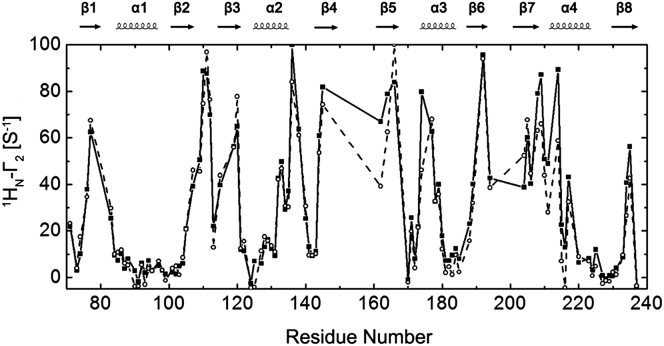
To investigate the driving forces for the calculated structure ensemble, we acquired PRE data at different salt concentrations using a mutant with a spin-label attached at N148. As expected, the intradomain PREs (E71–S154) were not influenced by ionic strength (Fig. 9). Residues displayed significant PRE differences at 0 and 200 mM NaCl, which were concentrated in a region from the C-terminal end of β7 to the middle of α4. If a structure is stabilized mainly by electrostatic interactions, this structure will be altered by salt because electrostatic interactions decrease with the increase of ionic strength. If a structure is stabilized by hydrophobic interactions, this structure will not be affected by salt. According to the NMR-derived ensemble, the spin-label at N148 in RRM1 is close to the region from the end of β7 to the middle of α4 in structure E4 and is also close to the center of the RRM2 β-sheet (β5–β8) in structure E1. If our structure ensemble is correct in geometry and stabilization force, the residues from the end of β7 to the middle of α4 will have larger PREs at lower salt, while those in the RRM2 β-sheet will have similar PREs at higher and lower salt concentrations. This prediction agrees very well with our experimental observation, demonstrating that the calculated ensemble represents the true structures of PubRRM12 in solution.

Figure 9.

PRE data of PubRRM12 with a MTSL at N148 recorded at 0 (▪) and 200 mM (○) NaCl.

Discussion

The method proposed here determines di-domain protein structure ensemble by rotating and shifting one domain relative to the other, which uses only six orthogonal parameters to fully define the conformation of each protein conformer. In this method, the linker’s conformation is neglected because the function of a multidomain protein is often related to the domain-domain orientation and separation rather than the linker conformation. Previous rigid-body-based methods (20, 21, 22, 25, 26, 47, 60) solve structure ensembles by focusing on structures of the linker that connects two rigid domains. The linker’s backbone has at least 2n degrees of freedom for each conformer, where n is the number of residues in the linker. For an ensemble with m conformers, the total degrees of freedom for OPEO (6m+m-1) is much smaller than those for other methods (2nm+m-1) when n > 6. Hence our method should be much more efficient in identifying optimal structure ensemble than previous methods, but it cannot be used to determine the conformations of the linker. To obtain realistic linker conformations and consider energy minimization of each conformer, we will develop a more sophisticated PNGA-based protocol.

Structure ensemble determination from PREs is often achieved by optimizing the agreement between experimental and back-calculated PREs (or Q factor). Because the calculated PREs depend on the number of conformers, conformer structures, and populations, increasing the calculated PRE values of a cluster of protons can be achieved by reducing distances of a spin-label to the protons in a particular conformer (changing structure of a conformer), increasing the conformer population, or adding one more conformer to the existing ensemble. Thus, a small Q-factor value can be achieved by identifying an optimal ensemble with correct conformer number, structures, and populations or by finding a larger ensemble in which one or more true conformers are missing and some false conformers exist. If an optimization procedure is not efficient enough to find the correct ensemble, the second type of overfitting will occur easily. Our results demonstrate that the overfitting can be avoided with the method OPEO. This is accomplished by using a minimal number of fitting parameters or variables to define a structure ensemble and by employing a more efficient optimization protocol to identify the optimal ensemble.

Here we propose to use a three-pseudo-conformer ensemble to approximately represent the multiple conformations of a flexible MTSL. With this approximation, the synthetic PREs can match the back-calculated PREs extremely well with Q factors as small as ∼0.1, but the calculated structure ensembles still deviate from the input reference ensemble by as much as 6.5 Å even in the absence of PRE uncertainties. In a real system, PRE uncertainties exist due to measurement errors, protein dynamics, unaccounted spin-label dynamics, anisotropic tumbling of protein, incomplete spin-labeling, and spin-label reduction. To assess the effect of such potential uncertainties on the quality of calculated structure ensembles, we assume the uncertainties can be accounted by adding two random errors to each synthetic PRE: one absolute error (3 s⁻¹, equivalent to a ∼4% measurement error in ¹H R₂ for the diamagnetic sample) and one proportional error of 30% of the PRE value. The order parameter (S²), which reflects the mobility of an electron-H_N vector, includes two contributions: one from the vector orientation fluctuation caused mainly by rotational motions and the other from vector length fluctuation caused by domain-domain translational motions and spin-label dynamics. Iwahara et al. (56) found that the S² correlates with the effective vector length and it increases from 0.68 to 0.85 with the increase of the length from 18 to 25 Å. Because the electron-H_N vectors used in our calculations are long (>13 Å), the variation in S² should be relatively small. For PubRRM12, the localized correlation times (τ_r) derived from different amides were in a range of 8–10 ns (Fig. S9) because of anisotropic tumbling and domain dynamics, so the variation in τ_c^app (τ_r^∗S²) can be as large as ±20%. If incomplete spin-labeling occurs, 95% labeling will result in underestimation of PRE values by ∼5%. MTSL reduction is very slow and its effect can be neglected if the PRE data are collected for less than one day by using freshly prepared samples. Taken all of these potential errors together, the uncertainties in PREs are still smaller than the random noise added to the synthetic data (±30%). As shown above, the quality of the ensemble derived from PREs is insensitive to PRE uncertainties, provided that the uncertainties are <30%. Therefore, the complications caused by spin-label and protein dynamics as well as anisotropic tumbling can be ignored if the required structural quality is relatively low (>6.5 Å in RMSD). If a system is more dynamic and more anisotropic than PubRRM12, the quality of the ensemble obtained with the approach proposed here will be lower.

To achieve higher structural quality, rigid spin-labels such as unnatural amino acids (61) and MSTL analogs (55) shall be used to avoid the spin-label ensemble approximation. For rigid spin-labels, the anisotropic tumbling effect can be incorporated easily by modifying Eq. 2. When a large spin-label either rigid or flexible is used, its interference with domain-domain interactions shall be avoided. If the spin-label is located in a domain-domain interface, the spin-label tag may change domain-domain interactions and result in artificial structural members in the calculated ensemble. In this case, SAXS can be used to examine whether any interference exists, provided the interference is significant enough to change domain-domain separation. In addition, the incomplete spin-labeling effect shall be corrected by measuring the extent of labeling by mass spectrometry. The labeling extent can also be estimated from 2D NMR spectra used for PRE measurements when it is <90%. It is noteworthy that the correction is not needed for the spins whose chemical shifts in the labeled species are different from those in the unlabeled species.

The structure ensemble of Pub1p is significant different from its homolog U2AF65, which has been reported previously in Mackereth et al. (19) and Huang et al. (60). Although individual domain structures of U2AF65 and PubRRM12 are very similar, their amino-acid sequences (identity of 27.6% and similarity of 35.3%) are very different (Fig. S11). Examining the electrostatic potential of PubRRM12 (Fig. 7) and U2AF65 (Fig. 5 in Huang et al. (60)), we see that the RRM2 surface of PubRRM12 is totally negative, but that of U2AF65 contains both positively and negatively charged patches. The interactions through a negative charge region (D206 and E207) in RRM1 and a positive charge region (K286, K328, and R334) in RRM2 for U2AF65 are no longer available for PubRRM12. Moreover, U2AF65 has a much longer linker (32 amino acids) than PubRRM12 (10 amino acids), implying that U2AF65 can sample much more conformations than PubRRM12. Therefore, the differences in the electrostatic potential and linker length contribute to the very different structure ensembles of the two homolog proteins.

The mechanism of a single RRM domain binding to RNA/DNA is well understood (57). The four β-strands form a plastic platform for nucleic acid binding. The N- and C-terminal regions, together with loops, can enhance the binding affinity. To bind to longer single-stranded RNA/DNA, two or more RRM domains are required to form a larger binding platform. However, the molecular mechanism of recognition of RNA/DNA by tandem RRM domains is still not well understood. RNA-free U2AF65 was initially found to exist in two distinct conformers in solution: one open state corresponding to the RNA-bound conformation, and one closed state in which the RNA-binding surface of RRM1 is partially blocked by the two helices of RRM2 (19). Based on the structures, a conformational selection mechanism coupled with a population shift of the two states has been proposed for recognition of polypyrimidine tract RNA by U2AF65. Nevertheless, a minor induced-fit mechanism could not be ruled out (19). A more recent study on the same U2AF65 has shown that U2AF65 exists in a large number of conformers (60). In the ensemble a significant portion resembles the previously proposed closed state, a small portion resembles the open state, and many other conformers differ from the open and closed states. This result still underscores the possible contribution of the conformational selection mechanism in the RAN recognition by U2AF65.

In all of the four PubRRM12 conformers obtained here, the RNA-binding platform of RRM1 is nearly fully occupied by RRM2 and the linker. The binding platform of RRM2 is partially blocked by RRM1 in structures E1–E3, while it is unblocked in E4. None of the conformers adopts a fully open conformation to readily interact with single-stranded RNA/DNA. Very likely, Pub1p binds to a DNA or RNA through an induced-fit mechanism. First, a part of the RNA/DNA binds to the RRM2 domain in E4. In the meantime, RRM1 changes the orientation to open its binding platform. Subsequently, the RRM1 domain in the open conformation binds to the second part of the RNA/DNA. Once E4 completes the binding to the nucleic acid, other ensemble members can shift to E4.

Conclusions

A multidomain protein with weak domain-domain interactions often adopts more than one structure in solution. Determination of all the structures is the key to understand how the protein functions, which is still challenging. The overfitting problem commonly suffered by most methods may hinder elucidation of the structure-function relationship because false and true structures cannot be discriminated. As demonstrated on reference ensembles with predefined structures, the method proposed here overcomes the problem by enhancing optimization efficiency via use of a minimal number of parameters to define structures and a more efficient optimization protocol as well as by establishing a new overfitting indicator—the O factor.

MTSL is widely used as a spin-label in structure determination, but it is flexible and can adopt multiple conformations. No matter how complicated its dynamics is, the positions of a MTSL can be represented by a small number of pseudo conformers in structure ensemble determination from PRE data. When the required accuracy of a structural ensemble is not high (∼6.5 Å), the use of three pseudo conformers is a good choice because the quality of PRE-derived ensembles is not improved significantly but the computational time increases greatly with the increase of the pseudo spin-label conformer number.

PubRRM12 exists in four conformers in solution that are in fast exchange in the NMR time regime. Individual conformers can be stabilized by hydrophobic, electrostatic, or both hydrophobic and electrostatic interactions. Because none of the conformers adopts an open conformation to readily interact with single-stranded RNA/DNA, PubRRM12 very likely uses an induced fit mechanism to recognize RNA or DNA.

Author Contributions

D.Y. and G.G. designed the research; W.L., J.Z., J.-S.F., and G.T. performed the research; and W.L. and D.Y. wrote the article.

Editor: H. Jane Dyson.