Abstract
Trimers with one attractive bead and two repulsive beads, similar to recently synthesized trimer patchy colloids, were simulated with flat-histogram Monte Carlo methods to obtain the stable self-assembled structures for different shapes and interaction potentials. Extended corresponding states principle was successfully applied to self-assembling systems in order to approximately collapse the results for models with the same shape, but different interaction range. This helps us directly compare simulation results with previous experiment, and good agreement was found between the two. In addition, a variety of self-assembled structures were observed by varying the trimer geometry, including spherical clusters, elongated clusters, monolayers, and spherical shells. In conclusion, our results help to compare simulations and experiments, via extended corresponding states, and we predict the formation of self-assembled structures for trimer shapes that have not been experimentally synthesized.
1 Introduction
Self-assembly is a promising method to manufacture new materials with novel properties. 1–5 Recent advances in colloidal synthesis of anisotropic particles have allowed for improved design of the particles and the superstructures into which they assemble. 6–8 In addition to repulsive interactions stemming from shape anisotropy, attractive anisotropic interactions between colloids may be introduced by adding depletant molecules to the solution. 9 Computer simulations and theoretical models have also been used to understand and predict the properties of assemblies from their basic building blocks. 10–13
Trimer colloids were recently synthesized with one attractive bead and two repulsive beads, where the attractive and repulsive interactions are governed by the smoothness or roughness of the bead surfaces in the presence of depletant particles in solution. 14,15 Trimers of a single shape were experimentally synthesized and observed to form elongated structures. 15 These trimers were also studied computationally in order to analyze the self-assembled structures and compare with experiment. 15 Other previous simulation studies include trimers with different number of attractive beads, 16,17 dimers, 14,18–21 and tetramers. 22 Recently, Avvisati and Dijkstra simulated trimers with tunable interaction range and bond length in order to study the competition between self-assembly and macroscopic phase separation. 23 In our previous work, we studied the self-assembly and macroscopic phase separation for a variety of trimer shapes with one attractive bead. But these trimer shapes did not corresponded to the experimentally synthesized geometry, and the interactions (range of the potential with respect to the particle size) were not similar to experiment. 24 In this work, we simulate shorter interaction ranges (no macroscopic phase separation) 25 than our previous work, 24 which are comparable to the experimental system.
To compare our simulation results with experiment and between different computational models, we use the law of extended corresponding states (ECS), which is based on equating second virial coefficients. 26 Originally proposed by Noro and Frenkel for isotropic particles exhibiting macroscopic phase separation, ECS is a useful way to draw comparisons between models and identify which ones are essentially equivalent. 26,27 Foffi and Sciortino found that patchy particles also obey ECS near the gas-liquid critical point. 28 In addition, ECS has been used to study the phase behavior of active particle suspensions. 29 In this work, we investigate this concept for self-assembling systems. Although ECS has been previously used for self-assembling systems, 15 by matching the second osmotic virial coefficient of experiments and simulations at one condition, ECS has not been systematically validated for self-assembling systems with different interaction ranges.
In this work, we perform Wang-Landau Transition-Matrix Monte Carlo (WL-TMMC) simulations of trimers with one attractive bead and two repulsive beads for a variety interaction ranges and trimer shapes. In order to simulate short-ranged interactions with highly attractive potentials, several advanced algorithms were employed to improve sampling, including configurational bias, geometric cluster algorithm, and aggregation volume bias. 30–34 We find that extended corresponding states can be successfully applied to self-assembling systems. The results for different interaction ranges collapsed by shifting their interaction strength, provided that they are sufficiently short-ranged. In addition, we predict that changes in the size of the repulsive beads and the bond lengths of the experimental structure result in the formation of spherical clusters, elongated clusters, spherical shells and monolayers.
This paper is organized as follows. In Section 2, we describe the trimer models and associated interaction potentials. The simulation methods are described in Section 3. In Section 4, the results and discussion section is split into a section on comparing different models for the experimental trimer geometry in Section 4.1 and exploring different self-assembled structures formed by a variety of trimer geometries in Section 4.2. Finally, conclusions are provided in Section 5.
2 Models
The trimers were composed of one attractive bead (blue) and two repulsive beads (red), as illustrated in Figure 1. The relative placement of the two repulsive beads with respect to the central attractive bead was defined by the bond angle, θ, and the bond length, L. In this work, the two bond lengths between either repulsive bead and the attractive bead were equal, and the trimers were rigid. The interaction between two beads, i and j, was modeled by a modified, shifted-force Lennard-Jones (LJ) potential,
Fig. 1.
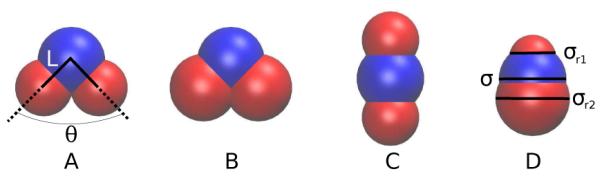
The trimer models investigated in this work are illustrated using VMD. 36 The blue bead represents the smooth colloidal bead, and is attracted to other blue beads. All other pair interactions are purely repulsive.
| (1) |
| (2) |
where ri j is the center-to-center separation distance between two beads, is the potential cut-off, and σi j = (σi + σ j)/2. The parameter ε is the well depth of the LJ potential interaction. The parameter σ is the length scale (or diameter) of the interaction site (or bead). The diameter of the blue, attractive bead, σ , was fixed while the diameter of the red, repulsive beads, σr1 and σr2, were varied independently. The range of the attractive interactions was tuned with the parameter, α, as shown in Figure 2.
Fig. 2.
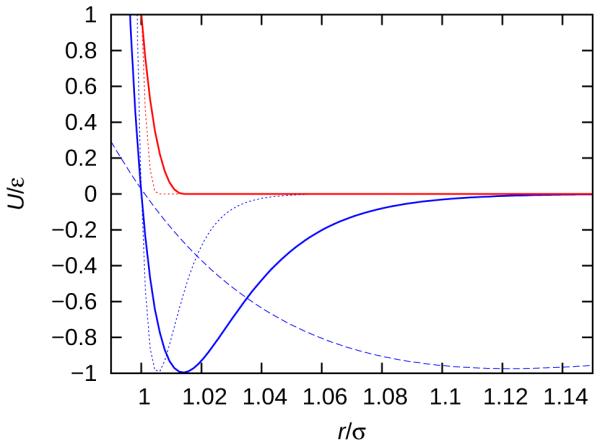
The potential energy of interaction, given by Equation 1, for α = 6 (dashed line), α = 50 (solid line) and α = 128 (dotted line). The blue lines show the attractive interactions between smooth beads, shown in Figure 1. The red lines show the repulsive interactions between the rough beads, shown in Figure 1.
In this work, we study four geometrically distinct trimer models (A, B, C and D), which are shown in Figure 1 and listed in Table 1 for the various models§. Model A is the same shape as the recently synthesized colloidal trimer. 15 The remaining models B, C and D are variations of the experimental structure that we investigated to predict the formation of self-assembled structures for trimer colloid shapes that have not been experimentally synthesized. Model B has larger repulsive beads than model A. Model C is a linear version of model A, and model D is also linear, but with size-asymmetric repulsive beads. Interactions between beads were chosen to mimic those observed experimentally. The experimental colloidal trimers possess short range attractive interactions with a center-to-center separation distance up to approximately 1.02σ. 15 This attractive interaction is due to the favorable excluded volume overlap of colloidal beads with a smooth surface in depletant, 14 and can be captured by high values of the parameter α. Here we studied the behavior of α = 6, 12, 24, 50 and 128. To distinguish between different model geometries and interaction ranges, we use the following naming convention: Mα, where M denotes the model type and α denotes interaction range. The short range attractive interactions for α = 50 and α = 128 more closely resemble the attractive range of the colloids than the α = 6 case, which was utilized in our previous work. 24 For interactions between attractive, blue beads, the potential cutoff distance, , was 1.08, 1.2, 3, 3 and 3 for α = 128, 50, 24, 12, and 6, respectively. The rough colloidal beads have less excluded volume overlap, and were therefore modeled as being purely repulsive. All pair-wise interactions involving the repulsive, red beads were made purely repulsive by setting the cutoff to , also known as the Weeks-Chandler-Andersen potential. 35
Table 1.
The parameters of the trimer models investigated in this work, and computed values for the excluded volume (see Appendix A) and the theta temperature, B22(βεθ) = 0.
| model | σ r1 | σ r2 | L/σ | θ | α | Vex/σ3 | β ε θ |
|---|---|---|---|---|---|---|---|
| A | 0.85 | 0.85 | 0.57 | 91° | n/a | 1.009(1) | 5.13(3) |
| A6 | 0.85 | 0.85 | 0.57 | 91° | 6 | 1.009(1) | 1.36(1) |
| A50 | 0.85 | 0.85 | 0.57 | 91° | 50 | 1.009(1) | 5.25(1) |
| A128 | 0.85 | 0.85 | 0.57 | 91° | 128 | 1.009(1) | 6.35(2) |
| B50 | 1 | 1 | 0.57 | 91° | 50 | 1.315(1) | 5.97(2) |
| B128 | 1 | 1 | 0.57 | 91° | 128 | 1.315(1) | 7.04(5) |
| C50 | 0.85 | 0.85 | 0.57 | 180° | 50 | 1.009(1) | 5.80(2) |
| D50 | 0.7 | 1.1 | 0.3 | 180° | 50 | 0.806(1) | 5.93(2) |
The second osmotic virial coefficient, B22, has been found to be useful in comparing models via extended corresponding states, 26,28 and is a measure of the average potential energy between two particles. By equating the second virial coefficients of two different models, the relative location of their coexistence curves may be estimated, provided that both models are sufficiently short-ranged. The second osmotic virial coefficient is defined as
| (3) |
| (4) |
where r is the relative position and orientation between two particles, V is the domain of possible positions and orientations, β = 1/kBT, and T is the temperature. Note that the notation for B22 is not related to the notation for model B. For the LJ potential, the second osmotic virial coefficient was numerically computed by Monte Carlo integration, as described in Appendix B.
The theta temperature is defined by the condition B22(β εθ) = 0, and is provided in Table 1 for the various models. The theta temperature, β εθ, is analogous to the Boyle temperature of a gas.
3 Methods
The self-assembly of the trimers was investigated with Wang-Landau Transition-Matrix Monte Carlo (WL-TMMC) simulations 37–39 in the grand-canonical ensemble. This simulation method computes the free energy, potential energy, pressure and detailed structural information as a function of trimer density (or concentration) at constant β ε (constant temperature or ε), in a single simulation. The equilibrium simulation of these self-assembling systems was computationally expensive, where a single simulation was composed of hundreds of billions of Monte Carlo trials. The Monte Carlo trials are described in Section 3.1. Details of the WL-TMMC simulations are provided in Section 3.2, and the methods to analyze the structure of the clusters are described in Section 3.3.
3.1 Monte Carlo Trials
Models with short-ranged attractions and deep well-depths (e.g., α = 50 or 128 and β ε > 7) require Monte Carlo algorithms that efficiently simulate the formation and destruction of energetically stable clusters. The following three Monte Carlo algorithms involving collective motion or biased configurational sampling were implemented to overcome large energy barriers.
The first of these algorithms is the Geometric Cluster Algorithm (GCA). 30,31 The GCA is a rejection-free algorithm that samples cluster translation, rotation, creation and destruction more efficiently than traditional single particle moves. 40,41 The algorithm proceeds as follows. A trimer and a pivot point in space are randomly selected, and the trimer is reflected about the pivot. All other trimers which interact with the pivoted trimer, in both the old and newly pivoted positions, are then attempted to be pivoted with a probability related to the pair interaction energy between the two trimers. Each attempted pivot was carried out recursively until all the interacting trimers were attempted to be pivoted. To avoid inefficient moves involving pivots of most of the trimers in the system, the pivot point was confined to a cubic box centered on the first randomly selected trimer. The size of this bounding cubic box was tuned via 5 % changes every 106 trials, in order to obtain an average target number of trimers involved in a pivot, set to Nmax/5. Note that while the conventional rigid cluster moves implemented in our previous work 24 could not create or destroy clusters due to detailed balance, the GCA does not suffer from this limitation. The algorithm was optimized to minimize the number of pair-wise computations. With this implementation, the energy change of the entire GCA move was deduced from the stored pairwise interactions involving particles which were rejected from all attempted pivots.
The second algorithm that was implemented to overcome sampling difficulties was the configurational-bias (CB) method with multiple first bead (MFB) insertions. 32,42 This method allows the individual beads of the trimer to be sequentially grown in a computationally efficient manner. In this work, each bead was grown with six trials. For insertions, deletions, or regrowths of the entire trimer, this included multiple first beads. Trimers were also partially regrown, and only one trial position was used for the trivial one-bead partial regrowths. Although CB is traditionally optimized for high densities, the CB method naturally complements the third and final algorithm described below.
The aggregation volume bias (AVB) method was the third Monte Carlo move that was implemented to improve sampling. 33,34,43–46 The aggregation volume bias method has been shown to improve sampling of strongly associating fluids and was well-suited for the strong, short-ranged interactions studied in this work. This is because the AVB method targets transitions between the outside and inside of the chosen aggregation volume, which mimics the formation and destruction of clusters. The aggregation volume was defined by the distance between attractive beads greater than σ and less than rc, independent of the repulsive beads. Because the aggregation volume definition ignores the location of the repulsive beads, a significant number of AVB attempts lead to overlap with repulsive beads. This simplified the AVB implementation, in comparison to the alternative method of defining a trimer orientation-dependent aggregation volume. But this implementation without orientation dependence was efficient in tandem with the CB algorithm, because the CB algorithm is likely to accept the non-overlapping configurations while growing the timers one bead at a time. Thus, for the grand-canonical insertion moves with AVB, CB and MFB, the first bead was an attractive bead, which was inserted within the aggregation volume of another randomly selected attractive bead. For entire trimer regrowths using AVB, CB and MFB, the AVB2 and AVB3 algorithms were employed for multiple first bead insertions of the attractive bead. For AVB2 and AVB3, the relative probability to select in-to-out or out-to-in moves was 50 %. For more details on the implementation of the combined AVB, CB and MFB algorithm, see Appendix C.
In addition to the three Monte Carlo moves described above, the following Monte Carlo trials were also utilized, as described previously. 24 These trials included single trimer translation, rotation, insertion and deletion, smart Monte Carlo, 47 rigid cluster translation and rotations, and parallel configuration swaps. Refer to Ref. 24 for implementation details of these trials. The rigid trimer rotations were performed about the centroid of the positions of the three beads. Table 2 summarizes all of the Monte Carlo trials that were employed in this work, and provides the relative weights for the probabilities of attempting each type. The relative weights of the different trials were chosen such that the computer would spend roughly equal amounts of time processing the different trials, optimized for the high density simulations. This weighting strategy avoided an inefficient scenario where the majority of computer time was spent on one type of trial, when that trial may not sample well in a particular region of phase space.
Table 2.
Monte Carlo trials and relative weights for the probability of selection.
| trial | weight |
|---|---|
| single-trimer translation or rotation | 5 |
| single-trimer insertion or deletion | 5/4 |
| smart Monte Carlo | 1/Nmax |
| cluster translation or rotation | 1/Nmax |
| parallel configuration swap | 10−4 |
| geometric cluster algorithm | 5/Nmax |
| CB and MFB insertion or deletion | 0.9 |
| CB, AVB, and MFB insertion or deletion | 0.1 |
| CB, AVB2, and MFB regrowth | 1/12 |
| CB, AVB3, and MFB regrowth | 1/12 |
| CB two-bead partial regrowth | 1/2 |
| one-bead partial regrowth | 1/2 |
3.2 Grand Canonical Wang-Landau Transition-Matrix Monte Carlo Simulations
The Wang-Landau Transition-Matrix Monte Carlo method in the grand-canonical ensemble is a flat-histogram method used to obtain the free energy and potential energy as a function of trimer density (or concentration) at constant β ε (temperature or ε). The trimer concentration, ρ, ranges from 0 to Nmax/V, where Nmax is the maximum number of trimers and V = L3 is the volume of the cubic periodic boundary. The self-assembling “phase diagram” was then constructed from a series of constant β ε simulations. The Wang-Landau method computes the free energy based on visited states statistics, while the Transition-Matrix method computes the free energy based on transition statistics between states. The combination of these two methods allows one to benefit from both the fast estimate of the free energy using visited states, and also improved long-term convergence using transitions between states. 48 The methods used to determine convergence are described in the previous work. 24 The simulations were parallelized with overlapping subsets of the concentration range assigned to individual processors, while attempting configuration swaps between processors, as described previously. 24
A series of grand canonical WL-TMMC simulations were performed for Nmax = 250, L = 9σ, and β μ − 3 ln(Λ/σ) = −4 to −6, where μ is the chemical potential and Λ is the thermal de Broglie wavelength. For each model listed in Table 1, simulations were conducted at constant 1/β ε in the range [0.09, 0.15] with a spacing of 0.005. In order to verify that system-size dependent effects were small, additional simulations were performed with L/σ = 8, 9.5 at 1/β ε = 0.125 for α = 50 and at 1/β ε = 0.115 for α = 128. For L = 8σ , Nmax = 140. For L = 9.5σ , Nmax = 265. Error bars in density were then obtained as the standard deviation from the three independent simulations at L/σ = 8, 9, 9.5. In all cases, the error bars in density were smaller than the symbols for figures in Section 4. Error bars in β ε were simply determined by the spacing between simulations.
3.3 Structural Analysis
Clusters, which were identified for rigid cluster moves and structural analysis, were defined as all trimers having an attractive bead within the cut-off distance, rc, from at least one other attractive bead in the cluster, obtained via a recursive flood-fill algorithm. Statistics on the clusters were accumulated every attempted cluster move, after the simulation swept more than one time, where a sweep was defined as satisfying the condition that each macrostate had been visited from a different macrostate at least 100 times. After one sweep, trimer configurations were stored every 105 trials in a compressed binary format for further analysis.
The boundaries between the different self-assembled structures were obtained from the WL-TMMC simulations. One of these boundaries occurred at the low density (or concentration) boundary of the self-assembled structure, and is referred to as the critical micelle concentration (CMC). The CMC is defined as the lowest concentration at which micellar clusters form. After the concentration is increased beyond the CMC, the concentration of the free trimers and premicellar aggregates remains approximately constant within a range of concentrations. 49 Thus, the high concentration boundary or limit of the micellar cluster is taken to be the maximum concentration at which the concentration of free trimers is approximately constant. The critical micelle temperature (CMT) is the highest temperature (or lowest ε) at which micelles could exist. This temperature is not a true thermodynamic critical point, and was simply named by analogy to the critical micelle concentration. 50 Finally, spherical clusters change into elongated clusters at low temperature (or high ε). More details for determining these boundaries may be found in Ref. 24.
4 Results and Discussion
We studied the thermodynamic phase behavior of a variety of self-assembling trimers with different interaction potentials and geometries. In Section 4.1, Noro-Frenkel extended corresponding states is applied to self-assembly of the experimental structure (model A) in order to compare models with varying interaction ranges, and compare the models with experiment. Then, in Section 4.2, various trimer geometries (i.e., models B, C and D), were examined in order to predict the formation of self-assembled structures which include spherical clusters, elongated clusters, spherical shells and monolayers.
4.1 Comparison of Experiment and Models with Different Interactions
Self-assembly phase diagrams were computed for a given trimer shape using WL-TMMC simulations in the grand canonical ensemble. Note that microscopic self-assembled structures do not represent a thermodynamic phase, and therefore the term phase diagram is used loosely to refer to the structures that form in different regions of phase space, β ε and ρσ 3. The stable regions for the elongated clusters of models A50 and A128 are shown in Figure 3. The clusters formed here can be described as elongated micelles. As β ε is decreased, the elongated structures eventually break apart. In addition, a critical or minimum concentration of trimers is required to form self-assembled structures (i.e., the CMC), and this critical concentration decreases as β ε increases. Finally, the high concentration boundary is insensitive to β ε, relative to the sensitivity of the CMC with respect to β ε (see Ref. 24 for definition of this boundary). Although models A50 and A128 possess the same geometry, the phase diagrams are quantitatively different because model A128 has a shorter interaction range than A50. In this section, we quantitatively compare these two models, and compare with experiment, by applying Noro-Frenkel extended corresponding states.
Fig. 3.

Self-assembly phase diagrams for models A50 (red) and A128 (black). Elongated clusters form at concentrations above the critical micelle concentration, shown by the black x and red + symbols. The dashed line along the critical micelle concentration is a linear fit to the data. The critical micelle β ε is shown by the triangle. The high concentration boundary of the micellar fluid is shown by the solid line. Error bars were obtained as the standard deviation from three independent simulations. The snapshot is a representative configuration of model A50 at the state point shown by the black circle symbol.
Assuming that Noro-Frenkel extended corresponding states applies to self-assembling systems, we seek to equate the second osmotic virial coefficient, B22 of models over the entire range of β ε values of interest. While other studies have matched second virial coefficients in self-assembling systems at a particular value of β ε, 15 it is not clear what assumptions and errors may be involved in using the matched second virial coefficient at one β ε to compare the entire range of β ε of interest. In general, the mapping between two models may require that each state point be matched individually. The second osmotic virial coefficient for models A6, A12, A24, A50 and A128 are shown in Figure 4. However, for sufficiently short-ranged interaction (α ≥ 24), the curves can be approximately collapsed by shifting each curve by their respective theta temperatures, β εθ, as shown in Figure 5. Note that the theta temperature is a function of both the particle geometry and interaction range.
Fig. 4.

The second osmotic virial coefficient for A6 (blue solid square), A12 (green star), A24 (blue open square), A50 (black +) and A128 (red x). The error bars are smaller than the symbols.
Fig. 5.
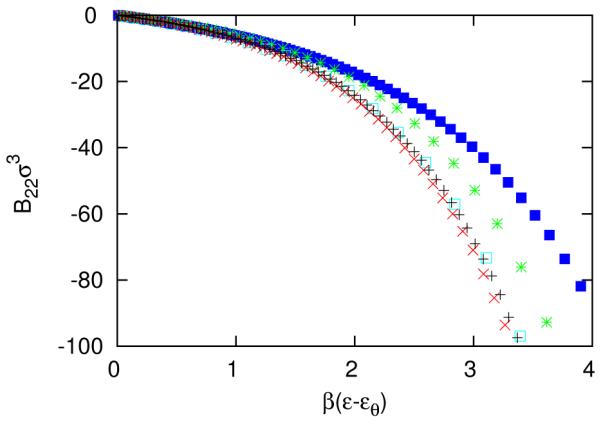
The second osmotic virial coefficient, shifted by the theta solvent condition, B22(β εθ ) = 0, with the same colors and symbols as in Figure 4.
In order to understand the collapse due to shifting in β ε, consider the second virial coefficient for two square-well (SW) models with different interaction strength parameters (ε1, ε2) and interaction range parameters (λ1, λ2), but the same hard core diameter, σ . The square well potential is defined as
| (5) |
where λ determines the attractive interaction range. The second osmotic virial coefficient for the SW may be evaluated analytically with Equation 3,
| (6) |
For the two different SW models to have the same B22 with different interaction strengths, ε1 and ε2, and different interaction ranges, λ1 and λ2, the following condition must be true,
| (7) |
For short-ranged potentials (i.e., λ → 1), as illustrated in Figure 3, at self-assembling conditions, eβε >> 1. This condition is true for short-ranged patchy models, when the attractive interactions is large enough to overcome steric repulsions and promote clustering. With the condition eβε >> 1, Equation 7 reduces to
| (8) |
Thus, the difference between ε1 and ε2 is a function of the relative interaction ranges for models with equivalent B22. Therefore, for sufficiently short-ranged potentials, the B22 curves of two different ranged models may be collapsed by shifting β ε by a constant factor. A similar argument may be applied to the Lennard-Jones potentials, Equation 1, if the potentials are sufficiently short ranged that they may be mapped onto square-well potentials. In this short-ranged limit, the effective hard sphere diameter is insensitive to β ε. Any value of the second osmotic virial coefficient may be chosen to shift and collapse the data. This simplifies comparison with experimental data, where it is more convenient to obtain the second osmotic virial coefficient at only one depletant concentration. In addition, this approach also simplifies the comparison between many different models, and may be used to determine when a model should be considered sufficiently short-ranged. For example, in comparing between many models with different interaction ranges, such as Figure 7 of Avvisati and Dijkstra, 23 it is possible that shorter-ranged interactions could have collapsed upon shifting the interaction strength by a constant.
Fig. 7.
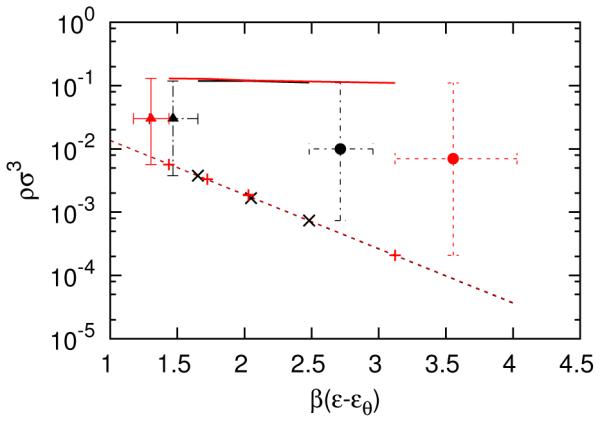
Self-assembly phase diagrams for models B50 and B128, shifted by β εθ. The symbols and colors are as described in the caption of Figure 3. The red and black circles are the spherical to elongated cluster transitions for B50 and B128, respectively.
The phase diagrams for models A50 and A128, shown in Figure 6, were shifted by β ε∗, defined by B22(β ε∗) = −11.1σ 3, which is the experimentally reported second osmotic virial coefficient. 15 This choice of β ε∗ allows meaningful comparison with experiment, where β εθ is not known. As predicted by extended corresponding states (ECS), the CMC for A50 and A128 collapse onto a single curve after shifting by and for α = 50 and 128, respectively. The results for models A50 and A128 may also be compared with the experimental and simulation results of Wolters et al. using ECS. The data sets from Figure 9 of Wolters et al. corresponding to φparticles = 0.01 were taken using Plot Digitizer 2.6.6, and they were shifted by , corresponding to their reported second virial coefficient value of B22(β ε∗) = −11.1σ 3. These two curves are given in Figure 6. The error bars in the experiment were too large to quantitatively evaluate the relative performance of the simulations. To further investigate the differences in our data for models A50 and A128 with the simulation data of Wolters et al., we also calculated the B22 for the simulation model of Wolters et al. as outlined in Appendix B, and obtained a value of . Using this value of , the simulation data set of Wolters et al. shows better agreement with the models A50 and A128. We note that differences in the simulation data of Wolters et al. and this work can be attributed to differences in simulation methodology (e.g., canonical ensemble with single particle moves versus grand canonical ensemble with flat histogram methods and collective particle moves). While the cause of the discrepancy cannot be determined without further investigation, this comparison between simulation results of different models demonstrates the usefulness of ECS.
Fig. 6.
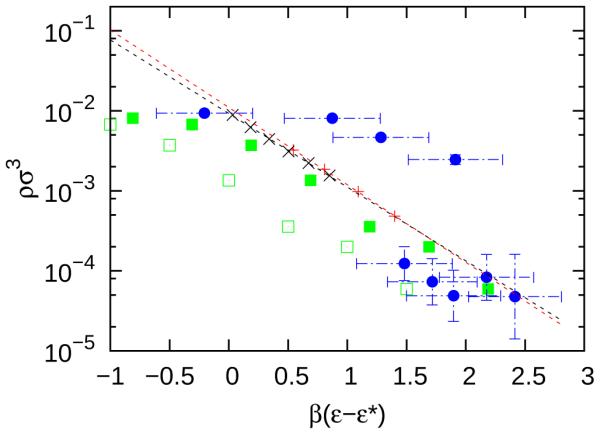
The concentration of free trimers (i.e., the CMC), shifted by ε∗, for model A simulations and previously published experimental data. 15 From this work A50, (red +) and A128, (black x) models are shown. The red and black dashed lines are the linear fits to the CMC for A50 and A128, respectively. In addition, simulations (green open squares) and experiments (blue circles) are shown from Wolters et al. 15 with . Finally, the shifted simulation results of Wolters et al. with are shown as green solid squares.
The critical micelle concentrations (CMC) for both A50 and A128 are expected to collapse onto a single curve upon shifting, following an analytical theory developed for self-assembly, independent of extended corresponding states. For short-ranged potentials, the CMC can be given by 14
| (9) |
where Vex is the excluded volume of a trimer (see Table 1), ρVex is the volume fraction of free monomers and premicellar aggregates, ζ is the width of the attractive potential well, and is the average number of bonds in one trimer. Upon inspection of Equation 9, the CMC’s for models with different interaction ranges, but the same geometry, are shifted by a constant, in agreement with Equation 8. This is because ln ρ in Equation 9 is a linear function of β ε with a slope that is independent of interaction range. The CMC for both A50 and A128 were fit to Equation 9 using least-squares minimization, and was found to be 4.5 and 4.2, respectively. These values of are in agreement with Wolters et al.
4.2 Simulations of Self-Assembled Structures for Various Geometries
In this section, variations on the experimental structure, models B, C and D, were investigated in order to study the formation of self-assembled structures for trimer geometries that have not been experimentally synthesized. To begin, model B, which has larger repulsive beads than model A, was found to form both spherical and elongated clusters. Different interaction ranges for model B collapsed upon shifting to match the B22. Finally, models C and D are shown to form monolayers and spherical shells, respectively.
The phase diagrams for models B50 and B128 are shown in Figure 7, shifted by β εθ. Increasing the size of the repulsive beads stabilized spherical clusters under some conditions. These spherical clusters became elongated above a certain value of β ε, resulting in a qualitatively similar type of phase diagram as previously found for a different geometry. 24 The critical micelle concentrations for the B50 and B128 models also collapsed onto a single curve using extended corresponding states, as shown in Figure 7. The average number of bonds, , was 4 for both B models. The number of bonds, , was expected to be lower than the model A value of ≈ 4.5, because model B possesses larger repulsive ears than model A. The number of bonds was also expected to decrease when transitioning from elongated to spherical clusters. The low β ε boundary between the spherical to elongated cluster regions for both the B50 and B128 models were within two standard deviations. The differences in the boundaries for models B50 and B128 may be the result of the arbitrariness in the definition of the CMT, which is also discussed in Ref. 24. In addition, boundaries in β ε were determined with less precision than boundaries in concentration, because the grand canonical simulations were performed at constant β ε, and thus data at finer intervals of β ε were not available and would require more simulations. The high concentration boundaries of the micellar fluid were in relatively good agreement. Discrepancies between the results for α = 50 and α = 128 may be due to subtle changes in the shape of the particles. For example, the shoulder of the repulsive interactions, shown in Figure 2, changes the effective sizes of the beads. Although these changes may be small, it is possible they significantly affected the stability of self-assembled clusters.
A variety of self-assembled structures, shown in Figure 8, formed for the trimer particles with one attractive bead. For model A50, the straight tubular structure, shown in Figure 8a and 8b was the predominant self-assembled structure, and was described previously. 15 This straight tubular structure is visually characterized by its cross-section of four trimers, and the straight line-up of the beads with respect to the long axis of the elongated cluster. Spiral elongated clusters, similar to those described previously, 15 were also observed, and occurred more frequently at lower values of β ε. When the size of the repulsive beads was increased to that of model B50, spiral tubular structures become the predominant self-assembled structure at higher values of β ε, as shown in Figure 8c. The spiral structures, are characterized by a cross section of roughly three trimer particles, rather than four, with each successive trimer rotated about the long axis of the elongated cluster. Spherical clusters were also found for model B50 at lower values of β ε, as shown in Figure 8d. Note that the spherical clusters were not simply formed by a nucleation of an elongated cluster, because multiple stable spherical clusters coexist without forming elongated clusters. When the bond angle for model A50 was increased to 180°, resulting in model C50, mono-layers readily formed, as shown in Figure 8e. Finally, spherical shells were engineered from a conical-shaped trimer, model D50, as shown in Figure 8f. Although only one particular trimer shape has been created in experiments, 15 our simulations suggest that many different structures may self-assemble from trimer particles with one attractive bead by changing the trimer geometry.
Fig. 8.
The following selected structures are illustrated: straight elongated clusters of model A50 with β ε = 8 (a), the same elongated cluster as “a” from a different angle (b), two spiral elongated clusters of model B50 with β ε = 10 (c), spherical clusters of model B50 with β ε = 8 (d), mono-layer of model C50 with β ε = 8 (e), and spherical shells of model D50 with β ε = 8 (f). The blue boxes represent the periodic boundaries.
5 Conclusion
The self-assembly of trimer colloids with one attractive bead and two repulsive beads was computationally investigated for different interaction ranges and particle shapes. The stability region in the ρσ 3-β ε plane of the resulting self-assembled structures was obtained over a range of trimer densities and interaction strengths by using Wang-Landau Transition-Matrix Monte Carlo simulations in the grand canonical ensemble. Extended corresponding states was applied to self-assembling systems to compare models with different interactions ranges, but the same shape. In particular, the second osmotic virial coefficients of the two models may be equated by shifting the interaction strength by a constant. This constant shift in the interaction strength led to collapse of the results over the entire range of state points of interest. In addition, various trimer geometries were also investigated, and were found to form spherical clusters, elongated clusters, monolayers and hollow spherical clusters (e.g., vesicles).
In future work, one may investigate potentials that possess attractive interactions that are shorter-ranged than the ones studied in this work by using the adhesive hard sphere model. 51,52 The adhesive hard sphere model may be similar to the limit of α → ∞ for Equation 1. But the difficulties of sampling short range interactions with deep well depths increase for larger values of α. For the adhesive hard sphere model, the well width effectively vanishes, and special simulation techniques are required. 51
The continuous potentials studied in this work are important to develop because they may be more readily simulated with molecular dynamics simulations. For extended corresponding states, the collapse of the second osmotic virial coefficients, shown in Figure 5, was demonstrated for continuous potentials that require numerical computation of the virial coefficients, in addition to discontinuous potentials that are more amenable to theoretical calculations. Molecular dynamic studies of the kinetics of cluster formation, and the effect of shear on self-assembly, may be the subject of future publications.
Acknowledgments
H.W.H. acknowledges support from a National Research Council postdoctoral research associateship at the National Institute of Standards and Technology. J. M. acknowledges support from the U.S. Department of Energy, Office of Basic Energy Science, Division of Material Sciences and Engineering under Award (DESC0013979). Use of the high-performance computing capabilities of the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation (NSF) grant no. TG-MCB-120014, is gratefully acknowledged.
A Excluded Volume
Excluded volume, Vex/σ3, was computed numerically by assuming the beads are hard spheres with a diameter equal to their σ parameter. 35 The calculation is similar to that described in Ref. 24; however, the effective size of the excluded probe is zero in this work. In practice, the excluded volume was computed numerically by overlaying the trimer with a cubic grid of np = 109 points and a side length, equal to the largest σ plus the maximum intra-particle distance from a bead to the center-of-mass. The excluded volume, Vex, is obtained by counting the number of grid points which are inside at least one of the hard spheres of the trimer, no,
| (10) |
By computing the excluded volume of one hard sphere and comparing to theoretical value of πσ3/6, the numerical error is expected to be on the order of 10−4σ3.
B Second Osmotic Virial Coefficient
The second osmotic virial coefficient for continuous potentials (e.g., Equation 2) was numerically computed by Monte Carlo integration.
| (11) |
where ri is the relative position and orientation of a second trimer with respect to the first trimer, f (ri; β ε) is given by Equation 4, and i = 1, …, Ntrial randomly chosen positions and orientations of a second trimer with respect to the first. For more details, see the implementation described in Ref. 24. In this work, B22/σ 3 was computed in increments of 1/β ε of 0.001, and the standard deviations were obtained from a series of block averages of Ntrial = 108.
C Aggregation Volume Bias in Tandem with Configuration Bias
Although aggregation volume bias (AVB), configuration bias (CB) and multiple first bead (MFB) insertions have been described elsewhere, 32–34,42–45 the combination of the two bias methods is not fully documented in a single source in the literature. An AVB trial focuses on the region of space that a particle will be moved, inserted or deleted. In this work, only the first bead is considered for AVB trials, and the aggregation volume is defined without any orientation dependence. To simplify notation, the following short-hand names will be used. AV refers to the aggregation volume. M is the particle to be moved in regrowths, added in insertions, or removed in deletions. R is the region of the aggregation volume for the target particle (i.e., “in” or “out”). The volume inside the AV is vin, and the volume outside the AV is vout = V − vin. The number of particles inside the AV is nin, and nout outside the AV. Aggregation volumes are defined for specific pairs of bead types. Thus, nin only counts the number of beads in the AV that match the correct type. In this work, only smooth, blue beads are considered in the AVB algorithm, and therefore the number of particles, N = nin + nout.
For grand-canonical insertions and deletions of particles with AVB, CB and MFB, the algorithm proceeds as follows. The target particle, J is selected randomly among all particles (reject if N = 0). R is the “in” region of J, and . There is an equal probability of attempting an insertion or deletion. For insertions, the Metropolis acceptance probability for the trial is given by
| (12) |
where z = σ 3eβ μ /Λ3 and WCB is the Rosenbluth term from configurational bias. To compute WCB, the first bead of M is randomly inserted in R for a total of k random trials. The ith trial for the first bead, b = 1, is selected with a probability
| (13) |
| (14) |
where is the potential energy of the first bead (b = 1) of M in the ith trial position with all other particles. After selection of the ith trial, the remaining b = 2 to nb beads are sequentially grown from k trial positions each.
| (15) |
For deletions, M is selected randomly from R and the Metropolis acceptance probability is
| (16) |
To compute WCB, the position of the first bead of M and k − 1 other random positions of the first bead of M in R are used to compute w1. Following Equations 14 and 15, WCB is computed for the remaining beads for the original position of the beads in M, and k − 1 other random positions, subject to the intramolecular potential, as described elsewhere for CB. 42
For regrowths with either AVB2 or AVB3, in tandem with CB and MFB, one begins by selecting Rnew and Rold, which are the AV regions for the “new” and “old” configurations in the CB algorithm. For regrowths with AVB2, CB and MFB, the algorithm proceeds as follows. The target particle J is selected randomly (reject if N ≤ 1). Next, the type of move is chosen to be “out → in” or “in → out” of the AV of particle J with a probability Pbias or 1 − Pbias, respectively. If the “out → in” move type is chosen, Rnew is the “in” region of J and Rold is the “out” region of J. The Metropolis acceptance probability for the “out → in” move is
| (17) |
where and are the “new” and “old” Rosenbluth weights determined by growing the beads with configurational bias, as described below. If the “in → out” move type is chosen, Rnew is the “out” region of J and Rold is the “in” region of J. The Metropolis acceptance probability for the “in → out” move is
| (18) |
For regrowths with AVB3, CB and MFB, the algorithm proceeds as follows. Two particles, K and J, are randomly selected with the condition that J and K do not have non-overlapping AV’s (reject entire trial if all AV’s overlap, or N ≤ 2). Next, the type of move is chosen to be “out → in” or “in → out” with a probability Pbias or 1 − Pbias, respectively. If the “out → in” move type is chosen, Rnew is the “in” region of J and nin = . The “old” configuration is then randomly chosen to be “in K” or “out J” with equal probability. If “in K” is chosen, Rold is the “in” region of K, and . Otherwise, Rold is the “out” region of J, and . The Metropolis acceptance probability for the “out → in” move is
| (19) |
If the “in → out” move type is chosen, Rold is the “in” region of J, and . The “new” configuration is then randomly chosen to be “in K” or “out J” with equal probability. If “in K” is chosen, Rnew is the “in” region of K, and . Otherwise, Rnew is the “out” region of J, and . The Metropolis acceptance probability for the “in → out” move is
| (20) |
To grow the remaining beads in the CB algorithm and compute WCB, the remaining algorithm is the same for either AVB2 or AVB3, once Rnew and Rold are determined, as described above. The Rosenbluth factors, and , are computed from the “new” and “old” configurations. M is selected randomly in Rold (reject if not possible). The trial positions and Rosenbluth factor for the “new” configuration, is computed as follows. The first bead in M is placed in Rnew for a total of k trials, and the ith trial is selected with probability given by Equation 13. After selection of the ith trial for the first bead, the remaining beads are sequentially grown from k trial positions each, and . The Rosenbluth factor for the “old” configuration, is computed as follows. The first bead in M is placed in Rold for a total of k trials, including the original position. w1 is computed via Equation 14 for the k trials. The Rosenbluth factor for the remaining beads, wb, are computed for k trials, including the original position, and . The regrowth trial move is then subject to the Metropolis acceptance criteria.
Footnotes
Contribution of the National Institute of Standards and Technology, not subject to U.S. Copyright.
This model possesses the same square-well and hard-sphere interactions as reported in Ref 15
References
- 1.Zheng W, Jacobs HO. Adv. Funct. Mater. 2005;15:732–738. [Google Scholar]
- 2.Grzybowski BA, Wilmer CE, Kim J, Browne KP, Bishop KJM. Soft Matter. 2009;5:1110–1128. [Google Scholar]
- 3.Ozin GA, Hou K, Lotsch BV, Cademartiri L, Puzzo DP, Scotognella F, Ghadimi A, Thomson J. Mater. Today. 2009;12:12–23. [Google Scholar]
- 4.Soukoulis CM, Wegener M. Nat. Photonics. 2011;5:523–530. [Google Scholar]
- 5.Vignolini S, Yufa NA, Cunha PS, Guldin S, Rushkin I, Stefik M, Hur K, Wiesner U, Baumberg JJ, Steiner U. Adv. Mater. 2012;24:OP23–OP27. doi: 10.1002/adma.201103610. [DOI] [PubMed] [Google Scholar]
- 6.Glotzer SC, Solomon MJ. Nat. Mater. 2007;6:557–562. doi: 10.1038/nmat1949. [DOI] [PubMed] [Google Scholar]
- 7.Chen Q, Bae SC, Granick S. Nature. 2011;469:381–384. doi: 10.1038/nature09713. [DOI] [PubMed] [Google Scholar]
- 8.Sacanna S, Pine DJ, Yi G-R. Soft Matter. 2013;9:8096–8106. [Google Scholar]
- 9.Cademartiri L, Bishop KJM, Snyder PW, Ozin GA. Philos. Trans. R. Soc. London, Ser. A. 2012;370:2824–2847. doi: 10.1098/rsta.2011.0254. [DOI] [PubMed] [Google Scholar]
- 10.Bianchi E, Blaak R, Likos CN. Phys. Chem. Chem. Phys. 2011;13:6397. doi: 10.1039/c0cp02296a. [DOI] [PubMed] [Google Scholar]
- 11.Damasceno PF, Engel M, Glotzer SC. Science. 2012;337:453–457. doi: 10.1126/science.1220869. [DOI] [PubMed] [Google Scholar]
- 12.Bechinger C, Sciortino F, Ziherl P. Physics of Complex Colloids. IOS Press; 2013. [Google Scholar]
- 13.Bianchi E, Capone B, Kahl G, Likos CN. Faraday Discuss. 2015;181:123–138. doi: 10.1039/c4fd00271g. [DOI] [PubMed] [Google Scholar]
- 14.Kraft DJ, Ni R, Smallenburg F, Hermes M, Yoon K, Weitz DA, Blaaderen A. v., Groenewold J, Dijkstra M, Kegel WK. Proc. Natl. Acad. Sci. USA. 2012;109:10787–10792. doi: 10.1073/pnas.1116820109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wolters JR, Avvisati G, Hagemans F, Vissers T, Kraft DJ, Dijkstra M, Kegel WK. Soft Matter. 2015;11:1067–1077. doi: 10.1039/c4sm02375g. [DOI] [PubMed] [Google Scholar]
- 16.Jiménez-Serratos G, Gil-Villegas A, Vega C, Blas FJ. J. Chem. Phys. 2013;139:114901. doi: 10.1063/1.4820530. [DOI] [PubMed] [Google Scholar]
- 17.Khan S, Haaga J, Gunton JD. J. Chem. Phys. 2015;143:024906. doi: 10.1063/1.4926537. [DOI] [PubMed] [Google Scholar]
- 18.Hong L, Cacciuto A, Luijten E, Granick S. Langmuir. 2008;24:621–625. doi: 10.1021/la7030818. [DOI] [PubMed] [Google Scholar]
- 19.Munaò G, O’Toole P, Hudson TS, Costa D, Caccamo C, Giacometti A, Sciortino F. Soft Matter. 2014;10:5269–5279. doi: 10.1039/c4sm00544a. [DOI] [PubMed] [Google Scholar]
- 20.Munaò G, O’Toole P, Hudson TS, Costa D, Caccamo C, Sciortino F, Giacometti A. J. Phys. Condens. Mat. 2015;27:234101. doi: 10.1088/0953-8984/27/23/234101. [DOI] [PubMed] [Google Scholar]
- 21.Avvisati G, Vissers T, Dijkstra M. J. Chem. Phys. 2015;142:084905. doi: 10.1063/1.4913369. [DOI] [PubMed] [Google Scholar]
- 22.Barz B, Urbanc B. J. Phys. Chem. B. 2014;118:3761–3770. doi: 10.1021/jp412819j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Avvisati G, Dijkstra M. Soft Matter. 2015;11:8432–8440. doi: 10.1039/c5sm02076j. [DOI] [PubMed] [Google Scholar]
- 24.Hatch HW, Mittal J, Shen VK. J. Chem. Phys. 2015;142:164901. doi: 10.1063/1.4918557. [DOI] [PubMed] [Google Scholar]
- 25.Vliegenthart GA, Lodge JFM, Lekkerkerker HNW. Physica A. 1999;263:378–388. [Google Scholar]
- 26.Noro MG, Frenkel D. J. Chem. Phys. 2000;113:2941–2944. [Google Scholar]
- 27.Platten F. J. Chem. Phys. 2015;142:174905. doi: 10.1063/1.4919127. [DOI] [PubMed] [Google Scholar]
- 28.Foffi G, Sciortino F. J. Phys. Chem. B. 2007;111:9702–9705. doi: 10.1021/jp074253r. [DOI] [PubMed] [Google Scholar]
- 29.Schwarz-Linek J, Valeriani C, Cacciuto A, Cates ME, Marenduzzo D, Morozov AN, Poon WCK. Proc. Natl. Acad. Sci. USA. 2012;109:4052–4057. doi: 10.1073/pnas.1116334109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Liu J, Luijten E. Phys. Rev. Lett. 2004;92:035504. doi: 10.1103/PhysRevLett.92.035504. [DOI] [PubMed] [Google Scholar]
- 31.Liu J, Luijten E. Phys. Rev. E. 2005;71:066701. doi: 10.1103/PhysRevE.71.066701. [DOI] [PubMed] [Google Scholar]
- 32.Siepmann JI, Frenkel D. Mol. Phys. 1992;75:59–70. [Google Scholar]
- 33.Chen B, Siepmann JI. J. Phys. Chem. B. 2001;105:11275–11282. [Google Scholar]
- 34.Chen B, Siepmann JI, Oh KJ, Klein ML. J. Chem. Phys. 2001;115:10903–10913. [Google Scholar]
- 35.Weeks JD, Chandler D, Andersen HC. J. Chem. Phys. 1971;54:5237–5247. [Google Scholar]
- 36.Humphrey W, Dalke A, Schulten K. J. Mol. Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 37.Errington JR. J. Chem. Phys. 2003;118:9915–9925. [Google Scholar]
- 38.Shell MS, Debenedetti PG, Panagiotopoulos AZ. J. Chem. Phys. 2003;119:9406–9411. [Google Scholar]
- 39.Rane KS, Murali S, Errington JR. J. Chem. Theory Comput. 2013;9:2552–2566. doi: 10.1021/ct400074p. [DOI] [PubMed] [Google Scholar]
- 40.Whitelam S, Geissler PL. J. Chem. Phys. 2007;127:154101. doi: 10.1063/1.2790421. [DOI] [PubMed] [Google Scholar]
- 41.Rossi L, Soni V, Ashton DJ, Pine DJ, Philipse AP, Chaikin PM, Dijkstra M, Sacanna S, Irvine WTM. Proc. Natl. Acad. Sci. USA. 2015;112:5286–5290. doi: 10.1073/pnas.1415467112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Frenkel D, Smit B. Understanding Molecular Simulation: From Algorithms to Applications. Academic Press; 2002. [Google Scholar]
- 43.Chen B, Siepmann JI. J. Phys. Chem. B. 2000;104:8725–8734. [Google Scholar]
- 44.Chen B, Siepmann JI, Oh KJ, Klein ML. J. Chem. Phys. 2002;116:4317–4329. [Google Scholar]
- 45.Chen B, Siepmann JI, Klein ML. J. Phys. Chem. A. 2005;109:1137–1145. doi: 10.1021/jp0463722. [DOI] [PubMed] [Google Scholar]
- 46.Loeffler TD, Sepehri A, Chen B. J. Chem. Theory Comput. 2015;11:4023–4032. doi: 10.1021/acs.jctc.5b00466. [DOI] [PubMed] [Google Scholar]
- 47.Rossky PJ, Doll JD, Friedman HL. J. Chem. Phys. 1978;69:4628–4633. [Google Scholar]
- 48.Shen VK, Siderius DW. J. Chem. Phys. 2014;140:244106. doi: 10.1063/1.4884124. [DOI] [PubMed] [Google Scholar]
- 49.Jusufi A, Panagiotopoulos AZ. Langmuir. 2015;31:3283–3292. doi: 10.1021/la502227v. [DOI] [PubMed] [Google Scholar]
- 50.Floriano MA, Caponetti E, Panagiotopoulos AZ. Langmuir. 1999;15:3143–3151. [Google Scholar]
- 51.Kranendonk WGT, Frenkel D. Mol. Phys. 1988;64:403–424. [Google Scholar]
- 52.Miller MA, Frenkel D. J. Chem. Phys. 2004;121:535–545. doi: 10.1063/1.1758693. [DOI] [PubMed] [Google Scholar]



