Sensitivity to Interaural Time Differences Conveyed in the Stimulus Envelope: Estimating Inputs of Binaural Neurons Through the Temporal Analysis of Spike Trains

Abstract

Sound-source localization in the horizontal plane relies on detecting small differences in the timing and level of the sound at the two ears, including differences in the timing of the modulated envelopes of high-frequency sounds (envelope interaural time differences (ITDs)). We investigated responses of single neurons in the inferior colliculus (IC) to a wide range of envelope ITDs and stimulus envelope shapes. By a novel means of visualizing neural activity relative to different portions of the periodic stimulus envelope at each ear, we demonstrate the role of neuron-specific excitatory and inhibitory inputs in creating ITD sensitivity (or the lack of it) depending on the specific shape of the stimulus envelope. The underlying binaural brain circuitry and synaptic parameters were modeled individually for each neuron to account for neuron-specific activity patterns. The model explains the effects of envelope shapes on sensitivity to envelope ITDs observed in both normal-hearing listeners and in neural data, and has consequences for understanding how ITD information in stimulus envelopes might be maximized in users of bilateral cochlear implants—for whom ITDs conveyed in the stimulus envelope are the only ITD cues available.

INTRODUCTION

The classic duplex theory of sound localization (Strutt 1907) posits two mechanisms by which sound sources on the horizontal plane are localized. For sounds of relatively long wavelength compared to the size of the head (low frequencies), sensitivity to small differences in the time of arrival of a sound at the two ears (interaural time differences (ITDs)) underpins the ability to locate the sound source (Thompson 1882) and contributes to the ability to hear out sounds in background noise (“cocktail party” listening, Ruggles and Shinn-Cunningham 2011). For normal-hearing listeners, localization accuracy is most acute for ITDs conveyed in the temporal fine structure (TFS) of sounds with frequencies in the range 500–900 Hz (Bilsen and Raatgever 1973) and degrades rapidly around 1.3 kHz, above which listeners tend to rely more on interaural differences in the level to determine source location.

Nevertheless, although valid to a first approximation, the dichotomy suggested by the duplex theory is not strict. In particular, human listeners are also sensitive to ITDs conveyed in the modulated stimulus envelope of high-frequency sounds (e.g., Henning 1974), sensitivity also evident in the responses of neurons in the lateral superior olive (LSO; Joris and Yin 1995), inferior colliculus (IC; Yin et al. 1984), and, albeit less prominently, the medial superior olive (MSO; Joris 1996; Gai et al. 2014). While sensitivity to envelope ITDs is likely less relevant to acoustic hearing (e.g., Devore and Delgutte 2010), it is of higher importance for users of bilateral cochlear implants (CIs)—an increasingly common class of listeners for whom perception of sound is generated by implanted electrical devices that convey acoustic information direct to auditory nerve fibers as a series of modulated electrical pulses. To this end, investigators have sought to improve binaural hearing in CI listeners by assessing performance using different envelope shapes, with rapid, short pulses, separated by relatively long intervals, deemed most effective in conveying high-quality ITD information (e.g., Laback et al. 2011).

Here, we demonstrate how features of the stimulus envelope—particularly the speed of the rising envelope and the duration of the pause between successive slopes—influence the ITD sensitivity of high-frequency neurons. In particular, we show how the interaction of timed excitatory and inhibitory circuits results in neuron- and envelope-specific ITD sensitivity. Detailed insights are facilitated by combining three investigation tools: (1) a broad repertoire of stimulus envelopes previously employed to determine factors influencing ITD discrimination performance perceptually (Klein-Hennig et al. 2011) and neurally (Dietz et al. 2013), (2) a novel method of visualizing neural response patterns, and (3) a neuron-specific binaural model. The data provide a logical framework in which to understand the limits to performance in envelope ITD coding for individual neurons as well as for understanding the principles underlying binaural interactions more generally.

MATERIALS AND METHODS

Experimental Materials and Methods

The experimental recording methods and neural data analyzed in this study have been reported previously (Dietz et al. 2013). Data were derived from extracellular recordings made from 71 well-isolated single neurons in the inferior colliculus (IC) of 15 adult tri-colored guinea pigs under urethane anesthesia at the UCL Ear Institute. The surgical procedures and recording equipment were described in detail by Dietz et al. (2014) and are only briefly reiterated here.

Each cycle of the stimulus envelope was constructed from four segments, identical to those used by Klein-Hennig et al. (2011): (1) a pause segment with zero amplitude, (2) an attack segment identical to the rising portion of a squared sinusoid, (3) a sustained segment with a constant amplitude, and (4) a decay segment identical to the falling portion of a squared sinusoid. The ITD was applied after multiplying the tonal carrier with the envelope resulting in a full waveform shift. The “fine” recording range of the ITD was between ±2 ms and consisted of responses to 25 evenly spaced ITDs, i.e., a 167-μs spacing. The “coarse” recording range of ITD extended from −8.33 to +28.33 ms and had a 1.67-ms ITD spacing. The asymmetric ITD range was due to technical reasons. The stimuli were presented via Tucker-Davis Technologies RPvdsEx and necessary memory limitation enforced the selection of specific delay elements resulting in this ITD range.

The stimulus duration was always an integer multiple of the cycle duration (starting and stopping in the modulation trough) and was as close to 1 s as possible (990–1010 ms). The interstimulus interval was at least 300 ms (again, technical RPvdsEx related reasons prohibited to specify an exact interval). The dataset reported here comprises 16 different envelope shapes with an average of 38 different ITDs recorded between 4 and 10 times (mean = 7.8), depending on how well the isolation of the single-neuron recording was maintained.

A search stimulus consisting of ongoing 50-ms presentations of pure tones was used to isolate neurons. The setup allowed for presenting these tones diotically (standard), ipsilateral only, contralateral only (highest success rate), or with an interaural time difference. First approximations of the neuron’s response threshold and characteristic frequency (CF) were made. Each neuron’s CF was determined by recording a frequency-versus-level response area spectrally flanking an initial CF estimate. Neurons included in the present study all have CFs > 1500 Hz. Envelope ITD sensitivity was tested with a reduced set of conditions, including the highest and lowest segment durations, and only the coarse, 1.67-ms ITD grid. As soon as the experimenter identified ITD sensitivity to at least one envelope shape, the main recording was initiated.

The main recording duration lasted between 56 and 140 min for each isolated neuron. The stimulus presentation order was chosen so as to record conditions with identical envelope shapes en bloc. Within each block, the ITD was successively increased. Thereafter, for the next run, the presentation order was reversed. In these reversed runs, the carrier was inverted in one channel in order to cancel out potential residual tuning to the carrier ITD (SUMCOR, Joris 2003). Stimuli were presented via calibrated earphones with an amplitude maximum approximately 20 dB above the pure-tone threshold at the CF of the neuron.

Modeling Methods

The full model developed in the present study is based on the primary neural projections up to the binaural interaction stage in the brainstem. The model consists of three stages: (I) the auditory nerve (AN), (II) the cochlear nucleus (CN), and (III) the binaural interaction stage. The medial nucleus of the trapezoid body (MNTB) is modeled as an inhibitory relay with no synaptic delay and is not explicitly included in the model. No assumption is made in the model where the primary binaural interaction takes place—logically this could be the MSO ipsilateral to the recording site or the contralateral LSO. To limit the parameter space of the model, neural stages between the superior olivary complex (SOC) and the IC, such as the dorsal nucleus of the lateral lemniscus (DNLL), were not included in the model. The IC responses measured empirically were assumed as being inherited from the primary binaural interaction site.

Input Signals

Stimuli were generated in the same way as for the experimental data collection but using MATLAB (MathWorks, Natick, MA). Whereas the stimulus carrier frequency during the experiment was set to a neuron’s CF, in the simulation, it was always 4 kHz and the stimulus level was fixed at 40 dB SPL at each ear.

Auditory Nerve Model

The AN model by Zilany et al. (2009) was used to generate the synaptic inputs to the CN model. This AN model was developed to model the cat auditory nerves, which have different cochlear tuning and temporal phase-locking properties to the guinea pig. In the response feature we are focused on here, i.e., firing rate and phase locking to stimulus envelopes at a relatively low modulation rate, this model provides a good approximation for the AN responses in guinea pig. This AN model incorporates detailed descriptions of cochlear tuning and non-linearity, inner hair cell (IHC) transduction, IHC-AN synapse, and refractoriness. Twenty medium spontaneous rate (SR) AN fibers, simulated by 20 repetitions of one stimulus, projected to the respective CN model neurons (see below) on each side. Medium-SR AN fibers were used because they provide good phase locking and relatively high firing rate, thus are well suited for the purpose of the model. The CF of all AN fibers was always 4 kHz. It is worth noting that the medium-SR AN model has a threshold of about 20 dB SPL for CF tones; thus, the 40-dB SPL stimulus level used in the model is roughly 20 dB above the threshold. This corresponds well with the empirical experiment in the present study where the stimulus level was set at 20 dB above the neuron’s threshold. At this stimulus level, the response rate of the AN model was midway between the spontaneous rate and the saturation rate.

Cochlear Nucleus Model

Two types of CN models were used to generate inputs to the binaural interaction model: the primary-like CN model and the onset-type CN model. The primary-like CN model acts as a relay, each receiving the responses from one AN fiber and sending this response to the binaural interaction neuron (BIN). Modeling the primary-like CN neuron as a relay represents an oversimplification of the physiology (no enhancement in fine structure phase locking, etc), but we justify it here in terms of maintaining the simplicity of the model, without losing its essential features. Given the current focus on envelope phase locking, the relay model was a reasonable approximation because the high-CF primary-like CN neurons show similar phase locking to modulation as the AN, especially at low stimulus levels such as the 20 dB above threshold used in the present study (Frisina et al. 1990). The one-to-one projection from AN to primary-like CN neuron is a reasonable assumption, given the estimated number of AN fibers (1–4) innervating spherical bushy cells (Osen 1970; Ryugo and Sento 1991; Nicol and Walmsley 2002). The onset-type CN neurons were simulated by single-compartment Hodgkin-Huxley (HH) models developed by Rothman and Manis (2003a, b). Five onset-type CN model neurons converge onto the BIN, and each onset-type CN model receives inputs from 20 AN fibers. Compared with the primary-like CN model, the degree of convergence (20 AN fibers) and the projection of onset-type CN model neurons directly onto the BIN are less well supported anatomically. Their purpose was largely to simulate IC inputs that are sensitive to envelope slopes. The HH-type models were implemented using NEURON (Hines and Carnevale 1997), a broad-purpose, neuron-simulation environment. Software written in MATLAB (MathWorks, Natick, MA) was used to initialize the model parameters before each simulation and to analyze the data after each simulation. For both types of CN models, no synaptic delay was included in their AN inputs.

The membrane characteristics of the onset-type CN model are the same as for the type II CN cell model developed by Rothman and Manis (2003a, b). The type II CN model was used here to simulate slope-sensitive inputs to the IC because of its phasic response pattern to positive current steps. It has been shown that phasic firing neurons are associated with slope-sensitive responses to time varying inputs (Beraneck et al. 2007; McGinley and Oertel 2006; Gai et al. 2010). As shown in Figure 1, the onset-type CN model only responded at the stimulus onset in response to a 200-ms tone presented at CF (Fig. 1D). The onset-type CN model also shows sensitivity to envelope slopes, i.e., strong onset response to steep slopes (Fig. 1E) and weak response to shallow slopes (Fig. 1F). In contrast, the primary-like CN model shows a sustained response to CF tones and is also less sensitive to envelope slopes (Fig. 1A–C).

FIG. 1.

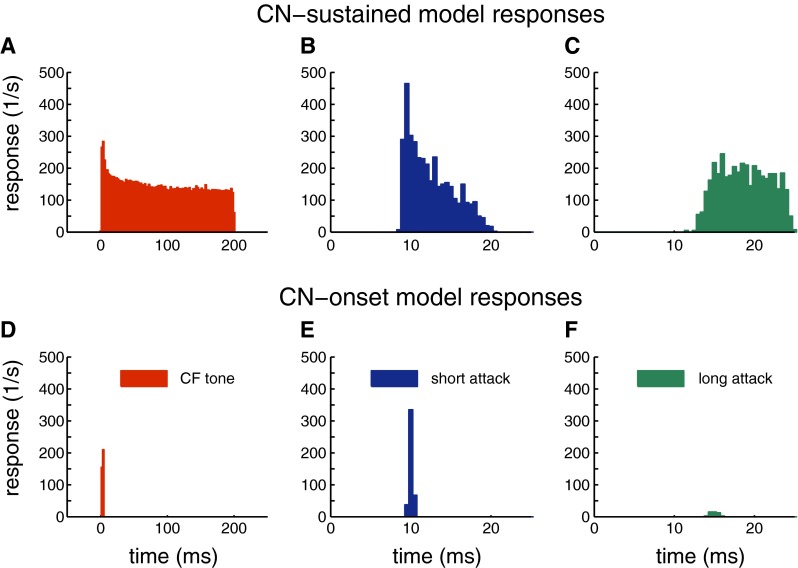
Examples for CN model responses. A–C primary-like CN model responses. D–F onset-type CN model responses. A, D CN responses to a 200-ms tone at the CF of the CN model (4000 Hz) and 40 dB SPL. B, E CN responses to steep attack envelope (Figs. 2, 3, 4, and 5G). C, F CN responses to shallow attack envelope (Figs. 2, 3, 4, and 5H).

Each spike generated by the AN model elicits an excitatory postsynaptic conductance (PSC), and the total synaptic conductance waveform is the superposition of all the excitatory PSCs occurring during the stimulus. Each PSC was described as the difference of two exponentials (rising and falling components). Specifically, each excitatory PSC was expressed as

$$g_e\left(t\right)=\frac{G_E}{G_{\mathit{norm}}}\left[exp\left(-t/{\tau }_{E\_\mathit{fall}}\right)-exp\left(-t/{\tau }_{E\_\mathit{rise}}\right)\right]$$ 1

where ${\tau }_{E\_\mathit{rise}}$ and ${\tau }_{E\_\mathit{fall}}$ refer to the attack and decay time constants for excitation, respectively. The normalization factor was chosen to be G_norm = exp ( − t_p/ − t_{E_fall}) − exp ( − t_p/ − t_{E_rise}) so that the peak conductance was $G_E$ and the peak latency was

$$t_p=\frac{{\tau }_{E\_\mathit{rise}}\ast {\tau }_{E\_\mathit{fall}}}{{\tau }_{E\_\mathit{fall}}-{\tau }_{E\_\mathit{rise}}}\mathit{In}\frac{{\tau }_{E\_\mathit{fall}}}{{\tau }_{E\_\mathit{rise}}}\mathit{with}{\tau }_{E\_\mathit{fall}}>{\tau }_{E\_\mathit{rise}}$$ 2

In the onset CN model, ${\tau }_{E\_\mathit{rise}}$ was set to 0.1 ms, ${\tau }_{E\_\mathit{fall}}$ was set to 1 ms and $G_E$ was set to 3 nS. The reversal potential was 0 mV for excitatory synapses. The resting potential for the onset CN model was −64.9 mV.

Model of Binaural Interaction

As for the onset-type CN simulations, single-compartment HH models were used to model BINs. The HH-type BIN model was the same as in a previous study of LSO responses to monaural SAM tones (Wang and Colburn 2012) and localization with bilateral cochlear implants (Kelvasa and Dietz 2015). It is a single-compartment model with three ion channels in the membrane: a sodium channel, a high-threshold potassium channel (KHT), and a “leak” channel. No hyperpolarization-activated channel or low-threshold potassium channel (KLT) was included in the model. The membrane of the model is thus specified by the membrane capacitance ${\mathrm{C}}_{\mathrm{m}}$ = 31.4 pF, the leak conductance ${\mathrm{g}}_{\mathrm{leak}}$ = 31.4 nS, the sodium conductance ${\mathrm{g}}_{\mathrm{N}\mathrm{a}}$ = 8000 nS, and the high-threshold potassium conductance ${\mathrm{g}}_{\mathrm{K}\mathrm{H}\mathrm{T}}$ = 1200 nS.

Other biophysical parameters of this model, such as the mathematical characterization of the ion channels, were described previously by Wang and Colburn (2012) and Rothman and Manis (2003b). Depending on the specific neuron, the BIN model receives excitatory and/or inhibitory CN inputs from both sides (e.g. Fig. 2J). The MNTB is modeled as an inhibitory relay (sign inverter) between the CN and the binaural interaction whenever inhibitory inputs are required.

FIG. 2.

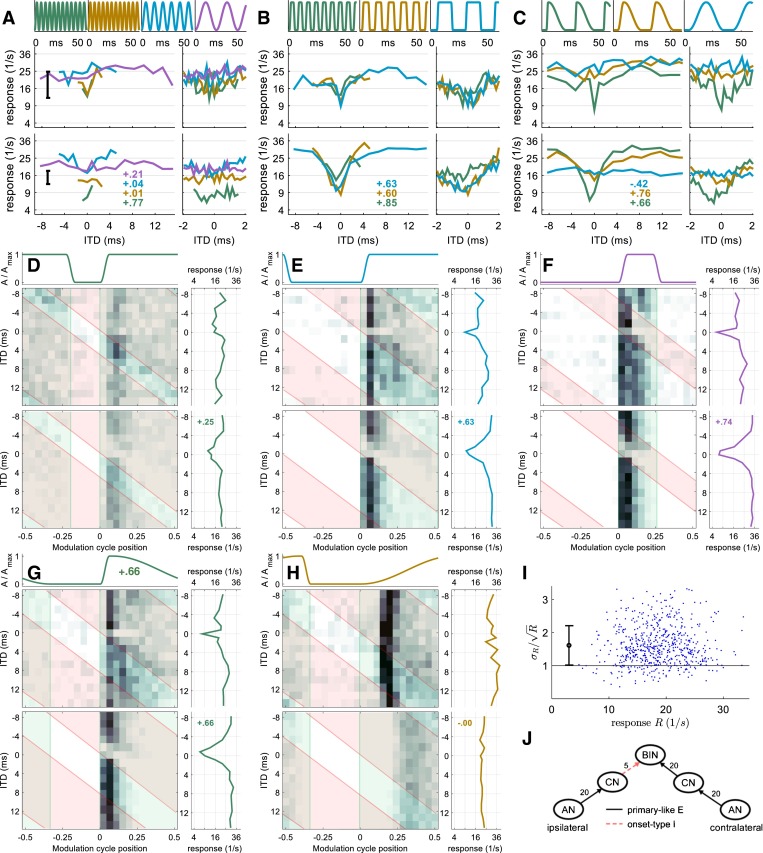
Neuron 1 (CF = 10,800 Hz): A–H data model comparison. Each panel consists of envelope waveform (top), recorded data (middle), and modeled data (bottom). Inset numbers indicate the correlation between modeled and recorded rate-vs.-ITD function. A–C: example rate-vs.-ITD functions for ten different envelope shapes. A Sinusoidal amplitude modulation (SAM) with different frequencies (333, 200, 100, and 40 Hz). The large plot on the left covers ITDs across the whole modulation cycle (1.67 ms ITD spacing), whereas the small plots on the right show ITDs in the [−2 + 2] ms interval that were recorded with a finer ITD spacing of 167 μs. B Pseudo-square-wave modulation. Attack and decay duration are fixed to 1.5 ms; pause and peak duration are identical and varied systematically: 2 ms (143 Hz), 4 ms (91 Hz), and 11 ms (40 Hz). C Variation of attack duration. Peak, decay, and pause duration are kept constant at 0.5, 15, and 8 ms, respectively. Attack durations are 1.5 ms (40 Hz), 5 ms (35 Hz), and 15 ms (26 Hz). D–H Five example 2D histograms showing response rate as a function of modulation cycle position and ITD. All five envelope shapes have a cycle duration of 25 ms (40 Hz). The transparent green area indicates when the contralateral envelope is non-zero, and the transparent red area comprises the moments when the ipsilateral envelope is non-zero. D–F Pseudo-square-wave modulated envelopes (1.5-ms attack and decay) with different duty cycles: D 4-ms pause, 18-ms peak; E 11-ms pause, 11-ms peak (same as 40-Hz condition in B); F 18-ms pause, 4-ms peak. The green area indicates when the contralateral (predominantly excitatory) envelope is high; the red area indicates when the ipsilateral envelope is high. Averaging across the modulation cycle results in the respective rate-vs.-ITD function, which is plotted to the right of each 2D histogram; G 8-ms pause, 1.5-ms short attack, and a shallow 15-ms long decay slope (same as the 1.5-ms attack condition in C). H This envelope is the temporal inversion of G, with a shallow 15-ms long attack and a steep 1.5-ms decay. Despite the clear phase locking in both recorded and modeled data, there is no more rate-vs.-ITD tuning with this envelope. I Test if the response rates are in line with a Poisson distribution: for response rates generated by a Poisson process, the standard deviation divided by the square root of the mean response for all ∼600 conditions should be rate independent and in the stricter sense it should on average be 1. For this neuron, rate independence appears to be given but the average ratio is 1.6. J Sketch of the model. BIN stands for binaural interaction neuron. Numbers on each projection indicate the number of inputs.

The HH-type BIN model receives either 20 inputs from the primary-like CN model or 5 inputs from the onset-type CN model. The estimated numbers of excitatory and inhibitory inputs to a single LSO cell are both around ten (Sanes 1990). The number of inputs to the MSO is less-well characterized anatomically, but a recent modeling study suggests that greater than 4 inputs are required to obtain realistic output from an MSO model (Franken et al. 2014). Thus, the numbers in the model are not unreasonable given the estimated number of inputs for the primary binaural interaction neurons in the brainstem.

The synaptic model describing the synapse between the CN and binaural interaction follows the same equations as those presented earlier for the synapse between the AN and the onset CN model. In addition to excitatory inputs, inhibitory inputs were also included in the binaural model. Synaptic inhibition is given in the same form as in Eqs. (1) and (2) with corresponding parameters ${\tau }_{I\_\mathit{rise}}$, ${\tau }_{I\_\mathit{fall}}$, and $G_I$. The reversal potential was −70 mV for inhibitory synapses. Table 1 summarizes the membrane parameters and the synaptic parameters for the HH-type binaural models, respectively. In the binaural model, ${\tau }_{E\_\mathit{rise}}$ was always set to be 1/10 of ${\tau }_{E\_\mathit{fall}}$, so only ${\tau }_{E\_\mathit{fall}}$ is reported in Table 1.

TABLE 1.

Synaptic parameters for the binaural interaction model

IC cell no.	Contralateral E				Ipsilateral I				Ipsilateral E				CD
	CN input	Number of inputs	${str}_{e\_\mathit{con}}$	${\tau }_{e\_\mathit{con}}$	CN input	Number of inputs	${str}_{i\_ips}$	${\tau }_{i\_ips}$	CN input	Number of inputs	${str}_{e\_ips}$	${\tau }_{e\_ips}$
1	Primary-like	20	1 nS	1 ms	Onset-type	5	3 nS	2 ms	N/A	N/A	N/A	N/A	300 μs
2	Onset-type	5	3 nS	1 ms	Primary-like	20	1.5 nS	2 ms	N/A	N/A	N/A	N/A	900 μs
3	Primary-like	20	0.3 nS	5 ms	N/A	N/A	N/A	N/A	Primary-like	20	0.05 nS	5 ms	300 μs
4	Primary-like	2	8 nS	1 ms	Primary-like	2	20 nS	2 ms	Onset-type	5	2.4 nS	1 ms	0 μs

The BIN model was permitted, at most, four inputs from the CN: excitatory (E) and inhibitory (I) inputs from contralateral side, and E and I inputs from the ipsilateral side. For the four example neurons described in the RESULTS, the model parameters were optimized in the following procedure:

• Step 1:

  the number and the type of the inputs to the IC were inferred from the 2D histogram (see the next section for details). For simplicity, each input (E or I) was either onset-type or sustained-type. In this step, only the 2D histograms in the 40-Hz pseudo-square-wave conditions (Fig. 2D–F) were used to determine the IC input types.

• Step 2:

  synaptic parameters (strength and time constant) for all the CN inputs to the BIN were systematically varied in fixed steps, and all the other parameters were fixed. In this step, the characteristic delay of the BIN was fixed at zero. The BIN model responses were then compared to the empirical data by visual inspections, and the synaptic parameters that produced the best fit to the data in the square-wave envelope shape conditions and steep/shallow attack slope conditions (e.g., Fig. 2D–H) were considered optimal. Visual inspection was used because it was difficult to use a single metric to gauge how good the fit was for all the data in multiple conditions, including both the rate-vs.-ITD functions and the 2D histograms.

• Step 3:

  after the synaptic parameters were optimized, the characteristic delay (CD) between the inputs to the binaural interaction was set to maximize the correlation coefficient between model and experimentally recorded rate-vs.-ITD functions. The mean correlation is taken from three pseudo-square-wave envelope shapes (see, e.g., Fig. 2D–F). Discrete CDs were tested at 300-μs steps. Because it is the relative delay between the excitatory and inhibitory inputs that determines the shape of the ITD tuning curve, the CD in the model can be introduced in only one of the inputs.

The simulation results reported in the RESULTS section are based on the final models with the optimal synaptic parameters from step 2 and the best CD from step 3 (see Table 1).

Data Visualization Methods

Methods for graphical visualization of the neural responses were identical for experimental and model data (Figs. 2, 3, 4, and 5). Rate-vs.-ITD functions were plotted with two different ITD ranges: a main panel comprising the ITD in the interval [−8.33; +15] ms, with spacing of 1.67 ms, and a subpanel for the interval [−2.0; +2.0] ms, with spacing of 167 μs. The rate is plotted on a quadratic ordinate axis. Rate-vs.-ITD changes would appear even more pronounced on the more typical linear axis. However, this axis scaling has the advantage that spike-count variance is displayed as a constant vertical range independent of mean rate (shown), assuming spikes are generated by a Poisson process. In other words, the vertical difference between two ITDs on such an equal variance scale is proportional to the neural discriminability between these ITDs (see Dietz et al. 2013 for details). The Poisson assumption was tested and is visualized in panel I (Figs. 2, 3, 4, and 5). With equal variance on the employed axes proven, it is not necessary to plot error bars to each data point. Instead, the average standard deviation is plotted for each neuron in panel A (Figs. 2, 3, 4, and 5)

FIG. 3.

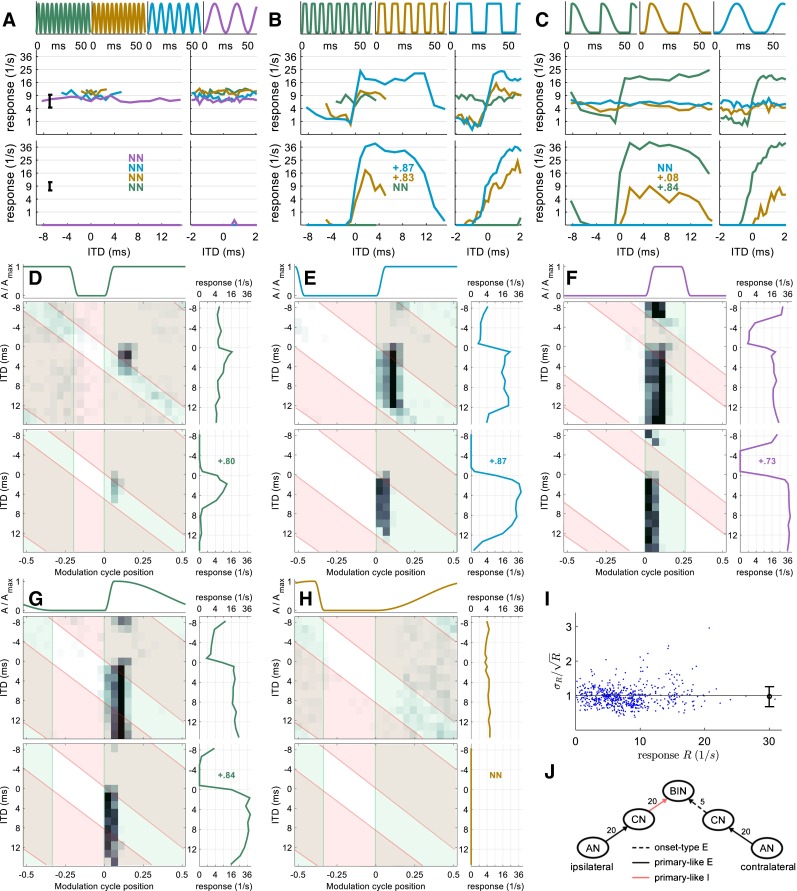
Neuron 2 (CF = 6000 Hz). Same format as Figure 2. While this neuron is also EI-type, it is modeled with sustained ipsilateral inhibition and onset-type contralateral excitation, as indicated in J. Response rates of this neuron satisfy the Poisson assumption (I).

FIG. 4.

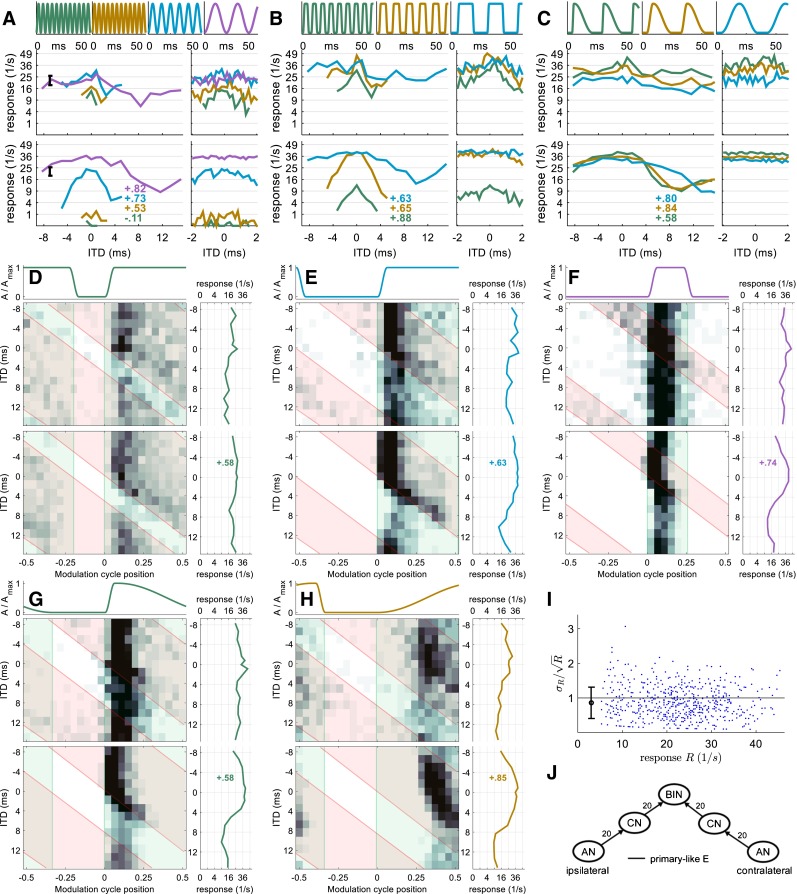
Neuron 3 (CF = 9,600 Hz). Same format as Figures 2 and 3. This EE-type neuron is modeled with sustained excitation from both sides. Response rates of this neuron satisfy the Poisson assumption (I).

FIG. 5.

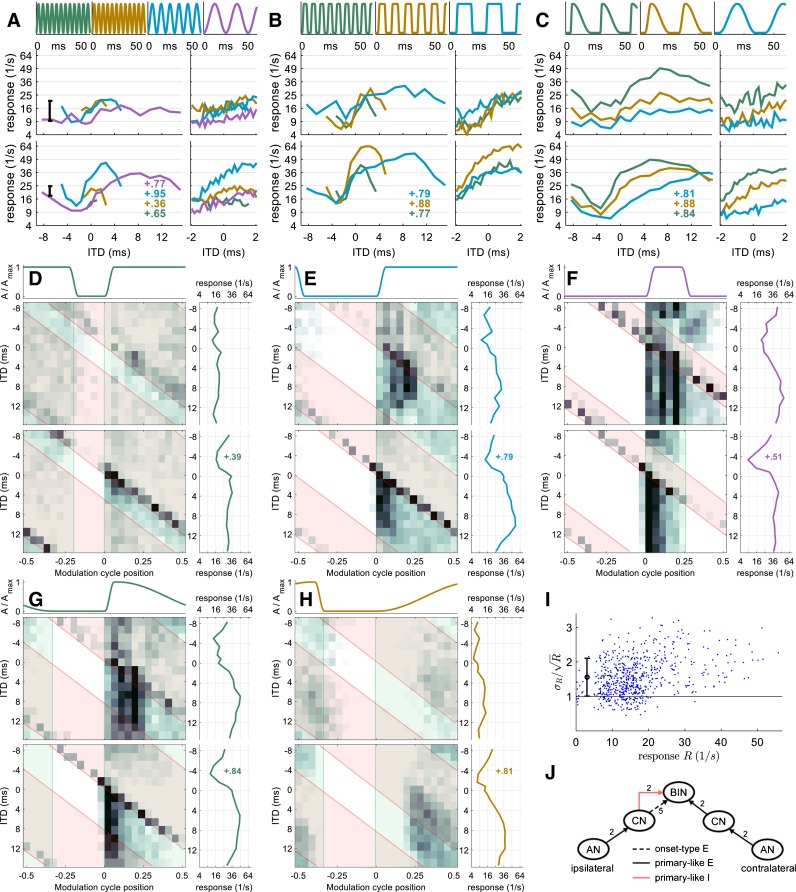
Neuron 4 (CF = 4500 Hz). Same format as Figures 2, 3, and 4. This EIE three-input-type neuron is modeled with sustained ipsilateral inhibition, onset-type ipsilateral excitation, and sustained contralateral excitation.

In addition, 2D rate-vs.-ITD-vs.-AM cycle histograms (here, referred to as 2D histograms) indicate that when in the AM cycle the neural responses occur but, in contrast to traditional AM cycle histograms, they simultaneously show how these histograms depend on ITD. The estimated response latency of the neuron was subtracted so that the response time can be related to the modulation cycle position. The latency was estimated by the response onset in a condition with a steep, 1.5-ms short, rising envelope segment (typically the envelope shape with 18-ms pause).

A transparent green area is plotted in the histograms when the magnitude of the contralateral envelope is non-zero and a transparent red area comprises the moments when the ipsilateral envelope is non-zero. For this type of display only conditions with a 25-ms cycle duration (40 Hz) are employed. The AM cycle is separated into 25 time bins.

RESULTS

Experimental and simulated data are presented for each of the four exemplar neurons outlined in the MATERIALS AND METHODS. For each example (Figs. 2, 3, 4, and 5), the data plots within each panel are arranged such that the envelope shape is illustrated along the top row, the experimental data in the middle, and the model simulation results of the corresponding neural circuit model at the bottom of the panel. The four exemplar neurons were selected because they were among those neurons showing the strongest ITD tuning (to at least one envelope shape) and because they were representatives of the three main classes of interaction: excitatory-excitatory (EE), excitatory-inhibitory (EI), and excitatory-inhibitory- excitatory (EIE). The standard response type for envelope ITD sensitivity is EI (e.g., Joris and Yin 1995), from which two examples were chosen. EI neurons also underpin neural sensitivity to interaural level differences (ILDs), a property of many neurons in the LSO of the brainstem, where excitatory input from the ipsilateral ear and inhibitory input from the contralateral, converge to generate this binaural property. LSO neurons are also the most likely candidates to generate EI-type sensitivity to envelope ITDs, and many of these neurons project to the contralateral IC (rendering their excitatory-inhibitory polarity opposite to that of the LSO). A second study based on these data, focusing on population analysis, is currently under review.

Neuron 1—Excitatory-Inhibitory Type

The rate-vs.-ITD functions of neuron 1—the first example neuron—showed a steep trough at ITD = 0 ms for all five envelope shapes with steep rising flanks (1.5-ms duration) and at least 8-ms pause duration (Fig. 2B, C). The remaining eight envelopes for neuron 1 generated rather ITD-independent response rates of 20–30 sp/s. Notably, the steep trough was absent in response to the slightly less-steep envelope with 5-ms attack duration (Fig. 2C, brown line). The influence of peak duration—tangential to this analysis—can only be compared across panels: the waveform in Figure 2D differs from the brown waveform in Figure 2B only in terms of the “peak” duration (and consequently in modulation rate). The corresponding rate ITD functions, however, differ considerably. For this neuron, stimuli with a shorter peak duration tend to generate stronger trough-type ITD tuning.

Extending the visual analysis to the 2D rate-vs.-ITD-vs.-AM cycle histograms (Fig. 2D–H), it can be inferred that the neuron has a sustained-type contralateral excitation. When the contralateral envelope is non-zero (green area), the response is high. In contrast, the ipsilateral envelope (red area) does not enhance the response in any way, suggesting that this neuron has no excitatory input from the ipsilateral side. If the onset in both ears occurs synchronously (ITD = 0), the onset response is suppressed (except Fig. 2H, which is discussed later). This, apparently ipsilateral, inhibition appears to be largely onset in nature, i.e., not sustained through the duration of the stimulus envelope, as it is ineffectual if the onset of the ipsilateral AM cycle starts before that of the contralateral side (i.e., when ITDs are negative).

These observations were then employed as a starting point for constructing the features and inputs of a model neuron displaying the same binaural response characteristics, after which we varied the parameters of the binaural inputs to match other properties of the response (see MATERIALS AND METHODS for details of the fitting process).

The model data—illustrated directly beneath the experimental data—demonstrate that the model reproduces most of the response characteristics of neuron 1. First, excitation from the contralateral side and onset-type inhibition from the ipsilateral side are apparent; only the sustained response is weaker in the model compared to the data. Second, there is good correspondence between the rate-vs.-ITD functions for model and neural data, by both visual comparison and correlation coefficients (inset numbers in Fig. 2A−H). For SAM tones, the model reproduced the more-or-less flat rate-vs.-ITD curve of neuron 1. The trough in the rate-vs.-ITD function at the highest modulation frequencies (200 and 333 Hz) is likely coincidental since the error bar (in Fig. 2A) reveals that the spike-rate standard deviation is slightly larger than the small (and speculatively systematic) ITD tuning. For square-wave amplitude-modulated (SqAM) tones (Fig. 2B), the model reproduces the trough-type ITD sensitivity exhibited by neuron 1 for all modulation frequencies tested. There is a good match between the rate-vs.-ITD functions of the model and the neuron, evidenced by the similarity of rate-vs.-ITD functions measured over the smaller ITD range. Finally, when parameters of the rising slope of the envelope were varied, the model also captures the main effect of the envelope slope observed in the data, i.e., strong ITD sensitivity to steep, short slopes and weak, or no, ITD sensitivity to shallow slopes. The main discrepancy here is that the model appears to show a slightly deeper trough in response to rising slopes of intermediate duration than was observed experimentally (Fig. 2C, brown curves).

In Figure 2G, H, the stimulus envelopes are highly asymmetric. The envelope in Figure 2G shows a steep and short (1.5-ms) rising envelope segment and a shallow and long (15-ms) decay segment. The envelope in Figure 2H is the temporally inverted version of this, with a 15-ms attack and a steep 1.5-ms decay. As shown in Figure 2C, the condition with a steep and short attack generates a strongly modulated rate-vs.-ITD function, which is absent in the temporally inverted condition. Nevertheless, this particular neuron also demonstrates a strong onset response if the envelope has a shallow, long attack (Fig. 2H). Indeed, the firing rate is slightly higher in this condition compared to that in response to the steep, short attack. Such a strong, and highly phase-locked, onset response to the shallow attack is unique in our population of 71 neurons. Here, the model correctly reproduces the rate-vs.-ITD function but it fails to account for the higher overall firing rate and the strong onset response evident in Figure 2H.

Neuron 2—Excitatory-Inhibitory Type

Similar to neuron 1, neuron 2 shows relatively little ITD tuning to SAM tones (Fig. 3A). Further, the overall firing rate is insensitive to the modulation frequency of SAM tones. For SqAM tones, neuron 2 shows broad peaks and troughs in rate-vs.-ITD functions for 40- and 91-Hz modulation (Fig. 3B), with a steep increase in rate moving from negative to positive ITDs (contralateral leading). The resulting shapes of the rate-vs.-ITD function are similar to the stimulus envelope within a cycle.

Figure 3C shows the responses of neuron 2 when the rising slope of the envelope was varied and indicates that ITD sensitivity was generated only for the steepest slope, with essentially flat rate-vs.-ITD functions in response to shallower slopes. Due to the breadth of the peaks/troughs in Figure 3B, C, it is not immediately clear from the rate-vs.-ITD functions whether the responses of neuron 2 are likely to be generated by binaural excitatory inputs, or by excitation from one ear and inhibition from the other. Nevertheless, conditions with very different pause and peak durations help to disambiguate between the two possibilities: In the rotated rate-vs.-ITD function at the right side of Figure 3F, the rate-vs.-ITD function is characterized by a fairly narrow trough, of equivalent duration to that of the peak portion of the envelope, and a broad peak corresponding to the long pause. This suggests that this neuron might have an “EI” interaction in which a sustained-type inhibition excises the response to the stimulus envelope, leaving an inverted version of the envelope as resulting rate-vs.-ITD function. This hypothesis is further supported by the 2D histograms: The highest firing rates in Figure 3D–F occur largely at the onset of each cycle of the contralateral envelope (green boxes), suggesting an onset-dominated excitatory input from the contralateral side. These onset responses are also strongly modulated by the ITD. Specifically, the responses are completely suppressed when the ipsilateral envelope is non-zero (red boxes), indicating strong, sustained inhibition from the ipsilateral side. When the slope is shallow, this neuron shows weak, sustained responses that are insensitive to ITDs. All of these 2D histograms clearly suggest binaural interaction with onset-type contralateral excitation and sustained ipsilateral inhibition.

A model with these types of inputs reproduces the main features in the responses of neuron 2 (Fig. 3J). 2D histograms in Figure 3D–H confirm that the temporal pattern of the model responses generally matches that of neuron 2. The model also reproduced the broad peak/trough in the rate-vs.-ITD functions and simulated the effect of modulation rate and the steepness of the rising slope on ITD sensitivity (Fig. 3A–C). The main discrepancy between the neuron and the model lies in the firing rate. The neuron has a non-zero firing rate for negative ITDs and for cases with no ITD sensitivity. In contrast, the model shows zero firing for those conditions. This issue is revisited in the Discussion.

Neuron 3—Excitatory-Excitatory Type

Neuron 3 is an example of the small population of recorded IC neurons that show peak-type rate-vs.-ITD functions (Fig. 4A–C). In fact, it shows peak type tuning for more envelope shapes than any other neuron of the class. For SAM tones and SqAM tones, the rate-vs.-ITD function shows a peak at zero ITD. This peak is small and broad at low modulation frequencies, becoming larger and sharper as the modulation frequency increases. For this neuron, the rising slope has little effect on the ITD sensitivity; for all types of slopes tested, the rate-vs.-ITD function shows a weak, broad peak. The 2D histograms confirm that the peak-type ITD sensitivity of neuron 3 is generated by an EE interaction (Fig. 4D–F). Neuron 3 appears to receive sustained excitation from the contralateral side, since action potentials are generated throughout the peak duration of the contralateral envelope. Some action potentials are generated when the contralateral envelope is low and the ipsilateral envelope is high (Fig. 4F, red area excluding the overlap with green area), indicating that neuron 3 also receives weak sustained excitation from the ipsilateral side. The EE interaction is clearly evident in the 2D histograms as the neural responses are significantly enhanced in regions where both envelopes are high. In Figure 4G, neuron 3 shows strong onset responses and weak sustained responses to contralateral excitation for the steep slope. For the shallow slope, neuron 3 shows a sustained response to contralateral excitation (Fig. 4H). In both cases, the firing rate is enhanced for ITD regions where the ipsilateral envelope is above zero.

The model with two sustained excitatory inputs, a strong input from the contralateral side and a weak one from the ipsilateral, captures features of the 2D histograms generated from the data and resembles the neural response in other ways. For example, the model’s rate-vs.-ITD functions capture the peak-type ITD sensitivity, although in some cases, the rate-vs.-ITD tuning was stronger in the model simulation (e.g., Fig. 4C), and the overall firing rate of the model neuron is not always identical to the respective experimental data (Fig. 4A, B).

Neuron 4—Excitatory-Inhibitory-Excitatory Type

Both the rate-vs.-ITD function and, more so, the 2D histograms of neuron 4 suggest influences from three inputs. From the 2D histograms (Fig. 5D–F), it can be inferred that one input is sustained excitation from the contralateral side, as indicated by the neural activity delineated by the green boxes. Another apparent input is sustained inhibition from the ipsilateral side, as indicated by the suppression of the response to contralateral excitation when the ipsilateral envelope is above zero (red boxes). A third input is onset-type excitation from the ipsilateral side, which generates the diagonal response pattern present at the onset of the ipsilateral cycle (red boxes). These inputs are also visible in Figure 5G for the condition with a steep, rising slope. When the rising slope is shallow, sustained firing to contralateral excitation dominates the neural responses with only a weak contribution from the ipsilateral inhibition. The onset-type ipsilateral excitation is absent in the condition with shallow attack (Fig. 5H), a pattern similar to neuron 2. Due to the two ipsilateral inputs, neuron 4 does not exhibit one of the typical peak-, step-, or trough-type ITD sensitivity. Instead, its rate-vs.-ITD functions show both a peak and a trough with the steepest slope located around zero ITD (Fig. 5A–C). This response pattern is usually referred to as intermediate-type (Kuwada et al. 1987; Batra et al. 1993) and has been associated with additional input besides the usual EE or EI binaural inputs (Batra et al. 1997a, b; McAlpine et al. 1998).

The model for neuron 4 also has the same type of inputs as inferred from the neuron’s response, namely, sustained contralateral excitation, sustained ipsilateral inhibition, and onset-type ipsilateral excitation. Unlike previous neuron models, two versions of the model were fitted for neuron 4, one with 20 primary-like CN inputs as neurons 1–3, and a second with only 2 primary-like CN inputs. The number of onset-type CN inputs remained fixed at 5 for both versions of the model. The additional version of the model was employed because the model with 20 primary-like CN inputs failed to reproduce the strong sustained response driven by contralateral excitation. Only the simulation results using two primary-like CN inputs are reported here (Fig. 5). The influences from the three inputs are clearly visible in the simulated 2D histograms (Fig. 5D–H); the simulated sustained response produced by contralateral excitation matches the response of neuron 4 reasonably well. The simulated rate-vs.-ITD functions also reproduced the intermediate-type ITD sensitivity of neuron 4, showing a peak at positive ITDs and a trough at negative ITDs. Further, the breadth of the peak and trough appears to follow the modulation frequency of the envelope, also in good agreement with the experimental data. Finally, the steepest rising slope again produces more strongly modulated rate-vs.-ITD tuning than do the shallower slopes, both in the empirical data and in the simulation results. One quantitative difference between the neuron and the model lies in the overall firing rate, with the model showing slightly higher firing rates than the neuron, especially at preferred ITDs.

Population Analysis

Of the 71 neurons for which responses were obtained, it was possible, for 43 of these, to classify both the shape of the rate-vs.-ITD function and the main inputs from the 2D histograms. The results from this classification, based on visual inspection of the 50 % duty cycle SqAM condition (Figs. 2, 3, 4, and 5E), are shown in Table 2. For cases in which no ITD sensitivity was evident in response to this envelope shape, the classification was performed based on the SqAM condition with 18-ms pause (Figs 2, 3, 4, and 5F). The other 28 neurons typically showed only weak ITD tuning, even for the 18-ms pause condition. The four example neurons were representatives of the four most common classes of neural responses and cover all rate-vs.-ITD function shapes. The observed troughs were typically sharper tuned than the peaks.

TABLE 2.

Classification of the neural population by input type and rate-vs.-ITD function shape

	Peak	Trough	Step/Int	Sum
EE	7			7
EI		6	8	14
EIE	5	1	16	22
Sum	11	8	24	43

The most common input type for each of the four rate-vs.-ITD function shapes is marked in bold. One representative from each of these classes was selected as example neuron

EIE neurons make up half of this population. However, based on inspection of the temporal response patterns, two inputs are dominant in 6 of the 22 EIE neurons: in 5 of these neurons, the rate-vs.-ITD function is peak shaped and the excitatory inputs are dominant. One EIE-type neuron classified as trough shape has a narrow trough embedded in a broad, weakly modulated peak.

We also examined how well rate-vs.-ITD functions of each model neuron correlate with those obtained experimentally. With the neural population classified into three different groups of rate-vs.-ITD functions according to their shape, the correlation coefficient of the response rates can be compared to neurons from the same class as the model, and to neurons from the other two rate-vs.-ITD function shape classes (Fig. 6). This was performed for the three sqAM waveforms with f_m = 40 Hz that were used to fit the model (Fig. 6, top row), and three waveforms that were not used for model fitting to this point, in fact not at all compared with the model output. These new waveforms are also sqAM envelopes but with constant pause duration of 8 ms and three different hold durations (sustained segment). In particular, the condition with only 0.5-ms hold duration (blue diamonds in Fig. 6) challenges the model, as its duty cycle is shorter than any to which the model was fitted.

FIG. 6.

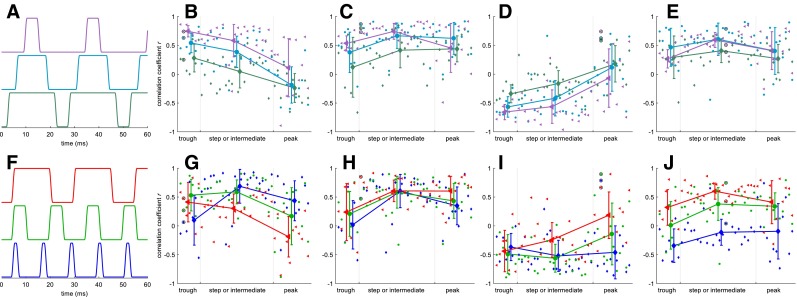
Correlation coefficient between the rate-vs.-ITD functions of the four model neurons and the corresponding rate-vs.-ITD function for each of 43 IC neurons. Top row: data for three 40-Hz envelopes on which the models were fitted (compare to Fig. 1 D–F). A Envelope shapes. B–E Correlation between data and models 1–4. Larger symbols with error bars indicate group average and standard deviation. The data points from the respective example neurons 1–4 are marked by black circles. Bottom row: same as top row but for three untrained envelope shapes (constant pause of 8 ms with variable hold duration of 0.5, 4, and 14 ms). The blue diamond in the black circle in H is hidden beneath the green circle and therefore not visible. For each isolated data point, the confidence interval cannot be not specified. However, a noise floor was estimated assuming Poisson noise in the response rate: the standard deviation of correlation values was then 0.09. Therefore, 95 % significance can be expected from correlation values >0.18. Precision increases with higher baseline correlation.

For the trained envelopes, all four models show the largest average correlation with the rate-vs.-ITD functions of their own shape class. This generalizes to the untrained envelope shapes for model neurons 2, 3, and 4, but not for model neuron 1: for the envelope with 0.5-ms hold duration, there is no average correlation between trough-type neurons and the trough-type model 1, not even for example neuron 1, to which the model was fitted. The absence of a correlation shows that not all aspects of neural responses are captured by the model. The possibility remains, therefore, that the processing of model 1 is very different to that of actual trough-type neurons, and that the model fitted to the trained conditions is merely one of several possible parameter fits. For model 3, the model appears to correlate well only to the specific neuron to which it was fitted. The reason for this is that neuron 3 is actually an untypical peak-type neuron in that it has peak-type tuning to almost all envelopes. Most other neurons of this (peak-type) class show ITD sensitive to only a very few envelope shapes. These can be identified by the positive correlation values. Several neurons were only sensitive to envelopes not investigated in Figure 6 and show no clear positive correlation with the model. However, these other peak-type neurons would not have been better exemplary neurons for two reasons: first, each neuron showed ITD sensitivity to a unique set of envelope shapes so there is, in fact, no typical representative of the peak-type class. Second, a model of a neuron that is not ITD sensitive to several, or even the majority, of envelopes is not useful in terms of correlating its flat rate-vs.-ITD function with any other rate-vs.-ITD function. Notwithstanding these caveats, the model shows a high, positive correlation to the six rate-vs.-ITD functions of the, admittedly unique, example neuron 3 to which the model was fitted. Most remarkably, the correlation in the untrained 0.5-ms hold duration envelope is +0.785 for the example neuron 3 and negative for 41 of the remaining 42 neurons.

In addition to the correlation analysis, we also examined how the model results varied as the synaptic parameters changed. Figure 7 shows the influence of changing $G_E$ for two of the sqSAM conditions in model neuron 4 (EIE). These conditions tended to generate strong ITD tuning. It is clear that in both envelope conditions (Fig. 7C, D), increasing $G_E$ increased overall firing rates, and made the trough less prominent. In comparison, some of the 16 EIE neurons (e.g., the four thicker, colored lines in Fig. 7A, B) show similar ITD tuning as the model versions. From this, it can be speculated that some of the variation across the 16 neurons may be due in part to differences in excitatory conductance. Other properties that follow from changing the strength of the excitatory conductance are apparent in the four examples from the EIE intermediate-type population: for example, the shift in the position from negative to positive ITD with increasing overall response rate in Figure 7C, D is also visible in the 18-ms pause condition (Fig. 7A), but not in the 4-ms condition (Fig. 7B).

FIG. 7.

A Rate-vs.-ITD function for all 16 EIE intermediate and step-type neurons from the population for the SqAM envelope with 4-ms pause and 4-ms hold duration, f _m = 91 Hz. The green trace is from example neuron 4. The other three colored traces are from EIE neurons which appear to have similar input types and time constants as example neuron 4 and appear to differ primarily in their excitatory conductance. B Same as A but for the envelope with 18-ms pause and 4-ms hold duration, f _m = 40 Hz. C, D Rate-vs.-ITD functions for nine different excitatory conductances to the same stimuli as for A and B, respectively. Values in C indicate excitatory conductance in nS. The dashed trace is from model neuron 4.

DISCUSSION

We have demonstrated that a combination of binaural brain circuits, featuring either purely excitatory or mixed excitatory-inhibitory mechanisms, can explain the relative sensitivity of auditory-midbrain neurons to different features of the (binaural) sound envelope. Complementary to studies investigating isolated transient envelopes (e.g., Heil 1998), the current study focuses on the influence of a periodic envelope in the ongoing portion of a stimulus, disregarding any influence of stimulus onset.

Consistent with data obtained from stimulation of one ear only (e.g., Zheng and Escabí 2008), IC neurons show a wide range of response characteristics. With the addition of the ITD dimension, no pair of neurons within the population could be modeled with exactly the same parameters. The only substantial number of neurons (about 20 %) that could be identified as showing broadly consistent features were neurons classified as EI neurons, showing onset-type contralateral excitation and sustained ipsilateral inhibition, such as example neuron 2 (Fig. 3). The four example neurons were therefore chosen to represent the main types of response patterns observed in the majority of neurons. In particular, the example neurons exhibit strongest ITD tuning for envelopes with a long pause or a steep attack (e.g., neurons 1, 2, and 4), a feature consistent with human psychoacoustic data (Klein-Hennig et al. 2011; Dietz et al. 2015), in vitro MSO data (Gai et al. 2014) and with the responses of IC neurons to monaural stimulation (Neuert et al. 2001). Perhaps most importantly, the stimulus envelope shape most commonly employed in previous studies of envelope coding—sinusoidal amplitude modulation—was largely ineffectual in generating strong ITD dependence in neural firing rates. Indeed, many neurons highly sensitive to ITDs conveyed in other envelope shapes (e.g., example neuron 2) were entirely insensitive to ITDs conveyed in SAM tones, even for the same rate of modulation. This highlights the importance of a fast attack in generating ITD sensitivity in stimulus envelopes and suggests that previous studies employing SAM tones have grossly underestimated the proportion of midbrain and brainstem neurons sensitive to envelope ITDs. These findings together with the physiological differences between fine structure ITD circuits and envelope circuits (e.g., in vitro MSO vs. LSO data, Remme et al. 2014) provide a reference for future CI sound coding strategies to improve sound localization for bilateral CI subjects.

It is worth noting that studies of IC responses in the awake rabbit have shown large effects of anesthesia on envelope ITD processing (Chung et al. 2015). Indeed, anesthesia used in the present study may account for why most neurons show weak or no ITD sensitivity to envelopes at high modulation rates (see SAM condition in Figs. 2, 3, 4, and 5A). However, most of the conditions on which we focused had relatively low modulation rates (e.g., 40 Hz in Figs. 2, 3, 4, and 5C–H) for which IC responses are less likely to be strongly affected by the effect of anesthesia.

Based on binaural inputs estimated for each individual neuron, the model captures the main effects of the envelope shape on the ITD sensitivity in the IC, i.e., the steepness of the AM attack and the pause duration prior to each AM attack. A key observation is that the model also accommodates the range of very different response patterns across individual neurons, by changing model parameters within a physiologically plausible range. The model also has predictive power; for example, while the parameters were initially not fitted to the data shown in Figures 2, 3, 4, and 5G, H, the EE-type model predicted a similar rate-vs.-ITD tuning for the steep attack (Fig. 4G) compared to the shallow attack (Fig. 4H). This is not the case for any of the pure EI-type neurons (Figs. 2 and 3), which putatively receive their binaural input from the LSO rather than the MSO. From the experimental data alone, it is not clear whether or not this represented a systematic relationship rather than a coincidence.

The fact that each neural model can reproduce the firing patterns of the example IC neuron in response to a relatively large set of different stimuli provides strong support for the hypothesis that the synaptic inputs can be inferred from the rate-vs.-ITD function and the 2D histograms. Nevertheless, there are some clear discrepancies between the model simulation and the neural data. One example is the non-zero firing rate at non-preferred ITDs (Fig. 3). In the experimental data, firing rates are all above zero, even at non-preferred ITDs. In contrast, the model neuron shows no firing at non-preferred ITDs and the firing rate is also zero when ITD tuning is absent. Here, the response pattern is generated by strong ipsilateral inhibition that completely suppresses the contralateral excitation. When the strength of the inhibition was reduced in the model, response rates at non-preferred ITDs became positive. However, reducing the strength of the inhibitory input also generated ITD tuning in the model for conditions where neural responses showed no such sensitivity (e.g., Fig. 3A). One possible explanation for the lack of tuning in some of the neural rate-vs.-ITD functions is the lack of envelope phase locking to the inhibitory input for these conditions. This explanation, however, appears to be inadequate for the lowest modulation frequency in Figure 3A (40 Hz), since it would require the inhibition to be slower than is physiologically observed in the LSO (Sanes 1990). Spontaneous activity for this neuron is zero and is unlikely to be the explanation for the non-zero firing rate at non-preferred ITDs. It is possible that some monaurally driven inputs, i.e., ITD insensitive inputs, combined with the binaural responses of model neuron 2 might explain the non-zero firing rate in this neuron.

We have successfully reproduced most of the response patterns of our recorded IC neurons using realistic LSO membrane parameters. The LSO pathway has been associated with EI-type binaural interactions (e.g., Joris and Yin 1995), making it the likely neural circuit underlying the response pattern of neurons 1 and 2. Both clearly show influences from contralateral (relative to the IC recording site) excitation and ipsilateral inhibition. It is less clear, however, whether the LSO pathway also underlies the responses of neurons 3 and 4, because both of these neurons are also clearly influenced by ipsilateral excitation. The LSO as a possible source of IC neurons with EE properties cannot be ruled out since there have been reports of EE-type LSO neurons in gerbils (Kil et al. 1995). On the other hand, the MSO, normally associated with EE-type binaural interactions, also represents a possible source of input generating the response patterns of neurons 3 and 4. Compared with the LSO, however, responses of high-frequency MSO neurons are less often reported and details of their membrane properties less well known. Alternatively, responses of the example IC neurons could be generated at sites farther along the auditory pathway than the SOC, such as the DNLL or the IC itself. For example, an IC neuron with ipsilateral and contralateral input could equally well give rise to the observed response patterns.

Varying the excitatory synaptic strength in the model reproduced some of the variations observed in the IC population (Fig. 7). In general, however, variations of only a single parameter cannot fully account for variability of response patterns, even within the subpopulation of EIE intermediate-type neurons. This is not surprising, as multiple factors in the synaptic inputs can affect the IC responses. The number of inputs to the BIN model also affects the simulated response, mainly in the temporal pattern (see results on neuron 4). Reducing the number of primary-like CN inputs from 20 to 2 dramatically enhanced sustained responses driven by contralateral excitation. When the number of inputs was large, the high onset-to-sustained ratio in the primary-like response (Fig. 1A, steep decay in response rate within the first 25 ms) was well preserved in the synaptic current of the BIN, which gave rise to weak sustained response in BIN. With smaller number of inputs and stronger synaptic strength, this high onset-to-sustained ratio is largely reduced in the synaptic current, leading to an enhanced sustained response in BIN. Even though these effects are somewhat expected, they nonetheless increase the flexibility of the model: it is likely that the model can account for most of the variability in the responses among the IC population when multiple parameters in the model are fitted for each neuron’s response pattern.

The specific binaural nuclei contributing to the responses of neurons 1–3 may not be of primary importance when seeking to investigate mechanisms by which binaural sensitivity is generated in the IC, because these neurons can be explained by two main inputs only, and thus only one stage of binaural interaction. However, the actual circuit from brainstem to IC may play a role in understanding and modeling of the responses of neuron 4: the three main inputs result in two distinct anatomical arrangements—(1) three inputs converge onto one coincidence-detector neuron or (2) two stages of coincidence detection exist, each with two inputs. Case (2) can be further subdivided into cases with different pairs interacting first. Due to design limitations, the model considers only case (1), and this might account for the (relatively small) discrepancies between the model and the data: for example, responses to ipsilateral excitation generate more or less at equal-magnitude responses throughout the entire contralateral cycle (diagonal pattern in Fig. 5F). In the model, however, the response to the ipsilateral excitation is much stronger when the contralateral envelope is high than when it is low. This discrepancy may be explained by ipsilateral excitation directly projecting to the IC neuron itself.

Through a combination of a diverse set of envelope shapes employed in our recordings, and a detailed analysis of neural firing rates and temporal response patterns, it is possible to explain the responses of individual binaural neurons in the IC and to estimate the specific set of synaptic inputs each neuron receives from neurons in the binaural brainstem. Together, the model and the data provide the means of understanding at a physiological level the relative importance of different components of the stimulus envelope in driving ITD sensitivity, and how this depends on the neuron’s individual synaptic inputs.

In conclusion, the 2D histogram provides a novel approach to visualize the data such that general classes of the binaural inputs are readily available. Built upon the information inferred from the 2D histograms, the neural models demonstrate that the range of IC response patterns can be quantitatively explained by biologically plausible circuits and parameters. These analysis methods can be very useful tools to investigate binaural mechanisms underlying neural representation and processing of binaural stimuli that are more physiologically relevant, e.g., to develop optimal envelope shapes and enhanced ITDs for cochlear implants.

Compliance with Ethical Standards

Conflict of Interests

The authors declare that they have no conflict of interest.