Boomerang: A Method for Recursive Reclassification

Summary

While there are many validated prognostic classifiers used in practice, often their accuracy is modest and heterogeneity in clinical outcomes exists in one or more risk subgroups. Newly available markers, such as genomic mutations, may be used to improve the accuracy of an existing classifier by reclassifying patients from a heterogenous group into a higher or lower risk category. The statistical tools typically applied to develop the initial classifiers are not easily adapted towards this reclassification goal. In this paper, we develop a new method designed to refine an existing prognostic classifier by incorporating new markers. The two-stage algorithm called Boomerang first searches for modifications of the existing classifier that increase the overall predictive accuracy and then merges to a pre-specified number of risk groups. Resampling techniques are proposed to assess the improvement in predictive accuracy when an independent validation data set is not available. The performance of the algorithm is assessed under various simulation scenarios where the marker frequency, degree of censoring, and total sample size are varied. The results suggest that the method selects few false positive markers and is able to improve the predictive accuracy of the classifier in many settings. Lastly, the method is illustrated on an acute myeloid leukemia dataset where a new refined classifier incorporates four new mutations into the existing three category classifier and is validated on an independent dataset.

1. Introduction

Prognostic classifiers are used to guide treatment decisions and provide patient counseling in many clinical settings. For example, in acute myeloid leukemia (AML), three prognostic risk groups – unfavorable, intermediate, and favorable – defined by cytogenetics have distinct differences in survival and can guide suitability for bone marrow transplantation (Slovak et al., 2000). The tumor-node-metastasis (TNM) staging systems has provided the backbone of staging in many solid tumors (Edge et al., 2010); however, despite its widespread use, the TNM staging system has only modest predictive accuracy (Gönen and Weiser, 2010). Therefore, as new biologic or environmental markers become available, it is of clinical interest to identify markers that improve the overall accuracy of an existing classifier. These new markers can modify and refine one or more of the existing groups by shifting a subgroup of patients into a higher or lower risk category. While various statistical methodologies exist to develop an initial prognostic classifier, to our knowledge there are no systematic ways to refine an existing classifier by incorporating new markers.

To develop an initial classifier, tree-based methods such as classification and regression trees (CART) can be used to suggest simple and interpretable risk groups based on combinations of binary covariate splits (Breiman et al, 1984). Multiple authors have extended this methodology to the survival setting including among others: Segal (1988), Davis and Anderson (1989), and LeBlanc and Crowley (1992, 1993). Model building techniques such as stepwise or penalized re gression (Tibshirani, 1997) could also be used by defining a risk score that is then categorized into risk groups.

While these methods can develop new prognostic classifiers, they are not designed to modify an existing classifier by incorporating newly available markers. To illustrate this using CART methodology, a tree could be grown within each of the existing unfavorable, intermediate, and favorable risk categories to evaluate whether combinations of the new markers are associated with prognosis. Subgroups with differential survival are identified within each category, but it is unclear how to recombine the subgroups across the multiple trees to form the new unfavorable, intermediate, and favorable risk groups. Alternatively, variable selection using a regression model could be implemented to find a subset of new markers that are significantly associated with survival or have a significant interaction with the existing classifier. While this approach can provide a continuous risk score, it does not provide a new risk categorization system to use in clinical care.

This paper addresses this methodological gap by developing a new algorithm, called Boomerang, for risk reclassification. The algorithm starts with an existing classifier and searches among new markers for modifications that improve the overall predictive accuracy. At completion the algorithm returns to the pre-specified number of risk groups, typically the same number as the existing classifier. The algorithm presented here is illustrated using one measure of predictive accuracy, the concordance probability estimate (CPE) (Gönen and Heller, 2005). In this setting CPE can be interpreted as the probability that, for a randomly selected pair of patients, the ordering of the risk is consistent with the ordering of the outcomes (i.e., higher risk patients corresponding to shorter survival times). While our algorithm is illustrated using CPE, any metric of predictive accuracy could be used instead.

The paper continues with Section 2 providing a motivating example where the analysis goal is to develop a refined classifier. Section 3 provides an overview of the data setup and details of the two-stage algorithm. The section then proposes two resampling techniques to evaluate the improvement of the new refined classifier. Section 4 presents various simulation scenarios to assess the performance of the algorithm. Section 5 illustrates the use of the algorithm by applying it to risk classification in AML. The paper concludes in Section 6 with discussion of key results and implications for future use.

2. Motivating Example

In AML, cytogenetics characterize the chromosomal abnormalities in the malignant clone of the cancer and it is used to classify patients into one of three categories: favorable risk, intermediate risk, and unfavorable risk. While these three groups have significantly different survival (Slovak et al., 2000), heterogeneity in survival remains within each group. Patel et al (2012) explored how genetic profiling of patients could be used to reclassify patients by combining selected somatic mutations with cytogenetics to define a new three category system. The study included 398 patients who were previously enrolled in a clinical trial examining dosing regimens of chemotherapy. The existing risk classifier divided the cohort into the three cytogenetics-based groups: unfavorable (16%), intermediate (65%), and favorable (19%). Thirty-five percent were censored for the overall survival endpoint. A total of 17 genes, ranging in mutation frequency from 2% to 37%, were examined to see if any mutational combinations could refine and improve upon cytogenetics alone. The analysis goal was to develop a new three category system that has higher predictive accuracy.

Two CART strategies could be employed to analyze these data. A single tree could be grown with both cytogenetics and the mutational data. If grown using logrank splitting, this results in a total of 11 leaves in the unpruned tree that partition the covariate space. While the first split separated the intermediate and favorable cytogenetic groups from the unfavorable group, the favorable and intermediate groups were not separated until further down the tree; this classifier would be difficult to interpret in the clinical scenario. A second approach is to grow three separate trees within each of the cytogenetic risk groups. This results in 10 leaves across the three trees, with one split in the unfavorable cytogenetics tree, five splits in the intermediate tree, and one split in the favorable tree. The trees from these two CART-based strategies are provided in the Web Appendix.

Traditional pruning approaches, which remove branches of a single tree, are not designed to combine leaves across different branches or across separate trees. Amalgamation procedures, such as discussed in Ciampi et al. (1986), can combine leaves across different branches of a single tree but have not been applied to merge across separate trees. Without methodology and software available to refine a prognostic classifier, Patel et al. improvised a data-analytic strategy to develop the new classifier in the AML analysis. The amalgamation procedure is further discussed in Section 4, and we return to the AML analysis in Section 5.

3. The Boomerang Method

3.1 Overview

The methodological goal is to improve the predictive accuracy of an existing classification system by incorporating new genomic markers. Boomerang is comprised of a Forward Process and a Backward Process. In the Forward Process, the algorithm creates intermediary risk classifications by iteratively dividing one of the existing risk group into two subgroups by a selected genomic marker until further divisions no longer satisfy pre-defined splitting criteria. In the Backward Process, subregions are selectively merged until the pre-selected number of final risk groups is reached. The resulting classifier is a Boolean expression combining the existing risk groups and new markers. While the final size of the classifier can be any number of risk groups, the remainder of the manuscript returns to the same number of risk groups in the original classifier.

3.2 Boomerang Algorithm

For patient i = 1, …, n, we observe Y_i =min (C_i, T_i), the minimum of the underlying censoring time C_i and survival time T_i, along with the corresponding censoring indicator δ_i = I{T_i ⩽ C_i}. Covariates {x} can be separated into {x_C, x_G}, where x_C has dimension n × 1 and represents the existing classifier and x_G represents the p new genomic markers and is of dimension n × p.

The existing classifier divides the covariate space into K disjoint regions, R₁, …, R_K, and the collection of regions for the classifier is denoted $V^K={\{R_h\}}_{h=1}^K$. For region R_h, h = 1, …, K, we define an indicator function B_h(x) = I {x: x ∈ R_h}, and collection of functions as {B₁(x), …, B_K(x)}.

A region can be subdivided by a genomic marker x_j at a threshold c by the following indicators: $S_{x_j,c}^{+}=I\{x:x_j>c\}$ and $S_{x_j,c}^{-}=I\{x:x_j\le c\}$. For region R_h, this results in two subregions defined by $B_h(x)S_{x_j,c}^{+}$ and $B_h(x)S_{x_j,c}^{-}$. Let V^K(h, j, c) denote an expansion of the existing classifier where region R_h is split by x_j at the value c; this expanded classification system is represented by the functions,

$$\{B_1(x),\dots ,B_h(x)S_{x_j,c}^{-},B_h(x)S_{x_j,c}^{+},\dots ,B_K(x)\}.$$

While the split indicator notation naturally applies to binary and ordered covariates, modifications can extend the notation to include subsets of values for nominal categorical covariates.

The algorithm is illustrated using CPE to assess the discriminatory ability of the classifier. CPE is evaluated using the estimated coefficients from a proportional hazards model. While denoting $\eta (x)={\displaystyle {\sum }_{h=1}^K{\beta }_h{B}_h(x)}$ with β₁ = 0, the estimated coefficients are derived from partial likelihood

$$l(\beta )={\displaystyle \prod _{i=1}^n\frac{e^{\eta (x_i)}}{{\left[{\displaystyle {\sum }_{j\in Q(y_i)}{e}^{\eta (x_j)}}\right]}^{{\delta }_i}},}$$

where Q(y_i) represents the risk set at time y_i (Kalbfleisch and Prentice, 1980). For $V^K={\{R_h\}}_{h=1}^K$, CPE can then be estimated using

$$F(V^K)={\displaystyle \sum _{h,h^{\prime }=1}^K\frac{n_h{n}_{h^{\prime }}}{n(n+1)}{\left\{1+\exp ({\widehat{\beta }}_h-{\widehat{\beta }}_{h^{\prime }})\right\}}^{-1}},$$

where n_h and n_h′ are the number of patients whose covariates are within regions R_h and R_h′, and n is the overall sample size.

The general Forward Process iteratively searches for the largest improvement in CPE by finding

$$(h^{\ast },j^{\ast },c^{\ast })=\underset{h,j,c}{\arg max}\left[F(V^K(h,j,c))-F\left(V^K\right)\right],$$

with the corresponding difference of d_h*,j*,c*. The one-step expanded system where region R_h* is split by marker x_j* at a threshold c^* is denoted V^K+1 = V^K(h^*, j^*, c^*), where the K+1 regions are arbitrarily enumerated. Iterative application of this results in the following process:

Forward Process

• Step 1: Specify the minimum increase in the selected metric Δ for a split to be admissible. Also select the minimum number of patients (n_min) and observed failure times or events (e_min) required in each subregion.

• Step 2: Start with the initial system V^K with the index s = 0. Among all possible region and marker combinations which satisfy n_min and e_min, determine

  $$\underset{h,j,c}{\arg max}\left[F(V^{K+s}(h,j,c))-F\left(V^{K+s}\right)\right].$$ (1)

• Step 3: If d_h*,j*,c* > Δ, define V^K+(s+1) = V^K+s (h^*, j^*, c^*).

• Step 4: Repeat steps 2–3 updating the index s + 1 until no further split satisfies the Δ,n_min, and e_min parameters. Let V^M denote the fully expanded system to initiate the Backward Process.

To determine the final classifier, the Backward Process considers merging any two partitions in the expanded system V^M. For notational convenience, let W^M = V^M and consider W^M(h, h′) = {R₁, R₂, … R_h ∪ R_h′, …, R_M} the W^M system with regions R_h and ${R^{\prime }}_h$ merged. In this process, the algorithm searches for the M − 1 system with the highest predictive accuracy by finding

$$(h^{\ast },{h^{\prime }}^{\ast })=\underset{h,h^{\prime }}{\arg max}F(W^M(h,h^{\prime })).$$ (2)

The one-step reduced system is denoted W^M−1 = W^M(h^*, h′^*) and similar to the Forward Process the M − 1 regions are arbitrarily enumerated. The process continues as follows:

Backward Process

• Step 1: Select the number of risk categories K′ in the final classification system.

• Step 2: Among all $(\begin{array}{c}M\\ 2\end{array})$ possibilities, find h^* and h′^* combination in (2) that maximizes F(W^M(h, h′)).

• Step 3: Let W^M−1 = W^M(h^*, h′^*), which can be generalized as W^M−s. 

• Step 4: Continue with the previous two steps, updating the index s + 1 with each iteration, until M − s = K′. Let W^K′ denote the partition for the final classifier.

3.3 Implementation

In addition to selecting the minimum number of patients and observed events in each partition, the algorithm requires a minimum increase (Δ) in predictive accuracy for a division to be permissible. A large Δ may prevent any division beyond the existing classifier or may miss potential marker-by-marker interactions identified later in the Forward Process. However, too small of a Δ may result in expansions driven mostly by noise. While the analyst can select this tuning parameter upfront, an initial cross-validation procedure can also be utilized to select this parameter. This is illustrated in the Reclassification in AML section, using 10-fold cross-validation to select Δ. In this process, 9/10^th of the data are randomly selected and used to develop a new modified classifier for one potential Δ; this classifier is applied to the group of patients not selected. The CPE for the potential Δ is calculated once all patients have a reclassified risk group. This is repeated for several potential Δ values along a grid, where the entire cross-validation process is repeated. The Δ that provides the largest average CPE is selected for the Forward Process.

3.4 Evaluation of the New Classifier

Ideally a new classifier will be evaluated on an independent dataset or a separate validation cohort. Unfortunately, in many clinical scenarios, such data are not available at the time of analysis or the current data are too limited to split into training and validation cohorts. Data resampling techniques exist to estimate the bias of over-fitting in an adaptive procedure when new risk groups may need to be evaluated on the same data upon which they were derived. The bias-adjusted bootstrap is one technique that can be used to estimate the predictive accuracy of the final classifier (Efron and Tibshirani, 1994). In this procedure, the algorithm is refitted on a bootstrap sample of the data, and the refined classifier from the bootstrap sample is applied to the original dataset. The bias is calculated as the difference in CPE from the within-bootstrap sample estimate and the estimate when the refined classifier is applied to the original data. The average bias is calculated over multiple bootstrap samples, and this average bias is subtracted from the CPE estimate of the final classifier from the original dataset. This method is illustrated in the Reclassification in AML section below.

In addition to a final estimate of predictive accuracy, it is often of interest to assess whether the new classifier results in a statistically significant improvement in the selected metric over the original prognostication. Let F(V^K) denote the metric from the original classifier and F(W^K′) from the final refined classifier. The permutation test is constructed by permuting the rows of the matrix x_G a total of L times over the triplet of survival time, failure indicator, and original classification. The entire refinement process is repeated and the statistic $F(W_l^{K^{\prime }})$ is calculated for each permutation. Any procedure such as a preselection of markers or cross-validation to identify Δ should be included within the analysis of the each permuted data set. The p-value to evaluate the observed increase in predictive accuracy using the permutation-based null distribution is calculated using

$$\frac{1}{L}{\displaystyle \sum _{l=1}^{L}I\{F(W_l^{K^{\prime }})⩾F(W^K)\}}.$$

4. Simulation Studies

The performance of the Boomerang method is evaluated under three scenarios motivated by the results of Patel et al (2012). In Null Scenario 1, existing classifier V^K represents the true risk structure of the data; the new x_G markers are non-informative and do not improve the true classification of the data. While this is not a realistic scenario in many clinical settings, it is included here to assess the potential for false positive marker selection. Null Scenario 2 considers an existing classifier that does not perfectly reflect the true structure of the data, but the misclassification is independent of the x_G markers included in the algorithm. Therefore, the new markers cannot improve upon the accuracy of the existing system. This scenario represents a clinical situation where, for example, the cohort under consideration is more heterogenous than the one in which the classifier was developed and validated. In the final scenario Alternative the existing system misclassifies some patients; however, now a subset of the x_G markers can be utilized to correctly reclassify these patients.

In all three scenarios, the number of risk groups in both the true and the existing classifier is three. Survival times are generated from a Weibull distribution with a shape parameter of 0.7 and scale parameters of λ₁ = 15, λ₂ = 3.5, and λ₃ = 0.9 depending on the underlying risk group. The censoring times are drawn from a uniform distribution corresponding to approximately 30% or 50% censoring. A total of 20 binary markers are generated from a binomial distribution with a mutational frequency of 0.15 or 0.30 depending on the simulation. All markers are independent of survival times except for markers x₁, x₂, x₃, and x₄ in the Alternative Scenario. In this scenario, patients in the existing intermediate risk group with markers x₁ or x₂ should be reclassified as part of the new favorable risk group. Patients in the existing unfavorable group with marker x₃ and those in the favorable group with marker x₄ should all be reclassified as part of the new intermediate risk group. Null Scenario 2 mirrors the simulation step of the Alternative Scenario; however, now the markers that could improve the predictive accuracy (z₁, z₂, z₃, and z₄) are unobserved.

The CPE for the true classifier depends on the scenario and marker frequency. Under the Alternative Scenario, the CPE for the true classifier correctly reclassifying all patients was designed to have a CPE of 0.68 for a marker frequency of 15% and 0.68 for a marker frequency of 30%. Under Null Scenario 1, the true classifier is the existing one, and it has a CPE of 0.69. Under Null Scenario 2, with the data x₁, …, x₂₀, the best classifier is also the existing one, and it was designed to have a CPE of 0.66 for a marker frequency of 15% and 0.63 for a marker frequency of 30%. Had z₁ to z₄ been observed and available, the best CPE value would be the same as in the Alternative Scenario. While modest, the CPE values from these simulated classifiers are typical to what is seen in cancer prognostication where survival heterogeneity will likely remain to some extent within risk groups.

The simulation set-up is provided in Table 1. R₁, R₂, and R₃ and the defined functions B₁(x), B₂(x), and B₃(x) represent the existing classifier for the unfavorable, intermediate, and favorable risk groups. In each simulation, the sample was evenly split into the three risk groups. The algorithm is evaluated on a total sample size of 300 and 600 patients.

Table 1.

Scale parameters for the three simulations scenarios.

	Weibull Scale Parameter
Null Scenario 1	λ1B1(x) + λ2B2(x) + λ3B3(x)
Null Scenario 2	$\begin{array}{c}{\lambda }_1{B}_1(x)+{\lambda }_2{B}_2(x)+{\lambda }_3{B}_3(x)+({\lambda }_2-{\lambda }_1)B_1(x)S_{z_3}^{+}\\ +({\lambda }_3-{\lambda }_2)max\{B_2(x)S_{z_1}^{+},B_2(x)S_{z_2}^{+}\}+({\lambda }_2-{\lambda }_3)B_3(x)S_{z_4}^{+}\end{array}$
Alternative Scenario	$\begin{array}{c}\hfill {\lambda }_1{B}_1(x)+{\lambda }_2{B}_2(x)+{\lambda }_3{B}_3(x)+({\lambda }_2-{\lambda }_1)B_1(x)S_{x_3}^{+}\hfill \\ \hfill +({\lambda }_3-{\lambda }_2)max\{B_2(x)S_{x_1}^{+},B_2(x)S_{x_2}^{+}\}+({\lambda }_2-{\lambda }_3)B_3(x)S_{x_4}^{+}\hfill \end{array}$

To assess over-optimism in the adaptive procedure, a separate independent data set is simulated in each scenario to evaluate the bias in the final CPE estimate; the total sample size, censoring distribution, and marker frequency remain the same as the data under which the refined classifier was generated.

Cross-validation was used to select the minimum improvement ΔCPE for a split to be admissible. The potential values of Δ evaluated in the procedure included

$$\{1.0,0.05,0.02,0.015,0.01,0.0075,0.005,0.0025,0.001\}.$$

The first value of 1.0 is included to return the original classification system. In addition to Δ, a split was required to have at least 15 patients and 5 observed failures in all considered partitions.

Table 2 summarizes the results from 1,000 simulations of the data generating process. The first row provides the results of Null Scenario 1 with a marker frequency of 15%, 30% censoring, and 300 patients. On average, the algorithm selected Δ = 0.12 and the original classifier was returned in 97% of the simulations. Among markers x₁ to x₂₀ on average less than 0.1 were selected. The estimated CPE for the original classifier, refined classifier evaluated within sample, and the refined classifier evaluated on an independent data set are 0.69, 0.69, and 0.68, respectively. Comparing across the various Null Scenario 1 simulations, the higher marker frequency resulted in the more frequent return of the original classifier. The general performance improved with the larger cohort size.

Table 2.

Simulation results evaluating reclassification with 20 new markers under Null Scenario 1, Null Scenario 2, and the Alternative Scenario. CPE Start is the concordance estimate of the existing classifier and Final is the final refined classifier unadjusted for over-optimism. CPE Independent is the final classifier applied to an independent validation data set. The results are averaged over 1,000 replications.

Sample Size	Marker Frequency	Censoring	ΔCPE	Org. Classifier Returned	Average Number Selected			CPE
					(X1, …, X20)	(X1, …, X4)	(X5, …, X20)	Start	Final	Independent
Null Scenario 1
300	0.15	0.28	0.12	0.97	<0.1			0.69	0.69	0.68
300	0.15	0.49	0.11	0.94	0.1			0.68	0.69	0.68
300	0.30	0.28	0.15	0.99	<0.1			0.69	0.69	0.69
300	0.30	0.49	0.17	0.97	<0.1			0.68	0.69	0.68
600	0.15	0.28	0.10	0.99	<0.1			0.69	0.69	0.69
600	0.15	0.49	0.11	0.95	<0.1			0.69	0.69	0.69
600	0.30	0.28	0.11	0.99	<0.1			0.69	0.69	0.69
600	0.30	0.49	0.12	0.98	<0.1			0.69	0.69	0.68
Null Scenario 2
300	0.15	0.30	0.13	0.91	0.2			0.66	0.66	0.65
300	0.15	0.52	0.12	0.85	0.2			0.66	0.66	0.66
300	0.30	0.32	0.17	0.76	0.3			0.63	0.63	0.63
300	0.30	0.54	0.17	0.68	0.5			0.63	0.64	0.63
600	0.15	0.31	0.11	0.95	0.1			0.66	0.66	0.65
600	0.15	0.52	0.12	0.86	0.2			0.66	0.66	0.66
600	0.30	0.32	0.11	0.76	0.4			0.63	0.63	0.63
600	0.30	0.54	0.13	0.66	0.6			0.63	0.64	0.63
Alternative
300	0.15	0.31	0.063	0.43		0.9	0.2	0.65	0.67	0.66
300	0.15	0.52	0.105	0.68		0.4	0.2	0.66	0.66	0.66
300	0.30	0.32	0.040	0.14		2.2	0.3	0.63	0.67	0.65
300	0.30	0.54	0.089	0.33		1.2	0.6	0.63	0.66	0.64
600	0.15	0.31	0.009	0.04		2.8	0.2	0.65	0.68	0.67
600	0.15	0.52	0.029	0.18		1.8	0.4	0.66	0.68	0.67
600	0.30	0.32	0.006	< 0.01		3.4	0.3	0.63	0.67	0.67
600	0.30	0.54	0.018	0.05		2.7	0.4	0.63	0.67	0.66

Compared with Null Scenario 1, Null Scenario 2 had more difficulty returning the original classifier. The performance was modestly better for the lower marker frequency; this may be due partly to the relatively low misclassification of the existing classifier when the mutant status of z₁, …, z₄ occurs in only 15% of the patients. Depending on the simulation, the algorithm selected on average up to 0.6 out of the 20 markers. This false marker selection in the greedy procedure resulted in an increase in estimated CPE for the within-sample final estimate in some scenarios and a corresponding drop in CPE when the modified classifier was applied to an independent data set.

In the final scenario Alternative, cross-validation selected a smaller Δ than the null scenarios, ranging from 0.006 to 0.105, correctly recognizing the signal in the data. This resulted in the original classifier returned less frequently than the two null scenarios. Across the various Alternative scenarios, the algorithm selected on average between 0.4 to 3.4 of the four markers x₁ to x₄ that improve the predictive accuracy, and between 0.2 to 0.6 of the 16 noise markers. Similar to the other scenarios, the general performance improved with lower censoring and a larger sample size. While the within sample CPE estimate was inflated over the estimate when the classifier was applied to an independent dataset, there was an improvement in accuracy over the original existing classifier in all scenarios except one where the sample size and marker frequency was low and censoring was high.

The bias adjustment technique outlined in Section 3.4 was run as a illustrative example under the Alternative Scenario for 300 and 600 patients when the marker frequency and censoring was 30%. The bias was estimated using 10 bootstrap samples of each simulated data set. The bias-adjusted CPE for 600 patients was 0.67, the same as the unadjusted value. For the smaller sample size, the adjusted CPE was 0.65, down from an unadjusted value of 0.67.

As a comparison to our method, we modified the amalgamation procedure of Ciampi et al. (1986) for the reclassification scenario. Three separate trees were grown within each of the existing risk groups using logrank splitting. The procedure requires the logrank p-value for all candidate splits to achieve a predetermined α level. To mirror the Boomerang algorithm, we additionally required at least 15 patients and 5 observed failures in each partition. After growing was complete, the amalgamation procedure was modified so leaves from the different trees could be combined. Merging was based on reiteratively combining the two leaves with the smallest logrank statistic. This process continued until the final three category classifier was reached. The results from this “Three Trees” approach for 300 and 600 patients are provided in the Web Appendix. The procedure used α=0.05 as illustrated in Ciampi et al. (1986). While able to correctly identify more of the markers x₁ to x₄ than the Boomerang algorithm under the Alternative, the method selected up to 2 to 3 noise markers under the various null scenarios. This resulted in a lower average CPE value when the refined classifier was applied to a validation data set. Due to this higher false positive selection, we did not further consider this tree-based approach.

5. Reclassification in AML

This section illustrates the proposed Boomerang algorithm using AML data outlined in Section 2. In addition to the primary cohort described above, there was an independent validation cohort that included a total of 84 patients with 13, 47, and 24 in the unfavorable, intermediate, and favorable cytogenetic groups. Approximately 30% of the patients were censored for the overall survival endpoint. The validation cohort did not include sequencing for the WT1 marker; therefore, this marker was removed from this illustrative analysis.

Similar to the previous section, a total of 15 patients and 5 deaths were required in each partition in the Forward Process. Cross-validation selected a Δ value of 0.0025. The results of the algorithm are shown in Table 3. Before reclassification, the frequencies for the unfavorable, intermediate, and favorable cytogenetic risk categories were 16%, 65%, and 19%, respectively. After reclassification, the frequencies were 29%, 34%, and 38%, respectively. The algorithm reclassified 41 patients with intermediate cytogenetic risk as part of the new unfavorable risk, and 60 as part of the new favorable risk. The favorable and unfavorable cytogenetic groups were not reclassified. The overall frequency of the selected markers in the final refined classifier were DNMT3A (23%), IDH2 (8%), FLT3 (38%), and NPM1 (31%).

Table 3.

The refined risk groups for AML patients using the Boomerang algorithm. The Forward Process partitioned the Intermediate Cytogenetic risk group into five regions based on four somatic mutations.

New Risk Classification	Cytogenetic Risk + Mutations
Favorable Risk	Favorable Cytogenetics Intermediate Cytogenetics & IDH2MT Intermediate Cytogenetics & IDH2WT & FLT3WT & NPM1MT
Intermediate Risk	Intermediate Cytogenetics & IDH2WT & FLT3WT & NPM1WT Intermediate Cytogenetics & IDH2WT & FLT3MT & DNMT3AWT
Unfavorable Risk	Intermediate Cytogenetics & IDH2WT & FLT3MT & DNMT3AMT Unfavorable Cytogenetics

MT: mutant; WT: wild-type

Kaplan-Meier survival plots are provided in Figure 1 for the revised risk classifier in both the primary and validation cohorts. Panel (A) is the existing cytogenetics classifier for the primary cohort and Panel (B) provides the seven groups from the end of the Forward Process as shown in Table 3. The refined three category system is shown in panel (C). The classifier based just on cytogenetics had a CPE estimate of 0.58, and this increased to 0.63 without adjusting for overoptimisim. The bias-adjusted CPE estimate for the revised classifier is 0.61, and the permutation-based p-value for the improvement in CPE is <0.001.

Figure 1.

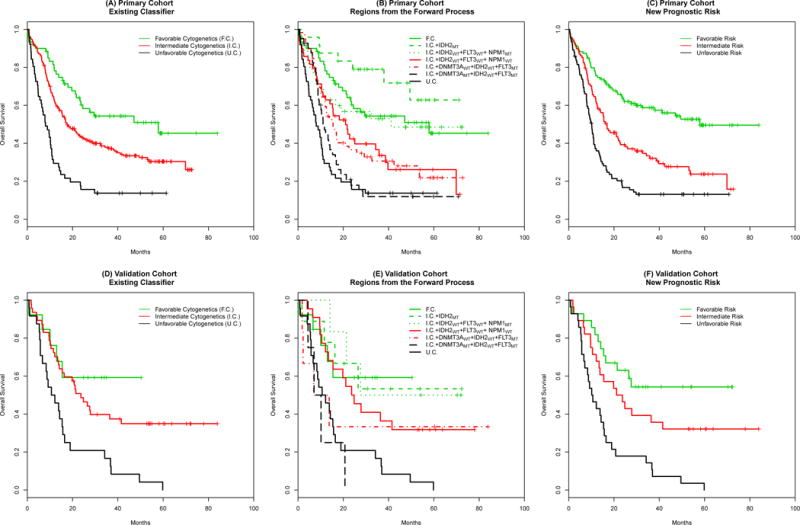
Kaplan-Meier survival curves of the revised risk classification in AML. Panels (A) and (D) show the existing classifier for the primary and the validation cohorts. Panels (B) and (E) show the seven groups identified in the Forward Process, and panels (C) and (F) show the overall survival for the final revised classifier for the two cohorts. F.C., I.C., and U.C. represent the favorable, intermediate, and unfavorable cytogenetics groups in the existing classifier. MT and WT indicate the mutant and wild-type status for the new somatic mutations.

The original cytogenetic categories for the smaller validation cohort is provided in Panel (C). Panel (D) and (E) provide survival curves for the intermediary groups and revised classifier. While Panel (D) is provided to mirror Panel (B), we note that these survival curves may be challenging to interpret with the limited sample size. The revised classifier had an increase in CPE from 0.61 to 0.64.

Both the resampling methods used in the primary cohort and the CPE estimates in the separate validation cohort provide evidence that the Boomerang algorithm resulted in an improvement in the predictive ability for AML risk classification.

6. Discussion

This paper presents a novel method for refining a prognostic classifier by incorporating new markers. The algorithm is designed for the clinical scenario where the existing categorical classifier has been well validated though heterogeneity exists in one or more risk groups. In such a case, the algorithm allows one to explore refinements in the existing classifier that improve the overall predictive accuracy. Using Boolean expression, the updated classifier is easy to interpret and implement in the clinical setting. The systematic forward and backward steps and the use of resampling techniques assess the improvement in predictive accuracy when independent data are not available.

There are key differences in the growing and merging process of the Boomerang algorithm compared to a tree-based approach with a modified amalgamation procedure. In the tree approach, a node is partitioned based on the binary split that maximizes a statistic such as the logrank test; this two-group test is evaluated locally within the covariate space defined by that node. The amalgamation procedure discussed in Ciampi et al. similarly merges leaves based on a two-group comparison of survival, and the two groups with the smallest test statistic are merged. This differs from our proposed methodology. As a classifier is further partitioned in the Boomerang algorithm, it remains focused on finding the division that maximizes the predictive accuracy of the entire classifier, instead of maximizing a two-group comparison within a single partition. Similarly, as we consider merging two regions in an expanded classifier with M regions, we are searching for the classifier with M − 1 regions that has the largest CPE estimate. Merging here is again done with respect to maximizing a statistic over the entire classifier, not minimizing a two-group statistic. Our proposed approach is more aligned with the reclassification goal and may be one of the reasons it outperforms the tree-based approach.

Our algorithm is illustrated using CPE, a model-based metric of discrimination ability that has the advantage of being independent of the censoring distribution (Gönen and Heller, 2005). Since some of the candidate risk groups evaluated by the algorithm will be small and likely contain few events, we felt it was important to have a metric that is not influenced by the amount of censoring. However, CPE has the disadvantage of assuming the data are well approximated by the proportional hazards model, an assumption that may be problematic for some data. For those who are more concerned with this, a c-index type measure may be preferable although it may come at the expense of being sensitive to higher levels of censoring. The relative strengths of various metrics for right-censored data have been previously evaluated and an informed choice can be made by studying the operating characteristics reported in the literature (Schmid and Potapov, 2012).

The simulations were designed to assess the performance of the algorithm under realistic clinical scenarios. Overall, the algorithm was able to improve the predictive accuracy over the initial classifier while selecting a small number of false positive markers. Under the null scenarios, the original classifier was frequently returned; under the alternative, CPE tended to improve appreciably when the refined classifier was applied to an independent data set. However, the simulations also illustrate the difficulty of identifying the correct markers as censoring increases and marker prevalence decreases. For example, in the alternative scenario with 300 patients and a marker prevalence of 15%, on average 15 patients will have intermediate risk and have the x₁ mutation. As 15 is the minimum partition size, only occasionally will the algorithm be able to identify this combination. Any additional combination in the intermediate risk group, such as the x₂ mutation, will be below the required partition size. However, while the minimum partition size is important, we found that the growing process in the algorithm more frequently stopped due to not satisfying the ΔCPE selected by cross-validation.

In addition, there may be clinical scenarios where the number of markers is large relative to the number of patients. Like many adaptive methods, the proposed algorithm may become increasingly unstable in higher dimensions. In such situations, an initial screening step can be implemented to identify markers with either the strongest univariate effect or strongest pairwise interaction with other markers. If resampling is used to assess the improvement of the final classifier, it is important to incorporate the marker screening process into the resampling technique.

The permutation-based resampling technique to assess the CPE improvement assumes independence between the existing classifier and the new markers. This can be modified if dependence is observed. One strategy would be to randomly generate new markers that are independent of survival but have the same frequency as the current markers and the same correlation to the existing classifier. Multiple data sets are generated and evaluated using the Boomerang algorithm to obtain the distribution of the CPE increase under the null, and the CPE improvement of the refined classifier is compared to this distribution.

In our experience, such as in the AML example, clinicians are frequently interested in reclassification within the same number of categories of the original classifier. While there is an argument to retain a parsimonious system, there may be situations where one would want to evaluate the performance of a classifier with more or fewer risk groups. The algorithm is easy to modify in the Backward Process to return a k−1 or k+ 1 system; however, additional work is required to determine how best to evaluate the marginal benefit of a refined classifier with a different number of categories.