Analysis of Translation Elongation Dynamics in the Context of an Escherichia coli Cell

Abstract

Understanding the mechanisms behind translation and its rate-limiting steps is crucial for both the development of drug targets and improvement of heterologous protein production with many biotechnological applications, such as in pharmaceutical and biofuel industries. Despite many advances in the knowledge of the ribosome structure and function, there is still much discussion around the determinants of translation elongation with experiments and computational studies pointing in different directions. Here, we use a stochastic framework to simulate the process of translation in the context of an Escherichia coli cell by gathering the available biochemical data into a ribosome kinetics description. Our results from the study of translation in E. coli at different growth rates contradict the increase of mean elongation rate with growth rate established in the literature. We show that both the level of tRNA competition and the type of cognate binding interaction contribute to the modulation of elongation rate, and that optimization of a heterologous transcript for faster elongation rate is achieved by combining the two. We derive an equation that can accurately predict codon elongation rates based on the abundances of free tRNA in the cell, and can be used to assist transcript design. Finally, we show that non-cognate tRNA-ribosome binding has an important weight in translation, and plays an active role in the modulation of mean elongation rate as shown by our amino-acid starvation/surplus studies.

Introduction

Protein synthesis plays an important role in biological systems because its products constitute most of the molecular machinery required for cell regulation, growth, and functionality. Studies involving synonymous codon substitution of rare codons have shown that these codons are associated with ribosome pausing. Their replacement by more frequent ones was observed to decrease protein specific activity (1, 2), which can be associated with protein misfolding, as different structural domains require different speeds to be formed (3). A better understanding of the determinants of translation elongation can contribute to the design of drugs to target translation deficiencies and it could improve the yield of recombinant proteins in host cells through the optimization of DNA sequences for faster translation.

Despite the advances in the knowledge of ribosome kinetics (such as the unveiling of the structure and function of several ribosomal domains with cryo-electron microscopy and x-ray crystallography (4, 5) or the development of bulk rapid-mixing kinetics and single-molecule experiments for the study of ribosome reaction kinetics and the dynamics of translation events (6, 7, 8)), the dynamics of the translation process and its rate-limiting steps are still not completely understood. The availability of cognate tRNA for a codon is generally accepted as the determinant of translation elongation rate. However, studies of computational or experimental character that attempt to identify the rate-limiting steps of translation have not been able to provide a consensus on this matter. A computational study of translation using a mechanistic model has found that the competition among cognate tRNAs and the nonspecific binding tRNAs (near-cognate (nc) and noncognate (non) tRNAs) is the rate-limiting step in translation (9). Another computational study has identified specifically the competition between cognate and near-cognate tRNAs as the determinant in translation rates (10). More recently, in a computational model that does not take competition into account, the concentration of ternary complex aa-tRNA:GTP:EF-Tu was found to limit elongation rate (11). In two recent experimental studies involving synonymous codon replacements, the key factor in translation elongation rate was attributed to the tRNA availability in somewhat different ways. Spencer et al. (12) showed that the determinant of codon translation modulation is the availability of cognate tRNA with Watson-Crick versus wobble interactions, whereas Rosenblum et al. (13) suggested that cognate tRNA abundance is the key factor.

Recent stochastic models enable the study of the translation dynamics for an organism’s representative set of mRNA sequences (14, 15), which allows for the study of more complex dynamics such as ribosome crowding effects and the dynamics of tRNA availability in a whole-cell context. This is more difficult to address with deterministic models. These stochastic models take into account the fluctuations on the availability of tRNA and ribosomal resources, but despite their complexity, they do not provide a complete kinetics for competition. Using a stochastic framework, we simulate the translation process based on the available ribosome kinetics as determined in the literature (16, 17, 18, 19), which describes fully the tRNA competition and differentiates between a cognate Watson-Crick (WC) and a cognate wobble (WB) tRNA binding interaction. We simulate the simultaneous translation of a representative pool of Escherichia coli mRNA sequences under a range of different growth rates for which the number of ribosomes and the concentrations of each tRNA species are known. We show that two distinct mechanisms modulate the speed at which each codon is translated: (1) the amount of competitor tRNA and (2) the type of cognate binding interaction (WC versus WB), which, combined, optimize elongation rate of a heterologous transcript added to the cell. Formulating the translation process deterministically by extending previous work (9), we derive an equation that estimates the codon elongation rates based on the amount of free competitor and cognate (WC, WB) tRNAs. We compare the predictions of this equation with the ones from our stochastic model, and we show its potential to assist with the design of optimized heterologous transcripts by synonymous codon substitution.

Materials and Methods

Stochastic model of E. coli translation machinery

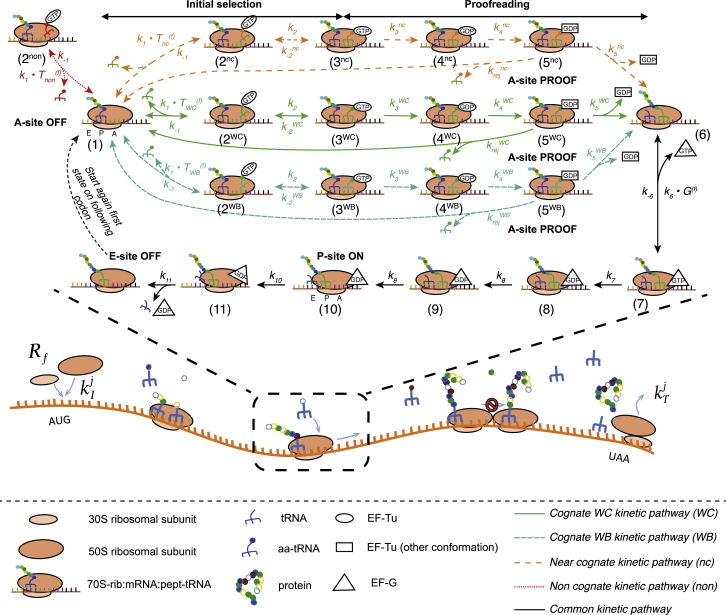
The ribosome kinetics for translation elongation cycle of each codon of an mRNA sequence was obtained from in vitro experiments detailed in Table S1 in the Supporting Material and is represented schematically in Fig. 1. The four different kinetic pathways (cognate Watson-Crick (WC), cognate wobble (WB), near-cognate (nc), and non-cognate (non)) represent the different types of tRNA binding to the mRNA-ribosome complex (see Supporting Materials and Methods S1). The ribosome kinetics for WC, nc, and non are obtained from Wohlgemuth et al. (16) at 20°C. The ribosome kinetics for WB was obtained from Kothe and Rodnina (19) at 20°C, where cells not expressing tRNA-Ala2 had their matching codon GCC decoded by the isoacceptor tRNA-Ala1B via a wobble binding interaction. Based on these biochemical assays, the translation elongation cycle is divided into two stages where the codon-anticodon match is evaluated, resulting in the possibility of rejecting the tRNA: the initial selection stage (states 1–3) and the proofreading stage (states 5–1). After the tRNA accommodation and peptide bond formation from states 5 to 6, the ribosome kinetics for the mRNA-tRNA translocation between states 6 and 11 is a combination of rate-limiting steps from Pan et al. (18) at 25°C and the remaining steps are from Peske et al. (17) at 37°C (fast rate constants that do not limit the system). During the step at which the translated codon and tRNA are shifted to the P-site (states 9–10), the next codon of the mRNA sequence is placed at the A-site for decoding and at the same time the deacylated-tRNA that was previously at the P-site is translocated to the E-site. In our model we assume that: (1) the ribosome kinetics for WB binding interaction is the same independently of the type of wobble mismatch and codon involved; and (2) the translocation kinetics is common to the WC, WB, and nc binding interactions, as the kinetic steps no longer depend on the codon-anticodon interaction. Furthermore, the kinetics of the tRNA charging with an amino acid and binding with EF-Tu, mediated by EF-Ts, is not taken into account in the model. We instead assume that the tRNA is instantaneously recharged after leaving the ribosome E-site and that the finalized ternary complex aa-tRNA:GTP:EF-Tu is readily available for binding with the ribosome, and hence not limiting translation. This assumption is consistent with the observation that 90% of EF-Tu is estimated to be present in the form of the ternary complex (20). We also note that at steady state the rates of uncharged tRNA degradation (>120 min in Mohanty et al. (21)) and aa-tRNA degradation (100–1000 h in Hentzen et al. (22)) occur on a much longer timescale than the timescale for the cycle of elongation until the tRNA is released from the E-site (see Table 1). This leads to the rate of tRNA charging being equal to the rate of tRNA release from the E-site and to the rate of aa-tRNA binding to the A-site. For simplicity, tRNA throughout the text denotes the finalized ternary complex aa-tRNA:GTP:EF-Tu ready to bind to the mRNA-ribosome complex.

Figure 1.

Schematic representation of the ribosome kinetics of the translation elongation cycle during which a polypeptide is synthesized following the decoding of its corresponding mRNA sequence. The four pathways represent the different types of codon-anticodon interaction (WC, WB, nc, and non). After the tRNA accommodation and peptide bond formation from state 5 to state 6, the subsequent kinetic pathway is assumed to be common for the different types of binding interactions, as the kinetic steps no longer depend on the codon-anticodon recognition. $T_{WC}^{\left(f\right)}$, $T_{WB}^{\left(f\right)}$, $T_{nc}^{\left(f\right)}$, and $T_{\text{non}}^{\left(f\right)}$ are the concentration of free cognate WC, cognate WB, and near-cognate and non-cognate tRNAs, respectively, for the codon being translated. A-site OFF, A-site PROOF, and E-site OFF correspond to the positions where tRNA is released from the mRNA-ribosome complex and P-site ON corresponds to the position where ribosome translocation to the next codon occurs and hence the tRNA in the A-site is placed in the P-site and the one in P-site is placed in the E-site. To see this figure in color, go online.

Table 1.

Statistics on Mean Ribosome Occupancy Time Lags and Total Number of Events per Decoding Stage and Binding Type

	WC	WB	nc	non
${\overline{\Delta t}}_{bi}^{A\mathbf{-}OFF}$[× 10−2 s]	0.36 (0.006)	0.48 (0.009)	3.9 (0.009)	1.2 (0.0008)
$N_{bi}^{A\mathbf{-}OFF}$	70,961	86,665	4,651,313	15,757,894
%a	30.92	31.8	98.9	100
${\overline{\Delta t}}_{bi}^{A\text{-}PROOF}\left[\text{s}\right]$	0.16 (0.003)	0.51 (0.01)	0.31 (0.001)	—
$N_{bi}^{A\mathbf{-}PROOF}$	790	75,871	50,877	—
%a	0.34	27.85	1.08	—
${\overline{\Delta t}}_{bi}^{P\mathbf{-}ON}\left[\text{s}\right]$	0.70 (0.01)	1.00 (0.02)	0.83 (0.002)	—
${\overline{\Delta t}}_{bi}^{E\mathbf{-}OFF}\left[\text{s}\right]$	3.09 (0.05)	3.41 (0.07)	3.29 (0.008)	—
$N_{bi}^{P\mathbf{-}ON/E\text{-}OFF}$	157,731	109,924	843	—
%a	68.74	40.35	0.02	—
$t_{\text{codon}}^{bi}\left[\text{s}/\text{aa}\right]$	1.82	1.54	0.74	0.69

Values in parentheses are standard deviations.

^aFraction of bi events (WC, WB, nc, and non) per decoding stage (A-site OFF, A-site PROOF, and P-site ON/E-site OFF).

We simulated the dynamics of translation with an exact continuous-time stochastic algorithm (23) based on previous work (24), which allows studying the dynamics of the simultaneous translation of different mRNA species assuming a fixed total amount of tRNA and ribosomal resources (tRNA^T, R^T). The algorithm accounts (1) for the need of ribosome binding space on the beginning of the decoding region for translation initiation to take place; (2) for the “traffic jam effect” due to ribosome queuing when slower codons are being translated; (3) for the fluctuations between active and free ribosomes (R^a, R^f); and (4) it was here further improved to account for fluctuations between active and free tRNA molecule abundances (tRNA^a, tRNA^f) by allowing the dynamic tracking of the position of the tRNA molecules inside the ribosome during translation. A list with the tRNA-codon binding interactions is presented in Tables S2 and S3. From the possible tRNA choices, we selected the species that will participate in the binding reaction based on a distribution that takes into account the amount of available molecules for each species at the time of the binding. Once a tRNA species is selected for binding with the mRNA-ribosome complex, its amount decreases by one unit. Rejection of the tRNA molecule during initial selection stage (states 1–3 or A-site OFF) or proofreading stage (states 5–1 or A-site PROOF), or simple deacylated-tRNA release from the ribosomal E-site (states 11–1 or E-site OFF) will result in the increase of the respective tRNA species amount by one unit.

Translational resources and mRNA cell composition

The concentrations of each tRNA species in E. coli at growth rates 0.4, 0.7, 1.07, and 1.6 h⁻¹ were obtained from the experiments reported in Dong et al. (25). We estimated the total number of tRNA molecules (tRNA^T) and ribosomes (R^T) per cell at each growth rate from the values reported in Bremer and Dennis (26). The tRNA^T was used with the total tRNA concentration ([tRNA^T]) to compute the respective cell volumes at the given growth rates. The values obtained for the cell volumes were inside the range determined for E. coli in Kubitschek and Friske (27) (see Supporting Materials and Methods S2 and Fig. S1 in the Supporting Material for further details on this estimation and Table S4 for values). Finally, the number of tRNA molecules for each of the tRNA species at each growth rate was computed from their respective concentrations and the cell volume.

We computed the average number of mRNA copies per E. coli cell at each growth rate from the mRNA synthesis rate per cell in the function of growth rate as reported in Bremer and Dennis ((26); and see Supporting Materials and Methods S3 and Fig. S2 for further details on this estimation and Table S4 for values). Because we lack data on the mRNA sequences and respective copy numbers expressed at each of the growth rates under study (for which we do have available tRNA concentration data), we constructed the mRNA pools of the cell at each condition by formulating a homogeneity criterion based on the fact that E. coli expresses mRNA in low copy number (28). This criterion assumes that the mRNA pools are qualitatively similar across the four growth rates and enforces them to approximate both the average mRNA length and the codon usage frequency (CU) of E. coli. The $C{U}_j$ is a measure of the fraction of each codon j present in the genome of an organism, and thus is a measure independent of growth rate. The validity of this assumption was shown by comparing the mRNA expression in E. coli at low (29) and high (30) growth rates (Table S5). The complete formulation of the homogeneity criterion is explained in Supporting Materials and Methods S3. Briefly, from the list of E. coli mRNA species encoding proteins only and excluding pseudogenes obtained from the E. coli K12 strain in EcoGene 3.0 (31), we selected, based on the criterion, a subset of the listed mRNA species with 52% of the sequences in this subset classified as essential genes. Although the identity of the mRNA species was preserved in the cell at the different four growth rates, the individual copy numbers were varied to match the estimated average number of mRNA sequences per cell. The E. coli K12 CU was obtained from the Genomic tRNA database (32). To differentiate between the CU based on the genome and that of the CU frequency based purely on the set of mRNA copies present in a cell, we defined the mRNA codon usage frequency (mCU) as a measure of the fraction of each codon j ($mC{U}_j$) present in the mRNA pools at each growth rate. Such values were enforced to approximate the ones of E. coli CU (see Fig. S3 for a comparison between CU and mCU at each growth rate).

The concept of interaction-based mRNA codon usage frequency ($IBmC{U}_{{\text{tRNA}}_i}$) is introduced here to quantify the frequency of codons in the system that interact with tRNA species i and are classified under a certain basepair binding interaction. The $IBmC{U}_{{\text{tRNA}}_i}^{bi}$ is computed with the following expression:

$$IBmC{U}_{{\text{tRNA}}_i}^{bi}=\sum _{{\text{codon}}_j\text{with}\text{bi}\text{for}{\text{tRNA}}_i}mC{U}_j,$$ (1)

where $mC{U}_j$ is summed over all codon species j that bind to the tRNA species i with the binding interaction bi. As mentioned above, there are four possible binding interactions (WC, WB, nc, and non) and we further defined a fifth one to account for all cognate binding interactions: $IBmC{U}_{{\text{tRNA}}_i}^{\text{cogn}}=IBmC{U}_{{\text{tRNA}}_i}^{\text{WC}}+IBmC{U}_{{\text{tRNA}}_i}^{\text{WB}}$.

Codon elongation rate

We derived an expression for the codon elongation rate ($k_{\text{eff}}$) in function of the free cognate (WC and WB), near-cognate (nc), and non-cognate (non) tRNA concentrations and the ribosome kinetic parameters. This derivation was based on a deterministic model of translation (9), which was extended to account for the differentiation between two types of cognate binding interactions, for the possibility of nc misincorporation and for tRNA rejection at the proofreading stage (see Supporting Materials and Methods S4). Inserting the values of the kinetic rate constants from Table S1 we obtained an expression to compute $k_{\text{eff}}^j$ for each codon j

$$k_{\text{eff}}^j=\frac{T_{WC,j}^f+0.5884\times T_{WB,j}^f+2.6233\times {10}^{-4}\times T_{nc,j}^f}{0.0104+0.4556\times T_{WC,j}^f+0.6864\times T_{WB,j}^f+0.0613\times T_{nc,j}^f+0.0171\times T_{\text{non},j}^f},$$ (2)

where the variables are the free WC, WB, near-cognate, and non-cognate tRNA concentrations to codon j.

Simulation of translation in E. coli cell

The cell composition at 37°C and ribosome kinetics described above was used to simulate the translation dynamics for an E. coli cell. The translation initiation rate constants (k_I) for each mRNA species were calibrated such that the system reached a 80% ribosome activity in each simulated pool as estimated in Bremer and Dennis (26) (see Supporting Materials and Methods S5). The termination rate constants (k_T) values were kept high so that it was not a rate-limiting step in translation, as had been observed in Racle et al. (33) and Arava et al. (34). Simulations were performed for E. coli at growth rates 0.4, 0.7, 1.07, and 1.6 h⁻¹ and for the translation of seven synonymous Firefly Luciferase transcripts in an E. coli cell growing at 1.07 h⁻¹. Simulations were performed individually for each transcript and only one copy of the transcript was added to the pool of mRNA copies in a cell at 1.07 h⁻¹. The design of the transcripts was based on synonymous codon substitution that yields the same Luciferase amino-acid sequence (see Supporting Materials and Methods S6 and Table S6 for mRNA sequences). The data was extracted from the simulations during a time interval for which the system was at steady state (see example for 1.07 h⁻¹ in Figs. S4 and S5). All simulation results were averaged over a large number of repetitions of the same simulation.

Results and Discussion

General translation properties of the cell in function of growth rate

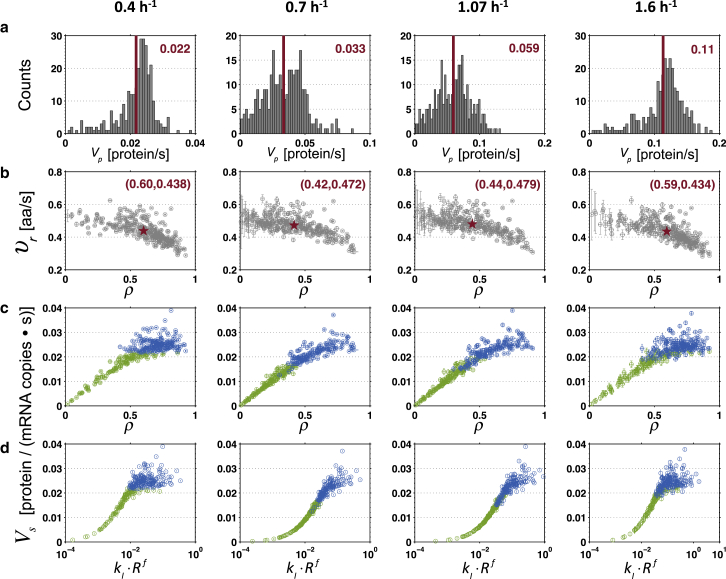
We studied the distribution of the protein synthesis rate (V_p) for each growth rate (Fig. 2 a). The mean V_p among the mRNA species is observed to increase with the growth rate, along with the increase in translation resources (see Table S2). Interestingly, the mean elongation rate (υ_r) (Eq. S6 and Supporting Materials and Methods S7) is observed first to increase and then decrease with growth rate, which is accompanied by a respective decrease and increase in the mean ribosomal density (ρ) (Eq. S7 and Supporting Materials and Methods S7), contrary to the estimations in Bremer and Dennis (26) where it increases with growth rate (Fig. 2 b). Despite this difference, we found good agreement with the mean distance between ribosomes estimated in Bremer and Dennis (26) and our computed values (Eq. S8 and Supporting Materials and Methods S7) for each growth rate using the ρ-values of each mRNA species from our simulations and assuming the ribosome has the size of one nucleotide L_R = 0 (Fig. S6 a). However, the real length of the ribosome covers ∼12 codons, which is accounted for in our simulations, and performing the computation with the correct ribosome length shows that the values from the literature overestimate the true mean distance between ribosomes. The effect observed above results directly from the inverse changes in mean ρ, given that the mean tRNA activity (i.e., the fraction of tRNA species bound to ribosomes (see Eq. S9 and Supporting Materials and Methods S7)) of all tRNA species is similar for the different growth rates (Fig. S6 c), and that the average of the fold changes in abundance from all tRNA species at each growth rate relative to 0.4 h⁻¹ is fairly constant (Fig. S6 d). This suggests no major changes in the ratio between cognate and competitor tRNA concentrations that could affect υ_r.

Figure 2.

(a) Distribution of protein synthesis rate (V_p) for the different growth rates. The red bar and number represent the mean V_p among all mRNA species. (b) Elongation rate (υ_r) for each mRNA species in function of the ribosomal density (ρ) for the different growth rates. The red star and text represent the mean (ρ, υ_r) from all the mRNA species in the cell. Vertical and horizontal error bars represent standard deviation from 100 repeated simulations. (c and d) Specific protein synthesis rate (V_s) for each mRNA species in function of the ribosomal density (ρ) (c) and in function of the initiation rate (k_I × R^f) (d) for the different growth rates. Green and blue color-code separates the data points that have a V_p below or above the mean V_p among all mRNA species, respectively. Vertical and horizontal error bars represent standard deviation from 100 repeated simulations. To see this figure in color, go online.

Interestingly, with the increase in growth rate, the V_p distribution shifts from having one peak to a bimodal distribution and back again to having just one peak, suggesting a systemic change in the control of the synthesis rate. Previous computational and experimental studies have shown for different organisms that translation of most mRNA species is initiation- or elongation-limited (33, 34). In particular, computational studies have shown that the specific protein synthesis rate (V_s), i.e., the rate of proteins produced per number of copies of an mRNA species (see Supporting Materials and Methods S7), is limited by translation initiation for low values of ρ; by translation termination for high values of ρ; and reaches a maximum for moderate values of ρ for which translation elongation becomes limiting (9, 35, 36). We observe that the cells simulated at growth rates 0.4 and 1.6 h⁻¹ have a higher number of mRNA species that cluster in a more stable region of the V_s curve with higher ρ and higher initiation rate (k_I × R^f), indicating that these are mostly elongation-limited, whereas the cells at growth rates 0.7 and 1.07 h⁻¹ have their mRNA species clustered into two groups that correlate with the V_p bimodal distributions: one group with lower ρ for which translation is mostly initiation-limited and a second group with higher ρ-values for which translation is mostly elongation-limited (Fig. 2, c and d). A decrease bigger than 20% in the ratio between R^f and the total number of mRNA copies at 0.7 and 1.07 h⁻¹ with respect to the one at 0.4 h⁻¹ suggests a limitation in free ribosome resources (Fig. S6 b). Thus, it appears that under low and high growth rates that the system optimizes protein translation with higher V_s for the mRNA species, whereas for intermediate growth rates, translation initiation regulates protein synthesis. Consequently, at growth rates 0.4 and 1.6 h⁻¹, there is a higher proportion of mRNA species limited by translation elongation—a limitation that corresponds to more ribosome blocking (higher ρ) due to queuing of ribosomes downstream of the sequences and lower υ_r, so that the overall mean υ_r of the entire mRNA pool decreases (Fig. 2 b).

Although these results were obtained from simulations considering a homogeneous mRNA pool across mRNA conditions (see Supporting Materials and Methods S3), they are valid for any choice on pool composition as long as the total number of ribosomes and mRNAs in the system remains as parameterized here. This is consequence of the calibration performed on the initiation rates to force the cell at each growth rate to have 80% of its ribosomes active in translation. This leads to a steady state where, for each growth condition, the level of free ribosomes will always consist of the remaining 20%, which is independent of the individual ribosome profiles of each sequence. If the ratio between free ribosomes and total amount of mRNAs is maintained independently of the mRNA pools used, the shifts on average ribosomal densities will be observed because they constitute a direct effect of the competition among translating mRNAs for free ribosomes, which in turn, directly influence the level of ribosome crowding along the mRNA sequences.

Determinants of elongation rate

We investigate further the determinants of translation elongation rate by focusing on the analysis of the cell at growth rate 1.07 h⁻¹ (highest mean υ_r and moderate mean ρ) and the production of a heterologous protein. The results discussed below are similar for the four growth rates, and thus are independent of the changes in ρ, unless otherwise stated.

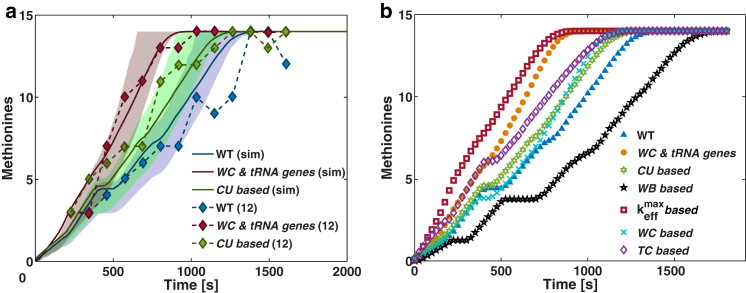
To qualitatively validate the model and its parameters, we separately simulate the translation of four Luciferase transcripts in an E. coli cell growing at 1.07 h⁻¹, we postprocess the translation time profiles of the transcripts (see Supporting Materials and Methods S7 and S8) and we compare our results with the ones from pulse-chase experiments performed by Spencer et al. (12). For the simulations, we use the same Luciferase transcripts as in Spencer et al. (12), which consist of a wild-type (WT) Luciferase transcript and three other sequences whose designs follow different criteria based on synonymous codon substitution: codons with existing WC decoding tRNA isoacceptors combined with high tRNA gene copy number (WC and tRNA genes), codons with the highest genome codon usage frequency (CU-based), and codons without WC decoding tRNA isoacceptors (WB-based; see criteria detail in Supporting Materials and Methods S6 and mRNA sequences in Table S6). The mean time-evolution curves of methionine level from our in silico pulse-chase performed on the WT, WC, and tRNA genes and CU-based transcripts (no experimental curve available for WB-based) show good agreement with the experimental curves from Spencer et al. (12) (Fig. 3 a). The experimental curves obtained at 37°C, and hence with faster elongation rate, were calibrated for comparison with our system at 20–25°C by multiplying the time axis by a factor of 23 s (Supporting Materials and Methods S8). The deviations between the simulated and experimental curves are accounted for by the distribution of the simulated curves that generated our mean time-evolution curves of methionine level.

Figure 3.

(a) Comparison between simulated (sim) and experimental time-evolution curves of methionine level obtained from experiments in Spencer et al. (12) for WT Luciferase and for two of its synonymous transcripts (WC and tRNA genes and CU-based). Bounds represent the 25th and 75th quartile of the distribution from the in silico pulse-chase curves. Time axis from the experimental data points was adjusted with the same calibration factor used for the methionine labeling time (see Supporting Materials and Methods S8). (b) In silico pulse-chase performed during the translation of seven heterologous transcripts yielding the same amino-acid sequence based on different synonymous codon substitution criteria in E. coli cells at 1.07 h⁻¹. The time-evolution curves of methionine level result from the average of 4000 repeated simulations. The curves are plotted with the bounds representing the 25th and 75th quartile of their sample distribution in Fig. S7. To see this figure in color, go online.

Three other Luciferase transcripts were designed where codons were replaced by their synonyms based on existing WC decoding tRNA isoacceptors (WC-based), based on the highest cognate tRNA concentration (TC-based), and based on the highest codon elongation rate ($k_{\text{eff}}^{\max }$-based) (more detail about criteria can be found in the Supporting Materials and Methods). For the design of the $k_{\text{eff}}^{\max }$-based transcript we computed the codon elongation rate ($k_{\text{eff}}^j$) of each codon species j with Eq. 2, using the steady-state tRNA concentrations obtained after simulating an E. coli cell at 1.07 h⁻¹. The WC and tRNA genes and $k_{\text{eff}}^{\max }$-based transcripts present the fastest elongation rates ((Fig. 3 b); for translation time profiles, see Fig. S8) and highest protein synthesis rates when compared to the WT transcript (28 and 28.6%, respectively; see Fig. S9 a), with $k_{\text{eff}}^{\max }$-based being more optimal. These two transcripts differ only in the use of two codon species (one encoding for glutamine and the other for serine) that, combined, appear in 43 positions along the 585-codon sequence. The similarity between these two transcripts is explained by the previously observed correlation between tRNA abundance and its gene copy number (25, 37, 38), and the fact that k_eff of a codon is maximized by high concentration of cognate WC tRNA and low competition. Only the WB-based transcript leads to a decrease in protein synthesis (∼20% less translated protein; see Fig. S9 a) relative to the WT transcript. We tested a transcript where the 20 first codons were not changed and confirmed that the different pulse-chase curves between WT and $k_{\text{eff}}^{\max }$-based are a result of changes in elongation rate rather than initiation (Fig. S9 b). Nevertheless, we note here that even though a transcript is optimized for elongation by synonymous codon substitution with the purpose of increasing protein production levels, the translation initiation rate, which is dictated by the beginning of the transcript’s sequence and the steady-state R^f of the host cell, has a major impact on the gain in protein production with respect to the WT in its rate-limiting regime (as seen above with the specific protein synthesis rate (V_s), and is further discussed in Fig. S9, b–d).

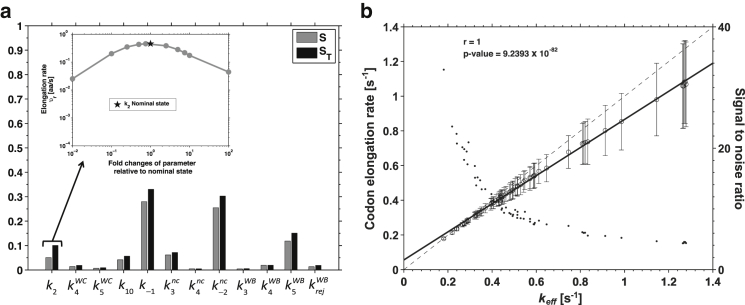
These findings are supported by sensitivity analysis of the ribosome kinetic parameters with respect to υ_r. After performing an initial screening on the 25 kinetic rate constants to identify the insignificant ones (Fig. S10), we use a Monte Carlo-based numerical procedure for variance-based global sensitivity analysis (39). We then determine the ribosome kinetic rate constants that most influence the value of υ_r observed for an mRNA transcript (Fig. 4 a; results are valid for any mRNA species, as the ribosomal kinetic pathway is the same for all codons). The analysis shows no dominant rate constants (all sensitivity indices < 0.4), but their order of influence, as ranked by their main effects ($S_{k_i}$), indicates that $k_{-1}$, $k_{-2}^{nc}$, and $k_5^{WB}$ are the most influential rate constants, which indicates that there are two decoding stages of the ribosome that determine υ_r: (1) rejection of competitor tRNA ($k_{-1}$ and $k_{-2}^{nc}$) during initial selection, and (2) accommodation of cognate WB tRNAs ($k_5^{WB}$). Interestingly, although the influence of $k_2$ on υ_r is mostly due to interaction effects ($S_{T_{k_i}}$), we observe that the nominal value (obtained from experiments) of $k_2$ seems to be optimized to yield the highest υ_r (inset in Fig. 4 a). Analysis of the system for the parameters at 37°C and for the in vivo parameters deduced from in vitro ones (40) showed a redistribution of the rate-limiting steps (Fig. S11, a and b), where cognate binding interaction ($k_5^{WB}$) becomes more important than the overall tRNA competition ($k_{-1}$ and $k_{-2}^{nc}$). This finding supports the discussions on tRNA competition as observed at in vitro conditions presenting an inhibitory effect on translation elongation that would decrease translation efficiency if maintained at in vivo conditions (40, 41). The fact that the ratio between each ribosome kinetic rate constant at 37°C and then at 20°C is approximately the same (except for the initial tRNA binding rate constant and at least until the tRNA accommodation for which we have values to compare) would explain why our results at 20–25°C match so well the experiments performed at 37°C (12). We note here that when we combine the ribosome kinetics at 20–25°C with the parameters of the system at 37°C (such as total number of ribosomes, total number of tRNAs, and total number of mRNAs), we also perform a scaling of the initiation rate to bring the translation process to the conditions at 37°C by enforcing 80% ribosomes to be active in translation. If in this system the ribosome kinetics were to be replaced by a faster kinetics, such as the one at 37°C, the resulting effect would be a faster elongation rate due to the ribosomes’ faster movement along the sequence and a faster update of the number of free ribosomes. This is so because elongation rate at 37°C is expected to increase, and such increase would happen uniformly for all sequences as the ribosome kinetics is assumed equal for all codons. However, if the system was to be submitted to the same scaling condition that, on initiation, enforces an 80% ribosome activity, the steady state reached for this system would be the same as the one obtained with a ribosome kinetics at 20°C.

Figure 4.

(a) Main and total effect ($S_{k_i},S_{T_{K_i}}$) on the value of υ_r due to a change in rate constant k_i. (Inset) Changes in υ_r in function of the changes on $k_2$ for a range of two orders of magnitude below and above its nominal value (star). (b) Codon elongation rate obtained from stochastic simulations ($k_{\text{stoch}}$) versus the codon elongation rate constant ($k_{\text{eff}}$; open circles). Each data point corresponds to one of the 61 codons taking part in the translation elongation. Linear regression line is represented by a continuous line. The Pearson correlation coefficient (r) and p-value are indicated. The dashed line is the one-to-one function for comparison. The signal/noise from $k_{\text{stoch}}$ corresponding to each codon is represented by the dots and remains higher than 1 for all codons, starting to stabilize for the codons with higher elongation rates. To see this figure in color, go online.

These results support the optimality of $k_{\text{eff}}^{\max }$-based transcript design as less competition and higher rate of accommodation for cognate WB improves $k_{\text{eff}}$ values. Furthermore, the high correlation (Fig. 4 b) between the codon elongation rates obtained from our stochastic simulations (k_stoch; see translation time profiles in Supporting Materials and Methods S7) and k_eff for each codon (Fig. 4 b) indicates that k_eff is a high accuracy predictor of codon elongation rate of slow codons (i.e., codons limiting translation). Stochastic queuing effects that are dependent on the mRNA sequence downstream introduce variability on the measured k_stoch for fast codons and bias the codon elongation rate toward values that are lower than the ones expected in a theoretical system without ribosome-queuing interference.

Key factors on tRNA activity

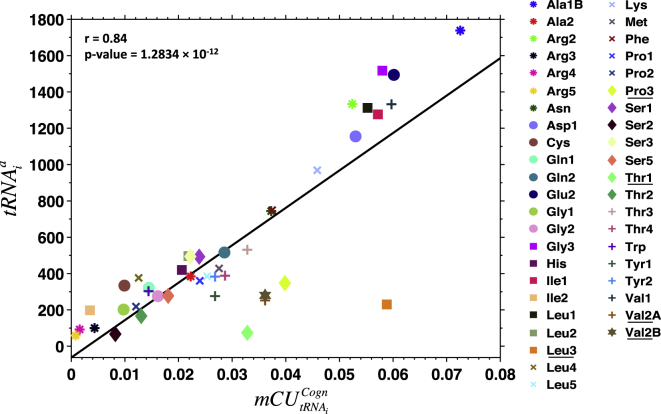
The amount of tRNA available for translation used to estimate k_eff dictates both the cognate and competitor tRNA concentrations for each codon, and directly depends on the amount of tRNA that is active in translation, i.e., occupying the ribosomes. We estimate the mean ribosome occupancy time lag (${\overline{\Delta t}}_{bi}^{ds}$) and the total number of events ($N_{bi}^{ds}$) per decoding stage (ds) and binding interaction (bi) using Eq. S10 for the WT Luciferase transcript in an E. coli cell growing at 1.07 h⁻¹. The decoding stages are A-site OFF, A-site PROOF, P-site ON, and E-site OFF (see Fig. 1 and Supporting Materials and Methods S9), and the possible binding interactions are WC, WB, nc, and non. The statistics obtained here are valid for any mRNA sequence and growth rate. Higher ribosomal densities increase both ${\overline{\Delta t}}_{bi}^{\text{P}\text{-}\text{ON}}$ and ${\overline{\Delta t}}_{bi}^{\text{E}\text{-}\text{OFF}}$ because of slower translocation of the ribosome, but the proportions between the events remain the same (results not shown). Note that ${\overline{\Delta t}}_{bi}^{ds}$ values result directly from the intrinsic ribosome kinetics and, as such, they are very similar for all the different tRNA-codon interactions, except for P-site ON and E-site OFF decoding stages. Here, the ribosome translocation time depends on the ribosome queuing downstream of the mRNA sequence (Fig. S12), whereas the number of events depends on the codon species and the free tRNA abundances (Fig. S13). Most of the tRNAs involved in cognate binding interactions (68.74 and 40.35% for WC and WB, respectively) are accepted for peptidyl bond formation and occupy the ribosome until its release at the E-site after a long ${\overline{\Delta t}}_{WC}^{\text{E}\text{-}\text{OFF}}$ or ${\overline{\Delta t}}_{WB}^{\text{E}\text{-}\text{OFF}}$ has occurred (Table 1). Thus, tRNA species with higher cognate-based mRNA codon usage frequency ($IBmC{U}_{{\text{tRNA}}_i}^{\text{cogn}}$) (see Eq. 1) also have higher frequency of events that result in E-site release, and subsequently are active in translation in higher amounts as shown by the correlation found in Fig. 5. However, there is a difference of ∼28% between WB and WC binding interactions that will not reach decoding stage E-site OFF and will instead end up with the tRNA being rejected at proofreading stage (A-site PROOF), which is a much faster event than for E-site OFF. Deviation from the regression line corresponds to cases for which the proportion of $IBmC{U}_{{\text{tRNA}}_i}^{WC}$ is very low, and $IBmC{U}_{{\text{tRNA}}_i}^{WB}$ is not high enough to compensate for the number tRNA molecules that could be active if there was high $IBmC{U}_{{\text{tRNA}}_i}^{WC}$ instead of $IBmC{U}_{{\text{tRNA}}_i}^{WB}$. Such are the cases of the outliers Leu3, Pro3, Val2A, and Val2B in Fig. 5 (see proportion of $IBmC{U}_{{\text{tRNA}}_i}^{WC}$ and in Fig. S14). Thr1 deviates from the regression line because it is the species with the lowest concentration in the cell and with an abundant isoacceptor (Thr3) (Fig. S15). Therefore, the probability of Thr1 to bind with the ribosome is reduced and hence its activity is not representative of the $IBmC{U}_{\text{Thr}1}^{\text{cogn}}$. Because a small number of near-cognate binding interactions can reach A-site PROOF and E-site OFF decoding stages (1.08 and 0.02%, respectively), $IBmC{U}_{{\text{tRNA}}_i}^{nc}$ can be high enough such that the number of A-site PROOF or E-site OFF events can compensate for a low $IBmC{U}_{{\text{tRNA}}_i}^{\text{cogn}}$ or a high proportion of $IBmC{U}_{{\text{tRNA}}_i}^{WB}$ with respect to $IBmC{U}_{{\text{tRNA}}_i}^{WC}$, and hence contribute to a higher tRNA activity (which is the case of Val1 in Fig. S15).

Figure 5.

Number of tRNA molecules of species i active in translation ($tRN{A}_i^a$) in function of its respective cognate interaction-based mRNA codon usage frequency ($IBmC{U}_{{\text{tRNA}}_i}^{\text{cogn}}$). The Pearson correlation coefficients (r) and the p-values are indicated. Correlation outliers are underlined in the legend. To see this figure in color, go online.

From $N_{bi}^{ds}$ presented in Table 1 we compute a total of 2.4% of cognate binding events among all possible binding events, and only 1.3% of these 2.4% resulted in a complete codon translation (reaching P-site ON, thus leaving the A-site free for the binding of a new tRNA). The larger bulk of translation binding events consists of interactions with competitor tRNAs (97.6%), which support tRNA competition as a determinant of elongation rate. We compute the average time of codon translation per incorporated amino acid and per binding interaction ($t_{\text{codon}}^{\text{bi}}$) using Eq. S11. The fact that $t_{\text{codon}}^{\text{non}}$ is of the same order of magnitude as $t_{\text{codon}}^{\text{nc}}$ (Table 1) implies that non-cognate binding interactions cannot be dismissed on the basis of these being fast events, contrary to the assumption made by Fluitt et al. (10). This assumption is used in recent translation modeling attempts (14, 15) where these interactions are ignored based on being fast and all competition in the system is resumed to near-cognate binding interactions. In fact, although the total time spent per non-cognate binding interaction is small (${\overline{\Delta t}}_{\text{non}}^{\text{A}\text{-}\text{OFF}}\approx 1.2\times {10}^{-2}\text{s}$), one needs to take into account that these binding events have a very high frequency of occurrence. If we compute the ratio between the total time spent per near-cognate interaction and non-cognate interaction $\left(\left({\overline{\Delta t}}_{nc}^{\text{A}\text{-}\text{OFF}}\times N_{nc}^{\text{A}\text{-}\text{OFF}}+{\overline{\Delta t}}_{nc}^{\text{A}\text{-}\text{PROOF}}\times N_{nc}^{\text{A}\text{-}\text{PROOF}}+{\overline{\Delta t}}_{nc}^{\text{E}\text{-}\text{OFF}}\times N_{nc}^{\text{E}\text{-}\text{OFF}}\right)/\left({\overline{\Delta t}}_{\text{non}}^{\text{A}\text{-}\text{OFF}}\times N_{\text{non}}^{\text{A}\text{-}\text{OFF}}\right)\right)$, we observed that this value is very close to 1, implying that non-cognate events are as important as near-cognate ones. Nevertheless, despite the high number of near-cognate binding events, we estimate that near-cognate misincorporation occurs only once for each 318-cognate WC- and WB-complete codon translations, resulting in an error frequency of ∼3 × 10⁻³, which is in the range of the E. coli in vivo measurements (42, 43, 44, 45, 46, 47). These results underline the significance of competition in the dynamics of translation elongation; they remain valid for in vivo conditions (Fig. S11 c) despite the observed decrease of the effect of tRNA competition in translation and subsequent decrease in error frequency of a factor of 3.

Global effects of amino-acid starvation and surplus in the cell

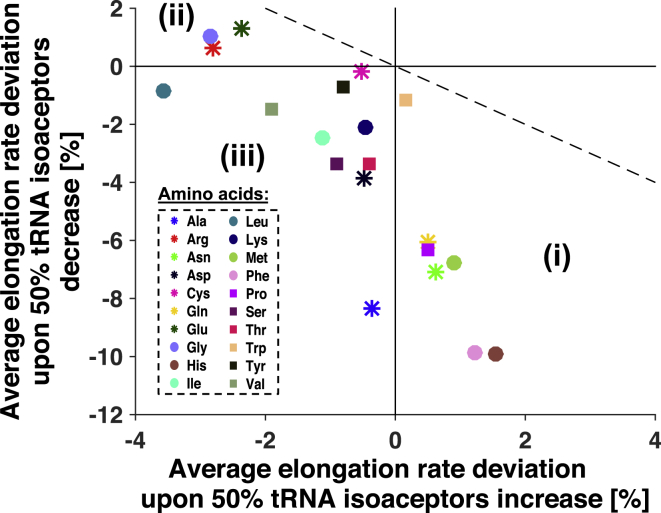
Given the role that tRNA availability plays in elongation rate, an interesting question is how the surplus or starvation of certain amino acids will globally affect elongation rate in the cell. To answer this question, we simulate 20 times the cell at growth rate 1.07 h⁻¹, and in each simulation we increase or decrease the concentration of each tRNA isoacceptors for the same amino acid by 50% of their literature values at the given growth rate. Analysis of the relative deviation of the average elongation rate from all mRNA species with respect to the standard case at 1.07 h⁻¹ shows three regimes according to the effect of the increase/decrease of the amino-acid concentrations on the average elongation rate in the cell (Fig. 6). Similar results were obtained when the concentrations where changed by 20 and 50% for each tRNA species separately (Fig. S16), and analysis of these results revealed the mechanisms behind the observed effects (details in Fig. S17). The amino acids Phe, His, Met, Asn, Pro, and Gln in regime i generally limit translation in the cell under starvation conditions and improve elongation rates under surplus. These amino acids have isoacceptor tRNAs that are among the ones whose cognate (specially WB type) codons have very slow codon elongation rates, and present a low ratio between codon elongation rate and cognate codon mCU on the mRNA sequences in the cell (Figs. S18 and S19). On the other hand, the amino acids Gly, Glu, and Arg in regime ii generally limit translation in the cell under surplus by increasing the competition on their near- and non-cognate codons, and generally improve translation under starvation conditions due to diminished competition pressure. These amino acids have tRNA isoacceptors that are among the species in the cell that are present in highest abundances (Fig. S15) and, as a consequence, their cognate codons have the highest codon elongation rates (Fig. S19). In the case of Leu, the negative effect on elongation rate due to the surplus of its tRNA isoacceptor Leu1 prevails; however, the combined effect from all its isoacceptors under starvation is characteristic of regime iii. The amino acids in regime iii are the ones that have an effect similar to ii, but to a smaller extent under surplus due to the increase in competition resulting from their combined isoacceptor high abundances or high $IBmC{U}_{{\text{tRNA}}_i}^{nc}+IBmC{U}_{{\text{tRNA}}_i}^{non}$. However, under starvation, their cognate codon elongation rates are negatively affected by the high $IBmC{U}_{\text{tRNA}}^{\text{cogn}}$ demanding free tRNA.

Figure 6.

Relative deviation of the average elongation rate from all mRNA species in the cell, upon combined 50% decrease of the abundance of all tRNA isoacceptors. This is per amino-acid type in function of the relative deviation of the average elongation rate from all mRNA species in the cell upon one-at-a-time 50% increase of the abundance of the same tRNA isoacceptors per amino-acid group. One-to-one line (dashed) plotted for comparison. To see this figure in color, go online.

Overall, starvation of a tRNA or an amino acid has a more pronounced effect on the cell’s translation behavior because it acts upon the rate-limiting codons. Nevertheless, the global effects of competition on translation elongation due to transient changes in nutrient supply introduce into the cell another level of regulation of the patterns of protein synthesis as a response to stress. Our stochastic framework has the potential to study the surplus/starvation effect of changes in the amount of tRNA competition on the elongation of the different mRNA species in detail, which is not the case in the most recent stochastic approach for modeling translation (15) where the effect of diminished competition pressure for the amino acids Gly, Glu, and Arg has not been observed, concluding instead that all types of amino-acid starvation only lead to a decrease of the mean elongation rate in the cell.

Conclusions

In this work we used a stochastic framework to model the translation process based on the available ribosome kinetics that describes tRNA competition while discriminating between cognate Watson-Crick and wobble interactions, and we simulated the simultaneous translation of a representative pool of E. coli mRNA sequences under a range of different growth rates (0.4, 0.7, 1.07, and 1.6 h⁻¹) with parameters obtained from the literature. The variation of the mean elongation rate from all mRNA species observed with the change in cell growth rate resulted from a systems response to an alteration of the ratio between free ribosomal resources and the number of mRNA copies that required those resources. Control of translation is observed to shift between initiation and elongation, which is characterized by a change in the ribosomal densities, and thus fine-tunes the protein synthesis of the mRNA species in the cell. We do not observe an increase in the mean elongation rate with growth rate as estimated in Bremer and Dennis (26), from where the data was collected. The way mean elongation rate is usually estimated (26, 48) takes only into account the protein synthesis and the number of free ribosomes, which both increase with growth rate (not necessarily in a proportional way), and not the changes that can occur in ribosomal density and that affect elongation rate. Our results are consistent with what is expected from a system where the codon elongation rate is determined by the ribosome kinetics and the free tRNA concentrations, and where the elongation rate is determined by the combined effect of the multiple codon elongation rates and the ribosomal density along a sequence (which is also influenced by the initiation rate). For a system where tRNA competition effects are not observed to change radically with growth rate and the mRNA pool is qualitatively constant (such as here, despite the change in tRNA levels), the mRNA species being translated will present a maximum elongation rate under initiation-limiting conditions and a lower elongation rate under elongation-limiting conditions (if the ribosomal density is such that high ribosome queuing interaction negatively impacts elongation). These results suggest that the actual mean elongation rate is thus no longer well represented by just the amount of protein synthesis in the system, as for some mRNA species the highest protein synthesis is achieved by crowding the sequence with ribosomes, which may result in lower elongation rate. This implies that the actual elongation rate of some mRNA species may remain constant under different growth rates, whereas for others it may decrease as a result of the level of ribosome crowding. This is consistent with the observation of an approximately constant elongation rate for lacZ for increasing growth rates (49).

Our sensitivity analysis results showed that the level of tRNA competition and the type of cognate binding interaction (WC versus WB) determines elongation rate, as shown by sensitivity analysis. The design of heterologous transcripts based on optimizing the sequence with synonymous codons that minimize tRNA competition and maximize the WC binding interactions with their cognate tRNAs was shown to lead to higher protein production. However, there is a tradeoff between protein production level and elongation rate due to ribosome crowding effects. We proposed an equation to assist the design of optimized mRNA sequences that compute the codon elongation rate (k_eff) of a codon given that the amount of free tRNA species in the host organism is known. Nevertheless, because this equation will only help to design a sequence with codons that have high codon elongation rates, final protein specific activity will need to be tested, as it has been demonstrated that cotranslational folding of proteins during the translation of slow codons is essential for correctly creating specific domains determining the protein activity (1, 2, 3).

The analysis of our system showed that non-cognate binding interactions do, in fact, contribute to the competition level as much as the near-cognate ones do—contrary to the assumption made by Fluitt et al. (10) that these can be ignored based on their fast interactions, thus assuming that all competition in the system is resumed by near-cognate binding interactions. Furthermore, the existing stochastic models (14, 15) of translation use the latter results to estimate a factor for the tRNA competition, which is fixed per codon and is integrated in the codon elongation. This competition factor is estimated using the total amount for each tRNA species in the cell instead of the free transient tRNA amount that can be obtained at each step of the simulation, and as a consequence the effect of competition from changes in tRNA availability is no longer representative of the actual state of the cell. Because we accounted for these, we observed in our surplus/starvation studies the effect of changes in the amount of tRNA competition on the elongation of the different mRNA species. Similar studies performed in Shah et al. (15) failed to observe this effect, concluding that all types of amino-acid starvation only lead to a decrease of the mean elongation rate in the cell.

Furthermore, the results presented here, which were obtained from a ribosome kinetics at 20–25°C, were validated for higher temperature of 37°C. This is more consistent with in vivo conditions, and for the deduced in vivo kinetic rates obtained in Rudorf et al. (40). Analysis of the system for the parameters at 37°C and for the in vivo parameters deduced from in vitro ones (40) were found to support a translation model for which tRNA competition, although still an important factor, has a lower impact in translation elongation rate then the type of cognate decoding (40, 41).

In conclusion, our stochastic framework has proven to be effective in the analysis of a complex system such as translation. Literature describing the parameters for translation resources and specifically the ribosome kinetics is widely available for E. coli. The use of parameters and data pertaining to a specific organism establishes the framework for the study and modeling of systems with an amount of components corresponding to the size of a biologically meaningful translation system—one that does not need to rely on the use of simplified parameter regimes. Furthermore, because the ribosome decoding center has been shown to be highly conserved among species during evolution (50) and similarities have been reported in the function of the different elongation factors in both bacteria and eukaryotes (51), the results observed in this work remain therefore valid for other organisms. This framework is a valuable tool for the systematic study of translation. Adding information on ribosome or polysome profiling experiments, as well as mRNA sequencing data for the specific conditions under study when available, can be valuable to the systems-level analysis of translation in the cell. This framework could thus be used for future work focused on: (1) exploring particular patterns of translation in certain mRNA sequences that could then be clustered by functionality and by codon frequency, (2) studying the impact of changing the sequence of certain endogenous genes on the translation of the other mRNA sequences in the cell, and (3) studying the impact of expressing heterologous genes on the translation of other mRNA sequences.

Author Contributions

J.P.V., J.R., and V.H. formulated the model; J.P.V. and J.R. wrote the software code; and J.P.V., J.R., and V.H. analyzed the results and wrote the article.

Editor: Richard Bertram.

Supporting Citations

References (52, 53, 54, 55, 56, 57, 58, 59) appear in the Supporting Material.