Abstract
Polymerization of sickle hemoglobin (HbS) is the primary pathogenic event of sickle cell disease. For insight into the nature of the HbS polymer fiber formation, we develop a particle model—resembling a coarse-grained molecular model—constructed to match the intermolecular contacts between HbS molecules. We demonstrate that the particle model predicts the formation of HbS polymer fibers by attachment of monomers to rough fiber ends and the growth rate increases linearly with HbS concentration. We show that the characteristic 14-molecule fiber cross section is preserved during growth. We also correlate the asymmetry of the contact sites on the HbS molecular surface with the structure of the polymer fiber composed of seven helically twisted double strands. Finally, we show that the same asymmetry mediates the mechanical and structural properties of the HbS polymer fiber.
Introduction
Sickle cell disease (SCD) is an inherited anemia that arises from a single point mutation, from glutamate to valine, in the hemoglobin molecule (1). The genetic cause of the disease was identified by Linus Pauling, who called it the first molecular disease (2). The primary pathophysiological event in SCD is that sickle hemoglobin (HbS) polymerizes into long fibers under deoxygenated conditions. The fibers distort the morphologies of red blood cells (RBCs) and dramatically alter their mechanical and rheological properties (3, 4, 5). In combination with several associated processes, sickling of RBCs leads to vaso-occlusion and related organ and systemic damage (6, 7). The polymerization of HbS has been modeled with a double nucleation mechanism (8, 9). According to this mechanism, homogeneous nucleation of HbS polymer fibers is followed by fiber growth and branching by secondary nucleation of new fibers on top of existing ones. Homogeneous nucleation is a stochastic process that overcomes the energy barrier of nucleation and leads to the creation of the first embryo of a sickle hemoglobin fiber. The presence of the nucleation barrier makes nucleation events rare. Once a nucleus forms, HbS fibers grow quickly, likely by the addition of HbS monomers (8, 10, 11, 12, 13). The chirality of HbS molecules, which lack internal planes of symmetry, results in a particular structure of the HbS fiber, comprised of seven double strands in the style of a twisted rope (14, 15). The HbS fibers are quite stiff and their mechanical properties, such as bending rigidity κ and persistence length lp, can be measured from the amplitude of the thermal fluctuations as Wang et al. (16), Turner et al. (17), and Li et al. (18). In this method, the bending rigidity and persistence length of the HbS fiber can be calculated from the following equations,
| (1) |
| (2) |
where L is the length of the HbS polymer fiber, and is the normal deviation of the HbS polymer fiber-end from its average position. Experimental measurements (16, 17) of the bending rigidity showed that κ was ∼5.2 × 10−25 Nm2, corresponding to a persistence length of lp ≈ 121 μm.
Computational modeling and simulations of sickle RBCs and sickle blood have provided understanding on how sickle RBCs behave in microfluidic channels and how these behaviors may affect vaso-occlusion (19). For example, a coarse-grained, multiscale RBC model (20, 21) has been employed to quantify the hemodynamic and rheological characteristics of blood flow with SCD under various physiological conditions (22, 23). Available evidence indicates that the adhesion interaction between the sickle RBCs and vasculature walls plays a profound effect on the hemodynamics of sickle blood (24). Furthermore, numerical models have provided useful insights into the mechanisms of HbS fiber nucleation and growth. To this end, Dou and Ferrone (25) developed a kinetic model of HbS polymerization that explained the formation of polymer domains inside RBCs. Their results demonstrated the transformation of a single fiber to wheat-sheaf bundles and then to spherulitic domains. Dynamic simulations of self-assembly of HbS confirmed that hydrophobic interactions among HbS molecules are necessary for the formation of HbS fibers (26). Different coarse-grained HbS polymer fiber models have also been introduced to simulate the dynamic behavior such as zipping and unzipping dynamics of HbS fibers, demonstrating the decisive role of fiber frustration and compression (18, 27). However, to the best of our knowledge, no model has been developed before that can accurately describe the growth of HbS polymer fibers, specifically in reproducing the structure of twisted HbS fibers.
In this study, we simulate the formation process of HbS polymer fibers assuming that a nucleus already exists. We aim to model the dynamics of HbS polymerization at the molecular level and gain insights into the nature of the HbS polymer fiber formation. We employ coarse-grained molecular dynamics (CGMD) to simulate the growth of HbS polymer fiber and probe the structural and mechanical properties of the fiber. The rest of the article is organized as follows. In Materials and Methods, we briefly describe the particle-based model and simulation method. In Results and Discussion, we then present and discuss our numerical results and summarize the findings. We then present the conclusion.
Materials and Methods
Model and simulation method
HbS molecule model
Hemoglobin (Hb) is a protein molecule inside a red blood cell that carries oxygen (O2) from the lungs to the body tissues and returns carbon dioxide (CO2) from the tissues back to the lungs. It consists of four connected globin subunits. Normal adult hemoglobin (HbA) contains two α- and two β-globin subunits. HbS is a variant form of Hb found in individuals with SCD. It differs from HbA by a single amino acid: valine replaces glutamate at the sixth position on the surface of the β-subunit, causing the hemoglobin to become less soluble under decreasing oxygen concentrations and to polymerize into HbS fibers.
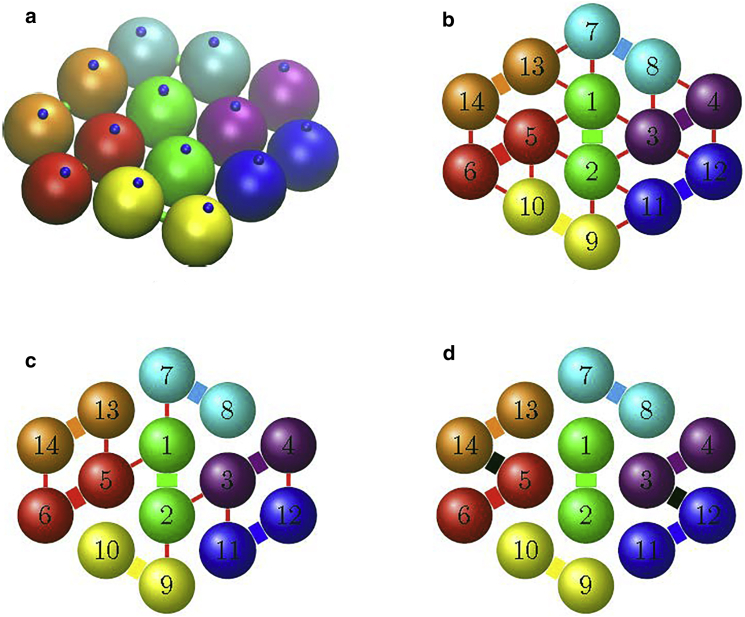
The HbS polymer structure is relatively well understood. Electron microscopy and x-ray diffraction from HbS crystals with molecular arrangement similar to that in the fiber have identified three types of contacts, illustrated in Fig. 1 a: (1) intra-double-strand axial contacts, highlighted in blue (2); intra-double-strand lateral contacts, green; and (3) inter-double-strand contacts, red (28, 29, 30, 31). Accordingly, we proposed a coarse-grained patchy particle model (32, 33) for the HbS molecules. In this model, a sickle hemoglobin molecule is represented by a rigid sphere with a set of patches on its surface. Intermolecular interactions are localized at these patches to distinguish and describe the different types of contact spots (Fig. 1 b), i.e., the coarse-grained model has two axial (blue) patches, and one lateral (green) patch, which are involved in the intra-double-strand contacts. Inter-double-strand attraction is considered implicitly in the coarse-grained particle model, and is described by the attractive term of the Lennard-Jones potential. In addition, we introduce two perpendicular vectors p and q (Fig. 1, b and d) to describe the orientation of a patchy particle.
Figure 1.
Mesoscopic model of HbS polymer fiber. (a) Structure of a sickle hemoglobin molecule highlighting the residues participating in three types of contacts. Green and blue mark the lateral and axial intra-double-strand contacts, while red marks the inter-double-strand contacts. (b) Extended patchy particle model of HbS molecules. A sickle hemoglobin molecule is represented as a patchy particle with three (two blue and one green) patches, whose colors correspond to those in (a). The red contact type is treated implicitly; for clarification, a pseudo-patch colored in red represents one possible location for such a contact. For more possible locations of red contact types, we refer to Fig. 2b. (c) Structure of a sickle hemoglobin double strand. (d) Representation of a sickle hemoglobin double strand in the patchy particle model. To see this figure in color, go online.
HbS fiber nucleus
In this study we focus on the growth dynamics of HbS molecules and the polymerized structure of HbS polymer fiber, so we assume that a sickle hemoglobin fiber nucleus already exists and it is initially placed at the center of the model system. The structure of the HbS fiber nucleus, including the relative position and orientation of each HbS molecule, is designed to match the known structure of the HbS polymer fiber (15); see Fig. 2 a. The twisted rope structure consists of an inner core of four strands surrounded by a sheath of 10 strands. These 14 strands are grouped into seven double stands as indicated in Fig. 2 a. We modified the relative position and orientation values of HbS molecules in a small range, and we found that their influence on the growth dynamics of HbS polymer fiber is quite small. Hence, in the following study, we carried out CGMD simulations using the known structure of the HbS fiber nucleus, with fixed relative position and orientation of HbS molecules.
Figure 2.
(a) Model structure of the HbS fiber nucleus. Particles of the same color are within the same double strand. Intra- and inter-double-strand contacts between HbS particles are based on (b) the Dykes-Rodgers’ model, (c) the Carragher’s model, and (d) the Roufberg-Ferrone’s model. Thick lines represent lateral intra-double-strand contacts, while thin red lines represent inter-double-strand contacts. Thick black lines represent additional contacts. To see this figure in color, go online.
Interactions
To model the anisotropic interactions between HbS molecules, we hypothesize that two HbS molecules interact through their patches and that patches only form contacts with patches of the same type. We divide the patch sites into two types, active and inactive, depending on whether another HbS molecule is attached to a site or not. Sites between two bound molecules are considered inactive, while open sites are active. In addition, we assume that two HbS molecules interact only when their patches are within the range of attractive interaction. Specifically, the attractive interaction is represented by
| (3) |
where A and B are used to determine the strength and range of the interaction, r is the distance between two patch sites of interacting HbS molecules (and not between molecular centers), and rc sets the distance cutoff. This potential is analogous to the attractive term of the Morse potential, which is a popular potential energy function used to model intermolecular interaction. If an active site and an inactive site come into a close contact, i.e., less than a constant δ, an axial bond is built between the two HbS molecules (see the blue bond in Fig. 1 d). Considering that the distance between two residues in contact regions is mostly in the range 0.3–0.6 nm (31), we set δ as 0.5 nm. To model the activation barrier EA for attachment of a sickle hemoglobin molecule to a fiber, we assume that only a fraction f of the HbS molecules within the proper distance from a site forms a bond. The fraction f relates to EA as f ∼ exp(−EA/kBT), with EA = 28 kJ mol−1 and f = 1.3 × 10−5 (12).
The elasticity of the intermolecular bond (34) is modeled as
| (4) |
where k = 2 is the bond strength, and λ = 1.5 nm is the maximum extension of the bond. Similarly, lateral bonds with k = 1 and λ = 1.5 nm can be built (see the green bond in Fig. 1 d). Hence, two HbS molecules combine to form a molecular contact, and the HbS polymer fiber grows.
The helical twist of HbS polymer fibers is caused by deviations of the stacked HbS molecules from translational alignment (26, 35). To model this helical twist, we consider angle-bending potentials between axial vectors and , and lateral vectors and of two neighboring HbS molecules in the same strand. These potentials are given by
| (5) |
| (6) |
where and are the bending strength of angle bending potentials in axial and lateral directions, respectively; and are angles between each pair of vectors, and and are the corresponding equilibrium values of these two angles. The misorientation of the HbS molecules with respect to the fiber axis is dictated by the low molecular symmetry.
The inter-double-strand contact holds the seven double strands together and stabilizes the HbS polymer fiber. There are three hypotheses for the possible inter-double-strand contact, i.e., Dykes-Rodgers’ model (Dykes et al. (36) and Rogers et al. (37)), Carragher’s model (Carragher et al. (15)), and Roufberg-Ferrone’s model (Roufberg and Ferrone (38)). Compared to Dykes-Rodgers’ model, Carragher’s model has a lower number of contacts. In Roufberg-Ferrone’s model, two additional contacts are assumed to generate two pairs of double-strand partners. Based on these three hypotheses, we set the inter-double-strand contacts (see Fig. 2, b–d). The bonds in inter-double-strand contacts are mostly of the van der Waals type; we model them with the Lennard-Jones potential
| (7) |
where ε is the well depth and a measure of the strength of the contacts; and is the equilibrium separation, at which repulsive and attractive forces balance. The Lennard-Jones potential is a function of the distance r between the center-of-mass of two HbS particles. The attractive term of the Lennard-Jones potential is with a cutoff at a distance of 7 nm, and it describes the attractive interaction between HbS particles in adjacent double strands. In the Dykes-Rodgers’ model and the Carragher’s model, we set ε = 1; in the Roufberg-Ferrone’s model, we set ε = 2 to enhance the interactions of the two additional β6 contacts. To avoid particle interpenetration, each HbS particle is considered to have an excluded volume that is inaccessible to other particles in the simulation volume. The excluded volume effect is represented by the repulsive term of the Lennard-Jones potential.
Simulation method and model parameters
We simulate the growth dynamics of HbS molecules using the CGMD method. In CGMD simulation, the position, orientation, and momentum of a particle representing a sickle hemoglobin molecule is updated in a continuous phase space at discrete time steps (39). The translational and rotational motions as well as pairwise interacting forces of the particles are represented by Langevin equations
| (8) |
| (9) |
where and are center-of-mass linear velocity and angular velocity of particle i; and are force and torque exerted on particle i; and are random force and torque, respectively; and and are friction coefficients. For numerical integration of the equations of motion, we use the velocity Verlet algorithm with a finite time step of 0.0001τ, where τ is the timescale of CGMD simulation. Here we note that the timestep must be chosen sufficiently short to avoid discretization errors, because the bond-stretching potential for bonded HbS particles and the Lennard-Jones potential for nonbonded HbS particles are quite stiff. All runs are performed in a NVT ensemble using a Langevin thermostat (40).
Because the hemoglobin molecule is nearly ellipsoidal with volume of 6 × 5 × 5 nm (41), we choose the diameter of spherical patchy particle d = 5.3 nm; this parameter represents the characteristic length scale λp of the model system. According to previous experimental measurements on the length distribution of HbS polymer fibers (42), we know that >70% of polymer fibers are shorter than 800 nm, so we choose a cuboid simulation box of size 800 × 65 × 65 nm with periodic boundary conditions. HbS particles are placed randomly into the simulation box. The total number of HbS particles is set at 11,000, thus the volume concentration of HbS particles is ϕp = 26%. The latter value corresponds, with HbS molecular volume of 0.74 g/cm3, to the average HbS concentration in erythrocytes of sickle cell patients, 35 g/dL (43, 44).
To determine the equilibrium angle in Eq. 5 and in Eq. 6, we require that the pitch length and the number of HbS molecules in each turn of modeled HbS polymer fibers to match the experimental values. In Cartesian coordinates, a circular helix can be described by the following relations
| (10) |
where a is the radius, and 2πb is the pitch length. The HbS polymer fiber has an average radius of ∼11 nm and a mean helical pitch length of ∼270 nm. In addition, there are, on the average, 46 HbS monomers in each turn (15). Equation 10 indicates that with = 11.5° and = 7.8°, we would get a pitch length of ∼270 nm and 46 HbS molecules in each turn, which correspond to the experimental values. To explore the effect of these two parameters on the structural and mechanical properties of HbS fibers, we vary them within a range centered at the above values.
Parameters and of the angle bending potential are related to the bending rigidity κ of HbS polymer fiber. To compute the bending rigidity κ of a sickle hemoglobin fiber, we apply the thermal fluctuation method described in Turner et al. (17) and Li et al. (18). We find that the simulated values of bending rigidity κ at and are very close to the experimental bending rigidity value of ∼κ = 5.2 × 10−25 Nm2 (17). Therefore, we have chosen the values and in our simulations.
The choice of parameters in Eqs. 3 and 4 is far more flexible. In this study, we choose B = 2 for the attractive interaction of both blue and green patches. To ensure that the inner double strands can reach a sufficient number of free HbS molecules during polymerization, the value of the interaction strength parameter for the inner two double strands is made larger than those for the outer five double strands, i.e., and for blue patches with rc = 1.5, and A = 2.0 and rc = 0.5 for green patches. A set of simulations has been performed by changing these parameters and our simulation results show that the final structure of HbS polymer is insensitive to these parameters. To illustrate the effect of molecular chirality on the mechanical and structural properties of HbS polymer fiber, we systematically vary the axial chiral angle in the range from 0.0° to 18.0° and examine the modulated pitch length and bending persistence length of the HbS polymer fiber.
Results and Discussion
Formation dynamics of HbS polymer fiber
The three-dimensional CGMD simulations of HbS polymer formation address the roles of the intermolecular interactions, including the intra- and inter-double-strand contacts, and molecular symmetry affects the HbS fiber structure. As expected, we find that without the attractive intra-double-strand interactions no HbS aggregates are observed in the simulations. The combination of intra- and inter-double-strand interactions in the Dykes-Rodgers’ model and angle bending yields a twisted HbS polymer fiber consisting of seven double strands (see Fig. 3 a). The HbS polymer fiber has a radius of ∼11 nm and a helical pitch length of ∼270 nm, which is in accordance with the experimental characterizations of the HbS polymer fiber. It takes 24.6 h for such a typical simulation of 2.5 × 106 timesteps, performed with 64 MPI tasks at four Xeon E5-2650 processors (Intel, Santa Clara, CA).
Figure 3.
(a) Structure of HbS polymer fiber obtained from CGMD simulations using the Dykes-Rodgers’ model. Strands belonging to same double strand are colored identically. The HbS nucleus is in the middle of the fiber. Each strand within the fiber twists with good synchronization to maintain the structure of seven double strands. A hexagonally shaped cross section is shown for clarity. (b) Unstable structure of HbS fiber obtained from CGMD simulation using Carragher’s model. (c) Sequential snapshots of the formation of HbS polymer fiber. For clarity, only the HbS particles in the HbS fiber are shown while the free HbS molecules in growth medium are not. To see this figure in color, go online.
Using Carragher’s model of intermolecular contacts, we observed that the double strands split (Fig. 3 b), indicating that the simulations have failed to reproduce the fiber structure. One possible reason is that the interactions between double strands in this model are too weak to keep the HbS fiber stable. This simulation result is consistent with the analysis by Cretegny and Edelstein (30). By contrast, the Roufberg-Ferrone and Dykes-Rodgers models yield similar structures of the HbS fibers, with nearly identical pitch length; the fiber structures resulting from both models are consistent with the experimental observations. It is worth pointing out that Roufberg-Ferrone’s model cannot be used alone, because it focuses on the two β6 contacts without considering the other inter-double-strand contacts; hence, in this study, this model was always used together with Dykes-Rodgers’ model.
A direct observation of the dynamics of formation of HbS polymer fibers at the molecular level is important for understanding the corresponding mechanism. However, this process is too fast to be captured even with the current state-of-the-art experimental techniques. Hence, the simulations provide an alternative means to understand this process. In Fig. 3 c and Movie S1 in the Supporting Material, we present a typical evolution of a sickle hemoglobin polymer fiber. These observations reveal that HbS particles initially rapidly aggregate onto the HbS nucleus and form a short HbS polymer fiber (see Fig. 3 c). HbS particles in the vicinity of the newly generated fiber are attracted to its ends and attach to them, resulting in a persistent growth in both directions leading to a long twisted HbS fiber. Throughout the simulations the fiber thickness of 14 molecules was preserved and the fiber did not thicken or lose strands. This observation agrees with experimental results. The simulations clearly demonstrate that the growth of HbS fibers is due to the attachment of HbS monomers, rather than by association of precursor aggregates performed in the growth medium. This result is consistent with analyses of experimental data on the growth of HbS polymer fibers (11, 12, 45). In addition, we find that the active sites on the HbS fiber surface are not always in the same layer in the direction perpendicular to the fiber axis, so individual strands may vary in length. We conclude that the growth of HbS polymer fiber is not a layer-by-layer process. In addition, we observe that fibers never branch. This observation suggests that experimentally observed fiber branching that leads to numerous distinct morphologies of sickle RBCs requires additional processes, which are not a part of this model, such as heterogeneous nucleation of new fibers.
Influence of HbS monomer concentration on the growth rate of HbS fiber
The growth rate of HbS polymer fiber is a fundamental aspect of SCD pathology. One solution parameter that determines the growth rate is the concentration of HbS in the growth medium. To illustrate the effect of the HbS concentration on HbS polymer fiber growth, we systematically vary this parameter and examine the modulated growth rate for a series of growth media that contain HbA, HbS, and hybrid HbAS. The growth rate j is expected to be a linear function of HbS activity a, which, in turn, is the product of the activity coefficient γ, and HbS concentration C, a = γC (11, 12, 45). The coefficient γ is determined by the volume fraction of all Hb species in the growth medium. Hence, to explore the dependence of the growth rate on C, in the simulations we kept the total Hb concentration constant so that the coefficient γ remains approximately constant.
We evaluate the growth rate of HbS polymer fibers from the increase of the number of HbS particles of an individual fiber with time. We find that the average growth rate of the HbS fiber increases with the increase of HbS concentration in an approximately linear fashion (Fig. 4), which is in agreement with theoretical predictions and experimental observations (45).
Figure 4.
Dependence of the growth rate, j, of HbS polymer fiber on the concentration of HbS monomers, C, at constant total Hb concentration. Note that error bars are included, but the deviation is quite small. To see this figure in color, go online.
From Fig. 4, we also find that the concentrations of HbS monomers at very low or high levels have some significant effect on the growth of HbS fiber. The calculated growth rate at a very low or high concentration of HbS monomers is somewhat lower than the corresponding value in the fitting curve. This may arise from the fact that the HbS polymer fiber only grows at its ends by monomer addition. At a low initial concentration of HbS monomers in the model system, the concentration of free HbS monomers in the vicinity of the fiber end would be readily depleted. The likely reason for the slower growth rates at high concentrations is the competition between the ends of adjacent strands for supply of monomers.
Structural and mechanical properties of HbS polymer fiber
The pathology of SCD is controlled by HbS polymer fibers that distort the RBC morphologies and make them rigid. This is, in turn, related to the structural and mechanical properties of HbS fibers, such as their intrinsic stiffness. Here, we analyze the variations of twist and bend in HbS polymer fiber to probe effects of the intermolecular interactions on the HbS fiber structural and mechanical properties.
Influence of molecular chirality on the helical pitch length of HbS polymer fiber
Pitch length, which is defined as the length over which the HbS polymer fiber twists through a full revolution, 360°, affects the structural property (twist) of HbS polymer fiber. The pitch length s of a sickle hemoglobin polymer fiber can be calculated from the dihedral angle, ϕ, between neighboring HbS particles in the same strand with respect to the fiber axis, using the geometric relationship
| (11) |
where l is the length of the fiber along its axis. In experiments, the pitch length is observed to vary along the HbS fiber with a mean value of ∼270 nm.
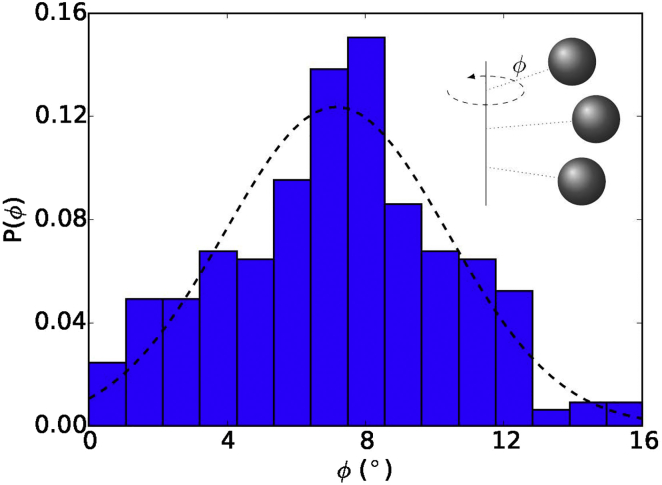
From the simulated HbS polymer fiber structure, we calculate the dihedral angle ϕ and obtain its distribution (see Fig. 5). The angular distribution is well approximated by a Gaussian function, where we can get the mean value of this distribution as ∼7.4° with a standard derivation ∼3.5°, which agrees well with the experimental estimated mean value of ∼7.5° with a standard derivation of ∼2.7° (15). The approximate pitch length is then determined through Eq. 11. In this case, the pitch length is SM = 55, corresponding to a physical value of sp = 292 nm. (The length scale of the model system is λp = 5.3 nm, thus sp = sM × λp = 55 × 5.3 = 292 nm.)
Figure 5.
Histogram of dihedral angles ϕ between neighboring HbS monomers. The histogram follows a nearly Gaussian distribution (dashed line). (Inset) Schematic of dihedral angle that is perpendicular to fiber axial direction. To see this figure in color, go online.
The experimental observation shows that the distribution of HbS polymer fiber pitch length is statistically equivalent to a Gaussian distribution (15). We conducted a series of independent simulations with completely independent initial positions of free HbS particles but with the same interaction parameters, which give us a group of HbS polymer fibers with different pitch lengths. We then calculated the interaction energy among HbS particles in a sickle hemoglobin polymer fiber with different helical pitch lengths (see Table 1). Our results show that the energy difference between these cases is small. One possible reason is that we use the same interaction parameters in these different simulation cases. However, a small change in the distance (or angle) between two adjacent HbS particles can bring an apparent change in pitch length; this may help us to explain the existence of variable pitch lengths observed in HbS polymer fibers. When Dykes-Rodgers’ model is used, the average pitch length is 284.3 nm. The Roufberg-Ferrone model yields an average pitch length of 285.2 nm.
Table 1.
Energy Difference of HbS Polymer Fiber with Different Helical Pitch Length
| Simulation Case | Pitch Length (nm) | Energy Difference (kBT) |
|---|---|---|
| I | 265.0 | −0.28 |
| II | 265.2 | 0.00 |
| III | 286.8 | 0.44 |
| IV | 288.2 | −0.31 |
| V | 292.2 | −0.36 |
Here we choose the data from simulation case II as a reference point. For comparison, the average total energy of one layer in a sickle hemoglobin polymer fiber is ∼−40.0 kBT.
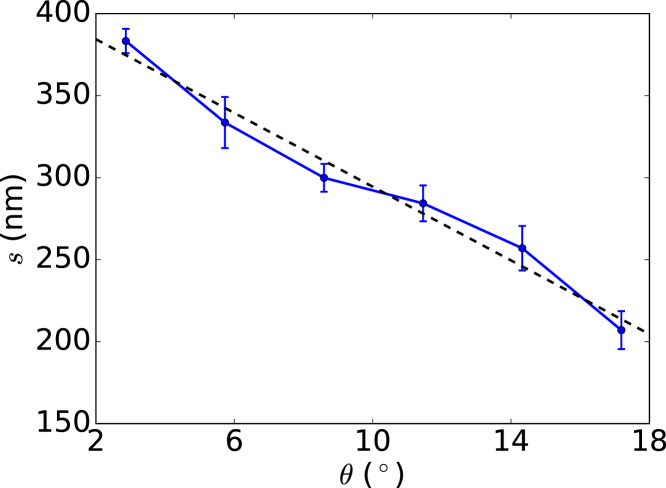
It is of fundamental and practical interest to study the structure of a twisted HbS polymer fiber under the influence of intermolecular interaction such as chiral interaction. From this, we determine the fiber pitch length s at different equilibrium values of axial chiral angle (using Dykes-Rodgers’ model); see Fig. 6. We find that s decreases linearly with , which indicates that weak chiral interaction results in high pitch length.
Figure 6.
Functional dependence of fiber pitch length, s, of HbS polymer on axial chiral angle, . To see this figure in color, go online.
Influence of molecular chirality on the bending rigidity of HbS polymer fibers
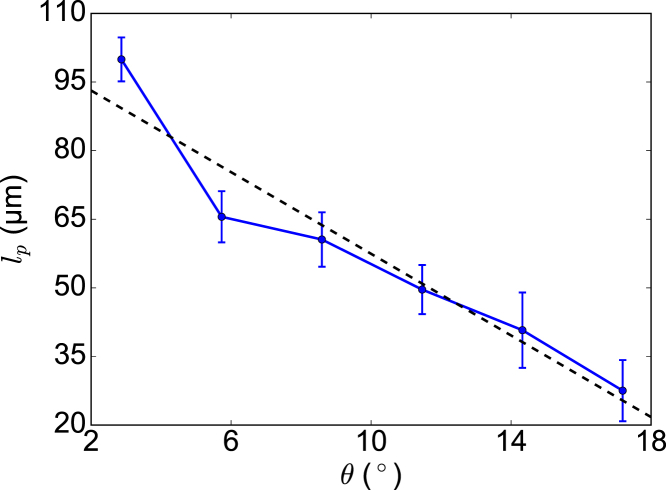
The thermally driven shape fluctuations of HbS polymer fibers can be used to obtain their bending rigidity. In this study, we measure deviations, δu(L), of the end of a sickle hemoglobin polymer fiber from a straight line joining its other end. The mean-squared amplitude of this deviation is directly related to the bending rigidity κ and persistence length lp, as shown in Eqs. 1 and 2. When the Dykes-Rodgers model is used, the average value of lp is 49.6 μm; with the Roufberg-Ferrone model, the average value of lp is 59.4 μm, which means a stronger bending rigidity of HbS fiber due to the additional β6 contacts.
The measured bending persistence length lp of HbS polymer fiber with respect to axial chiral angle (using Dykes-Rodgers’ model) is plotted in Fig. 7. We find that lp decreases nearly linearly with increasing , which indicates that weak chirality may result in a larger bending persistence length. The numerical results are consistent with the theoretical analysis by Park and Oh (46). However, the theoretical model assumed that the diameter of the HbS polymer fiber is much greater than the strand diameter, hence the formula they derived cannot be used here to predict the bending rigidity of HbS polymer fibers.
Figure 7.
Functional dependence of bending persistence length, lp, of HbS polymer fiber on axial chiral angle . To see this figure in color, go online.
Through Eq. 1, we find that the molecular chirality is associated with the bending rigidity, i.e., the HbS polymer fiber becomes stiffer with the decrease of molecular chirality. When aligning with other fibers, it is easy for them to distort the cell morphologies and decrease their deformability. Thus, the molecular chirality is a critical determinant of the mechanical properties of HbS polymer fibers and the rheological properties of sickle RBCs.
Conclusion
In this article, we have studied the growth of HbS polymer fiber by assuming a preexisting nucleus using CGMD simulations. We developed a coarse-grained patchy particle model of HbS by considering that each particle has three types of contact sites, and that the azimuthal angles between them vary. The locations of the contact sites between HbS molecules were designed to describe the molecular arrangement in a sickle hemoglobin fiber.
Using this model, we demonstrated that the formation process of HbS polymer fiber occurs through monomer addition, but does not follow a layer-by-layer growth mode. We found that our model, using the Dykes-Rodgers and Roufberg-Ferrone hypotheses, reproduces the complex structure of HbS polymer fiber, i.e., a twisted structure of seven double strands, but Carragher’s hypothesis failed. We analyzed the interaction energy among HbS particles in HbS polymer fibers with different helical pitch length and found that the interaction energy difference between two simulation cases is quite small. These findings may facilitate the understanding of variable pitch length observed in HbS polymer fibers. In addition, we found that the molecular chirality is the critical determinant of the mechanical and structural properties of HbS polymer fiber.
Our model does not allow detachment of HbS molecules from the fiber. Hence, it fails to account for the equilibrium between fibers and growth medium. This deficiency will be accounted for in future work. Furthermore, our model does not include fiber-fiber interactions. Hence, it is not clear whether the choice of interaction strength parameters of double strands affects the way fibers grow (such as fiber branching) or not. A previous study has shown that fiber branching can be the result of splitting of a single HbS fiber from a parent bunch of several single fibers (4). To address this issue, we will modify this model by assuming a preexisting parent fiber and allowing fiber branching in future work. Additional extensions should target a hybrid model constructed by combining this coarse-grained HbS model with particle-based composite models, which account separately for the lipid bilayer and cytoskeleton but also include explicitly/implicitly the transmembrane proteins, of the human RBC membrane (47, 48, 49) and the whole RBC (50, 51). Such models will be employed to investigate the uncoupling phenomenon of the cytoskeleton from the lipid bilayer in SCD due to HbS polymerization and growth (52), and probe the influence of HbS polymer fibers on the morphological and mechanical properties of sickle RBCs. Furthermore, in combination of these integrated methods with a mesoscopic sickle RBC model developed by Lei and Karniadakis (24), ultimately, computations that encompass all molecular and cellular scales could be used to investigate the entire process from deoxygenation and nucleation to vaso-occlusion in SCD. Such simulations would potentially answer questions concerning with the link among HbS polymerization, cell sickling, blood flow alteration, and eventual vaso-occlusive crisis, which may reveal new paradigms for therapeutic treatments.
Author Contributions
L.L., X.L., P.G.V., and G.E.K. designed research; L.L. and X.L. performed research; X.L., P.G.V., and G.E.K. contributed new reagents/analytic tools; L.L., X.L., P.G.V., and G.E.K. analyzed data; L.L., X.L., P.G.V., and G.E.K. wrote the article.
Acknowledgments
L.L. and X.L. thank Zhen Li and Xin Bian for helpful discussions.
The work described in this article was supported by National Institutes of Health grant No. U01HL114476. An award of computer time was provided by the Innovative and Novel Computational Impact on Theory and Experiment program. This research used resources of the Argonne Leadership Computing Facility, which is a Department of Energy Office of Science User Facility supported under contract No. DE-AC02-06CH11357. This research also used resources of the Oak Ridge Leadership Computing Facility, which is a Department of Energy Office of Science User Facility supported under contract No. DE-AC05-00OR22725.
Editor: Nathan Baker.
Footnotes
One movie is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30120-5.
Contributor Information
Xuejin Li, Email: xuejin_li@brown.edu.
George Em Karniadakis, Email: george_karniadakis@brown.edu.
Supporting Material
References
- 1.Ingram V.M. Abnormal human haemoglobins. III. The chemical difference between normal and sickle cell haemoglobins. Biochim. Biophys. Acta. 1959;36:402–411. doi: 10.1016/0006-3002(59)90183-0. [DOI] [PubMed] [Google Scholar]
- 2.Pauling L., Itano H.A., Wells I.C. Sickle cell anemia a molecular disease. Science. 1949;110:543–548. doi: 10.1126/science.110.2865.543. [DOI] [PubMed] [Google Scholar]
- 3.Eaton W.A., Hofrichter J. Hemoglobin S gelation and sickle cell disease. Blood. 1987;70:1245–1266. [PubMed] [Google Scholar]
- 4.Samuel R.E., Salmon E.D., Briehl R.W. Nucleation and growth of fibres and gel formation in sickle cell haemoglobin. Nature. 1990;345:833–835. doi: 10.1038/345833a0. [DOI] [PubMed] [Google Scholar]
- 5.Ballas S.K., Mohandas N. Sickle red cell microrheology and sickle blood rheology. Microcirculation. 2004;11:209–225. doi: 10.1080/10739680490279410. [DOI] [PubMed] [Google Scholar]
- 6.Stuart M.J., Nagel R.L. Sickle-cell disease. Lancet. 2004;364:1343–1360. doi: 10.1016/S0140-6736(04)17192-4. [DOI] [PubMed] [Google Scholar]
- 7.Du E., Diez-Silva M., Suresh S. Kinetics of sickle cell biorheology and implications for painful vasoocclusive crisis. Proc. Natl. Acad. Sci. USA. 2015;112:1422–1427. doi: 10.1073/pnas.1424111112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ferrone F.A., Hofrichter J., Eaton W.A. Kinetics of sickle hemoglobin polymerization. II. A double nucleation mechanism. J. Mol. Biol. 1985;183:611–631. doi: 10.1016/0022-2836(85)90175-5. [DOI] [PubMed] [Google Scholar]
- 9.Vekilov P.G. Sickle-cell haemoglobin polymerization: is it the primary pathogenic event of sickle-cell anaemia? Br. J. Haematol. 2007;139:173–184. doi: 10.1111/j.1365-2141.2007.06794.x. [DOI] [PubMed] [Google Scholar]
- 10.Ferrone F.A., Hofrichter J., Eaton W.A. Kinetics of sickle hemoglobin polymerization. I. Studies using temperature-jump and laser photolysis techniques. J. Mol. Biol. 1985;183:591–610. doi: 10.1016/0022-2836(85)90174-3. [DOI] [PubMed] [Google Scholar]
- 11.Galkin O., Nagel R.L., Vekilov P.G. The kinetics of nucleation and growth of sickle cell hemoglobin fibers. J. Mol. Biol. 2007;365:425–439. doi: 10.1016/j.jmb.2006.10.001. [DOI] [PubMed] [Google Scholar]
- 12.Vekilov P.G., Galkin O., Nagel R.L. Determination of the transition-state entropy for aggregation suggests how the growth of sickle cell hemoglobin polymers can be slowed. J. Mol. Biol. 2008;377:882–888. doi: 10.1016/j.jmb.2008.01.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ferrone F.A. The delay time in sickle cell disease after 40 years: a paradigm assessed. Am. J. Hematol. 2015;90:438–445. doi: 10.1002/ajh.23958. [DOI] [PubMed] [Google Scholar]
- 14.Crepeau R.H., Edelstein S.J. Polarity of the 14-strand fibers of sickle cell hemoglobin determined by cross-correlation methods. Ultramicroscopy. 1984;13:11–18. doi: 10.1016/0304-3991(84)90052-4. [DOI] [PubMed] [Google Scholar]
- 15.Carragher B., Bluemke D.A., Josephs R. Structural analysis of polymers of sickle cell hemoglobin. I. Sickle hemoglobin fibers. J. Mol. Biol. 1988;199:315–331. doi: 10.1016/0022-2836(88)90316-6. [DOI] [PubMed] [Google Scholar]
- 16.Wang J.C., Turner M.S., Briehl R.W. Micromechanics of isolated sickle cell hemoglobin fibers: bending moduli and persistence lengths. J. Mol. Biol. 2002;315:601–612. doi: 10.1006/jmbi.2001.5130. [DOI] [PubMed] [Google Scholar]
- 17.Turner M.S., Briehl R.W., Josephs R. Anisotropy in sickle hemoglobin fibers from variations in bending and twist. J. Mol. Biol. 2006;357:1422–1427. doi: 10.1016/j.jmb.2006.01.071. [DOI] [PubMed] [Google Scholar]
- 18.Li H., Ha V., Lykotrafitis G. Modeling sickle hemoglobin fibers as one chain of coarse-grained particles. J. Biomech. 2012;45:1947–1951. doi: 10.1016/j.jbiomech.2012.05.016. [DOI] [PubMed] [Google Scholar]
- 19.Chiang E.Y., Frenette P.S. Sickle cell vaso-occlusion. Hematol. Oncol. Clin. North Am. 2005;19:771–784. doi: 10.1016/j.hoc.2005.08.002. [DOI] [PubMed] [Google Scholar]
- 20.Pivkin I.V., Karniadakis G.E. Accurate coarse-grained modeling of red blood cells. Phys. Rev. Lett. 2008;101:118105. doi: 10.1103/PhysRevLett.101.118105. [DOI] [PubMed] [Google Scholar]
- 21.Fedosov D.A., Caswell B., Karniadakis G.E. A multiscale red blood cell model with accurate mechanics, rheology, and dynamics. Biophys. J. 2010;98:2215–2225. doi: 10.1016/j.bpj.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lei H., Karniadakis G.E. Quantifying the rheological and hemodynamic characteristics of sickle cell anemia. Biophys. J. 2012;102:185–194. doi: 10.1016/j.bpj.2011.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Li X.J., Du E., Karniadakis G.E. Patient-specific blood rheology in sickle-cell anaemia. Interface Focus. 2016;6:20150065. doi: 10.1098/rsfs.2015.0065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lei H., Karniadakis G.E. Probing vasoocclusion phenomena in sickle cell anemia via mesoscopic simulations. Proc. Natl. Acad. Sci. USA. 2013;110:11326–11330. doi: 10.1073/pnas.1221297110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dou Q., Ferrone F.A. Simulated formation of polymer domains in sickle hemoglobin. Biophys. J. 1993;65:2068–2077. doi: 10.1016/S0006-3495(93)81237-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li X., Caswell B., Karniadakis G.E. Effect of chain chirality on the self-assembly of sickle hemoglobin. Biophys. J. 2012;103:1130–1140. doi: 10.1016/j.bpj.2012.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Li H., Lykotrafitis G. A coarse-grain molecular dynamics model for sickle hemoglobin fibers. J. Mech. Behav. Biomed. Mater. 2011;4:162–173. doi: 10.1016/j.jmbbm.2010.11.002. [DOI] [PubMed] [Google Scholar]
- 28.Watowich S.J., Gross L.J., Josephs R. Intermolecular contacts within sickle hemoglobin fibers. J. Mol. Biol. 1989;209:821–828. doi: 10.1016/0022-2836(89)90610-4. [DOI] [PubMed] [Google Scholar]
- 29.Watowich S.J., Gross L.J., Josephs R. Analysis of the intermolecular contacts within sickle hemoglobin fibers: effect of site-specific substitutions, fiber pitch, and double-strand disorder. J. Struct. Biol. 1993;111:161–179. doi: 10.1006/jsbi.1993.1047. [DOI] [PubMed] [Google Scholar]
- 30.Cretegny I., Edelstein S.J. Double strand packing in hemoglobin S fibers. J. Mol. Biol. 1993;230:733–738. doi: 10.1006/jmbi.1993.1195. [DOI] [PubMed] [Google Scholar]
- 31.Harrington D.J., Adachi K., Royer W.E., Jr. The high resolution crystal structure of deoxyhemoglobin S. J. Mol. Biol. 1997;272:398–407. doi: 10.1006/jmbi.1997.1253. [DOI] [PubMed] [Google Scholar]
- 32.Glotzer S.C. Self-assembly of patchy particles. Nano Lett. 2004;4:1407–1413. doi: 10.1021/nl0493500. [DOI] [PubMed] [Google Scholar]
- 33.Pawar A.B., Kretzschmar I. Fabrication, assembly, and application of patchy particles. Macromol. Rapid Commun. 2010;31:150–168. doi: 10.1002/marc.200900614. [DOI] [PubMed] [Google Scholar]
- 34.Rector D.R., van Swol F., Henderson J.R. Simulation of surfactant solutions. I. Micelle formation in the bulk phase. Mol. Phys. 1994;82:1009–1031. [Google Scholar]
- 35.Yang Y., Meyer R.B., Hagan M.F. Self-limited self-assembly of chiral filaments. Phys. Rev. Lett. 2010;104:258102. doi: 10.1103/PhysRevLett.104.258102. [DOI] [PubMed] [Google Scholar]
- 36.Dykes G.W., Crepeau R.H., Edelstein S.J. Three-dimensional reconstruction of the 14-filament fibers of hemoglobin S. J. Mol. Biol. 1979;130:451–472. doi: 10.1016/0022-2836(79)90434-0. [DOI] [PubMed] [Google Scholar]
- 37.Rodgers D.W., Crepeau R.H., Edelstein S.J. Pairings and polarities of the 14 strands in sickle cell hemoglobin fibers. Proc. Natl. Acad. Sci. USA. 1987;84:6157–6161. doi: 10.1073/pnas.84.17.6157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Roufberg A., Ferrone F.A. A model for the sickle hemoglobin fiber using both mutation sites. Protein Sci. 2000;9:1031–1034. doi: 10.1110/ps.9.5.1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Miller T.F., Eleftheriou M., Martyna G.J. Symplectic quaternion scheme for biophysical molecular dynamics. J. Chem. Phys. 2002;116:8649–8659. [Google Scholar]
- 40.Schneider T., Stoll E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B. 1978;17:1302–1322. [Google Scholar]
- 41.Erickson H.P. Size and shape of protein molecules at the nanometer level determined by sedimentation, gel filtration, and electron microscopy. Biol. Proced. Online. 2009;11:32–51. doi: 10.1007/s12575-009-9008-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Briehl R.W., Mann E.S., Josephs R. Length distributions of hemoglobin S fibers. J. Mol. Biol. 1990;211:693–698. doi: 10.1016/0022-2836(90)90070-3. [DOI] [PubMed] [Google Scholar]
- 43.Mohandas N., Johnson A., Groner W. Automated quantitation of cell density distribution and hyperdense cell fraction in RBC disorders. Blood. 1989;74:442–447. [PubMed] [Google Scholar]
- 44.Beutler E. The sickle cell diseases and related disorders. In: Kaushansky K., Williams W.J., editors. Williams Hematology. 6th Ed. McGraw-Hill Medical; New York: 2001. pp. 581–605. [Google Scholar]
- 45.Aprelev A., Liu Z., Ferrone F.A. The growth of sickle hemoglobin polymers. Biophys. J. 2011;101:885–891. doi: 10.1016/j.bpj.2011.05.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Park J.W., Oh A.G. Bending rigidity of yarns. Text. Res. J. 2006;76:478–485. [Google Scholar]
- 47.Li H., Lykotrafitis G. Two-component coarse-grained molecular-dynamics model for the human erythrocyte membrane. Biophys. J. 2012;102:75–84. doi: 10.1016/j.bpj.2011.11.4012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Li H., Lykotrafitis G. Erythrocyte membrane model with explicit description of the lipid bilayer and the spectrin network. Biophys. J. 2014;107:642–653. doi: 10.1016/j.bpj.2014.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Zhang Y., Huang C., Suresh S. Multiple stiffening effects of nanoscale knobs on human red blood cells infected with Plasmodium falciparum malaria parasite. Proc. Natl. Acad. Sci. USA. 2015;112:6068–6073. doi: 10.1073/pnas.1505584112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Peng Z., Li X., Suresh S. Lipid bilayer and cytoskeletal interactions in a red blood cell. Proc. Natl. Acad. Sci. USA. 2013;110:13356–13361. doi: 10.1073/pnas.1311827110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Li X., Peng Z., Karniadakis G.E. Probing red blood cell mechanics, rheology and dynamics with a two-component multi-scale model. Philos. Trans. A Math. Phys. Eng. Sci. 2014;372:20130389. doi: 10.1098/rsta.2013.0389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Liu S.C., Derick L.H., Palek J. Uncoupling of the spectrin-based skeleton from the lipid bilayer in sickled red cells. Science. 1991;252:574–576. doi: 10.1126/science.2020854. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.