On the reliability of peptide nonplanarity seen in ultra‐high resolution crystal structures

Abstract

Ultra‐high resolution protein crystal structures have been considered as relatively reliable sources for defining details of protein geometry, such as the extent to which the peptide unit deviates from planarity. Chellapa and Rose (Proteins 2015; 83:1687) recently called this into question, reporting that for a dozen representative protein structures determined at ∼1 Å resolution, the diffraction data could be equally well fit with models restrained to have highly planar peptides, i.e. having a standard deviation of the ω torsion angles of only ∼1° instead of the typically observed value of ∼6°. Here, we document both conceptual and practical shortcomings of that study and show that the more tightly restrained models are demonstrably incorrect and do not fit the diffraction data equally well. We emphasize the importance of inspecting electron density maps when investigating the agreement between a model and its experimental data. Overall, this report reinforces that modern standard refinement protocols have been well‐conceived and that ultra‐high resolution protein crystal structures, when evaluated carefully and used with an awareness of their levels of coordinate uncertainty, are powerful sources of information for providing reliable information about the details of protein geometry.

Introduction

Since the mid‐1990s, there has been a large increase in the number of protein structures solved at resolutions of near 1 Å and better, primarily due to the greater availability of intense synchrotron X‐ray sources and techniques for rapid‐cooling of protein crystals to cryogenic temperatures for data collection.1 At such resolutions the diffraction data are sufficiently extensive that the geometric restraints that define the expected bond lengths, angles, and planarity become less important and less influential,2, 3 and the coordinate uncertainties for well‐ordered parts of the protein drop down into the range of 0.01 to 0.05 Å.3, 4, 5 For these reasons, such ultra‐high resolution protein crystal structures have been considered reliable sources for gaining insight into features of protein geometry that differ from the standard expected molecular geometries. Examples include: the geometric distortions of ligands and protein groups in enzyme active sites;6, 7, 8, 9, 10 the systematic variation in peptide backbone bond angles as a function of the backbone conformation in commonly observed regions of ϕ,ψ‐space11 and in rarely observed high‐energy transition conformations;12 and a level of nonplanarity of the peptide unit in proteins much greater than expected based on data from lower resolution protein crystal structures that were strongly influenced by peptide planarity restraints.13

In the case of peptide nonplanarity, our group¹³ built on the work of others5, 14, 15 to show that in protein structures determined at 1 Å resolution and better, the ω torsion angles (defined by the Cα_i−1‐C_i−1‐N_i‐Cα_i atoms and equal to 180° for a perfectly planar trans peptide unit) are rather broadly distributed. The standard deviation was ∼6.3° for trans peptide bonds with about 12% and 0.5% of residues deviating more than 10°and 20°, respectively, from planarity. As not all parts of a crystal structure have the same level of reliability, we examined the electron density of every peptide with ω ≥ 20° from planar to assess which were reliable; then using the reliable examples, we showed that these highly nonplanar peptides are not just in active sites, but represent a mundane aspect of protein structure that simply reflects the “frustration”16, 17, 18 that occurs as proteins fold into their tertiary structures. We (see Fig. 3D of Berkholz et al.13) and others14, 19 made very clear that such levels of deviation from planarity are fully consistent with the estimate originally defined by Pauling that deviations of ∼10° from planarity would come at a cost of about 1 kcal/mol.20

Figure 3.

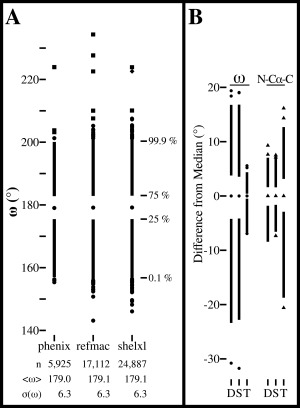
ω‐angle distributions from three refinement programs and distortion of the N‐Cα‐C angle caused by the tight ω restraints. (A) ω‐angle distributions for 40, 92, and 137 structures identified by CR²¹ as having been refined at ≤1 Å resolution by Phenix, Refmac and SHELX, respectively (lists provided in Supporting Information files). For each refinement package (identified by name), the number of refined residues, the mean and standard deviation of ω, and a Tufte boxplot27 are shown. In each boxplot, the central dot marks the median, the upper line extends from the 75th percentile to the 99.9th percentile, the lower line extends from the 25th to the 0.1st percentile and the most extreme 0.1% of observations at each end are shown as individual circles, squares or diamonds. For each distribution, observations were manually checked for the quality of the fit to their electron density starting with the furthest outlier and continuing until a reliably modeled example was found. Observations were categorized as incorrect (squares), unable to be assessed due to unavailable data (diamonds), or reliable (circles). (B). Tufte boxplots27 showing the distributions of the ω (circles) and N‐Cα‐C (triangles) angles relative to their median values for residues in the dozen test structures. The left plots show ω for the structures as deposited (D), and re‐refined using standard (S) or tight (T) ω‐restraints, and the right plots similarly show the N‐Cα‐C angles. Standard deviations for the ω distributions are: 6.5°, 6.5°, and 1.0°. For the N‐Cα‐C angle distributions the standard deviations are 2.5°, 2.3°, and 4.6°.

Recently, Chellapa and Rose (CR) challenged these conclusions, calling into question whether such deviations from planarity are “a necessary implication from the available data”21 and also incorrectly claiming that the reports of such deviations from planarity are “raising doubts about Pauling's consequential inference that distortions from planarity come at significant energetic cost.” To support their claims of such deviations not being reliably determined, they reported that re‐refinements of twelve ultra‐high resolution protein structures using tighter restraints on ω yielded alternative protein models in which the ω angles were much closer to 180°, “without consequent reduction in reported evaluation metrics (e.g., R‐values).”21 They also claimed that even for ultra‐high resolution structures different refinement packages led to “distinctly different ω‐angle signatures,” indicating that one cannot rely on ultra‐high resolution crystal structures to obtain unbiased and accurate geometric details.

Here, we report that there are multiple shortcomings of the study by CR and that their conclusions are not valid. It is certainly true that refinements as done by CR using much tighter ω restraints do yield structures that have lower deviations from planarity, but it is far from true that these alternative models provide equally good fits to the diffraction data. Two key shortcomings in the CR study were a failure to carry out proper control refinements, and, even more importantly, a primary reliance on global statistics to evaluate model quality rather than the inspection of difference electron density maps and 2Fo‐Fc maps to assess details of how well each model agrees with its data.

Refinement Protocols

In order to reinvestigate the effects of tightened ω restraints on model quality, we used the same 12 structures studied by CR (Table 1), and re‐refined them just as they described,21 with a specific seed used for all refinements to ensure consistency and repeatability. Briefly, starting from each PDB entry, an initial round of five cycles of refinement was done, using “phenix.refine” with the options “strategy = individual_sites,” “wc = 0,” and “main.random_seed = 2772306.” The resulting model was then used as the input for two subsequent parallel refinements: one used the same tight ω restraint that was applied by CR; the other was done to serve as a control refinement and used a standard ω restraint. These refinements were each run for five cycles using the following options: “strategy = individual_sites + individual_sites_real_space + individual_adp+occupancies,” “wxc_scale = 0.4,” “optimize_xyz_weight = True,” “optimize_adp_weight = True,” “optimize_mask = True,” “wc = 1,” and “main.random_seed = 2772306.” The “tight” refinements differed from the standard refinements only by setting “omega_esd_override_value = 0.5.” In the following sections, these two refinements will be called “standard” and “tight.” Coordinate and other files related to this paper but not available in the PDB are available at http://biochem.science.oregonstate.edu/content/structural-resources.

Table 1.

The application of Tight ω‐Restraints Significantly Increases Overall R‐Values over the 12 Test Cases

			Depositedb		R work			R free
PDB ID	Software	Resa	R work	R free	Std.c	Tightc	Δc	Std.c	Tightc	Δc
2CWS	SHELXL	1.00	10.8	13.8	10.9	11.7	0.8	12.8	13.8	1.0
2GUD	REFMAC	0.94	14.5	15.5	13.6	14.1	0.5	15.2	16.1	0.9
2OV0	SHELXL	0.75	12.8	13.9	13.1	13.7	0.6	14.1	14.7	0.6
2P5K	REFMAC	1.00	13.5	15.9	13.0	13.2	0.2	15.4	15.9	0.5
2PNE	REFMAC	0.98	14.1	17.0	13.5	14.5	1.0	16.4	17.5	1.1
2QSK	REFMAC	1.00	13.9	16.1	13.7	14.2	0.5	15.9	16.5	0.6
3D1P	REFMAC	0.98	12.3	13.4	12.2	12.7	0.5	13.5	14.1	0.6
3F7L	SHELXL	0.99	11.9	14.2	11.7	11.8	0.1	14.0	14.3	0.3
3QL9	PHENIX	0.93	12.8	13.6	11.9	11.9	0.0	12.8	13.1	0.3
4AQO	REFMAC	0.99	12.8	16.4	13.0	13.7	0.7	16.6	16.9	0.3
4JP6	REFMAC	1.00	15.8	18.4	16.5	16.6	0.1	18.9	19.1	0.2
4MTU	SHELXL	0.97	14.1	15.7	14.3	14.8	0.5	15.4	15.8	0.4
	Average	0.96					0.5			0.6
	σ	0.07					0.3			0.3
	P valued				3.0E‐04			3.8E‐05

^aResolution (in Å).

^b R _work and R _free values (in %) recalculated by Phenix for each model as deposited in the pdb (as was done by CR²¹).

^cReports R‐values (in %) for models from refinement using standard ω‐restraints (Std) or tight ω−restraints (tight), and the “tight – std” difference (Δ).

^dA paired, two‐tailed t‐test was used to obtain P values.

R‐values are consistently worse with the tight ω restraints

The R‐values of our parallel re‐refinements of each ultra‐high resolution structure are reported in Table 1, with the R‐values calculated by Phenix of the deposited models also provided for comparison. The models produced by the tight ω restraints had R _work values ranging from 0.0 to 1.0% higher and R _free values ranging from 0.2 to 1.1% higher (Table 1). The statistical significance of this consistent decrease in the overall agreement of the model to the data seen over the dozen structures was assessed using a paired two‐tailed t‐test. The P values of 0.00003 and 0.0000038 for the changes in R _work and R _free, respectively (Table 1), show that even just based on these overall R‐values, the standard ω restraint produces models that are significantly better than the tight ω restraint.

CR did not see such a consistent difference in the overall R‐values because they compared the R‐values of the structures refined using tight ω restraints to the R‐values calculated for the structures as they were deposited. The shortcoming of that comparison is that it is not properly controlled for all changes but the tightness of the ω restraint. For instance, for PDB entry 3QL9, the re‐refinement using Phenix with tight ω restraints lowered R _work and R _free by 0.9 and 0.5% respectively compared with the R‐values of the deposited coordinates (Table 1). While one might be tempted to conclude that tightening the ω restraints led to a better model, it is crucial to note that one has also changed the refinement program from an older version of Phenix (the coordinates were deposited in 2011) to a newer version. Indeed, as shown by our control refinement using the current version of Phenix with the standard ω restraint, R _work decreased by the same amount, and R _free decreased by 0.3% more (Table 1). Thus, the decrease in R‐values seen was due to something about the newer version of Phenix, rather than due to tightening the ω restraint.

Also, while changes in R‐values on the order of 0.5 to 1% may seem small, such changes are actually quite notable. In this regard, we note that crystallographers often expend much effort toward the end of a refinement trying to get structural details just right, and at this stage a drop in R _free in the 0.5 to 1.0% range is seen as a strong validation that the changes made were worthwhile. Also, when the R‐values are as low as the ones for the structures analyzed here, a drop from, say, 14% to 13% is a substantial fractional improvement, especially given that overall R‐values are global indicators that are not very sensitive to small changes in the positions of a small subset of atoms in a large protein structure.2

Electron density maps show that models from tight ω restraints are not correct

As a global statistic, R‐values are fairly insensitive to the incorrect positioning of a few atoms, and are unsuitable for evaluating whether any particular part of a model is correct. For this reason, the decisions about how to improve a structure during crystallographic refinement are made based on inspection of electron density maps, and as noted in a recent review about how to avoid pitfalls during structure determination: “a model must always be thoroughly scrutinized visually against electron density maps before accepting it as final.”22 At the ultra‐high resolutions of the structures studied here, well‐ordered parts of the protein have atoms fully resolved, making interpretation relatively easy.

For all 12 test cases, inspection of the electron density map reveals that in the tightly restrained structures some peptide units are very clearly incorrectly fit.¹

As a dramatic example we consider the peptide between residues 189 and 190 in PDB entry 2CWS, for which the standard refinement led to a peptide with ω ∼33° from planarity. For this peptide, the tight restraints produced a structure that placed atom 190‐N well outside of the strong 2Fo‐Fc density for that atom [Fig. 1(A)], and for which the difference map has a very large pair of positive and negative peaks further making clear that the 190‐N atom needs to be shifted in order to agree with the data [Fig. 1(B)]. In difference electron density maps for mostly well‐fit models, the root‐mean‐square electron density of the map (ρ _rms; also commonly called σ) is taken as an upper limit of its noise level (since many peaks are due to signal). In general, peaks that are smaller than ±3 × ρ _rms are considered not reliably distinguishable from noise and the larger the peak the more significantly it indicates something that is wrong with the model.2 This pair of ∼13 × ρ _rms peaks [Fig. 1(B)] is a glaring indicator of an atom in the wrong position. In contrast, the Fo‐Fc difference map calculated using the model refined by standard restraints does not show any such peaks at this location (data not shown). Among the other 11 test‐case structures refined with “tight” restraints, two have a largest difference peak associated with a peptide plane that also has a peak height of greater than 10 × ρ _rms. For the other nine structures, the strongest peptide‐plane‐associated difference peaks are between 5 and 10 ρ _rms, heights that are smaller but still very significant.

Figure 1.

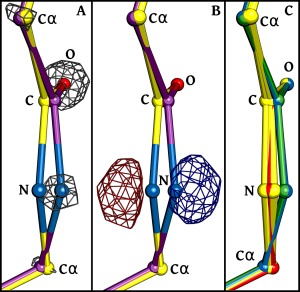
Evidence from electron density that tight ω‐restraints lead to incorrect models. Backbone atoms (labeled C, N, O, and Cα) of the peptide unit between residues 189 and 190 of PDB‐ID 2CWS are shown for multiple models, using atom coloring (oxygen—red; nitrogen—blue; carbon—as defined for each model). (A) The model resulting from refinement using tight ω‐restraints (yellow carbons; ω = 175.6°) is shown along with its 2Fo‐Fc electron density (grey mesh; contoured at 7.5 × ρ _rms), revealing that the N‐atom is clearly placed incorrectly. Additionally shown is the model resulting from refinement using standard ω‐restraints (purple carbons; ω = 147.2°) which does fit the electron density well. (B) The same structures are shown with the Fo‐Fc difference electron density also calculated using the tightly‐restrained model. Negative (red mesh) and positive (blue mesh) density are contoured at ±7.5 × ρ _rms. (C) Shown are the models from 10 pairs of independent refinements done either using tight ω‐restraints (yellow) or standard ω‐restraints (blue). The deposited model (green) and the model refined by CR²¹ (red) are also shown.

To test whether a single pair of refinements carried out for each structure can be taken as a reliable representative of the structures that could result from each refinement protocol, we carried out a set of independent refinements from different starting models and assessed how much spread occurred in the atom positions.11, 24, 25 For PDB entry 2CWS, we created ten different starting models using the “shake” algorithm of Phenix with the setting “modify.sites.shake = 0.2;” this randomly moves the model atoms so that the mean shift of all atoms is 0.2 Å. Then each of these 10 models was re‐refined using the “tight” and “standard” protocols and the same experimental data. The results were that the rms spread of backbone atoms within the standard and tight sets of 10 structures was just 0.011 Å and 0.017 Å, respectively. Visually, for the 189 to 190 peptide in structure 2CWS, the 10 structures created using each refinement protocol are very tightly clustered so that the atomic shift that occurred between protocols for the 190‐N atom is quite reliably defined [Fig. 1(C)]. Furthermore, the 2CWS coordinate set generated by CR using tight restraints is situated in the midst of the 10 tightly restrained structures we generated, and the original PDB entry is situated in the midst of the 10 “standard” structures [Fig. 1(C)]. We conclude from these observations that, at these resolutions, a single refinement provides representative coordinates with a precision of <0.02 Å for well‐ordered parts of the structure. Interestingly, this “shake” experiment also validates that using tight ω restraints does somewhat degrade the overall R‐values: for the 10 tight refinements, the mean R _work/R _free were 11.5 ± 0.5 (SD)/13.8 ± 0.5, and for the 10 standard refinements, the mean R _work/R _free were 11.2 ± 0.3/13.2 ± 0.4. Comparing R‐values from the 10 tight refinements with those from the 10 standard refinements using a paired t‐test yields P values of 0.1 and 0.02 for R _work and R _free, respectively. Given that all of the tightly restrained models are incorrect for the peptide before residue 190 [Fig. 1(C)], the lack of significance for the change in R _work using a P < 0.05 criterion does not indicate the models are equally valid, but underscores the unsuitability of this global statistic for assessing details of model quality.

Tightly restraining ω causes shifts in many atoms in excess of their positional uncertainty

For a more global analysis of how the uncertainty in atomic positions compares with the atomic shifts caused by the tight ω restraints, we calculated for each peptide a “peptide shift ratio” by dividing the shift in positions that occurred between the tight and standard refinements by an estimate of the positional uncertainty of the atoms (as defined in the Fig. 2 legend). This ratio increases fairly linearly as a function of how much ω deviated from 180° in the standard refinement (Fig. 2). When |ω − 180°| is ∼5°, nearly all peptides exhibit a shift that is greater than the estimated coordinate uncertainty, and for |ω − 180°| ∼10°, nearly all peptides have been shifted more than triple their experimental uncertainty. This shows that across the dozen test structures the nonplanarity of peptides having ω over ∼5° away from 180° can be considered to be defined reliably enough that the structure restrained to be planar is not an equally valid alternate interpretation, but in fact is a model that is not consistent with the diffraction data.

Figure 2.

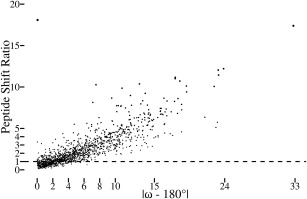
Significant atomic shifts are caused by tight ω restraints. Plotted for each peptide in the dozen test structures is the peptide shift ratio (defined below) as a function of the degree to which ω deviates from 180° in the standard refinement. For each atom in a structure refined using standard restraints, the standard uncertainty in the position of each atom4 was estimated using the Online_DPI webserver.26 Also, the shift for each atom between the standard vs. tight ω refined structures was calculated. Noting that the tight restraints often lead mostly to shifts in the central C, O, and N atoms of a peptide (e.g. Fig. 1), we defined a “peptide shift ratio” for each peptide as the rms of the shifts of the three central atoms in the peptide (i.e. O_i‐1, C_i‐1, and N_i) divided by the rms of the estimated standard uncertainties of the same three atoms. A value of 1 means that the rms shift in the atom positions is equal to the uncertainty in the positions of those atoms. The most nonplanar residue in the dataset is the 2CWS 189‐190 peptide shown in Figure 1. The one outlier in the plot is the 179 to 180 peptide from PDB entry 3QL9 with an ω angle in the standard refinement that is only 0.1° from planar but for which the backbone oxygen shifts ∼0.4 Å to yield a peptide shift ratio of ∼18. This can be rationalized in that this peptide oxygen has high anisotropy and that the method used to estimate the positional uncertainty does not take the anisotropy into account.26

At these resolutions, ω angle distributions do not depend on refinement software

An additional argument provided by CR,21 that the tight restraints led to valid alternative models, was that Phenix, Refmac, and SHELX led to “distinctly different” distributions of ω angles, with the same mean but “significantly different tails” (see Fig. 5 of that article). Using the same set of structures that they used, we repeated the analysis and found that in fact the ω‐distributions are remarkably similar, closely matching with regard to the median, the standard deviation, the 25th and 75th percentiles and even the 0.1st and 99.9th percentiles [Fig. 3(A)]. With regard to assessing the upper and lower limits of the extreme outliers, as was pointed out by Berkholz et al.,13 it is crucial to inspect the electron density maps to remove examples that are not reliable. Doing this leaves no outliers over 40° from planar in any of the sets [Fig. 3(A)], and leaves the Refmac and SHELX distributions having slightly more extreme outliers, which is reasonable as three to four times as many residues are included in those distributions. Also, that the detailed values of the extreme outliers differs for each distribution makes sense, because the sets contain different proteins. The remarkable similarity of these distributions is consistent with the expectation that at resolutions near 1 Å, the diffraction data are sufficiently extensive that differences in restraints used by different refinement packages should have little influence on the resulting structure.2, 11 Further support for this conclusion is that when a comparison is made of the ω distributions for the same set of structures refined by different programs, even the outliers match within a few degrees [compare plots D and S in the Fig. 3(B) left hand panel].

Tight ω restraints cause unreasonable secondary distortions

An interesting observation pointed out by CR but not further discussed was that the application of tight ω restraints during refinement also results in a wider spread of N‐Cα‐C angles. We have confirmed this observation [Fig. 3(B)], and find it easy to explain. As we have noted (see Fig. 2 legend), forcing nonplanar peptides to become planar tends to involve shifts of the peptide C, O and N atoms, and any movement of the backbone C and/or N atoms will change the N‐Cα‐C angle. As an example, for the 2CWS 189‐190 peptide (Fig. 1) ω changes from 147.2° to 175.6° between the standard and tight refinements, with the N‐Cα‐C angle of residue 189 changing minimally from 111.6° to 112.8°, but that of residue 190 changing from 105.7° to 92.1°. As we have made clear above, this “alternative” model does not agree with the diffraction data (e.g. Fig. 1), and such levels of distortion of an N‐Cα‐C angle are unprecedented even in ultra‐high resolution structures.

Synthesis

We hope that the above analyses lay to rest any concerns that may have been raised by CR,21 and reinforce what has been known for decades in the protein crystallographic community: that ultra‐high resolution structure determinations of proteins have unique value for defining accurate protein structures.3, 5 We also hope that we have made clear the limited value of global metrics, and the importance of inspecting electron density maps to assess the reliability of any given feature in a crystal structure. In this example, we have shown that, in particular, peptide nonplanarity in ultra‐high resolution protein crystal structures is unequivocally supported by experimental evidence, and that alternative models in which peptide units are forced to be highly planar are clearly not compatible with the data. Using highly increased ω restraints during refinements leads to notably worse R‐values, shifts in the positions of atoms that are well beyond the experimental uncertainty, a worsening of other aspects of protein geometry, and most importantly, clear regions of disagreement between the model and the electron density maps.

One additional point we would like to clarify relates to the broad claim of CR²¹ that “a refined protein crystal structure is essentially an under‐determined model.” They supported this point by quoting the abstract of a paper by DePristo et al.28 who wrote that “disregarding structural heterogeneity introduces degeneracy into the structure determination process, as many single, isotropic models exist that explain the diffraction data equally well. The large differences among these models imply that the accuracy of crystallographic structures has been widely overestimated. Further, it suggests that analyses that depend on small differences in the relative positions of atoms may be flawed.” What apparently was not recognized by CR is that in this statement the authors were only referring to low and medium resolution structures, where “heterogeneity is difficult to identify and model, and are therefore approximated by a single, average conformation with isotropic variance.”28

In contrast, for structures determined at near 1 Å resolution heterogeneity is relatively easy to identify and model, and anisotropic motions of atoms are also accounted for. Indeed, DePristo et al.28 explicitly point this out in their introduction: “Modeling anisotropic motion and structural heterogeneity has been limited to proteins that diffract to atomic resolution, due to the necessity for a high parameter‐to‐observation ratio.” So the comment that “a refined protein crystal structure is essentially an under‐determined model”, is only accurate for structures solved at medium to low resolution, and explains why the more planar ω angles seen in those structures cannot be taken as reliable.13, 14 CR's comment does not apply to the structures solved at resolutions near 1 Å and better, as these are sufficiently over‐determined that they are able to provide insights into the true details of protein geometry.

Finally, we want to repeat in closing, that the levels of deviation from planarity seen in the ultra‐high resolution protein structures and in small molecule peptides are not at all in conflict with Pauling's ideas about the planarity of the peptide bond, but are strikingly consistent with them.19 We fully recognize that for protein structure prediction, it has been and still can be very helpful to assume that peptide planarity is absolute, but this must be recognized as a simplification that in itself is not consistent with Pauling's thinking about the peptide unit. That accounting accurately for such geometric details is of practical value was recently provided by a study showing that for protein prediction with Rosetta can be enhanced by allowing ω torsion angles to deviate from planarity at the levels seen in ultra‐high resolution structures.29

Supporting information

Supporting Information