Modeling confounding by half-sibling regression

Abstract

We describe a method for removing the effect of confounders to reconstruct a latent quantity of interest. The method, referred to as “half-sibling regression,” is inspired by recent work in causal inference using additive noise models. We provide a theoretical justification, discussing both independent and identically distributed as well as time series data, respectively, and illustrate the potential of the method in a challenging astronomy application.

We assay a method for removing the effect of confounding noise, based on a hypothetical underlying causal structure. The method does not infer causal structures; rather, it is influenced by a recent thrust to try to understand how causal structures facilitate machine learning tasks (1).

Causal graphical models as pioneered by (2, 3) are joint probability distributions over a set of variables $X_1,\dots ,{\mathit{X}}_{\mathit{n}}$, along with directed graphs (usually, acyclicity is assumed) with vertices $X_i$, and arrows indicating direct causal influences. By the causal Markov assumption, each vertex $X_i$ is independent of its nondescendants, given its parents.

There is an alternative view of causal models, which does not start from a joint distribution. Instead, it assumes a set of jointly independent noise variables, one for each vertex, and a “structural equation” for each variable that describes how the latter is computed by evaluating a deterministic function of its noise variable and its parents (2, 4, 5). This view, referred to as a functional causal model (or nonlinear structural equation model), leads to the same class of joint distributions over all variables (2, 6), and we may thus choose either representation.

The functional point of view is useful in that it often makes it easier to come up with assumptions on the causal mechanisms that are at work, i.e., on the functions associated with the variables. For instance, it was recently shown (7) that assuming nonlinear functions with additive noise renders the two-variable case identifiable (i.e., a case where conditional independence tests do not provide any information, and it was thus previously believed that it is impossible to infer the structure of the graph based on observational data).

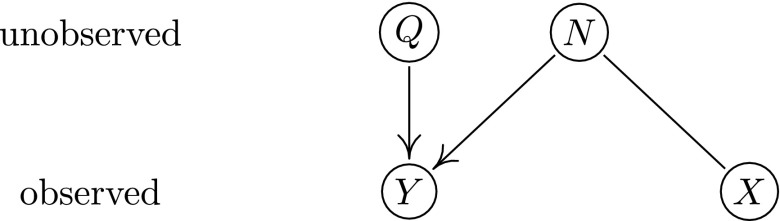
In this work we start from the functional point of view and assume the underlying causal graph shown in Fig. 1. In the present paper, $N,Q,X,Y$ are random variables (RVs) defined on the same underlying probability space. We do not require the ranges of the RVs to be $\mathrm{ℝ}$, and, in particular, they may be vectorial; we use $n,q,x,y$ as placeholders for the values these variables can take. All equalities regarding RVs should be interpreted to hold with probability one. We further (implicitly) assume the existence of conditional expectations.

Fig. 1.

We are interested in reconstructing the quantity Q based on the observables X and Y affected by noise N, using the knowledge that $\left(N,X\right)\mathrm{╨}Q$. Note that the involved quantities need not be scalars, which makes the model more general than it seems at first glance. For instance, we can think of N as a multidimensional vector, some components of which affect only X, some only Y, and some both X and Y.

Note that, although the causal motivation was helpful for our work, one can also view Fig. 1 as a directed acyclic graph (DAG) without causal interpretation, i.e., as a directed graphical model. We need Q and X (and, in some cases, also N) to be independent (denoted by $Q\mathrm{╨}X$), which follows from the given structure no matter whether one views this as a causal graph or as a graphical model.

In the section Half-Sibling Regression, we present the method. Following this, we describe the application and provide experimental results, and conclusions. Note that the present work extends a conference presentation (8). Proofs that are contained in ref. 8 have been relegated to Supporting Information.

Half-Sibling Regression

Suppose we are interested in the quantity Q, but, unfortunately, we cannot observe it directly. Instead, we observe Y, which we think of as a degraded version of Q that is affected by noise N. Clearly, without knowledge of N, there is no way to recover Q. However, we assume that N also affects another observable quantity (or a collection of quantities) X. By the graph structure, conditional on Y, the variables Q and X are dependent (in the generic case); thus X contains information about Q once Y is observed (although $X\mathrm{╨}Q$). This situation is quite common if X and Y are measurements performed with the same apparatus, introducing the noise N. In the physical sciences, this is often referred to as “systematics,” to convey the intuition that these errors are not simply due to random fluctuations but are caused by systematic influences of the measuring device. In our application below, both types of errors occur, but we will not try to tease them apart. Our method addresses errors that affect both X and Y, for instance by acting on N, no matter whether we call them random or systematic.

We need to point out a fundamental limitation at the beginning. Even from infinite data, only partial information about Q is available, and certain degrees of freedom remain. In particular, given a reconstructed Q, we can always construct another one by applying an invertible transformation to it, and incorporating its inverse into the function computing Y from Q and N. This includes the possibility of adding an offset, which we will see below.

The intuition behind our approach is as follows. Because $X\mathrm{╨}Q$, X cannot predict Q and thus Q’s influence on Y. It may contain information, however, about the influence of N on Y, because X is also influenced by N. Now suppose we try to predict Y from X. As argued above, whatever comes from Q cannot be predicted; hence only the component coming from N will be picked up. Trying to predict Y from X is thus a vehicle to selectively capture N’s influence on Y, with the goal of subsequently removing it, to obtain an idealized estimate of Q referred to as $\widehat{Q}$.

Definition 1.

$$\widehat{Q}≔Y-E\left[Y|X\right]$$ [1]

We first show that $\widehat{Q}$ reconstructs Q (up to its expectation $E\left[Q\right]$) at least as well as $Y-E\left[Y\right]$ does.

Proposition 1. For any RVs $Q,X,Y$ that satisfy $Q\mathrm{╨}X$, we have

$$E\left[{\left(Q-E\left[Q\right]-\left(Y-E\left[Y\right]\right)\right)}^2\right]\ge E\left[{\left(Q-E\left[Q\right]-\widehat{Q}\right)}^2\right].$$

The above also holds true if we subject Y to some transformation before substituting it into [1] and Proposition 1. Note that it is conceivable that our procedure might benefit from such a transformation; however, finding it is not a topic of the present paper. See also the discussion on the function g following [2].

Proof. We have

$$\begin{array}{l}E\left[{\left(Q-E\left[Q\right]-\left(Y-E\left[Y\right]\right)\right)}^2\right]\\ =E\left[{\left(Q-Y-E\left[Q\right]+E\left[Y\right]\right)}^2\right]\\ \ge E\left[{\left(Q-Y-E\left[Q-Y|X\right]\right)}^2\right]\\ =E\left[{\left(Q-E\left[Q\right]-\widehat{Q}\right)}^2\right].\end{array}$$

Note that the two terms related by the inequality in Proposition 1 differ exactly by the amount $\text{Var}\left[E\left[Q-Y|X\right]\right]$. This is due to Lemma 1 (Supporting Information) and the law of total variance $\text{Var}\left[Q-Y\right]=\text{Var}\left[E\left[Q-Y|X\right]\right]+E\left[\text{Var}\left[Q-Y|X\right]\right]$.

Our method is surprisingly simple, and although we have not seen it in the same form elsewhere (including standard works on error modeling, e.g., ref. 9), we do not want to claim originality for it. Related tricks are occasionally applied in practice, often using factor analysis to account for confounding effects (10–15). However, those methods usually aim at removing spurious associations between at least two variables (which could erroneously be attributed to a nonexisting causal influence of one variable on another one), whereas our method aims at reconstructing a single variable of interest. Common to these methods and ours is the idea that removal of the disturbing influence is enabled by the fact that it perturbs several or even a large number of variables at the same time, and by strong assumptions about how the disturbance acts (such as linearity or parametric models). Note that our variable X is referred to as “negative controls” in ref. 15.

We next propose an assumption that allows for a practical method to reconstruct Q up to an additive offset. The assumption allows a theoretical analysis that provides insight into why and when our method works.

Additive Systematic Error.

Inspired by recent work in causal inference, we use nonlinear additive noise models (7). Specifically, we assume that there exists a function f such that

$$Y=Q+f\left(N\right).$$ [2]

We do not consider the more general form $Y=g\left(Q\right)+f\left(N\right)$ because, without additional information, g would not be identifiable. Note, moreover, that, although for ref. 7, the input of f is observed and we want to decide if it is a cause of Y, in the present setting, the input of f is unobserved (16) and the goal is to recover Q, which, for ref. 7, played the role of the noise.

Complete Information.

For an additive model [2], our intuition can be formalized: In this case, we can predict the additive component in Y coming from N, remove the confounding effect of N, and thus reconstruct Q (up to an offset)—which is exactly what we want.

Proposition 2. Suppose $N,X$ are RVs, and f is a measurable function. If there exists a function ψ such that

$$f\left(N\right)=\psi \left(X\right),$$ [3]

i.e., $f\left(N\right)$ can in principle be predicted from X perfectly, then we have

$$f\left(N\right)=E\left[f\left(N\right)|X\right].$$ [4]

If, moreover, the additive model assumption [2] holds, with RVs $Q,Y$ and $Q\mathrm{╨}X$, then

$$\widehat{Q}=Q-E\left[Q\right].$$ [5]

In our main application below, N will be systematic errors from an astronomical spacecraft and telescope, Y will be a star under analysis, and X will be a large set of other stars. In this case, the assumption that $f\left(N\right)=\mathit{\psi }\left(X\right)$ has a concrete interpretation: It means that the device can be self-calibrated based on measured science data only (17) (as opposed to requiring separate calibration data).

Proposition 2 provides us with a principled recommendation on how to remove the effect of the noise and reconstruct the unobserved Q up to its expectation $E\left[Q\right]$: We need to subtract the conditional expectation (i.e., the regression) $E\left[Y|X\right]$ from the observed Y (Definition 1). The regression $E\left[Y|X\right]$ can be estimated from observations $\left(x_i,y_i\right)$ using (linear or nonlinear) off-the-shelf methods. We refer to this procedure as “half-sibling regression” to reflect the fact that we are trying to explain aspects of the child Y by regression on its half-sibling(s) X to reconstruct properties of its unobserved parent Q.

Note that $m\left(x\right)≔E\left[f\left(N\right)|X=x\right]$ is a function of x, and $E\left[f\left(N\right)|X\right]$ is the RV $m\left(X\right)$. Correspondingly, [4] is an equality of RVs. By assumption, all RVs live on the same underlying probability space. If we perform the associated random experiment, we obtain values for X and N, and [4] tells us that, if we substitute them into m and f, respectively, we get the same value with probability 1. Eq. 5 is also an equality of RVs, and the above procedure therefore not only reconstructs some properties of the unobservable RV Q—it reconstructs, up to the mean $E\left[Q\right]$, and with probability 1, the RV itself.

In practice, of course, the accuracy will depend on how well the assumptions of Proposition 2 hold. If the following conditions are met, we may expect that the procedure should work well:

• i)X should be (almost) independent of Q—otherwise, our method could possibly remove parts of Q itself and thus throw out the baby with the bath water. A sufficient condition for this to be the case is that N be (almost) independent of Q, which often makes sense in practice, e.g., if N is introduced by a measuring device in a way independent of the underlying object being measured. Clearly, we can only hope to remove noise that is independent of the signal; otherwise, it would be unclear what is noise and what is signal. A sufficient condition for $N\mathrm{╨}Q$, finally, is that the causal DAG in Fig. 1 correctly describes the underlying causal structure.

Note, however, that Proposition 2, and thus our method, also applies if NQ, as long as $X\mathrm{╨}Q$ (see Prediction Based on Noneffects).

• ii)The observable X is chosen such that Y can be predicted as well as possible from it; i.e., X contains enough information about $f\left(N\right)$, and, ideally, N acts on both X and Y in similar ways such that a “simple” function class suffices for solving the regression problem in practice.

This may sound like a rather strong requirement, but we will see that, in our astronomy application, it is not unrealistic: X will be a large vector of pixels of other stars, and we will use them to predict a pixel Y of a star of interest. In this kind of problem, the main variability of Y will often be due to the systematic effects due to the instrument N also affecting other stars, and thus a large set of other stars will indeed allow a good prediction of the measured Y.

Note that it is not required that the underlying structural equation model be linear—N can act on X and Y in nonlinear ways, as an additive term $f\left(N\right)$.

In practice, we never observe N directly, and thus it is hard to tell whether the assumption of perfect predictability of $f\left(N\right)$ from X holds true. We now relax this assumption.

Incomplete Information.

We now provide a stronger result for $\widehat{Q}$ [1], including the case where $f\left(N\right)$ does not contain all information about X.

Proposition 3. Let f be measurable, $N,Q,X,Y$ be RVs with $Q\mathrm{╨}X$, and $Y=Q+f\left(N\right)$. The expected squared deviation between $\widehat{Q}$ and $Q-E\left[Q\right]$ satisfies

$$E\left[{\left(\widehat{Q}-\left(Q-E\left[Q\right]\right)\right)}^2\right]=E\left[\text{Var}\left[f\left(N\right)|X\right]\right].$$ [6]

Note that Proposition 2 is a special case of Proposition 3: if there exists a function ψ such that $\psi \left(X\right)=f\left(N\right)$, then the right-hand side of [6] vanishes. Proposition 3 drops this assumption, which is more realistic: Consider the case $X=g\left(N\right)+R$, where R is another RV. In this case, we cannot expect to reconstruct the variable $f\left(N\right)$ from X exactly.

There are, however, two settings where we would still expect good approximate recovery of Q: (i) If the standard deviation (SD) of R goes to zero, the signal of N in X becomes strong and we can approximately estimate $f\left(N\right)$ from X; see Proposition 4. (ii) Alternatively, we observe many different effects of N. In the astronomy application below, Q and R are stars, from which we get noisy observations Y and X. Proposition 5 below shows that observing many different $X_i$ helps reconstructing Q, even if all $X_i$ depend on N through different functions $g_i$ and their underlying (independent) signals $R_i$ do not follow the same distribution. The intuition is that, with increasing number of variables, the independent $R_i$ “average” out, and thus it becomes easier to reconstruct the effect of N.

Proposition 4. Assume that $Y=Q+f\left(N\right)$ and let

$$X^s≔g\left(N\right)+s\cdot R,$$

where R, N, and Q are jointly independent, $s\in \mathrm{ℝ}$, $f\in C_b^0\left(\mathrm{ℝ}\right)$, g is invertible, and $g,g^{-1}\in C^0\left(\mathrm{ℝ}\right)$. Then

$${\widehat{Q}}^s\stackrel{L^2}{\to }Q-E\left[Q\right]\hspace{0.17em}\mathit{as}\hspace{0.17em}s\to 0,$$

where ${\widehat{Q}}^s≔Y-E\left[Y|X^s\right]$.

Proof. We have for $s\to 0$ that

$$\begin{array}{ccc}& s\cdot R& \stackrel{P}{\to }0\\ \Rightarrow & g\left(N\right)+s\cdot R-g\left(N\right)& \stackrel{P}{\to }0\\ \stackrel{\ast }{\Rightarrow }& g^{-1}\left(g\left(N\right)+s\cdot R\right)-N& \stackrel{P}{\to }0\\ \stackrel{\ast }{\Rightarrow }& f\left(g^{-1}\left(g\left(N\right)+s\cdot R\right)\right)-f\left(N\right)& \stackrel{P}{\to }0\\ \Rightarrow & {\psi }_s\left(X^s\right)-f\left(N\right)& \stackrel{P}{\to }0\end{array}$$

for some ${\psi }_s$ that is bounded in s (the implications $\mathrm{\ast }$ follow from the continuous mapping theorem). (The notation $\stackrel{P}{\to }$ denotes convergence in probability with respect to the measure P of the underlying probability space.) This implies

$$E\left[f\left(N\right)|X^s\right]-f\left(N\right)\stackrel{L^2}{\to }0$$

because

$$E\left[{\left(f\left(N\right)-E\left[f\left(N\right)|X^s\right]\right)}^2\right]\le E\left[{\left(f\left(N\right)-{\psi }_s\left(X^s\right)\right)}^2\right]\stackrel{}{\to }0$$

($L^2$ convergence follows because f is bounded). However, then

$$\begin{array}{c}Q-E\left[Q\right]-{\widehat{Q}}^s=-f\left(N\right)-E\left[Q\right]+E\left[f\left(N\right)+Q|X^s\right]\\ =E\left[f\left(N\right)|X^s\right]-f\left(N\right)\stackrel{L^2}{\to }0.\end{array}$$

Proposition 5. Assume that $Y=Q+f\left(N\right)$ and that ${\mathbf{X}}_d≔\left(X_1,\dots ,X_d\right)$ satisfies

$$\begin{array}{cc}{X}_i≔g_i\left(N\right)+R_i,& i=1,\dots ,d,\end{array}$$

where all $R_i$, N, and Q are jointly independent, $f\in C_b^0\left(\mathrm{ℝ}\right)$, $g_i\in C^0\left(\mathrm{ℝ}\right)$ for all i, ${\displaystyle {\sum }_{i=1}^{\infty }\frac{1}{i^2}\text{var}\left(R_i\right)<\mathrm{\infty }}$, and

$${\tilde{g}}_d≔\frac{1}{d}{\displaystyle \sum _{j=1}^d{g}_j}$$

is invertible with ${\left({\tilde{g}}_d^{-1}\right)}_d$ uniformly equicontinuous. Then

$${\widehat{Q}}_d\stackrel{L^2}{\to }Q-E\left[Q\right]\hspace{0.17em}\mathit{as}\hspace{0.17em}d\to \infty ,$$

where we define ${\widehat{Q}}_d≔Y-E\left[Y|{\mathbf{X}}_d\right]$.

Prediction Based on Noneffects of the Noise Variable.

Although Fig. 1 shows the causal structure motivating our work, our analysis does not require a directed arrow from N to X. For the method to work in the sense of Propositions 2 and 3, we need additivity [2], $X\ma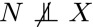thrm{╨}Q$, and , to ensure that X contains information about N. We can represent this by an undirected connection between the two (Fig. 2), and note that such a dependence may arise from an arrow directed in either direction, and/or another confounder that influences both N and X. (Imagine that N is noise induced by a CCD, and X is a nearby thermometer. Both X and N will be affected by the unobserved true temperature T on the CCD and any amplifiers. The measured temperature does not have a causal effect on N, but nevertheless, it contains information about N that the regression can use.)

Fig. 2.

Causal structure from Fig. 1 when relaxing the assumption that X is an effect of N.

Knowledge about a possibly complex causal structure can help in choosing the right regression inputs X. Recall that the Markov Blanket of a node contains its parents, its children, and its children’s other parents (2). Ideally, we would want X to comprise the largest possible subset of N’s Markov Blanket containing information about N, subject to the constraint that $X\mathrm{╨}Q$ (for an example, see Fig. S1).

Fig. S1.

Example for Prediction based on Noneffects of the Noise Variable. The condition that the regression input X should satisfy $X\mathrm{╨}Q$ rules out its component $X_1$. As a consequence, although $X_3$ is contained in N’s Markov blanket, it is no longer useful as a regression input when predicting Y, because it only contains information about Y conditional on $X_1$. In the end, we are left with only $X_2$ for prediction of Y.

Half-Sibling Regression for Time Series

Above, we have modeled the data as an independent and identically distributed (i.i.d.) sample. In practice, however, the data may be drawn from random processes that inherit a time structure. We now generalize the i.i.d. method to the time series setting.

Model Assumptions.

Suppose we are given two time series, ${\left(X_t\right)}_t$, ${\left(Y_t\right)}_t$, with an ordered discrete index set, say $\mathrm{\mathbb{Z}}$, that are generated according to the structural equation

$$\begin{array}{cc}\forall t\mathrm{\in \mathbb{Z}}& \{\begin{array}{l}{Y}_t=f\left(N_t\right)+Q_t\\ X_t=g\left(N_t\right)+R_t\end{array}\end{array}$$ [7]

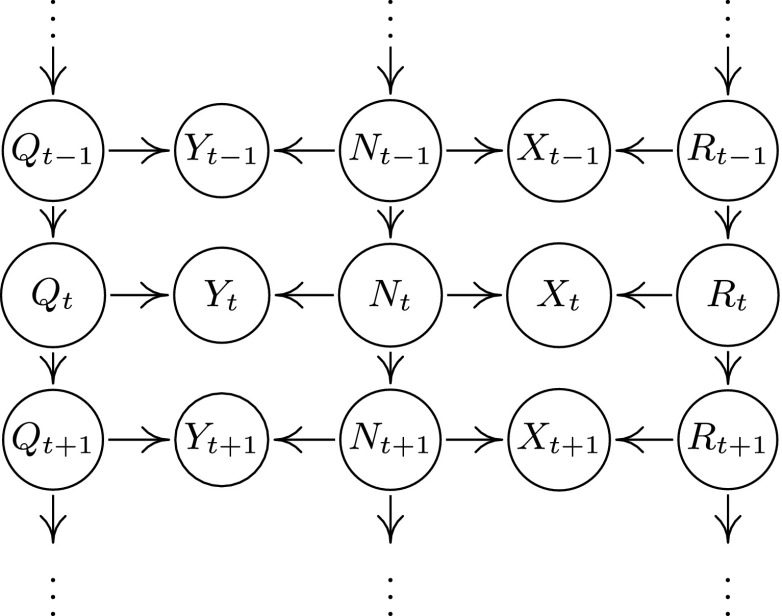
with three unobserved time series ${\left(Q_t\right)}_t$, ${\left(N_t\right)}_t$, and ${\left(R_t\right)}_t$ that are independent of each other. Fig. 3 shows an example with order one processes. As before, our goal is to reconstruct the hidden time series ${\left(Q_t\right)}_t$.

Fig. 3.

Special case of the time series model. ${\left(Q_t\right)}_t$, ${\left(N_t\right)}_t$, and ${\left(R_t\right)}_t$ are (jointly) independent of each other, but each one may be autocorrelated. Regressing $Y_t$ on ${\left(X_t\right)}_t$ unblocks only paths avoiding $Q_t$: the estimate ${\widehat{Y}}_t≔Y_t-E\left[Y_t|{\left(X_t\right)}_t\right]$ of $Y_t$ does not regress out any variability caused by $Q_t$ and is more accurate than the i.i.d. estimate $Y_t-E\left[Y_t|X_t\right]$. Regressing $Y_t$ on $Y_{t-1}$ unblocks two paths: one avoiding $Q_t$, and the other not. The first may enhance the estimate of $Q_t$; the second, however, may worsen it. In general, the contribution of both parts cannot be separated. However, they can for particular time series ${\left(Q_t\right)}_t$.

Exploiting the Time Dependencies.

Contrary to the i.i.d. case, $Q_t$, $N_t$, and $R_t$ are now influenced by their own past $Q_{t-s}$, $N_{t-s}$, and $R_{t\mathrm{-}s}$, respectively, whereas $Y_t$ and $X_t$ are only influenced by $Q_t$ and $N_t$, respectively, as in the i.i.d. case. This may induce a time dependency in both ${\left(X_t\right)}_t$ and ${\left(Y_t\right)}_t$. We will now focus on how to exploit them to improve the reconstruction of ${\left(Q_t\right)}_t$.

In the i.i.d. case, we estimated $Q_t$ with ${\widehat{Q}}_t^S≔Y_t-E\left[Y_t|X_t\right]$. In principle, we can now use the time dependency of ${\left(X_t\right)}_t$ by regressing $Y_t$ on the whole future and past of ${\left(X_t\right)}_t$. This leads to the possibly improved estimator ${\widehat{Q}}_t^T≔Y_t-E\left[Y_t|{\left(X_t\right)}_{t\in \mathrm{\mathbb{Z}}}\right]$. In some situations, it may also be useful to exploit the time dependency of ${\left(Y_t\right)}_t$. However, contrary to the regression of $Y_t$ on $X_t$ [or ${\left(X_t\right)}_t$], blindly regressing $Y_t$ onto ${\left(Y_s\right)}_{s\ne t}$ may regress out parts of $Q_t$ and deteriorate the results. To see this, consider Fig. 3: Although the covariates ${\left(X_t\right)}_t$ do not contain any information about $Q_t$, the covariate $Y_{t-1}$, for example, does; see d separation (3). Therefore, regressing $Y_t$ on other values $Y_s$, $s\ne t$, can, in general, remove information of $Q_t$ from $Y_t$. This may change, however, if we make additional assumptions about $Q_t$. This is the purpose of Signals with Compact Support.

Signals with Compact Support.

We now assume that $Q_t$ can be expressed as $Q_t=h\left(S_t,F_t\right)$; that is, we replace the first equation in [7] with

$$Y_t=f\left(N_t\right)+h\left(S_t,F_t\right),$$ [8]

where $N_{t_1}$, $S_{t_2}$, and $F_{t_3}$ are jointly independent for all choices of $t_1,t_2$, and $t_3$, and h is a fixed function. Denoting by ${\mathrm{ℐ}}_{\text{transit}}≔\left[t_0-\mathrm{\Delta }/2;t_0+\mathrm{\Delta }/2\right]$ a window of width $\mathrm{\Delta }$ around $t_0$, we further assume that

$$F_t=c\hspace{0.17em}\text{for}\hspace{0.17em}t\notin {\mathrm{ℐ}}_{\text{transit}},$$ [9]

where c is a constant. In the example of exoplanet search described below, we use $h\left(s,f\right)=s\cdot f$, and $c=1$. ${\left(S_t\right)}_t$ corresponds to the stellar brightness (which is variable), and the signal of interest, ${\left(F_t\right)}_t$, is the multiplicative change in the observed brightness due to a partial occlusion of the observed star by a planet passing through the line of sight between star and telescope. Such transits are centered around some $t_0$ and have a length $\mathrm{\Delta }$, which we think of as an RV. The RVs $F_t$ for $t\in {\mathrm{ℐ}}_{\text{transit}}$ describe the shape of the transit. Eq. 9, however, also covers additive effects, using $h\left(s,f\right)=s+f$ and $c=0$. We assume that $t_0$ is unknown and that $\mathrm{\Delta }$ can be bounded by some α: $\mathrm{\mathbb{P}}\left(\mathrm{\Delta }<\alpha \right)=1$. The goal is to detect the transits, i.e., the regions where $F_t\ne c$. We now describe the method that we will later apply to the exoplanet data set.

Method.

In the i.i.d. case, we proposed to predict each $Y_t$ from the other stars $X_t$ and then use the residuals as a reconstruction for $Q_t$ (up to its mean). If we are really interested in the detection of transits ${\left(F_t\right)}_t$ rather than in reconstructing $Q_t=h\left(S_t,F_t\right)$, we can attempt to filter out the autoregressive (AR) component of ${\left(Y_t\right)}_t$ that comes from ${\left(f\left(N_t\right)\right)}_t$ and ${\left(S_t\right)}_t$, as long as this does not affect $F_t$. Consider $\alpha ,\delta \in {\mathrm{\mathbb{N}}}_{>0}$ with $\mathrm{\mathbb{P}}\left(\mathrm{\Delta }<\mathit{\alpha }\right)=1$, as above. Here, δ specifies the size of windows in past and future that we will use as regression inputs. Define $\mathcal{W}≔\left[-\alpha -\delta ,-\alpha \right]\mathrm{\cup }\left[\alpha ,\alpha +\delta \right]$. We further write $Y_{t+\mathcal{W}}≔{\left(Y_{t+s}\right)}_{s\in \mathcal{W}}$. The method consists of the following steps.

Half-Sibling Regression for Time Series

• i)Choose a test set containing those points where we want to predict, with indices ${\mathrm{ℐ}}_{\text{test}}$. Construct a training set, with indices ${\mathrm{ℐ}}_{\text{train}}$, containing all those points that are separated by more than $\alpha +\delta$ from the test set.
• ii)Regress $Y_t$ on $Y_{t+\mathcal{W}}$ and $X_t$ using all $t\in {\mathrm{ℐ}}_{\text{train}}$ for training and hyperparameter tuning. Use the resulting model for predicting ${\widehat{Y}}_t$ from $Y_{t+\mathcal{W}}$ and $X_t$ for all $t\in {\mathrm{ℐ}}_{\text{test}}$.

In principle, ${\mathrm{ℐ}}_{\text{test}}$ may be a singleton, in which case we build a model for a single test point. If we have to do this for every possible choice of that point, computational requirements become rather large. In practice, we thus use a test set that contains roughly a third of the data, which means we need to carry out the above procedure three times to build models for all possible test points.

Because the signal of interest $F_t$ differs from c only on a compact support, we are able to prove that the method does not destroy any relevant information about the transits in $F_t$, as long as we carefully choose the parameters α and δ.

Proposition 6. Assume that, for any $t\in \mathrm{\mathbb{Z}}$, we have $Y_t=f\left(N_t\right)+h\left(S_t,F_t\right)$ with $F_t$ as in [9]. Assume further that ${\widehat{Y}}_t≔\varphi \left(Y_{t+\mathcal{W}},X_t\right)$ with $\varphi \left(y,x\right)=E\left[Y_t|Y_{t+\mathcal{W}}=y,X_t=x\right]$ constructed by half-sibling regression for time series as described above; here, ϕ is well defined if we assume that the conditional distribution of $Y_t$ given $f\left(N_{t+\mathcal{W}}\right)+S_{t+\mathcal{W}}$ and $X_t$ does not depend on t. Then

$${\widehat{Y}}_t\mathrm{╨}{F}_t\hspace{1em}for\hspace{0.17em}all\hspace{0.17em}t\in {\mathrm{ℐ}}_{\text{transit}}.$$ [10]

As a consequence, we can use ${\widehat{Y}}_t$ to correct the observed $Y_t$, and we never remove any information about the transit $F_t$. The proof is immediate because, for a fixed $t_{test}\in {\mathrm{ℐ}}_{\text{transit}}$, we have that $Y_t$, $Y_{t+\mathcal{W}}$, and $X_t$ for $t\in {\mathrm{ℐ}}_{\text{train}}$, as well as $Y_{t_{test}+\mathcal{W}}$ and $X_{t_{test}}$, are independent of $\left(\mathrm{\Delta },{\left(F_t\right)}_{t\in {\mathrm{ℐ}}_{\text{transit}}}\right)$.

In general, ${\widehat{Y}}_t$ will not be independent of $F_t$ for $t\notin {\mathrm{ℐ}}_{\text{transit}}$; in other words, correction of $Y_t$ using ${\widehat{Y}}_t$ (e.g., by subtraction) may distort the signal outside of the transit time window ${\mathrm{ℐ}}_{\text{transit}}$. This is visualized in Fig. 4. In practice, the training set usually contains more than one transit. In this case, we cannot prove [10]. However, we would only expect a real distortion of the transit signal if the transits are abundant and thus form a significant fraction of the training set; again, see Fig. 4.

Fig. 4.

Simulated transit reconstruction using half-sibling regression for time series, but without regressing on $X_t$. From bottom to top: ${\left(F_t\right)}_t$, ${\left(Y_t\right)}_t$, ${\left({\widehat{Y}}_t\right)}_t$ with $Y_t=S_t{F}_t$, and ${\widehat{Q}}_t≔{\left(Y_t-{\widehat{Y}}_t\right)}_t$. The estimate ${\widehat{Y}}_t$ was trained using ridge regression with regularization parameter $\mathit{\lambda }=0.1$. Transits were also present in the training set. Note that the transit itself is preserved. However, some artifacts (here: bumps) are introduced to the right and left of the transit.

Applications

Synthetic I.I.D. Data.

We first analyze two simulated data sets.

Increasing relative strength of N in a single X.

We consider 20 instances (each time we sample 200 i.i.d. data points) of the model $Y=f\left(N\right)+Q$ and $X=g\left(N\right)+R$, where f and g are randomly chosen sigmoid functions and the variables N, Q, and R are normally distributed. The SD for R is chosen uniformly between 0.05 and 1, and the SD for N is between 0.5 and 1. Because Q can be recovered only up to a shift in the mean, we set its sample mean to zero. The distribution for R, however, has a mean that is chosen uniformly between $-1$ and 1, and its SD is chosen from the vector $\left(\mathrm{1,0.5},0.25,0.125,0.0625,0.03125,0\right)$. Proposition 4 shows that, with decreasing SD of R, we can recover the signal Q. SD zero corresponds to the case of complete information (Proposition 2). For regressing Y on X, we use the function gam (penalized regression splines) from the R package mgcv; Fig. 5 shows that this asymptotic behavior can be seen on finite data sets.

Fig. 5.

(Left) We observe a variable $X=g\left(N\right)+R$ with invertible function g. If the variance of R decreases, the reconstruction of Q improves because it becomes easier to remove the influence $f\left(N\right)$ of the noise N from the variable $Y=f\left(N\right)+Q$ by using X; see Proposition 4. (Right) A similar behavior occurs with increasing the number d of predictor variables $X_i=g_i\left(N\right)+R_i$; see Proposition 5. Both plots show 20 scenarios, each connected by a thin line.

Increasing number of observed ${\mathrm{X}}_{\mathrm{i}}$ variables.

Here, we consider the same simulation setting as before, this time simulating $X_i=g_i\left(N\right)+R_i$ for $i=1,\dots ,d$. We have shown, in Proposition 5, that, if the number of variables $X_i$ tends to infinity, we are able to reconstruct the signal Q. In this experiment, the SD for $R_i$ and Q is chosen uniformly between 0.05 and 1; the distribution of N is the same as above. It is interesting to note that even additive models (in the predictor variables) work as a regression method (we use the function gam from the R package mgcv on all variables $X_1,\dots ,X_d$ and its sum $X_1+\dots +X_d$). Fig. 5 shows that, with increasing d, the reconstruction of Q improves.

Exoplanet Light Curves.

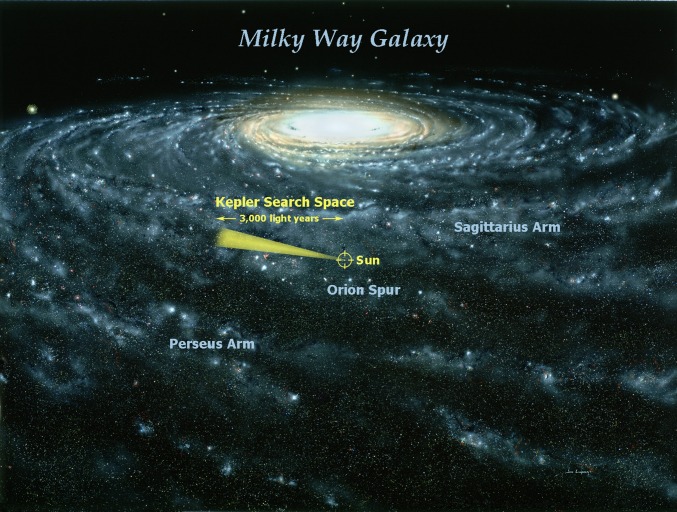
The field of exoplanet search has recently become one of the most popular areas of astronomy research. This is largely due to the Kepler space observatory launched in 2009. Kepler observed a small fraction of the Milky Way in search of exoplanets. The telescope was pointed at the same patch of sky for more than 4 y (Fig. 6 and Fig. S2). In that patch, it monitored the brightness of 150,000 stars (selected from among 3.5 million stars in the search field), taking a stream of half-hour exposures using a set of Charge-Coupled Device (CCD) imaging chips.

Fig. 6.

View of the Milky Way with position of the Sun and depiction of the Kepler search field. Image courtesy of © Jon Lomberg.

Fig. S2.

Kepler search field as seen from Earth, located close to the Milky Way plane, in a star-rich area near the constellation Cygnus. Image courtesy of NASA/Carter Roberts/Eastbay Astronomical Society.

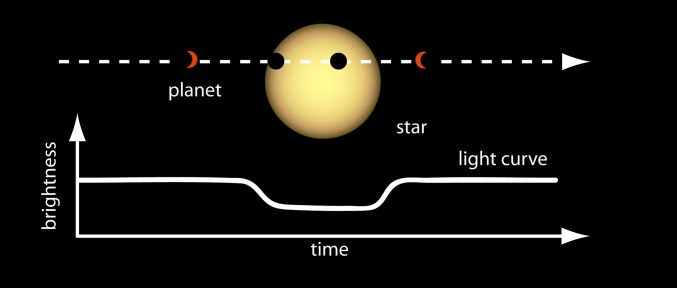
Kepler detects exoplanets using the transit method. Whenever a planet passes in front of their host star(s), we observe a tiny dip in the light curve (Fig. S3). This signal is rather faint, and, for our own planet as seen from space, it would amount to a brightness change smaller than ${10}^{-4}$, lasting less than half a day, taking place once a year, and visible from about half a percent of all directions. The level of required photometric precision to detect such transits is one of the main motivations for performing these observations in space, where they are not disturbed by atmospheric effects and it is possible to observe the same patch almost continuously using the same instrument.

Fig. S3.

Sketch of the transit method for exoplanet detection. As a planet passes in front of its host star, we can observe a small dip in the apparent star brightness. Image courtesy of NASA Ames.

For planets orbiting stars in the habitable zone (allowing for liquid water) of stars similar to the Sun, we would expect the signal to be observable, at most, every few months. We thus have very few observations of each transit. However, it has become clear that there are a number of confounders introduced by spacecraft and telescope leading to systematic changes in the light curves that are of the same magnitude or larger than the required accuracy. The dominant error is pointing jitter: If the camera field moves by a fraction of a pixel (for Kepler, the order of magnitude is 0.01 pixels), then the light distribution on the pixels will change. Each star affects a set of pixels, and we integrate their measurements to get an estimate of the star’s overall brightness. Unfortunately, the pixel sensitivities are not precisely identical, and, even though one can try to correct for this, we are left with significant systematic errors. Overall, although Kepler is highly optimized for stable photometric measurements, its accuracy falls short of what is required for reliably detecting Earth-like planets in habitable zones of Sun-like stars.

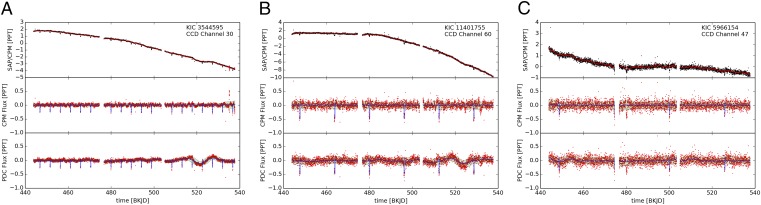
We obtained the data from the Mikulski Archive for Space Telescopes (see archive.stsci.edu/index.html). Our system, which we abbreviate as cpm (Causal Pixel Model), is based on the assumption that stars on the same CCD share systematic errors. If we pick two stars on the same CCD that are far away from each other, they will be light years apart in space, and no physical interaction between them can take place. The light curves (Fig. S4) nevertheless have similar trends, caused by systematics. We use linear ridge regression (see Supporting Information) to predict the light curve of each pixel belonging to the target star as a linear combination of a set of predictor pixels. Specifically, we use 4,000 predictor pixels from about 150 stars, which are selected to be closest in magnitude to the target star. (The exact number of stars varies with brightness, as brighter stars have larger images on the CCD and thus more pixels.) This is done because the systematic effects of the instruments depend somewhat on the star brightness; e.g., when a star saturates a pixel, blooming takes place, and the signal leaks to neighboring pixels. To rule out any direct optical cross-talk by stray light, we require that the predictor pixels are from stars sufficiently far away from the target star (at least 20 pixels distance on the CCD), but we always take them from the same CCD (note that Kepler has a number of CCDs, and we expect that systematic errors depend on the CCD). We train the model separately for each month, which contains about 1,300 data points. (The data come in batches, which are separated by larger errors, since the spacecraft needs to periodically redirect its antenna to send the data back to Earth.) Standard ${\ell }_2$ regularization is used to avoid overfitting, and parameters (regularization parameter and number of input pixels) were optimized using cross-validation. Nonlinear kernel regression was also evaluated but did not lead to better results. This may be due to the fact that the set of predictor pixels is relatively large (compared with the training set size), and, among this large set, it seems that there are sufficiently many pixels that are affected by the systematics in a rather similar way as the target.

Fig. S4.

Stars on the same CCD share systematic errors. A and B show pixel fluxes (brightnesses) for two stars: KIC 5088536 (A) and KIC 5949551 (B); here, KIC stands for Kepler Input Catalog. Both stars lie on the same CCD but are far enough apart so that there is no stray light from one affecting the other. Each panel shows the pixels contributing to the respective star. Note that there exist similar trends in some pixels of these two stars, caused by systematic errors.

If we treat the data as i.i.d. data, our method removes some of the intrinsic variability of the target star. This is due to the fact that the signals are not i.i.d., and time acts as a confounder. If, among the predictor stars, there exists one whose intrinsic variability is very similar to the target star, then the regression can attenuate variability in the latter. This is unlikely to work exactly, but, given the limited observation window, an approximate match (e.g., stars varying at slightly different frequencies) will already lead to some amount of attenuation. Because exoplanet transits are rare, it is very unlikely (but not impossible) that the same mechanism will remove some transits.

Note that, for the purpose of exoplanet search, the stellar variability can be considered a confounder as well, independent of the planet positions that are causal for transits. To remove this, we use as additional regression inputs also the past and future of the target star (see Proposition 6). This adds an AR component to our model, removing more of the stellar variability and thus increasing the sensitivity for transits. In this case, we select an exclusion window around the point of time being corrected, to ensure that we do not remove the transit itself. Below, we report results where the AR component uses as inputs the three closest future and the three closest past time points, subject to the constraint that a window of ±9 h around the considered time point is excluded. Choosing this window corresponds to the assumption that time points earlier than −9 h or later than +9 h are not informative for the transit itself. Smaller windows allow more accurate prediction, at the risk of damaging slow transit signals. Our code is available at https://github.com/jvc2688/KeplerPixelModel.

To give a view on how our method performs, cpm is applied on several stars with known transit signals. After that, we compare them with the Kepler Presearch Data Conditioning (PDC) method (see keplergo.arc.nasa.gov/PipelinePDC.shtml). PDC builds on the idea that systematic errors have a temporal structure that can be extracted from ancillary quantities. The first version of PDC removed systematic errors based on correlations with a set of ancillary engineering data, including temperatures at the detector electronics below the CCD array, and polynomials describing centroid motions of stars. The current PDC (18, 19) performs principal component analysis (PCA) on filtered light curves of stars, projects the light curve of the target star on a PCA subspace, and subsequently removes this projection. PCA is performed on a set of relatively quiet stars close in position and magnitude. For non-i.i.d. data, this procedure could remove temporal structure of interest. To prevent this, the PCA subspace is restricted to eight dimensions, strongly limiting the capacity of the model (20).

In Fig. 7, we present corrected light curves for three typical stars of different magnitudes, using both cpm and PDC. In our theoretical analysis for the i.i.d. case, we dealt with additive noise, and could deal with multiplicative noise, e.g., by log transforming. In practice, neither of the two models is correct for our application. If we are interested in the transit (and not the stellar variability), then the variability is a multiplicative confounder. At the same time, other noises may be better modeled as additive (e.g., CCD noise). In practice, we calibrate the data by dividing by the regression estimate and then subtracting 1, i.e.,

$$\frac{Y}{E\left[Y|x\right]}-1=\frac{Y}{E\left[Y|x\right]}-\frac{E\left[Y|x\right]}{E\left[Y|x\right]}=\frac{Y-E\left[Y|x\right]}{E\left[Y|x\right]}.$$

Effectively, we thus perform a subtractive normalization, followed by a divisive one. This works well, taking care of both types of contaminations.

Fig. 7.

Corrected fluxes using our method, for three example stars, spanning the main magnitude (brightness) range encountered. We consider a bright star (A), a star of moderate brightness (B), and a relatively faint star (C). SAP stands for Simple Aperture Photometry (in our case, a relative flux measure computed from summing over the pixels belonging to a star). In A−C, Top shows the SAP flux (black) and the cpm regression (red), i.e., our prediction of the star from other stars. Middle shows the cpm flux corrected using the regression (for details, see Applications, Exoplanet Light Curves), and Bottom shows the PDC flux (i.e., the default method). The cpm flux curve preserves the exoplanet transits (little downward spikes), while removing a substantial part of the variability present in the PDC flux. All x axes show time, measured in days since January 1, 2009.

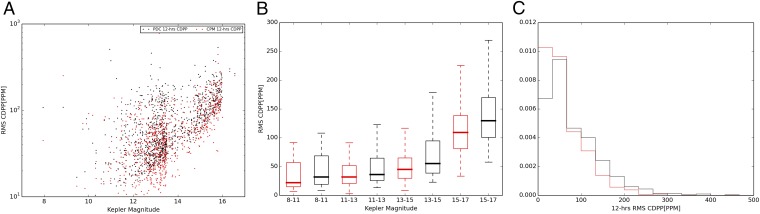
The results illustrate that our approach removes a major part of the variability present in the PDC light curves, while preserving the transit signals. To provide a quantitative comparison, we ran cpm on 1,000 stars from the whole Kepler input catalog (500 chosen randomly from the whole list, and 500 random G-type Sun-like stars), and estimated the Combined Differential Photometric Precision (CDPP) for cpm and PDC. CDPP is an estimate of the relative precision in a time window, indicating the noise level seen by a transit signal with a given duration. The duration is typically chosen to be 3 h, 6 h, or 12 h (21). Shorter durations are appropriate for planets close to their host stars, which are the ones that are easier to detect. We use the 12-h CDPP metric, because the transit duration of an Earth-like planet is roughly 10 h. Fig. 8 presents our CDPP comparison of cpm and PDC, showing that our method outperforms PDC. This is no small feat, because PDC incorporates substantial astronomical knowledge (e.g., in removing systematic trends). It should be noted, however, that PDC’s runtime is much smaller than that of cpm.

Fig. 8.

Comparison of the proposed method (cpm) to the Kepler PDC method in terms of CDPP (see Applications, Exoplanet Light Curves). A shows our performance (red) vs. the PDC performance in a scatter plot, as a function of star magnitude (note that larger magnitude means fainter stars, and smaller values of CDPP indicate a higher quality as measured by CDPP). B bins the same dataset and shows box plots within each bin, indicating median, top quartile, and bottom quartile. The red box corresponds to cpm, and the black box refers to PDC. C shows a histogram of CDPP values. Note that the red histogram has more mass toward the left (i.e., smaller values of CDPP), indicating that our method overall outperforms PDC, the Kepler “gold standard.”

Conclusion

We have assayed half-sibling regression, a simple yet effective method for removing the effect of systematic noise from observations. It uses the information contained in a set of other observations affected by the same noise source. We have analyzed both i.i.d. and time series data. The main motivation for the method was its application to exoplanet data processing, which we discussed in some detail, with rather promising results. However, we expect that it will have applications in other domains as well.

Our method may enable astronomical discoveries at higher sensitivity on the existing Kepler satellite data. Moreover, we anticipate that methods to remove systematic errors will further increase in importance: By May 2013, two of the four reaction wheels used to control the Kepler spacecraft were dysfunctional, and, in May 2014, NASA announced the K2 mission, using the remaining two wheels in combination with thrusters to control the spacecraft and continue the search for exoplanets in other star fields. Systematic errors in K2 data are significantly larger because the spacecraft has become harder to control. In addition, NASA is planning the launch of another space telescope for 2017. The Transiting Exoplanet Survey Satellite (tess.gsfc.nasa.gov/) will perform an all-sky survey for small (Earth-like) planets of nearby stars. To date, no Earth-like planets orbiting Sun-like stars in the habitable zone have been found. This is likely to change in the years to come, which would be a major scientific discovery. In particular, although the proposed method treats the problem of removing systematic errors as a preprocessing step, we are also exploring the possibility of jointly modeling systematics and transit events. This incorporates additional knowledge about the events that we are looking for in our specific application, and it has already led to promising results (20).

Further Proofs

Proof of Proposition 2: Due to [3], we have

$$E\left[f\left(N\right)|X\right]=E\left[\psi \left(X\right)|X\right]=\psi \left(X\right)=f\left(N\right).$$

To show the second statement, consider the conditional expectation

$$E\left[Y|X\right]=E\left[Q+f\left(N\right)|X\right].$$

Using $Q\mathrm{╨}X$ and [4], we get

$$E\left[Y|X\right]=E\left[Q\right]+f\left(N\right)=E\left[Q\right]+Y-Q.$$

Recalling Definition 1 completes the proof.

Before proving Proposition 3, we observe that $E\left[f\left(N\right)|X\right]$ is a good approximation for $f\left(N\right)$ whenever $f\left(N\right)$ is almost determined by X.

Lemma 1. For any two RVs $Z,X$, we have

$$E\left[{\left(Z-E\left[Z|X\right]\right)}^2\right]=E\left[\text{Var}\left[Z|X\right]\right].$$ [S1]

Here, $E\left[Z|X\right]$ is the RV $g\left(X\right)$ with $g\left(x\right)=E\left[Z|X=x\right]$, and $\text{Var}\left[Z|X\right]$ is the RV $h\left(X\right)$ with $h\left(x\right)=\text{Var}\left[Z|X=x\right]$. Then [S1] turns into

$$E\left[{\left(Z-g\left(X\right)\right)}^2\right]=E\left[h\left(X\right)\right].$$ [S2]

Proof of Lemma 1: Note that, for any RV Z, we have

$$\text{Var}\left[Z|X=x\right]=E\left[{\left(Z-E\left[Z|X=x\right]\right)}^2|X=x\right],$$

by the definition of variance, applied to the variable ${Z|}_{X=x}$. Hence

$$\text{Var}\left[Z|X\right]=E\left[{\left(Z-E\left[Z|X\right]\right)}^2|X\right],$$

where both sides are functions of X. Taking the expectation w.r.t. X on both sides yields

$$E\left[\text{Var}\left[Z|X\right]\right]=E\left[{\left(Z-E\left[Z|X\right]\right)}^2\right],$$

where we have used the law of total expectation $E\left[E\left[W|X\right]\right]=E\left[W\right]$ on the right-hand side.

Proof of Proposition 3: We rewrite the argument of the square in [6] as

$$\begin{array}{c}\widehat{Q}-\left(Q-E\left[Q\right]\right)\\ =Y-E\left[Y|X\right]-Q+E\left[Q\right]\\ =f\left(N\right)+Q-E\left[f\left(N\right)|X\right]-E\left[Q|X\right]-Q+E\left[Q\right]\\ =f\left(N\right)-E\left[f\left(N\right)|X\right].\end{array}$$

Here, the last step uses $E\left[Q|X\right]=E\left[Q\right]$, which follows from $Q\mathrm{╨}X$.

The result follows using Lemma 1 with $Z≔f\left(N\right)$.

Proof of Proposition 5: By Kolmogorov’s strong law, we have for

$${\overline{\mu }}_d≔\frac{1}{d}{\displaystyle \sum _{i=1}^{d}E\left[R_i\right]}$$

that

$$\begin{array}{ccc}& \frac{1}{d}{\displaystyle {\sum }_{i=1}^d{R}_i-{\overline{\mu }}_d}& \stackrel{P}{\to }0\\ \Rightarrow & \frac{1}{d}{\displaystyle {\sum }_{i=1}^d\left(g_i\left(N\right)+R_i\right)-{\overline{\mu }}_d-{\tilde{g}}_d\left(N\right)}& \stackrel{P}{\to }0\\ \stackrel{\ast }{\Rightarrow }& {\tilde{g}}_d^{-1}\left(\frac{1}{d}{\displaystyle {\sum }_{i=1}^d\left(g_i\left(N\right)+R_i\right)-{\overline{\mu }}_d}\right)-{\tilde{g}}_d^{-1}\left({\tilde{g}}_d\left(N\right)\right)& \stackrel{P}{\to }0\\ \Rightarrow & {\tilde{g}}_d^{-1}\left(\frac{1}{d}{\displaystyle {\sum }_{i=1}^d{X}_i-{\overline{\mu }}_d}\right)-N& \stackrel{P}{\to }0\\ \stackrel{\ast \ast }{\Rightarrow }& f\left({\tilde{g}}_d^{-1}\left(\frac{1}{d}{\displaystyle {\sum }_{i=1}^d{X}_i-{\overline{\mu }}_d}\right)\right)-f\left(N\right)& \stackrel{P}{\to }0\\ \Rightarrow & {\psi }_d\left({\mathbf{X}}_d\right)-f\left(N\right)& \stackrel{P}{\to }0\end{array}$$

for some ${\psi }_d$ that are uniformly bounded in d (the implication $\mathrm{\ast }$ follows from uniform equicontinuity, implication $\mathrm{\ast \ast }$ by the continuous mapping theorem). This implies

$$E\left[f\left(N\right)|{\mathbf{X}}_d\right]-f\left(N\right)\stackrel{L^2}{\to }0$$

because

$$E\left[{\left(f\left(N\right)-E\left[f\left(N\right)|{\mathbf{X}}_d\right]\right)}^2\right]\le E\left[{\left(f\left(N\right)-{\psi }_d\left({\mathbf{X}}_d\right)\right)}^2\right]\to 0.$$

[The convergence of the right hand side follows from ${\psi }_d\left({\mathbf{X}}_d\right)-f\left(N\right)\stackrel{P}{\to }0$ and boundedness of ${\psi }_d\left({\mathbf{X}}_d\right)-f\left(N\right)$.] However, then

$$\begin{array}{c}Q-E\left[Q\right]-{\widehat{Q}}_d=-f\left(N\right)-E\left[Q\right]+E\left[f\left(N\right)+Q|{\mathbf{X}}_d\right]\\ =E\left[f\left(N\right)|{\mathbf{X}}_d\right]-f\left(N\right)\stackrel{L^2}{\to }0.\end{array}$$

A Note on Related Work

In its supplement, ref. 15 assays a related idea for the case of linear relations with multivariate variables. In this work, Y is a vector of log expression levels of some genes of interest, and the generating model

$$Y=X\beta +W\alpha +E$$ [S3]

is assumed, where X represents some factors of interest, e.g., some vector-valued disease state, W denotes some unobserved covariates (such as sample quality), E is a random noise term, and β and α are matrices of regression coefficients. $W\alpha$ is the unwanted term because W may be a latent common cause of X and Y which makes the estimation of the regression vector β difficult. The correction method assumes that there are some control genes that are not influenced by the factors X of interest, that is, the restriction of [S3] to those genes reads

$$Y_c=W{\alpha }_c+E_c.$$

W is estimated from $Y_c$ via factor analysis, which allows removal of the unwanted term $W\alpha$ from [S3]. Unlike ours, the method is restricted to linear models.

A crucial feature of our approach is that an explicit estimation of the noise term N is not necessary, which is particularly convenient when it influences Y in a nonlinear way.

The method of ref. 15 has recently been further developed (22).

Ridge Regression

Suppose we are given an i.i.d. sample $\left(X_1,Y_1\right),\dots ,\left(X_n,Y_n\right)$ from $Y\in \mathrm{ℝ}$, $X\in {\mathrm{ℝ}}^d$. Then, for any $\lambda >0$ (regularization parameter), the solution to the problem

$$\widehat{\beta }≔\underset{\beta \in {\mathrm{ℝ}}^d}{\text{argmin}}{\displaystyle \sum _{i=1}^n{\left(Y_i-{\beta }^t{X}_i\right)}^2+\lambda {\Vert \beta \Vert }_2}$$

is given by (e.g., ref. 23)

$$\widehat{\beta }≔{\left({\mathbf{X}}^{\mathbf{t}}\mathbf{X}+\lambda \mathbf{I}\right)}^{-\mathbf{1}}{\mathbf{X}}^{\mathbf{t}}\mathbf{Y},$$

where the $n\times d$ matrix $\mathbf{X}$ and the $n\times 1$ matrix $\mathbf{Y}$ contain the data points.

For a light curve of duration 3 mo, our approach took about 7 h on a single core (Ivy Bridge x86_64 3.0 GHz), training the 3 mo separately, i.e., about 2 h for each month comprising around 1,300 data points. We had to solve about 1,300 linear systems of dimension about 1,300 for a 1-mo light curve. There were four parameters to be tuned: the number of predictor pixels, autoregression window size, and L2 regularization parameters for both components (regression from the other stars, and autoregression on past and future of the light curve itself). The parameters were tuned by first considering a representative subset of around 20 light curves and performing cross-validation. This led to different values for each light curve, but we found that we were able to choose a set of values uniform across the light curves that led to essentially the same cross-validation errors. We thus used these values for all light curves. We found that the results were robust with respect to changing the regularization parameter by an order of magnitude (up or down).