Significance
The potential energy stored in ion gradients across cell membranes drives nutrients in and out of cells by cotransport proteins, e.g., uphill glucose accumulation in cells by sodium cotransporters. Insight into the mechanism of cotransport has been obtained from high-resolution atomic structures of the transporters, but further progress requires dynamic information about ion and substrate movements through the proteins. We have used multiple long molecular-dynamic simulations and electrophysiological assays to explore the dynamics of the transport cycle. Ligands bound to sodium-dependent glucose transporters are released to the cytoplasm stochastically, whereas release to the external solution is ordered with sugar first. The order of events is intimately tied to how the protein converts the energy stored in an ion gradient into a sugar gradient.
Keywords: transporter, SGLT, simulation, kinetics, symporter
Abstract
Secondary active transporters, such as those that adopt the leucine-transporter fold, are found in all domains of life, and they have the unique capability of harnessing the energy stored in ion gradients to accumulate small molecules essential for life as well as expel toxic and harmful compounds. How these proteins couple ion binding and transport to the concomitant flow of substrates is a fundamental structural and biophysical question that is beginning to be answered at the atomistic level with the advent of high-resolution structures of transporters in different structural states. Nonetheless, the dynamic character of the transporters, such as ion/substrate binding order and how binding triggers conformational change, is not revealed from static structures, yet it is critical to understanding their function. Here, we report a series of molecular simulations carried out on the sugar transporter vSGLT that lend insight into how substrate and ions are released from the inward-facing state of the transporter. Our simulations reveal that the order of release is stochastic. Functional experiments were designed to test this prediction on the human homolog, hSGLT1, and we also found that cytoplasmic release is not ordered, but we confirmed that substrate and ion binding from the extracellular space is ordered. Our findings unify conflicting published results concerning cytoplasmic release of ions and substrate and hint at the possibility that other transporters in the superfamily may lack coordination between ions and substrate in the inward-facing state.
Transport of sugar molecules across membranes is virtually ubiquitous in biology, and it is of central importance in human health. The uptake of glucose is especially crucial due to its pivotal role in cellular metabolism and energy production. In mammals, glucose is absorbed in the small intestine and kidney via sodium-dependent glucose transporters (SGLTs), which localize to the apical membrane and concentrate glucose in the epithelia. SGLTs fall into the large leucine-transporter (LeuT) structural family of secondary active transporters that have evolved to concentrate a wide array of substrates across membranes using the energy stored in the Na+ electrochemical potential gradient. For symporters in this family, transport occurs by an alternating access mechanism (1) in which the transporter first binds ligands in an outward-facing conformation, and then transitions to an inward-facing conformation that releases the cargo to the cytoplasm. The order of ion and substrate binding and unbinding is likely tied to the function of the transporter, making it possible to convert the energy stored in the ion gradient into a substrate gradient, and vice versa when these proteins operate in reverse.
Extensive biochemical uptake assays and electrophysiological studies of SGLTs have led to a view of Na+/glucose cotransport in which Na+ binding precedes sugar binding on the external face of the transporter. Kinetic models adhering to this mechanism satisfactorily account for the steady-state currents and pre–steady-state charge movements of hSGLT1 as a function of voltage and the extracellular sodium and sugar concentrations (2). According to these models, the SGLT transport cycle comprises the ordered binding of Na+ ions and glucose before translocation of the fully loaded carrier to the internal side (Fig. 1A). Although the binding order and partial reaction steps corresponding to Na+ and sugar binding to the extracellular face are well understood for hSGLT1 (3) and vSGLT (4, 5), less is known about substrate release to the cytoplasm, i.e., symmetrical release (glucose off before Na+), Na+ before glucose, or random. Models of symmetrical release (Fig. 1A) fit the existing data, but the experiments were not designed to directly probe the order of release to the intracellular space. Meanwhile, molecular simulations of the bacterial homolog, vSGLT, in the inward-facing state have revealed a different picture in which Na+ exits the transporter before sugar (6–8). Thus, there are two opposing views on how release occurs during the pumping cycle, and here, we present additional of experiments on hSGLT1 and simulations on vSGLT designed to resolve these differences.
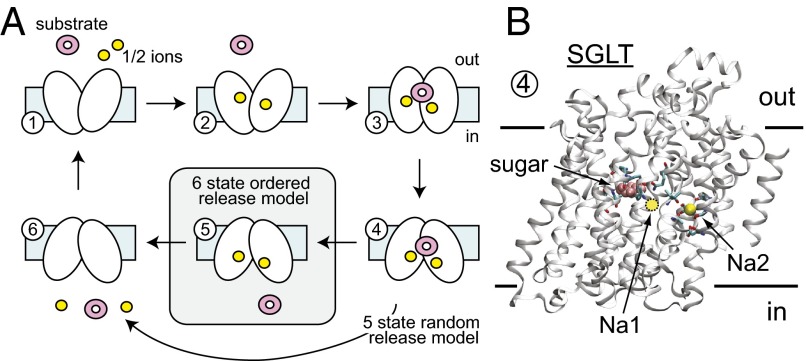
Fig. 1.
Kinetic scheme for SGLT substrate and ion transport. (A) Each number represents a conformation (state) that the carrier occupies in sequence during the transport cycle. Influx experiments suggest an ordered binding scheme for substrate (pink) and sodium (yellow) at the extracellular face, but the order of events for the inward-facing state are less clear. The standard six-state model in which substrate unbinds before Na+ was developed previously and nicely fits existing data. However, previous simulations on the bacterial transporter vSGLT suggest that Na+ may unbind first. Here, we highlight a third possibility, skipping state 5, in which substrate and ion binding are independent and occur in a random order. vSGLT carries out transport with one ion, whereas hSGLT1 uses two. The arrows indicate the direction corresponding to inward pumping; however, SGLT is fully reversible, as exploited in this study. (B) Structure of SGLT in the inward-facing conformation bound to Na+ and sugar (state 4). The structure is of vSGLT (PDB ID code 3DH4), which does not contain an Na1 Na+ binding site. The approximate position of the Na1 site in hSGLT1 is marked with a yellow circle based on functional data (13).
We carried out 21 substrate release simulations on the inward-facing state of vSGLT (Fig. 1B) to compile statistics on the order and biophysical nature of unbinding. At the same time, we examined the cytoplasmic release of Na+ and glucose from hSGLT1 using whole-cell patch-clamp electrophysiology. The experimental Na+/glucose currents were compared with calculations from a mathematical model using either the standard scheme in Fig. 1A or a modified scheme in which substrate unbinding to the cytoplasm is unordered. The simulations, experiments, and mathematical modeling all support the claim that substrate and Na+ release to the intracellular compartment are random events that are not ordered.
Results
Na+ and Sugar Release from the Inward-Facing Conformation of vSGLT Are Independent.
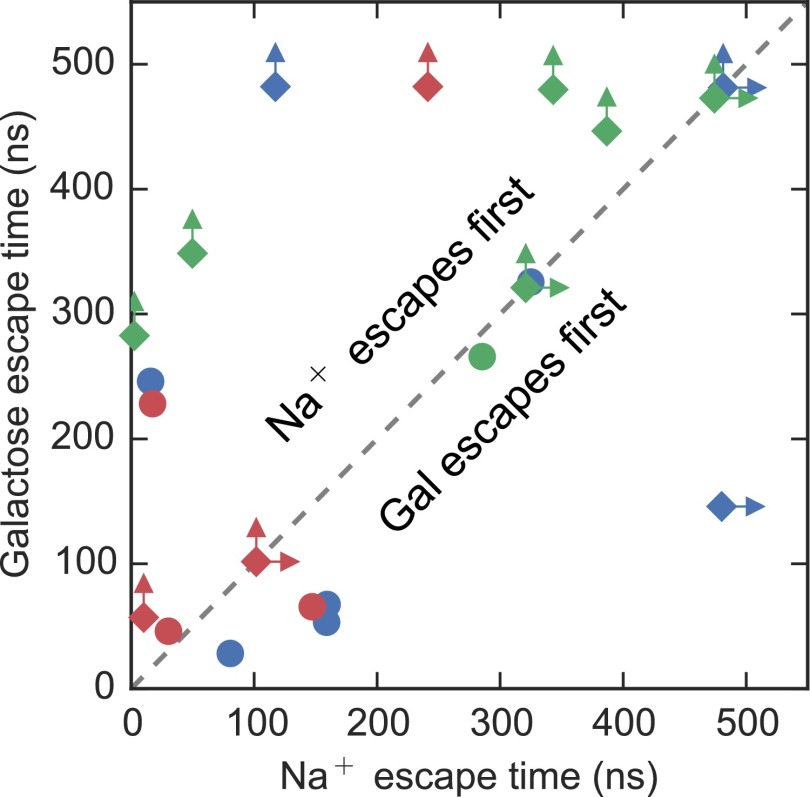
Earlier simulations of vSGLT, initiated from the inward-facing conformation with Na+ and galactose bound in their crystallographic poses, observed rapid sodium release that triggered conformational changes in the protein that permitted subsequent sugar unbinding (7). Here, we revisit those results by examining 21 individual simulations initiated under similar conditions. To generate as many independent galactose escape events as possible, we terminated single simulations at the time of galactose release, or at a time before 480 ns, not allowing any simulation to extend beyond 480 ns. This resulted in nearly 6.5 μs of aggregate simulation time. Each of the points in Fig. 2 represents the time of escape of galactose (ordinate) and sodium (abscissa) from those simulations. Points that fall above the diagonal line indicate that sodium escaped first, whereas points below the line had sugar escape first, and points on the line involved simultaneous escape times. In 10 of the 21 events, sodium exited before galactose release, but in contrast to previous studies (6–9) the escape time ranged up to 400 ns (Fig. 2). Along the diagonal are four cases in which Na+ and galactose both failed to exit, and one case in which they both exited simultaneously. The six remaining events are novel in that galactose exited before Na+ departure. For those simulations terminated before galactose was released, we believe that an escape event would have been observed if the simulations were further extended, consistent with the trajectories in which sugar exited, because the substrate was generally quite mobile in the binding pocket.
Fig. 2.
Lifetimes of bound states for galactose and Na+. Scatter plot of time of release of galactose and Na+ from the sugar and Na2 binding sites, respectively, for each simulation. Trajectories originating from the same initial model of vSGLT (as described in ref. 21) are shown as distinct colors. Simulations that were terminated before full unloading of sugar and/or Na+ are represented by diamonds with one or two arrows indicating that Na+ (right arrow) and/or galactose (up arrow) is still bound. We posit that galactose failing to exit before the simulations ended is a function of the simulation timescale and not due to any structural constraints. All other trajectories are shown as circles.
Previously, we reported an escapement mechanism in which initial Na+ release from the Na2 binding site triggers a rotameric flip in the side chain of the large aromatic amino acid Y263, which makes up part of a thin inner gate, to create a cavity for galactose exit into the cytoplasm. We termed this rotameric conformation of Y263 the permissive state. Although two of the eight intracellular sugar release simulations occur via this exact series of events, we also observe substrate release sequences that differ in their ordering. Two more escapes occur via flipping of Y263 to the permissive state but Na+ remains bound (7), whereas another four occur without Y263 undergoing a rotamer change, as reported by Li and Tajkhorshid (10) (Fig. S1). Furthermore, the occupancy of the Na2 site does not appear to alter the Y263 rotamer distribution (Fig. S2), potentially ruling out allosteric coupling between the thin inner gate and the Na2 sodium binding site in the inward-facing state. Together with the finding that sugar can exit before Na+ release (Fig. 2), it is likely that internal release of sodium and substrate from the inward-occluded structure is uncoordinated with very little, if any, global changes in the protein’s conformation.
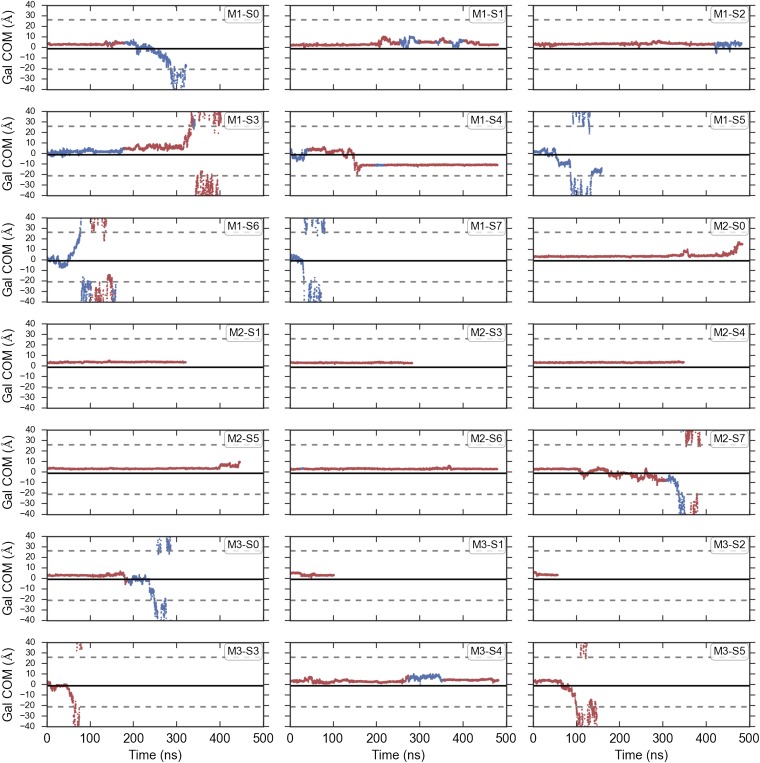
Fig. S1.
Galactose escape and Y263 rotamer conformation. For each of the simulations, the center of mass of the galactose molecule is shown projected onto the z axis. The points along the trajectory are colored red if Y263 is in the crystallographic rotamer conformation and blue if it is in the alternative rotameric state. The boundaries of the membrane are shown as dashed lines, and the center of mass of the side-chain atoms of Y263 in the crystallographic conformation is shown as a solid black line.
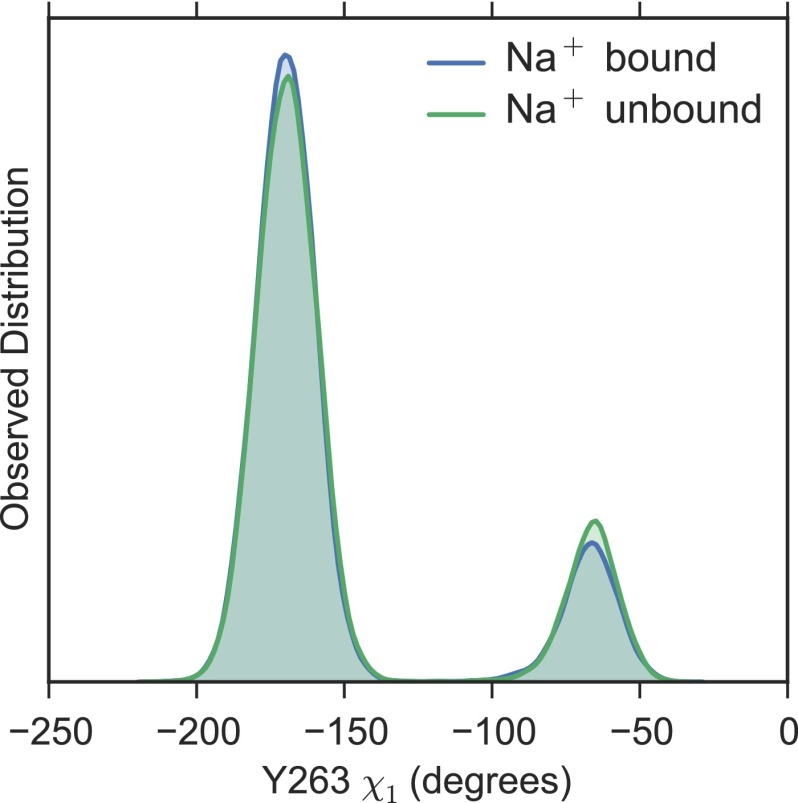
Fig. S2.
Rotamer conformations of Y263 with and without Na+. Distribution of the dihedral angle of Y263 with Na+ present (blue) or absent (green) from the Na2 site. The Na2 site is categorized as being occupied if any Na+ ion in the simulation box is within 4.5 Å of the either oxygen atom in the carboxyl group of D189. It is difficult to distinguish between the distributions due to the high degree of overlap.
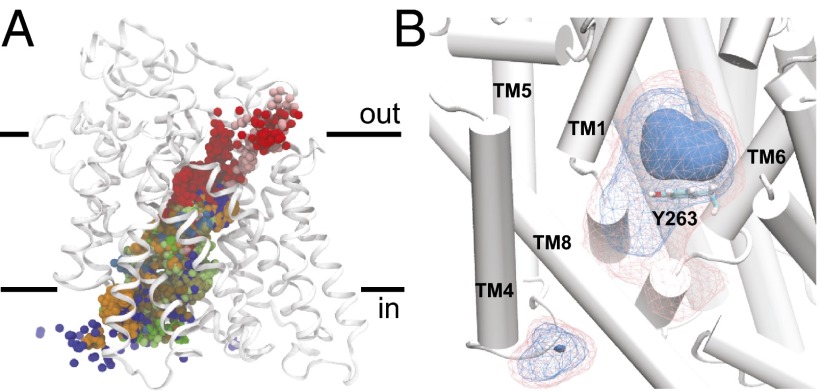
Superimposing the coordinates of galactose from all of the simulation data reveals that the substrate explores the entire intracellular cavity during exit (Fig. 3A). Visual inspection of individual trajectories and analysis of the protein–sugar contacts, indicates that, as galactose escapes, there is no clear sequence of residues visited during exit. Last, we calculated a volumetric map, detailing the observed density of galactose throughout the simulation box, again using the entire dataset. Not surprisingly, the most populated region corresponds to the location of galactose in the X-ray structure (dark blue region above Y263 in Fig. 3B). Furthermore, a simple clustering based on galactose root-mean-squared displacement indicates that the pose of the cluster center is close to the crystallographic pose (Fig. S3). We note that there is a region of enhanced density for galactose distal from the galactose binding site, wedged between the intracellular ends of TMs 4 and 9 (residues S177, I178, N371, V396, and R400). This density arises from a single trajectory, where galactose binds at this location and remains for >300 ns. At this time, it is unclear whether this site has any physiological relevance. Recently, a putative secondary binding site for galactose in the intracellular vestibule below Y263 was reported (11). In that study, both experimental assays and computational modeling suggested that both this site and the crystallographic sugar binding site could be occupied simultaneously. Our escape simulations significantly sampled this region below Y263, as shown in the density map in Fig. 3B. We docked a second galactose molecule into the intracellular cavity, revealing a pose similar to the one reported by Li et al. (11), and this configuration fell within the second most populated cluster from the sugar release simulations (Fig. S3). Thus, it is possible that the residues highlighted in Fig. S3 form a secondary binding site that has been significantly weakened in the inward-facing conformation. However, as galactose in the X-ray site unbinds, it does not always pass through this second site as it stochastically explores the intracellular cavity on its way to the cytoplasm.
Fig. 3.
Galactose escape trajectories. (A) Center of mass of galactose from every escape simulation. Each simulation is shown in a different color. (B) Density of galactose taken from all simulation data. The densest region of occupancy is shown as a solid surface directly above Y263 (shown as sticks), and two isocontours of decreasing density are shown in wireframe in blue and pink, respectively. TM9 is removed for clarity.
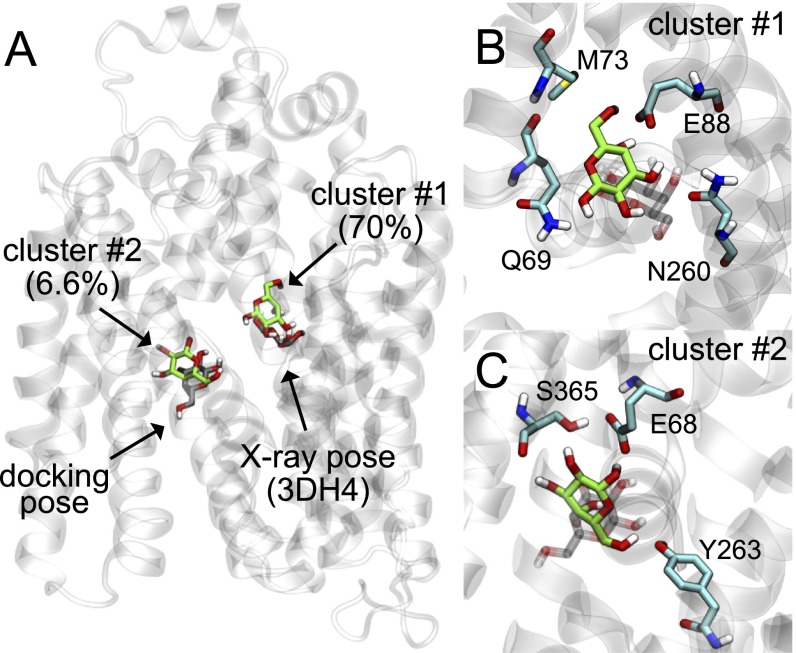
Fig. S3.
Clustering analysis of galactose molecules from sugar release simulations. (A) The vSGLT structure (PDB ID code 3DH4) with resolved galactose (gray molecule on Right) and the generator for the most populated cluster (green), which contains 70% of the data. The Schrŏdinger Glide XP software package (44) was used to dock (rigid receptor/flexible ligand) a second galactose molecule into the intracellular cavity resulting in the pose on the Left (gray). This pose occupies the second most populated cluster (6.6% of the data) with the cluster generator shown in green. Clustering was carried out using MSMBuilder3 in concert with MDTraj (41). The K-centers algorithm was used with a square Euclidean metric and 500 clusters. (B) Magnified image of the top cluster generator (green) and resolved galactose molecule from the 3DH4 structure (gray). (C) Magnified image of the second most populated cluster generator (green) with docked pose (gray). The docked pose and cluster generator contain three of the residues identified by Li et al. in their recent work (11).
Long Na+ Dwell Times and Ion Rebinding Events.
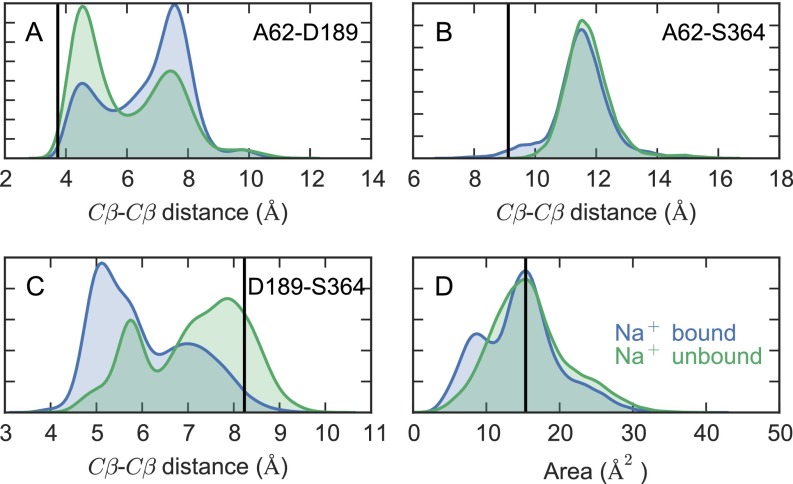
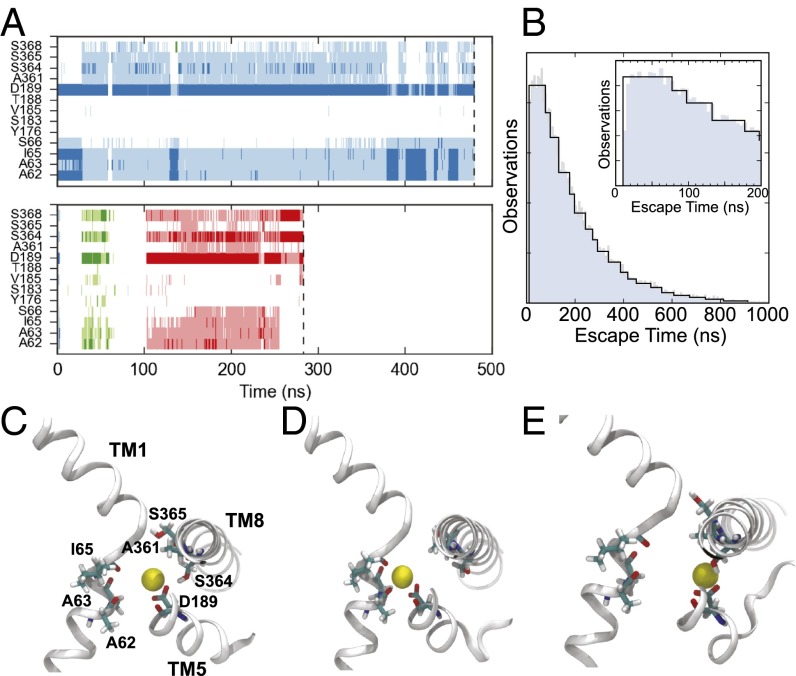
The sodium ion in the Na2 site of the outward-facing LeuT structure is tightly coordinated by residues on TM1 and TM8. However, TM1 and TM8 are too far apart in the inward-facing vSGLT crystal structure to form good contacts with the ion (12), and earlier simulations showed rapid unbinding from the site on the 10-ns timescale (6–8). Interestingly, our present simulations show a broad range of dwell times dominated by quick releases, as seen before, but we also observe very long-lived bound states lasting 480 ns as in the simulation shown in Fig. 2. The site does not reorganize to cause increased coordination, but, rather, the site widens (Fig. S4), as we observed previously (7), and a variable number of residues stabilize the ion as shown in Fig. 4A for two trajectories (see Fig. S5 for all 21 simulations). There is a slight propensity for the Na2 site to close in the presence of Na+ (Fig. S4D). The primary contact is D189, which has a typical Na+ to carboxyl oxygen distance less than 3 Å, and the equivalent position in hSGLT1 (D204) was shown to be involved in Na+ binding to Na2 (13). Additionally, A62, A63, I65, and S364 all contact the Na+ to different degrees. Individual snapshots illustrate the role of these residues but also highlight that a well-coordinated proteinaceous shell is not needed to retain the ion in the transporter (Fig. 4 C–E). We also observed events where Na+ ions from bulk solution rebind to the empty Na2 site, as shown in the lower panel of Fig. 4A, providing evidence that this position is likely the sodium binding site required for transport, albeit one that is probably weakened compared with the tight coordination of Na+ observed in alternative conformations of other LeuT-superfamily members. It is interesting to speculate that these rebinding events are representative of how the system progresses through the transport cycle when operating in reverse.
Fig. S4.
Residue–residue distance distributions in the Na2 site. Distributions of the Cβ–Cβ distances between (A) A62 and D189, (B) A62 and S364, and (C) D189 and S364, in the presence and absence of Na+ in the Na2 site. (D) The area of the triangle formed by the three residues. The black vertical line in each panel is the value observed in the 3DH4 X-ray structure.
Fig. 4.
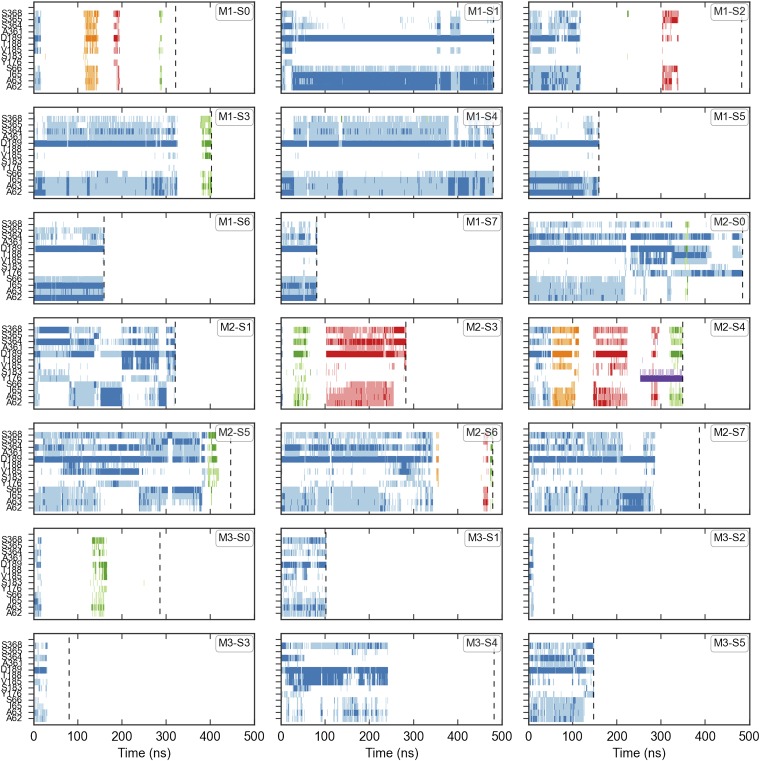
Properties of Na+ binding and release. (A) Na+ interactions with key Na2 binding site residues for two arbitrary trajectories. Time points where the sodium is within 3 Å of the residue’s backbone carbonyl or terminal side-chain oxygen are shown as either dark blue, green, or red. When the Na+ is between 3 and 4.5 Å from the same set of atoms, the time point is shown as either light blue, green, or red. The different primary colors represent distinct Na+ ions, where the ion initially placed in the Na2 site is shown in blue. The end of the trajectory is denoted by a vertical dashed line. (B) Na+ escape time distribution calculated from 30,000 simulated trajectories of the Na+ binding MSM transition matrix. The Inset focuses on the first 200 ns shown in the main panel. (C–E) Representative Na+ coordinations observed in the simulation trajectories. Sections TM1, 5, and 8 are shown in cartoon representations, whereas A62, A63, I65, D189, A361, S364, and S365 are shown as sticks.
Fig. S5.
Na+ interactions with key Na2 binding site residues. The different primary colors represent distinct Na+ ions, where the ion initially placed in the Na2 site is shown in blue. Time points where the sodium is within 3 Å of the residue’s backbone carbonyl or terminal side-chain oxygen are shown as dark colors. When the Na+ is between 3 and 4.5 Å from the same set of atoms, the time point is shown as a lighter shade of the same color. The end of the trajectory is denoted by a vertical dashed line.
A Markov State Model of Ion Escape.
Although the Na+ escapes observed in the simulations suggest that ions initially bound in the Na2 site have a broad dwell time distribution dominated by shorter times, our sample size is insufficient to estimate the complete distribution directly. We therefore sought to further quantify Na+ release dynamics by developing a Markov state model (MSM) of the process, parameterized by the complete set of simulated trajectories. To capture the full ionic configuration of the system in a reduced set of discrete states, we represented each snapshot in terms of the occupancy of Na+ ions in a set of concentric shells around 13 key residues located in and around the Na2 site. This representation of the system follows the solvent-shell featurization framework, first developed to include solvent degrees of freedom in MSMs (14). Its extension to treat ion conformations is natural, and the method cleanly handles the indistinguishability of ions, is invariant to translation and rotation of the transporter, and captures local protein conformational changes in the ion binding site. The solvent-shell model in principle would also account for both first and second shell coordination of the ion, where the latter would involve bridging waters. The data, however, suggest that second shell coordination does not appear to be important in the ion retention seen in our simulations.
Trajectories projected into the solvent-shell space were preprocessed using time-structure independent component analysis (15, 16) and were then assigned to a discrete set of states using K-centers clustering. From the state-to-state transition counts, we constructed a MSM. All of the steps involved with the construction and validation of the model were performed using MSMBuilder3 (17), and complete details are presented in Materials and Methods and SI Materials and Methods (Figs. S6 and S7 and Table S1).
Fig. S6.
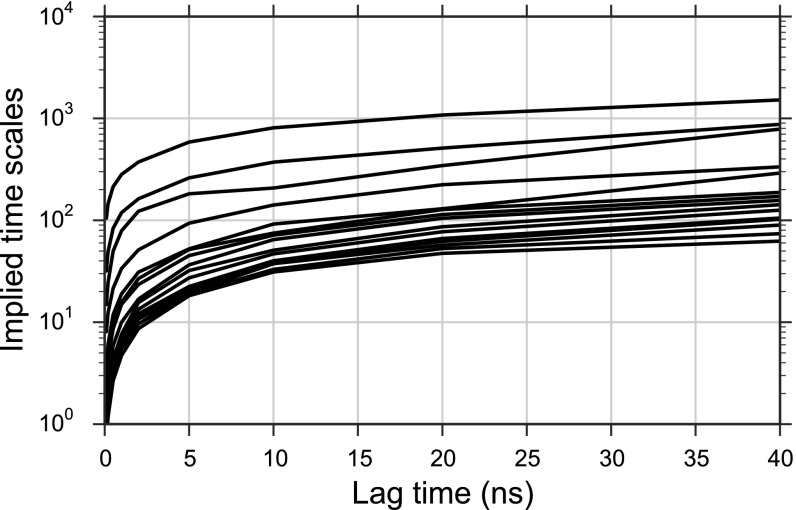
MSM implied timescales. Implied time scales calculated from the MSM transition probability matrix as a function of lag time.
Fig. S7.
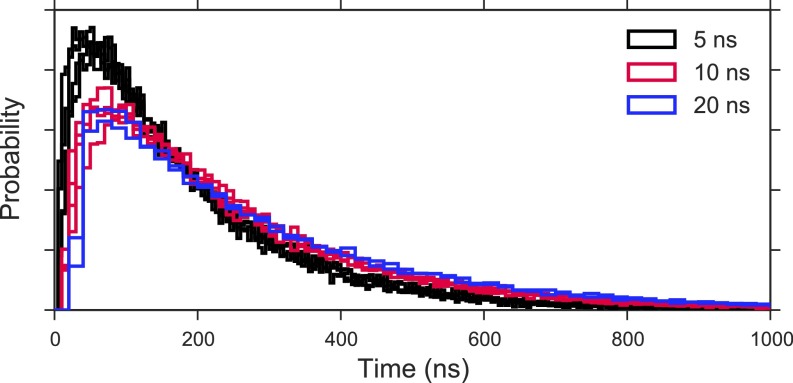
Na+ escape first passage time distributions. Na+ escape time distribution calculated from 30,000 simulated trajectories of the MSM transition matrix for models with varying lag time and hyperparameters. Models are selected based on well-behaved implied timescales and GMRQ scoring criteria described in the text.
Table S1.
MSM hyperparameters were tuned via grid search
| Hyperparameter | Grid search values |
| No. of tICA components | 1, 2, 3, 4 |
| tICA lag time, ns | 1, 2, 5 |
| No. of MSM microstates | 25, 50, 100, 200, 400, 800 |
| MSM lag time, ns | 0.1, 0.2, 0.5, 1, 2, 5, 10, 20 |
From the validated MSM, we used a kinetic Monte Carlo scheme to generate an ensemble of simulated Na+ escape trajectories initialized from the crystallographic placement of the ion in the Na2 site. Monte Carlo simulations were terminated once the ion exited the transporter as defined by entering a state without any Na+ ions within 6 Å of the 13 residues that define the Na2 site. The distribution of time required for the Na+ to exit the transporter is shown in Fig. 4B for one model. The distribution displays a broad range of Na+ dwell times, spanning the range observed in the underlying MD trajectories. It is peaked, however, over escape times of 10–80 ns in duration, consistent with typically fast Na+ release from the inward-facing state captured in the crystallographic structure. Longer Na+ residence times on the timescale of hundreds of nanoseconds have diminished, but nonnegligible probability. The general shape of the distribution suggests that, at the level of spatial coarse graining imposed by the MSM’s state space, exit of Na+ from the Na2 site is dominated by a single energetic barrier. The source of the barrier is not clear, however, and it may arise from interactions with many residues.
Extracellular Substrate Release from an Inward-Facing State.
The inward-facing conformation of vSGLT provides a nearly continuous water-filled cavity from just below the sugar binding site to the intracellular bulk. This, or closely related conformational states, are poised to release both Na+ and sugar through that passage, and consistent with a strict alternating-access mechanism, the X-ray structure exhibits a thick outer gate that occludes the substrate site from the extracellular space. Simulations of vSGLT have revealed that this outer gate is permeable to water, which crosses the transporter through the sugar binding site, and that water flow is modulated by the transient formation of an opening on the extracellular face of the transporter (18–21).
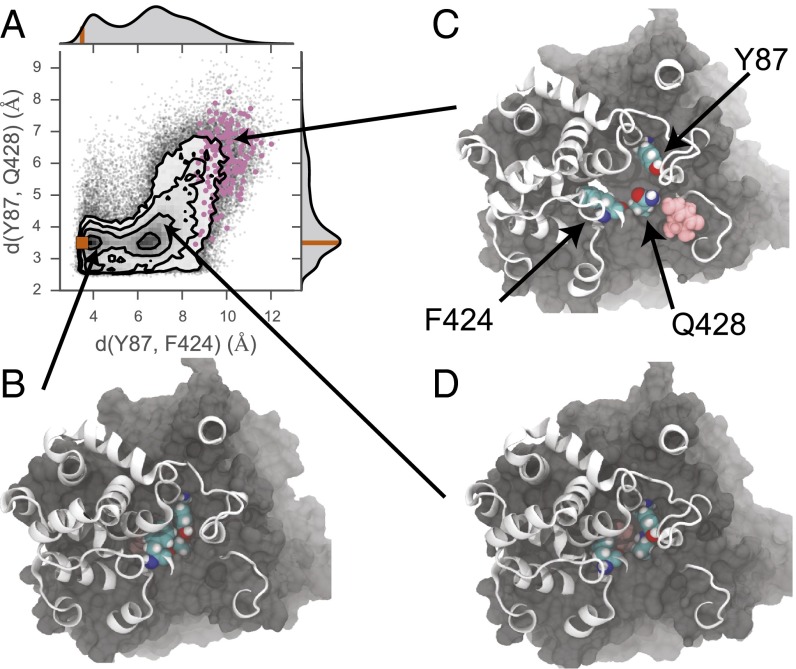
In 2 of our 21 simulations, the galactose escapes to the extracellular bulk through the same opening. Although the cavity is often large enough to permit water movement into the protein from the extracellular side, its size is typically too small to accommodate the larger galactose molecule. The size of the hole depends little on backbone deformations, but instead is a feature of side-chain conformations. In particular, the relative distances between Y87, F424, and Q428 largely determine whether galactose is presented with a steric barrier to exit. Fig. 5A shows the observed distribution of distances between Y87 and F424, and Y87 and Q428, measured as the minimum distance between atom centers in each residue. Although the crystallographic distances are well represented in the observed population of separation distances, a second maximum exists in the Y87–F424 distribution at ∼7 Å. As the galactose moves past these residues to escape to the extracellular side, the separation distance must expand into the tail of the Y87–F424 distribution in concert with an expansion in the minimum separation distance between Y87 and Q428. Points corresponding to the distances observed during the escapes are highlighted in Fig. 5A, and representative conformations are shown for both the rare conformation permissive to galactose exit (Fig. 5C) as well as the dominant conformations observed in the dataset, which do not appear to permit outward exit (Fig. 5 B and D). A rough estimate based on this data suggests that the inward-facing state of the transporter spends ∼8% of its time in a conformation compatible with outward sugar escape. These gate opening events occur in just under one-half of the simulations, and there are several instances where the gate opens and then tightly recloses.
Fig. 5.
Galactose exit through the extracellular gate. (A) The joint distribution of the minimum distance between Y87 and F424, and Y87 and Q428. Overlaid on the distribution are the observed distances from the simulation (gray points) and the crystallographic distances (orange point). The observed distances occurring when the galactose has a position along the z axis between 11 and 15 Å above the center of mass of the core helices are colored in pink. The marginal probability distribution for each residue–residue distance is shown on the upper and right axes, where the orange line on each correspond to the distances observed in the crystal structure (PDB ID code 3DH4). Residue positions are shown in C. (B–D) Molecular representation of the transporter in various conformational states of the extracellular gate. All protein atoms with z positions <12 Å are shown in surface representation, and all residues above that height are shown in cartoon representations. Y87, F424, and Q428 are shown in VDW representation, as is the galactose molecule in pink. (B) Conformation corresponding to the minima containing the crystallographic structure. (C) Conformation with a fully open extracellular gate, permitting galactose exit. (D) Conformation with the Y87–F424 distance expanded relative to the crystal structure, corresponding to the second minimum along this axis. The galactose is obscured in B and D due to the partial to full closure of the outer gate.
Experimental Tests of Ion and Substrate Release from Human SGLT1.
Given that our original simulations performed on vSGLT (7) failed to support the accepted view that sugar release precedes ion escape (2), we devised a set of experiments to explicitly test the order of binding/unbinding at the cytoplasmic and extracellular faces. If the binding or release of cargo is a multistep, ordered process, as depicted in the six-state model in Fig. 1, it is possible to inhibit the transporter after substrate translocation by increasing the intracellular concentration of the substrate. This process, known as transinhibition, can be induced by either the driving ion or the substrate, where inhibition is most profound when the concentration of the cargo molecule that comes off first is increased due to “trapping” of the transporter in a state that cannot directly reset to the outward-facing state. Thus, we measured steady-state Na+/glucose currents in the presence of various intracellular solutions to determine those sets of conditions that would inhibit transport, making it possibly to tease apart the order of unbinding to the cytoplasm. Unfortunately, vSGLT expression is poor in oocytes, so we carried out these studies on the closely related human homolog, human SGLT1. We also tested the order of binding to the extracellular face by exploiting the fact that SGLTs can operate reversibly, making it possible to translocate sugars from the inside to the outside of the cell.
Binding to the Extracellular Face Is Ordered.
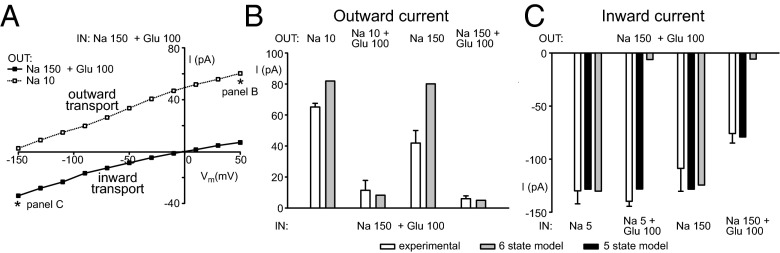
The Na+/glucose current–voltage (I–V) curve recorded from a typical cell in whole-cell mode shows zero current in the absence of an applied voltage when the inner and outer solutions contain 150 mM Na+ and 100 mM glucose (black squares, Fig. 6A). Moving to negative voltages drives Na+ into the cell along the normal transport cycle giving rise to an inward current, whereas positive voltages expel Na+ as the transporter operates in reverse. When Na+ in the extracellular solution is dropped to 10 mM, only outward currents can be measured over the entire voltage range (white squares), indicating that hSGLT1 is operating in reverse. Data taken in the outward transport mode shown in Fig. 6B was recorded at +50 mV (asterisk/ Fig. 6B), and the measurements along the inward transport cycle shown in Fig. 6C were recorded at −150 mV (asterisk/ Fig. 6C). The rationale for these voltage choices is that, although the glucose-induced current is voltage dependent, it becomes voltage independent at the extreme voltages (+50 and −150 mV) (3), allowing us to compare currents measured in cells with the values obtained with simulations.
Fig. 6.
Transinhibition of hSGLT1. (A) Current–voltage relationship of inward (black square) and outward (white squares) currents from a typical cell expressing hSGLT1. The patch pipette was filled with Na+ (150 mM) plus glucose (100 mM). (B) Transinhibition of outward currents measured in HEK-293T cells expressing hSGLT1 (white bars) or predicted by computer simulations (gray bars) using the standard six-state model. Experimental data are means and SEM (n = 9). (C) Transinhibition of inward currents measured cells expressing hSGLT1 (white bars) or predicted by six-state simulations (gray bars) or by five-state simulation (black bars). Experimental data are means and SEM (n = 7).
We first explored binding from the outside by operating under conditions that favor outward transport (Fig. 6B). Substantial outward current could only be evoked with high intracellular Na+(150 mM) and glucose (100 mM) (Fig. S8A). The largest outward current was measured in the presence of low, 10 mM Na+ in the extracellular solution, and increasing the extracellular Na+ 15-fold to 150 mM resulted in only a 35% reduction of the outward current (white bars in Fig. 6B). However, the addition of 100 mM glucose to the extracellular media dramatically reduced the current by 83–93% in low or high Na+, respectively, indicating transinhibition by glucose. To further validate the protocol, we carried out mathematical calculations with our original six-state kinetic model (2) (Fig. 1A, Materials and Methods, and SI Materials and Methods and Table S2), which assumes that ions bind the substrate for both outward- and inward-facing states (gray bars in Fig. 6B). Without any additional parameter modification, the computed outward currents matched the experimental data and were able to predict glucose transinhibition of the outward currents, whereas extracellular Na+ has only a minor effect. Thus, both the patch-clamp experiments and the kinetic modeling support the standard notion that glucose is first off in reverse transport, and hence, it is the last to bind from the outside when undergoing forward transport.
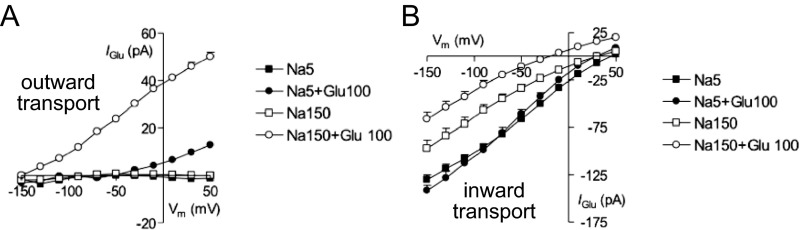
Fig. S8.
Voltage dependence of inward and outward currents. (A) Outward currents measured in the presence of 10 mM Na+ in the extracellular solution. Transinhibition of the outward current was tested with four different intracellular solutions: 5 mM Na+ (black squares), 5 mM Na+ plus 100 mM glucose (black circles), 150 mM Na+ (white squares), and 150 mM Na+ plus 100 mM glucose (white circles). Symbols are means and SEM (n = 9). (B) Inward currents measured in the presence 150 mM Na+ and 100 mM glucose in the extracellular solution. The intracellular solutions and corresponding symbols are the same as those used in A. Symbols are means and SEM (n = 9).
Table S2.
Model parameters for the five-state kinetic model
| k12 = 50,000 M−2⋅s−1 | k21 = 300 s−1 | ε12 = 0.3 | ε21 = 0.3 |
| k16 = 600 s−1 | k61 = 25 s−1 | ε16 = 0.7 | ε61 = 0.7 |
| k23 = 45,000 M−1⋅s−1 | k32 = 20 s−1 | ε23 = 0 | ε32 = 0 |
| k34 = 50 s−1 | k43 = 50 s−1 | ε34 = 0 | ε43 = 0 |
| k46 = 10 s−1 | k64 = 3,750,000 M−3⋅s−1 | ε46 = 0 | ε64 = 0 |
Ion and Substrate Release to the Cytoplasm Is Unordered.
Next, we determined the order of unbinding to the cytoplasm by manipulating the internal concentrations and recording inward currents, induced by extracellular Na+ and glucose, in an attempt to identify conditions that cause transinhibition (Fig. S8B). Remarkably, three conditions with vastly different concentration values (low Na+, high Na+, and low Na+ and high glucose) did not affect the magnitude of the inward current (white bars in Fig. 6C). In fact, only very high intracellular Na+ and glucose concentrations could reduce the transport rate, but only by about 50%. We then compared the computed currents from the standard six-state mathematical model (gray bars) to the experimental results. Calculations from the model predict that intracellular Na+ alone does not have any effect on Na+/glucose inward current, whereas 100 mM glucose (in high and low Na+) cause a strong transinhibition. Although the first prediction is in good agreement with our experimental data, the model fails to explain our results in the presence of glucose. Because sugar comes off first, the model predicts strong transinhibition in the presence of 100 mM glucose, whereas the overall currents in low and high Na+ in the absence of glucose are in good agreement. Similarly, additional simulations in which Na+ unbinds first predict that intracellular Na+ alone would block inward transport. The failure of the six-state model to predict the effect of internal substrates on inward current, coupled with lack of order in substrate release observed in our vSGLT simulations, led us to construct a model in which Na+ and glucose exits are merged into a single step (Table S3). Such a model directly corresponds to the scenario in which unbinding is not ordered. The five-state model correctly predicts the observed experimental results: Na+ or glucose alone do not affect the inward current, and the simultaneous presence of Na+ and glucose are required to decrease inward transport by 50% (black bars in Fig. 6C). Thus, our simulations of vSGLT as well as our experiments and kinetic modeling of hSGLT1 all suggest that substrate unbinding is uncorrelated in SGLTs.
Table S3.
Model parameters for the six-state kinetic model
| k12 = 50,000 M−2⋅s−1 | k21 = 300 s−1 | ε12 = 0.3 | ε21 = 0.3 |
| k16 = 600 s−1 | k61 = 25 s−1 | ε16 = 0.7 | ε61 = 0.7 |
| k23 = 45,000 M−1⋅s−1 | k32 = 20 s−1 | ε23 = 0 | ε32 = 0 |
| k34 = 50 s−1 | k43 = 50 s−1 | ε34 = 0 | ε43 = 0 |
| k45 = 800 s−1 | k25 = 0.01 s−1 | ε45 = 0 | ε54 = 0 |
| k65 = 4,500 M−2⋅s−1 | k56 = 16 s−1 | ε56 = 0 | ε65 = 0 |
SI Materials and Methods
Markov State Model of Na+ Binding/Unbinding Process.
A Markov state model (MSM) of Na+ binding/unbinding from the Na2 site of vSGLT was constructed using the solvent-shells framework first introduced by Harrigan et al. (14). MSMs reduce the complex dynamics of a process in the fully atomistic phase space, into a set of transition rates between discrete states, parameterized by the simulation data. Here, the movement of Na+ in and out of the Na2 site is described by transforming the trajectory data into the occupancy of Na+ in a set of concentric shells surrounding 13 key residues in and around the site. Specifically, we selected the backbone carbonyl oxygen atoms of A62, A63, I65, V185, and A361, the side-chain hydroxyl oxygens of S66, Y176, S183, T188, S364, S365, and S368, and the two carboxyl oxygens of D189 based on inspection of the most prevalent contacts sodium made with the transporter in the region of the Na2 site during the simulations. Around each of the selected atoms, we define shells extending radially from its center, 1.5 Å in width. The instantaneous Na+ density in each shell specifies a vectorial representation of each snapshot with dimensions as follows:
| [S1] |
where is the index of the solute atom (here the oxygen atoms described above), is the index of the shell, and specifies the Na+ ion. Each shell j is parameterized by the radial distance, from solute atom i, and extends from to with a midpoint, . The distance between Na+ k and solute atom i, , parameterizes the indicator function , which equals 1 if Na+ ion k is in the jth shell of solute atom i and zero otherwise. All of the elements of are therefore zero if none of the sodium ions in the simulation are within 6 Å of any of the 14 solute oxygen atoms, representing an apo Na2 site.
After transforming each of the trajectories into its solvent shell representation, we applied time-independent component analysis (tICA) to further reduce the dimensionality of the model space before constructing the MSM (15, 16). The transformation of the trajectories was performed using the WetMSM plugin (14) for MSMBuilder3 (17). All subsequent model building and analysis was also performed using MSMBuilder3 in concert with MDTraj (41).
We then built a large number of candidate MSMs by varying the set of model parameters, namely the number of microstates (clusters), tICA components, and both the lag time of the MSM and the lag time used in determining the tICA components. The grid of parameters is shown in Table S1, and iterating over all combinations of parameters resulted in 576 distinct models. These models were evaluated with regard to the convergence of their implied timescales, their generalized matrix Rayleigh quotient (GMRQ) (42) using threefold cross-validation, as well as the convergence of the first passage time distribution of Na+ escape from the Na2 site determined via kinetic Monte Carlo simulations.
To select a model from among the 576 candidates, we first examined the implied timescales across the range of lag times, τ, computed from the eigenvalues of each MSMs transition probability matrix, , as follows:
| [S2] |
where is the ith eigenvalue of . The implied timescales of a model tend to plateau, becoming approximately constant for long lag times when the model’s dynamics are Markovian. We therefore discarded all models whose slowest implied timescales were still increasing over the entire range of selected lag times. Furthermore, for all parameter sets, lag times less than ∼5 ns were in the rising transient phase of the implied timescale curves so models with lag times <5 ns, were also not considered (Fig. S6).
Finally, threefold cross validation using the rank-3 GMRQ objective function was used to minimize overfitting of the model (42). Models with less than 200 states tended to provide a better balance between the test and training scores.
Generating Long Escape Trajectories from a MSM Using Kinetic Monte Carlo.
From each of the MSMs that showed a good balance between the training and test GMRQ scores as well as well-behaved implied timescales, we used a kinetic Monte Carlo scheme to generate long Na+ escape trajectories to determine the first passage time distribution of this process. For each model we evaluated, we first mapped the crystallographic conformation of Na+ in the Na2 site to one of the MSM microstates. Starting from that microstate, we then generated a long trajectory by sampling the transition probability matrix of the MSM as follows. For a MSM in state i at time t, the probability of transitioning to state j at time is given by the element of , . To propagate the model forward one time step τ, we generate a uniformly distributed random number, R on the interval , and select the state j if . This process is repeated until we reach the state corresponding to the fully apo Na2 site where all of the Na+ ions in the system are in the bulk and >6 Å away from any of the solute atoms. The time required to reach this state is recorded, and then a new trajectory is initiated starting at from the microstate corresponding to the crystallographic conformation. We repeated this procedure 30,000 times to construct an estimate of the first passage time distribution Na+ escape from each model.
Distributions of first passage times for the tested models are shown in Fig. S7. For each lag time examined, the distributions show a high degree of similarity, independent of variations in the other hyperparameters (number of microstates, number of tICA components, and tICA lag time). In agreement with the implied timescale convergence behavior, we observe little difference in the overall shape of the first passage time distributions calculated at lag times of 10 and 20 ns, whereas models with a 5-ns lag time produce escape time distributions displaying slightly faster kinetics. We therefore selected from among the models with a 10-ns lag time to maximize the amount of total sampling used.
Mathematical Model of SGLT1 Transport.
The set of differential equations for the six-state kinetic model is described in the manuscript by Parent et al. (2). For the five-state model presented here, the related equations are as follows:
| [S3] |
where is the occupancy probability for state i, and . Transitions between states and are represented by rate constants : . Eyring rate theory is used to describe the dependence of rate constants on membrane potential (V):
| [S4] |
where is a voltage-independent rate, is the equivalent charge movement (up to the transition state between ), and F, R, and T have their usual physicochemical meanings (2). Na+ and sugar binding on external and internal membrane surfaces is represented by rate constants:
The current () associated with each transition is given by , where e is elementary charge (2). Total current (I) associated with SGLT1 is , and is the total number of transporters in the oocyte plasma membrane.
Computer simulations for the five- and six-state models were performed using Berkeley Madonna 8.0.1. The predictions of the models were examined using voltage pulse protocols for comparison with the electrophysiological experiments. The voltage pulse protocol was simulated by determining the occupancy probabilities at a given holding potential ( = −50 mV). At each test voltage ( ranging from +50 and −150 mV), the time course of the occupancy probabilities was obtained by numerically integrating the system of differential equations using the Runge–Kutta method. Cotransporter currents and steady-state current–voltage relations were calculated as functions of extracellular and intracellular Na+ and glucose concentrations.
The voltage-independent rate constants () and parameters for the five-state model are provided in Table S2. The base rate is determined by enforcing microscopic reversibility:
The voltage-independent rate constants () and parameters for the six-state model are provided in Table S3, where the and rates were determined from microscopic reversibility:
For completeness, we have performed other simulations which are not reported here. Because the net charge transferred between is 1.0 (13), and the stoichiometry for hSGLT1 is 2 Na+:1 glucose, simulations were performed with 1 net charge transferred from . These were performed with different and values, but under the constraint . Our finding was that the results are qualitatively similar, that is, the voltage dependence of the transitions between and does not affect the conclusions that the intracellular release of Na+ and glucose is uncoordinated.
Simulations with TM0.
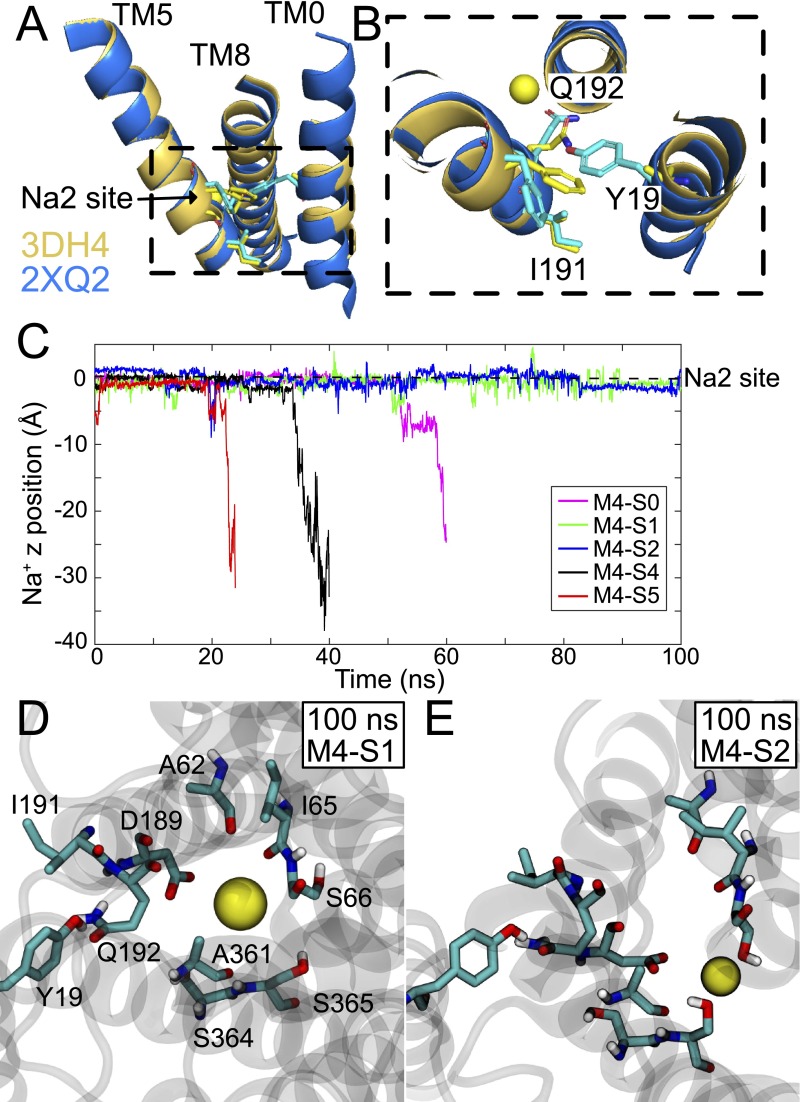
The full structure of vSGLT including the TM0 helix was constructed using MODELLER, version 9.15 (30), along with the galactose-bound crystal structure (PDB ID code 3DH4) and the well-resolved TM0 helix from the apo structure (PDB ID code 2XQ2). Subsequence models are referred to as M4. The structural alignment of TM5 and TM8 of 2XQ2 onto 3DH4 results in a good superposition of the TM0 backbone atoms allowing us to unambiguously assign the residues in TM0, which were deposited as alanine residues in 3DH4 (Fig. S9 A and B). The first unassigned alanine in the 3DH4 structure aligns with F10 in the 2XQ2 structure, and the resulting assignment is identical to the one predicted by Mazier et al. (9). One hundred models were generated, and the MODELLER DOPE score, along with visual inspections of side-chain rotamers of TM0, led to the final model selection used for all subsequent simulations. The protein along with the galactose substrate and the crystallographic Na+ were oriented with respect to the z axis using Orientation of Proteins in Membranes (OPM) (43) and then inserted into a 1-palmitolyl-2-oleoyl-sn-glycero-3-phosphatidylethanolamine (POPE) membrane using the CHARMM-GUI Membrane Builder (31). The system was then solvated in a rectangular box 94 94 102 Å3 in size containing 85,000 atoms and neutralized with 150 mM Na+ and Cl−.
Fig. S9.
vSGLT simulations with TM0 helix. (A) Superposition of 3DH4 structure (gold) onto the 2XQ2 structure (blue) using only the Cα atoms of TM5 and TM8. TM0 backbone from both structures align well. Y19, I191, and Q192 are represented as sticks (cyan from 2XQ2, yellow from 3DH4). (B) Magnified view of dashed box in A. Y19 in TM0 from 2XQ2 is positioned to interact with Q192 in TM5, as predicted by Mazier et al. (9). Although Q192 adopts a slightly different conformation in 3DH4 and 2XQ2, I191 is identical in both structures. (C) Position of bound Na2 Na+ ion in time. Time 0 corresponds to the end of equilibration, and z equal zero is the starting position of Na+ in the X-ray site. Release to the cytoplasm was assumed for z values less than −10 Å. Results for model M4-S3 is not pictured because the Na+ was lost to the cytoplasm before the end of equilibration. The Na+ in models M4-S1 and M4-S2 remains bound for the entire 100-ns simulation. The coordination of the Na+ in the Na2 site at 100 ns for model M4-S1 (D) and model M4-S2 (E). Model M4-S1 retains many of the Na+ contacts observed in the 3DH4 X-ray structure, whereas model M2-S2 does not. In all simulations, Y19 remains directly hydrogen bonded to Q192 throughout most of the simulation. Occasionally, a water molecule mediates the interaction, as observed in ref. 9, but we never observe Y19 form a hydrogen bond to the backbone atoms of I191. A list of Na+ exit times is provided in Table S4.
Next, the system was minimized with NAMD, version 2.9 (37), using conjugate gradient for 10,000 steps. Coordinates were saved at six different times during the minimization procedure: 2,000 (S0), 6,000 (S1), 7,000 (S2), 8,000 (S3), 9,000 (S4), and 10,000 (S5) steps. Simulations were carried out using the CHARMM36 parameter set [CHARMM22 with CMAP correction for the protein (32, 33), CHARMM force field for pyranose monosaccharides for galactose (35), and CHARMM36 for lipids (34)] using a TIP3P water model (36). Each system (S0–S5) was subjected to gradual heating from 10 to 310 K at a rate of 20 K every 15 ps using temperature reassignment. During the heating phase, the dynamics were carried out in a constant volume/temperature (NVT) ensemble with the Na2 site Na+, galactose heavy atoms, and protein backbone heavy atoms restrained with a 10 kcal⋅mol−1⋅Å−2 harmonic force constant. The side-chain and lipid head group heavy atoms were restrained with a 5 kcal⋅mol−1⋅Å−2 force constant. After reaching 310 K, the force constraints were decreased by one-half, and a fast 25-ps simulation in the NVT ensemble was carried out. Next, we switched to an NPT ensemble using the Langevin piston barostat with a 200-fs piston period and 100-fs piston decay constant to maintain the pressure at 1 bar. Temperature was maintained at 310 K using Langevin dynamics with 1 ps−1 damping coefficient. Constraints were gently reduced over the next 1.2 ns, and each system was then allowed to equilibrate for 5 ns without restraints. Finally, each system was simulated for 100 ns or until the Na+ escaped from the Na2 site (Fig. S9C). Bond lengths between hydrogen and heavy atoms were constrained with the SHAKE algorithm, and a 1-fs time step was used for heating and the initial NPT phase, followed by a 2-fs time step for the remainder of the simulations. The particle mesh Ewald summation was applied with an interpolation order of 6 along the grid. The van der Waals interactions were smoothly switched to zero between 11 and 12 Å.
Discussion
Sodium-dependent transporters use the energy stored in the sodium electrochemical potential gradients to accumulate a wide range of small molecules. How ions and substrates interact with the protein to drive the transport cycle is central to understanding transporter function. Here, we took advantage of the fact that these transporters can operate reversibly to test the order of binding at the extracellular face. With high intracellular glucose and Na+, we recorded outward (reverse) currents at +50 mV, and we established that external glucose causes transinhibition whereas high external Na+ does not (Fig. 6B). This finding confirms previous research suggesting that, under forward transport, Na+ binds to the transporter first followed by glucose. Through the manipulation of internal concentrations, we then determined that neither high glucose alone nor high Na+ caused transinhibition, which could not be described with the standard six-state kinetic model that assumes glucose unbinding before Na+ release (22). Calculations with a modified five-state kinetic model in which unbinding is random and independent reproduced the experimental results (Fig. 6C). Thus, the experiments and kinetic modeling indicate that sugar and Na+ unbinding is not ordered, which is surprising because past modeling suggested ordered release (3, 22). That said, we acknowledge that these previous experiments did not carefully probe the influence of intracellular ion and substrate concentrations on transport.
Our simulations carried out on vSGLT also support the claim that intracellular Na+ and sugar release occurs in a random, independent manner (Fig. 2). Generating 21 simulations ranging from 100 to 500 ns is computationally demanding, but essential for drawing mechanistic conclusions given the inherent stochastic nature of proteins operating in a thermal environment. Our observation that galactose sometimes escapes before Na+ is based on our observation of long ion dwell times. Previously, two other groups proposed that conformational changes within the Na2 site could result in a stronger affinity of vSGLT for sodium. We had hoped that the MSM would reveal specific conformations of the Na2 site that corresponded to long Na+ dwell times; however, this was not the case, and instead the distribution of escape times was monoexponential with many different coordination states (Fig. 4 C–E). Mazier et al. (9) observed Na+ remaining in the Na2 site for 60 ns and attributed the increased stability of the ion to their inclusion of the TM0 helix, which contributes a conserved tyrosine into the Na2 interaction network. TM0 was not well resolved in the initial vSGLT structure and is often excluded from simulations (6–8, 10, 18, 21, 23, 24), including the ones presented here. We explored the role of TM0 by carrying out six additional vSGLT simulations with TM0 included (SI Materials and Methods and Table S4). We observed one Na+ release before the completion of equilibration, three releases between 20 and 60 ns, and two simulations where Na+ remained bound out to 100 ns (Fig. S9). These times are quite consistent with those presented in Figs. 2 and 4; thus, the presence of this transmembrane helix alone is not sufficient to account for increased Na+ stability as demonstrated by our results in its absence. Meanwhile, Bisha et al. (23) carried out a set of metadynamics simulations to reveal local rearrangements within Na2 that increased Na+ coordination resulting in longer dwell time up to 70 ns. Our work suggests that the Na+ ion is occasionally well coordinated by multiple protein residues in Na2, but these direct interactions are not required to maintain an occupied binding site. Importantly, Na+ is not pulling together TM5 and TM8, which would be needed to close the intracellular vestibule and help reset the transporter to an outward-facing state. Thus, the states in Fig. 4 C and D are quite distinct from the ion coordination states observed in the outward-facing LeuT Na2 binding site because the protein plays the dominant role in ion coordination for LeuT (25), but the vSGLT states shown here involve both protein and bridging water molecules. Last, we speculate that the variable distribution of dwell times observed in the simulations is related to the stochastic nature of ion release from an electrostatically favorable site with multiple metastable poses rather than the protein switching to a high-affinity ion-binding state.
Table S4.
Sodium escape times with TM0
| Simulation | Escape time |
| M4-S0 | 60 ns |
| M4-S1 | Entire 100 ns |
| M4-S2 | Entire 100 ns |
| M4-S3 | During equilibration |
| M4-S4 | 35 ns |
| M4-S5 | 21 ns |
Previous estimates of glucose and Na+ binding to hSGLT1 from the extracellular space, during inward transport at −150 mV, suggest values of 0.15 and 1.3 mM, respectively (26). This low glucose value corroborates our data in Fig. 6B, in which 100 mM external glucose effectively suppresses transport due to trapping hSGLT1 in the glucose-bound state, which cannot proceed through the rest of the cycle. Meanwhile, previous studies exploring outward transport of rabbit SGLT1 at 0 mV reported much higher cytoplasmic values of 35–50 mM for αMDG in 100 mM NaCl (27, 28)—200–300 times greater than the for inward transport. Similarly, the for Na+ binding is 10 times larger for outward transport compared with inward transport—12 versus 1.3 mM, respectively (26). These increased values for ion and substrate binding from the cytoplasm cannot explain our data alone, as our experiments in Fig. 6C used internal glucose concentrations at least two times higher than the reported values, and we still failed to observe any current reduction. Thus, although the binding is weaker, only independent binding of the ion and substrate explains the data. Our vSGLT simulations of the inward-facing state were carried out in 150 mM NaCl, and we observed 25 unbinding events and 18 rebinding events. Although we hesitate to make solid estimates of the Na+ value to this state, these counts suggest a value greater than 150 mM, which is even weaker than the of 12 mM estimated for hSGLT1 (26). Last, in our previous simulations, we computed the galactose binding free energy to the inward-facing state to be 1–2 kBT (7), again consistent with the weak value reported for rabbit SGLT1 (27, 28).
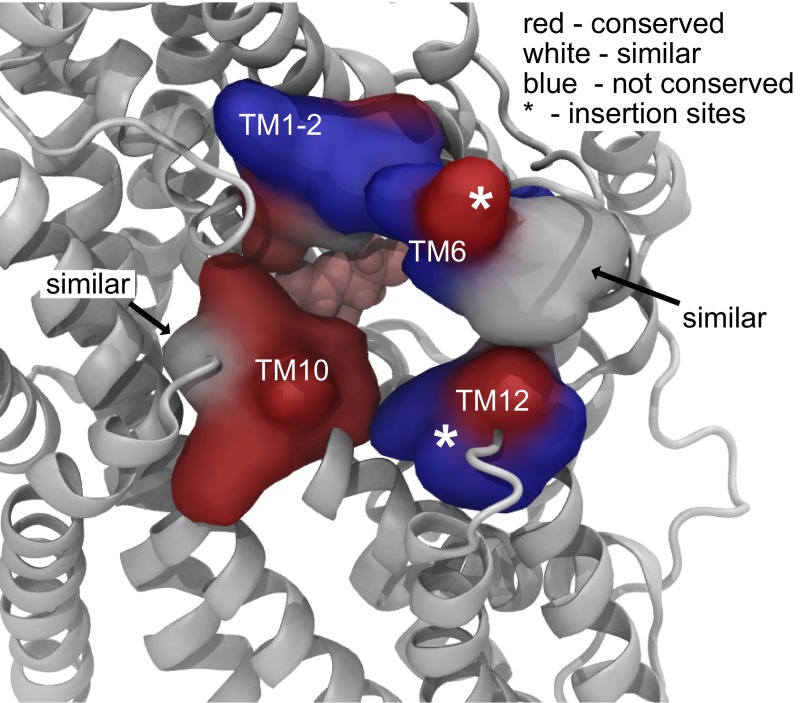
Finally, we want to comment on our finding that galactose exits through the outer gate in 2 out of 21 simulations of vSGLT. The exits are facilitated by side-chain motions of the residues forming the gate rather than a global change in protein conformation. This pathway is shared by water (18–21), but we have never observed Na+ exit through the external gate in 10.8 μs of simulation (6.5 μs reported here plus an additional 4.3 μs). This backflux of sugar indicates that the coupling ratio for Na+ to galactose transport may increase above 1 for vSGLT, as a rough estimate from the observed 10 galactose exits (8 to the cytoplasm and 2 to the extracellular solution) suggests a stoichiometry of 1.25, which may be experimentally indistinguishable from 1. These outward escapes would also reduce the maximal sugar gradient achievable by vSGLT, but we note that the marine bacterium Vibrio parahaemolyticus quickly converts galactose to galactose-6-phosphate, as do many nonepithelial cells, which would potentially obviate concerns about maintaining a sugar gradient. There is no evidence that mammalian SGLTs have a reduced coupling ratio, and our simulations of water flow through vSGLT predict permeability values larger than those measured for hSGLT1, suggesting that closure of the gates may be more tightly coordinated in hSGLT1 (21). There are two insertions in loops of hSGLT1/2 near the extracellular gate that are not present in vSGLT (21), and in general, the conservation along the outer pathway is low (Fig. S10), potentially allowing for a tighter seal in mammalian SGLTs. For hSGLT1, approximately two Na+ ions are coupled to inward sugar transport, but we have found that mutation of the large hydrophobic side chains of the external gates to cysteine also increases the coupling ratio to as high as 6–1 for F453C (F424 in vSGLT) (29). This decreased coupling ratio suggests that mutations in the outer gate increase the probability that partially transported sugars return to the external solution.
Fig. S10.
The outer gate is poorly conserved from vSGLT to hSGLT1. Pictured is a snapshot of vSGLT from a simulation in which the outer gate opens widely. The view is from the extracellular solution, and galactose can be seen in the binding site (pink). The outer gate residues are represented by their molecular surface, and they have been classified into three categories: conserved (red), similar (white), and nonconserved (blue). There are two stretches of amino acids inserted into hSGLT1/2 that are not present in vSGLT (21), and these insertion sites are indicated by asterisks in TM6 and TM12.
There is a large number of sodium-dependent cotransporters that adopts the same fold as SGLT, often referred to as the leucine-transporter fold. Superfamily members include the neurotransmitter sodium symporters (NSS). Given the structural similarity of all of these proteins, we believe that the order of substrate and ion binding at the cytoplasmic face may be similar in other family members. At the extracellular face, ordering is likely tied to increased substrate affinity that occurs once the ions bind the outward-facing state; however, the inward-facing state appears to have low affinity to both molecules and a concomitant loss of coordination between sites. It will be interesting to see whether simulations of the inward-facing conformation of family members that have both Na1 and Na2 Na+ sites also show random release. The experimental data presented here suggest that the cation can bind to the Na2 site from the cytoplasm, and that galactose follows the same pathway through vSGLT in the forward and reverse directions, but what triggers the opening of the external gate to permit Na+ and galactose to exit into the external solution? In general, the order of events is intimately tied to the transporter’s operation as it moves through the pumping cycle. The picture provided here at the intracellular face will help us understand the forces and conformational changes required for resetting the system to the outward-facing state.
Materials and Methods
Simulations.
Molecular-dynamics simulations of vSGLT were generated as previously described (21). The trajectories described therein form the basis for the current analysis. Briefly, four independent all-atom models of monomeric vSGLT based on the inward-occluded, galactose-bound state X-ray structure [Protein Data Bank (PDB) ID code 3DH4] (12), were embedded in a POPE lipid bilayer, using MODELLER (30) and the CHARMM-GUI Membrane Builder (31). The models were parameterized using the CHARMM22 force field (32) with CMAP corrections (33) for the protein, the CHARMM36 lipid force field (34), the CHARMM pyranose monosaccharides parameter set for the galactose (35), and the TIP3P explicit water model (36). Each model was initially minimized and equilibrated using NAMD 2.7 (37). Final coordinates and velocities from these runs were used as initial conditions for simulations on the Anton special-purpose supercomputer (38) and were not used in any subsequent analysis. Complete details of the simulations protocol, including simulations with TM0, are provided in ref. 21, and details of the analysis in this work are given in SI Materials and Methods.
Reagents and Solutions.
The standard extracellular solution (Na+ buffer) contained the following (in mM): 150 NaCl, 2 KCl, 1 CaCl2, 1 MgCl2, and 10 Hepes at pH 7.4. Choline chloride was use to maintained osmotic balance when extracellular Na+ concentration was reduced. Mannitol (100 mM) was added to the extracellular solution when the intracellular solution contained 100 mM glucose to maintain osmotic balance. The standard intracellular solution contained the following (in mM): 145 CsCl, 5 NaCl, 11 EGTA, and 10 Hepes at pH 7.4. For high Na+ intracellular solution, 145 mM CsCl was substituted with 145 mM Na+ (150 mM Na+ total). One hundred millimolar glucose was added to the standard intracellular solution or high Na+ solution as indicated.
Cell Culture and Transfection.
Human embryonic kidney 293T cells (HEK293T) cells were purchased from the American Type Culture Collection and maintained in culture as described elsewhere (39). Cells were grown until 50–70% confluence and then transfected using the Effectene kit (Qiagen) with 1 μg of the hSGLT1-IRES plasmid following protocol instructions as described (39).
Whole-Cell Patch-Clamp Recording.
Our procedure for whole-cell patch-clamp experiments has been explained elsewhere (39). In brief, experiments were performed 2 d after transfection. Cells were plated on 12-mm poly-l-lysine–coated glass coverslips and selected on the basis of fluorescence intensity of GFP using a Nikon diaphot epifluorescence microscope (Nikon). During the experiment, cells were kept at the holding potential = −60 mV and gravity perfused using a set of 0.25-mm cannulas positioned near the cell. For recordings at constant holding potential, currents were filtered at 2 kHz and digitized at 1 kHz. Steady-state kinetics were determined using a voltage step protocol. The membrane voltage was stepped from = −60 mV to the test potential ranging between −150 and in +50 mV in 20-mV increments for a duration of 100 ms and averaged over three sweeps. In this case, the current was filtered at 2 kHz and digitized at 50 kHz. Steady-state glucose currents () were obtained by subtracting the baseline current recorded in Na+ buffer plus phlorizin (Pz) from the total current measured in Na+ buffer plus glucose:
| [1] |
Outward glucose currents were calculated by subtracting the records in the presence of phlorizin from corresponding traces in the presence of 150 or 10 mM Na+:
| [2] |
The concentration of phlorizin used to inhibit hSGLT1 depends on the external Na+ concentration. In 150 mM Na+, 100 μM phlorizin inhibits 95% [ = 0.14 μM (40)], whereas in 10 mM Na+ phlorizin concentration has to be increased to 200 μM to observe a 80% inhibition of the inward glucose current.
Mathematical Model of SGLT1 Transport.
The differential equations corresponding to the five- and six-state models of Na+/glucose cotransport were solved with Berkeley Madonna 8.0.1. The time course of the occupancy probabilities for each state in the cycle were obtained by numerically integrating the differential equation using the Runge–Kutta method. The cotransport currents were obtained from the occupation probabilities, and the system was run to steady state to generate current–voltage values as a function of intracellular and extracellular Na+ and glucose concentrations. A full description of the simulation details together with the equations are presented in SI Materials and Methods.
Acknowledgments
We thank Frank V. Marcoline, Michael Bokoch, and Pushkar Pendse for helpful discussions. We also acknowledge Matthew Jacobson for his help with small-molecule docking. Simulations were performed on the Anton special-purpose supercomputer provided by the National Resource for Biomedical Supercomputing (NRBSC), the Pittsburgh Supercomputing Center (PSC), and the Biomedical Technology and Research Center for Multiscale Modeling of Biological Systems through Grant P41GM103712-S1 from the National Institutes of Health and Grant PSCA00015P (to M.G.). The Anton machine at NRBSC/PSC was generously made available by D. E. Shaw Research. Simulations were also performed at the San Diego Supercomputer Center through the support of Grant MCB-80011 (to M.G. and J.L.A.) from the Extreme Science and Engineering Discovery Environment, which is supported by National Science Foundation Grant ACI-1053575. This work was supported by National Institutes of Health Grants GM089740 (to M.G. and J.M.R.), T32-DK061296 (to J.L.A.), DK19567 (to E.M.W.), and GM078844 (to J.A.). The work of S.C. was supported by a start-up fund from Daegu Gyeongbuk Institute of Science and Technology.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1525378113/-/DCSupplemental.
References
- 1.Jardetzky O. Simple allosteric model for membrane pumps. Nature. 1966;211(5052):969–970. doi: 10.1038/211969a0. [DOI] [PubMed] [Google Scholar]
- 2.Parent L, Supplisson S, Loo DD, Wright EM. Electrogenic properties of the cloned Na+/glucose cotransporter: II. A transport model under nonrapid equilibrium conditions. J Membr Biol. 1992;125(1):63–79. doi: 10.1007/BF00235798. [DOI] [PubMed] [Google Scholar]
- 3.Wright EM, Loo DD, Hirayama BA. Biology of human sodium glucose transporters. Physiol Rev. 2011;91(2):733–794. doi: 10.1152/physrev.00055.2009. [DOI] [PubMed] [Google Scholar]
- 4.Veenstra M, Lanza S, Hirayama BA, Turk E, Wright EM. Local conformational changes in the Vibrio Na+/galactose cotransporter. Biochemistry. 2004;43(12):3620–3627. doi: 10.1021/bi0357210. [DOI] [PubMed] [Google Scholar]
- 5.Turk E, Gasymov OK, Lanza S, Horwitz J, Wright EM. A reinvestigation of the secondary structure of functionally active vSGLT, the vibrio sodium/galactose cotransporter. Biochemistry. 2006;45(5):1470–1479. doi: 10.1021/bi052160z. [DOI] [PubMed] [Google Scholar]
- 6.Li J, Tajkhorshid E. Ion-releasing state of a secondary membrane transporter. Biophys J. 2009;97(11):L29–L31. doi: 10.1016/j.bpj.2009.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Watanabe A, et al. The mechanism of sodium and substrate release from the binding pocket of vSGLT. Nature. 2010;468(7326):988–991. doi: 10.1038/nature09580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zomot E, Bahar I. The sodium/galactose symporter crystal structure is a dynamic, not so occluded state. Mol Biosyst. 2010;6(6):1040–1046. doi: 10.1039/b927492h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mazier S, Quick M, Shi L. Conserved tyrosine in the first transmembrane segment of solute:sodium symporters is involved in Na+-coupled substrate co-transport. J Biol Chem. 2011;286(33):29347–29355. doi: 10.1074/jbc.M111.263327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Li J, Tajkhorshid E. A gate-free pathway for substrate release from the inward-facing state of the Na+-galactose transporter. Biochim Biophys Acta. 2012;1818(2):263–271. doi: 10.1016/j.bbamem.2011.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li Z, et al. Identification of a second substrate-binding site in solute-sodium symporters. J Biol Chem. 2015;290(1):127–141. doi: 10.1074/jbc.M114.584383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Faham S, et al. The crystal structure of a sodium galactose transporter reveals mechanistic insights into Na+/sugar symport. Science. 2008;321(5890):810–814. doi: 10.1126/science.1160406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Loo DD, Jiang X, Gorraitz E, Hirayama BA, Wright EM. Functional identification and characterization of sodium binding sites in Na symporters. Proc Natl Acad Sci USA. 2013;110(47):E4557–E4566. doi: 10.1073/pnas.1319218110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Harrigan MP, Shukla D, Pande VS. Conserve water: A method for the analysis of solvent in molecular dynamics. J Chem Theory Comput. 2015;11(3):1094–1101. doi: 10.1021/ct5010017. [DOI] [PubMed] [Google Scholar]
- 15.Pérez-Hernández G, Paul F, Giorgino T, De Fabritiis G, Noé F. Identification of slow molecular order parameters for Markov model construction. J Chem Phys. 2013;139(1):015102. doi: 10.1063/1.4811489. [DOI] [PubMed] [Google Scholar]
- 16.Schwantes CR, Pande VS. Improvements in Markov state model construction reveal many non-native interactions in the folding of ntl9. J Chem Theory Comput. 2013;9(4):2000–2009. doi: 10.1021/ct300878a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Beauchamp KA, et al. MSMBuilder2: Modeling conformational dynamics at the picosecond to millisecond scale. J Chem Theory Comput. 2011;7(10):3412–3419. doi: 10.1021/ct200463m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Choe S, Rosenberg JM, Abramson J, Wright EM, Grabe M. Water permeation through the sodium-dependent galactose cotransporter vSGLT. Biophys J. 2010;99(7):L56–L58. doi: 10.1016/j.bpj.2010.08.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sasseville LJ, Cuervo JE, Lapointe JY, Noskov SY. The structural pathway for water permeation through sodium-glucose cotransporters. Biophys J. 2011;101(8):1887–1895. doi: 10.1016/j.bpj.2011.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li J, et al. Transient formation of water-conducting states in membrane transporters. Proc Natl Acad Sci USA. 2013;110(19):7696–7701. doi: 10.1073/pnas.1218986110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Adelman JL, et al. Structural determinants of water permeation through the sodium-galactose transporter vSGLT. Biophys J. 2014;106(6):1280–1289. doi: 10.1016/j.bpj.2014.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Loo DD, Hirayama BA, Karakossian MH, Meinild AK, Wright EM. Conformational dynamics of hSGLT1 during Na+/glucose cotransport. J Gen Physiol. 2006;128(6):701–720. doi: 10.1085/jgp.200609643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bisha I, Laio A, Magistrato A, Giorgetti A, Sgrignani J. A candidate ion-retaining state in the inward-facing conformation of sodium/galactose symporter: Clues from atomistic simulations. J Chem Theory Comput. 2013;9(2):1240–1246. doi: 10.1021/ct3008233. [DOI] [PubMed] [Google Scholar]
- 24.Bisha I, Rodriguez A, Laio A, Magistrato A. Metadynamics simulations reveal a Na+ independent exiting path of galactose for the inward-facing conformation of vSGLT. PLoS Comput Biol. 2014;10(12):e1004017. doi: 10.1371/journal.pcbi.1004017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yamashita A, Singh SK, Kawate T, Jin Y, Gouaux E. Crystal structure of a bacterial homologue of Na+/Cl−-dependent neurotransmitter transporters. Nature. 2005;437(7056):215–223. doi: 10.1038/nature03978. [DOI] [PubMed] [Google Scholar]
- 26.Quick M, Tomasevic J, Wright EM. Functional asymmetry of the human Na+/glucose transporter (hSGLT1) in bacterial membrane vesicles. Biochemistry. 2003;42(30):9147–9152. doi: 10.1021/bi034842x. [DOI] [PubMed] [Google Scholar]
- 27.Eskandari S, Wright EM, Loo DD. Kinetics of the reverse mode of the Na+/glucose cotransporter. J Membr Biol. 2005;204(1):23–32. doi: 10.1007/s00232-005-0743-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sauer GA, Nagel G, Koepsell H, Bamberg E, Hartung K. Voltage and substrate dependence of the inverse transport mode of the rabbit Na+/glucose cotransporter (SGLT1) FEBS Lett. 2000;469(1):98–100. doi: 10.1016/s0014-5793(00)01255-2. [DOI] [PubMed] [Google Scholar]
- 29.Sala-Rabanal M, et al. Bridging the gap between structure and kinetics of human SGLT1. Am J Physiol Cell Physiol. 2012;302(9):C1293–C1305. doi: 10.1152/ajpcell.00397.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sali A, Blundell TL. Comparative protein modelling by satisfaction of spatial restraints. J Mol Biol. 1993;234(3):779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
- 31.Jo S, Kim T, Im W. Automated builder and database of protein/membrane complexes for molecular dynamics simulations. PLoS One. 2007;2(9):e880. doi: 10.1371/journal.pone.0000880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.MacKerell AD, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102(18):3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 33.Mackerell AD, Jr, Feig M, Brooks CL., 3rd Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J Comput Chem. 2004;25(11):1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 34.Klauda JB, et al. Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types. J Phys Chem B. 2010;114(23):7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Guvench O, et al. Additive empirical force field for hexopyranose monosaccharides. J Comput Chem. 2008;29(15):2543–2564. doi: 10.1002/jcc.21004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79(2):926–935. [Google Scholar]
- 37.Phillips JC, et al. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26(16):1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shaw DE, et al. Millisecond-Scale Molecular Dynamics Simulations on Anton. ACM; New York: 2009. [Google Scholar]
- 39.Hummel CS, et al. Glucose transport by human renal Na+/d-glucose cotransporters SGLT1 and SGLT2. Am J Physiol Cell Physiol. 2011;300(1):C14–C21. doi: 10.1152/ajpcell.00388.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hummel CS, et al. Structural selectivity of human SGLT inhibitors. Am J Physiol Cell Physiol. 2012;302(2):C373–C382. doi: 10.1152/ajpcell.00328.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.McGibbon RT, et al. Mdtraj: A modern open library for the analysis of molecular dynamics trajectories. Biophys J. 2015;109(8):1528–1532. doi: 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.McGibbon RT, Pande VS. Variational cross-validation of slow dynamical modes in molecular kinetics. J Chem Phys. 2015;142(12):124105. doi: 10.1063/1.4916292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lomize MA, Lomize AL, Pogozheva ID, Mosberg HI. OPM: Orientations of proteins in membranes database. Bioinformatics. 2006;22(5):623–625. doi: 10.1093/bioinformatics/btk023. [DOI] [PubMed] [Google Scholar]
- 44.Friesner RA, et al. Glide: A new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. J Med Chem. 2004;47(7):1739–1749. doi: 10.1021/jm0306430. [DOI] [PubMed] [Google Scholar]