Early life stages contribute strongly to local adaptation in Arabidopsis thaliana

Significance

Organisms are often adapted to local environmental conditions. Yet, the contribution of genetic differences expressed during early life stages to the magnitude and genetic basis of local adaptation are poorly known. We planted seeds of recombinant inbred lines derived from a cross between populations of the model plant Arabidopsis thaliana in Italy and Sweden at the parental sites, and mapped quantitative trait loci (QTL) for fitness and its components. Natural selection strongly favored the local genotype during seedling establishment, and QTL for establishment contributed to local adaptation and genetic fitness tradeoffs. The results demonstrate that adaptive differentiation during early life stages can be strong and should be considered for a full understanding of the ecology and genetics of local adaptation.

Abstract

The magnitude and genetic basis of local adaptation is of fundamental interest in evolutionary biology. However, field experiments usually do not consider early life stages, and therefore may underestimate local adaptation and miss genetically based tradeoffs. We examined the contribution of differences in seedling establishment to adaptive differentiation and the genetic architecture of local adaptation using recombinant inbred lines (RIL) derived from a cross between two locally adapted populations (Italy and Sweden) of the annual plant Arabidopsis thaliana. We planted freshly matured, dormant seeds (>180 000) representing >200 RILs at the native field sites of the parental genotypes, estimated the strength of selection during different life stages, mapped quantitative trait loci (QTL) for fitness and its components, and quantified selection on seed dormancy. We found that selection during the seedling establishment phase contributed strongly to the fitness advantage of the local genotype at both sites. With one exception, local alleles of the eight distinct establishment QTL were favored. The major QTL for establishment and total fitness showed evidence of a fitness tradeoff and was located in the same region as the major seed dormancy QTL and the dormancy gene DELAY OF GERMINATION 1 (DOG1). RIL seed dormancy could explain variation in seedling establishment and fitness across the life cycle. Our results demonstrate that genetically based differences in traits affecting performance during early life stages can contribute strongly to adaptive differentiation and genetic tradeoffs, and should be considered for a full understanding of the ecology and genetics of local adaptation.

Identifying the ecological and genetic mechanisms underlying local adaptation, defined as the local genotype outperforming nonlocal genotypes (1), is a central problem in evolutionary biology. Local adaptation is common in both plant and animal species (2–5), promotes the maintenance of genetic variation (6, 7), and is a key component of models of speciation (8, 9). However, the relative importance of traits contributing to adaptive differentiation and their underlying genetic architecture remain poorly known (1, 7, 10, 11). One key question is whether local adaptation results from genetic tradeoffs (antagonistic pleiotropy) in which locally favored alleles reduce fitness elsewhere or is caused by alleles that are conditionally neutral (favored in the home environment but selectively neutral in other environments). Empirical studies have rarely detected genetic tradeoffs (12–14), but these studies typically include only part of the life cycle (3, 5, 15), possibly resulting in a systematic underestimation of the magnitude of adaptive differentiation and of the occurrence of genetically based tradeoffs.

Early life stages can be expected to play a prominent role in local adaptation. First, selection can be particularly severe during the first part of the life cycle when organisms are vulnerable and suffer from high mortality rates (15–19). Second, conditions early in life often have cascading effects on later life-history traits (16, 20, 21). For example, resource availability during the juvenile stage can affect subsequent survival and fecundity (20). Moreover, these delayed life-history effects may be transmitted across generations in the form of maternal effects (16, 20, 21).

So far, early life stages have received little attention in studies exploring the magnitude and genetic basis of local adaptation (15, 16). For instance, field experiments with plants are usually based on the transplantation of seedlings (12–14, 22–28) and therefore do not assess the importance of possible adaptive differentiation and genetic tradeoffs expressed at the seed and germination stage. Indirect evidence suggests that the seed stage may contribute considerably to local adaptation. Field studies have shown that germination timing is subject to strong natural selection in a wide range of plant species (15, 29). In many species, the timing of germination is controlled by seed dormancy, which is a heritable trait (30, 31) that shows evidence of adaptive differentiation. Up to 90% of the plant species in temperate regions produce seeds that are dormant at maturation (31), and intraspecific genetic variation in seed dormancy has been documented along altitudinal (32, 33) and latitudinal gradients (34–36). Moreover, sequence variation in the dormancy gene DELAY OF GERMINATION 1 (DOG1) in Arabidopsis thaliana indicates local adaptation (34), and the level of seed dormancy has been shown to be important for establishment success in novel environments (37).

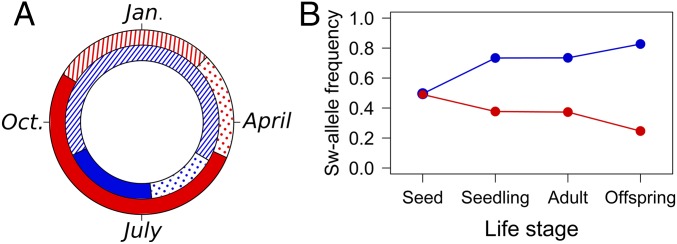
We studied the contribution of early life stages to local adaptation by examining the adaptive significance and genetic basis of differences expressed during the seed and seedling stages in the annual plant A. thaliana. To do so, we used a recombinant inbred line (RIL) population derived from a cross between two natural populations from close to the southern and northern limits of its native range (Italy and Sweden). Both populations have a winter-annual life cycle: They germinate and produce a rosette in the fall, flower in the following spring, and disperse ripe seeds in early summer. However, the length of the seed stage is more than twice as long in the natural population in Italy as in Sweden (Fig. 1A). Consistent with this difference, the seeds produced by the Italian genotype have a higher dormancy level than the seeds produced by the Swedish genotype (38), meaning that they require a longer period of after-ripening to become germinable. This higher dormancy level is likely an adaptation to prevent germination during the long and dry Italian summers, which pose a high mortality risk for seedlings. Nine quantitative trait loci (QTL) have been identified underlying the difference in seed dormancy of these populations, with the main-effect QTL colocalizing with the dormancy gene DOG1 (38). Previous reciprocal transplant experiments have demonstrated that the two populations show strong local adaptation (14, 39) and that relatively few genomic regions can explain much of the adaptive divergence of the two populations (14). However, because the plants in the QTL mapping experiments were planted at the field sites as seedlings (14), fitness effects of genes influencing the seed and germination stage may have been missed.

Fig. 1.

Life cycle variation in A. thaliana. (A) The length of the major life stages in natural populations in Italy (red) and Sweden (blue). Filled areas: seed stage, hatched areas: vegetative stage; dotted areas: reproductive stage. (B) Change in frequency of the Swedish allele at the marker closest to the mean point estimate of the fitness QTL Q9 within one generation in the RIL population planted in Italy (red) and Sweden (blue). The frequency of the Swedish allele is given among seeds planted (Seed), among established seedlings (Seedling), among plants alive at harvest (Adult), and among fruits produced (Offspring, based on RIL median number of fruits produced).

We conducted a reciprocal transplant experiment including the complete A. thaliana life cycle by planting >180,000 seeds representing >200 RILs at the native field sites of the parental genotypes in the period when seed dispersal occurred in the natural populations. Because both the level and the genetic basis of seed dormancy are affected by maternal environmental conditions during seed maturation (38, 40), we produced the experimental seeds at the field sites where they were to be planted. We estimated the strength of selection during different life stages and mapped QTL for fitness and its components (seedling establishment, survival, and fecundity). One advantage of using RILs is that traits measured in different experiments can easily be linked (41). Here we quantified selection on seed dormancy by relating RIL performance in the present experiment to estimates of seed dormancy obtained for the same RILs in a previous study (38).

We hypothesized that (i) selection during seedling establishment contributes to local adaptation, (ii) local alleles of establishment QTL increase fitness and contribute to fitness tradeoffs, and (iii) variation in seedling establishment can be explained by differences in seed dormancy. Our results demonstrate that early life stages are subject to strong natural selection and play a prominent role in local adaptation.

Results

Selection During Seedling Establishment Contributes Strongly to Fitness Differences Between the Parental Genotypes.

At both sites, the total fitness (number of fruits per viable seed planted) of the local genotype was much higher than that of the nonlocal genotype [significant genotype × site interaction in two-way generalized linear models (GLM); Fig. 2 and Tables S1 and S2], resulting in selection coefficients of 0.92 (Italy) and 0.93 (Sweden; Table S1). In Italy, the local genotype had 14.4 times higher fitness than the nonlocal genotype; this higher fitness was the result of 2.8 times higher establishment success (number of seedlings alive at the end of the germination period per viable seed planted) and 4.8 times higher fecundity (number of fruits per surviving plant). In Sweden, the local genotype had 13.0 times higher fitness than the nonlocal genotype, mainly because of a 10.0 times higher establishment success. Frequent monitoring of germination in Sweden indicated that the higher establishment success of the local genotype (18% vs. 1.8%; Table S1) was explained by a markedly higher proportion of seeds germinating (mean ± SE: Swedish parental genotype, 33.3 ± 2.1%, n = 80; Italian parental genotype, 3.1 ± 0.5%, n = 79), although the survival of young seedlings until the assessment of establishment success at the end of the germination period was somewhat lower (62 ± 3%, n = 80 vs. 71 ± 6%, n = 46).

Fig. 2.

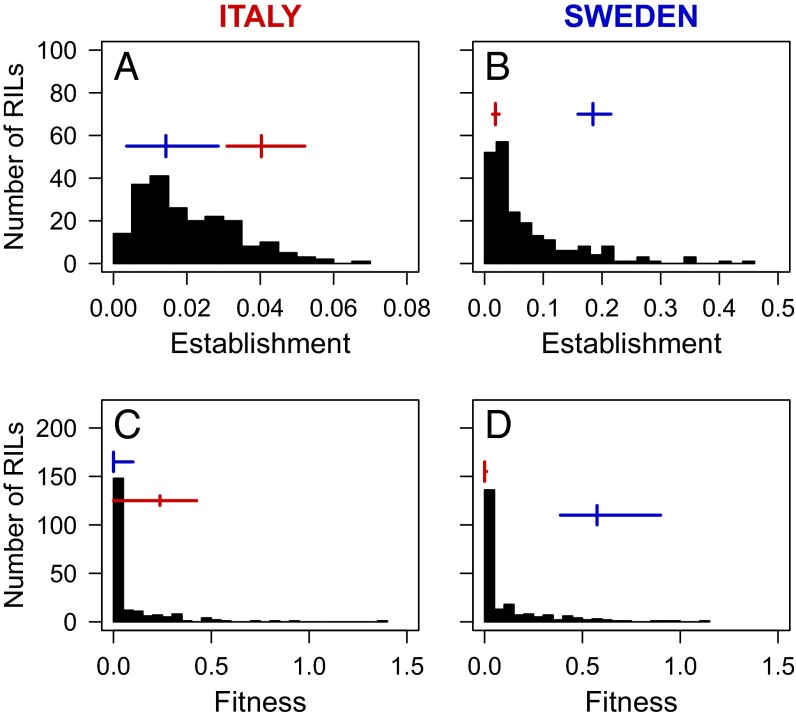
Frequency distributions of mean establishment and median fitness of 209 RILs in Italy (A and C) and 219 RILs in Sweden (B and D). The vertical and horizontal lines show the mean establishment and median fitness values of the Italian (red) and Swedish (blue) genotype with corresponding 95% confidence intervals. Note the difference in the scale of the x axis for establishment in A and B.

Table S1.

Fitness of the Italian and Swedish genotypes of A. thaliana

Variable	Site	Italian genotype	n	Swedish genotype	n	s
Total fitness	Italy	3.290 ± 1.059	80	0.229 ± 0.130	14	0.93
	Sweden	0.105 ± 0.034	79	1.365 ± 0.233	80	0.92
Establishment	Italy	0.0403 ± 0.0054	80	0.0143 ± 0.0063	14	0.65
	Sweden	0.0184 ± 0.0029	79	0.1847 ± 0.0145	80	0.90
Survival	Italy	1.00 ± 0	47	1.00 ± 0	5	0
	Sweden	0.75 ± 0.07	40	0.90 ± 0.03	79	0.17
Fecundity	Italy	62.06 ± 16.61	47	12.80 ± 4.31	5	0.79
	Sweden	7.55 ± 1.93	33	7.96 ± 1.05	71	0.05

Mean (±SE) fitness (number of fruits produced per viable seed planted), and its components establishment (number of seedlings alive at the end of the germination period per viable seed planted), survival (proportion of plants surviving to reproduce) and fecundity (fruit production of survivors) of the Italian and Swedish genotype of Arabidopsis thaliana, and the selection coefficients (s) quantifying the strength of selection (s = 1 − [mean fitness of less fit genotype/mean fitness of fittest genotype]).

Table S2.

Effect of site and genotype on fitness and its components of the parental genotypes

Response	Source of variation	df/Δdf	Deviance	F or χ2	P
Establishment*	Site	250/1	842.5	6.3	0.013
	Genotype	250/1	1,225.8	122.8	<0.001
	Site × genotype	249/1	821.9	59.7	<0.001
Survival†	Site	NA	NA	NA	NA
	Genotype	118/1	101.1	4.3	0.037
	Site × genotype	NA	NA	NA	NA
Fecundity‡	Site	153/1	222.9	44.0	<0.001
	Genotype	153/1	179.2	0.3	0.605
	Site × genotype	152/1	183.9	5.4	0.020
Fitness‡	Site	250/1	153.4	30.2	<0.001
	Genotype	250/1	137.8	14.5	<0.001
	Site × genotype	249/1	144.2	19.0	<0.001

The effects of site (Italy vs. Sweden) and genotype (Italian vs. Swedish) on fitness and on the three fitness components establishment, survival, and fecundity of the parental genotypes were analyzed with GLMs. The significance of each explanatory variable and interaction term was tested by comparing the change in deviance between the full model and a reduced model. For survival, we tested the effect of genotype only in Sweden, because in Italy all plants of both parental lines survived. Significant P-values are shown in bold.

^*Quasibinomial error distribution with logit link, F-test.

^†Binomial error distribution with logit link, χ²-test.

^‡Negative binomial error distribution with log link, χ²-test.

Local Alleles of Establishment QTL Are Favored by Selection and Contribute to Fitness Tradeoffs.

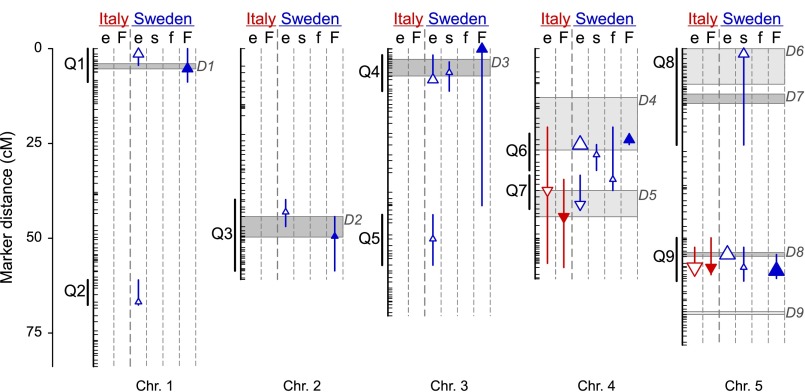
For total fitness and all three fitness components at both sites, some RILs had phenotypic values beyond the 95% confidence intervals of the parental genotypes, suggesting transgressive segregation (Fig. 2 and Fig. S1). We identified five QTL for total fitness in Sweden that together explained 35.0% of the variance among RILs, and two QTL in Italy explaining 13.3% of the variance in RIL fitness (Fig. 3 and Table S3). Among the three fitness components, we identified the greatest number of QTL for establishment (eight QTL in Sweden, two QTL in Italy), followed by survival (four QTL in Sweden, zero QTL in Italy) and fecundity (one QTL in Sweden, zero QTL in Italy; Fig. 3 and Table S3). In total, we identified nine distinct QTL for total fitness and the fitness components; all QTL for total fitness overlapped with establishment QTL. The local genotype was favored for all QTL, with the exception of one establishment QTL with a moderate effect size in Sweden (Q7), for which the Swedish allele was associated with lower establishment. Two epistatic interactions were detected, one for establishment (Q6 × Q9) and one for survival (Q4 × Q6) in Sweden, but both had only weak effects (Fig. S2 and Table S3).

Fig. S1.

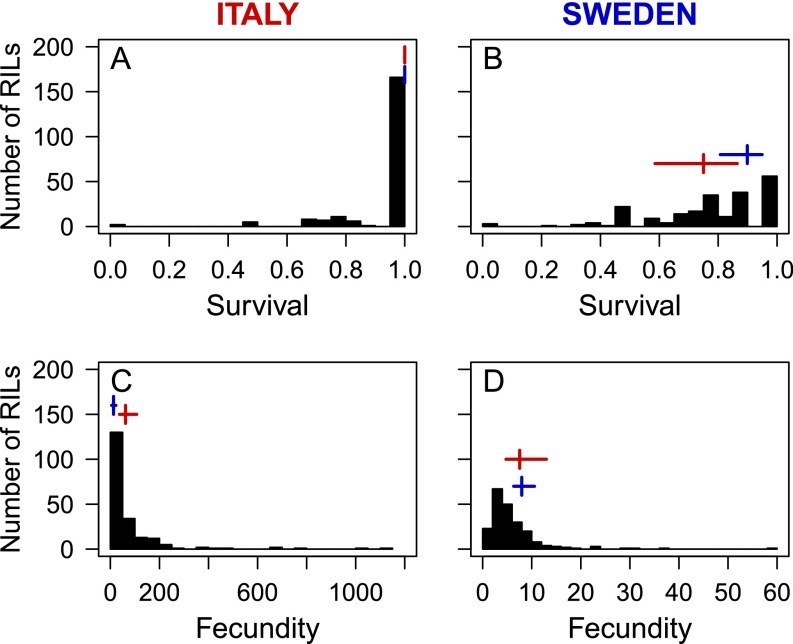
Frequency distributions of mean survival and fecundity of 209 RILs in Italy (A and C) and 219 RILs in Sweden (B and D). The vertical and horizontal lines show the mean survival and fecundity values of the Italian (red) and Swedish (blue) genotype with corresponding 95% confidence intervals. Note the difference in the scale of the x axis for fecundity in C and D.

Fig. 3.

QTL identified for total fitness (F; closed symbols) and its components establishment (e), survival (s), and fecundity (f) (open symbols) in Italy (red) and Sweden (blue). The triangle (with vertical line) shows the point estimate (with 95% Bayesian credible interval) of the QTL position. The orientation of the triangle indicates the effect of the Swedish genotype (upward, higher phenotype value; downward, lower phenotype value), and the size of the triangle represents the proportion of phenotypic variance among RILs explained by the QTL (small, ≤5%; medium, 5–10%; large, ≥10%). The black vertical lines specify the locations of the distinct QTL identified for total fitness and the fitness components (Q1–Q9; Methods). The boxes present the 95% Bayesian credible intervals for dormancy QTL (D1–D9) identified in one maternal environment (light gray) and the range of point estimates for dormancy QTL detected in more than one maternal environment (dark gray) in a previous study of the same RIL population (38).

Table S3.

QTL and epistatic interactions detected for fitness and its components establishment, survival and fecundity in a seed transplant experiment in Italy and Sweden

		Fitness				Establishment				Survival				Fecundity
QTL	Chr	Position (95% Bayes)	LOD	Effect size	PVE	Position (95% Bayes)	LOD	Effect size	PVE	Position (95% Bayes)	LOD	Effect size	PVE	Position (95% Bayes)	LOD	Effect size	PVE
Italy
Q7	4	44.3* (34.5–57.7)	3.3	−0.096	6.6	37.4 (20.7–56.6)	4.1	−0.008	7.2	—	—	—	—	—	—	—	—
Q9	5	57.7 (49.9–59.6)	3.8	−0.097	7.5	57.7 (52.4–58.6)	8.6	−0.011	16.0	—	—	—	—	—	—	—	—
Full model			6.5		13.3		11.9		23.1	—	—	—	—	—	—	—	—
Sweden
Q1	1	5.3* (0.0–8.8)	4.2	0.101	6.0	1.4 (1.4–4.4)	9.5	0.050	9.4	—	—	—	—	—	—	—	—
Q2	1	—	—	—	—	66.8 (61.0–67.6)	4.4	0.033	4.1	—	—	—	—	—	—	—	—
Q3	2	49.58* (44.3–58.6)	3.4	0.089	4.8	43.1 (39.8–46.9)	1.3	0.017	1.2	—	—	—	—	—	—	—	—
Q4	3	0.1 (0.0–41.4)	4.5	0.104	6.4	8.2 (1.7–8.2)	7.3	0.044	7.1	6.3* (3.5–11.2)	2.3	0.079	4.2	—	—	—	—
Q5	3	—	—	—	—	50.2 (43.8–57.1)	1.0	0.015	0.9	—	—	—	—	—	—	—	—
Q6	4	24.0* (22.4–24.3)	4.2	0.102	6.0	25.3* (25.3–25.3)	12.1	0.069	12.4	28.0 (25.3–32.1)	2.1	0.072	3.8	—	—	—	—
Q7	4	—	—	—	—	41.1* (33.4–42.3)	6.5	−0.049	6.3	—	—	—	—	34.5 (20.7–37.4)	1.8	2.46	3.8
Q8	5	—	—	—	—	—	—	—	—	1.4* (0.0–25.4)	2.8	0.090	5.2	—	—	—	—
Q9	5	58.6 (54.3–60.6)	9.4	0.153	14.2	54.3* (54.3–54.3)	14.8	0.064	15.6	57.7 (52.4–61.3)	0.4	0.033	0.7	—	—	—	—
Q6xQ9	—	—	—	—	—	—	0.1	−0.006	0.1	—	—	—	—	—	—	—	—
Q4xQ6	—	—	—	—	—	—	—	—	—	—	0.1	0.020	0.3	—	—	—	—
Full model			20.5		35.0		40.5		57.3		7.6		15.0		1.8		3.8

The chromosome (chr), point estimate in cM with 95% Bayesian credible interval (95%Bayes), LOD score, effect size, and the percentage of variance explained (PVE) are given for each QTL detected. QTL were considered to be the same when their 95% Bayesian credible intervals were <15.2 cM and overlapped with each other. QTL with a credible interval >15.2 cM that overlapped with the point estimate of another QTL are placed under that QTL or under the QTL with the shortest distance between the point estimates if it overlapped with more than one QTL and are shown in italic type. A positive effect size indicates that the Swedish genotype is associated with a higher phenotypic value than is the Italian genotype.

^*The point estimate overlaps with the credible intervals <15.2 cM for distinct dormancy QTL identified in one maternal environment or the range of point estimates for dormancy QTL detected in two or more maternal environments in the same RIL population (Fig. 3) (38).

Fig. S2.

Interaction plots for the two epistatic interactions detected between QTL for establishment in Sweden (A) and QTL for survival in Sweden (B). The mean ± SE phenotype for each genotype × genotype combination is indicated.

The effects of all six QTL for total fitness varied between the two sites (significant QTL × environment interactions). Total fitness QTL Q9, which had the largest effect size and influenced establishment at both sites and survival in Sweden (Fig. 3), showed a clear tradeoff, with the local allele being favored at each site (contrasts in GLM, P < 0.05); the other five fitness QTL were conditionally neutral (Table S4). The tradeoff QTL Q9 was under strong selection: The frequency of the Swedish allele at the closest marker location was present in 49% (Italy) and 50% (Sweden) of the seeds sown at the start of the experiment and increased up to 83% among the fruits produced in Sweden but decreased to 25% among the fruits produced in Italy (Fig. 1B).

Table S4.

Effects of site and genotype of the six QTL on the number of fruits produced per viable seed planted

Source of variation	df/Δdf	Deviance	F	P
Site	397/1	88.2	5.8	0.016
Q1 (X1_2689578)	397/1	87.3	1.7	0.194
Q3 (X2_13716369)	397/1	88.5	7.5	0.007
Q4 (X3_656579)	397/1	90.2	15.2	<0.001
Q6 (X4_6498644)	397/1	91.2	19.5	<0.001
Q7 (X4_11157390)	397/1	92.3	24.9	<0.001
Q9 (X5_20095240)	397/1	88.0	4.9	0.027
Site × Q1	391/1	68.4	29.1	<0.001
Site × Q3	391/1	65.3	10.0	0.002
Site × Q4	391/1	65.0	8.1	0.005
Site × Q6	391/1	64.4	4.8	0.029
Site × Q7	391/1	66.2	15.8	<0.001
Site × Q9	391/1	75.9	75.2	<0.001

Effects of site (Italy vs. Sweden) and genotype (Italian vs. Swedish) were examined with GLMs with quasi-Poisson error distribution and log link function. The significance of each explanatory variable and interaction term was tested by comparing the change in deviance between the full model and a reduced model with an F-test. Significant P-values are shown in bold.

Seed Dormancy Explains Variation in RIL Establishment and Has Cascading Effects Across the Life Cycle.

Seeds were planted soon after maturation, i.e., at a time when seed dormancy differs strongly between the two parental genotypes and varies widely in the RIL population (38). To examine the adaptive significance of seed dormancy, we related dormancy estimates obtained for field-matured seeds of the same RILs in a previous experiment (38) to RIL germination behavior and performance in the present experiment. In Sweden, RIL dormancy level was negatively related to the proportion of seeds germinating (Spearman rank correlation, r_s = −0.66, P < 0.001) and was positively correlated with the timing of germination (r_s = 0.34, P < 0.001) and the survival of young seedlings from germination until the assessment of establishment success at the end of the germination period (r_s = 0.30, P < 0.001).

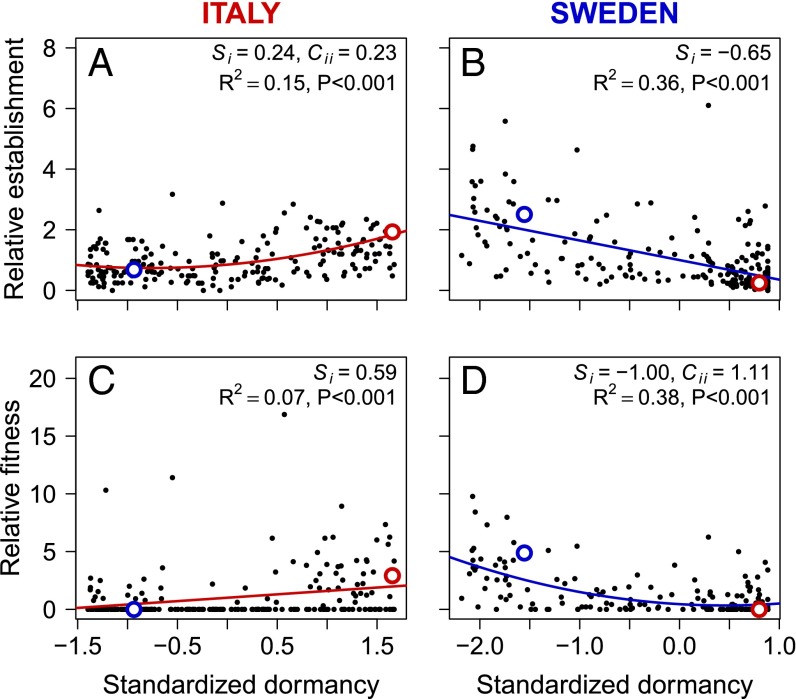
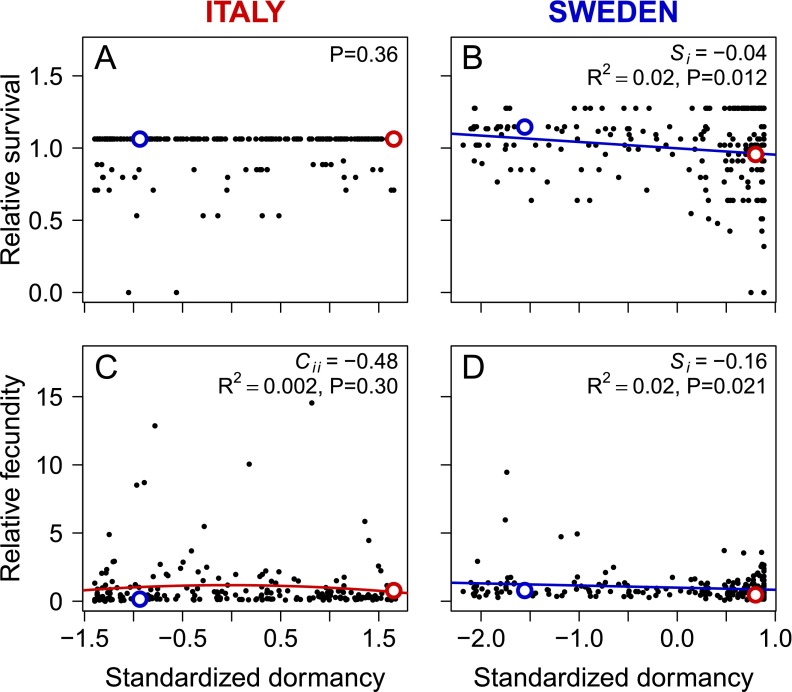
We found divergent selection on seed dormancy, with low dormancy favored in Sweden and high dormancy favored in Italy (Fig. 4 C and D and Table S5). This divergent selection was the result of strong directional selection on seed dormancy during seedling establishment at both sites (Fig. 4 A and B and Table S5). In Sweden, there was also weak but significant selection for low seed dormancy via survival (S_i = −0.04) and fecundity (S_i = −0.16) (Fig. S3 and Table S5). In Italy, there was no selection on dormancy via survival and only weak stabilizing selection through fecundity (Fig. S3 and Table S5). At both sites, the local parental genotype had a dormancy level associated with higher fitness than that of the nonlocal genotype, which is consistent with adaptive differentiation in seed dormancy (Fig. 4).

Fig. 4.

The relationship between standardized mean dormancy and relative mean establishment (A and B) and relative median fitness (C and D) of 209 RILs in Italy (A and C) and 219 RILs in Sweden (B and D). Statistically significant linear (S_i) and quadratic (C_ii) selection differentials are indicated (Table S5). Parental mean and median values are shown with red (Italian genotype) and blue (Swedish genotype) circles.

Table S5.

Linear (S_i) and quadratic (C_ii) standardized selection differentials for seed dormancy in Italy and Sweden based on variation in total fitness and its components establishment, survival, and fecundity

Life cycle stage	Italy		Sweden
	Si	Cii	Si	Cii
Total fitness	0.588 (0.306, 0.883)	0.615 (−0.228, 1.323)	−0.999 (−1.290, −0.756)	1.105 (0.481, 1.768)
Establishment	0.242 (0.163, 0.316)	0.228 (0.009, 0.431)	−0.646 (−0.799, −0.514)	0.272 (−0.119, 0.651)
Survival	0.010 (−0.008, 0.032)	0.012 (−0.039, 0.070)	−0.044 (−0.074, −0.016)	−0.035 (−0.111, 0.045)
Fecundity	−0.095 (−0.321, 0.129)	−0.483 (−1.108, −0.045)	−0.156 (−0.419, −0.023)	0.092 (−0.222, 0.449)

The 95% confidence intervals estimated with bootstrapping are given in parentheses. Significant selection differentials (confidence intervals not including 0) are in bold.

Fig. S3.

The relationship between standardized mean dormancy and relative mean survival (A and B) and relative mean fecundity (C and D) of 209 RILs in Italy (A and C) and 219 RILs in Sweden (B and D). Statistically significant linear (S_i) and quadratic (C_ii) selection differentials for seed dormancy are indicated (Table S5). Parental mean and median values are shown with red (Italian genotype) and blue (Swedish genotype) circles.

Also the QTL mapping results suggest that seed dormancy influenced plant performance throughout the life cycle. The QTL for total fitness (four of six distinct QTL), establishment (three of eight distinct QTL), and survival (two of four distinct QTL) had point estimates that overlapped with dormancy QTL identified in the same RIL population (Fig. 3 and Table S3) (38). Moreover, the Bayesian credible interval of the fitness tradeoff QTL Q9 overlapped with the position of the major dormancy QTL D8 and the underlying dormancy gene DOG1 (38).

Discussion

Our results demonstrate that genetic differences expressed during early life stages can play an important role in local adaptation. We planted locally produced seeds of A. thaliana at experimental sites in Italy and Sweden at the time of seed dispersal and found strong selection against the nonlocal genotype during the establishment phase. This selection during establishment contributed to a markedly higher total fitness of the local genotype. Moreover, with one exception, local alleles of the eight distinct establishment QTL were favored, and the major QTL for establishment and total fitness showed evidence of a fitness tradeoff. The results emphasize the need to include early life stages in assessments of adaptive population differentiation and the genetic architecture of local adaptation.

In Sweden, selection against the nonlocal genotype resulted mainly from selection during the establishment phase, whereas in Italy fecundity also contributed strongly to the fitness difference. For most organisms, the relative contribution of different life stages to local adaptation is not known, because most studies do not include the whole life cycle but instead use a single fitness component or an indirect measure of performance such as growth rate in assessments of adaptive differentiation (2–5). We found that genetic differences expressed during early life stages can contribute strongly to adaptive differentiation, but also that their relative importance for overall fitness differences may vary among environments. These results illustrate that the whole life cycle must be considered for a comprehensive understanding of local adaptation.

Genetic tradeoffs (locally favored alleles that reduce fitness elsewhere) are expected to be the main cause of local adaptation (13), but so far conditionally neutral alleles (favored in the home environment but selectively neutral in other environments) have been more commonly detected in mapping studies (22–24, 26, 27, but see 12–14). We detected one fitness tradeoff (Q9) among the two and five fitness QTL identified in Italy and Sweden, respectively, and at both sites this QTL had the largest effect on fitness of all QTL detected. This QTL overlaps with a fitness QTL detected in a previous reciprocal transplant experiment conducted with the same RIL population in which seedlings instead of seeds were planted. In that experiment, however, the Italian genotype at this QTL was favored by selection at both sites (14). Our finding demonstrates that genetic tradeoffs can escape detection if early life stages are not considered. Compared with the previous study based on the transplantation of seedlings (14), our study included fewer RILs, replication per RIL was lower (especially in Italy because of low rates of seedling establishment; Fig. 2A), and the experiment was conducted in one rather than three years. Lower statistical power thus may explain why fewer fitness QTL were detected in the current experiment (13, 14).

Differences in RIL seedling establishment could be explained by divergent selection on seed dormancy. Our measure of seed dormancy reflects the after-ripening period required for seeds to become germinable (38). As expected, seed dormancy was negatively related to the proportion of seeds that germinated during the experiment and was positively related to germination timing in Sweden, where frequent monitoring of germination (once or twice per week) allowed us to quantify these relationships. Seed dormancy should evolve to match the timing of germination optimal for subsequent establishment and reproduction. The optimal length of the period spent as dormant seed should differ in Italy and Sweden because of differences in the duration of the dry summer period, which poses a high mortality risk for seedlings. Italian summers are more than twice as long as the Swedish summers, and, as predicted, we detected strong selection for low seed dormancy in Sweden and for high dormancy in Italy. This result is consistent with the difference in seed dormancy between the parental lines (Fig. 4), and latitudinal gradients in dormancy observed in A. thaliana and also in the sea beet Beta vulgaris ssp. maritima (34–36).

Both the selection analysis and the QTL mapping suggest that seed dormancy influences not only seedling establishment but also survival and fecundity. This result is expected because seed dormancy affects not only the timing of germination and therefore the conditions for the newly emerged seedlings, but also the seasonal environment during later life-history stages. Cascading effects of environmental conditions during early life stages across the rest of the life cycle have been reported for several plant and animal species (15, 20, 21), including A. thaliana (16, 37). Such cascading effects make it even more important to consider early life stages and maternal effects to capture the full magnitude of local adaptation in any organism.

At both sites, less than 10% of the planted seeds resulted in established seedlings (Fig. 2), as is common among plants with small seeds when sown under natural conditions (42, 43). Seedling establishment success depends on the proportion of seeds germinating and seedling survival. The frequent monitoring of germination in Sweden indicated that in total 33% (Swedish genotype) and 3% (Italian genotype) of the seeds germinated during the experiment and that about two-thirds of these seedlings survived until establishment success was scored. Thus a substantial fraction of the seeds may have entered the soil seed bank, which is a regular feature of many annual and short-lived herbs including A. thaliana (31).

Our fitness estimates have not taken into account the possibility that dispersed seeds may emerge as seedlings from the seed bank in the following years, but there is reason to believe that recruitment from the seed bank should, if anything, increase the advantage of the local genotype at both sites. Many plant species express annual dormancy cycles in the seed bank (31), and a reciprocal seed burial experiment conducted at the same field sites showed that these dormancy cycles differ between the Italian and Swedish genotypes (44). In Sweden, field-matured seeds of the Swedish genotype stored in the soil germinated to a higher proportion when excavated during the germination period in the year following burial (77%) than during the first year (30%), whereas buried seeds of the Italian genotype did not germinate in either year (44). This lack of germination of the Italian genotype is consistent with life-cycle models of A. thaliana predicting that genotypes with high dormancy levels grown at northern locations (Finland in the case of the model examined) will stay in the seed stage year-round (45). At the Italian field site, the Swedish genotype has been found to lose seed dormancy more rapidly than the Italian genotype (44), which should result in an earlier timing of germination. Integrated life-cycle models of A. thaliana indeed predict that at southern locations (Spain), low-dormancy genotypes will germinate in September, which is about a month earlier than the genotypes with high-dormancy levels (45). At the Italian field site, dry periods can occur until October (44), and the later seasonal dormancy loss of seeds in the seed bank is likely to give the Italian genotype a fitness advantage. Taken together, both the results from the seed burial experiment (44) and predictions from integrated life-cycle models (45) suggest that the advantage of the local genotype would increase if the fate of seeds in the seed bank were taken into account, and that the estimates of adaptive differentiation obtained in the present study thus are conservative.

In conclusion, early life stages are known to be under strong selection (15–19) and to have cascading effects across the whole life cycle (16, 20, 21), but they are seldom included in studies on the genetic basis of local adaptation (12–14, 22–28). By conducting a reciprocal transplant experiment including the whole life cycle and maternal effects, we have shown that selection during early life stages contributes strongly to both the magnitude and the genetic basis of adaptive differentiation among natural populations of A. thaliana. Our results demonstrate that the magnitude of local adaptation can be underestimated, and that genetic tradeoffs may be missed if early life stages are not included. Therefore, it is crucial to consider the whole life cycle for a full understanding of the ecology and genetics of local adaptation.

Methods

Study System.

We used a RIL population derived from a cross between two natural populations of A. thaliana from the northern (Sweden: 62°48′N, 18°12′E) and southern (Italy: 42°07′N, 12°29′E) margins of its native range. Despite striking differences in temperature regime between the two sites (39), both the Italian and Swedish populations are winter annuals (Fig. 1A). The RILs are genotyped for 348 SNP markers evenly spaced across the five nuclear chromosomes of the Columbia physical map. Detailed information about the RIL genotyping and linkage map construction can be found in Ågren et al. (14).

Reciprocal Transplant Experiment.

The reciprocal transplant was conducted in experimental gardens located at the sites of the source populations. The seeds used for the experiment were produced at the respective field sites by maternal plants (398 RILs and both parental genotypes) that were planted as 10- to 14-d-old seedlings in the field (14). The average temperature during seed maturation (2 wk before seed harvest) was 11.3 °C (range 3.2–21.2 °C) in Italy and 13.0 °C (range 5.4–24.4 °C) in Sweden (based on hourly recordings). All ripe seeds were collected during the natural seed dispersal period (April 16–20, 2012 in Italy, June 27–July 1, 2012 in Sweden) and for each site pooled by genotype with an average of 11.5 (range 3–23) replicate plants per genotype in Italy and 10.0 (range 3–24) replicate plants in Sweden.

At each site, the reciprocal seed sowing experiment had a randomized block design consisting of 20 plug trays with 160 cells each (individual cells 27 mm wide × 55 mm deep) that were distributed in 10 blocks (two plug trays per block). The trays were filled with local soil in Italy and with an equal mixture of local sand, gravel, and unfertilized peat in Sweden. The trays were sunk into the ground after the removal of all A. thaliana plants within 5 m of the field experiment to minimize the risk of contamination with nonexperimental seeds.

We randomly selected 209 RILs in Italy and 219 RILs in Sweden from the 398 RILs planted at the field sites for inclusion in the present experiment. If a line had not produced sufficient seeds for three or more replicates, it was replaced with another randomly chosen line. The two parents and 196 RILs were planted at both sites. We planted up to 10 replicates per RIL and 80 replicates per parental genotype, with each replicate consisting of 40 seeds sown in one cell of a plug tray. Because not every line had enough seeds available for 10 replicates, the average final sample size was 9.2 (range 3–10) replicates per RIL in Italy and 9.7 (range 3–10) replicates per RIL in Sweden. For the parental genotypes, we sowed 80 replicates of the Italian genotype but because of poor seed production only 14 replicates of the Swedish genotype in Italy, and 79 replicates of the Italian genotype and 80 replicates of the Swedish genotype in Sweden. The seeds were planted at the field site as soon as possible after harvest (9 d after harvest in Italy and 17 d after harvest in Sweden). After sowing, the seeds were exposed to the local weather conditions and were not watered or protected in any way. In Sweden, we recorded the number of seedlings, their developmental stage, and their position within the cell once or twice per week from seed planting until the end of the germination period. From these observations we estimated the cumulative proportion of the seeds that germinated, the survival of young seedlings from germination until the assessment of establishment success, and the mean timing of germination for each cell. The Italian genotype germinated later than the Swedish genotype [mean ± SE: 47.5 ± 2.5 d after sowing (n = 46) vs. 43.2 ± 1.0 d after sowing (n = 80)].

At both sites, the number of established plants was recorded after the end of the natural germination period (February 4, 2013 in Italy, before the start of flowering; October 11, 2012 in Sweden, before the arrival of snow). For each cell, we calculated establishment as the number of established plants divided by the number of seeds planted. The establishment rate for all lines was far below 100%, and we therefore estimated the viability of the experimental seeds of each line × site combination with a germination test on fertilized agar after 2 wk of cold stratification to remove potential dormancy (38). We used a sample of 40–100 seeds per RIL and parental genotype from the same harvest that had been retained for this purpose. The great majority of the RILs (91% in Italy, 87% in Sweden) and both parental lines had seed viabilities >95%. We corrected RIL mean germination proportion and RIL mean seedling establishment based on the estimated seed viability. The number of established plants was 1,732 in Italy and 6,783 in Sweden, resulting in a mean establishment rate of 0.021 and 0.074, respectively. We quantified contamination of the experiment with nonexperimental seeds by scoring seedling establishment in control cells placed in the two outer rows of each tray (400 cells per site) and in randomly selected positions in the tray interior (620 in Italy, and 186 in Sweden). The control cells had a mean establishment rate of 0.004 in both Italy and Sweden, i.e., fivefold lower in Italy and 19-fold lower in Sweden than the mean establishment in cells where seeds were planted.

Directly after seedling establishment was recorded, all seedlings but the most central in each cell were removed to prevent confounding effects of establishment success and competition intensity. The remaining seedling was monitored until fruit maturation. At fruit maturation (April 26–28, 2013 in Italy, June 24–26, 2013 in Sweden), we recorded the survival (from the moment of thinning of established seedlings until fruit maturation) and fecundity (number of fruits containing viable seeds) of surviving plants. We calculated total fitness as the number of fruits produced per planted viable seed (establishment × survival × fecundity), using the focal plant as a proxy for the survival and fecundity of removed seedlings. We expect the focal plant to be representative in this respect, because the SD of germination timing among the germinated seedlings within each cell (5.5 d) was much smaller than the range of variation in mean germination timing among RILs (34.1–76.4 d after sowing).

Selection on the Parental Genotypes.

All statistical analyses were performed in R version 3.1.2 (46). We tested the effects of site, genotype, and their interaction on establishment, survival, fecundity, and total fitness of the parents with GLM. We used a binomial distribution with logit link function for the phenotypes which could vary only from 0 to 1 (establishment and survival, with quasi-likelihood estimation to correct for overdispersion for establishment), and a negative binomial distribution with log link function for overdispersed phenotypes with count values (fecundity and fitness) using the MASS package (47). For survival, we tested the effect of genotype only in Sweden, because all plants of the two parental genotypes survived in Italy. We tested the significance of each explanatory variable and the interaction term by comparing the change in deviance between the full model and reduced model (site + genotype + site × genotype vs. site + genotype; site + genotype vs. genotype; site + genotype vs. site) with an F- or χ²-test. We quantified the strength of selection with the selection coefficient, s = 1 − (mean fitness of less fit genotype/the mean fitness of the fittest genotype).

QTL Analysis.

We mapped QTL for total fitness and its components (establishment, survival, and fecundity) in Italy and Sweden. For each RIL, survival was calculated as the proportion of plants surviving. We used RIL mean values for establishment and fecundity. Because of low establishment success and strong selection, RIL replication was strongly reduced for survival and fecundity, in particular in Italy, decreasing the genetic effects compared with random environmental effects and increasing the effect of outliers, especially for total fitness. We therefore used RIL median values for total fitness.

The QTL mapping was performed in R/qtl (41, 48) using Haley–Knott regression with genotype probabilities of the genetic markers and pseudomarkers in gaps >2 cM, 5% significance thresholds for incorporating additive and epistatic QTL calculated from 10,000 permutations, and final QTL model selection with the automated stepwise algorithm (14, 38, 49, 50). Because the stepwise algorithm is sensitive to deviations from the normal distribution, we quantile-normalized establishment and fecundity at both sites before analysis to obtain a normal distribution (41). Quantile normalization did not improve the distribution of survival and total fitness at the two sites, and we therefore analyzed these four phenotypes with two separate but complementary QTL analyses (38, 50) conducted as described above. First, we analyzed each phenotype as a binary trait (RIL survival proportions <1 vs. 1; RIL median fitness 0 vs. >0), specifying a binary model in the QTL analysis. Second, we analyzed variation in survival among RILs with proportion of surviving seedlings <1 and variation in fitness among RILs with median fitness >0 after quantile-normalization of the data. For total fitness in Italy, the highest number of QTL was detected with the binary dataset, including the single QTL identified with the quantile-normalized zero-excluded dataset. For survival and total fitness in Sweden, the quantile-normalized analysis resulted in the greatest number of QTL identified and included the QTL detected with the binary dataset. No QTL was detected for survival in Italy in any analysis. For the survival and fitness phenotype of each site, we built the final QTL models from the model that identified the greatest number of QTL (total fitness in Italy, binary data of 209 RILs; survival and total fitness in Sweden, quantile-normalized subset of 159 and 112 RILs, respectively). We fitted the final QTL models for all phenotypes with ANOVA using the untransformed data to calculate the logarithm of the odds (LOD) score, effect size, and percentage of variance explained for each QTL.

To identify colocalization of QTL detected for different phenotypes and in different environments, we considered 95% Bayesian credible intervals and point estimates (14, 38, 49, 50). Because wider credible intervals increase the likelihood of colocalization, we used stricter colocalization criteria for QTL with credible intervals larger than the arbitrary threshold of one-fourth of the length of the smallest chromosome (15.2 cM). Identified QTL were classified as distinct if their 95% Bayesian credible intervals were <15.2 cM and nonoverlapping or if the credible interval was >15.2 cM and nonoverlapping with the point estimate of another QTL. We considered that the identified QTL colocalized with dormancy QTL detected in the same RIL population (38) when its point estimate fell within the 95% Bayesian credible interval of a dormancy QTL identified in one maternal environment or within the range of point estimates for dormancy QTL detected in more than one maternal environment.

Fitness Tradeoffs.

We estimated QTL × environment interactions for the six fitness QTL using a GLM with quasi-Poisson error distribution. We identified the marker closest to the point estimate for each QTL detected at one site and to the mean position of the point estimates weighted by their LOD scores for fitness QTL Q9, which was detected at both sites. We tested the effect of QTL genotype, site, and all QTL × site interactions by comparing the change in deviance between the full model and reduced model (QTL genotype + site + QTL genotype × site vs. QTL genotype + site; QTL genotype + site vs. QTL genotype; QTL genotype + site vs. site) with an F-test. We tested the effect of QTL genotype on fitness at each of the two sites with contrasts using the Contrast package in R (51).

Selection on Seed Dormancy.

For each field site, we quantified the form and strength of genotypic selection on seed dormancy in the RIL population across the whole life cycle, and through individual fitness components (establishment, survival, and fecundity). We used estimates of the mean dormancy levels of seeds produced at the two field sites obtained for the same RILs in a previous experiment (38). Seed dormancy was quantified as 1 − germination proportion after 12 wk of after-ripening at room temperature; this measure captures most of the among-RIL variation in dormancy level of field-matured seeds and reflects the after-ripening time needed for the seeds to become germinable (38). For each site, we calculated RIL relative fitness based on its median total fitness (see QTL analysis above) and on its mean establishment, survival, and fecundity, respectively. To estimate the standardized selection differential (52, 53), we regressed RIL relative fitness on RIL standardized dormancy separately by site. The linear selection differential (S_i) was obtained from a model including only the linear term; the quadratic selection differential (C_ii) was obtained by doubling the quadratic regression coefficient from a model that included both the linear and the quadratic term (53, 54). The residuals of the regression analyses did not have a normal distribution, so we validated the results by calculating 95% confidence intervals of the estimated coefficients with the bias-corrected and accelerated method by resampling the data 10,000 times with the Boot package in R (55). We examined the relationships between RIL dormancy level and RIL mean germination proportion, timing of germination, and seedling survival in Sweden with Spearman rank correlations.