Abstract
Inferring causal effects from observational and interventional data is a highly desirable but ambitious goal. Many of the computational and statistical methods are plagued by fundamental identifiability issues, instability, and unreliable performance, especially for large-scale systems with many measured variables. We present software and provide some validation of a recently developed methodology based on an invariance principle, called invariant causal prediction (ICP). The ICP method quantifies confidence probabilities for inferring causal structures and thus leads to more reliable and confirmatory statements for causal relations and predictions of external intervention effects. We validate the ICP method and some other procedures using large-scale genome-wide gene perturbation experiments in Saccharomyces cerevisiae. The results suggest that prediction and prioritization of future experimental interventions, such as gene deletions, can be improved by using our statistical inference techniques.
Keywords: interventional–observational data, invariant causal prediction, genome database validation, graphical models
In this article, we discuss statistical methods for causal inference from perturbation experiments. As this is a rather general topic, we focus on the following problem: based on data from observational and perturbation settings, we want to predict the effect and outcome of an unseen and new intervention or perturbation. Taking applications in genomics as an example, a typical task is as follows: based on observational data from wild-type organisms and interventional data from gene knockout or knockdown experiments, we want to predict the effect of a new gene knockout or knockdown on a phenotype of interest. For example, the organism is the model plant Arabidopsis thaliana, the gene knockouts correspond to mutant plants, and the phenotype of interest is the time it takes until the plant is flowering (1).
From a methodological viewpoint, the prediction of unseen future interventions belongs to the area of causal inference where one aims to quantify presence and strength of causal effects among various variables. Loosely speaking, a causal effect is the effect of an external intervention (or say the response to a “What if I do?” question). The corresponding theory, e.g., using Pearl’s do-operator (2), provides a link between causal effects and perturbations or randomized experiments. We mostly assume here that all of the variables in the causal model (for inferring causal effects) are observed: the case with hidden variables is mentioned only briefly in a later section, although it is an important theme in causal inference (due to the problem of hidden confounding variables) (cf. refs. 2 and 3).
A popular and powerful route for causal modeling is given by structural equation models (SEMs) (2, 4). We consider a set of random variables , and we often denote by , emphasizing that Y is our response variable of interest (e.g., a phenotype of interest). The main building blocks of a SEM are as follows: (i) an underlying true causal influence diagram for the random variables , formulated with a directed graph D whose nodes correspond to the variables, most often with a directed acyclic graph (DAG); (ii) each of the random variables is modeled as a function of their parental variables, given by the graph D, and an error term. The system of structural equations is then as follows:
| [1] |
where denotes the set of parents of node j in the underlying graph or DAG D and are error terms that are jointly independent. Furthermore, for , denotes the variables , and the arrow “” is emphasizing that is caused (or influenced) by , which is a stronger statement than an algebraic equality.
The most commonly used model for an intervention at one or several variables has been pioneered by Pearl (cf. ref. 2): the do-operation is setting the single variable to a deterministic value x, which corresponds to replacing the structural equations [1] for with ; analogously, the do-operation can be applied to several variables simultaneously. The distribution of Y when doing an intervention can be derived via the truncated Markov factorization (2, 3, 5) or by the backdoor adjustment formula, and we can then consider quantities like the expected response Y when having done an intervention at putting its value to x:
| [2] |
For more details, we refer to ref. 2. The do-operation has been generalized to probabilistic “soft” interventions where the intervention value (little x in the notation above) becomes a random variable (6). Furthermore, a so-called “mechanism change” with an intervention at variable with index j is replacing the conditional probability distribution , corresponding to the jth equation in the SEM [1], by another distribution (7). In addition, “fat-hand” interventions (8) (with uncertain intervention targets) and activity interventions (9) (simultaneous mechanism changes of all children of a variable) have been used to model interventions in molecular biology. For the do-interventions, it is sufficient to know the SEM because the intervention itself is fully specified by the known quantities j and x. We will discuss in a section below that do-interventions can be too simple for certain applications.
Identifiability and Estimation from Data
One of the major challenges is the estimation of the SEM [1] from observational or a mix of observational and interventional data. We are particularly interested in high-dimensional settings where the number of variables can be much larger than sample size, as in many applications from, e.g., genomics and genetics.
A first complication concerns identifiability: the data-generating probability distribution(s) might be represented by different structures (acyclic directed graphs) D and corresponding different functions in the SEM [1]. The different graph structures D that can generate the data-generating distribution(s) build an equivalence class . Situations where this equivalence class is large (and hence the degree of identifiability is low) occur when the data-generating distribution is observational and the SEM in [1] is either fully nonparametric with no specified additional structure or when the functions are linear and the error terms are Gaussian (cf. ref. 2). More identifiability is possible when the data-generating distribution corresponds to a mix of observational and interventional data (7–12) or when the SEM has additional structure. Regarding the latter, it is possible to identify from the observational data distribution P the single underlying causal DAG: the most prominent examples are linear, non-Gaussian, acyclic models (LiNGAM) where the functions are linear but all error terms are non-Gaussian (13), the functions are nonlinear and the error terms are additive (14, 15), or the functions are linear with Gaussian error terms that all have the same variances (16).
Algorithms and Methods.
Given data, we want to estimate the SEM in [1] (its equivalence class if it is not identifiable), and based on this, we often aim to estimate the total causal average effect (see also [2]) or its generalization when intervening at more than one variable. If the underlying causal DAG D is not identifiable from the distributions, we can only obtain bounds for .
For linear Gaussian SEMs, estimation of the Markov equivalence class based on observational data can be done by penalized maximum-likelihood estimation (17) or by constraint-based methods with the PC-algorithm using conditional independence testing (3, 18). Based on the estimated Markov equivalence class, lower bounds for the absolute value of the parameter can be derived using a computationally efficient strategy (19). The setting with a mix of observational and interventional data and estimation of the corresponding smaller Markov equivalence class is discussed in ref. 20. Bayesian methods for structure and parameter estimation include those in refs. 8, 9, 21, and 22. Theoretical performance guarantees in the high-dimensional setting with underlying sparse DAGs have been given in refs. 19, 23, and 24.
For identifiable models, some other estimation strategies have been proposed. For linear SEMs with non-Gaussian errors (LiNGAM), one can make use of independent component analysis (13), and for additive SEMs, proposals include independence testing of residuals (15) or penalized nonparametric maximum-likelihood estimation (25). Based on an estimated causal graph, the quantity in [2] can be nonparametrically inferred using marginal integration for the backdoor formula adjustment (26).
Sometimes, the direct (instead of total) causal effects are of interest. They are typically given by the parameters of a graphical or SEM. For example, the edge function in [1] encodes all of the direct effects from to , or the parameter in [4] describes the direct effect of to Y.
Challenges and Validation.
There are a number of difficulties that occur, implying that estimation of a causal graph or influence diagram or of a total causal effect is a very ambitious goal, particularly in the high-dimensional context where p is much larger than sample size. Even with simulated data from a specific model under consideration, one often needs a substantial sample size to ensure that the estimated (equivalence class of) graphs or causal effects are fairly accurate. The supporting mathematical theory is often of crude asymptotic nature as sample size tends to infinity and does not advance more detailed understanding; for an exception, presenting some more refined convergence rates, see ref. 24. Furthermore, the faithfulness assumption can become rather severe for moderate dimensions already (27, 28). (A distribution P is faithful with respect to a DAG D if all conditional and marginal dependencies among the variables can be derived from the DAG D.)
Quantifying uncertainty.
When using methods based on estimating first a causal graph or an equivalence class thereof and subsequently inferring the direct or total causal average effect, it seems difficult to accurately quantify uncertainty in terms of confidence bounds. Confidence regions based on sample-splitting procedures are rather unreliable and much worse than for inferring association in regression models (29). Thus, in absence of “error bars,” one cannot draw reliable confirmatory conclusions. We will discuss later a recently proposed methodology that provides confidence intervals for direct causal effects, in the setting with not only observational but also additional, rather general kind of interventional data.
Validation.
Because (asymptotic as sample size tend to infinity) correctness of causal inference relies on strong assumptions, with some of them being uncheckable in practice, a central point is their empirical validation with new interventional data. Perhaps best posed is the validation of the “total causal effect.” [A total causal effect of X to Y measures the overall effect on Y when doing a perturbation at X. Its expected value (as a function of x) is defined in ref. 2.] This can be done by holding out some interventional test data. Mathematically, we aim to predict the expected value in [2]. The prediction error is then a measure between the estimated quantity of , based on the training data, and the actual value of the variable Y under the perturbation in a new (test data) intervention experiment. Instead of this qualitative measure, we can also test for the existence of a total causal effect. Mathematically, this is the case if is different from for some x; see [2]. To validate this in empirical data, we define below a notion of (total) “strong intervention effect” (SIE); it is a binary event and allows to validate whether a method (based on training data) was successful in correctly predicting the binary outcome of a SIE being present or absent in new test data.
We note that a procedure that is estimating direct causal effects, as most causal prediction methods do, can also be used to predict total (strong) intervention effects; for more details, see SI Appendix.
Validation of estimated lower bounds of the total causal effects in a large-scale gene deletion experiment for yeast has been performed in ref. 30: however, the result depends in a rather sensitive way on how a true positive finding is defined. We thus suggest next a conservative notion for validation of total causal effects.
We propose here the criterion of SIE, which is well suited for validation with large-scale interventions having one measurement each, such as gene knockdowns or deletions. It conservatively classifies total intervention (causal) effects as being strong or not. Consider a variable that is intervened on and a response variable Y of interest.
SIE.
The intervention of variable on the response Y is strong if both of the following events occur:
-
i)
the intervened variable has a value that is below or above all values of variable seen in other interventional/observational data (with no intervention on );
-
ii)
the response variable Y has a value below or above the range of values of Y in all other interventional/observational data (with no intervention on Y).
Thus, the definition of an SIE is based on a given dataset. An SIE of to Y corresponds to an event with corresponding extreme behavior of the realized values of the two variables. It is an estimate of presence or absence of a strong total causal effect. We note that, for a given Y, there can only be at most one that fulfills the criterion. Therefore, the criterion is conservative, meaning that not all non-SIE effects are noncausal.
The existence of a “direct causal effect” is difficult to extract from hold-out interventional validation data, unless we adopt a model that we want to avoid for validation purposes. (In an SEM as in [1], there is a direct effect from X to Y if X is a parent of Y.) In Validation: Gene Perturbation Experiments, we consider scores measuring direct effects using external information from a genome database and transcription factor (TF) binding based on ChIP-on-chip data as a source of indirect evidence for a direct effect. With such approaches, we have to keep in mind that the external source of validation might be very noisy and error-prone. In particular, it turns out to be difficult to predict SIEs from external information alone.
Causal Inference Based on Invariance Across Experiments
We outline here a recently published method (31) that exploits the fact that the data arise from different experimental conditions or perturbations. In the advent of big-data scenarios, the latter setting with heterogeneous data sources becomes more common. The method has a few crucial benefits addressing some of the difficulties mentioned in the previous section: (i) an “automatic identifiability” property (see the discussion after [5]); (ii) some confidence bounds for inferring causal variables (see [5]); (iii) the flexibility that the interventions and perturbations do not need to be exactly specified; and (iv) avoiding some typically unstable and complicated estimation of a graph (or an equivalence class of graphs) from data.
The method is based on invariance of conditional distributions across intervention experiments from a rather general type. The role of invariance in causal inference has received some attention in the literature (2, 32–34). To the best of our knowledge, however, the work in ref. 31 is the first of its kind that exploits invariance of conditional distributions for statistical estimation and confidence statements.
As before, we consider a response or target variable of interest, denoted by Y, and a p-dimensional predictor variable . We assume a setting with data for different experimental settings . For example, with in the context of gene perturbation experiments, the experimental settings could correspond to observational data () and data from unspecified interventions (). We could also consider a larger set of experimental settings when having in addition data from say two gene-specific interventions, encoded in addition by and . Thereby, is a vector of the response variable and an design matrix, containing the different data points in the setting e. It is important to point out that we have more than say observational data only (assuming that does contain more than one element of experimental settings). We use a linear model for the response or target variable:
| [3] |
where the error or noise term has mean zero. We note that the regression vector and the noise term are unknown or unobservable, respectively. An intercept that is constant across environments could be added, but we will not do so here for notational simplicity. We refer to SI Appendix for some potential violations of the assumed linearity in [3].
The response variables in [3] are assumed to correspond to a linear SEM:
| [4] |
where is a noise term that is independent from , and is unique and equals the parental set of Y and corresponds to the coefficients (edge weights) in such a SEM. The variables and are generated from a rather general class of interventions on X. We require that these interventions, or the corresponding experimental settings, are such that the following invariance assumption holds. (The invariance assumption will be exploited in the next section: the main idea will be to look for components of the regression vector that are invariant among experimental settings.)
Invariance Assumption.
For and from [4], define a vector γ such that and . Then:
We note that are the causal variables for Y (sometimes called the direct causes of Y) and the distribution for (for all ) is equal to the one of in [4].
As an example, consider experimental settings that arise from do-interventions (2) at variables different from Y in a SEM as in [4]: then the invariance assumption holds.
We give in the following a simple example under noise interventions. Assume the SEM for a target of interest Y and two potentially causal variables is given by the following (to improve readability, we omit the superscript “e” and write instead of ):
where are independent with mean zero and unit variance and the strength of the noise is a function of the environment. The true causal parent of Y is just the second variable . A simple regression from Y on the two variables will put a nonzero regression coefficient on both variables (even though is a child of Y in the causal graph and hence not causal for Y, it has predictive power for the outcome Y). For the causal discovery, we propose, intuitively speaking, to look through all possible subsets S of . For each subset S, we ask whether it is possibly a parental set of the outcome of interest by checking an invariance property across different environments. For the true causal parents, the regression coefficients when regressing Y on and the residual variance will be identical across environments. Let be the optimal regression coefficient when regressing Y onto for a given subset S of predictor variables (a function of the environment e) and let be the residual variance of . The two environments are defined in this example by a change in the noise level so that and (this fact does not have to be known; the change could also consist of do-interventions or other types of interventions on , and we do not require knowledge of the precise location or type of intervention). The regression coefficients and residual variances in the two environments are then given for all possible subsets of variables by Table 1.
Table 1.
Invariance example
| Set | Invariant? | Invariant? | ||||
| — | — | Yes | 2 | 5 | No | |
| 4/9 | 5/12 | No | 18/81 | 5/6 | No | |
| 1 | 1 | Yes | 1 | 1 | Yes | |
| (2/5, 1/5) | (1/4,1/2) | No | 1/5 | 1/2 | No |
We can see from Table 1 that both the optimal regression coefficient and the residual variance stay constant in all environments for the true set of causal parents (here, if S is equal to ), whereas the residual variance changes for all other subsets of variables, including the empty set that would correspond to Y being a root node in the SEM. The invariant causal prediction (ICP) method works by collecting all subsets S of variables for which we cannot statistically reject the hypothesis that is identical in all environments and can also not reject the hypothesis that is constant in all environments . In the population example above, only satisfies this invariance. Once we have collected all subsets S of variables for which we cannot reject invariance, we take the empirical estimate to be the intersection across all of the subsets with the invariance property (where we cannot statistically reject the hypothesis of invariance); that is, we look for variables that are common among all invariant subsets. For sufficiently many data points, in the example this yields the answer , and we thus detect that variable 2 has to be causal for the outcome Y. Note that, if we just observed a single environment, we would see invariance for all subsets S, including the empty set (because invariance across one environment always holds). The intersection across all invariant sets would thus be the empty set, and we could not determine that one or more of the variables is causal for the outcome of interest from observational data alone. The same phenomenon would occur if the strengths and of the noise in both environments had the same value.
Invariant Prediction Method.
Having data as in [3] from various experimental settings, the main idea (as outlined in the example above) is to look for sets of predictor variables that leave the corresponding regression vectors and noise terms invariant across experimental settings. This is the basis of the invariant prediction method (31) (more details in SI Appendix). Here, we simply present the main result.
As with any causal inference method, one might face identifiability problems. This is a fundamental and unavoidable issue. However, assuming the invariance assumption, the ICP approach will lead to a set (SI Appendix, formula S.4), which has the following confidence property:
| [5] |
for some prespecified confidence level such as 0.95 or 0.99. [The set depends on the data, and hence is random when interpreting the data as usual as realizations of random variables.] Thus, when applying the method many times to different datasets, we expect that in approximately of the cases, all of the selected variables are causal (i.e., direct causes). The main assumption for deriving the statement in [5] is the invariance assumption. As described above, it holds if the experimental settings come from a rather broad class of interventions that do not directly act on the response variable Y (SI Appendix). As an example where this assumption is plausible in practice, consider gene perturbation experiments and assume a phenotypic response Y and predictor variables corresponding to expression values of all of the genes in the genome (the columns of the matrix X). Suppose that the interventions act on some of the (possibly vaguely specified) genes, such as gene deletions or gene knockdowns. Then, these interventions do not directly target the response Y, and thus, the main assumption outlined above is satisfied.
The elegance of the method and of the statement is that we do not need to know or specify whether a causal variable is identifiable from the data-generating probability distribution: the method automatically takes care about potential identifiability problems. (We do not know whether the method is complete: that is, whether all direct causal effects that are identifiable from the data-generating distribution would be correctly detected by the method.)
Heterogeneity in Big Data.
The ICP method outlined above crucially depends on the fact that we have access to different experimental conditions from . In presence of say observational data alone ( consisting of one experimental setting only, i.e., ), we would not detect any causal variable. [Causal inference from observational data would require approaches based on, e.g., fitting SEMs and graphical modeling (Identifiability and Estimation from Data).]
With the ICP method, the degree of identifiability increases as the space of experimental settings becomes larger. Denote the causal variables that are identifiable from the invariance assumption by (SI Appendix, formula S.1). We then have that
| [6] |
meaning that for we have . Sufficient conditions under which , that is the causal variables are uniquely identifiable, have been worked out for linear Gaussian SEMs, requiring that is sufficiently “rich” and form a certain class of interventions (31).
From [6], we conclude that with a larger amount of experimental settings (“more heterogeneity”) we have higher degree of identifiability of causal effects. Thus, in the setting of big data with a large space of experimental settings, we have an advantage to exploit invariance across a large . For example, with gene perturbation experiments discussed below, it can be of interest to consider experimental settings not only from different gene interventions but also arising from change of environments from potentially different datasets.
The ICP method can deal with a general variety of experimental settings, including observational data, known interventions of a certain type at a known variable, random interventions at an unknown variable, or observational data in a changed environment. We emphasize the importance that one does not need to know what the working experimental conditions from actually mean. In practice, it is often difficult to know whether an intervention has been done at, e.g., one specified variable only, or to specify the kind of intervention that has been done, e.g., a do-intervention (2) or a “soft” intervention (6). The fact that one does not need to specify the nature of an experimental setting in contributes to robustness and generality of the procedure. The only necessary background knowledge regarding the types of interventions is that they do not target the response variable Y itself.
It has been assumed so far that is the set of the true available experimental settings, but this is not necessary. In principle, we can construct the working experimental settings as we like and still obtain [5], as long as the invariance assumption is satisfied with respect to . (The data in such a constructed experimental setting has then a mixture distribution. For an experiment , the mixture distribution is , where is the entire space of all possible experimental settings, are positive weights summing up to 1, and are probability distributions.)
Invariance in Presence of Hidden Variables.
The ICP method from the previous section implicitly assumes that there are no hidden confounding variables. The method can be generalized to situations where invariant effects correspond to causal effects in SEMs where the intervention or perturbation does not have an effect on the hidden variables (35). Further explanation is beyond the scope of this paper.
Software
Comparing different approaches for detection of causal effects is in practice often cumbersome as they use very different implementations. To address this issue, we provide a software package CompareCausalNetworks (36) for the R language (37). It provides a unified interface to the following methods: GES [Greedy Equivalence Search (17)], CAM [Causal Additive Model (25)], Lingam [Linear, Non-Gaussian, Acyclic Models (13)], rfci (38) (really fast causal inference), and pc [PC-algorithm (3)], which are all classically applied to observational data only, as well as GIES [Greedy Interventional Equivalence Search (12)], which is making explicit use of the knowledge where interventions took place. The ICP methods are implemented as ICP and hiddenICP (allowing for hidden variables) in the R package InvariantCausalPrediction. They use the knowledge of the environment where an observation took place (for example, whether it is part of the observational or interventional data) but are not requiring knowledge about the precise nature of the interventions. As a further benchmark, we also implement cross-validated sparse regression as a method regression and offer the option of using stability selection (39) on all implemented methods.
Validation: Gene Perturbation Experiments
We consider large-scale gene deletion experiments in yeast (Saccharomyces cerevisiae) (40). Genome-wide mRNA expression levels are measured for 6,170 genes: 160 observational data points from wild-type individuals and 1,479 interventional data arising from single gene deletions (1,479 perturbation/deletion experiments where a single gene has been deleted from a strain). The goal is to predict the expression levels of all (except the deleted) genes of a new and unseen single gene deletion intervention. More precisely, denoting the expression levels of the genes by variables with , we want to predict whether significantly changes when deleting gene j (for each of the 6,170 different responses Y).
For this task, we aim to obtain a confidence statement from the ICP method for in [4], or to estimate using other methods, describing the direct causal effect of on Y. We then use the strong direct effects [ranked according to the proportion of times the effect gets selected/top-ranked when running each procedure on 50 random subsamples of the data (39)] as a proxy for the strong total effect of to Y, because we expect strong direct and strong total effects to be very similar to each other (SI Appendix).
We use the following separation into training and validation data. We divide the 1,479 interventional data into five blocks . We use as training data all 160 observational data points and four blocks with and , of interventional data, and the validation data are the remaining block . Therefore, we can predict the effects from the interventions from block without having used these interventional data in the training set. By repeating the separation into training and validation data five times, each gene perturbation is held out once and we can use it to validate the predictions.
For the ICP method, we use a very simple labeling of experimental settings: , where corresponds to observational data and to all interventional data (regardless which gene has been targeted to be knocked down). As discussed above, when choosing a small set , we might pay a price in terms of statistical power to detect significant causal variables. On the other hand, due to potential off-target effects of interventions, pooling all interventions into one experimental setting is more robust against “noisy interventions” that potentially affect many genes. As significance level, we use a level of corresponding to a probability greater or equal to 0.99 in the confidence statement in [5]. We repeat the experiment on subsamples of the data in the spirit of stability selection (39, 41) and rank the edges in order of decreasing selection frequency. [For the ICP method, there is a directed edge from gene j to k if: gene k is the response variable and gene j is an element of the selected causal variables . For methods using directed graphical modeling, the meaning of “directed edge” is given by the corresponding DAG.] Going down this list, we check whether the prediction of a directed edge from gene j to gene k is “successful” in the sense of an SIE as defined before (where gene j corresponds to the X variable and gene k to the response variable Y). Note that the SIE is an estimate of the total causal effect. Among 9,125,430 possible edges, there are 10,757 interventions (about 0.1% of all edges) that we classify as strongly successful with this criterion.
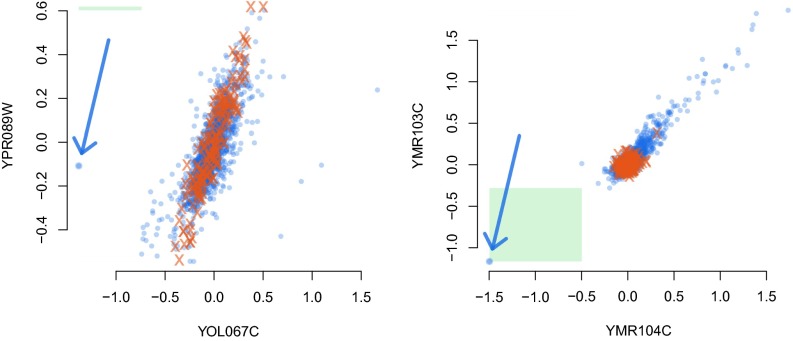
Fig. 1 shows two examples. On the left is a pair of genes YOL067C,YPR089W that was selected due to the high correlation between the two genes on observational data. When intervening on YOL067C (the gene on the x axis), the activity of gene YPR089W is still well within its usual range and the intervention is deemed not successful according to our criterion. The right side shows the pair YMR104C,YMR103C. The edge from the first to the second one of these genes is the most frequently selected edge by our method of ICP. It is selected because the model for observational and interventional data fits equally well to the data (and there is no other explanation using other genes that would achieve this). This is in contrast to the gene pair on the left, where the interventional data have a much broader variance around a regression fit than the observational data.
Fig. 1.
The activities of two pairs of genes. Observational data are shown as red crosses and interventional data as blue circles. A blue arrow marks the experiment where an intervention on gene YOL067C occurs (activity shown on the x axis in the left panel) and analogously in the right panel. The intervention on the Left is deemed not “strongly successful” [not fulfilling (i) in the definition of an SIE] as the activity of gene YPR089W (y axis) under the intervention is well within its usual range. The intervention on the Right is called strongly successful as the activity of YMR103C (y axis) under the intervention is outside of the previously seen range and likewise for the gene YMR104C on which the intervention occurs (strongly successful area is marked by the green box).
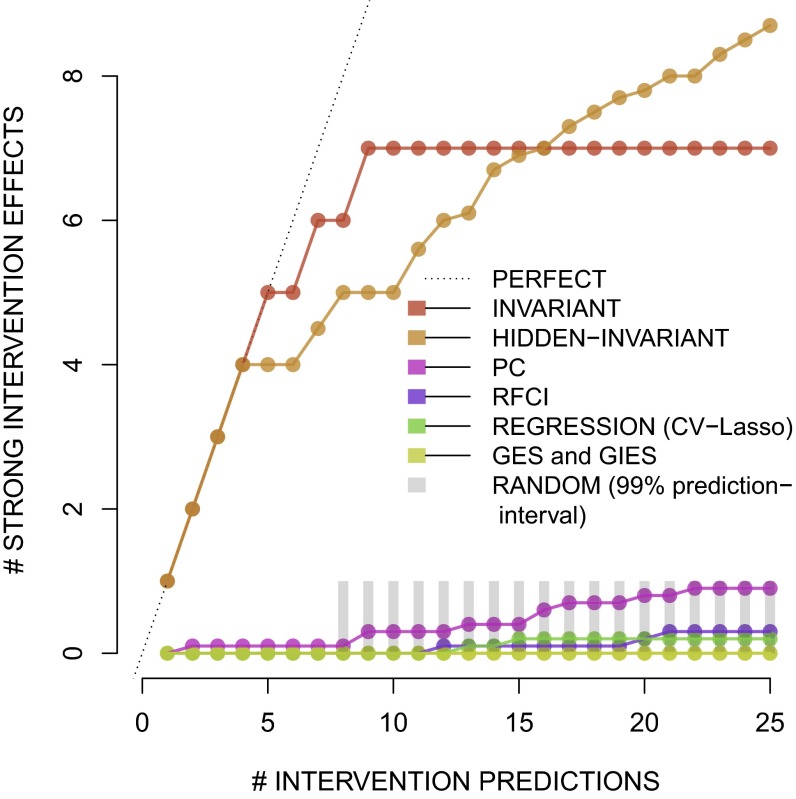
For the K most often selected edges, we can check how many of the corresponding interventions were strongly successful on the test data. Fig. 2 shows results for several methods, where gene pairs are ordered by the selection frequency for each method when fitting models on 100 random bootstrap samples of the data. In case of equal selection frequency, we compute the expected number of SIEs when breaking the ties randomly. The number of SIEs among the most frequently selected gene pairs can thus take a noninteger value in the presence of ties. As a crude benchmark, we can first look at the success of random guessing. If choosing randomly, we will with probability of at least 95% not predict a single SIE for and the expected number of selected SIE with random guessing is just for . With ICP (allowing for hidden variables or not), the first four top edges correspond to an SIE.
Fig. 2.
The average number of successful interventions (y axis) against the number of selected edges (x axis) for various methods.
As a comparison, we show results for GES, GIES, PC, RFCI, and a regression-based estimate, where we always choose the first 25 ranked candidate genes with stability selection. These methods are fitted with the default values once on just observational data and then also (as shown here) on both observational and interventional data, but the difference between the two is very small, with the results that use interventional data (the ones shown) slightly superior. All of the considered methods yield estimates of direct effects, but we validate with SIE which is estimating the total effect (justification in SI Appendix).
To give an impression of the computational complexity of the algorithms, Table 2 shows the runtime of used methods (with the same settings as used to produce the other results on the whole dataset) on a single core of a 2.8-GHz processor when estimating the causal graph for either the first 50, 500, or 5,000 genes. The runtimes reported here do not include the prescreening (SI Appendix), as this was a common preprocessing step for all methods.
Table 2.
Timing comparisons in minutes
| No. genes | |||
| Method | 50 | 500 | 5,000 |
| ICP | 0.233 | 2.64 | 27.7 |
| hiddenICP | 0.012 | 0.12 | 1.4 |
| pc | 0.004 | 0.10 | 2.4 |
| rfci | 0.004 | 0.12 | 3.6 |
| ges | 0.002 | 0.80 | 1,002.4 |
| gies | 0.010 | 4.06 | 842.8 |
| Regression | 0.069 | 0.70 | 7.5 |
One question is whether a mechanism is already known that links the top-scoring gene pairs. If so, this can be viewed as a validation of the SIEs one can see in the data. The question can be turned around, however. We can ask whether we could predict the SIEs just using biological background knowledge.
To this end, we extracted six scores that measure interactions between gene pairs from a bioinformatics source, the Saccharomyces Genome Database (SGD) based on ref. 42 at yeastmine.yeastgenome.org. This database contains over gene interactions collected by the BioGRID public resource from the scientific literature. Interactions are categorized as either “physical” or “genetic,” and a subset of each is labeled as manually curated. For all gene pairs, we queried the database for an interaction and interpret the “bait” to “hit” directionality of the interaction as a direct causal effect from bait to hit. [One has to keep in mind that this interpretation is questionable. The presence of an edge in the database indeed may suggest the presence of a direct causal relation, but the directionality of the edge in the database need not coincide with the directionality of the causal relation but could point in the opposite direction. Furthermore, the fact that two proteins bind (physical interaction) or that two genes have a nonlinear interaction on some phenotype (genetic interaction) does not yet imply that there is a causal relation between the gene expression levels.] This resulted in six binary scores for gene pairs. Scores A, B, and C use the following, respectively: (A) both physical and genetic interactions, (B) only physical interactions, and (C) only genetic interactions. Scores D, E, and F are similar but use only the subsets of manually curated interactions.
In addition, we used ChIP-on-chip data from ref. 43 as another source of indirect evidence for validation. The dataset contains binding activity of a subset of genes that function as TFs and regulate the expression levels of other genes. A binary score was constructed by matching the binding activity at confidence level for 118 TFs with the SGD naming scheme, resulting in 8,073 nonzero entries.
Table 3 shows the number of gene pairs that have both an SIE and also a nonzero value in the scores from the yeastgenome.org and TF datasets among all of more than 9 million possible gene pairs. There are 10,679 gene pairs with an SIE, 8,073 with a score on TF, and the number of gene pairs with a score on A–F are given by 109,549, 38,377, 73,688, 17,778, 8,581, 10,324, respectively. Table 3 shows that the number of pairs that have both an SIE and score is substantially higher compared with a situation where these measures would be independent. Using Fisher’s exact test, these associations are significant at level less than for all scores. Still, the overlap is rather small, as just a few hundred out of all 10,679 gene pairs with an SIE have a nonvanishing score. We note that, although SIE measures the total effect and the six yeastgenome.org scores A–F and TF are more related to direct effects, some joint occurrences are interesting to look at; see also the discussion on validation in Challenges and Validation. [A strong direct effect is expected to result in a strong total effect (SI Appendix).]
Table 3.
Overlap between SIEs and scores from yeastgenome.org and TF bindings
| A | B | C | D | E | F | TF | |
| No. gene pairs with both SIE and score | 327 | 92 | 267 | 105 | 60 | 61 | 117 |
| Expected no. under independence | 128.2 | 44.9 | 86.2 | 20.8 | 10.0 | 12.1 | 9.5 |
We also show the 20 gene pairs that are most frequently selected with the ICP method in Table 4, starting with the most frequently selected pair “YMR104C YMR103C.” The columns show whether the pairs have an SIE and whether an interaction is indicated by the nonzero score A–F from yeastgenome.org dataset and by a nonzero score TF from the ChIP-on-chip data.
Table 4.
Top 20 stable results from ICP
| Rank | Cause | Effect | SIE | A | B | C | D | E | F | TF |
| 1 | YMR104C | YMR103C | ✓ | |||||||
| 2 | YPL273W | YMR321C | ✓ | |||||||
| 3 | YCL040W | YCL042W | ✓ | |||||||
| 4 | YLL019C | YLL020C | ✓ | |||||||
| 5 | YMR186W | YPL240C | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| 6 | YDR074W | YBR126C | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| 7 | YMR173W | YMR173W-A | ✓ | |||||||
| 8 | YGR162W | YGR264C | ||||||||
| 9 | YOR027W | YJL077C | ✓ | |||||||
| 10 | YJL115W | YLR170C | ||||||||
| 11 | YOR153W | YDR011W | ✓ | ✓ | ||||||
| 12 | YLR270W | YLR345W | ||||||||
| 13 | YOR153W | YBL005W | ||||||||
| 14 | YJL141C | YNR007C | ||||||||
| 15 | YAL059W | YPL211W | ||||||||
| 16 | YLR263W | YKL098W | ||||||||
| 17 | YGR271C-A | YDR339C | ||||||||
| 18 | YLL019C | YGR130C | ||||||||
| 19 | YCL040W | YML100W | ||||||||
| 20 | YMR310C | YOR224C |
Out of the top 20 pairs from the ICP method, 7 show an SIE (measuring a total effect), as already seen in Fig. 2. Four pairs correspond to an indication of an interaction based on the scores A–F derived from the yeastgenome.org database. Just a single pair shows both an SIE and a positive interaction score. Even though the overlap is small, both results on their own are significant, if compared with random sampling of gene pairs, as shown in Table 5. As the causes from these top 20 pairs include no TFs found in the TF dataset, there is no overlap with the corresponding score.
Table 5.
Significance of top 20 ICP results
| Score | Strong effects among top 20 ICP results | Expected no. under random guessing | P value |
| SIE | 7 | ||
| A | 3 | ||
| B | 3 | ||
| C | 2 | ||
| D | 2 | ||
| E | 1 | ||
| F | 2 | ||
| TF | 0 | 1 |
Application to Flow Cytometry Data
As another example of the possible applications of invariant prediction, we consider the flow cytometry data of ref. 44. The abundance of 11 biochemical agents is measured in several different environments. One of the environments can be considered as observational data without external interventions. In the other environments, different reagents have been added (or stimulants have been removed) that modify the behavior of some of the biochemical agents (see refs. 44 and 9 for a more detailed description of the experiments). [The description in ref. 9 is not entirely accurate: conditions 7 and 8 (activation by PMA and β2cAMP) are abundance interventions in combination with a global intervention, as the α-CD3 and α-CD28 activators were not applied in those conditions (in contrast with all other conditions, including the baseline).] Each environment contains between 700 and 1,000 samples. Here, we only use a subset of eight environments, the same ones that ref. 9 used, to allow comparison of the results.
A naive implementation of invariant prediction would try to find an invariant regression model for each of the 11 agents in turn, where invariance is measured across all eight environments simultaneously. The ICP method does not allow interventions on the target variable itself (see the discussion after [5] and also SI Appendix). We thus follow a slightly adapted strategy by comparing all 28 possible pairs of environments. For each pair of environments, we estimate the set of causal predictors using ICP. Taking the union of all of the estimated parental sets across the 28 pairs of environments leads to the graph of edges shown in Fig. 3 when controlling the overall familywise error rate at . We give a more detailed description of the application of the ICP method to the flow cytometry data in the SI Appendix.
Fig. 3.
The graph of estimated causal relations between the biochemical agents in the ref. 44 data. Blue edges are found by an invariant prediction approach, whereas red edges are found if allowing hidden variables and feedback with invariant prediction. Purple edges are found with invariant prediction whether allowing for hidden variables or not. The solid edges (including the gray edges) are all relations that have been reported in either the consensus network according to ref. 44, or the newly reported edges in ref. 44, 9, or 8. See also SI Appendix, Table S1.
Allowing for hidden variables with hiddenICP allows correlation between the noise input at different variables. Under a shift mechanism for the interventions described in more detail in ref. 35, the presence of feedback loops will not invalidate the output of hiddenICP (for details, see refs. 31 and 35). Some two-cycles can be seen to be selected by the method in Fig. 3. Of the 15 edges found by invariant prediction (with or without hidden variables), 12 have been previously reported in the literature. Each of the three previously unreported edges adds a reverse link to a previously reported edge. In general, one would expect feedback loops to be present in this system. However, there seems to be no consensus yet on the exact nature of these feedback loops. Therefore, we should consider what Sachs et al. (44) call the “consensus” network to be an incomplete description of a more complicated biological reality. SI Appendix, Table S1, gives a list of all of the edges that have been found by different causal discovery methods. Our estimated network in Fig. 3 also confirms quite well with the point estimate in ref. 35, which allows for interventions on the target variables but cannot produce confidence intervals and significance testing.
Conclusions
The recently developed ICP method (31) for causal inference is equipped with confidence bounds for inferential statements, without the need of prespecifying whether causal effects are identifiable or not. A notable feature of the approach is that with increased heterogeneity, in terms of more experimental settings, it automatically achieves better identifiability. The underlying invariance principle (invariance assumption) can be used if data from different experimental conditions (such as observational--interventional data) are available. We provide open-source software in the R language (36), which enables an easy use of the ICP method and comparing it to some other, well-known causal inference algorithms.
We validate the statistical ICP method for Saccharomyces cerevisiae. We consider new interventional gene deletion experiments that have not been used for training the method, and we also look at additional information from the SGD at yeastgenome.org and from TF binding based on ChIP-on-chip data. The validation itself has to be set up carefully to avoid validating spurious effects: we propose here the notion of an SIE. To increase the range of validation to other applications and datasets, we also considered flow cytometry data: the validation is on less rigorous grounds without hold-out intervention experiments and SIE, but it nevertheless allows to compare with existing results in the literature. The best validation is, in our opinion, successful prediction of the effects of previously unseen interventions, as demonstrated here for the ICP method and gene knockout data.
Supplementary Material
Acknowledgments
We thank Patrick Kemmeren for generously providing the gene perturbation data. J.M.M. and P.V. were supported by The Netherlands Organization for Scientific Research (VIDI Grant 639.072.410).
Footnotes
The authors declare no conflict of interest.
This paper results from the Arthur M. Sackler Colloquium of the National Academy of Sciences, “Drawing Causal Inference from Big Data,” held March 26–27, 2015, at the National Academies of Sciences in Washington, DC. The complete program and video recordings of most presentations are available on the NAS website at www.nasonline.org/Big-data.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1510493113/-/DCSupplemental.
References
- 1.Stekhoven DJ, et al. Causal stability ranking. Bioinformatics. 2012;28(21):2819–2823. doi: 10.1093/bioinformatics/bts523. [DOI] [PubMed] [Google Scholar]
- 2.Pearl J. Causality: Models, Reasoning and Inference. Cambridge Univ Press; New York: 2000. [Google Scholar]
- 3.Spirtes P, Glymour C, Scheines R. Causation, Prediction, and Search. 2nd Ed MIT Press; Cambridge, MA: 2000. [Google Scholar]
- 4.Bollen KA. Structural Equations with Latent Variables. Wiley; New York: 1989. [Google Scholar]
- 5.Robins J. A new approach to causal inference in mortality studies with a sustained exposure periodapplication to control of the healthy worker survivor effect. Math Model. 1986;7(9):1393–1512. [Google Scholar]
- 6.Markowetz F, Grossmann S, Spang R. 2005. Probabilistic soft interventions in conditional Gaussian networks. Tenth International Workshop on Artificial Intelligence and Statistics (AISTATS) (Society for Artificial Intelligence and Statistics, NJ), pp 214–221.
- 7.Tian J, Pearl J. Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence (UAI) Morgan Kaufmann; San Francisco: 2001. Causal discovery from changes; pp. 512–521. [Google Scholar]
- 8.Eaton D, Murphy K. Exact Bayesian structure learning from uncertain interventions. Proceedings of the Eleventh International Conference on Artificial Intelligence and Statistics (AISTATS) 2007;2:107–114. [Google Scholar]
- 9.Mooij JM, Heskes T. Proceedings of the 29th Annual Conference on Uncertainty in Artificial Intelligence (UAI) AUAI Press; Corvallis, OR: 2013. Cyclic causal discovery from continuous equilibrium data; pp. 431–439. [Google Scholar]
- 10.Meek C. Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence (UAI) Morgan Kaufmann; San Francisco: 1995. Causal inference and causal explanation with background knowledge; pp. 403–418. [Google Scholar]
- 11.Cooper G, Yoo C. Proceedings of the 15th Annual Conference on Uncertainty in Artificial Intelligence (UAI) Morgan Kaufmann; San Francisco: 1999. Causal discovery from a mixture of experimental and observational data; pp. 116–125. [Google Scholar]
- 12.Hauser A, Bühlmann P. Characterization and greedy learning of interventional Markov equivalence classes of directed acyclic graphs. J Mach Learn Res. 2012;13:2409–2464. [Google Scholar]
- 13.Shimizu S, Hoyer PO, Hyvärinen A, Kerminen AJ. A linear non-Gaussian acyclic model for causal discovery. J Mach Learn Res. 2006;7:2003–2030. [Google Scholar]
- 14.Hoyer PO, Janzing D, Mooij JM, Peters J, Schölkopf B. Advances in Neural Information Processing Systems 21 (NIPS) Curran Associates; Red Hook, NY: 2009. Nonlinear causal discovery with additive noise models; pp. 689–696. [Google Scholar]
- 15.Peters J, Mooij JM, Janzing D, Schölkopf B. Causal discovery with continuous additive noise models. J Mach Learn Res. 2014;15:2009–2053. [Google Scholar]
- 16.Peters J, Bühlmann P. Identifiability of Gaussian structural equation models with equal error variances. Biometrika. 2014;101:219–228. [Google Scholar]
- 17.Chickering DM. Optimal structure identification with greedy search. J Mach Learn Res. 2002;3:507–554. [Google Scholar]
- 18.Harris N, Drton M. PC algorithm for nonparanormal graphical models. J Mach Learn Res. 2013;14:3365–3383. [Google Scholar]
- 19.Maathuis MH, Kalisch M, Bühlmann P. Estimating high-dimensional intervention effects from observational data. Ann Stat. 2009;37:3133–3164. [Google Scholar]
- 20.Hauser A, Bühlmann P. Jointly interventional and observational data: Estimation of interventional Markov equivalence classes of directed acyclic graphs. J R Stat Soc B. 2015;77:291–318. [Google Scholar]
- 21.Heckerman D, Geiger D, Chickering DM. Learning Bayesian networks: The combination of knowledge and statistical data. Mach Learn. 1995;20:197–243. [Google Scholar]
- 22.Koller D, Friedman N. Probabilistic Graphical Models: Principles and Techniques. MIT Press; Cambridge, MA: 2009. [Google Scholar]
- 23.Kalisch M, Bühlmann P. Estimating high-dimensional directed acyclic graphs with the PC-algorithm. J Mach Learn Res. 2007;8:613–636. [Google Scholar]
- 24.van de Geer S, Bühlmann P. ℓ0-penalized maximum likelihood for sparse directed acyclic graphs. Ann Stat. 2013;41:536–567. [Google Scholar]
- 25.Bühlmann P, Peters J, Ernest J. CAM: Causal additive models, high-dimensional order search and penalized regression. Ann Stat. 2014;42:2526–2556. [Google Scholar]
- 26.Ernest J, Bühlmann P. Marginal integration for nonparametric causal inference. Electron J Stat. 2015;9:3155–3194. [Google Scholar]
- 27.Uhler C, Raskutti G, Bühlmann P, Yu B. Geometry of the faithfulness assumption in causal inference. Ann Stat. 2013;41:436–463. [Google Scholar]
- 28.Mooij JM, Cremers J. 2015. An empirical study of one of the simplest causal prediction algorithms. Proceedings of the UAI 2015 Workshop on Advances in Causal Inference, CEUR Workshop Proceedings (CEUR-WS.org, Aachen, Germany), Vol 1504, pp 30–39.
- 29.Bühlmann P, Rütimann P, Kalisch M. Controlling false positive selections in high-dimensional regression and causal inference. Stat Methods Med Res. 2013;22(5):466–492. doi: 10.1177/0962280211428371. [DOI] [PubMed] [Google Scholar]
- 30.Maathuis MH, Colombo D, Kalisch M, Bühlmann P. Predicting causal effects in large-scale systems from observational data. Nat Methods. 2010;7(4):247–248. doi: 10.1038/nmeth0410-247. [DOI] [PubMed] [Google Scholar]
- 31.Peters J, Bühlmann P, Meinshausen N. 2016. Causal inference using invariant prediction: Identification and confidence intervals (with discussion). arXiv:1501.01332.
- 32.Aldrich J. Autonomy. Oxf Econ Pap. 1989;41:15–34. [Google Scholar]
- 33.Schölkopf B, et al. Proceedings of the 29th International Conference on Machine Learning (ICML) Omnipress; New York: 2012. On causal and anticausal learning; pp. 1255–1262. [Google Scholar]
- 34.Bareinboim E, Pearl J. Advances in Neural Information Processing Systems 27 (NIPS) Curran Associates; Red Hook, NY: 2014. Transportability from multiple environments with limited experiments: Completeness results; pp. 280–288. [Google Scholar]
- 35.Rothenhäusler D, Heinze C, Peters J, Meinshausen N. Advances in Neural Information Processing Systems 28 (NIPS) Curran Associates; Red Hook, NY: 2015. Backshift: Learning causal cyclic graphs from unknown shift interventions; pp. 1513–1521. [Google Scholar]
- 36.Heinze C, Meinshausen N. 2015. CompareCausalNetworks. R package, version 0.1.1. Available at https://cran.r-project.org/web/packages/CompareCausalNetworks/CompareCausalNetworks.pdf. Accessed April 29, 2016.
- 37.R Development Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna: 2005. [Google Scholar]
- 38.Colombo D, Maathuis MH, Kalisch M, Richardson TS. Learning high-dimensional directed acyclic graphs with latent and selection variables. Ann Stat. 2012;40:294–321. [Google Scholar]
- 39.Meinshausen N, Bühlmann P. Stability selection (with discussion) J R Stat Soc B. 2010;72:417–473. [Google Scholar]
- 40.Kemmeren P, et al. Large-scale genetic perturbations reveal regulatory networks and an abundance of gene-specific repressors. Cell. 2014;157(3):740–752. doi: 10.1016/j.cell.2014.02.054. [DOI] [PubMed] [Google Scholar]
- 41.Breiman L. Heuristics of instability and stabilization in model selection. Ann Stat. 1996;24:2350–2383. [Google Scholar]
- 42.Cherry JM, et al. Saccharomyces Genome Database: The genomics resource of budding yeast. Nucleic Acids Res. 2012;40(Database issue):D700–D705. doi: 10.1093/nar/gkr1029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.MacIsaac KD, et al. An improved map of conserved regulatory sites for Saccharomyces cerevisiae. BMC Bioinformatics. 2006;7:113. doi: 10.1186/1471-2105-7-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sachs K, Perez O, Pe’er D, Lauffenburger DA, Nolan GP. Causal protein-signaling networks derived from multiparameter single-cell data. Science. 2005;308(5721):523–529. doi: 10.1126/science.1105809. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.