Inferring cortical function in the mouse visual system through large-scale systems neuroscience

Abstract

The scientific mission of the Project MindScope is to understand neocortex, the part of the mammalian brain that gives rise to perception, memory, intelligence, and consciousness. We seek to quantitatively evaluate the hypothesis that neocortex is a relatively homogeneous tissue, with smaller functional modules that perform a common computational function replicated across regions. We here focus on the mouse as a mammalian model organism with genetics, physiology, and behavior that can be readily studied and manipulated in the laboratory. We seek to describe the operation of cortical circuitry at the computational level by comprehensively cataloging and characterizing its cellular building blocks along with their dynamics and their cell type-specific connectivities. The project is also building large-scale experimental platforms (i.e., brain observatories) to record the activity of large populations of cortical neurons in behaving mice subject to visual stimuli. A primary goal is to understand the series of operations from visual input in the retina to behavior by observing and modeling the physical transformations of signals in the corticothalamic system. We here focus on the contribution that computer modeling and theory make to this long-term effort.

The neocortical sheet is a layered structure with a thickness that varies by a factor of two to three, whereas its surface area varies by 50,000 between the small smoky shrew and the massive blue whale. A unique hallmark of mammals, neocortex is a highly versatile, scalable, ∼2D computational tissue that excels at real time sensory processing across modalities and making and storing associations as well as planning and producing complex motor patterns. Neocortex consists of smaller modular units (columnar circuits that reach across the depth of cortex) broadly repeated iteratively across the cortical sheet. These modules vary considerably in their connectivity and properties between regions, with some controversy whether there is, indeed, a single canonical function performed by any and all neocortical columns.

A deep understanding of cortex necessitates measuring relevant biophysical variables, such as recording action and membrane potentials, and relating them to genetically identified cell types. Mapping, observing, and intervening in widespread but highly specific cellular activity are more readily accomplished in the mouse, Mus musculus, than in the human brain. The brain of the laboratory mouse is more than three orders of magnitude smaller than the human brain in weight (0.4 vs. 1,350 g) and contains 71 million vs. 86 billion nerve cells for the entire brain and 14 million vs. 16 billion nerve cells for neocortex (1).

The Allen Institute for Brain Science is engaged in a 10-y, high-throughput, milestone-driven effort to characterize all cortical cell types for the mouse cortex to build a small number of distinct experimental and computational platforms, called brain observatories, for studying behaving mice and to construct abstract and biophysically realistic models of cortical networks. All relevant data, including anatomical, physiological, transcriptional, behavioral, and modeling data, acquired are made freely and publicly available at www.brain-map.org.

Some theoretical questions that we seek to address are

• Canonical cortical computation: To what extent are the computational principles found in mouse primary visual cortex (V1) common to other visual areas, other sensory areas, and other cortical areas? What is the common computational motif, the canonical circuit, that recurs with variants throughout neocortex?

• Hierarchical computations: Do visual regions correspond to layers of a primarily feedforward hierarchical computation, in which each layer integrates features represented at previous layers, as a mechanism for object recognition? What is the function of top-down signals in cortex? Is neural computation best viewed as statistical inference?

• Neural population dynamics: How do the dynamics of neural populations reflect computations of visual representations, decisions, and motor planning that evolve over the time course of a behavioral trial? Are there repeatable trajectories in the space of multineuron activity that lead to different decisions made by the brain? What mechanistic neural models can give rise to the observed dynamics? Can their complexity be captured by low-dimensional models?

• Visual coding: How do visual thalamocortical areas represent information about the world? How is this representation affected by internal states, in particular vigilance? Is the representation of natural scenes efficient as in sparse coding models? Does this neural code use the correlation structure among neurons as in population coding? How does population dynamics change during learning a visual object recognition task?

We here describe recent progress in how modeling and theory contribute to understanding the operations of the cortical sheet.

Visual System of the Mouse

The goal of MindScope is to understand the computations performed by visual cortex in the young adult laboratory mouse. We chose the visual system (Fig. 1) not because mouse vision is a good model system for human vision, but because the visual modality is the one best understood in terms of anatomy, physiology, psychophysics, and computational models.

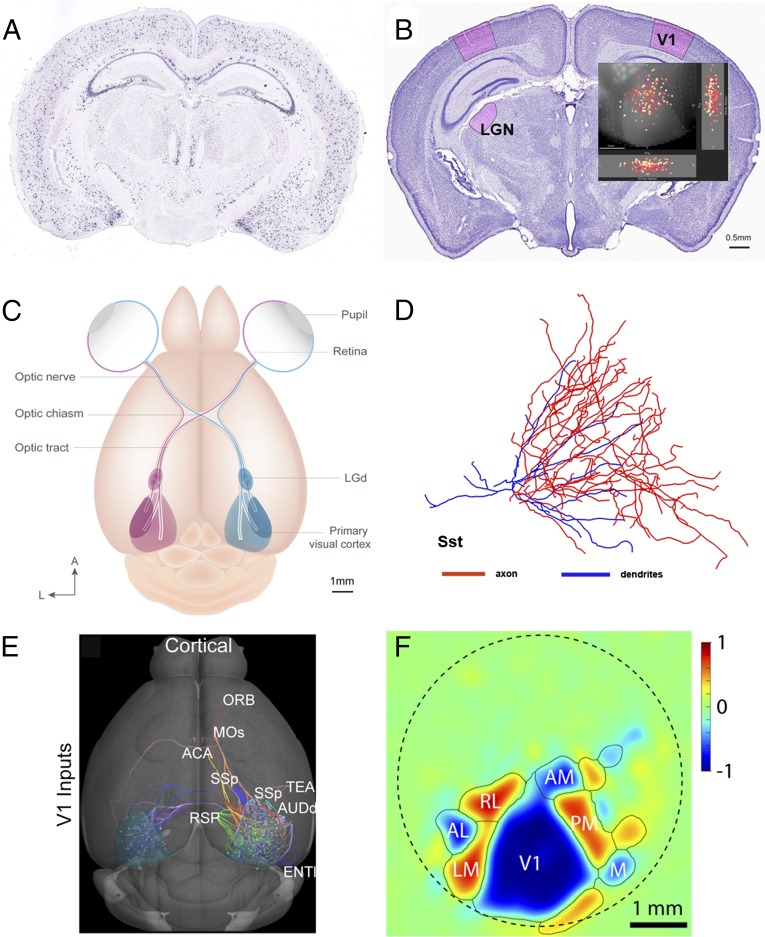
Fig. 1.

Mapping and analyzing cell type data. (A) A coronal view of the mouse brain showing in situ hybridization data from the Allen Brain Atlas for the Sst gene, a genetic marker for one class of inhibitory interneurons. (B) A view of the brain with the LGN and V1 outlined in red. Inset shows individual V1 Sst cells. (C) Overview of how right (red) and left (blue) visual fields are mapped from the retinas onto the LGN (also referred to as LGd) and from there, onto V1. Ganglion cells target more than 20 other brain structures other than the LGN. (D) A dendritic reconstruction of an Sst V1 interneuron, with its axon in blue and its dendrites in red. (E) V1 receives input from at least 40 distinct anatomical structures (cortical regions are shown) and projects to more than 34 regions (4). (ORB, orbital cortex; MOs, motor cortex; ACA, anterior cerebral artery; SSp, primary somatosensory cortex; TEA, tegmental area; AUDd, dorsal auditory stream; RSP, retrosplenial cortex; and ENT, entorhinal cortex.) (F) Functionally defined visual maps in the mouse visual cortex. V1 is surrounded by other visual regions, such as LM area, AL area, rostrolateral area (RL), anteromedial area (AM), PM area, and medial area (M).

In the common laboratory mouse (56-d-old male C57BL/6J), 6–7 million rods and 180,000 cones in each eye convert the incoming rain of photons into analog information that percolates through the retinal tissue and generates action potentials in 55,000 ganglion cells (2). There are at least 20 types of distinct ganglion cells, each one with distinct morphologies, response patterns, target cells, and molecular signatures. Each of these cell types tiles (that is, covers) visual space. Most of them project to the superior colliculus and close to two dozen other target structures. At least four of these cell types project to 18,000 neurons of the lateral geniculate nucleus (LGN), part of the visual thalamus (Fig. 1B). The axons of LGN cells, in turn, connect with some of 360,000 neurons of the V1 (Fig. 1C). Fig. 1D shows a dendritic reconstruction of a somatostatin (Sst) gene expressing V1 interneuron, with its axon in blue and its dendrites in red. The thalamocortical visual system consists of pathways from the retina through LGN to the V1 (Fig. 1C) and from there, to a wide network of other cortical regions (Fig. 1E). Wide-field imaging of cortical firing patterns through a 5-mm-diameter cranial window (perimeter marked with a dashed line in Fig. 1F) reveals at least 10 functionally active visual cortical areas (Fig. 1F). Finally, the cortical sheet exhibits layered structure, with five layers (labeled 1, 2/3, 4, 5, and 6) distinguishable and each layer hosting many different excitatory and inhibitory cell types. We have identified 42 distinct cell types in V1 alone using single-cell mRNA transcriptional clustering: 19 excitatory and 23 inhibitory neurons (3, 4) (casestudies.brain-map.org/celltax).

Models of Individual Neurons

A significant effort of MindScope is the characterization of components that comprise the cortex—synapses, neurons, and standard circuits that they form. To that purpose, we have set up a standardized pipeline characterizing electrical properties and morphology of individual neurons from brain slices coupled with the generation of point neuron and biophysical models of these cells.

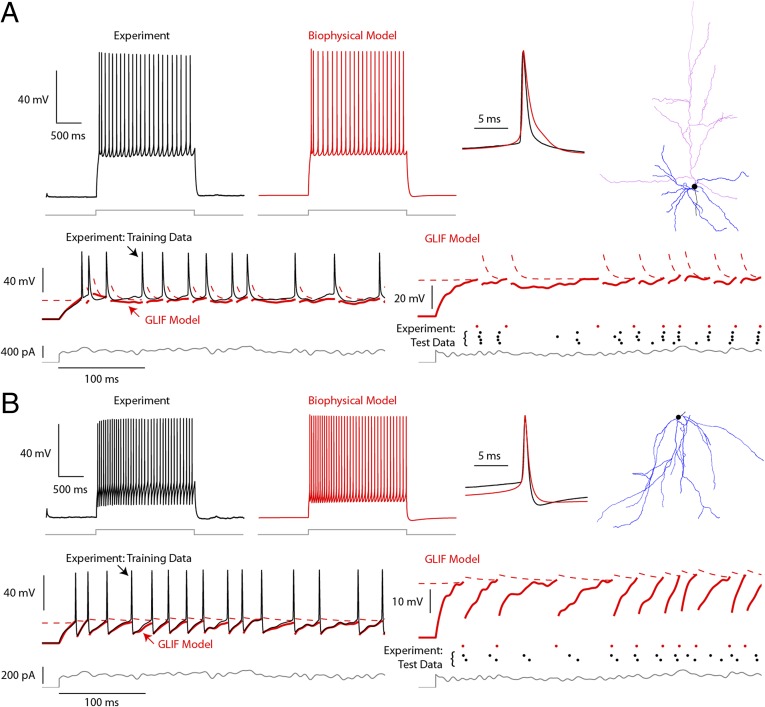
Computational models are tuned to reproduce experimentally recorded electrical data. Models for neurons from genetically labeled subpopulations in mouse V1 were generated, including both inhibitory and excitatory cells from different layers, displaying a range of intrinsic electrophysiological properties (Fig. 2). The ability of models to reproduce the spike times of experimental data is evaluated by a temporal explained variance metric. All models and evaluation criteria are freely shared through the Allen Cell Type Database (celltypes.brain-map.org/).

Fig. 2.

Single-cell biophysical and point neuron models. Data from (A) a fluorescently labeled excitatory neuron from genetically modified mouse (Rbp4-Cre tdTomato+) and (B) an SST-labeled inhibitory interneuron (Sst-Cre tdTomato+) (Fig. 1 A and D). A, Upper and B, Upper show examples of $V_m\left(t\right)$ generated by the associated biophysical models. Data (black) and models (red) are shown in response to current injections (gray), with close-up views of individual spikes superimposed. Morphological reconstructions of the modeled cells are shown in A, Right and B, Right, with apical dendrites colored in magenta and other dendrites colored in blue. A, Lower and B, Lower illustrate simpler point models (GLIF) for the same cells, which ignore the detailed morphology structure of the cell. Training data consist of at least three repeats of frozen pink noise: during the fit of the training data (black solid line), the membrane potential (red solid line) and threshold (red dashed line) are computed between spikes. Thus, the spiking histories of the model and the neuron are the same. Test data: during the testing phase, a different instantiation of noise is repeated at least twice, and the resulting spikes (black dots) are compared with the spikes produced by the model (red dots).

Point Neuron Models.

Generating models at different levels of granularity is important because of the multiscale nature of neuronal systems (5). We constructed a series of point neuron models of increasing complexity aimed at reproducing the temporal properties of spike trains (as opposed to subthreshold properties). Point neuron models take a somacentric view, in which the fundamental variable is the membrane potential at the soma, ignoring detailed dendritic morphology. The neuronal membrane potential has two different timescales: one characterizes the rapid changes during the action potentials, and the other characterizes slower subthreshold changes. This timescale separation, along with the highly stereotyped shape of action potentials, is the fundamental reason for the generation of hybrid dynamical systems. In these systems, a set of dynamical equations is followed until a condition is reached, at which point the values of the state variable(s) are reset. The leaky integrate and fire (LIF) model (6) is the best known example of a simple hybrid system where the membrane potential evolves until a threshold is reached, after which it is reset. Generalizations of LIF models that aim to better characterize neural spiking behavior include increasing the number of variables in the dynamical equations, thereby making the dynamical equations nonlinear (7), and making the reset rules more sophisticated (8).

To access the contribution of each mechanism to spike time reproduction, we constructed a series of increasingly complex models starting with the basic LIF model. We sequentially included (i) reset rules (spike-dependent changes in membrane potential and threshold caused by the activation and inactivation of ionic membrane conductance), (ii) after-spike currents (representing the slower effects of membrane conductance activated by an action potential), and (iii) voltage-dependent changes in threshold. To fit the parameters for the different mechanisms, we designed a series of stimuli specifically aimed at characterizing them, in which more complex models required more specific stimuli. For more complex models, the fitting of the mechanisms is iterative (similar to that in the work in ref. 9) followed by a final optimization step (similar to that in the work in ref. 10) to fine-tune parameters. The performance of the models was evaluated by time-based metrics on frozen noise not used for the generation of the models (Fig. 2). These models provide a baseline for reproducing neuronal firing patterns and can readily be used for large network simulations.

By keeping the number of added mechanisms low, these generalized leaky integrate and fire (GLIF) models represent a low-dimensional description of the true membrane dynamics. The challenge for this class of models is to prove that a low number of mechanisms can reproduce the salient features of activity. To test if the GLIF model is sufficient to reproduce spiking behavior for in vivo-like stimuli, we quantify the fraction of the variance of the biological spike train that can be explained by the model.

Biophysical Neuron Models.

A finer level of resolution is furnished by biophysical models, which aim to create a faithful and detailed representation of how visual information is processed in cortex with a direct link between the biological substrate—synapses, cell membranes, various neuronal compartments, and their biophysical properties—and the computations performed through their concerted activity. The aim of single-neuron biophysical models is to more precisely reproduce the general firing and subthreshold dynamics of neurons recorded under both slice conditions as well as in the behaving animal. The models use the approach in the work by Druckmann et al. (11) to evaluate performance by comparing the model and experimental values of specific electrophysiological features (average firing frequency, action potential width, etc.) computed, in its simplest form, from the somatic voltage response to somatic current injection in the slice.

Models are optimized and run using NEURON 7.3 (12). Passive parameters (intracellular resistivity and membrane capacitance) are first estimated by fitting a model without active conductance and then, fixed during the main optimization procedure, whereas the densities of active somatic conductance are tuned to optimize the response of the model to a step current. An additional mechanism describing intracellular ${\text{Ca}}^{2+}$ dynamics has two free parameters that are optimized: the time constant of ${\text{Ca}}^{2+}$ removal and the binding ratio of the ${\text{Ca}}^{2+}$ buffer. Other free parameters are the densities of a leak conductance in each type of cellular compartment: somatic, axonal, basal dendrite, and apical dendrite (when present). In total, 15–16 free parameters are tuned to optimize these models using a genetic algorithm procedure (11, 13). Several random seeds are used, and the best model across all runs is kept as the representative model for a given cell.

These biophysical models with passive dendrites, obtained for a variety of excitatory and inhibitory neurons (Fig. 2), reproduce experimentally recorded responses to training stimuli and generalize well to other stimuli.

One of the significant features of cortical neurons is active and voltage- and ion-dependent conductance along their dendritic morphologies. Such active conductance crucially impacts the transformation of synaptic inputs along the cellular morphology. For example, layer 5 pyramidal neurons in mouse V1 support a host of nonlinear mechanisms, such as somatic Na spikes, Ca-dependent plateau potentials, and NMDA spikes (14), hypothesized to offer different ways to integrate synaptic inputs. We are using the aforementioned optimization framework to account for spatial profiles of such active dendritic conductance, a computationally demanding process, and collaborating with the Blue Brain Project [Ecole Polytechnique Federale de Lausanne, (EPFL)] to implement active dendritic conductance. These optimizations capture features of back-propagating action potentials along dendrites as well as dendritic Ca spikes elicited at the Ca hot zone close to the main apical bifurcation of pyramids (similar to that in the work in ref. 14).

A key feature of the approach described above is that neuron models are produced for individual cells that were experimentally characterized rather than as an instantiation of a cell from a cell “type” based on the statistics of features defining the type [as done, for example, in the Blue Brain Project (15)]. Our approach is more difficult, because it is more constrained by data for each cell; however, it does not depend on any a priori cell taxonomy. This strategy is important, because no commonly agreed on taxonomy of cortical cell types has yet been created.

Systems-Level Models: Three Levels of Granularity

After characterization of the cellular building blocks, we next seek to investigate the emergent activity and computations of cortical networks related to retinal inputs. Building models at several levels of granularity is necessary to comprehend the neural correlates of visual perception and the computations performed by different components. We use three levels of granularity.

For a coarse characterization of cortical dynamics, we exploit an often used coding assumption that relevant variables are represented in the firing rate of a population of neurons. Using a statistical population density approach, one can then describe the dynamics of multiple active populations directly rather than by representing individual neurons separately (16). This approach allows for easier interpretation of the results and much faster simulation than with more elaborate models. The same method can be used to describe dynamics on mesoscopic scales, assuming that larger populations are homogeneous. Each cell type is, thereby, described by its own firing rate distribution.

In general, for inhomogeneous input or large and more complex synaptic connectivities, point neuron simulations are more appropriate, and one may use them to refine the number of cell types in determining cortical responses. This class of models treats each neuron as an independent entity, although the biophysical morphology of the neuron is ignored. Because these simulations have a larger number of parameters, some of which remain unconstrained, we focus on simulation efforts predicting responses of cell type-specific optogenetic perturbations.

Systems-level models that use biophysically realistic neurons attempt to show the effects of synapses, cell membranes, and various neuronal compartments on the network-level activity. Although these detailed simulations are computationally expensive and pose significant challenges for optimizing all relevant parameters, they enable a more direct understanding of biological properties and model parameters and permit a direct comparison between in silico and in vivo measurements.

Although currently, we perform independent simulations at these different levels of resolution, the ultimate aim is to produce multiscale simulations where a region of interest (e.g., V1) is modeled in biophysical detail, whereas closely associated regions (e.g., the rest of the visual system) are modeled with point neurons, and the rest of the brain is represented by population statistics.

Experimental data can parameterize neuronal simulations. However, even the most massive datasets leave the simulation underdetermined. More often, these data can provide strong validity constraints on neuronal models based on simulation results. When these constraining data are statistical in nature, fitting fine-scale models can be difficult whenever the relevant minimization objective function has stochastic terms. Because of their speed and deterministic dynamics, population statistic approaches can offer a complimentary alternative; parameter values can be tuned to satisfy validity constraints, and these tuned values can be substituted into fine-grained models. This multiscale modeling approach, which considers models at the scale best suited to data constraints, points to a synergy of modeling approaches, each tuned to its relevant domain.

Modeling Thalamic Input.

To characterize cellular responses in the behaving animal, systems-level models of cortical circuits rely on understanding the response properties of LGN neurons and their influence on V1 responses. Such a characterization has been performed under anesthesia (17), with six identified physiologically distinct cell classes. We have constructed a database of response characteristics and simplified filter-based models of these neurons in the awake mouse under different behavioral states. We then used simultaneous recordings obtained with high-density silicon probes to record the electrical activity of neurons in LGN and V1. Response properties were characterized using a variety of visual stimuli, such as sparse noise, drifting/stationary gratings, etc. Linear–nonlinear Poisson (LNP) models (18) were constructed to predict the output of LGN and V1 cells to a visual stimulus.

Although in general, these models provide a poor fit to test data on an individual trial basis ($R^2=0.02$), a repetition of the stimulus significantly improves the result to $R^2=0.51$. Cascade models (19) are a significant improvement: $R^2=0.5$; however, they are difficult to fit. We are using specially designed stimuli for these models: locally sparse noise, which allows independent characterization of subfields. A database of such models for LGN will allow systems-level cortical models to be simulated on exact spike trains for the images/movies that are used in the experimental training recordings.

Population Responses of a Cortical Column.

Population density modeling (20–22) offers an approach that is especially useful for systems composed of homogenous neuronal populations. Instead of simulating the dynamics of each neuron individually, a density distribution for the state variable evolves according to a master equation derived from the dynamics of the individual components. This approach significantly decreases computational resources necessary to simulate the system dynamics at the cost of averaging over heterogeneities in the populations. When summary statistics rather than single-neuron responses are external observables of interest, this tradeoff might tip in favor of a coarser-scale approach. When the true internal representation of the system is statistical (i.e., a population rate code), nothing is lost by the population statistic approach, and it is a more natural modeling technique to apply.

DiPDE (Integro-partial differential equation with displacement) (16) is a coupled population density equation solver that numerically computes the time evolution of the voltage density distribution of a population of neurons (23). Instead of solving one equation for the dynamics of each neuron, this method solves a displacement integropartial differential equation (the master equation) for the voltage density, assuming shot noise input with Poisson statistics. Because the dynamics of large numbers of homogeneous neurons is reduced to a single partial differential equation (PDE), simulations can be configured and run in a comparatively short amount of time but agree at the level of mean firing rates of large systems.

The speed of these simulations allows the use of statistics of neurons in the behaving animal together with constraints of well-measured structural data to optimize yet unknown parameters.

Fig. 3B compares the simulated output of a simplified cortical column model using population statistic modeling in DiPDE with the average result from 50 realizations of an LIF simulation with an analogous parameterization. We performed exhaustive simulation of the input–output relations of a fundamental cortical module to a cortical column (24).

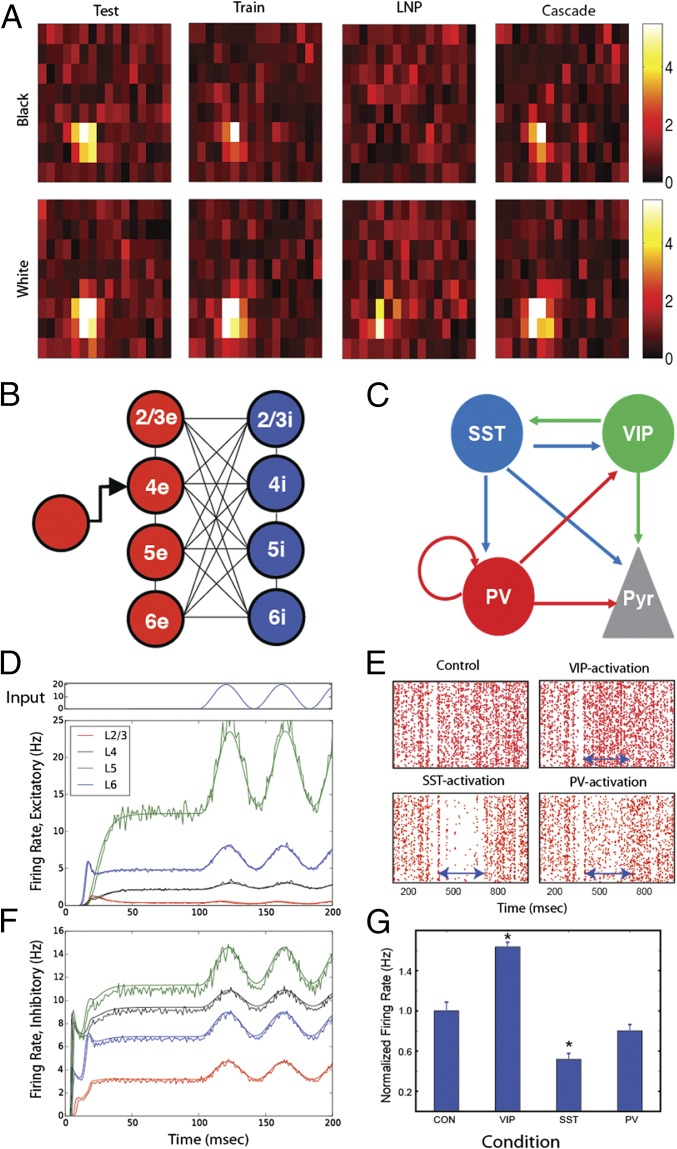
Fig. 3.

Population responses in LGN and V1 models. (A) Comparison of the receptive field of a mouse LGN cell using the mean firing rate. At one of 16 × 8 spatial pixels, (A, Upper) a black or (A, Lower) white square was flashed onto an otherwise gray screen. Column 1 shows the spatial receptive field recorded during the test period: a cell with distinct (Upper) off and (Lower) on subfields. Column 2 shows spatial receptive field recorded during the training period from which the models are constructed. The explained variance between test and training sets is $R^2=0.51$. In column 3, the holdout set responses of a single LNP model trained barely reconstruct the visual stimulus ($R^2=0.02$), whereas a cascade model with multiple LNP channels in column 4 has a vastly better performance with $R^2=0.50$. (B) Schematic of a simplified cortical column model [in the work by Potjans and Diesmann (24)]. Mean firing rate dynamics of an LIF simulation of the cortical column (noisy traces) is compared with the coupled population density equation solver DiPDE (smooth traces) for 2 × 4 populations of (D) excitatory and (F) inhibitory neurons (one each in four layers). At 100 ms, one layer 4 subpopulation is driven with an external sinusoidal input (pictured above), simulating LGN input. This simulation results in both linear and nonlinear mean firing rate responses of various populations. The two modeling approaches, DiPDE and LIF simulations, closely agree. (C) Schematic of the cell type-specific connectivity among inhibitory neurons used in the superficial layer of a cortical column model (Pyr, pyramidal neurons). (E) Action potentials of pyramidal neurons in superficial layers in control experiments and under interneuron expressing genes for PV, SST, and VIP cell activation conditions. Arrows indicate the period during which one of three inhibitory populations was activated. (G) The normalized firing rate (and SE) of the pyramidal neurons. *A significant difference between control and the specific simulation conditions (CON, control).

The methods of DiPDE are available as an open source software package written in Python [alleninstitute.github.io/dipde/; Gnu public license (GPL)] as a resource to the computational modeling community. The package includes several quick start examples as well as an out of the box implementation of the cortical column model discussed above.

Predicting Optogenetic Perturbation Responses.

The computational approach of using point neuron networks, in which cellular mechanisms and biophysics are replaced by simple LIF dynamics, has been successful in analyzing neural correlates of various cognitive functions, such as decision-making (25) and working memory (26). We adopted this approach to understand inhibitory cortical control by refining a large-scale cortical column model proposed earlier (24), replacing the single inhibitory interneuron cell types in the superficial layer with three distinct cell types expressing SST, vasoactive intestinal polypeptide (VIP), and parvalbumin (PV). The exact structure of the superficial layer circuits is based on the fraction of three inhibitory cell types (27) and the inhibitory connectivity described in ref. 28 (Fig. 3C).

Using modified column models, we first asked how each inhibitory cell type modulates the spiking activity of superficial pyramids by introducing excitatory currents mimicking optogenetic stimulation. Fig. 3E shows the raster plots of superficial pyramids in four different scenarios: control experiments without optogenetic stimulation and simulated PV, SST, and VIP interneuron activation between 400 and 700 ms. The effect of these manipulations (expressed as normalized firing rates of the pyramidal neurons in Fig. 3G) reveals that increases in excitability of three classes of inhibitory interneurons (VIP, SST, and PV) trigger a paradoxical increase, a decrease, and no change in the excitability of pyramidal neurons, respectively.

These results suggest that each inhibitory cell type has a unique functional role. The disinhibition induced by elevated VIP cell activity can result in increased sensitivity to sensory stimulus, consistent with experimental observations (29). The strong suppressive effects of SST cell activation can be useful in surround suppression (30). The functional roles of enhanced PV cell activity are not evident in our simulations. Instead, we note that pyramidal cells can quickly recover from inhibition induced by PV cells, indicating that PV cell mediating inhibition may be suitable for regulating pyramidal cell activity at fine temporal scales. Indeed, Cardin et al. (31) found that the optogenetic stimulation of PV cells increased γ-rhythms, reflecting the fine temporal dynamics. It should be noted that SST, PV, and VIP cells have multiple subclasses (3), and incorporating them into this model would be desirable.

Biophysically Detailed Network Models.

Our biophysical modeling effort aims to further bridge the gap between experimental observables and underlying cortical computations. The development of the model is driven by in-house electrophysiological and two-photon calcium imaging data from functional measurements in behaving animals. We are approaching the development of such a complex model from two directions. From one side, we are building a highly detailed model of the major input layer of V1 (namely, layer 4), with the primary focus on reproducing within-layer neural activity. From the other side, we are developing a biophysically detailed, multilayer cortical model, with the primary focus to recreate the extracellular potential recordings [local field potential (LFP), current source density, and extracellular spikes] along the full cortical depth. Both efforts are pursued using a common set of simulation tools and will be merged into a single, highly realistic cortical column.

In both directions, single-neuron representations of in vitro characterized cells (from appropriate layers) are replicated to describe a cortical region of 0.5 mm² in area and 0.1 mm in thickness for layer 4 and 0.86-mm-thick for the entire cortical column. The former contains 10,000 neurons, and the latter contains ∼24,500 neurons (about one-half of the biological cell density for computational efficiency), of which 80% are excitatory and 20% are inhibitory. Single cells are randomly positioned in physical space within their corresponding layers and randomly rotated along the cortical depth axis. Note that we use multiple copies of individual biophysical neuron models from the Allen Cell Types Database (see above). Furthermore, the database growth will enable an appropriate taxonomy of cell types, which will guide decisions on whether copies of individual cell models are representative enough or if extragenerative steps are required.

The connections and synaptic properties in the network models are established following distance- and cell type-dependent rules adopted from the literature (32–35) as well as based on in-house data. Synaptic connections are established between neurons based on the locations of their cell bodies, with synapses placed randomly over the dendritic tree (dependent on the type of connection, such as excitatory to excitatory, inhibitory to excitatory, etc.).

The layer 4 model is meant to simulate retinotopically mapped, visually evoked responses in V1 (Fig. 4A). For that purpose, one may use filters that operate in visual field space and represent responses of the LGN cells—currently, in a simple parametric functional form (to be replaced by the more sophisticated LNP filters described above). These filters convert movies into spike trains according to parameterization based on in-house LGN recordings, responding to local temporal increases and decreases in brightness (“on”- and “off”-type cells). For each biophysically detailed neuron in the layer 4 model, we choose a subset of on and off filters to supply inputs to the cell according to published experimental data (36) as well as in-house observations. As a result, arbitrary visual stimuli can be used as inputs to the layer 4 model.

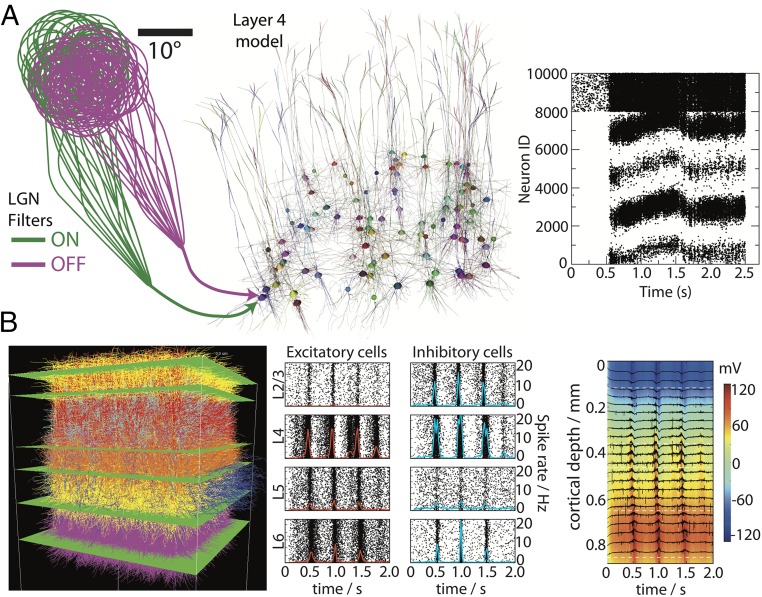
Fig. 4.

Large-scale biophysical simulations of mouse V1. (A) The layer 4 model and simulations. The LGN cells, supplying visual input to layer 4, are modeled as filters that produce spike trains in response to movies in visual space. For each neuron in the layer 4 model, a subset of on and off filters is chosen, and the spike trains generated by these filters are impinging onto the V1 cell; this situation is illustrated for one of the layer 4 neurons. The biophysically detailed model consists of 10,000 neurons; only 1% of these are shown. The simulated neuronal activity in response to visual stimulation with a drifting grating (between 0.5 and 2.5 s) is shown in Right. The first 8,000 neurons are pyramidal cells, and the rest are fast-spiking interneurons. Cells are grouped together according to their orientation preference of the drifting grating. (B, Left) Multilayer network of 24,500 interconnected, biophysically detailed neurons positioned in physical space and color-coded by layer and type. (B, Center) Population rasters and the corresponding spike rates (red lines, excitatory; blue lines, inhibitory neurons) in response to visual stimulus (drifting grating at 2 Hz). (B, Right) The laminar distribution of the simulated extracellular potential (black traces indicate $V_e$ as a function of time and specific depth; color indicates depth $V_e$) in response to neural activity.

With the feedforward LGN inputs and full recurrent connectivity within layer 4, the cells in the model receive several thousand synapses each. An essential part of the modeling process is the adjustment of synaptic weights to obtain realistic spike rates under condition of irregular activity within the network (i.e., avoiding epileptic-like, population-wide oscillations). After accomplished, initial series of simulations (Fig. 4A, Right) reproduce phenomena observed in the animal. For example, the distribution of firing rates in simulations is broadly consistent with the literature on V1 physiology (37) and in-house data, in that many cells remain silent or near-silent for many stimuli (i.e., exhibiting stimulus preference), the excitatory neurons spike at up to 10–20 Hz, and fast-spiking inhibitory neurons tend to fire at 10–40 Hz. Simulating visual stimulation by drifting gratings, we observe emergence of orientation tuning (which is absent in the simple filters currently used in this model to represent the feedforward inputs from LGN to V1); the distribution of orientation selectivity among cells in the model is consistent with experimental observations. The network also possesses rich dynamical behavior, with the responses within groups of cells following complex trajectories.

Input to the full, multilayer cortical column model (Fig. 4B) is simulated using both local connectivity and externally sourced input. For local input, the number of synaptic connections between neural populations is determined by scaling the integrated connectivity map (24) based on the fractions of short-range connections in visual cortex (38) originating from within a column of cortical tissue. Within a layer, cells are connected with the addition of periodic boundary conditions. For interlayer connections, the postsynaptic neurons are connected with uniform probability.

External input into the column is described by two mechanisms: LGN-like input and input representing long-range connections. The LGN input is modeled by spike trains into layer 4 excitatory cells as experimentally obtained in vivo during the presentation of visual stimuli (e.g., drifting grating at 2 Hz). Long-range connections are currently modeled by Poisson background spike trains but planned to be replaced by more meaningful dynamics from other brain areas using simpler models (i.e., LIF and statistical population methods).

One of the main purposes of the multilayer column model is to link biophysical computation with experimental observables, such as extracellular voltage ($V_e$) from silicon depth recordings, which have low-frequency components that are known as the LFP. The $V_e$ generated by transmembrane currents is computed along the column depth axis at locations 20 μm apart, corresponding to a virtual multielectrode array inserted vertically into the column’s center. The calculations are performed using the line source approximation method (39, 40) for the solution of Laplace equation governing $V_e$ distribution assuming a uniform conductivity (0.3 mS/mm) (Fig. 4B).

The synaptic weights and rate of background activity match firing rates as measured in vivo for each population, whereas the synaptic weights from local sources are tuned to find the network regime consistent with spike rates of evoked activity. Preliminary simulations show that, during otherwise irregular activity, excitatory neurons respond to LGN input with increased spiking up to 10 Hz, whereas inhibitory cells may reach 20 Hz (Fig. 4B). The magnitudes and overall dynamics of the simulated laminar $V_e$ in response to drifting gratings are consistent with experimental recordings reported in the literature (37) as well as in-house data. The modeled $V_e$ represents both spiking activity from cells with somata near the recording sites and slower activity (i.e., the LFP) coordinated across longer distances from more distant populations. Thus, such biophysical models are uniquely positioned to link between experimental observables, underlying biophysical processing and neural computation.

MindScope system modeling relies heavily on the experimental characterization of the cortex, and as such, the success or failure will be framed very much by what is feasible experimentally. For example, characterization of connection probabilities and synaptic strengths between various cell types in the cortex is very labor-expensive. If we follow our transcriptomic taxonomy of V1 neurons with 42 cell types (3), we will need to characterize ${42}^2=\mathrm{1,764}$ connection types, including their dependence on distance between cell bodies, layer location, etc., which will be challenging. A parallel approach is to reduce the large diversity of cell types into a small number of functional groups (e.g., one excitatory cell type per layer and a few layer-independent inhibitory cell types). This approach will require difficult tradeoffs regarding data, and assumptions will have to be made when building models. However, in this scenario the models will potentially have the biggest impact: in identifying crucial unconstrained aspects of the system on which experimental efforts could further focus. Another significant challenge is in creating an integrated multiresolution model as described above.

Models of Cortical Computations

In addition to mechanistic models that are fit with neural data to provide generative predictions of neural response, we are constructing higher-level computational models with task-oriented constraints. These constraints assign a computational role to the network, and training networks toward these tasks provide predictions of neural response and the “features” encoded by cortical activity.

The task of object recognition provides the first constraint. Taking cues from biology, the most powerful computational algorithms for this task are layered artificial neural networks. These networks use a feedforward structure composed of “simple” and “complex” feature summation and pooling units. Examples include HMAX (41, 42) and deep convolutional neural networks. It is not clear whether the mouse has an analog of the primate ventral stream as predicted by HMAX (Hierarchical Model and X). This latter question is important, and its answer will define the complexity and feasibility of this approach. The mouse visual system appears to have a broader anatomical structure than the macaque and therefore, may process visual information in very different ways.

The second constraint is the principle of sparse or efficient coding. Sparse coding models have been successful in describing the character of responses observed in primate V1. One can also use this principle as a means of understanding the lateral connectivity and feedback observed in cortex in addition to the feedforward computation described above. Importantly, although successful at predicting response properties, naive predictions for connectivity from such models often contradict what is known about biological connectivity, and therefore, there are important theoretical problems to tackle before we can rely on this method for defining our models of computation.

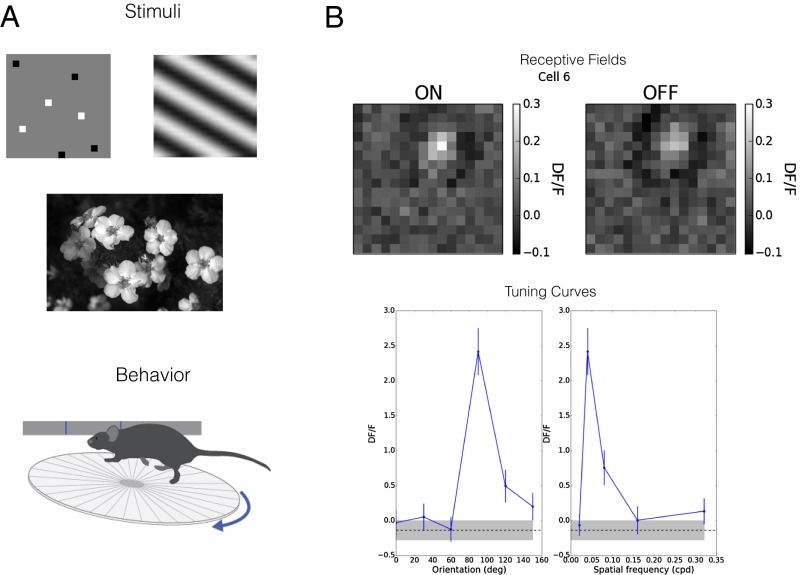
We are developing and fitting these models with a combination of mouse anatomy and neurophysiology. The necessary neurophysiological data comes from the Allen Brain Observatory (ABO, observatory.brain-map.org/visualcoding), an in-house effort to record under highly standardized conditions the dynamics of thousands of genetically identified neurons in visual cortex in running mice trained to respond to visual stimuli. The first ABO dataset is a survey of neural responses in visual regions [to begin with, V1, lateromedial (LM), anterolateral (AL), and posteromedial (PM)] to an array of stimuli: drifting and stationary gratings, locally sparse noise, natural images, and natural movies. The recording modality is two-photon calcium imaging from mice who are head-fixed but free to run on a disk, providing passive viewing from a “behaving” animal (Fig. 5A). This design presents its own challenge, because one must disentangle the effects of visual response from, for example, running modulation. Later versions of ABO will include detection and discrimination tasks. From the initial data, we are constructing a response model (e.g., receptive fields) for neurons in the visual pathway. Example receptive field and tuning curve are shown in Fig. 5B.

Fig. 5.

The Allen Brain Observatory. This in-house project is producing neuronal activity data from genetically identified neuronal populations in the behaving mouse using two-photon calcium imaging. (A) Responses are recorded to a variety of visual stimuli, including gratings, sparse noise, natural images, and natural movies, and across multiple regions, layers, and genetically defined cell types. (B) Example single-neuron response properties. Upper shows receptive fields from locally sparse noise separately for on (white) and off (black) stimuli (Fig. 3A). Lower shows example tuning curves for orientation and spatial frequency obtained from such imaging (in units of DF/F) in response to oriented gratings (cpd, cycles per degree; DF/F, relative change in fluorescence).

These models of computation exist at the coarsest, highest level of description, whereas the other models described in this paper are at finer detail and describe specific regions and circuits. Perhaps the most challenging problem is to relate these models across scales and levels of description, so that biophysical models can usefully inform the models of computation. This approach is daunting for a number of reasons, including the problem of relating different mechanistic descriptions of neural response.

Discussion

A number of models have been suggested to explain how fundamental neuronal stimulus response properties (such as orientation tuning) arise, with the most prominent one based on the seminal work by Hubel and Wiesel (43). Since then, many more classes of theories have been proposed, arguing that orientation tuning arises primarily from intracortical networks, a combination of feedforward and cortical inhibitory mechanisms, and in particular, feedforward mechanisms that include nonlinearities of individual cell types. However, how many of these theories are plausible given what we know about the biophysical properties of synapses and neurons in V1? Which of these postulations are most feasible and robust? These questions can be extended to even more conceptual models of visual processing and object recognition (41, 42), where it remains unknown which aspects of the suggested computations can be realized based on the detailed biophysics of neurons and networks. In this context, we plan to use biophysically realistic simulations to test many of these hypotheses and develop additional ones to help bridge the gap between higher-level functioning of the cortex and its biophysical surrogates. The project proposes to infer the structure and function of recurrent connectivity as well as feedback from higher areas and estimate the computational role that each area plays in the visual circuit.

The modeling part of MindScope shares some of the same goals as the Blue Brain Project/Human Brain Project at the EPFL in Switzerland (15). Their focus is on reproducing the firing behavior of rat somatosensory cortex in both slice and the animal using detailed biophysical models. They seek to incorporate all known biophysical and biochemical properties of brains (including detailed channel kinetics, vascularization, and so on) to explain rat behavior. Our goals are both more limited and more focused on a set of experimentally guided questions using a three levels of granularity model to isolate the relevant variables needed to understand any one specific phenomenon. At the same time, unlike the Blue Brain Project, MindScope is producing complete, free, and publicly accessible neuroanatomical, molecular, and physiological datasets (www.brain-map.org).

In summary, the overarching goal of MindScope is to understand the operations and the flexibility of cortical tissue in the mouse by comprehensively recording and analyzing cellular-level cortical responses. The project is carried out using behaving mice trained to perform simple visual discrimination tasks, with an integrated computational modeling effort, and using a large scale, team-based approach and open science.

SI Text

The members of the Project MindScope team are Costas Anastassiou, Anton Arkhipov, Chris Barber, Lynne Becker, Jim Berg, Barg Berg, Amy Bernard, Darren Bertagnolli, Kris Bickley, Adam Bleckert, Nicole Blesie, Agnes Bodor, Phil Bohn, Nick Bowles, Krissy Brouner, Michael Buice, Dan Bumbarger, Nicholas Cain, Shiella Caldejon, Linzy Casal, Tamara Casper, Ali Cetin, Mike Chapin, Soumya Chatterjee, Adrian Cheng, Nuno da Costa, Sissy Cross, Christine Cuhaciyan, Tanya Daigle, Chinh Dang, Bethanny Danskin, Tsega Desta, Saskia de Vries, Nick Dee, Daniel Denman, Tim Dolbeare, Ashley Donimirski, Nadia Dotson, Severine Durand, Colin Farrell, David Feng, Michael Fisher, Tim Fliss, Aleena Garner, Marina Garrett, Marisa Garwood, Nathalie Gaudreault, Terri Gilbert, Harminder Gill, Olga Gliko, Keith Godfrey, Jeff Goldy, Nathan Gouwens, Sergey Gratiy, Lucas Gray, Fiona Griffin, Peter Groblewski, Hong Gu, Guangyu Gu, Caroline Habel, Kristen Hadley, Zeb Haradon, James Harrington, Julie Harris, Michael Hawrylycz, Alex Henry, Nika Hejazinia, Chris Hill, Dijon Hill, Karla Hirokawa, Anh Ho, Robert Howard, Jaclyn Huffman, Ram Iyer, Tim Jarsky, Justin Johal, Tom Keenan, Sean Kim, Ulf Knoblich, Christof Koch, Ali Kriedberg, Leonard Kuan, Florence Lai, Rachael Larsen, Rylan Larsen, Chris Lau, Peter Ledochowitsch, Brian Lee, Chang-Kyu Lee, Jung-Hoon Lee, Felix Lee, Lu Li, Yang Li, Rui Liu, Xiaoxiao Liu, Brian Long, Fuhui Long, Jennifer Luviano, Linda Madisen, Veronica Maldonado, Rusty Mann, Naveed Mastan, Jose Melchor, Vilas Menon, Stefan Mihalas. Maya Mills, Catalin Mitelut, Kenji Mizuseki, Marty Mortrud, Lydia Ng, Thuc Nguyen, Julie Nyhus, Seung Wook Oh, Aaron Oldre, Doug Ollerenshaw, Shawn Olsen, Natalia Orlova, Ben Ouellette, Sheana Parry, Julie Pendergraft, Hanchuan Peng, Jed Perkins, John Phillips, Lydia Potekhina, Melissa Reading, Clay Reid, Brandon Rogers, Kate Roll, David Rosen, Peter Saggau, David Sandman, Eric Shea-Brown, Adam Shai, Shu Shi, Josh Siegle, Nathan Sjoquist, Kimberly Smith, Andrew Sodt, Gilberto Soler-Llavina, Staci Sorensen, Michelle Stoecklin, Susan Sunkin, Aaron Szafer, Bosiljka Tasic, Naz Taskin, Corinne Teeter, Nivretta Thatra, Carol Thompson, Michael Tieu, Dmitri Tsyboulski, Matt Valley, Wayne Wakeman, Quanxin Wang, Jack Waters, Casey White, Jennifer Whitesell, Derric Williams, Natalie Wong, Von Wright, Jun Zhuang, Zizhen Yao, Rob Young, Brian Youngstrom, Hongkui Zeng, and Zhi Zhou.